Сила тяжести: формула, определение

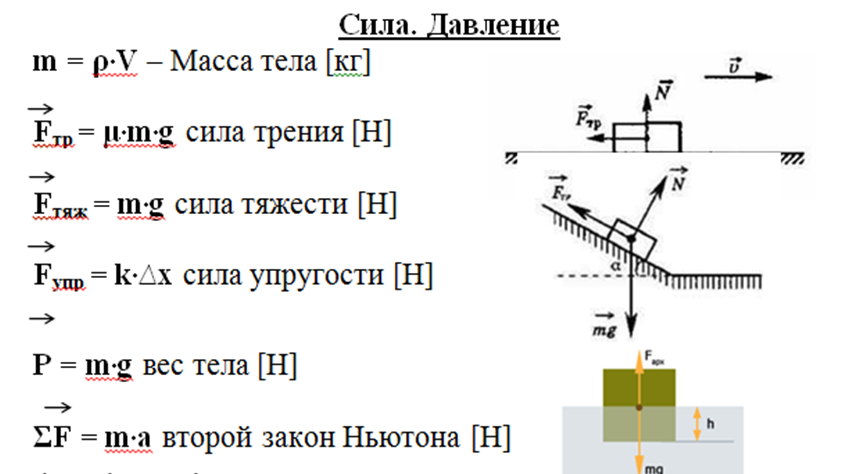
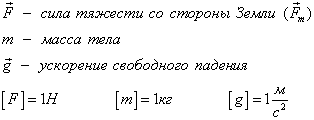Первая космическая скорость

Исаак Ньютон смог доказать, что причиной падения тел на Землю, движения Луны вокруг Земли и движения Земли вокруг Солнца является сила тяготения. Если камень бросить в горизонтальном направлении, его траектория будет отклонена от прямой линии под действием земной силы тяжести. Если же придать этому камню большую скорость, камень приземлится на большем расстоянии. Значит, существует такая скорость, при которой камень не приземлится, а начнет бесконечно вращаться вокруг Земли.

Определение
Первая космическая скорость — минимальная (для заданной высоты над поверхностью планеты) горизонтальная скорость, которую необходимо придать объекту, чтобы он совершал движение по круговой орбите вокруг планеты.

Вывод формулы первой космической скорости

Когда тело массой m вращается на некоторой высоте h, расстояние между ним и центром Земли равно сумме этой высоты и радиуса Земли. Поэтому сила тяготения между этим телом и Землей будет равна:

Движение тела вокруг планеты — частный случай движения тела по окружности с постоянной по модулю скоростью. Мы уже знаем, что такое тело движется с центростремительным ускорением, направленным к центру окружности. В данном случае центростремительное ускорение будет направлено к центру Земли. Это ускорение сообщает телу сила тяготения.

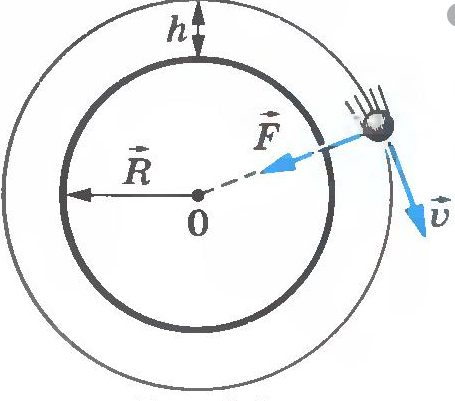
Так как тело движется на некоторой высоте h от поверхности Земли, центростремительное ускорение будет определяться формулой:

Подставив это ускорение в формулу второго закона Ньютона, получим силу, с которой Земля притягивает к себе тело массой m:

Приравняем правые части формул, следующих из закона всемирного тяготения и второго закона Ньютона, и получим:

Отсюда скорость, с которой должно тело массой m бесконечно вращаться вокруг Земли на высоте h, равна:

Скорость бесконечно вращающегося вокруг Земли тела не зависит от его массы. Она зависит только от высоты, на которой оно находится. Чем выше высота, тем меньше скорость его вращения.

Тело, вращающееся вокруг планеты, называется ее спутником. Чтобы любое тело стало спутником Земли, нужно сообщить ему некоторую скорость на поверхности планеты в горизонтальном направлении. Высота h в этом случае равна 0. Тогда эта скорость будет равна:

8 км/с — первая космическая скорость Земли.

Пример №3. Рассчитать первую космическую скорость для Венеры. Считать, что масса Венеры равна 4,87∙1024 кг, а ее радиус равен 6052 км.

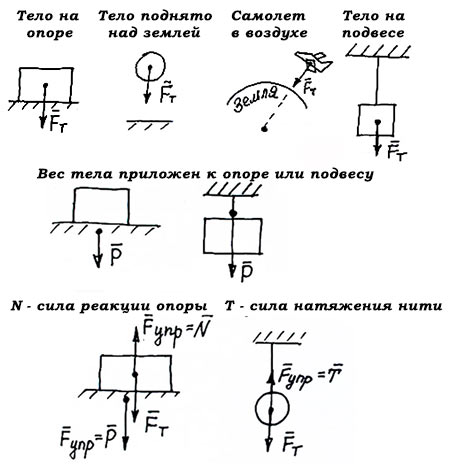
Сила реакции опоры

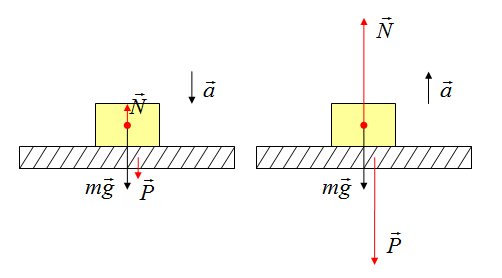
Представим очень тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры. Название силы «говорит» реагирует опора. Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, «сопротивляются».

Абсолютно любое тело, даже очень легкое (например,карандаш, лежащий на столе), на микроуровне деформирует опору. Поэтому возникает реакция опоры.

Специальной формулы для нахождения этой силы нет. Обозначают ее буквой , но эта сила просто отдельный вид силы упругости, поэтому она может быть обозначена и как

Сила приложена в точке соприкосновения предмета с опорой. Направлена перпендикулярно опоре.

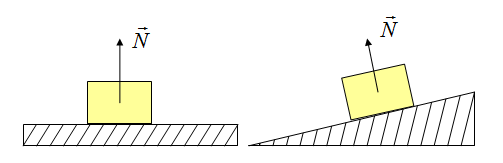
Так как тело представляем в виде материальной точки, силу можно изображать с центра

Убийственная тренировка пресса от олимпийской чемпионки

Роль гравитации для землян

Те условия, в которых мы живём, были бы невозможны без неё. Она удерживает нашу планету на одинаковом расстоянии от Солнца, не позволяет атмосфере покинуть пределы Земли, как и всему, что находится на её поверхности. Гравитационное притяжение Луны притягивает к себе моря, вызывая приливы океана.

Луна и приливы на Земле

Гравитация очень важна для нас. Мы не могли бы жить на Земле без неё. Тяготение Солнца удерживает Землю на орбите вокруг него на постоянном комфортном для жизни расстоянии. Сила притяжения удерживает нашу атмосферу и воздух, которым мы дышим.

Однако гравитация не везде одинакова на Земле. Она немного сильнее в местах с большей массой под землей, чем в местах с меньшей массой.

Проект «Свободное падение. Невесомость в лифте»

Во
время пребывания на космической станции
космонавтам приходится сталкиваться
с многочисленными неординарными
ситуациями. Вероятно, одно из главных
отличий жизни там наверху и здесь внизу
– это ощущение «невесомости». Ничего
не остаётся на месте, даже вы! Нет
гарантии, что вода потечёт вниз, и если
вы не пристегнёте себя к кровати, можете
проснуться в кладовой.

Многие
люди считают, что космонавты пребывают
в невесомости, потому что там нет
гравитации. Но как оказалось, космическая
станция подвержена воздействию
гравитации. Иначе как бы она оставалась
на орбите? Фактически, гравитация
Земли воздействует на космическую
станцию на 10% меньше, чем на поверхности.
Что же на самом деле происходит?

Когда
что-то находится на орбите, говорят, что
этот объект в состоянии свободного
падения – он падает через пространство,
без какого-либо противодействия. Но он
падает в том же темпе, в котором поверхность
Земли удаляется от него по кривой. Если
объект падает вертикально на 30 метров,
он также движется на таком же расстоянии
от поверхности Земли по горизонтали.
Обычно спутники падают, не ударяясь о
землю.

В
этом эксперименте вы сможете убедиться,
как свободное падение,
а также некоторые виды вертикального
движения, изучаемые в физике,
влияют на кажущийся вес объекта.

Ход эксперимента:

1. Для начала изучите падение воды.
2. Сделайте пару отверстий в дне чашки, наполните её водой. Понаблюдайте за тем, что происходит.
3. Теперь бросьте чашку в ведро. Каким образом изменился поток воды из чашки в воздухе?
4. Теперь можно исследовать, что происходит с весом в лифте.
5. Поместите предмет с небольшой массой на весы, определите его вес.
6. Держите весы возле пола, а затем быстро (но плавно) поднимите. Что происходит с весом?
7. Держите весы высоко в воздухе, а затем быстро (но плавно) опустите вниз. Что происходит с весом? Есть ли разница между этими двумя случаями?
8. Поднимитесь и спуститесь на несколько этажей в лифте. Возьмите с собой весы и предмет с небольшой массой.

Вывод:

В
первой части опыта сразу
после того, как вы налили воду в чашку,
она начинает вытекать через отверстия
на дне. Однако после того, как вы бросили
чашку вниз, вода перестала вытекать во
время падения.

Во
второй части опыта вес заметно
увеличивается, когда вы поднимаете весы
вверх, и уменьшается, когда вы их
опускаете. То же самое происходит в
процессе проведения эксперимента в
лифте. Почему? Говорят, будто в 1589 году
Галилей бросил два мяча разной массы с
Пизанской башни и заметил, что они упали
на землю одновременно. Когда астронавт
Дэвид Скот шагнул на поверхность Луны
в 1971 году, он воспроизвёл эксперимент
Галилея в практически полном вакууме
атмосферы Луны, используя перо и молот.
И действительно, оба предмета упали на
поверхность одновременно!

Возможно,
это звучит весьма парадоксально. Вы
можете подумать, что гравитация больше
влияет на молот и заставляет его упасть
быстрее. Действительно, молот сильнее
подвержен гравитационному
ускорению, чем перо. Однако из-за
того, что молот обладает более высокой
массой, для любой силы (включая гравитацию)
его сложнее сдвинуть с места. Постарайтесь
толкнуть магазинную тележку и автомобиль,
прилагая одинаковые усилия, и посмотрите,
что будет поддаваться легче. Сопротивление
движению отменяет более высокую
гравитационную силу.

Когда
вы бросаете чашку, вода и чашка падают
с одинаковой скоростью. Вода вытекает,
но чашка её подхватывает! Удивительно,
но вода моментально задерживается
внутри протекающей чашки.

То
же самое происходит с космонавтами на
борту космического корабля. Они кажутся
невесомыми не по причине отсутствия
гравитации, а потому что, как уже
упоминалось ранее, они всё время пребывают
в состоянии падения. То же самое происходит
и со всем, что находится на борту:
инструментами, продуктами питания,
одеждой. Космонавты на космической
станции подобны воде в чашке. Они падают
вместе со станцией и могут находиться
в состоянии невесомости.

Второй
эксперимент идёт следом. Вес – это
просто сила, воздействующая на ваше
тело, благодаря гравитации. Когда вы
поднимаете весы вверх, сила ваших рук
должна преодолеть гравитационную силу.
В этом случае вес кажется больше

Вес в
процессе движения называется кажущимся
весом, поскольку во внимание принимаются
и другие силы гравитации. Когда вы
опускаете весы вниз, сила ваших рук
уменьшает силу гравитации и кажущийся
вес снижается

Что
произойдёт с весом, если вы поднимете
весы, а затем бросите их? Как это
перекликается с первым экспериментом?

Эксперимент
в лифте не отличается, только в данном
случае моторы лифта делают работу за
вас. Как вы думаете, что бы произошло,
если бы кабель лифта порвался?

Значение в природе

Сила тяжести играет важную роль в процессах эволюции звёзд. Для звёзд, находящихся на этапе главной последовательности своей эволюции, сила тяжести является одним из важных факторов, обеспечивающих условия, необходимые для термоядерного синтеза. На заключительных этапах эволюции звёзд, в процессе их коллапса, благодаря силе тяжести, не скомпенсированной силами внутреннего давления, звёзды превращаются в нейтронные звёзды или чёрные дыры.

Сила тяжести очень важна для формирования структуры внутреннего строения Земли и других планет и тектонической эволюции её поверхности. Чем больше сила тяжести, тем большая масса метеоритного материала выпадает на единицу её поверхности. За время существования Земли её масса существенно увеличилась благодаря силе тяжести: ежегодно на Землю оседает 30-40 млн. тонн метеоритного вещества, в основном в виде пыли, что значительно превышает рассеяние лёгких компонентов верхней атмосферы Земли в космосе.

Без потенциальной энергии силы тяжести, непрерывно переходящей в кинетическую, круговорот вещества и энергии на Земле был бы невозможен.

Сила тяжести играет очень важную роль для жизни на Земле. Только благодаря ей у Земли есть атмосфера. Вследствие силы тяжести, действующей на воздух, существует атмосферное давление.

У всех живых организмов с нервной системой есть рецепторы, определяющие величину и направление силы тяжести и служащие для ориентировки в пространстве. У позвоночных организмов, в том числе человека, величину и направление силы тяжести определяет вестибулярный аппарат.

Наличие силы тяжести привело к возникновению у всех многоклеточных наземных организмов прочных скелетов, необходимых для её преодоления. У водных живых организмов силу тяжести уравновешивает гидростатическая сила.

Роль силы тяжести в процессах жизнедеятельности организмов изучает гравитационная биология.

«Всемирное тяготение. Сила тяжести»

Код ОГЭ 1.13. Всемирное тяготение. Закон всемирного тяготения. Сила тяжести. Ускорение свободного падения. Формула для вычисления силы тяжести вблизи поверхности Земли.  F = mg. Искусственные спутники Земли.

Закон всемирного тяготения не объясняет причин тяготения, а только устанавливает количественные закономерности.

Закон всемирного тяготения (И. Ньютон, 1667 г.): Тела притягиваются друг к другу с силой, прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними:  , где F – сила тяготения, m₁ и m₂ – массы взаимодействующих тел, r – расстояние между телами (центрами масс), G – гравитационная постоянная .

Закон справедлив для: 1) материальных точек; 2) однородных шаров и сфер; 3) концентрических тел.

Физический смысл гравитационной постоянной G: гравитационная постоянная G численно равна модулю силы тяготения, действующей между двумя точечными телами массой по 1 кг каждое, находящимися на расстоянии 1 м друг от друга.

Гравитационная постоянная G очень мала, и гравитационное взаимодействие существенно только при больших массах взаимодействующих тел.

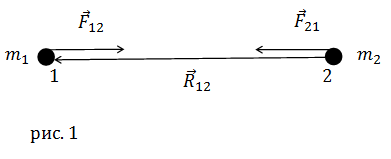
Внимание! Силы притяжения – центральные. В соответствии с третьим законом Ньютона:

Сила тяжести – частный случай силы всемирного тяготения. Рассмотрим взаимодействие планеты и тела (по сравнению с планетой тело можно считать материальной точкой).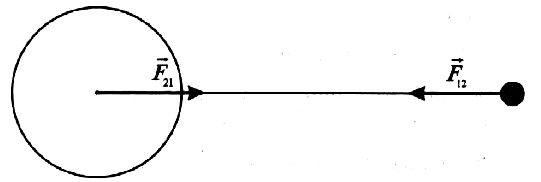
Изображённая на рисунке сила F₁₂ – сила притяжения тела к планете, которая и называется силой тяжести.

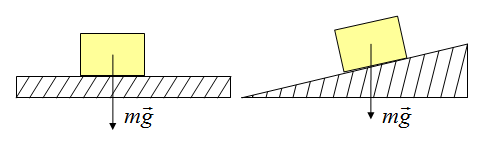
Применительно к ней формулу закона всемирного тяготения можно записать так:  , где m – масса тела, М – масса планеты, г –расстояние между телом и центром планеты, g – ускорение свободного падения. Тогда для ускорения свободного падения получаем:  . Если обозначить через R радиус планеты, а через h –расстояние до тела от поверхности планеты, то 

Сила тяжести и ускорение свободного падения направлены к центру масс планеты (перпендикулярно сферической поверхности планеты в данной точке).

 Ускорение, сообщаемое телу силой тяжести (ускорение свободного падения), зависит от:

•  массы планеты;
•  радиуса планеты;
•  высоты над поверхностью планеты;
•  географической широты (на Земле на полюсах g ~ 9,83 м/с2, на экваторе g ~ 9,79 м/с2);
•  наличия полезных ископаемых.

Внимание! Ускорение силы тяжести (свободного падения) не зависит от массы и других параметров тела!Внимание! При решении задач ускорение силы тяжести (свободного падения) принимается равным 10 м/с2

Конспект урока «Всемирное тяготение. Сила тяжести».

Следующая тема: «Импульс тела. Закон сохранения импульса».

Курение сигарилл

Основное преимущество при курении сигарилл по сравнению с сигарами заключается в простоте подхода их можно курить на ходу, как сигареты, для курения не требуется много времени, подходящей обстановки и специальных инструментов. Сигариллы намного крепче сигарет, поэтому ими лучше не затягиваться.

В подавляющее большинство сигарилл добавляются ароматизаторы, которые, впрочем, абсолютно безвредны. Самые распространённые вкусы это вишня и ваниль, существуют десятки других ароматов шоколад, персик, кокос, яблоко, арбуз, ягоды и так далее, чего душа ни пожелает.

Закон притяжения

Без присутствия силы тяжести стало бы невозможным происхождение многих, сейчас кажущихся нам естественными, вещей: так, не было бы схождение с гор лавин, течения рек, дождей. Атмосфера Земли может сохраняться исключительно благодаря воздействию силы тяжести. Планеты с меньшей массой, например, Луна или Меркурий, растеряли всю свою атмосферу довольно стремительными темпами и стали беззащитными перед потоками агрессивного космического излучения.

Атмосфера Земли сыграла решающее значение при процессе формирования жизни на Земле, ее. Помимо силы тяжести, на Земле воздействует также сила притяжения Луны. За счет ее близкого соседства (в космических масштабах), на Земле возможно существование отливов и приливов, а многие биологические ритмы являются совпадающими с лунным календарем

Силу тяжести, таким образом, нужно рассматривать в формате полезного и важного закона природы

Замечание 2

Закон притяжения считается универсальным и возможен к применению в отношении любых двух тел, обладающих определенной массой.

В ситуации, если масса одного взаимодействующего тела оказывается намного больше массы второго, говорится о частном случае гравитационной силы, для которого существует специальный термин, такой как «сила тяжести». Он применим к задачам, ориентированным на определение силы притяжения на Земле или иных небесных телах. При подставлении значения силы тяжести в формулу второго закона Ньютона, получаем:

$F = ma$

Здесь $а$ – ускорение силы тяжести, принуждающее тела стремиться друг к другу. В задачах, связанных с задействованием ускорения свободного падения, такое ускорение обозначают буквой $g$. С помощью собственного интегрального исчисления, Ньютону математически удалось доказать постоянную сосредоточенность силы тяжести в центре большего тела.

Методы измерения силы тяжести

Силу тяжести измеряют динамическими и статическими методами. Динамические методы используют наблюдение за движением тела под действием силы тяжести и измеряют время перехода тела из одного заранее определённого положения в другое. Они используют: колебания маятника, свободное падение тела, колебания струны с грузом. Статические методы используют наблюдение за изменением положения равновесия тела под действием силы тяжести и некоторой уравновешивающей её силы и измеряют линейное или угловое смещение тела.

Измерения силы тяжести бывают абсолютными и относительными. Абсолютные измерения определяют полное значение силы тяжести в заданной точке. Относительные измерения определяют разность силы тяжести в заданной точке и некоторого другого, заранее известного значения. Приборы, предназначенные для относительных измерений силы тяжести, называются гравиметрами.

Динамические методы определения силы тяжести могут быть как относительными, так и абсолютными, статические — только относительными.

Примечания

1. Сивухин Д. В. Общий курс физики. — М.: Физматлит, 2005. — Т. I. Механика. — С. 372. — 560 с. — ISBN 5-9221-0225-7.
2. Тарг С. М. // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 496. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
3. , с. 49.
4. Максимальное изменение силы тяжести, обусловленное притяжением Луны, составляет примерно ,25∗10−5{\displaystyle 0,25*10^{-5}} м/с2, Солнца ,1∗10−5{\displaystyle 0,1*10^{-5}} м/с2
5. , с. 71.
6. ↑ , с. 70.
7. , с. 82-83.
8. ↑ // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1998. — Т. 5. — С. 245—246. — 760 с. — ISBN 5-85270-101-7.
9. , с. 156.
10. , с. 200, 270.
11. , с. 128.
12. , с. 253-259.
13. ↑ Зубов В. П. Физические идеи древности // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 38, 54-55;
14. Зубов В. П. Физические идеи средневековья // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 114;
15. Зубов В. П. Физические идеи ренессанса // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 151;
16. ↑ Кузнецов Б. Г. Генезис механического объяснения физических явлений и идеи картезианской физики // отв. ред.
    Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 160-161, 169-170, 177;
17. , с. 7.
18. Кузнецов Б. Г. Основные принципы физики Ньютона // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 189-191;
19. Иваненко Д. Д. Основные идеи общей теории относительности // отв. ред. Григорьян А. Т., Полак Л. С.
    Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 300;
20. Грищук Л. П., Зельдович Я. Б. Тяготение // Физика космоса. Маленькая энциклопедия. — М., Советская энцилопедия, 1986. — С. 676
21. , с. 122.
22. Кабардин О.Ф., Орлов В.А., Пономарева А.В. Факультативный курс физики. 8 класс. — М.: Просвещение, 1985. — Тираж 143 500 экз. — С. 151 — 152
23. , с. 307.
24. , с. 70, 234.
25. , с. 208.
26. , с. 77.
27. , с. 48, 237-238.
28. , с. 289.
29. Зельманов А. Л. Многообразие материального мира и проблема бесконечности Вселенной // Бесконечность и Вселенная. — М., Мысль, 1969. — Тираж 12000 экз. — С. 283
30. Хромов С. П., Петросянц М. А. Метеорология и климатология. — М., МГУ, 2006. — ISBN 5-211-05207-2. — C. 67
31. П. Кемп, К. Армс Введение в биологию. — М.: Мир, 1988. — ISBN 5-03-001286-9. — Тираж 125000 экз. — С. 75
32. , с. 1-543.
33. ↑ Ландсберг Г. С. Элементарный учебник физики. Том 1. Механика, теплота, молекулярная физика. — М., Наука, 1975. — Тираж 350 000 экз. — С. 189-190
34. , с. 94-262.
35. У газовых гигантов «поверхность» понимается как область высот в атмосфере, где давление равно атмосферному давлению на Земле на уровне моря (1,013×105Па).
36. Данные взяты из статьи Википедии Ускорение свободного падения

Сферически симметричное тело

В соответствии с законом всемирного тяготения, сила гравитационного притяжения, действующая на материальную точку массой m{\displaystyle m} на поверхности сферически симметричного астрономического тела, имеющего массу M{\displaystyle M}, определяется соотношением:

F=G⋅M⋅mR2,{\displaystyle F=G\cdot {M\cdot m \over R^{2}},}

где G{\displaystyle G} — гравитационная постоянная, равная 6,67384(80)·10−11м3·с−2·кг−1, а R{\displaystyle R} — радиус тела. Данное соотношение справедливо в предположении, что распределение массы по объёму тела сферически симметрично. В этом случае сила гравитационного притяжения направлена к центру тела.

Модуль центробежной силы инерции Q{\displaystyle Q}, действующей на материальную частицу, выражается формулой:

Q=maω2,{\displaystyle Q=ma\omega ^{2},}

где a{\displaystyle a} — расстояние между частицей и осью вращения рассматриваемого астрономического тела, а ω{\displaystyle \omega } — угловая скорость его вращения. Центробежная сила инерции перпендикулярна оси вращения и направлена в сторону от неё.

Поправки, вносимые общей теорией относительности в закон всемирного тяготения Ньютона, в условиях Земли и других планет крайне малы (модуль гравитационного потенциала на поверхности Земли, равный половине квадрата второй космической скорости vII{\displaystyle v_{II}}, крайне мал по сравнению с квадратом скорости света c{\displaystyle c}: vII22c2∼10−10{\displaystyle {\frac {v_{II}^{2}}{2c^{2}}}\sim 10^{-10}}).

Что такое сила всемирного тяготения?

Притяжение существует не только между Землей и всеми телами, находящимися на ней, но и всеми телами между собой. Такое притяжение всех тел в нашей Вселенной называется всемирным тяготением.

Ты когда-нибудь видел, как магнит притягивает к себе различные предметы? Так вот, всемирное тяготение можно сравнить с магнитом: тела притягиваются не только к Земле, но и друг к другу.

На какие тела действует сила всемирного тяготения?

Эта сила действует абсолютно на все тела, которые имеют какой-либо, пусть даже самый незначительный вес. Именно благодаря такому притяжению мы не улетаем в открытый космос вместе с другими окружающими нас предметами, а остаемся на Земле.

Если бы сила притяжения отсутствовала, то любое подброшенное тело никогда бы не вернулось на Землю.

Согласно легенде, английский ученый Исаак Ньютон открыл закон всемирного тяготения после того, как на его глазах с дерева оторвалось яблоко и упало на землю. Ньютон задумался над тем, почему оно упало вертикально вниз, перпендикулярно земле, а не в сторону. Позже гениальный ученый сумел доказать, что все тела притягиваются друг к другу.

Ускорение и сила всемирного тяготения

Ускорение — это изменение скорости в течение единицы времени. Представь, что с большой высоты на Землю падает какое-либо тело. Пока расстояние до Земли очень большое, ее сила притяжения не так велика. Но по мере приближения тела к поверхности Земли сила притяжения Земли возрастает, и ускорение движения тела становится равным 9,8 м/с2. Например, если ты бросишь яблоко с большой высоты, скажем, с пятого этажа, оно будет лететь со скоростью 9,8 м/с спустя 1 секунду падения и уже 19,6 м/с после второй секунды. То есть с каждой секундой падения его скорость будет увеличиваться почти на 10 м/с!

Ускорение и масса тела

Ускорение не зависит от массы падающего тела

Например, два тела, падающие с одинаковой высоты, достигнут земли одновременно, при этом не важно, что падает — яблоко или машина. Конечно, если ты бросишь листик бумаги и камешек, то камешек окажется на земле раньше, но только лишь потому, что листику мешает падать сопротивление воздуха

Но если предположить, что листик бумаги и камешек будут падать вниз внутри высокого стеклянного цилиндра, из которого откачан воздух, то оба предмета достигнут дна одновременно.