Равнодействующая сила

Иллюстрация

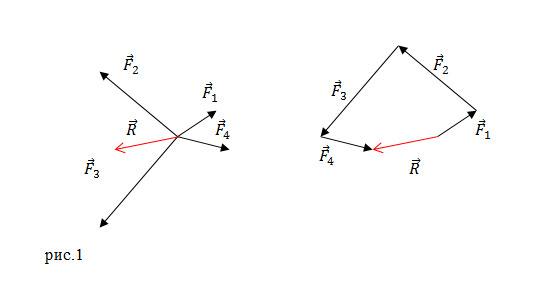
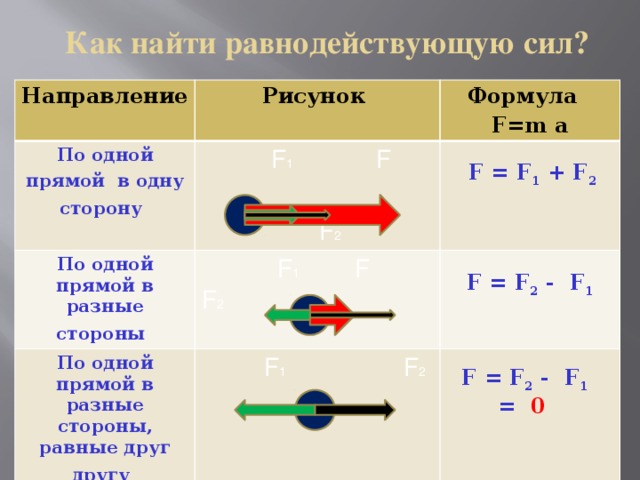
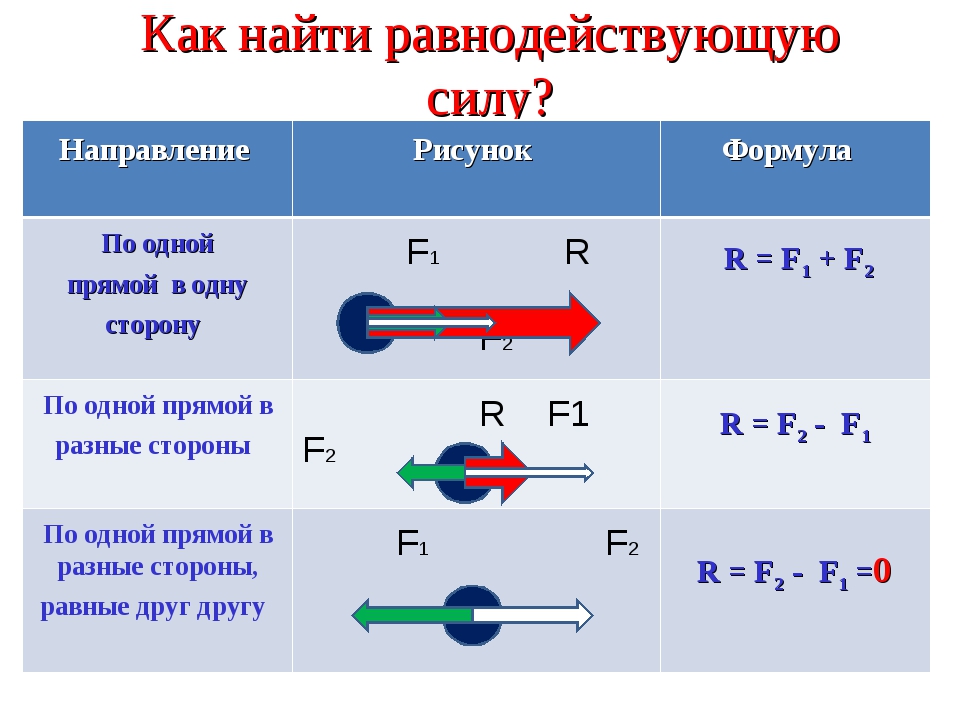
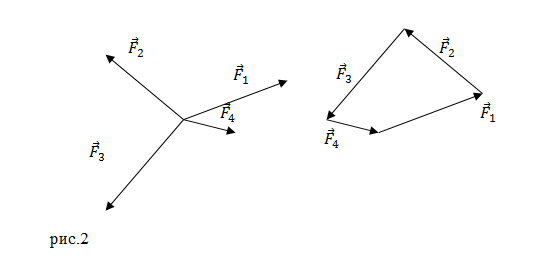
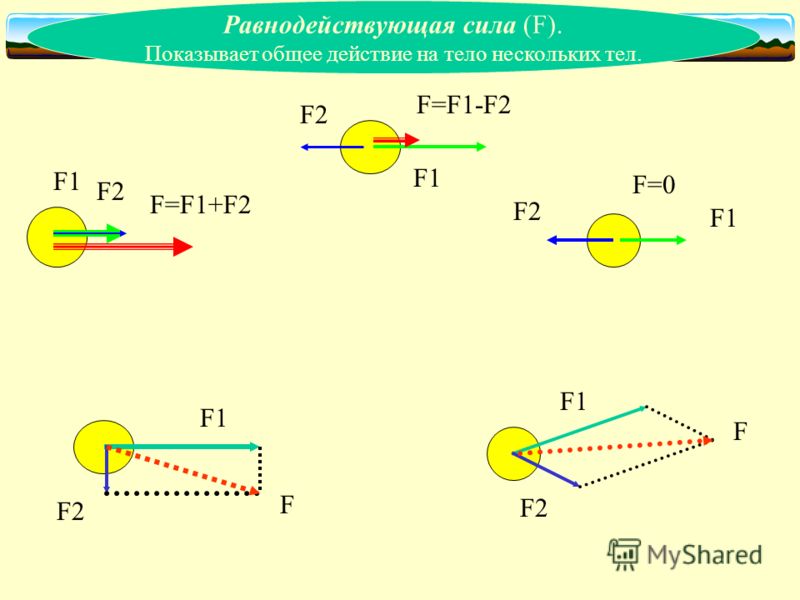
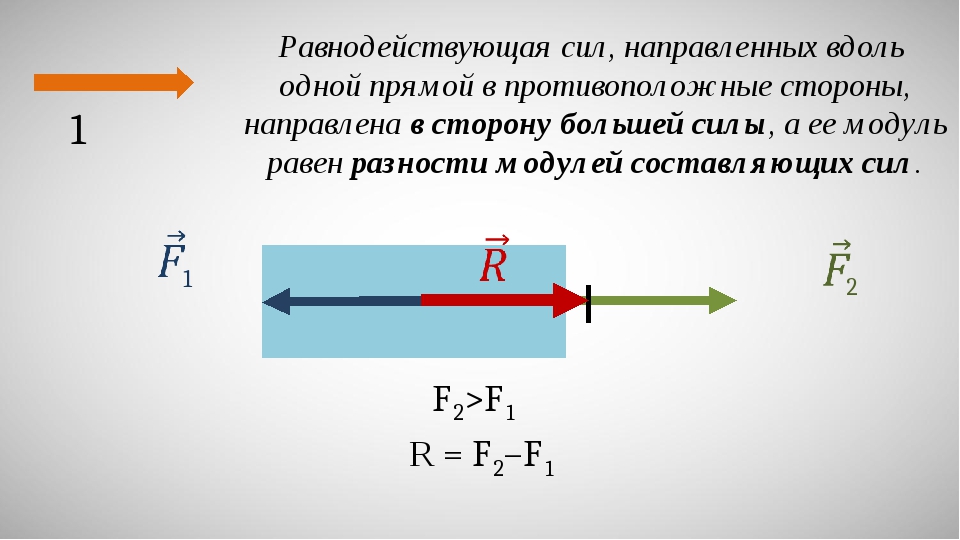
Схема иллюстрирует простые графические методы нахождения линии приложения равнодействующей силы простых плоских систем.

1. Линии приложения реальных сил и на самом левом рисунке пересекаются. После того, как векторное сложение выполнено «в местоположении », полученная результирующая сила преобразуется так, что линия ее приложения проходит через общую точку пересечения. Относительно этой точки все крутящие моменты равны нулю, поэтому крутящий момент результирующей силы равен сумме крутящих моментов фактических сил.F→1{\ displaystyle {\ scriptstyle {\ vec {F}} _ {1}}}F→2{\ displaystyle \ scriptstyle {\ vec {F}} _ {2}}F→1{\ displaystyle \ scriptstyle {\ vec {F}} _ {1}}F→р{\ displaystyle \ scriptstyle {\ vec {F}} _ {R}}
2. На рисунке в середине диаграммы показаны две параллельные действительные силы. После сложения вектора «в месте расположения » результирующая сила переводится в соответствующую линию приложения, где она становится равнодействующей . Процедура основана на разложении всех сил на составляющие, для которых линии приложения (бледные пунктирные линии) пересекаются в одной точке (так называемый полюс, произвольно установленный в правой части иллюстрации). Затем аргументы из предыдущего случая применяются к силам и их компонентам, чтобы продемонстрировать отношения крутящего момента.F→2{\ displaystyle \ scriptstyle {\ vec {F}} _ {2}}F→р{\ displaystyle \ scriptstyle {\ vec {F}} _ {R}}
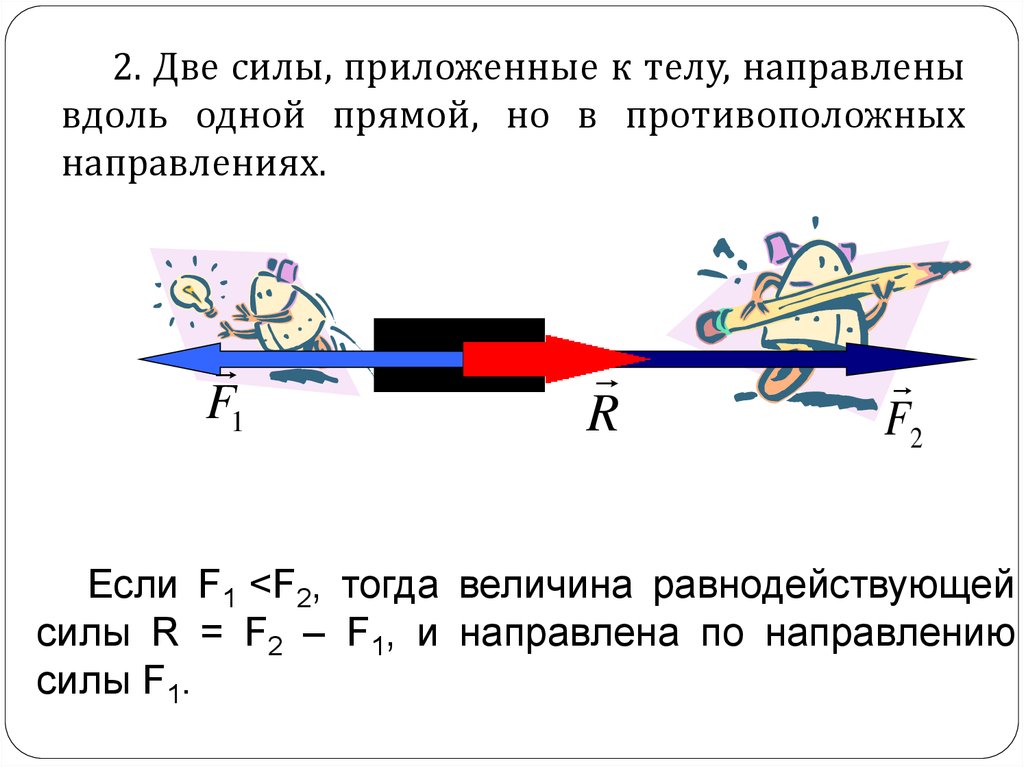
3. На крайнем правом рисунке показана пара , две равные, но противоположные силы, для которых величина результирующей силы равна нулю, но они создают чистый крутящий момент,    где   — расстояние между линиями их приложения. Это «чистый» крутящий момент, поскольку равнодействующей силы нет.τзнак равноFd{\ Displaystyle \ scriptstyle \ tau = Fd}d{\ displaystyle \ scriptstyle d}

Сложение сил

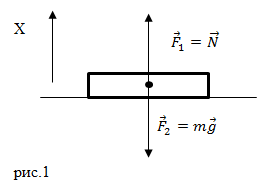
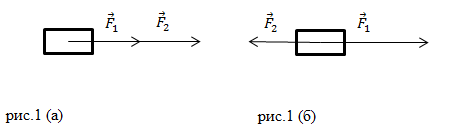
В случае, когда на тело действует n сил, говорят о равнодействующей силе, а формула второго закона Ньютона принимает вид:

$m\vec a = \sum\limits_{i=1}^n \vec F_i$.

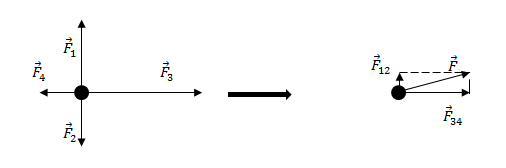
Рис. 1. Равнодействующая сил.

Поскольку F – векторная величина, сумма сил называется геометрической (или векторной). Такое сложение выполняется по правилу треугольника или параллелограмма, либо по компонентам. Поясним каждый метод на примере. Для этого запишем формулу равнодействующей силы в общем виде:

$F = \sum\limits_{i=1}^n \vec F_i$

А силу $F_i$ представим в виде:

$F = (F_{xi}, F_{yi}, F_{zi})$

Тогда суммой двух сил будет новый вектор $F_{ab} = (F_{xb} + F_{xa}, F_{yb} + F_{ya}, F_{zb} + F_{za})$.

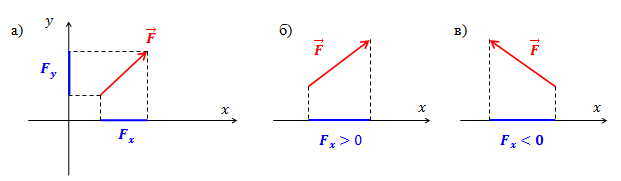
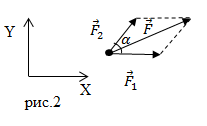
Рис. 2. Покомпонентное сложение векторов.

Абсолютное значение равнодействующей можно рассчитать так:

$F = \sqrt{(F_{xb} + F_{xa})^2 + (F_{yb} + F_{ya})^2 + (F_{zb} + F_{za})^2}$

Теперь дадим строгое определение: равнодействующая сила есть векторная сумма всех сил, оказывающих влияние на тело.

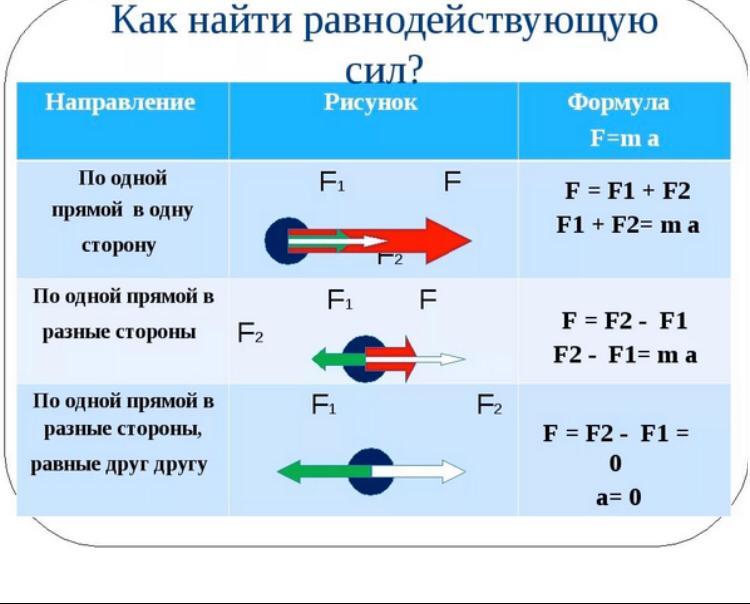
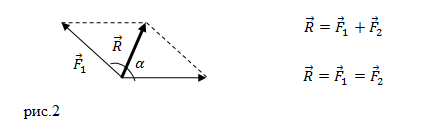
Разберем правила треугольника и параллелограмма. Графически это выглядит так:

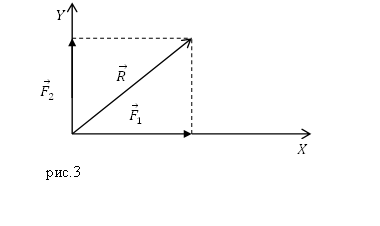
Рис. 3. Правило треугольника и параллелограмма.

Внешне они кажутся различными, но когда доходит до вычислений, сводятся к нахождению третьей стороны треугольника (или, что тоже самое, диагонали параллелограмма) по теореме косинусов.

Если сил больше двух, иногда удобней пользоваться правилом многоугольника. По своей сути – это всё тот же треугольник, только повторенный на одном рисунке некоторое количество раз. В случае, если по итогу контур получился замкнутым, общее действие сил равно нулю и тело покоится.

Определение равнодействующей геометрическим способом

Система сил, линии действия которых пересекаются в одной точке, называется сходящейся.

Необходимо определить равнодействующую системы сходящихся сил (F₁; F₂; F₃;…; F_n), где n – число сил, входящих в систему.

В соответствии со следствиями из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными к одной точке.

Используя свойство векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил.

При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.

Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называется геометрическим.

Многоугольник сил строится в следующем порядке.

1. Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпал с началом последующего.

2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.

3. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.

Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.

Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.

Если в системе три силы, образуется треугольник сил.

Геометрическим способом пользуются, если в системе три силы. При решении задач на равновесие тело считается абсолютно твердым (отвердевшим).

Задачи решаются в следующем порядке.

1. Определить возможное направление реакций связей.

2. Вычертить многоугольник сил системы, начиная с известных сил, в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура).

3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.

Смещение и вращение из-за силы

Точечные силы

Когда на частицу действует сила, она применяется к одной точке (объем частицы незначителен): это точечная сила, и частица является точкой ее приложения. Но внешняя сила, действующая на протяженное тело (объект), может быть приложена к ряду составляющих его частиц, т.е. может «распространяться» по некоторому объему или поверхности тела. Однако определение его вращательного воздействия на тело требует, чтобы мы указали его точку приложения (фактически, линию приложения, как объяснено ниже). Проблема обычно решается следующими способами:

• Часто объем или поверхность, на которую действует сила, относительно малы по сравнению с размером тела, так что их можно аппроксимировать точкой. Обычно нетрудно определить, является ли ошибка, вызванная таким приближением, допустимой.
• Если это неприемлемо (очевидно, например, в случае силы тяжести), такую ​​силу «объем / поверхность» следует описать как систему сил (компонентов), каждая из которых действует на отдельную частицу, и затем расчет должен быть выполнен для каждый из них отдельно. Такой расчет обычно упрощается за счет использования дифференциальных элементов объема / поверхности тела и интегрального исчисления. Однако в ряде случаев можно показать, что такая система сил может быть заменена одноточечной силой без фактического расчета (как в случае однородной гравитационной силы).

В любом случае анализ движения твердого тела начинается с модели точечной силы. И когда сила, действующая на тело, отображается графически, ориентированный линейный сегмент, представляющий силу, обычно рисуется так, чтобы «начать» (или «закончить») в точке приложения.

Твердые тела

Как сила ускоряет тело.

В примере, показанном на диаграмме напротив, единственная сила действует в точке приложения H на свободное твердое тело. Тело имеет массу , и его центр масс является точкой С . В приближении постоянной массы сила вызывает изменения в движении тела, описываемые следующими выражениями:
F→{\ displaystyle \ scriptstyle {\ vec {F}}}м{\ displaystyle \ scriptstyle m}

а→знак равноF→м{\ displaystyle {\ vec {a}} = {{\ vec {F}} \ over m}}   центр ускорения масс; и

α→знак равноτ→я{\ displaystyle {\ vec {\ alpha}} = {{\ vec {\ tau}} \ над I}}   — угловое ускорение тела.

Во втором выражении — крутящий момент или момент силы, тогда как — момент инерции тела. Крутящий момент, вызванный силой, — это векторная величина, определенная относительно некоторой контрольной точки:
τ→{\ displaystyle \ scriptstyle {\ vec {\ tau}}}я{\ displaystyle \ scriptstyle I}F→{\ displaystyle \ scriptstyle {\ vec {F}}}

τ→знак равнор→×F→{\ displaystyle {\ vec {\ tau}} = {\ vec {r}} \ times {\ vec {F}}}   — вектор крутящего момента, а

 τзнак равноFk{\ Displaystyle \ \ тау = Fk}   количество крутящего момента.

Вектор представляет собой вектор положения точки приложения силы, и в этом примере он обращается от центра масс в качестве опорной точки (см диаграмму). Отрезок прямой — это плечо рычага силы по отношению к центру масс. Как показано на рисунке, крутящий момент не изменяется (то же плечо рычага), если точка приложения перемещается вдоль линии приложения силы (пунктирная черная линия). Более формально это следует из свойств векторного произведения и показывает, что вращательное действие силы зависит только от положения линии ее приложения, а не от конкретного выбора точки приложения вдоль этой линии.
р→{\ displaystyle \ scriptstyle {\ vec {r}}}k{\ displaystyle \ scriptstyle k}F→{\ displaystyle \ scriptstyle {\ vec {F}}}

Вектор крутящего момента перпендикулярен плоскости, определяемой силой и вектором , и в этом примере он направлен к наблюдателю; вектор углового ускорения имеет то же направление. Правилу правой руки относится это направление к по часовой стрелке или против часовой стрелки , вращение в плоскости чертежа.
р→{\ displaystyle \ scriptstyle {\ vec {r}}}

Момент инерции рассчитывается относительно оси, проходящей через центр масс, параллельной крутящему моменту. Если тело, показанное на рисунке, представляет собой однородный диск, этот момент инерции равен . Если диск имеет массу 0,5 кг и радиус 0,8 м, момент инерции составляет 0,16 кгм 2 . Если сила составляет 2 Н, а плечо рычага 0,6 м, величина крутящего момента составляет 1,2 Нм. В показанный момент сила дает диску угловое ускорение α = τ / I = 7,5 рад / с 2 , а его центру масс — линейное ускорение a = F / m = 4 м / с 2. .
я{\ displaystyle \ scriptstyle I}язнак равномр22{\ displaystyle \ scriptstyle I = мистер ^ {2} / 2}

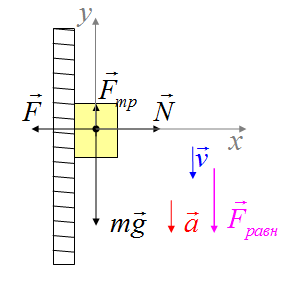
Связи и реакции связей

Все тела делятся на свободные и связанные.

Свободные тела – это тела, перемещение которых не ограничено.

Связанные тела – это тела, перемещение которых ограничено другими телами.

Тела, ограничивающие перемещение других тел, называют связями.

Силы, действующие от связей и препятствующие перемещению, называют реакциями связей. Реакция связи всегда направлена с той стороны, куда нельзя перемещаться.

Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей).

Связи делятся на несколько типов.

Связь – гладкая опора (без трения) – реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре.

Гибкая связь (нить, веревка, трос, цепь) – груз подвешен на двух нитях. Реакция нити направлена вдоль нити от тела, при этом нить может быть только растянута.

Жесткий стержень – стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня. Стержень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи.

Возможным перемещением точки называется такое бесконечно малое мысленное перемещение, которое допускается в данный момент.

Шарнирная опора. Шарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров.

Подвижный шарнир. Стержень, закрепленный на шарнире, может поворачиваться вокруг шарнира, а точка крепления может перемещаться вдоль направляющей (площадки). Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, так как не допускается только перемещение поперек опорной поверхности.

Неподвижный шарнир. Точка крепления перемещаться не может.

Стержень может свободно поворачиваться вокруг оси шарнира. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Ее изображают в виде двух составляющих: горизонтальной и вертикальной (R_x, R_y).

Защемление, или «заделка». Любые перемещения точки крепления невозможны.

Под действием внешних сил в опоре возникают реактивная сила и реактивный момент М_z, препятствующий повороту.

Реактивная сила представляется в виде двух составляющих вдоль осей координат:

R = R_x+ R_y.

Основное утверждение механики

Для описания движения тела можно взять любую систему отсчета. Обычно для этого используется система отсчета, связанная с Землей. Если какое-то тело меняет свою скорость, рядом с ним всегда можно обнаружить другое тело, которое на него действует. Так, если поднять камень и отпустить, он не останется висеть в воздухе, а упадет вниз. Следовательно, на него что-то подействовало. В данном случае сама Земля притянула камень к себе. Отсюда следует основное утверждение механики:

Основное утверждение механики

Изменение скорости (ускорение) тела всегда вызывается воздействием на него других тел.

Согласно утверждению, если на тело не действуют никакие силы, его ускорение будет нулевым, и оно будет либо покоиться, либо двигаться равномерно и прямолинейно (с постоянной скоростью).

Но в нашем мире мы не всегда это наблюдаем. И этому есть объяснение. Если тело покоится, оно действительно не меняет свою скорость. Так, мяч лежит на траве до тех пор, пока его не пнут. После того, как его пнут, он начинает катиться, но затем останавливается. Пока мяч катится, к нему больше не прикасаются. Казалось бы, согласно основному утверждению механики, мяч должен катиться вечно. Но этого не происходит, потому что на мяч действует сила трения, возникающая между его поверхностью и травой.

Свободное тело — тело, на которое не действуют другие тела. Свободное тело либо покоится, либо движется прямолинейно и равномерно.