Формула для вычисления дисперсии.среднее квадратическое отклонение. коэффициент вариации

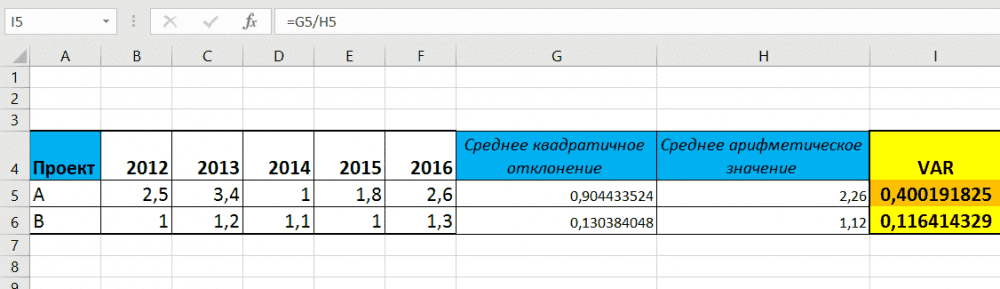
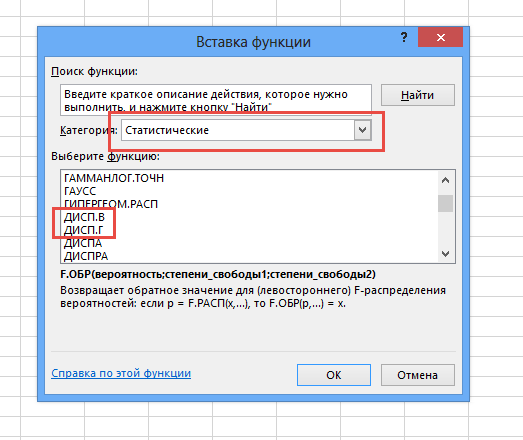
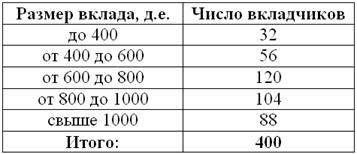
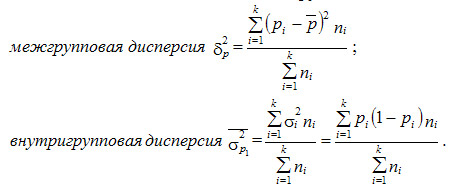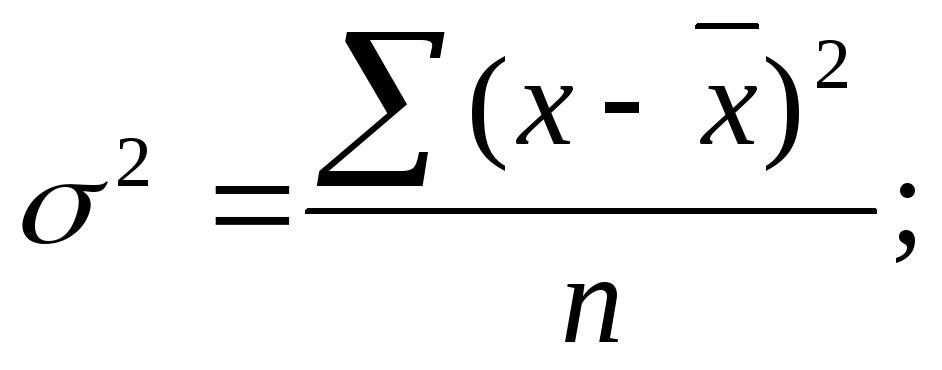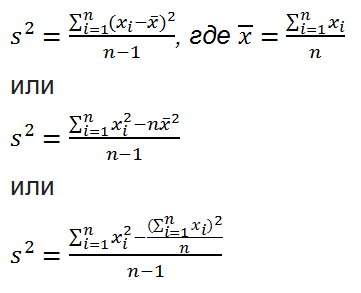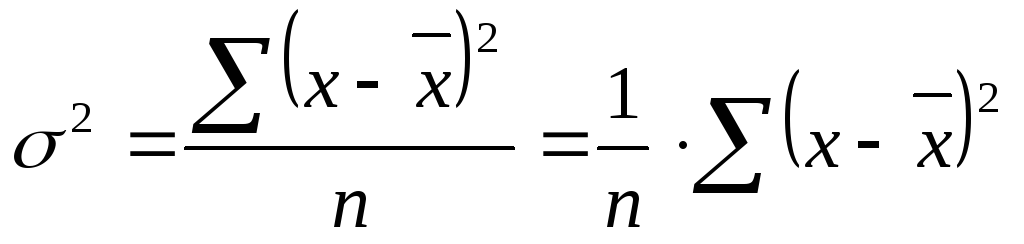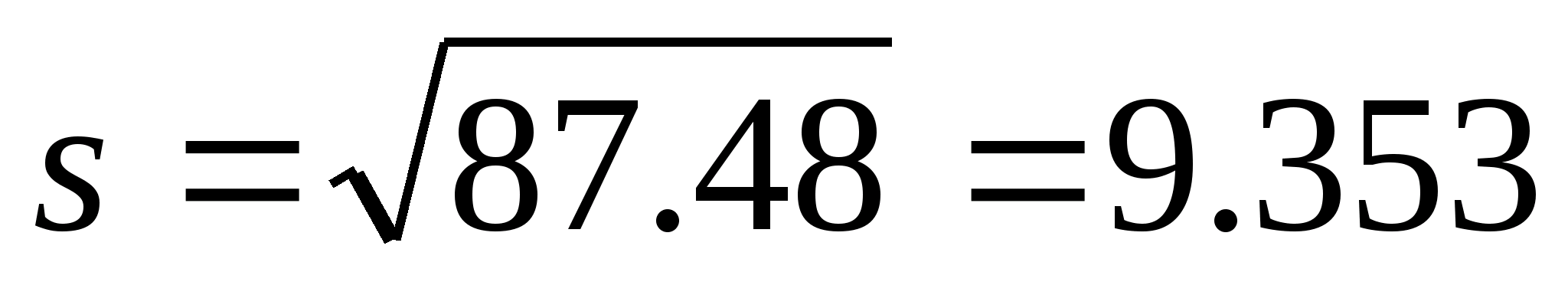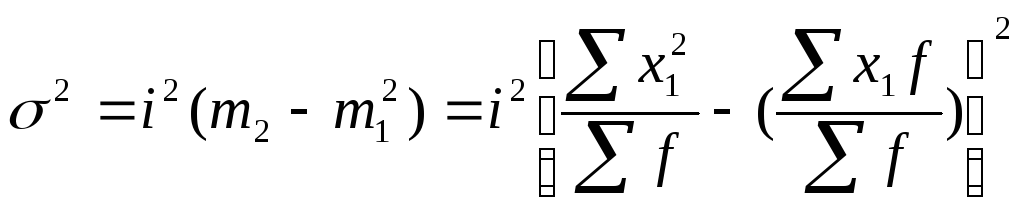Как рассчитать среднеквадратическое отклонение для AHT с помощью Microsoft Excel

Теперь, когда мы убедились, что вычислять стандартное отклонение AHT очень полезно, посмотрим, как это делается. Самый простой способ — использовать встроенные инструменты MS Excel. Для этого просто выполните такие действия:

• Занесите индивидуальные показатели AHT операторов в один столбец электронной таблицы.
• Используя функцию вычисления среднего арифметического AVERAGE (для русскоязычного MS Excel — СРЗНАЧ), рассчитайте среднее значение всех введенных данных. Excel не требует вычислять этот показатель отдельно, но он будет полезен для понимания итоговых результатов.
• Щелкните на любой свободной ячейке и выберите функцию оценки стандартного отклонения по выборке (STDEV или СТАНДОТКЛОН). Приложение попросит вас выделить группу цифр, которые вы будете использовать в расчете. Выделите все цифры, которые хотите использовать в анализе, и нажмите ENTER. Значение стандартного отклонения появится в открытой ячейке.

Правило трёх сигм

График плотности вероятности нормального распределения и процент попадания случайной величины на отрезки, равные среднеквадратическому отклонению.

Правило трёх сигм (3σ{\displaystyle 3\sigma }) — практически все значения нормально распределённой случайной величины лежат в интервале (x¯−3σ;x¯+3σ){\displaystyle \left({\bar {x}}-3\sigma ;{\bar {x}}+3\sigma \right)}. Более строго — приблизительно с вероятностью 0,9973 значение нормально распределённой случайной величины лежит в указанном интервале (при условии, что величина x¯{\displaystyle {\bar {x}}} истинная, а не полученная в результате обработки выборки).

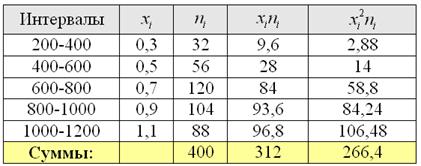
Расчет среднеквадратического отклонения

Для начала расчета среднеквадратического отклонения введите исходные числа в одно из полей ввода-вывода данных.
В первое поле можно ввести последовательность чисел, разделенных точкой с запятой (программа попытается так же преобразовать к стандартному виду, например, вставленную копию последовательности чисел с плавающей точкой, разделенных пробелами, запятой или точкой с запятой).
Во второе поле можно вводить числа по одному — они автоматически будут добавляться к данным первого поля, если расчет не запустился автоматически, кликните по зеленой кнопке, показывающей количество чисел в исследуемом массиве:
 

Введите исходные данные

Введите число

Сохранить исходный ряд данныхупорядочить данные по возрастаниюупорядочить данные по убываниювернуть исходную последовательность

Что-то пошло не так…
Прямое восхождение не может быть больше 24 часов,
минуты и секунды больше 60,
а склонение по абсолютной величине не должно быть больше 90°

OK

Среднеквадратическое отклонение, σ

Дисперсия, σ2

Среднее арифметическое, a_ср

Среднее линейное отклонение, δ

Коэффициент вариации, V

Размах вариации, R

Design by Sergey Ov for abc2home.ru

ВНИМАНИЕ! При перезагрузке страницы введенная информация не сохраняется, если Вы не сгенерировали код для записи результатов работы в командной строке:

Сохранить расчет среднеквадратического отклонения в истории браузера

Адресную строку с кодом из Ваших данных Вы можете можете переслать на любое устройство и воспроизвести на нем результаты расчетов

После того как будут введены хотя бы два исходных числа цвет квадратной кнопки на поле ввода данных должен поменяться с оранжевого на зеленый и автоматически начнется расчет среднеквадратического отклонения и сопутствующих параметров, если это не произошло, то кликните по зеленому полю кнопки.

• Среднее арифметическое — расчет онлайн, определение, формула
• Среднеквадратическое отклонение — расчет онлайн, определение, формула
• Среднее геометрическое — расчет онлайн, определение, формула
• Среднее гармоническое и среднее степенное — расчет онлайн, определения, формулы
• Среднее квадратическое — расчет онлайн, определение, формула

Практическое применение

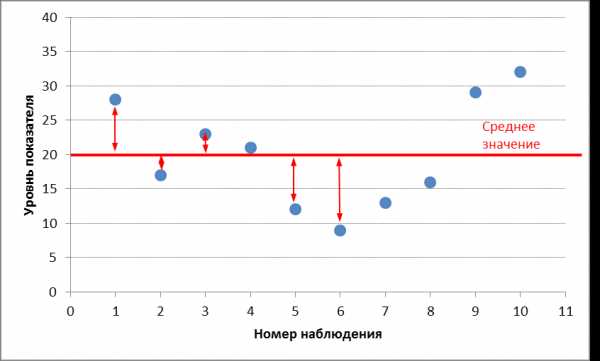
На практике среднеквадратическое отклонение позволяет определить, насколько значения в множестве могут отличаться от среднего значения.

Климат

Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой внутри континента. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.

Спорт

Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.

Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.

Дисперсия

Как
и среднее линейное отклонение, дисперсия
также отражает меру разброса данных
вокруг средней величины.

Формула
для расчета дисперсии выглядит так:

(для вариационных
рядов (взвешенная дисперсия))

(для несгруппированных
данных (простая дисперсия))

Где:
σ 2 –
дисперсия, Xi
–
анализируемsq
показатель (значение признака),
–
среднее значение показателя, f i –
количество значений в анализируемой
совокупности данных.

Дисперсия
— это средний квадрат отклонений.

Сначала
рассчитывается среднее значение, затем
берется разница между каждым исходным
и средним значением, возводится в
квадрат, умножается на частоту
соответствующего значения признака,
складывается и затем делится на количество
значений в данной совокупности.

Однако
в чистом виде, как, например, средняя
арифметическая, или индекс, дисперсия
не используется. Это скорее вспомогательный
и промежуточный показатель, который
используется для других видов
статистического анализа.

Упрощенный
способ расчета дисперсии

Среднеквадратическое
отклонение

Чтобы
использовать дисперсию дл анализа
данных из нее извлекают квадратный
корень. Получается так
называемое среднеквадратическое
отклонение
.

Кстати,
стандартное отклонение еще называют
сигмой – от греческой буквы, которой
его обозначают.

Среднеквадратическое
отклонение, очевидно, также характеризует
меру рассеяния данных, но теперь (в
отличие от дисперсии) его можно сравнивать
с исходными данными. Как правило,
среднеквадратические показатели в
статистике дают более точные результаты,
чем линейные. Следовательно,
среднеквадратическое отклонение
является более точным показателем меры
рассеяния данных, чем среднее линейное
отклонение.

Одним из основных инструментов статистического анализа является расчет среднего квадратичного отклонения. Данный показатель позволяет сделать оценку стандартного отклонения по выборке или по генеральной совокупности. Давайте узнаем, как использовать формулу определения среднеквадратичного отклонения в Excel.

Сразу определим, что же представляет собой среднеквадратичное отклонение и как выглядит его формула. Эта величина является корнем квадратным из среднего арифметического числа квадратов разности всех величин ряда и их среднего арифметического. Существует тождественное наименование данного показателя — стандартное отклонение. Оба названия полностью равнозначны.

Но, естественно, что в Экселе пользователю не приходится это высчитывать, так как за него все делает программа. Давайте узнаем, как посчитать стандартное отклонение в Excel.

18.3. Система двух случайных величин Двумерная случайная величина

До сих пор мы
рассматривали дискретные случайные
ве­личины, которые называют одномерными:
их возможные зна­чения определялись
одним числом. Кроме одномерных вели­чин
рассматривают также величины, возможные
значения ко­торых определяются
несколькими числами. Двумерную слу­чайную
величину обозначают через (X,
Y);
каждая из величин
X
и Y
называется компонентой (составляющей).
Обе величи­ны Х
и Y,
рассматриваемые одновременно, образуют
систему двух случайных величин. Например,
при штамповке стальных пластинок их
длина и ширина представляют собой
двумерную случайную величину.

Определение 1.
Законом распределения двумерной
случай­ной величины (X,
Y)
называют множество возможных пар чи­сел
(x_i,
y_j)
и их вероятностей
p(x_i,
y_j).
Двумерную случайную величину можно
трактовать как случайную точку А(Х,
Y)
на координатной плоскости.

Закон распределения
двумерной случайной величины обыч­но
задается в виде таблицы, в строках
которой указаны воз­можные значения
x_i
случайной величины X,
а в столбцах — возможные значения
y_j
случайной величины Y,
на пересече­ниях строк и столбцов
указаны соответствующие вероятности
p_ij.
Пусть случайная величина Х
может принимать п
значе­ний, а случайная величина Y
— т
значений. Тогда закон рас­пределения
двумерной случайной величины (X,
Y)
имеет вид

Из этой таблицы
можно найти законы распределения каждой
из случайных компонент. Например,
вероятность того, что слу­чайная
величина Х
примет значение х_k,
равна, согласно тео­реме сложения
вероятностей независимых событий,

Иными словами, для
нахождения вероятности Р(х_k)
нужно
просуммировать все т
вероятностей по k-му
столб­цу таблицы (18.21). Аналогично
получается вероятность то­го, что
случайная величина Y
примет возможное значение у_rР(у_r)
получается суммированием всех n
вероятностей r-й
стро­ки таблицы (18.21) (r
= 1,
2,
…
,m).
Отсюда следует, что
сумма всех
вероятностей в законе распределения
(18.21) равна единице:

Пример 1.
Задано распределение двумерной случайной
вели­чины:

Найти распределения
Х,
Y и Х
+
Y.

Решение.
В нашем случае возможные значения
случайной величины X:
х₁
= 1, х₂
= 2, x₃
= 3. Тогда, согласно формуле (18.22), имеем
P(x₁)
= 0,1
+
0,2 = 0,3,
P(x₂)
= 0,15
+
0,22 = 0,37,
Р(x₃)
= 0,12 + 0,21 = 0,33. Отсюда получаем закон
распреде­ления X:

Аналогично получаем
и для распределения Y:
у₁
= 1, y₂
= 2;
P(y₁)
= 0,1 + 0,15 +
0,12 = 0,37,
P(y₂)
= 0,2 + 0,22 + 0,21
= 0,63;

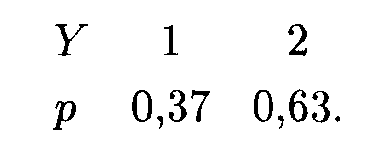
Теперь найдем
распределение
X+Y.
Возможные значения этой случайной
величины: 2, 3, 4 и 5. Соответствующие
вероятнос­ти Р(2)
= 0,1, Р(3)
= 0,15
+
0,2 = 0,35, Р(4)
= 0,12
+
0,22 = 0,34,
Р(5)
= 0,21. Отсюда находим искомое распределение:

В случае системы
двух случайных величин используются
кроме математических ожиданий и дисперсий
еще и другие числовые характеристики,
описывающие их взаимосвязь.

Коэффициент вариации не должен превышать по 44 ФЗ

Для унификации подхода к формированию НМЦК (начальной (максимальной) цены контракта, подписываемого с единственным поставщиком) при выполнении закупок в соответствии с ФЗ №44 «О контрактной системе в сфере закупок товаров, работ, услуг для обеспечения государственных и муниципальных нужд» разработаны методические рекомендации с методами и формулами расчета. А для участия в государственных торгах нужно составлять обоснование НМЦК. Расчет можно произвести в Excel.

Нормативный метод

Методика применяется в случаях, определенных законодательством (ст.19 ФЗ №44). Законодатель подразумевает использование предельных цен на товар, работу, услугу. В качестве источника информации применяется государственный реестр предельных отпускных цен.

• v – объем товара;
• цпред – предельная цена единицы товара.

Расчет НМЦК по 44-ФЗ в Excel:

Эта методика может использоваться совместно с методом сопоставимых рыночных цен.

Расчет в Excel

Рассчитать указанную величину в Экселе можно с помощью двух специальных функций СТАНДОТКЛОН.В
(по выборочной совокупности) и СТАНДОТКЛОН.Г
(по генеральной совокупности). Принцип их действия абсолютно одинаков, но вызвать их можно тремя способами, о которых мы поговорим ниже.

Способ 3: ручной ввод формулы

Существует также способ, при котором вообще не нужно будет вызывать окно аргументов. Для этого следует ввести формулу вручную.

Как видим, механизм расчета среднеквадратичного отклонения в Excel очень простой. Пользователю нужно только ввести числа из совокупности или ссылки на ячейки, которые их содержат. Все расчеты выполняет сама программа. Намного сложнее осознать, что же собой представляет рассчитываемый показатель и как результаты расчета можно применить на практике. Но постижение этого уже относится больше к сфере статистики, чем к обучению работе с программным обеспечением.

Пример расчета выборочной дисперсии и стандартного отклонения выборки.

После расчета геометрических и арифметических средних доходностей двух взаимных фондов в Примере (1) мы вычислили две меры дисперсии для этих фондов, размах и среднее абсолютное отклонение доходности (см.  Пример расчета размаха и среднего абсолютного отклонения для оценки риска).

Теперь мы вычислим выборочную дисперсию и стандартное отклонение выборки для доходности тех же двух фондов.

Таблица 15. Совокупная доходность двух взаимных фондов, 2008-2012 гг.
(повтор).

Год	Фонд Selected American Shares (SLASX)	Фонд T. Rowe Price Equity Income (PRFDX)
2008	-39.44%	-35.75%
2009	31.64	25.62
2010	12.53	15.15
2011	-4.35	-0.72
2012	12.82	17.25

На основании приведенных выше данных сделайте следующее:

1. Рассчитайте выборочную дисперсию доходности для (A) SLASX и (B) PRFDX.
2. Рассчитайте выборочное стандартное отклонение доходности для (A) SLASX и (B) PRFDX.
3. Сравните дисперсию доходности, измеренную стандартным отклонением доходности и средним абсолютным отклонением доходности для каждого из двух фондов.

Решение для части 1:

Чтобы вычислить выборочную дисперсию, мы используем Формулу 13 (значения отклонений приведены в процентах).

А. SLASX:

1. Среднее значение выборки:

\( \overline R \) = (-39.44 + 31.64 + 12.53 — 4.35 +12.82)/ 5 =
13.20/5 = 2.64%.

2. Квадратичные отклонения от среднего значения:

(-39.44 — 2.64)2 = (-42.08)2 = 1,770.73
(31.64 — 2.64)2 = (29.00)2 = 841.00
(12.53 — 2.64)2 = (9.89)2 = 97.81
(-4.35 — 2.64)2 = (-6.99)2 = 48.86
(12.82 — 2.64)2 = (10.18)2 = 103.63

3. Сумма квадратов отклонений от среднего составляет:

1,770.73 + 841.00 + 97.81 + 48.86 + 103.63 = 2,862.03.

4. Разделим сумму квадратов отклонений от среднего на (n — 1):

2,862.03/(5 — 1) = 2,862.03/4 = 715.51

B. PRFDX:

1. Среднее значение выборки:

\( \overline R \) = (-35.75 + 25.62 + 15.15 — 0.72 + 17.25)/5 = 21.55/5 = 4.31%.

2. Квадратичные отклонения от среднего значения:

(-35.75 — 4.31)2 = (-40.06)2 = 1,604.80
(25.62 — 4.31)2 = (21.31)2 = 454.12
(15.15 — 4.31)2 = (10.84)2 = 117.51
(-0.72 — 4.31)2 = (-5.03)2 = 25.30
(17.25 — 4.31)2 = (12.94)2 = 167.44

3. Сумма квадратов отклонений от среднего составляет:

1,604.80 + 454.12 + 117.51 + 25.30 + 167.44 = 2,369.17.

4. Разделим сумму квадратов отклонений от среднего на (n — 1):

2,369.17/4 = 592.29

Решение для части 2:

Чтобы найти стандартное отклонение, мы берем положительный квадратный корень из дисперсии.

A. Для SLASX, s = \( \sqrt 715.51 \) = 26.7%.

B. Для PRFDX, s = \( \sqrt 592.29 \) = 24.3%.

Решение для части 3:

Таблица 21 суммирует результаты части 2 для стандартного отклонения и включает результаты для MAD из Примера расчета размаха и среднего абсолютного отклонения для оценки риска.

Таблица 21. Два взаимных фонда: сравнение стандартного отклонения и среднего абсолютного отклонения (MAD).

Фонд	Стандартное отклонение (%)	Среднее абсолютное отклонение (%)
SLASX	26.7	19.6
PRFDX	24.3	18.0

Обратите внимание, что среднее абсолютное отклонение меньше стандартного отклонения. Среднее абсолютное отклонение всегда будет меньше или равно стандартному отклонению, потому что стандартное отклонение придает больший вес большим отклонениям, чем маленьким (помните, что отклонения возводятся в квадрат)

Поскольку стандартное отклонение является мерой дисперсии относительно среднего арифметического, мы обычно представляем  среднее арифметическое и стандартное отклонение вместе при анализе данных.

Когда мы имеем дело с данными, которые представляют собой временной ряд процентных изменений, представление геометрического среднего, представляющего собой сложную ставку скорости роста, также очень полезно.

В таблице 22 представлены исторические геометрические и арифметические средние доходности, а также историческое стандартное отклонение доходности для годовой и месячной доходности S&P 500.

Мы представляем эту статистику для номинальной (без поправки на инфляцию) доходности, чтобы мы могли наблюдать первоначальные величины доходности.

Таблица 22. Доходность рынка ценных бумаг: средние значения и стандартные отклонения.

Ставка доходности	Геометрическое среднее (%)	Среднее арифметическое (%)	Стандартное отклонение
S&P 500 (Годовая)	9.84	11.82	20.18
S&P 500 (Месячная)	0.79	0.94	5.50

коэффициент вариации

– это отношение стандартного отклонения к средней, выраженное в процентах:

И вот теперь совершенно без разницы, в д.е. мы считали:

или в тысячах д.е.:

Примечание: на практике часто считают именно через , но для оценки коэффициента вариации всей генеральной совокупности, конечно же, корректнее использовать исправленное стандартное отклонение .

В статистике существует следующий эмпирический ориентир:

– если показатель вариации составляет примерно 30% и меньше, то статистическая совокупность считается однородной. Это означает, что большинство вариант находится недалеко от средней, и найденное значение  хорошо характеризует центральную тенденцию совокупности.

– если показатель вариации составляет существенно больше 30%, то выборка неоднородна, то есть, значительное количество вариант находятся далеко от , и выборочная средняя плохо характеризует типичную варианту. В таких случаях целесообразно рассмотреть , а иногда и перцентили, которые делят вариационный ряд на части, и для каждого участка рассчитать свои показатели. Но это уже немного дебри статистики.

Другое преимущество относительных показателей – это возможность сравнивать разнородные статистические совокупности. Например, множество слонов и множество хомячков. Совершенно понятно, что дисперсия веса слонов по отношению к дисперсии веса хомяков будет просто конской, и их сопоставление не имеет смысла. Но вот анализ коэффициентов вариации веса вполне осмыслен, и может статься, что у слонов он составляет 10%, а у хомячков 40% (пример, конечно, условный). Это говорит о сбалансированном питании и размеренной жизни слонов. А вот хомяки там, то носятся с голодухи по полям, то отъедаются и спят в норах, и поэтому среди них есть много худощавых и много упитанных особей 🙂

Кроме коэффициента вариации, существуют и другие относительные показатели, но в реальных студенческих работах они почти не встречаются, и поэтому я не буду их рассматривать в рамках данного курса.

И сейчас, конечно же, задачки для самостоятельного решения:

Пример 17, на отработку терминов и формул:

а) Стандартное отклонение выборочной совокупности равно 5, а средний квадрат её вариант – 250. Найти выборочную среднюю.

б) Определите среднее квадратическое отклонение, если известно, что средняя равна 260, а коэффициент вариации составляет 30%.

и Пример 18, творческий:

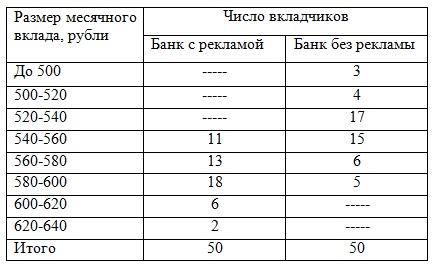
Производство стальных труб на предприятии (тонн) в 1-м полугодии составило:

Определить:
– среднемесячный объем производства;
– среднее квадратическое отклонение;
– коэффициент вариации.

Сделать краткие содержательные выводы. – Да, это тоже типичный пункт статистической задачи!

Обратите внимание, что здесь не понятно, выборочной ли считать эту совокупность или генеральной. И в таких случаях лучше не заниматься домыслами, просто используем обозначения без подстрочных индексов

Вообще, задачи на экономическую и промышленную тематику – самые популярные в статистике, и в моей коллекции их сотни. Но все они до ужаса однотипны, и поэтому я предлагаю их в терапевтической дозировке 🙂

Задание 8

Выполнить расчёты в Экселе – числа уже там, ну а инструкцию я на этот раз не привёл, поскольку люди вы уже опытные.

Краткое решение и ответ в конце урока, который подошёл к концу.

Следующее занятие не за горами, а уже за кочкой:

Решения и ответы:

Пример 17. Решение:

а) Используем формулу . По условию, , . Таким образом:

б) Используем формулу . По условию, , . Таким образом:

Ответ: а) , б)

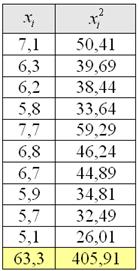
Пример 18. Решение: вычислим сумму вариант и сумму их квадратов:Найдём среднюю: тонны – среднемесячный объем производства за полугодие.Дисперсию вычислим по формуле:Среднее квадратическое отклонение: тонн.Коэффициент вариации:

Ответ:  тонны,  тонн,

Краткие выводы: за первое полугодие среднемесячный объём производства труб составил  тонны. Низкие показатели вариации говорят о стабильной ситуации на производстве.

(Переход на главную страницу)

Шаги

Часть 1 из 3:

Среднее значение

1. 1

   Возьмите наборе данных. Среднее значение – это важная величина в статистических расчетах.
   X
   Источник информации

   • Определите количество чисел в наборе данных.
   • Числа в наборе сильно отличаются друг от друга или они очень близки (отличаются на дробные доли)?
   • Что представляют числа в наборе данных? Тестовые оценки, показания пульса, роста, веса и так далее.
   • Например, набор тестовых оценок: 10, 8, 10, 8, 8, 4.

2. 2

   Для вычисления среднего значения понадобятся все числа данного набора данных.
   X
   Источник информации

   • Среднее значение – это усредненное значение всех чисел в наборе данных.
   • Для вычисления среднего значения сложите все числа вашего набора данных и разделите полученное значение на общее количество чисел в наборе (n).
   • В нашем примере (10, 8, 10, 8, 8, 4) n = 6.

3. 3

   Сложите все числа вашего набора данных.
   X
   Источник информации

   • В нашем примере даны числа: 10, 8, 10, 8, 8 и 4.
   • 10 + 8 + 10 + 8 + 8 + 4 = 48. Это сумма всех чисел в наборе данных.
   • Сложите числа еще раз, чтобы проверить ответ.

4. 4

   Разделите сумму чисел на количество чисел (n) в выборке. Вы найдете среднее значение.
   X
   Источник информации

   • В нашем примере (10, 8, 10, 8, 8 и 4) n = 6.
   • В нашем примере сумма чисел равна 48. Таким образом, разделите 48 на n.
   • 48/6 = 8
   • Среднее значение данной выборки равно 8.

Часть 2 из 3:

Дисперсия

1

Вычислите дисперсию. Это мера разброса данных вокруг среднего значения.
X
Источник информации

Эта величина даст вам представление о том, как разбросаны данные выборки.
Выборка с малой дисперсией включает данные, которые ненамного отличаются от среднего значения.
Выборка с высокой дисперсией включает данные, которые сильно отличаются от среднего значения.
Дисперсию часто используют для того, чтобы сравнить распределение двух наборов данных.

2

Вычтите среднее значение из каждого числа в наборе данных. Вы узнаете, насколько каждая величина в наборе данных отличается от среднего значения.
X
Источник информации

В нашем примере (10, 8, 10, 8, 8, 4) среднее значение равно 8.
10 — 8 = 2; 8 — 8 = 0, 10 — 2 = 8, 8 — 8 = 0, 8 — 8 = 0, и 4 — 8 = -4.
Проделайте вычитания еще раз, чтобы проверить каждый ответ

Это очень важно, так как полученные значения понадобятся при вычислениях других величин.

3

Возведите в квадрат каждое значение, полученное вами в предыдущем шаге.
X
Источник информации

При вычитании среднего значения (8) из каждого числа данной выборки (10, 8, 10, 8, 8 и 4) вы получили следующие значения: 2, 0, 2, 0, 0 и -4.
Возведите эти значения в квадрат: 22, 02, 22, 02, 02, и (-4)2 = 4, 0, 4, 0, 0, и 16.
Проверьте ответы, прежде чем приступить к следующему шагу.

4

Сложите квадраты значений, то есть найдите сумму квадратов.
X
Источник информации

В нашем примере квадраты значений: 4, 0, 4, 0, 0 и 16.
Напомним, что значения получены путем вычитания среднего значения из каждого числа выборки: (10-8)^2 + (8-8)^2 + (10-2)^2 + (8-8)^2 + (8-8)^2 + (4-8)^2
4 + 0 + 4 + 0 + 0 + 16 = 24.
Сумма квадратов равна 24.

5

Разделите сумму квадратов на (n-1). Помните, что n – это количество данных (чисел) в вашей выборке

Таким образом, вы получите дисперсию.
X
Источник информации

В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
n-1 = 5.
В нашем примере сумма квадратов равна 24.
24/5 = 4,8
Дисперсия данной выборки равна 4,8.

Часть 3 из 3:

Среднеквадратическое отклонение

1. 1

   Найдите дисперсию, чтобы вычислить среднеквадратическое отклонение.
   X
   Источник информации

   • Помните, что дисперсия – это мера разброса данных вокруг среднего значения.
   • Среднеквадратическое отклонение – это аналогичная величина, описывающая характер распределения данных в выборке.
   • В нашем примере дисперсия равна 4,8.

2. 2

   Извлеките квадратный корень из дисперсии, чтобы найти среднеквадратическое отклонение.
   X
   Источник информации

   • Как правило, 68% всех данных расположены в пределах одного среднеквадратического отклонения от среднего значения.
   • В нашем примере дисперсия равна 4,8.
   • √4,8 = 2,19. Среднеквадратическое отклонение данной выборки равно 2,19.
   • 5 из 6 чисел (83%) данной выборки (10, 8, 10, 8, 8, 4) находится в пределах одного среднеквадратического отклонения (2,19) от среднего значения (8).

3. 3

   Проверьте правильность вычисления среднего значения, дисперсии и среднеквадратического отклонения. Это позволит вам проверить ваш ответ.
   X
   Источник информации

   • Обязательно записывайте вычисления.
   • Если в процессе проверки вычислений вы получили другое значение, проверьте все вычисления с самого начала.
   • Если вы не можете найти, где сделали ошибку, проделайте вычисления с самого начала.

Видео в помощь

При статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.

Среднеквадратическое отклонение:

Стандартное отклонение
(оценка среднеквадратического отклонения случайной величины Пол, стены вокруг нас и потолок,x

относительно её математического ожидания на основе несмещённой оценки её дисперсии):

где — дисперсия ; — Пол, стены вокруг нас и потолок,i

-й элемент выборки; — объём выборки; — среднее арифметическое выборки:

Следует отметить, что обе оценки являются смещёнными. В общем случае несмещённую оценку построить невозможно. Однако оценка на основе оценки несмещённой дисперсии является состоятельной .

Прикладное значение среднеквадратического отклонения

Среднеквадратическое отклонение от отклонений значений исследуемых данных находит широкое прикладное применение в метрологии, экспериментальной физике и статистике.
При обработке результатов измерений во многих случаях их окончательные значения определяются как среднее арифметическое от значений, полученных в результате эксперимента, при этом среднеквадратическое отклонение величин будет являться оценкой ошибки измерений.
В свою очередь на основе минимизации среднеквадратических отклонений в 19 веке был разработан метод наименьших квадратов, который нашел широкое применение в таких областях как статистический, регрессионный анализ, обработка экспериментальных данных и вычислительная математика.

P.S. На этой странице используется Бета версия программы расчета среднеквадратического отклонения, об обнаруженных недочетах, а так же возможных пожеланиях просьба сообщить на форум сайта (окно для входа на форум находится в нижней части страницы).

1. Среднее арифметическоезначение (чаще используется термин, просто, «среднее арифметическое» или «среднее») множества заданных чисел определяется как число равное сумме всех чисел множества, делённой на их количество:

a_{ср.арифм} =  
a₁+ a₂+ …+ a_n
n
 

2. Если вычислено арифметическое среднее заданного множества чисел, то во многих случаях, становится желательной оценка рассеяния значений этих чисел относительно среднего. Оценка расходимости квадратов значений этих чисел от среднего и является оценкой дисперсии.
Вообще термин дисперсия появился в рамках теорий вероятностей. Одной из ее основополагающих характеристик является дисперсия случайной величины как мера разброса значений случайной величины относительно её математического ожидания.
Не углубляясь в дебри Тер-Вера, здесь приводим только используемую для наших расчетов формулу дисперсии:

σ 2 =  
(a₁ — a_cp)2 + (a₂ — a_cp)2 + …+ (a_n — a_cp)2
n
 

3. Среднее линейное отклонение определяется как среднее от абсолютных значений отклонений каждого из ряда чисел от их среднего арифметического:

δ =  
|a₁ — a_cp| + |a₂ — a_cp| + …+ |a_n — a_cp|
n
 

4. Коэффициент вариации ряда чисел — мера относительного разброса их значений; показывает, какую долю от среднего значения этой величины составляет её средний разброс. Исчисляется в процентах:

V =  

σ

a_ср
 
  × 100%

5. Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел. Таким образом, размах вариации может быть представлен следующей формулой:

R = a_max — a_min

Пример вычисления стандартного отклонения оценок учеников

Предположим, что интересующая нас группа (генеральная совокупность) это класс из восьми учеников, которым выставляются оценки по 10-бальной системе. Так как мы оцениваем всю группу, а не её выборку, можно использовать стандартное отклонение на основании смещённой оценки дисперсии. Для этого берём квадратный корень из среднего арифметического квадратов отклонений величин от их среднего значения.

Пусть оценки учеников класса следующие:

2, 4, 4, 4, 5, 5, 7, 9.{\displaystyle 2,\ 4,\ 4,\ 4,\ 5,\ 5,\ 7,\ 9.}

Тогда средняя оценка равна:

μ=2+4+4+4+5+5+7+98=5{\displaystyle \mu ={\frac {2+4+4+4+5+5+7+9}{8}}=5}

Вычислим квадраты отклонений оценок учеников от их средней оценки:

(2−5)2=(−3)2=9(5−5)2=2=(4−5)2=(−1)2=1(5−5)2=2=(4−5)2=(−1)2=1(7−5)2=22=4(4−5)2=(−1)2=1(9−5)2=42=16{\displaystyle {\begin{array}{lll}(2-5)^{2}=(-3)^{2}=9&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(7-5)^{2}=2^{2}=4\\(4-5)^{2}=(-1)^{2}=1&&(9-5)^{2}=4^{2}=16\\\end{array}}}

Среднее арифметическое этих значений называется дисперсией:

σ2=9+1+1+1+++4+168=4{\displaystyle \sigma ^{2}={\frac {9+1+1+1+0+0+4+16}{8}}=4}

Стандартное отклонение равно квадратному корню дисперсии:

σ=4=2{\displaystyle \sigma ={\sqrt {4}}=2}

Эта формула справедлива только если эти восемь значений и являются генеральной совокупностью. Если бы эти данные были случайной выборкой из какой-то большой совокупности (например, оценки восьми случайно выбранных учеников большого города), то в знаменателе формулы для вычисления дисперсии вместо n = 8 нужно было бы поставить n − 1 = 7:

σ2=9+1+1+1+++4+167≈4,57{\displaystyle \sigma ^{2}={\frac {9+1+1+1+0+0+4+16}{7}}\approx 4,57}

и стандартное отклонение равнялось бы:

σ=4,57≈2,14{\displaystyle \sigma ={\sqrt {4,57}}\approx 2,14}

Этот результат называется стандартным отклонением на основании несмещённой оценки дисперсии. Деление на n − 1 вместо n даёт неискажённую оценку дисперсии для больших генеральных совокупностей.

Правило трёх сигм

График плотности вероятности нормального распределения и процент попадания случайной величины на отрезки, равные среднеквадратическому отклонению.

Правило трёх сигм (3σ{\displaystyle 3\sigma }) гласит: вероятность того, что любая случайная величина отклонится от своего среднего значения менее чем на 3σ{\displaystyle 3\sigma }, — P(|ξ−Eξ∣<3σ)≥89{\displaystyle P(|\xi -E\xi \mid <3\sigma )\geq {\frac {8}{9}}}.

Практически все значения нормально распределённой случайной величины лежат в интервале (μ−3σ;μ+3σ){\displaystyle \left(\mu -3\sigma ;\mu +3\sigma \right)}, где μ=Eξ{\displaystyle \mu =E\xi } — математическое ожидание случайной величины. Более строго — приблизительно с вероятностью 0,9973 значение нормально распределённой случайной величины лежит в указанном интервале.