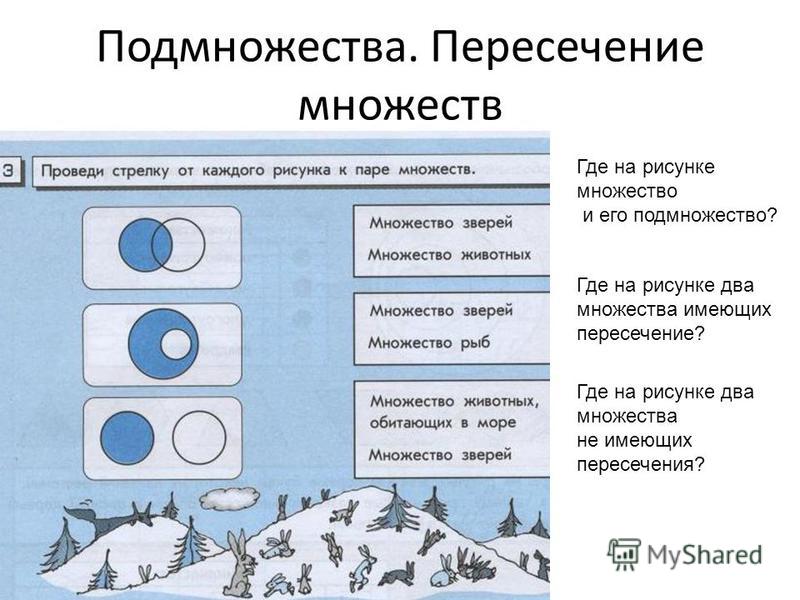
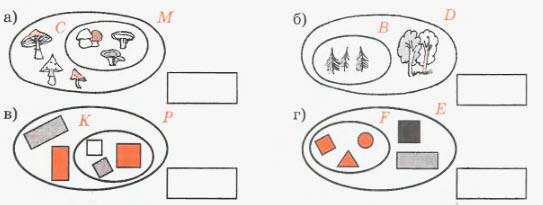
Множества,их элементы,поджмножества

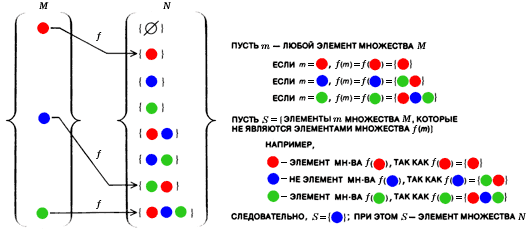
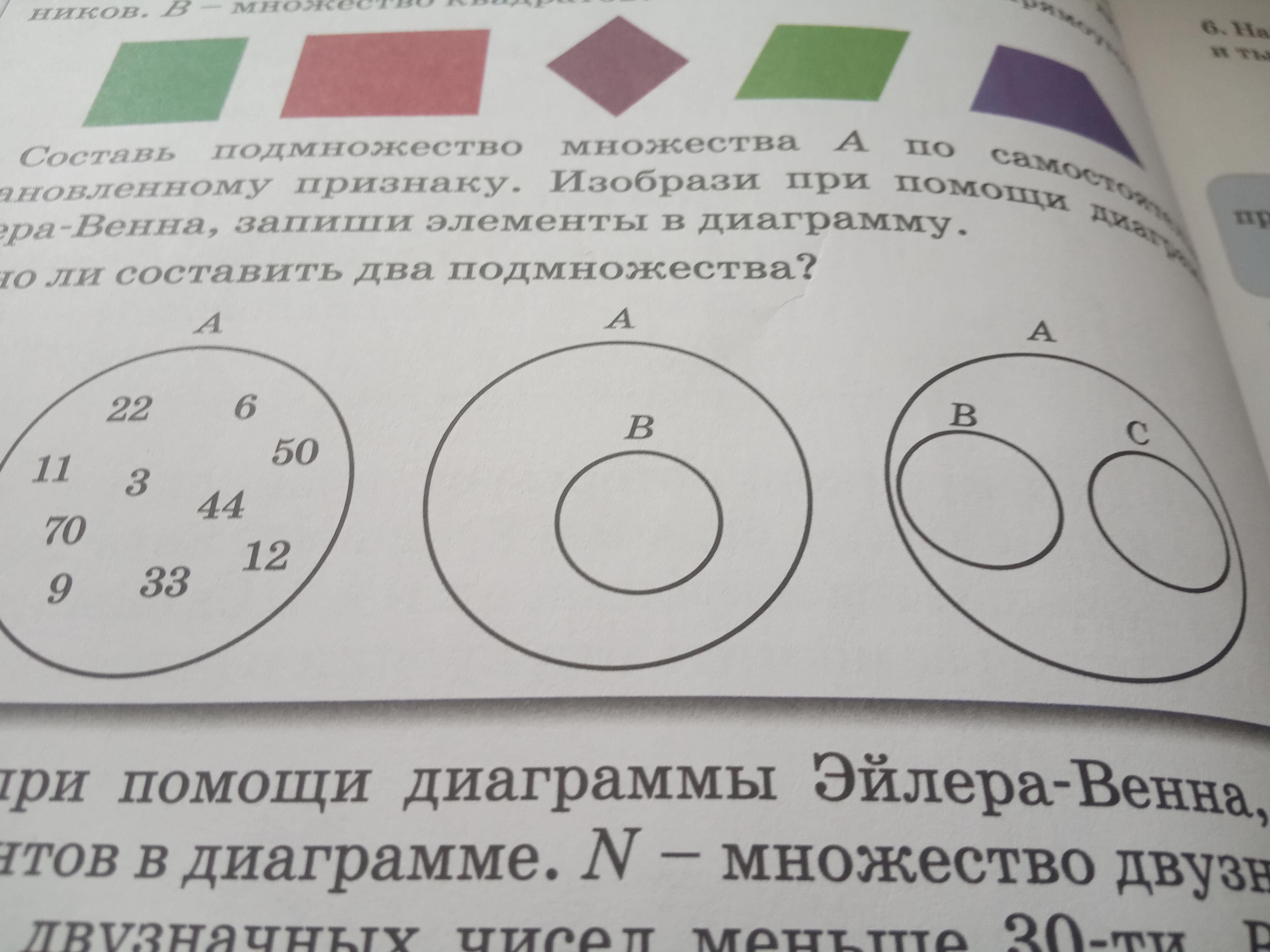
Примеры

Множества ∅, {}, {1,3,4}, {,1,2,3,4,5}{\displaystyle \varnothing ,~\{0\},~\{1,3,4\},~\{0,1,2,3,4,5\}} являются подмножествами множества {,1,2,3,4,5}.{\displaystyle \{0,1,2,3,4,5\}.}
Множества {∅,↑,oca}, {$,%,∗,↑}, {∅}, ∅{\displaystyle \{\varnothing ,\uparrow ,{\mbox{oca}}\},~\{\$,\%,*,\uparrow \},~\{\varnothing \},~\varnothing } являются подмножествами множества {$,%,∅,↑,∗,oca}.{\displaystyle \{\$,\%,\varnothing ,\uparrow ,*,{\mbox{oca}}\}.}
Пусть A={a,b}.{\displaystyle A=\{a,b\}.} Тогда P(A)={∅,{a},{b},{a,b}}.{\displaystyle {\mathcal {P}}(A)=\{\varnothing ,\{a\},\{b\},\{a,b\}\}.}
Пусть A={1,2,3,4,5},B={1,2,3},C={4,5,6,7}{\displaystyle A=\{1,2,3,4,5\},\;B=\{1,2,3\},\;C=\{4,5,6,7\}}. Тогда B⊂A,C⊄A.{\displaystyle B\subset A,\;C\not \subset A.}

Отображение множеств

Отображение множества во множество – это правило, по которому каждому элементу множества ставится в соответствие элемент (или элементы) множества . В том случае если в соответствие ставится единственный элемент, то данное правило называется однозначно определённой функцией или просто функцией.

Функцию, как многие знают, чаще всего обозначают буквой – она ставит в соответствие каждому элементу единственное значение , принадлежащее множеству .

Ну а сейчас я снова побеспокою множество студентов 1-го ряда и предложу им 6 тем для рефератов (множество ):

Векторы Матрицы Определители Комплексные числа (о, да!) Теория пределов Что такое производная?

Установленное (добровольно или принудительно =)) правило ставит в соответствие каждому студенту множества единственную тему реферата множества .

…а вы, наверное, и представить себе не могли, что сыграете роль аргумента функции =) =)

Элементы множества образуют область определения функции (обозначается через ), а элементы множества – область значений функции (обозначается через ).

Построенное отображение множеств имеет очень важную характеристику: оно является взаимно-однозначным или биективным (биекцией). В данном примере это означает, что каждому студенту поставлена в соответствие одна уникальная тема реферата, и обратно – за каждой темой реферата закреплён один и только один студент.

Однако не следует думать, что всякое отображение биективно. Если на 1-й ряд (к множеству ) добавить 7-го студента, то взаимно-однозначное соответствие пропадёт – либо один из студентов останется без темы (отображения не будет вообще), либо какая-то тема достанется сразу двум студентам. Обратная ситуация: если к множеству добавить седьмую тему, то взаимнооднозначность отображения тоже будет утрачена – одна из тем останется невостребованной.

Уважаемые студенты на 1-м ряду, не расстраивайтесь – остальные 20 человек после пар пойдут прибирать территорию университета от осенней листвы. Завхоз выдаст двадцать голиков, после чего будет установлено взаимно-однозначное соответствие между основной частью группы и мётлами…, а Вольдемар ещё и в магазин сбегать успеет =)

Теперь разберёмся со «школьной» функцией одной переменной. Пожалуйста, загляните на страницу Функции и графики (отроется на соседней вкладке), и в Примере 1 найдите график линейной функции .

Задумаемся, что это такое? Это правило , которое каждому элементу области определения (в данном случае это все значения «икс») ставит в соответствие единственное значение . С теоретико-множественной точки зрения, здесь происходит отображение множества действительных чисел во множество действительных чисел:

Первое множество мы по-обывательски называем «иксами» (независимая переменная или аргумент), а второе – «игреками» (зависимая переменная или функция).

Далее взглянем на старую знакомую параболу . Здесь правило каждому значению «икс» ставит в соответствие его квадрат, и имеет место отображение:

Итак, что же такое функция одной переменной? Функция одной переменной – это правило , которое каждому значению независимой переменной из области определения ставит в соответствие одно и только одно значение .

Как уже отмечалось в примере со студентами, не всякая функция является взаимно-однозначной. Так, например, у функции каждому «иксу» области определения соответствует свой уникальный «игрек», и наоборот – по любому значению «игрек» мы сможем однозначно восстановить «икс». Таким образом, это биективная функция.

! На всякий случай ликвидирую возможное недопонимание: моя постоянная оговорка об области определения не случайна! Функция может быть определена далеко не при всех «икс», и, кроме того, может быть взаимно-однозначной и в этом случае. Типичный пример:

А вот у квадратичной функции не наблюдается ничего подобного, во-первых: – то есть, различные значения «икс» отобразились в одно и то же значение «игрек»; и во-вторых: если кто-то вычислил значение функции и сообщил нам, что , то не понятно – этот «игрек» получен при или при ? Что и говорить, взаимной однозначностью здесь даже не пахнет.

Задание 2: просмотреть графики основных элементарных функций и выписать на листок биективные функции. Список для сверки в конце этого урока.

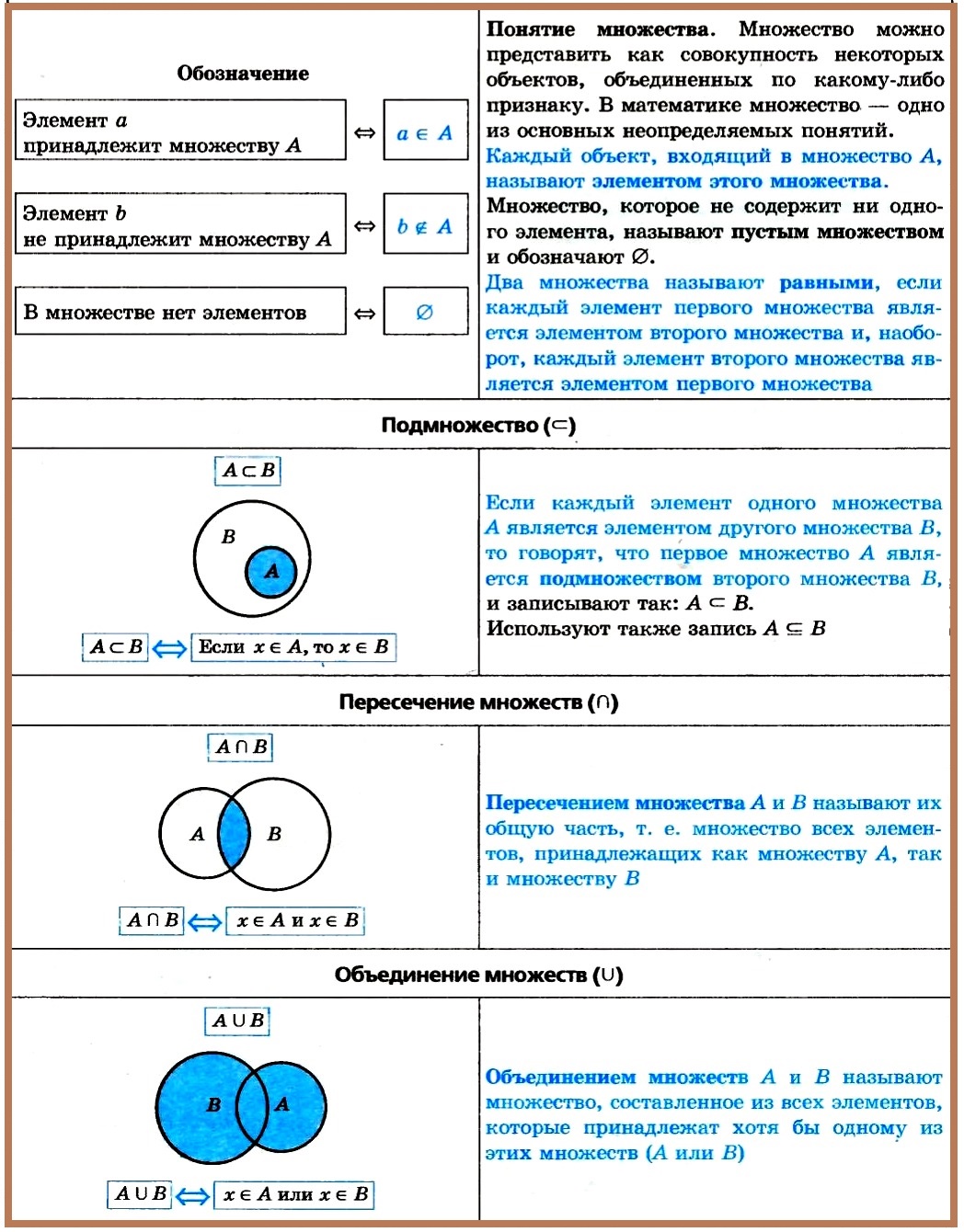
Обозначение множеств, подмножеств и их элементов

Чаще всего множества обозначаются латинскими буквами- $A, B, C , D, X, Y, Z, W$ и Т.Д.

Элементы множеств обозначаются строчными буквами $a,b,c,d,x,y,z$ и Т.Д.

Записать принадлежность некоторого элемента к некоторому множеству, например то, что некоторой элемент $a$ будет входить в множество $A$ математически можно так: $a\in A$.Прочитать данную запись можно так: a принадлежит множеству $A$.

Если же некоторый элемент, например, $b$ не принадлежит множеству $B$, то это записывается так: $b\notin B$.Читают эту запись так: $b$ не принадлежит множеству $B$

Например, если обозначить множество целых чисел за $A$, что тогда можно записать: $3\in A$, $7,5\notin B$

Пустое множество в математике обозначают так: $ᴓ$

Для обозначения того, что множество $B$ является подмножеством множества $A$, используют обозначение: Знак $\subset $ обозначает включение одного множества в другое множество.

Пример 1

Определить какие элементы из перечисленных $12,38,54,79,934$ будут входить в множество $A$- чисел кратных $3$.

Решение: По условию множество $A$ содержит в себе элементы, каждый из которых должен быть кратным, т.е. делится без остатка на $3.$ Значит для того чтобы определить будут ли заданные числа являться элементами множества $A$ нам надо проверить какие из них будут делится на $3$ без остатка, какие нет.

Вспомним признак делимости на $3$: Если сумма цифр, входящих в состав числа делится на $3$, то число делится на $3$ без остатка.

$12$ делится на $3$, т.к. сумма цифр числа $12$ равна $3$

число $38$ на $3$ без остатка делится не будет, т.к. сумма цифр $3+8=11$ не делится на $3$ без остатка

аналогично т.к. суммы цифр числа $54$ равна $9$ доказываем, что на $3$ оно делится, в число $74$ на $3$ делится не будет, т.к. сумма цифр равна $11.$

Найдем сумму цифр числа $934: 9+3+4=16$, число $16$ не кратно $3$ ,значит и число $934$ на $3$ без остатка делится не будет

Теперь сделаем вывод, какие числа будут являться элементами множества $A$:

Способы задания множеств

Существует два глобально различных способа задания множеств.

Первый заключается в том, что множество задается указанием всех его элементов. В таком случае говорят, что множество задано перечислением всех своих элементов или списком своих элементов. Перечислением элементов можно задать только конечные множества и при небольшом количестве элементов, входящих в него

Конечные множества с небольшим количеством элементов обычно записывают в фигурных скобках $\left\{a,b,c\right\}$

При таком способе задания множеств говорят, что множество задано перечислением его элементов.

Второй способ задания множеств применим как для конечных. так и для бесконечных множеств. Он заключается в том, что указывается свойство, которым обладает каждый элемент данного множества — множество задают описанием, т.е. указав его характеристическое свойство, т. е свойство, которым обладают все элементы этого множества и не обладают никакие другие объекты.

Пример 2

Например, с помощью описания можно задать такие множество натуральных чисел от $1$ до $9$ включительно. Характеристическим свойством, т. е. свойством, которым обладают все элементы этого множества для данных элементов будет являться то, что все они являются натуральными числами и каждое из них не меньше $1$ и не больше $9$. Перечислением указанное множество можно задать следующим образом:

$A=\left\{1\ ,2\ ,3,4,5,6,7,8,9\right\}$

Конечные и бесконечные множества

Множества, состоящие из конечного числа элементов, называются конечными множествами. Если же число элементов множества неограниченно, то такое множество называется бесконечным. Например, множество всех натуральных чисел бесконечно.

Рассмотрим два каких-либо множества $M$ и $N$ и поставим вопрос о том, одинаково или нет количество элементов в этих множествах.

Если множество $M$ конечно, то количество его элементов характеризуется некоторым натуральным числом — числом его элементов. В этом случае для сравнения количества элементов множеств $M$ и $N$ достаточно сосчитать число элементов в $M$ , число элементов в $N$ и сравнить полученные числа. Естественно также считать, что если одно из множеств $M$ и $N$ конечно, а другое бесконечно, то бесконечное множество содержит больше элементов, чем конечное.

Однако, если оба множества $M$ и $N$ бесконечны, то путь простого счета элементов ничего не дает. Поэтому сразу возникают такие вопросы: все ли бесконечные множества имеют одинаковое количество элементов, или же существуют бесконечные множества с большим и меньшим количеством элементов? Если верно второе, то каким способом можно сравнивать между собой количество элементов в бесконечных множествах? Этими вопросами мы теперь и займемся.

Примеры

Множества ∅, {}, {1,3,4}, {,1,2,3,4,5}{\displaystyle \varnothing ,~\{0\},~\{1,3,4\},~\{0,1,2,3,4,5\}} являются подмножествами множества {,1,2,3,4,5}.{\displaystyle \{0,1,2,3,4,5\}.}
Множества ∅, {,1,2,3,4,5}{\displaystyle \varnothing ,~\{0,1,2,3,4,5\}} являются тривиальными (несобственными) подмножествами множества {,1,2,3,4,5},{\displaystyle \{0,1,2,3,4,5\},} все остальные подмножества из элементов множества — нетривиальными или собственными.
Множества {∅,↑,oca}, {$,%,∗,↑}, {∅}, ∅{\displaystyle \{\varnothing ,\uparrow ,{\mbox{oca}}\},~\{\$,\%,*,\uparrow \},~\{\varnothing \},~\varnothing } являются подмножествами множества {$,%,∅,↑,∗,oca}.{\displaystyle \{\$,\%,\varnothing ,\uparrow ,*,{\mbox{oca}}\}.}
Пусть A={a,b}.{\displaystyle A=\{a,b\}.} Тогда P(A)={∅,{a},{b},{a,b}}.{\displaystyle {\mathcal {P}}(A)=\{\varnothing ,\{a\},\{b\},\{a,b\}\}.}
Пусть A={1,2,3,4,5},B={1,2,3},C={4,5,6,7}{\displaystyle A=\{1,2,3,4,5\},\;B=\{1,2,3\},\;C=\{4,5,6,7\}}. Тогда B⊂A,C⊄A.{\displaystyle B\subset A,\;C\not \subset A.}

Элемент множества

Объекты, из которых состоит множество, называют элементами множества или точками множества.
Множества чаще всего обозначают заглавными буквами латинского алфавита, его элементы — строчными. Если a{\displaystyle a} — элемент множества A{\displaystyle A}, то записывают a∈A{\displaystyle a\in A} («a{\displaystyle a} принадлежит A{\displaystyle A}»). Если a{\displaystyle a} не является элементом множества A{\displaystyle A}, то записывают a∉A{\displaystyle a\notin A} («a{\displaystyle a} не принадлежит A{\displaystyle A}»). В отличие от мультимножества каждый элемент множества уникален, и во множестве не может быть двух идентичных элементов. Иначе говоря, добавление к множеству элементов, идентичных уже принадлежащим множеству, не меняет его:

{6,11}={11,6}={11,11,6,11,6}{\displaystyle \{6,11\}=\{11,6\}=\{11,11,6,11,6\}}.

Равенство A=B{\displaystyle A=B} двух множеств означает

x∈A⟺x∈B.{\displaystyle x\in A\iff x\in B.}

Подмножества конечных множеств

Если исходное множество конечно, то у него существует конечное количество подмножеств. А именно, у n{\displaystyle n}-элементного множества существует 2n{\displaystyle 2^{n}} подмножеств (включая пустое). Чтобы убедиться в этом, достаточно заметить, что каждый элемент может либо входить, либо не входить в подмножество, а значит, общее количество подмножеств будет n{\displaystyle n}-кратным произведением двоек. Если же рассматривать только подмножества n{\displaystyle n}-элементного множества из k≤n{\displaystyle k\leq n} элементов, то их количество выражается биномиальным коэффициентом (nk){\displaystyle \textstyle {\binom {n}{k}}}. Для проверки этого факта можно выбирать элементы подмножества последовательно. Первый элемент можно выбрать n{\displaystyle n} способами, второй n−1{\displaystyle n-1} способом, и так далее, и, наконец, k{\displaystyle k}-й элемент можно выбрать n−k+1{\displaystyle n-k+1} способом. Таким образом мы получим последовательность из k{\displaystyle k} элементов, и ровно k!{\displaystyle k!} таким последовательностям соответствует одно подмножество. Значит, всего найдется n(n−1)…(n−k+1)k!=(nk){\displaystyle \textstyle {\frac {n(n-1)\dots (n-k+1)}{k!}}={\binom {n}{k}}} таких подмножеств.

Мощность

Мощность множества — характеристика множества, обобщающая понятие о количестве элементов для конечного множества таким образом, чтобы множества, между которыми возможно установление биекции были равномощны. Обозначается |A|{\displaystyle |A|} или ♯A{\displaystyle \sharp A}. Мощность пустого множества равна нулю, для конечных множеств мощность совпадает с числом элементов, для бесконечных множеств вводятся специальные кардинальные числа, соотносящиеся друг с другом по принципу включения (если A⊆B{\displaystyle A\subseteq B}, то |A|⩽|B|{\displaystyle |A|\leqslant |B|}) и распространением свойства мощности булеана конечного множества: |2A|=2|A|{\displaystyle |2^{A}|=2^{|A|}} на случай бесконечных множеств (само обозначение 2A{\displaystyle 2^{A}} мотивировано этим свойством).

Наименьшая бесконечная мощность обозначается ℵ{\displaystyle \aleph _{0}}, это мощность счётного множества. Мощность континуума, биективного булеану счётного множества обозначается c{\displaystyle {\mathfrak {c}}} или 2ℵ{\displaystyle 2^{\aleph _{0}}}. Континуум-гипотеза — предположение о том, что между счётной мощностью и мощностью континуума нет промежуточных мощностей.

Определение

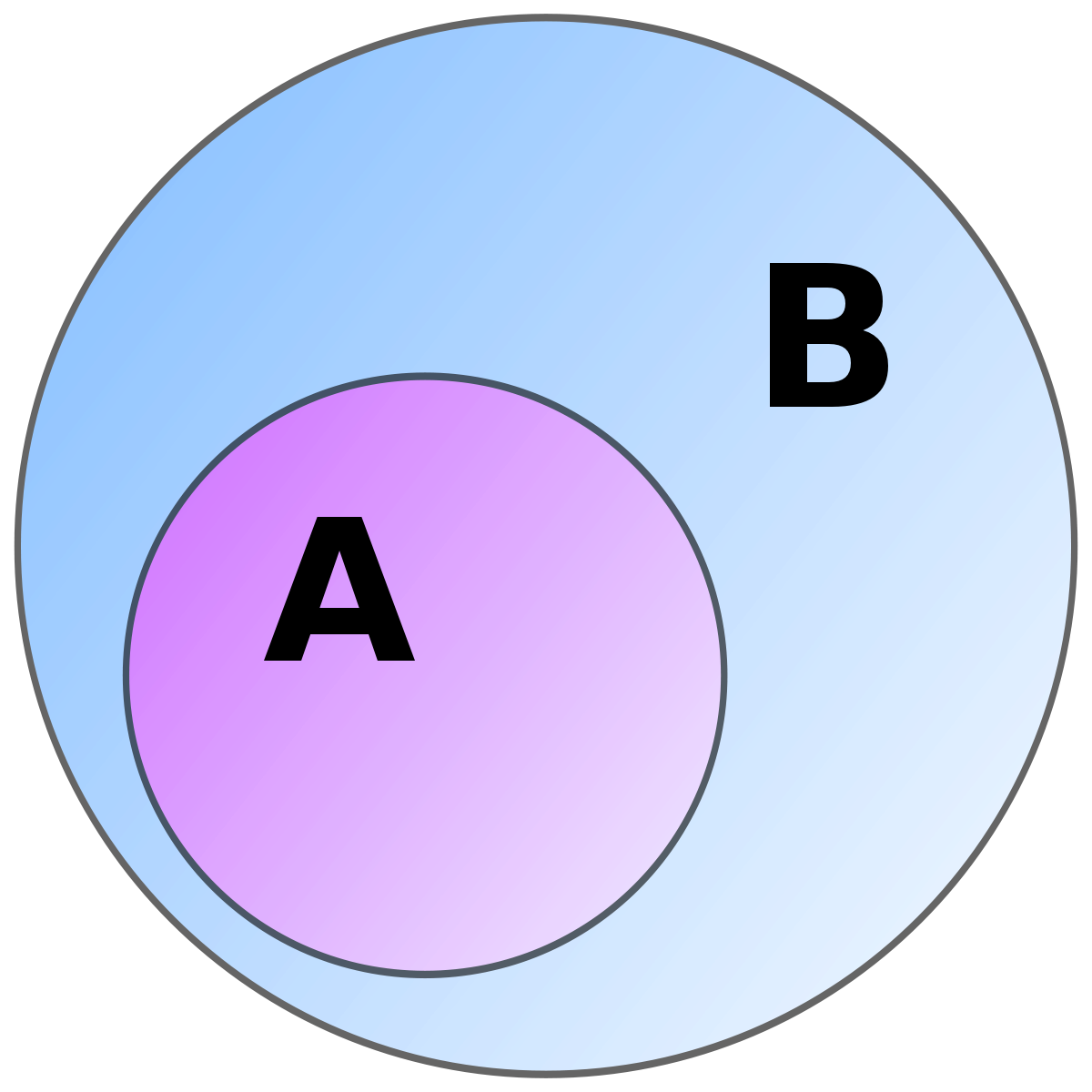
Множество A{\displaystyle A} называется подмножеством множества B{\displaystyle B}, если все элементы, принадлежащие A{\displaystyle A}, также принадлежат B{\displaystyle B}. Формальное определение:

(A⊂B)⇔(∀x(x∈A⇒x∈B)){\displaystyle (A\subset B)\Leftrightarrow \left(\forall x(x\in A\Rightarrow x\in B)\right)\,}.

Существует две системы символических обозначений для подмножеств:

«A{\displaystyle A} является подмножеством B{\displaystyle B}» обозначается	«A{\displaystyle A} является собственным подмножеством B{\displaystyle B}» обозначается	Примечание
A⊆B{\displaystyle A\subseteq B}	A⊂B{\displaystyle A\subset B}	Символ ⊆{\displaystyle \subseteq } является аналогом ≤{\displaystyle \leq }, то есть в случае A⊆B{\displaystyle A\subseteq B} допускается равенство A=B{\displaystyle A=B} множеств; символ ⊂{\displaystyle \subset } является аналогом <{\displaystyle <}, то есть в случае A⊂B{\displaystyle A\subset B} в B{\displaystyle B} есть элементы, которых нет в A{\displaystyle A}.
A⊂B{\displaystyle A\subset B}	A⊊B{\displaystyle A\subsetneq B}	Для понятия «подмножество» используется более простой символ, так как это понятие является более «фундаментальным».

Обе системы обозначений используют символ ⊂{\displaystyle \subset } в разных смыслах, что может привести к путанице. В данной статье мы будем использовать последнюю систему обозначений.

Множество B{\displaystyle B} называется надмно́жеством множества A{\displaystyle A}, если A{\displaystyle A} является подмножеством множества B{\displaystyle B}.

То, что B{\displaystyle B} является надмножеством множества A{\displaystyle A}, записывают B⊃A{\displaystyle B\supset A}, т.е.
(A⊂B)⇔(B⊃A).{\displaystyle (A\subset B)\Leftrightarrow (B\supset A)\,.}

Множество всех подмножеств множества A{\displaystyle A} обозначается P(A){\displaystyle {\mathcal {P}}(A)} и называется булеаном.

Собственное подмножество

Любое множество B{\displaystyle B} является своим подмножеством. Если мы хотим исключить B{\displaystyle B} из рассмотрения, мы пользуемся понятием со́бственного подмножества, которое определяется так:

Множество A{\displaystyle A} является собственным подмножеством множества B{\displaystyle B}, если A⊂B{\displaystyle A\subset B} и A≠B{\displaystyle A\neq B}.

Пустое множество является подмножеством любого множества. Если мы вдобавок хотим исключить из рассмотрения пустое множество, мы пользуемся понятием нетривиа́льного подмножества, которое определяется так:

Множество A{\displaystyle A} является нетривиальным подмножеством множества B{\displaystyle B}, если A{\displaystyle A} является собственным подмножеством B{\displaystyle B} и A≠∅{\displaystyle A\neq \varnothing }.

Множества. Операции над множествами

Ключевые слова конспекта: множества, операции над множествами, подмножество, пересечение множеств, объединение множеств, элемент множества, числовые множества, обозначение некоторых числовых множеств.

В жизни часто приходится встречаться с различными совокупностями объектов, объединёнными в одно целое по некоторому признаку. Для обозначения этих совокупностей используются различные слова. Например, говорят: «стадо коров», «букет цветов», «команда футболистов» и т. д.

В математике в целях единообразия для обозначения совокупностей употребляется единый термин — множество. Например, говорят: множество чётных чисел, множество двузначных чисел, множество правильных дробей со знаменателем 5.

Термин «множество» употребляется и тогда, когда речь идёт о нечисловых множествах. Например, говорят о множестве диагоналей многоугольника, о множестве точек координатной плоскости, о множестве прямых, проходящих через данную точку.

Объекты или предметы, составляющие множество, называют элементами множества. Например, число 89 — элемент мнoжества двузначных чисел; точка В — элемент мнoжества вершин многоугольника ABCDE.

Множeства бывают конечные и бесконечные. Например, множество двузначных чисел — конечное множество (оно содержит 90 элементов), а множество чётных чисел — бесконечное множество.

Конечное мнoжество может содержать миллиард элементов, 2 элемента, 1 элемент или даже не содержать ни одного элемента.

Пустое множeство — это мнoжество, не содержащее ни одного элемента. Для обозначения пустого мнoжества ввели специальный знак ∅.

Конечные множeства обычно записывают с помощью фигурных скобок. Например, множество вершин пятиугольника ABCDE можно записать так: {А, В, С, D, Е}, а множество двузначных чисел, кратных 15, так: {15, 30, 45, 60, 75, 90}. В таких случаях говорят, что множество задано перечислением его элементов.

Множeства принято обозначать большими буквами латинского алфавита. Например, рассмотренные выше множества вершин пятиугольника и двузначных чисел, кратных 15, можно обозначить соответственно буквами К и L и записать так: К = {А, В, С, D, Е}; L = {15, 30, 45, 60, 75, 90}.

Для основных числовых множеств введены специальные обозначения: множество натуральных чисел обозначают буквой N (от латинского слова natural — «естественный»), множество целых чисел — буквой Z (от немецкого слова zahl — «число»), множество рациональных чисел — буквой Q (от латинского слова quotient — «отношение»).

Число -8 является элементом мнoжества Z. Иначе говорят, что число -8 принадлежит множеству Z. Это предложение записывают короче: -8 ∈ Z. Число 0,17 не принадлежит множеству N (не является элементом множества N). Для выражения этого факта принята следующая запись: 0,17 ∉ N.

В тех случаях, когда задание множества перечислением элементов невозможно (как для бесконечного множества) или громоздко (как для конечного мнoжества с большим числом элементов), множество задают описанием, указав его характеристическое свойство, т. е. свойство, которым обладают все элементы этого множeства и не обладают никакие другие объекты.

Зададим с помощью описания некоторые мнoжества. Пусть А = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}. Зададим это множество описанием, используя понятие характеристического свойства. Множeство А можно охарактеризовать как «множество всех натуральных чисел от 1 до 14 включительно», или как «множество всех натуральных чисел, меньших 15», или, используя знаки ∈ , < и букву х для произвольного элемента множества А, как «множество значений х, где х ∈ N и х < 15».

Обозначения некоторых числовых множеств

Это конспект по математике на тему «Множества. Операции над множествами». Выберите дальнейшие действия:

Перейти к следующему конспекту:
Вернуться к списку конспектов по Математике.
Проверить знания по Математике.

Операции над подмножествами

Стандартные операции
над подмножествами, естественно,
применяются в теории вероятностей и
имеют вероятностную интерпретацию.

Дополнение

Дополнение
до подмножества A
— это подмножество

т. е. дополнением
к A
является подмножество, включающее в
себя все элементарные исходы, не
содержащиеся в A.
С точки зрения теории вероятностей
подмножество A
представляет событие, которое естественно
назвать отрицание A
или не-A.
Т.е. A
в опыте не произошло
(«не наступило»).

Объединение

Объединением
двух подмножеств A
и B
является подмножество

Соответственно
и интерпретация : произошло или A
или B.

Пересечение

Пересечением
двух подмножеств : A
и B
является подмножество

Соответственно
и интерпретация : и A
и B
произошли одновременно.

Разность

Разностью
двух подмножеств A
и B
является подмножество

Соответственно
и интерпретация : A
произошло, B
— нет.

Симметричная разность

Симметричной
разностью двух подмножеств A
и B
является подмножество

Соответственно
и интерпретация : произошло только одно
из этих двух событий.

Количество элементов в подмножестве

Если количество
элементов в подмножестве A
конечно, то будем
обозначать его так

Отношения между
подмножествами

Вложение

Подмножество
В
вложено в подмножество
A,
если любой элементарный
исход, содержащийся в B
также содержится и в A.

Интерпретация:

Стрелкой
Множества,их элементы,поджмножества
будем пользоваться также и для
утверждений типа: “из A
следует B” в формулировках
определений и теорем

из
B
следует A

Множества,их элементы,поджмножества

Т.е, если
произошло B, то произошло
и A.

Несовместность

Подмножества
A
и B
называются
несовместными
(непересекающимися), если они не содержат
общих элементарных исходов.

В теории
вероятностей это означает, что A
и B
одновременно произойти не могут.

Противоположность

Подмножества
A
и B
называются
противоположными или
дополнительными друг к другу, если они
несовместны и их объединение
достоверно.

В теории
вероятностей это означает, что в опыте
обязательно произойдет одно и только
одно из этих событий.

Формулы

Для
доказательства равенства двух
подмножеств A
и B
достаточно показать, что A
вложено в B,
и что B
вложено в A

Следующие
формулы позволяют выразить одни
операции с подмножествами через
другие. Доказательства проведите
сами.

Множества,их элементы,поджмножества

Полная группа
подмножеств

Полной группой
подмножеств называется конечный набор
или счетная последовательность попарно
несовместных подмножеств
объединение которых достоверно:

В опыте обязательно
произойдет одно и только одно из этих
событий.

Любые два противоположных
подмножества образуют полную группу
подмножеств.

Если пространство
элементарных исходов конечно или счетно,
то сами элементарные исходы являются
полной группой подмножеств.

Алгебра
и сигма-алгебра

При построении
математической модели случайного
объекта необходимо не только указать
все возможные элементарные исходы
опыта, но и определить (перечислить) все
возможные события, которые могут
произойти в этом опыте. Принято следующее
определение:

Алгебра событийAэто
набор подмножеств пространства
элементарных исходов
для которого выполняются следующие
условия:

Сигма — алгебра
событийFэто
набор подмножеств пространства
элементарных исходов
для которого выполняются следующие
условия:

и для любой счетной
последовательности

Очевидно, что любая
сигма-алгебра является алгеброй, но не
наоборот.

Колмогоров показал,
что естественной математической моделью
для множества событий является
сигма-алгебра.

Очевидным примером
сигма-алгебры является набор всех
подмножеств пространства элементарных
исходов – это наибольшая сигма-алгебра,
возможная на данном пространстве
элементарных исходов.

Наименьшая (тривиальная)
сигма-алгебра это следующий набор
подмножеств

Если алгебра или
сигма-алгебра содержит событие A
, то она обязана
содержать и отрицание A.
Поэтому минимальное
число подмножеств в нетривиальной
сигма-алгебре равно 4.

Алгебры и сигма-алгебры
обозначаем жирными наклонными латинскими
буквами.

Операции над множествами

Диаграмма Венна для A∩B{\displaystyle A\cap B}

Диаграмма Венна для A∪B{\displaystyle A\cup B}

Диаграмма Венна для A∖B{\displaystyle A\setminus B}

Диаграмма Венна для A△B{\displaystyle A\triangle B}

Бинарные операции

Основные бинарные операции, определяемые над множествами:

пересечение:

A∩B:={x∣x∈A∧x∈B}{\displaystyle A\cap B:=\{x\mid x\in A\land x\in B\}}.
объединение:

A∪B:={x∣x∈A∨x∈B}{\displaystyle A\cup B:=\{x\mid x\in A\lor x\in B\}}.

Если множества A{\displaystyle A} и B{\displaystyle B} не пересекаются, то A∩B=∅{\displaystyle A\cap B=\varnothing }. Их объединение обозначают также: A+B=A∪B{\displaystyle A+B=A\cup B}.

разность:

A∖B:=A∩B¯={x∣x∈A∧x∉B}{\displaystyle A\setminus B:=A\cap {\overline {B}}=\{x\mid x\in A\land x\notin B\}}.
симметрическая разность:

A△B≡A−˙B:={\displaystyle A\triangle B\equiv A{\dot {-}}B:=}

(A∪B)∖(A∩B)=A∩B¯+A¯∩B={\displaystyle (A\cup B)\setminus (A\cap B)=A\cap {\overline {B}}+{\overline {A}}\cap B=}

={x∣(x∈A∧x∉B)∨(x∉A∧x∈B)}{\displaystyle =\{x\mid (x\in A\land x\notin B)\lor (x\notin A\land x\in B)\}}.
декартово или прямое произведение:

A×B={(a,b)∣a∈A,b∈B}{\displaystyle A\times B=\{(a,\;b)\mid a\in A,\;b\in B\}}.

Для объяснения смысла операций часто используются диаграммы Венна, на которых представлены результаты операций над геометрическими фигурами как множествами точек.

Всякая система множеств, замкнутая относительно операций объединения и пересечения, образует относительно объединения и пересечения дистрибутивную решётку.

Унарные операции

Диаграмма Венна для (A∩B)∁{\displaystyle (A\cap B)^{\complement }}

Дополнение определяется следующим образом:

A¯≡A∁:={x∣x∉A}{\displaystyle {\overline {A}}\equiv A^{\complement }:=\{x\mid x\notin A\}}.

Операция дополнения подразумевает некоторый зафиксированный универсум (универсальное множество U{\displaystyle U}, которое содержит A{\displaystyle A}), и сводится к разности множеств с этим универсумом:

A¯=U∖A{\displaystyle {\overline {A}}=U\setminus A}.

Система множеств с фиксированным универсумом, замкнутая относительно операций объединения, пересечения с введённым таким образом дополнением образует булеву алгебру.

Булеан — множество всех подмножеств:

2X≡PX:={A∣A⊂X}{\displaystyle 2^{X}\equiv {\mathcal {P}}X:=\{A\mid A\subset X\}}.

Обозначение 2X{\displaystyle 2^{X}} происходит из свойства мощности множества всех подмножеств конечного множества:

|2X|=2|X|{\displaystyle \left|2^{X}\right|=2^{|X|}}.

Булеан 2X{\displaystyle 2^{X}} порождает систему множеств с фиксированным универсумом X{\displaystyle X}, замкнутую относительно операций объединения и пересечения, то есть, образует булеву алгебру.

Приоритет операций

Последовательность выполнения операций над множествами, как и обычно, может быть задана скобками. При отсутствии скобок сначала выполняются унарные операции (дополнение), затем — пересечения, затем — объединения и разности, которые имеют одинаковый приоритет. Операции одного приоритета выполняются слева направо. При этом надо иметь в виду, что в отличие от арифметических сложения и вычитания, для которых верно, что (a+b)−c=a+(b−c){\displaystyle (a+b)-c=a+(b-c)}, для аналогичных операций над множествами это неверно. Например, если A={1,3},B={1,2},C={2,3},{\displaystyle A=\{1,3\},B=\{1,2\},C=\{2,3\},} то (A∪B)∖C={1},{\displaystyle (A\cup B)\setminus C=\{1\},} но, в то же время, A∪(B∖C)={1,3}{\displaystyle A\cup (B\setminus C)=\{1,3\}}.

Действия над множествами. Диаграммы Венна

Диаграммы Венна (по аналогии с кругами Эйлера) – это схематическое изображение действий с множествами. Опять же предупреждаю, что я рассмотрю не все операции:

1) Пересечение множеств характеризуется логической связкой И и обозначается значком

Пересечением множеств и называется множество , каждый элемент которого принадлежит и множеству , и множеству . Грубо говоря, пересечение – это общая часть множеств:
Так, например, для множеств :

Если у множеств нет одинаковых элементов, то их пересечение пусто. Такой пример нам только что встретился при рассмотрении числовых множеств:

Множества рациональных и иррациональных чисел можно схематически изобразить двумя непересекающимися кругами.

Операция пересечения применима и для бОльшего количества множеств, в частности в Википедии есть хороший .

2) Объединение множеств характеризуется логической связкой ИЛИ и обозначается значком

Объединением множеств и называется множество , каждый элемент которого принадлежит множеству или множеству :

Запишем объединение множеств : – грубо говоря, тут нужно перечислить все элементы множеств и , причём одинаковые элементы (в данном случае единица на пересечении множеств) следует указать один раз.

Но множества, разумеется, могут и не пересекаться, как это имеет место быть с рациональными и иррациональными числами:

В этом случае можно изобразить два непересекающихся заштрихованных круга.

Операция объединения применима и для бОльшего количества множеств, например, если , то:

, при этом числа вовсе не обязательно располагать в порядке возрастания (это я сделал исключительно из эстетических соображений). Не мудрствуя лукаво, результат можно записать и так:

3) Разностью множеств и называют множество , каждый элемент которого принадлежит множеству и не принадлежит множеству :
Разность читаются следующим образом: «а без бэ». И рассуждать можно точно так же: рассмотрим множества . Чтобы записать разность , нужно из множества «выбросить» все элементы, которые есть во множестве :

Пример с числовыми множествами: – здесь из множества целых чисел исключены все натуральные, да и сама запись так и читается: «множество целых чисел без множества натуральных».

Зеркально: разностью множеств и называют множество , каждый элемент которого принадлежит множеству и не принадлежит множеству :
Для тех же множеств – из множества «выброшено» то, что есть во множестве .

А вот эта разность оказывается пуста: . И в самом деле – если из множества натуральных чисел исключить целые числа, то, собственно, ничего и не останется 🙂

Кроме того, иногда рассматривают симметрическую разность , которая объединяет оба «полумесяца»: – иными словами, это «всё, кроме пересечения множеств».

4) Декартовым (прямым) произведением множеств и называется множество всех упорядоченных пар , в которых элемент , а элемент

Запишем декартово произведение множеств : – перечисление пар удобно осуществлять по следующему алгоритму: «сначала к 1-му элементу множества последовательно присоединяем каждый элемент множества , затем ко 2-му элементу множества присоединяем каждый элемент множества , затем к 3-му элементу множества присоединяем каждый элемент множества »:

Зеркально: декартовым произведением множеств и называется множество всех упорядоченных пар , в которых . В нашем примере: – здесь схема записи аналогична: сначала к «минус единице» последовательно присоединяем все элементы множества , затем к «дэ» – те же самые элементы:

Но это чисто для удобства – и в том, и в другом случае пары можно перечислить в каком угодно порядке – здесь важно записать все возможные пары. А теперь гвоздь программы: декартово произведение – это есть не что иное, как множество точек нашей родной декартовой системы координат

А теперь гвоздь программы: декартово произведение – это есть не что иное, как множество точек нашей родной декартовой системы координат .

Задание для самостоятельного закрепления материала:

Выполнить операции , если:

1) ;
2)

Множество удобно расписать перечислением его элементов.

И пунктик с промежутками действительных чисел:

Напоминаю, что квадратная скобка означает включение числа в промежуток, а круглая – его невключение, то есть «минус единица» принадлежит множеству , а «тройка» не принадлежит множеству . Постарайтесь разобраться, что представляет собой декартово произведение данных множеств. Если возникнут затруднения, выполните чертёж 😉

Краткое решение задачи в конце урока.