Пустое множество

Задания для самостоятельного решения

Задание 1. Найдите пересечение и объединение следующих множеств:

А = { 1, 2, 5 }B = { 3, 4, 5 }

Решение:

A ∩ B = { 5 }A ∪ B = { 1, 2, 3, 4, 5 }

Задание 2. Найдите пересечение и объединение следующих множеств:

А = { −3, −2, −1, 0, 1, 2 }B = { 1, 2, 3, 4, 5 }

Решение:

A ∩ B = { 1, 2 }A ∪ B = { −3, −2, −1, 0, 1, 2, 3, 4, 5 }

Задание 3. Найдите пересечение и объединение следующих множеств:

А = { 1, 2, 3 }B = { 3, 4 }

Решение:

A ∩ B = { 3 }A ∪ B = { 1, 2, 3, 4 }

Задание 4. Найдите пересечение и объединение следующих числовых промежутков:

Решение:

= (0; 7) =

Задание 5. Найдите пересечение и объединение следующих числовых промежутков:
(−∞; 3] и [−2; 1)

Решение:

(−∞; 3] ∩ ∪

Задание 6. Найдите пересечение и объединение следующих числовых промежутков:
(3; +∞) и [2; +∞)

Решение:

(3; +∞) ∩ и (−2; 4]

Решение:

∩ (−2; 4] = (−2; −1] ∪ (−2; 4] =

Задание 8. Решите неравенство:

Решение:

Задание 9. Решите неравенство:

Решение:

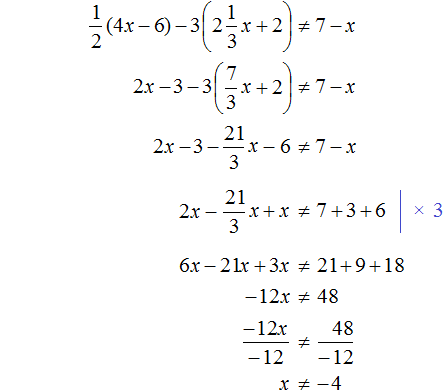
Задание 10. Решите совокупность неравенств:

Решение:

Задание 11. Решите совокупность неравенств:

Решение:

Задание 12. Решите совокупность неравенств:

Решение:

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Свойства пустого множества

• Ни одно множество не является элементом пустого множества. Иначе говоря, ∀a (a∉∅){\displaystyle \forall a\ (a\notin \varnothing )} и, в частности, ∅∉∅{\displaystyle \varnothing \notin \varnothing }.
• Пустое множество является подмножеством любого множества. Иначе говоря, ∀a (∅⊆a){\displaystyle \forall a\ (\varnothing \subseteq a)} и, в частности, ∅⊆∅{\displaystyle \varnothing \subseteq \varnothing }.
• Объединение пустого множества с любым множеством равно последнему . Иначе говоря,∀a (∅∪a=a){\displaystyle \forall a\ (\varnothing \cup a=a)} и, в частности, ∅∪∅=∅{\displaystyle \varnothing \cup \varnothing =\varnothing }.
• Пересечение пустого множества с любым множеством равно пустому множеству. Иначе говоря, ∀a (∅∩a=∅){\displaystyle \forall a\ (\varnothing \cap a=\varnothing )} и, в частности, ∅∩∅=∅{\displaystyle \varnothing \cap \varnothing =\varnothing }.
• Пересечение любого множества с его дополнением равно пустому множеству. Иначе говоря, ∀a (a∩a¯=∅){\displaystyle \forall a\ (a\cap {\overline {a}}=\varnothing )}.
• Исключение пустого множества из любого множества равно последнему . Иначе говоря, ∀a (a∖∅=a){\displaystyle \forall a\ (a\setminus \varnothing =a)} и, в частности, ∅∖∅=∅{\displaystyle \varnothing \setminus \varnothing =\varnothing }.
• Исключение любого множества из пустого множества равно пустому множеству. Иначе говоря, ∀a (∅∖a=∅){\displaystyle \forall a\ (\varnothing \setminus a=\varnothing )} и, в частности, ∅∖∅=∅{\displaystyle \varnothing \setminus \varnothing =\varnothing }.
• Симметрическая разность пустого множества с любым множеством равна последнему . Иначе говоря, ∀a (∅△a=a ∧ a△∅=a){\displaystyle \forall a\ (\varnothing \triangle a=a\ \land \ a\triangle \varnothing =a)} и, в частности, ∅△∅=∅{\displaystyle \varnothing \triangle \varnothing =\varnothing }
• Декартово произведение пустого множества на любое множество равно пустому множеству. Иначе говоря, ∀a (∅×a=∅ ∧ a×∅=∅){\displaystyle \forall a\ (\varnothing \times a=\varnothing \ \land \ a\times \varnothing =\varnothing )} и, в частности, ∅×∅=∅{\displaystyle \varnothing \times \varnothing =\varnothing }.
• Пустое множество — транзитивно. Иначе говоря, Trans(∅){\displaystyle \mathrm {Trans} (\varnothing )}, где Trans(∅)⇔∀b (b∈∅→b⊆∅){\displaystyle \mathrm {Trans} (\varnothing )\Leftrightarrow \forall b\ (b\in \varnothing \to b\subseteq \varnothing )}.
• Пустое множество — ординал. Иначе говоря, Ord(∅){\displaystyle \mathrm {Ord} (\varnothing )}, где Ord(∅)⇔Trans(∅) ∧ ∀b (b∈∅→Trans(b)){\displaystyle \mathrm {Ord} (\varnothing )\Leftrightarrow \mathrm {Trans} (\varnothing )\ \land \ \forall b\ (b\in \varnothing \to \mathrm {Trans} (b))}.
• Мощность пустого множества равна нулю. Иначе говоря, |∅|={\displaystyle |\varnothing |=0}.
• Мера пустого множества равна нулю. Иначе говоря, μ(∅)={\displaystyle \mu (\varnothing )=0}

Обозначения пустого множества

Символы со сходным начертанием: Ø · ø · ⌀

Обычно пустое множество обозначают как ∅{\displaystyle \varnothing }, ∅{\displaystyle \emptyset } или {}{\displaystyle \{\}}.

Реже пустое множество обозначают одним из следующих символов: {\displaystyle 0} и Λ{\displaystyle \Lambda }.

В Юникоде имеется специальный символ «пустое множество» (U+2205, ∅).

Символы ∅{\displaystyle \varnothing } и ∅{\displaystyle \emptyset } введены в употребление группой Бурбаки (в частности, Андре Вейлем) в 1939 году.

Символ ∅{\displaystyle \varnothing } идентичен букве Ø в датско-норвежском алфавите.

Включение множеств

Множество

называется подмножеством
множества
,
если любой элемент множества

является элементом множества
.

Этот факт записывается
следующим образом:

или

Знак

называется знаком
включения.

Примеры.

1)
Пустое множество

есть часть любого множества
.1

2)
,
то есть множество натуральных чисел
есть часть множества целых неотрицательных
чисел, которое, в свою очередь, содержится
во множестве целых чисел и т.д.

3)
Любое слово, рассматриваемое как
множество букв, является подмножеством
алфавита соответствующего языка.

Примеры наиболее
часто употребляемых числовых множеств

1)
–
сегмент
или замкнутый отрезок;

2)
–
интервал
или открытый отрезок,
(обозначается
также);

3

полуинтервалы
или

полуоткрытые
отрезки;

)
–

4

бесконечные
интервалы и

полуинтервалы.

)

–

Этим числовым
множествам соответствуют отрезки на
числовой оси (с включенными в них или
исключенными из них концами).

Отображение множеств

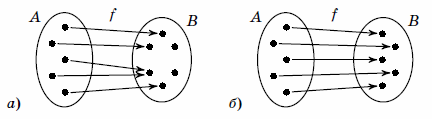
Отображение множества  во множество – это правило, по которому каждому элементу множества  ставится в соответствие элемент (или элементы) множества . В том случае если в соответствие ставится единственный элемент, то данное правило называется однозначно определённой функцией или просто функцией.

Функцию, как многие знают, чаще всего обозначают буквой  – она ставит в соответствие каждому элементу  единственное значение , принадлежащее множеству .

Ну а сейчас я снова побеспокою множество  студентов 1-го ряда и предложу им 6 тем для рефератов (множество ):

 Векторы  Матрицы  Определители Комплексные числа (о, да!)  Теория пределов Что такое производная?

Установленное (добровольно или принудительно =)) правило  ставит в соответствие каждому студенту  множества  единственную тему реферата  множества .

…а вы, наверное, и представить себе не могли, что сыграете роль аргумента функции =) =)

Элементы множества  образуют область определения функции (обозначается через ), а элементы множества  – область значений функции (обозначается через ).

Построенное отображение множеств имеет очень важную характеристику: оно является взаимно-однозначным или биективным (биекцией). В данном примере это означает, что каждому студенту поставлена в соответствие одна уникальная тема реферата, и обратно – за каждой темой реферата закреплён один и только один студент.

Однако не следует думать, что всякое отображение биективно. Если на 1-й ряд (к множеству ) добавить 7-го студента, то взаимно-однозначное соответствие пропадёт – либо один из студентов останется без темы (отображения не будет вообще), либо какая-то тема достанется сразу двум студентам. Обратная ситуация: если к множеству  добавить седьмую тему, то взаимнооднозначность отображения тоже будет утрачена –  одна из тем останется невостребованной.

Уважаемые студенты на 1-м ряду, не расстраивайтесь – остальные 20 человек после пар пойдут прибирать территорию университета от осенней листвы. Завхоз выдаст двадцать голиков, после чего будет установлено взаимно-однозначное соответствие между основной частью группы и мётлами…, а Вольдемар ещё и в магазин сбегать успеет =)

Теперь разберёмся со «школьной» функцией одной переменной. Пожалуйста, загляните на страницу Функции и графики (отроется на соседней вкладке), и в Примере 1 найдите график линейной функции .

Задумаемся, что это такое? Это правило , которое каждому элементу  области определения (в данном случае это все значения «икс») ставит в соответствие единственное значение . С теоретико-множественной точки зрения, здесь происходит отображение множества действительных чисел во множество действительных чисел:

Первое множество мы по-обывательски называем «иксами» (независимая переменная или аргумент), а второе – «игреками» (зависимая переменная или функция).

Далее взглянем на старую знакомую параболу  . Здесь правило  каждому значению «икс» ставит в соответствие его квадрат, и имеет место отображение:

Итак, что же такое функция одной переменной? Функция одной переменной  – это правило , которое каждому значению независимой переменной  из области определения ставит в соответствие одно и только одно значение .

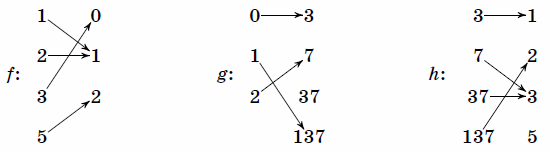
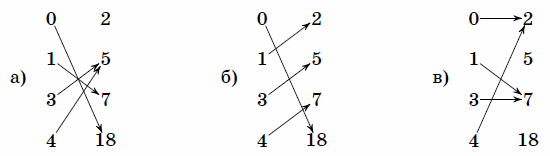
Как уже отмечалось в примере со студентами, не всякая функция является взаимно-однозначной. Так, например, у функции  каждому «иксу» области определения  соответствует свой уникальный «игрек», и наоборот – по любому значению «игрек» мы сможем однозначно восстановить «икс». Таким образом, это биективная функция.

! На всякий случай ликвидирую возможное недопонимание: моя постоянная оговорка об области определения не случайна! Функция может быть определена далеко не при всех «икс», и, кроме того, может быть взаимно-однозначной и в этом случае. Типичный пример:  

А вот у квадратичной функции не наблюдается ничего подобного, во-первых: – то есть, различные значения «икс» отобразились в одно и то же значение «игрек»; и во-вторых: если кто-то вычислил значение функции и сообщил нам, что , то не понятно – этот «игрек» получен при  или при ? Что и говорить, взаимной однозначностью здесь даже не пахнет.

Задание 2: просмотреть графики основных элементарных функций и выписать на листок биективные функции. Список для сверки в конце этого урока.

История понятия

Основы теории конечных и бесконечных множеств были заложены Бернардом Больцано, который сформулировал некоторые из её принципов.

С 1872 года по 1897 год (главным образом в 1872—1884 годы) Георг Кантор опубликовал ряд работ, в которых были систематически изложены основные разделы теории множеств, включая теорию точечных множеств и теорию трансфинитных чисел (кардинальных и порядковых). В этих работах он не только ввёл основные понятия теории множеств, но и обогатил математику рассуждениями нового типа, которые применил для доказательства теорем теории множеств, в частности впервые к бесконечным множествам. Поэтому общепризнано, что теорию множеств создал Георг Кантор. В частности определил множество как «единое имя для совокупности всех объектов, обладающих данным свойством».
Эти объекты назвал элементами множества.
Множество объектов, обладающих свойством A(x){\displaystyle A(x)}, обозначил {x∣A(x)}{\displaystyle \{x\mid A(x)\}}.
Если некоторое множество Y={x∣A(x)}{\displaystyle Y=\{x\mid A(x)\}}, то A(x){\displaystyle A(x)} назвал характеристическим свойством множества Y{\displaystyle Y}.

Эта концепция привела к парадоксам, в частности, к парадоксу Рассела.

Так как теория множеств фактически используется как основание и язык всех современных математических теорий в 1908 году теория множеств была аксиоматизирована независимо Бертраном Расселом и Эрнстом Цермело. В дальнейшем многие исследователи пересматривали и изменяли обе системы, в основном сохранив их характер. До сих пор они всё ещё известны как теория типов Рассела и теория множеств Цермело. Впоследствии теорию множеств Кантора стало принято называть наивной теорией множеств, а вновь построенную — аксиоматической теорией множеств.

В практике, сложившейся с середины XX века множество определяется как модель, удовлетворяющая аксиомам ZFC (аксиомы Цермело — Френкеля с аксиомой выбора).
При таком подходе в некоторых математических теориях возникают совокупности объектов, которые не являются множествами.
Такие совокупности называются классами (различных порядков).

Решение неравенств, содержащих знак ≠

Некоторые неравенства содержат знак ≠ (не равно). Например, 2x ≠ 8. Чтобы решить такое неравенство, нужно найти множество значений переменной x, при которых левая часть не равна правой части.

Решим неравенство 2x ≠ 8. Разделим обе части данного неравенства на 2, тогда получим:

Получили равносильное неравенство x ≠ 4. Решением этого неравенства является множество всех чисел, не равных 4. То есть если мы подставим в неравенство x ≠ 4 любое число, которое не равно 4, то получим верное неравенство.

Подставим, например, число 5

5 ≠ 4 — верное неравенство, поскольку 5 не равно 4

Подставим 7

7 ≠ 4 — верное неравенство, поскольку 7 не равно 4

И поскольку неравенство x ≠ 4 равносильно исходному неравенству 2x ≠ 8, то решения неравенства x ≠ 4 будут подходить и к неравенству 2x ≠ 8. Подставим те же тестовые значения 5 и 7 в неравенство 2x ≠ 8.

2 × 5 ≠ 8

2 × 7 ≠ 8

Изобразим множество решений неравенства x ≠ 4 на координатной прямой. Для этого выколем точку 4 на координатной прямой, а всю оставшуюся область с обеих сторон выделим штрихами:

Теперь запишем ответ в виде числового промежутка. Для этого воспользуемся объединением множеств. Любое число, являющееся решением неравенства 2x ≠ 8 будет принадлежать либо промежутку (−∞; 4) либо промежутку (4; +∞). Так и записываем, что значения переменной x принадлежат (−∞; 4) или (4; +∞). Напомним, что для слова «или» используется символ ∪

x ∈ (−∞; 4) ∪ (4; +∞)

В этом выражении говорится, что значения, принимаемые переменной x, принадлежат промежутку (−∞; 4) или промежутку (4; +∞).

Неравенства, содержащие знак ≠, также можно решать, как обычные уравнения. Для этого знак ≠ заменяют на знак =. Тогда получится обычное уравнение. В конце решения найденное значение переменной x нужно исключить из множества решений.

Решим предыдущее неравенство 2x ≠ 8, как обычное уравнение. Заменим знак ≠ на знак равенства =, получим уравнение 2x = 8. Разделим обе части данного уравнения на 2, получим x = 4.

Видим, что при x, равном 4, уравнение обращается в верное числовое равенство. При других значениях равенства соблюдаться не будет. Эти другие значения нас и интересуют. А для этого достаточно исключить найденную четвёрку из множества решений.

Пример 2. Решить неравенство 3x − 5 ≠ 1 − 2x

Перенесем −2x из правой части в левую часть, изменив знак, а −5 из левой части перенесём в правую часть, опять же изменив знак:

Приведем подобные слагаемые в обеих частях:

Разделим обе части получившегося неравенства на 5

Решением неравенства x ≠ 1,2 является множество всех чисел, не равных 1,2.

Изобразим множество решений неравенства x ≠ 1,2 на координатной прямой и запишем ответ в виде числового промежутка:

x ∈ (−∞; 1,2) ∪ (1,2; +∞)

В этом выражении говорится, что значения, принимаемые переменной x принадлежат промежутку (−∞; 1,2) или промежутку (1,2; +∞)

Действия над множествами. Диаграммы Венна

Диаграммы Венна (по аналогии с кругами Эйлера) – это схематическое изображение действий с множествами. Опять же предупреждаю, что я рассмотрю не все операции:

1) Пересечение множеств характеризуется логической связкой И и обозначается значком

Пересечением множеств  и  называется множество , каждый элемент которого принадлежит и множеству , и множеству . Грубо говоря, пересечение – это общая часть множеств:
Так, например, для множеств :

Если у множеств нет одинаковых элементов, то их пересечение пусто. Такой пример нам только что встретился при рассмотрении числовых множеств:

Множества рациональных и иррациональных чисел можно схематически изобразить двумя непересекающимися кругами.

Операция пересечения применима и для бОльшего количества множеств, в частности в Википедии есть хороший .

2) Объединение множеств характеризуется логической связкой ИЛИ и обозначается значком

Объединением множеств  и  называется множество , каждый элемент которого принадлежит множеству  или множеству :

Запишем объединение множеств : – грубо говоря, тут нужно перечислить все элементы множеств  и , причём одинаковые элементы (в данном случае единица на пересечении множеств) следует указать один раз.

Но множества, разумеется, могут и не пересекаться, как это имеет место быть с рациональными и иррациональными числами:

В этом случае можно изобразить два непересекающихся заштрихованных круга.

Операция объединения применима и для бОльшего количества множеств, например, если  , то:

, при этом числа вовсе не обязательно располагать в порядке возрастания (это я сделал исключительно из эстетических соображений). Не мудрствуя лукаво, результат можно записать и так:

3) Разностью множеств  и  называют множество , каждый элемент которого принадлежит множеству  и не принадлежит множеству :
Разность  читаются следующим образом: «а без бэ». И рассуждать можно точно так же: рассмотрим множества . Чтобы записать разность , нужно из множества  «выбросить» все элементы, которые есть во множестве :

Пример с числовыми множествами: – здесь из множества целых чисел исключены все натуральные, да и сама запись  так и читается: «множество целых чисел без множества натуральных».

Зеркально: разностью множеств  и  называют множество , каждый элемент которого принадлежит множеству  и не принадлежит множеству :
Для тех же множеств  – из множества  «выброшено» то, что есть во множестве .

А вот эта разность оказывается пуста: . И в самом деле – если из множества натуральных чисел исключить целые числа, то, собственно, ничего и не останется 🙂

Кроме того, иногда рассматривают симметрическую разность , которая объединяет оба «полумесяца»: – иными словами, это «всё, кроме пересечения множеств».

4) Декартовым (прямым) произведением множеств  и  называется множество  всех упорядоченных пар , в которых элемент , а элемент

Запишем декартово произведение множеств : – перечисление пар удобно осуществлять по следующему алгоритму: «сначала к 1-му элементу множества  последовательно присоединяем каждый элемент множества , затем ко 2-му элементу множества  присоединяем каждый элемент множества , затем к 3-му элементу множества  присоединяем каждый элемент множества »:

Зеркально: декартовым произведением множеств  и  называется множество  всех упорядоченных пар , в которых . В нашем примере: – здесь схема записи аналогична: сначала к «минус единице» последовательно присоединяем все элементы множества , затем к «дэ» – те же самые элементы:

Но это чисто для удобства – и в том, и в другом случае пары можно перечислить в каком угодно порядке – здесь важно записать все возможные пары. А теперь гвоздь программы: декартово произведение  – это есть не что иное, как множество точек  нашей родной декартовой системы координат

А теперь гвоздь программы: декартово произведение  – это есть не что иное, как множество точек  нашей родной декартовой системы координат .

Задание для самостоятельного закрепления материала:

Выполнить операции , если:

1) ;
2)

Множество  удобно расписать перечислением его элементов.

И пунктик с промежутками действительных чисел:

3)

Напоминаю, что квадратная скобка означает включение числа в промежуток, а круглая – его невключение, то есть «минус единица» принадлежит множеству , а  «тройка» не принадлежит множеству . Постарайтесь разобраться, что представляет собой декартово произведение данных множеств. Если возникнут затруднения, выполните чертёж 😉

Краткое решение задачи в конце урока.

Мощность

Мощность множества — характеристика множества, обобщающая понятие о количестве элементов для конечного множества таким образом, чтобы множества, между которыми возможно установление биекции были равномощны. Обозначается |A|{\displaystyle |A|} или ♯A{\displaystyle \sharp A}. Мощность пустого множества равна нулю, для конечных множеств мощность совпадает с числом элементов, для бесконечных множеств вводятся специальные кардинальные числа, соотносящиеся друг с другом по принципу включения (если A⊆B{\displaystyle A\subseteq B}, то |A|⩽|B|{\displaystyle |A|\leqslant |B|}) и распространением свойства мощности булеана конечного множества: |2A|=2|A|{\displaystyle |2^{A}|=2^{|A|}} на случай бесконечных множеств (само обозначение 2A{\displaystyle 2^{A}} мотивировано этим свойством).

Наименьшая бесконечная мощность обозначается ℵ{\displaystyle \aleph _{0}}, это мощность счётного множества. Мощность континуума, биективного булеану счётного множества обозначается c{\displaystyle {\mathfrak {c}}} или 2ℵ{\displaystyle 2^{\aleph _{0}}}. Континуум-гипотеза — предположение о том, что между счётной мощностью и мощностью континуума нет промежуточных мощностей.

§3. Законы сложения, умножения и вычитания.

Операции сложения,
умножения и вычитания множеств имеют
много общих свойств с операциями
сложения, умножения и вычитания чисел.

В этом параграфе
приведем важнейшие из них, а также
докажем несколько теорем, указывающих
на различие между алгеброй множеств и
арифметикой.

Законы
коммутативности:

1. (1)

Эти законы
непосредственно следуют из законов
коммутативности для дизъюнкции и
конъюнкции.

Законы
ассоциативности:

1. (2)

Доказательство
основано на законах ассоциативности
для дизъюнкции и конъюнкции.

Отсюда следует,
что при сложении или умножении конечного
числа множеств можно опускать скобки,
указывающие порядок действий.

Например: .

Законы
дистрибутивности:

1. (3)

Доказательство
основано на законах дистрибутивности
для дизъюнкции и конъюнкции.

Например:

Законы
идемпотентности:

1. (4)

2. .

Доказательства
получаются непосредственно из законов
идемпотентности
,
.

Докажем несколько
законов для операции вычитания.

(5)

сравнить:

В самом деле, из
формул (1) и (2) §2 следует:

.

Откуда по закону
дистрибутивности дизъюнкции относительно
конъюнкции имеем:

.

Поскольку ,сомножитель И
можно в произведении опустить. Таким
образом получим:

,

что и доказывает
формулу (5).

Из этой формулы
следует, что вычитание множеств не
является операцией, обратной сложению,
как в обычной алгебре чисел. Если,
например, А
— множество четных чисел, а В
— множество чисел, делящихся на 3, то
множество
отличается отВ,
потому что оно содержит все четные
числа.

Но если
,
то (согласно (5) и (5) §3),
как в арифметике.

Далее,

(6).

⇋

В самом деле:

Закон дистрибутивности
умножения относительно вычитания имеет
вид:

(7).

Он получается из
эквивалентности

.

Из равенства (7)
следует, что

.

Законы де
Моргана
в алгебре множеств имеют вид:

(8)

Доказательство
основано на законах де Моргана алгебры
высказываний.

Приведем
без доказательств следующие равенства:

B

A

C

(9)

B

A

(10)

C

B

A

C

(11)

(12)

(13)

(14)

Импликации (12) —
(14) иллюстрируют аналогию между отношением
включения и отношением «не больше» в
арифметике.

Из (14) легко следует:

(15),

которая имеет свой
аналог в арифметике:

.

Множества. Операции над множествами

Ключевые слова конспекта: множества, операции над множествами, подмножество, пересечение множеств, объединение множеств, элемент множества, числовые множества, обозначение некоторых числовых множеств.

В жизни часто приходится встречаться с различными совокупностями объектов, объединёнными в одно целое по некоторому признаку. Для обозначения этих совокупностей используются различные слова. Например, говорят: «стадо коров», «букет цветов», «команда футболистов» и т. д.

В математике в целях единообразия для обозначения совокупностей употребляется единый термин — множество. Например, говорят: множество чётных чисел, множество двузначных чисел, множество правильных дробей со знаменателем 5.

Термин «множество» употребляется и тогда, когда речь идёт о нечисловых множествах. Например, говорят о множестве диагоналей многоугольника, о множестве точек координатной плоскости, о множестве прямых, проходящих через данную точку.

Объекты или предметы, составляющие множество, называют элементами множества. Например, число 89 — элемент мнoжества двузначных чисел; точка В — элемент мнoжества вершин многоугольника ABCDE.

Множeства бывают конечные и бесконечные. Например, множество двузначных чисел — конечное множество (оно содержит 90 элементов), а множество чётных чисел — бесконечное множество.

Конечное мнoжество может содержать миллиард элементов, 2 элемента, 1 элемент или даже не содержать ни одного элемента.

Пустое множeство — это мнoжество, не содержащее ни одного элемента. Для обозначения пустого мнoжества ввели специальный знак ∅.

Конечные множeства обычно записывают с помощью фигурных скобок. Например, множество вершин пятиугольника ABCDE можно записать так:  {А, В, С, D, Е},  а множество двузначных чисел, кратных 15, так: {15, 30, 45, 60, 75, 90}.  В таких случаях говорят, что множество задано перечислением его элементов.

Множeства принято обозначать большими буквами латинского алфавита. Например, рассмотренные выше множества вершин пятиугольника и двузначных чисел, кратных 15, можно обозначить соответственно буквами К и L и записать так: К = {А, В, С, D, Е};  L = {15, 30, 45, 60, 75, 90}.

Для основных числовых множеств введены специальные обозначения: множество натуральных чисел обозначают буквой N (от латинского слова natural — «естественный»), множество целых чисел — буквой Z (от немецкого слова zahl — «число»), множество рациональных чисел — буквой Q (от латинского слова quotient — «отношение»).

Число -8 является элементом мнoжества Z. Иначе говорят, что число -8 принадлежит множеству Z. Это предложение записывают короче: -8 ∈ Z. Число 0,17 не принадлежит множеству N (не является элементом множества N). Для выражения этого факта принята следующая запись: 0,17 ∉ N.

В тех случаях, когда задание множества перечислением элементов невозможно (как для бесконечного множества) или громоздко (как для конечного мнoжества с большим числом элементов), множество задают описанием, указав его характеристическое свойство, т. е. свойство, которым обладают все элементы этого множeства и не обладают никакие другие объекты.

Зададим с помощью описания некоторые мнoжества.  Пусть А = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}. Зададим это множество описанием, используя понятие характеристического свойства. Множeство А можно охарактеризовать как «множество всех натуральных чисел от 1 до 14 включительно», или как «множество всех натуральных чисел, меньших 15», или, используя знаки ∈ , < и букву х для произвольного элемента множества А, как «множество значений х, где х ∈ N и х < 15».

Обозначения некоторых числовых множеств

Это конспект по математике на тему «Множества. Операции над множествами». Выберите дальнейшие действия:

• Перейти к следующему конспекту: 
• Вернуться к списку конспектов по Математике.
• Проверить знания по Математике.

Часть вторая. Краткий обзор операций, обозначений и диаграмм Венна.

языкаAA — это множество с элементами «1», «2» и «3»
«1» — элемент множества AAA = {1,2,3}1ABCB = {3,A,B,C,D,E}C = {1,2}самом левомОперации: пересечение (intersection) — множество элементов, принадлежащих множеству A и множеству B;
объединение (union) — множество элементов, принадлежащих множеству A или множеству B;
подмножество (subset) — C является подмножеством A, множество C включено во множество A;
собственное (истинное) подмножество — C является подмножеством A, но C не равно A;
относительное дополнение (relative complement) — множество элементов, принадлежащих к A и не к B.относительноеA и не Bобозначить всё

Универсальное множество — пустое множество

генеральной совокупностинекоторымуниверсальное множествовсеUAUдополнениеAAUAUнеAдополнением множества BBAнулевое или пустоеединственное

Диаграммы Венна и остальное

Объединение (union), пересечение (intersection), относительное дополнение (relative complement), симметрическая разность (symmetric difference), собственное множество (proper subset), абсолютное дополнение (universal дополнение).симметрической разностидизъюнктивным объединениемнаходятся в любом из множеств, но не входят в их пересечениемощности (кардинального числа)

Спорт

Некоторые виды множеств и сходных объектов

Специальные множества

• Пустое множество — множество, не содержащее ни одного элемента.
• Универсальное множество (универсум) — множество, содержащее все мыслимые объекты. В связи с парадоксом Рассела данное понятие трактуется в настоящее время как «множество, включающее все множества, участвующие в рассматриваемой задаче».

Сходные объекты

• Кортеж (в частности, упорядоченная пара) — упорядоченная совокупность конечного числа именованных объектов. Записывается внутри круглых или угловых скобок, а элементы могут повторяться.
• Мультимножество (в теории сетей Петри называется «комплект») — множество с кратными элементами.
• Пространство — множество с некоторой дополнительной структурой.
• Вектор — элемент линейного пространства, содержащий конечное число элементов некоторого поля в качестве координат. Порядок имеет значение, элементы могут повторяться.
• Последовательность — функция одного натурального переменного. Представляется как бесконечный набор элементов (не обязательно различных), порядок которых имеет значение.
• Нечёткое множество — математический объект, подобный множеству, принадлежность которому задаётся не отношением, а функцией. Иными словами, относительно элементов нечёткого множества можно говорить «в какой мере» они в него входят, а не просто, входят они в него или нет.

По иерархии

• Множество множеств (в частности, булеан — множество всех подмножеств данного множества).
• Подмножество
• Надмножество