Идеальный газ

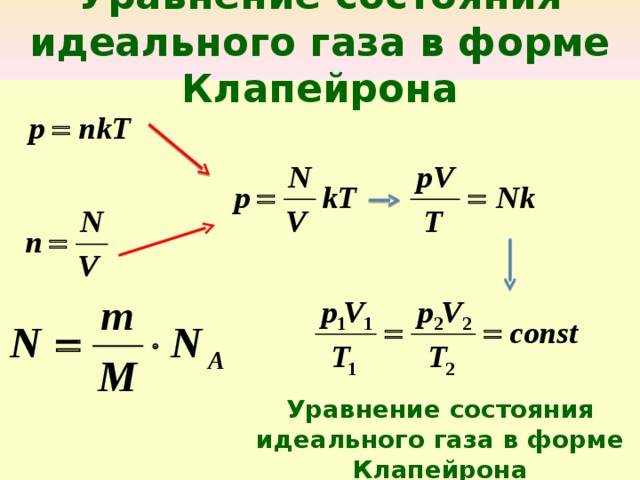
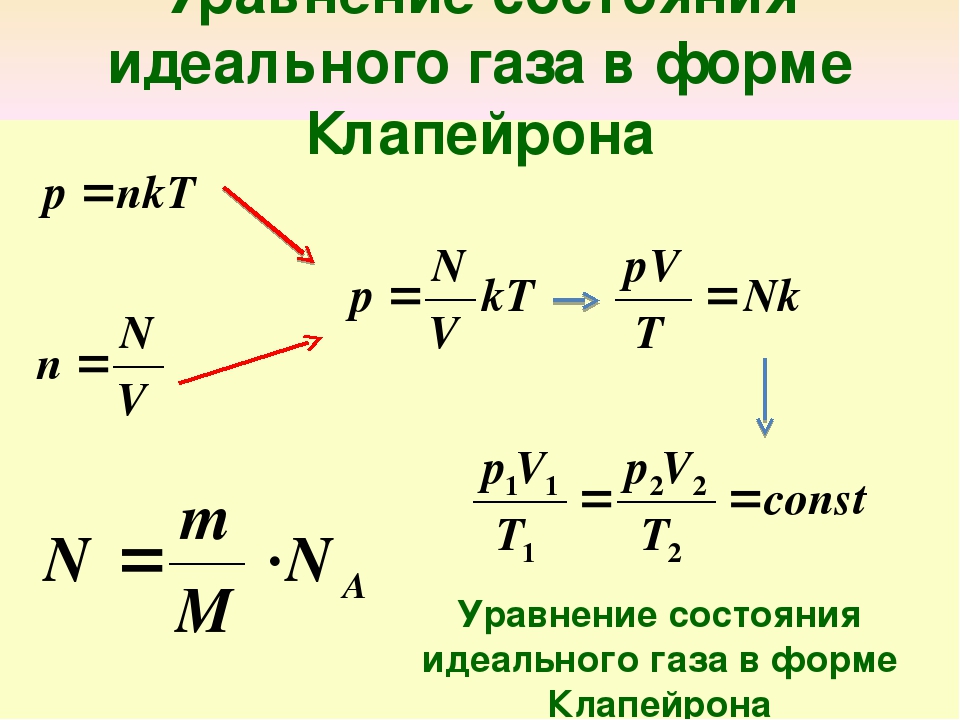
Уравнение положения идеального газа с учетом температуры

Физик Больцман утверждает, что средний показатель кинетической энергии частицы пропорционален абсолютному показателю температуры. Ек = 3/₂ кТ, где к = 1,38∙10-23, Т — температура. Работа идеального газа будет равна: Р = NkT/V, где N — количество молекул, V — объем сосуда. Если к этому показателю добавить концентрацию n = N/V, то вышеприведенная формула будет иметь такой вид: p = nkT. Эти два уравнения имеют различные формы записи, но они связывают для идеального газа давление, объем и температуру. Эти вычисления можно применять как к чистым газам, так и к их смесям. В последнем варианте под n нужно понимать все число молекул веществ, их суммарную концентрацию или полное количество молей в веществе.

Границы применения модели

Иеальный газ рассматривается в зависимости от поставленных задач. Если перед исследователем поставлена задача определить зависимость между температурой, объемом и давлением, то идеальным можно считать такое состояние вещества, при котором у газа наблюдается высокая точность до давлений, измеряемых несколькими десятками атмосфер. Но в случае изучения фазового перехода, например, испарения и конденсации, процесса достижения равновесия в газе, рассматриваемую модель нельзя применять даже при очень маленьком давлении. Давление газа на стенку пробирки происходит при хаотическом ударении молекул о стекло. Когда такие удары часты, организм человека может уловить эти изменения как непрерывное воздействие.

Температура

Вычислив только давление газа на стенки сосуда, нельзя определить средний показатель кинетической энергии его частиц.

Причем этого нельзя сделать ни для отдельной молекулы, ни для их концентрации. Поэтому для измерения параметров газа необходимо определять еще одну величину. Ею выступает температура, которая также связана с кинетической энергией молекул. Такой показатель выступает скалярной физической величиной. Температура описывает термодинамическое равновесие. В таком состоянии не происходит изменение параметров на микроуровне. Температура измеряется как отклонение от нулевого значения. Она характеризует насыщенность хаотического движения наименьших частиц газа. Она измеряется средним значением их кинетической энергии. Определяется этот показатель при помощи термометров в градусах различных отметок. Существует термодинамическая абсолютная шкала (Кельвина) и эмпирические ее разновидности. Они отличаются начальными точками.

Удельная и молярная теплоёмкость

Молярная теплоёмкость — теплоёмкость 1 моля вещества :

CM=Cν=1νδQΔT,{\displaystyle C_{M}={\frac {C}{\nu }}={\frac {1}{\nu }}{\frac {\delta Q}{\Delta T}},}

где ν=mM,{\displaystyle \nu =m/M,} m{\displaystyle m} — масса, M{\displaystyle M} — молярная масса вещества.

Теплоёмкость единичной массы вещества называется удельной теплоёмкостью и, в системе СИ, измеряется в Дж/(кг·К).

Формула расчёта удельной теплоёмкости:

c=CMM=δQmdT,{\displaystyle c={\frac {C_{M}}{M}}={\frac {\delta Q}{mdT}},}

где c — удельная теплоёмкость, m — масса нагреваемого (охлаждающегося) вещества.

Идеальные газы это

Идеальный газ подчиняется определенным законам в любой области температур и давлений. При неизменной температуре давление газа обратно пропорционально занимаемому им объему (закон Бойля-Мариотта):

pV = K_t

где K_t — постоянная, зависящая от температуры и массы in газа. Закон Бойля—Мариотта можно представить графически ветвью гиперболы в координатах р и V (рис.).

При постоянном объеме давление газа линейно изменяется с температурой (закон Шарля):

p= p(1 +αt)

где t— температура в °С; р— давление газа при 0°С; α — коэффициент пропорциональности, численно равный 1/₂₇₃. С помощью несложного алгебраического преобразования это уравнение можно привести к виду:

p= p(273 + t)/273

Заменив сумму (273+ t) величиной Т, получаем:

p= p(T/273)

(Т— температура по Кельвину).

Теперь закон Шарля принимает следующий вид:

p/T = Kυ[Kυ = f(V,m)]

В координатах р и Т закон Шарля выражается графически в виде прямой линии (рис. 2).

Рис. 2. Графическое выражение закона Шарля в координатах р и Т.

При постоянном давлении объем газа линейно изменяется с температурой (закон Гей-Люссака)

V = V(l+af),

где t и а имеют те же значения; V — объем газа при 0°С. Переходя к температурной шкале Кельвина, получаем:

V/T= К_Р [K_p = f(p, т)]

Закон Гей-Люссака выражается графически в координатах V и Т в виде прямой линии (рис. 3).

Переменные величины р и Т, описывающие состояние идеального газа, называются его основными параметрами состояния. Они связаны между собой простым соотношением

pV/T = K

где К — постоянная, зависящая только от массы m газа. Если принять тn=1 моль, то величина К перестает быть зависящей от каких-либо параметров. В этом случае ее обозначают латинской буквой R и называют универсальной газовой постоянной. Следовательно, для одного моля газообразного вещества можно написать:

В системе СИ

= 8,314 дж/моль • град

Для п молей уравнение состояния идеального газа принимает вид:

pV/T = nR

Рис. 3. Графическое выражение закона Гей-Люссака в координатах V и Т

Или, учитывая, что n = m/M (т — масса газа, М — его молекулярная масса),

Таким образом, измерив давление р, объем V и температуру Т массы m газа, легко можно вычислить его молекулярную массу из соотношения:

М = m(RT/pV)

Температура идеального газа прямо пропорциональна средней кинетической энергии поступательного движения его молекул

T ~ Ē_кин

Поскольку скорости движения каждой из N молекул различны то

Для двух идеальных газов, находящихся при одной и той же абсолютной температуре, m₁υ₁2=m₂υ₂2 или, что то же самое

Следовательно,

средняя квадратичная скорость движения молекул обратно пропорциональна корню квадратному из их массы.

При атмосферном давлении и температуре 300 К средние квадратичные скорости молекул водорода, кислорода и азота равны соответственно 1838, 461 и 493 м/сек. Благодаря незначительной молекулярной массе водород обладает гораздо более высокими скоростями диффузии по сравнению с другими газами. По этой причине он хорошо проводит теплоту и применяется для охлаждения подшипников мощных электрических машин.

При повышенной температуре газообразный водород довольно быстро диффундирует сквозь металлы, что приходится учитывать при конструировании химической aппаратуры. В процессе диффузии могут получаться различные гидриды постоянного и переменного составов. Например, в паровых котлах образуется гидрид железа, присутствие которого в толще металла снижает прочность стенок и может привести к взрыву.

Статья на тему Идеальный газ

← Предыдущая
Следующая →
Главная Строение вещества

Когда газ можно считать идеальным

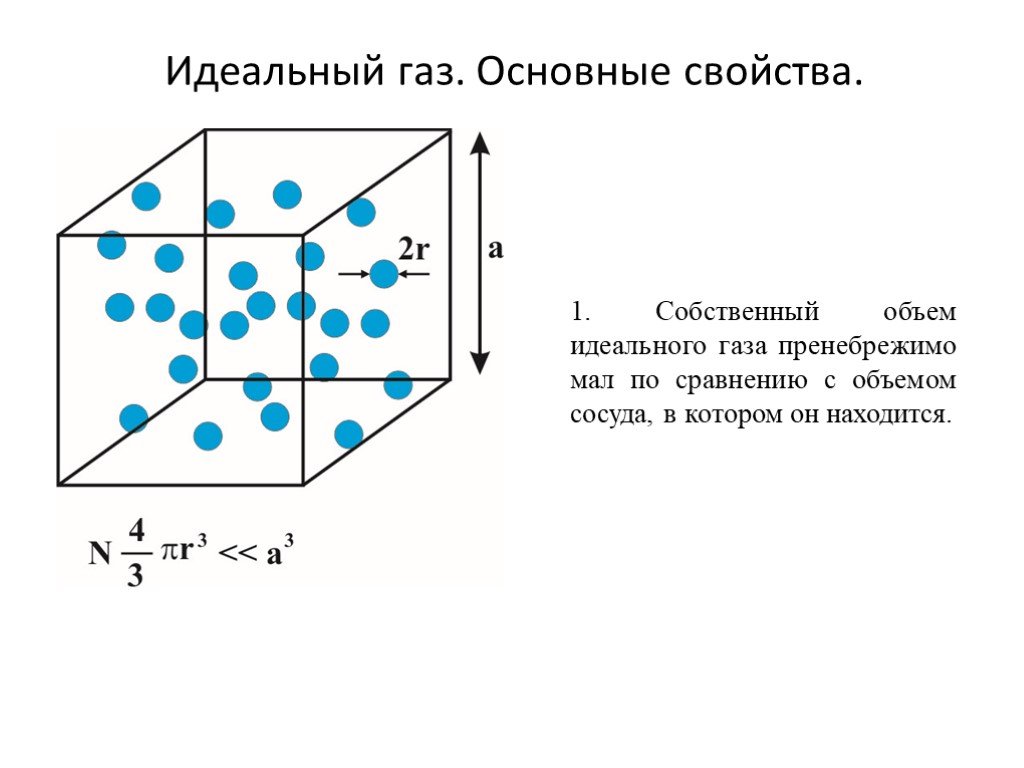
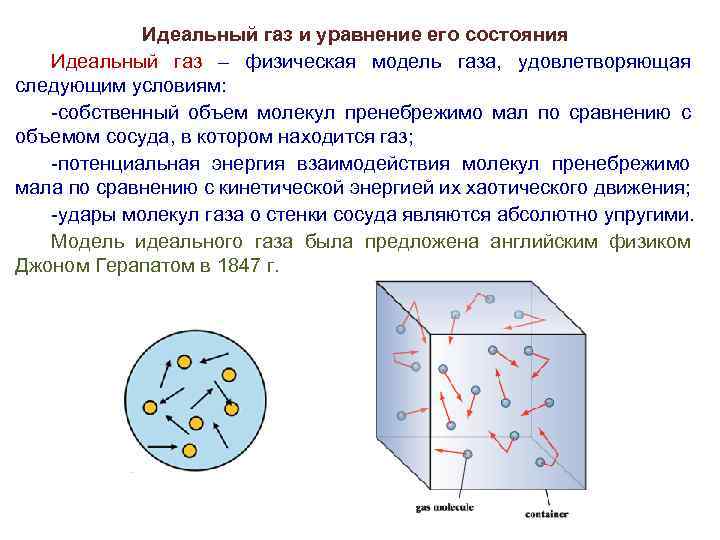
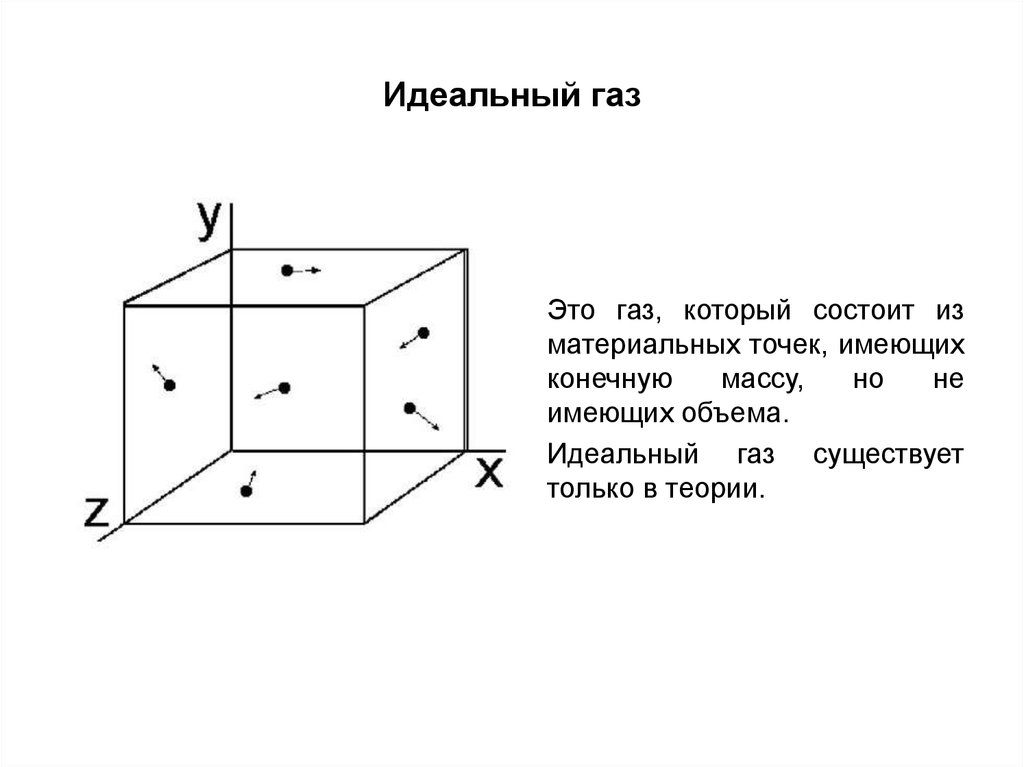
Существует несколько факторов, благодаря которым газ называется идеальным. Первым признаком является поведение молекул как абсолютно упругих тел, между ними отсутствуют силы притяжения. При этом газ будет очень разряжен. Расстояние между мельчайшими составляющими вещества будет гораздо больше размеров их самих. В таком случае тепловое равновесие будет достигаться мгновенно по всему объему. Чтобы достичь положения идеального газа в лабораторных условиях, реальный его тип разрежается соответствующим образом. Некоторые вещества в газообразном состоянии даже при комнатной температуре и нормальном атмосферном давлении практически не отличаются от идеального состояния.

Точки Бойля, кривая Бойля, температура Бойля

Рассмотрим отклонение свойств реального газа от свойств идеального газа с помощью PV,P{\displaystyle PV,P}-диаграммы. Из уравнения Клапейрона — Менделеева следует, что изотермы идеального газа на такой диаграмме изображаются горизонтальными прямыми. Воспользуемся уравнением состояния реального газа в вириальной форме. Для одного моля газа

PV=RT+BP+CP2+DP3+…{\displaystyle PV=RT+BP+CP^{2}+DP^{3}+…}

(Вириальное уравнение состояния реального газа)

где B,C{\displaystyle B,C} и D{\displaystyle D} — соответственно второй, третий и четвёртый вириальные коэффициенты, зависящие только от температуры. Из следует, что на PV,P{\displaystyle PV,P}-диаграмме ось ординат (P={\displaystyle P=0}) соответствует идеально-газовому состоянию вещества: при P→{\displaystyle P\to 0} вириальное уравнение состояния превращается в уравнение Клапейрона — Менделеева и, следовательно, положения точек пересечения изотерм с ординатой на рассматриваемой диаграмме соответствуют значениям RT{\displaystyle RT} для каждой из изотерм.

Из находим:

B=(∂(P,V)∂P)T,P=.{\displaystyle B=\left({\frac {\partial (P,V)}{\partial P}}\right)_{T,P=0}.}

(Второй вириальный коэффициент)

PV, P-диаграмма реального газа

Таким образом, в рассматриваемой системе координат наклон (то есть угловой коэффициент касательной) изотермы газа в точке пересечения этой изотермы с осью ординат даёт значение второго вириального коэффициента.

На PV,P{\displaystyle PV,P} -диаграмме изотермы, соответствующие температурам, меньшим некоторого значения TB{\displaystyle T_{B}} (называемого температурой Бойля) имеют минимумы, называемые точками Бойля.

Некоторые авторы в понятие «точка Бойля» вкладывают другое содержание, а именно, они исходят из единственности точки Бойля, понимая под ней точку на PV,P{\displaystyle PV,P}-диаграмме с нулевым давлением и температурой, равной температуре Бойля.

В точке минимума

(∂(P,V)∂P)T=,{\displaystyle \left({\frac {\partial (P,V)}{\partial P}}\right)_{T}=0,}

что всегда справедливо для идеального газа. Иными словами, в точке Бойля сжимаемости реального и идеального газов совпадают. Участок изотермы слева от точки Бойля соответствует условиям, когда реальный газ более сжимаем, чем идеальный; участок справа от точки Бойля соответствует условиям худшей сжимаемости реального газа по сравнению с идеальным.

Линию, являющуюся геометрическим местом точек минимумов изотерм на PV,P{\displaystyle PV,P}-диаграмме, называют кривой Бойля. Точке пересечения кривой Бойля с осью ординат соответствует изотерма с температурой, равной температуре Бойля. Это означает, что при температуре Бойля второй вириальный коэффициент обращается в нуль и температура Бойля есть корень уравнения

(∂(P,V)∂P)T,P=={\displaystyle \left({\frac {\partial (P,V)}{\partial P}}\right)_{T,P=0}=0.}

Ниже температуры Бойля второй вириальный коэффициент отрицателен, выше — положителен. Температура Бойля — важная характеристика кривой инверсии (в каждой точке которой дроссельный эффект равен нулю): при температурах ниже температуры Бойля возможно частичное сжижение газов при дросселировании (подробнее см. в книге).

Для газа, подчиняющегося уравнению Ван-дер-Ваальса,

TB=3.375TC,{\displaystyle T_{B}=3.375T_{C},}

где TC{\displaystyle T_{C}} — критическая температура. Для многих веществ примерное значение температуры Бойля даёт следующее эмпирическое соотношение:

TB≈(2.5÷2.75)TC.{\displaystyle T_{B}\approx (2.5\div 2.75)T_{C}.}

Из PV,P{\displaystyle PV,P}-диаграммы видно, что начальный участок изотермы с температурой Бойля, соответствующий сравнительно невысоким давлениям, достаточно близок к горизонтальной прямой, то есть при температуре газа, равной или близкой к температуре Бойля, реальный газ обладает свойствами, близкими к свойствам идеального газа.

Теплоёмкость идеального газа в изопроцессах

Адиабатический

В адиабатическом процессе теплообмена с окружающей средой не происходит, то есть dQ={\displaystyle dQ=0}. Однако, объём, давление и температура меняются, то есть dT≠{\displaystyle dT\neq 0}.

Следовательно, теплоёмкость идеального газа в адиабатическом процессе равна нулю: C=dT={\displaystyle C={0 \over dT}=0}.

Изотермический

В изотермическом процессе постоянна температура, то есть dT={\displaystyle dT=0}. При изменении объёма газу передаётся (или отбирается) некоторое количество тепла. Следовательно, теплоёмкость идеального газа равна плюс-минус бесконечности: C→±∞{\displaystyle C\to \pm \infty }

Изохорный

В изохорном процессе постоянен объём, то есть δV={\displaystyle \delta V=0} и, следовательно газ не совершает работы. Первое Начало Термодинамики для изохорного процесса имеет вид:

dU=δQ=νCVdT.(1){\displaystyle dU=\delta Q=\nu C_{V}dT.\qquad (1)}

А для идеального газа

dU=i2νRΔT.{\displaystyle dU={\frac {i}{2}}\nu R\Delta T.}

Таким образом,

CV=i2R,{\displaystyle C_{V}={\frac {i}{2}}R,}

где i{\displaystyle i} — число частиц газа.

Другая формула:

CV=Rγ−1,{\displaystyle C_{V}={\frac {R}{\gamma -1}},}

где γ{\displaystyle \gamma } — показатель адиабаты, R{\displaystyle R} — газовая постоянная газа.

Изобарный

Молярная теплоёмкость при постоянном давлении обозначается как Cp{\displaystyle C_{p}}. В идеальном газе она связана с теплоёмкостью при постоянном объёме соотношением Майера Cp=Cv+R{\displaystyle C_{p}=C_{v}+R}.
Уравнение Майера вытекает из первого начала термодинамики:

δQ=dU+δA,(2){\displaystyle \delta Q=\mathrm {d} U+\delta A,\qquad (2)}.

В рассматриваемом случае, согласно определению теплоёмкости:

δQ=CpdT,{\displaystyle \delta Q=C_{p}\mathrm {d} T,}

Учитываем, что работа газа равна :

δA=d(pV)=nRdT=pdV+Vdp=pdV,(Vdp=)(3){\displaystyle \delta A=\mathrm {d} (pV)=nR\mathrm {d} T\qquad =p\mathrm {d} V\qquad +V\mathrm {d} p\qquad =p\mathrm {d} V\qquad ,(V\mathrm {d} p\qquad =0)(3)}

Согласно уравнению Менделеева-Клапейрона для одного моля газа:

pdV=RdT.(4){\displaystyle p\mathrm {d} V=R\mathrm {d} T.\qquad (4)}

Подставляя уравнение (4) в (3) получаем:

δA=RdT(5){\displaystyle \delta A=R\mathrm {d} T\qquad (5)}

Так как энергия одной молекулы равна <e>=i2kT{\displaystyle <e>={\frac {i}{2}}kT} (6), то и внутренняя энергия в целом и при изобарном процессе будет определяться по соотношению (1). Следовательно, подставляя уравнения (1) и (5) в (2) получаем соотношение Майера.

Молекулярно-кинетическая теория позволяет вычислить значения молярной теплоёмкости для классического идеального газа газов через значение универсальной газовой постоянной исходя из уравнения (6) и предположения, что молекулы газа не взаимодействуют между собой:

для общего случая Cp=i+22R,{\displaystyle C_{p}={\frac {i+2}{2}}R,}
для одноатомных газов Cp=52R,{\displaystyle C_{p}={\frac {5}{2}}R,} то есть около 20.8 Дж/(моль·К);
для двухатомных газов и многоатомных газов с линейными молекуламиCp=72R,{\displaystyle C_{p}={\frac {7}{2}}R,} то есть около 29.1 Дж/(моль·К);
для многоатомных газов с нелинейными молекуламиCp=4R,{\displaystyle C_{p}=4R,} то есть около 33.3 Дж/(моль·К).

Теплоёмкости можно также определить исходя из уравнения Майера, если известен показатель адиабаты, который можно измерить экспериментально (например, с помощью измерения скорости звука в газе или используя метод Клемана — Дезорма).

Теплоёмкость реального газа может значительно отклонятся от теплоёмкости идеального газа. Так при температуре в 25 °С и атмосферном давлении атомарный водород имеет теплоёмкость 2,50R , а атомарный кислород — 2,63R. Также теплоёмкость реального газа зависит от температуры.

Литература

Андрющенко А. И. Основы технической термодинамики реальных процессов. — М.: Высшая школа, 1967. — 268 с.
Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.—Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
Белоконь Н. И. Основные принципы термодинамики. — Москва: Недра, 1968. — 112 с.
Бэр Г. Д. Техническая термодинамика. — М.: Мир, 1977. — 519 с.
Гуйго Э. И., Данилова Г. Н., Филаткин В. Н. и др. Техническая термодинамика / Под общ. ред. проф. Э. И. Гуйго. — Л.: Изд-во Ленингр. ун-та, 1984. — 296 с.
Додж Б. Ф. Химическая термодинамика в применении к химическим процессам и химической технологии. — М.: Иностранная литература, 1950. — 786 с.
Докторов А. Б., Бурштейн А. И. Термодинамика. — Новосибирск: Новосиб. гос. ун-т, 2003. — 83 с.
Еремин Е. Н. Основы химической термодинамики. — 2-е изд., испр. и доп. — М.: Высшая школа, 1978. — 392 с.
Кириллин В. А., Сычев В. В., Шейндлин А. Е. Техническая термодинамика. — 5-е изд., перераб. и доп. — М.: Изд. дом МЭИ, 2008. — 496 с. — ISBN 978-5-383-00263-6.
Коновалов В. И. Техническая термодинамика. — Иваново: Иван. гос. энерг. ун-т, 2005. — 620 с. — ISBN 5-89482-360-9.
Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин / Отв. ред. И. И. Новиков. — АН СССР. Комитет научно-технической терминологии. Сборник определений. Вып. 103. — М.: Наука, 1984. — 40 с.