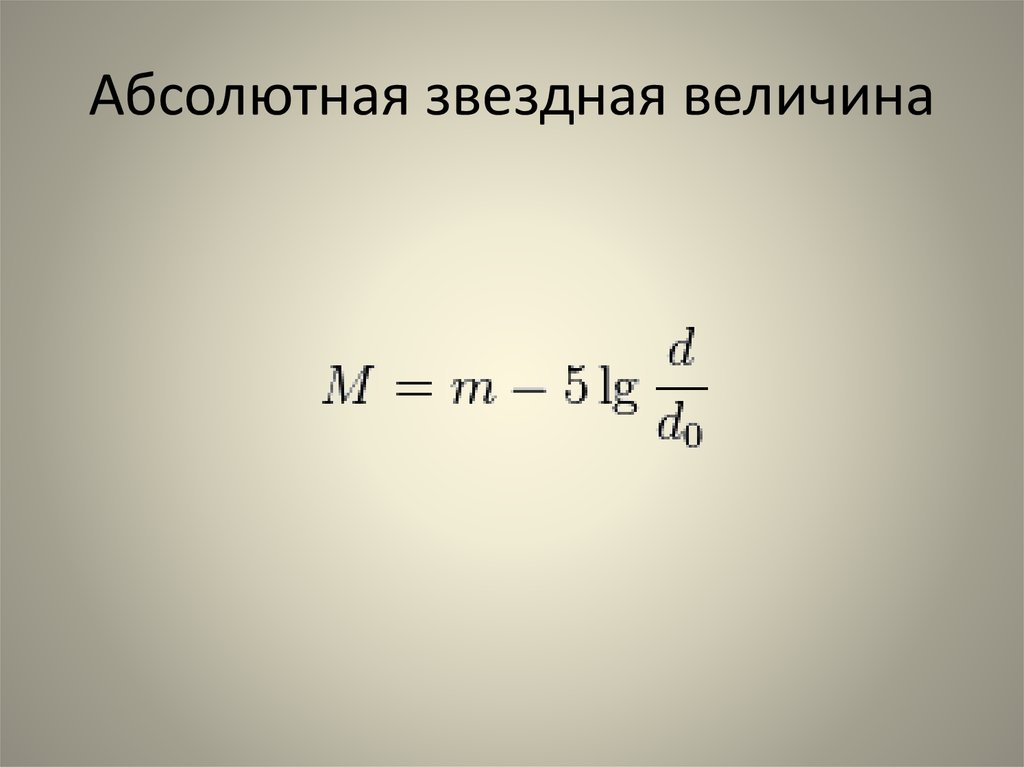Спектральная зависимость
Звёздная величина зависит от спектральной чувствительности приёмника излучения (глаза, фотоэлектрического детектора, фотопластинки и т. п.)
Болометрическая звёздная величина показывает полную мощность излучения звезды (то есть мощность излучения на всех длинах волн). Для её измерения применяется специальное устройство — болометр. Актуальность этой величины связана с тем, что некоторые звёзды (очень горячие и очень холодные) излучают преимущественно не в видимом спектре.
Однако чаще всего звёздные величины измеряют в определённых интервалах длин волн. Для этого разработаны фотометрические системы, в каждой из которых есть набор полос, перекрывающих разные диапазоны волн. В пределах каждой полосы чувствительность максимальна для некоторой длины волны и плавно спадает с удалением от неё.
Самой распространённой фотометрической системой является система UBV, которая состоит из трёх полос, перекрывающих разные интервалы длин волн. В ней для каждого объекта можно измерить 3 звёздные величины:
Визуальная звёздная величина (V) — звёздная величина в фильтре V, максимум пропускания которого близок к максимуму чувствительности человеческого глаза (555 нм).
«Синяя» звёздная величина (B) характеризует яркость объекта в синей области спектра; максимум чувствительности на длине волны около 445 нм.
Ультрафиолетовая звёздная величина (U) имеет максимум в ультрафиолетовой области при длине волны около 350 нм.
Разности звёздных величин одного объекта в разных диапазонах (для системы UBV это U − B и B − V) являются показателями цвета объекта: чем они больше, тем более красным является объект. Фотометрическая система UBV определена таким образом, чтобы показатели цвета звёзд спектрального класса А0V равнялись нулю.
Существуют и другие фотометрические системы, в каждой из которых может быть определён свой набор звёздных величин.
Фотографическая звёздная величина — определяется для спектральной чувствительности несенсибилизированной фотоэмульсии с максимумом чувствительности на длине волны 425 нм; по определению совпадает с визуальной звёздной величиной для звёзд А0V и блеском (6,0 ± 0,5)m. Вместе с фотовизуальной звёздной величиной использовалась в устаревшей фотографической системе звёздных величин.
Космические расстояния
Космические расстояния поражают своими масштабами, и, конечно, для их измерения не годятся наши земные километры. Одна из важнейших единиц измерения в астрономии — световой год. Это расстояние, которое проходит свет за год. Если учесть, что скорость света составляет 300 тысяч километров в секунду, то получается 9400 миллиардов километров. Это поражающее воображение число и используется астрономами в измерениях и вычислениях.
Самый далекий от нас космический объект, который можно увидеть невооруженным глазом, — это туманность Андромеды. Расстояние до нее от Земли составляет 2 миллиона световых лет. То есть тот свет, который мы видим сейчас, покинул туманность 2 миллиона лет назад. Мы видим ее такой, какой она была тогда. Как она выглядит сейчас, мы никогда не узнаем — у нас нет такой возможности.
Получается, что астрономия, по крайней мере тот ее раздел, который занимается далекими объектами, — это наука о прошлом. Глядя на ночное небо, мы видим прошлое звезд. Возможно, некоторые из них уже не существуют, но их свет только сейчас достиг нашей Солнечной системы.
Свет ближайшей к нам звезды, Солнца, доходит до Земли за 8 минут. Это не очень много, но все же и Солнце мы наблюдаем не в реальном времени. Замечая при помощи специальных приборов вспышку на Солнце, астрономы знают: на самом деле она произошла 8 минут назад. Самые отдаленные галактики, о существовании которых известно астрономам, находятся в 10-15 миллиардах световых лет он нас.
- Что такое звезды и какие они бывают?
- Яркость звезд и световой год
- Звездные карты: как найти объект на небе
- Красные гиганты, белые карлики, пульсары
Поделиться ссылкой
Светимость от А до Я
Источник излучения в звезде искать долго не приходится. Вся энергия, которая может покинуть светило, создается в процессе термоядерных реакций синтеза в звездном ядре. Атомы водорода, сливаясь под давлением гравитации в гелий, высвобождают громадное количество энергии. А в звездах помассивнее «горит» не только водород, но и гелий — порой даже более массивные элементы, вплоть до железа. Энергии тогда получается в разы больше.
Количество энергии, выделяемой во время ядерной реакции, напрямую зависит от массы звезды — чем она больше, тем сильнее гравитация сжимает ядро светила, и тем больше водорода одновременно превращается в гелий. Но не одна ядерная энергия определяет светимость звезды — ведь ее надо еще излучать наружу.
И тут вступает в игру площадь излучения. Ее влияние в процессе передачи энергии очень велико, что легко проверяется даже в быту. Лампа накаливания, нить которой нагревается до 2800 °C, за 8 часов работы существенно не изменит температуру в помещении — а обычная батарея температурой в 50–80 °C сумеет прогреть комнату до ощутимой духоты. Разницу в эффективности обуславливают отличия в количестве поверхности, излучающей энергию.
Соотношение площади ядра звезды и ее поверхности часто бывает соизмеримо с пропорциями нити лампочки и батареи — поперечник ядра может составлять всего одну десятитысячную общего диаметра звезды. Таким образом, на светимость звезды серьезно влияет площадь ее излучающей поверхности — то есть поверхности самой звезды. Температура тут оказывается не столь существенной. Накал поверхности звезды Альдебаран на 40% меньше температуры фотосферы Солнца — но из-за больших размеров, ее светимость превышает солнечную в 150 раз.
Получается, в вычислениях светимости звезды роль размеров важнее температуры и энергии ядра? На самом деле нет. Голубые гиганты с высокой светимостью и температурой обладают схожей светимостью с красными сверхгигантами, которые намного больше размерами. Кроме того, самая массивная и одна из наиболее горячих звезд, R136a1, обладает самой высокой яркостью среди всех известных звезд
До открытия нового рекордсмена, это ставит точку в дискуссии о наиболее важном для светимости параметре
Использование светимости в астрономии

Диаграмма Герцшпрунга — Рассела
Таким образом, светимость достаточно точно отражает как и энергию звезды, так и площадь ее поверхности — поэтому она задействована во многих классификационных диаграммах, используемых астрономами для сравнения звезд. Среди них стоить выделить диаграмму Герцшпрунга-Рассела, отображающую интересные закономерности в распределении звезд во Вселенной — например, по ней легко определить возраст звезды. Также на светимости базируется йеркская спектральная классификация звезд — именно в ней фигурируют такие термины «белые карлики» или «сверхгиганты».
Абзацем выше упоминалось о том, как температура звезды влияет на светимость. Эту зависимость астрономы используют для выяснения параметров звезды — особенно тогда, когда цвет, самый точный индикатор нагрева объекта, искажается гравитацией. Также яркость звезды косвенно связана с ее составом. Чем меньше в веществе светила элементов, тяжелее гелия и водорода, тем больше она может набрать массы — критической характеристики в определении яркости звезды.
https://youtube.com/watch?v=ai7unNTFjms
Измерение звездной величины
К сожалению, пока еще неизвестно никакого другого способа определять количество света, полученного от звезды, как судя по действию его на глаз. Две звезды считаются равными, когда они для глаза кажутся равной яркости. В этих условиях наше суждение весьма ненадежно. Потому наблюдатели старались придать больше точности, пуская в ход фотометры — инструменты для измерения количества света. Но даже при этих инструментах наблюдатель должен основываться на оценке глазом равенства блеска. Свет одной звезды увеличивается или уменьшается в определенной пропорции до тех пор. пока для нашего глаза он не покажется равным свету другой звезды; а эта последняя может быть и искусственной звездочкой, полученной при помощи пламени свечи или лампы. Степень увеличения или уменьшения определит разницу величин обоих звезд.
Когда мы стараемся прочно обосновать измерения блеска звезды, мы приходим к выводу, что эта задача довольно сложна. Прежде всего не все лучи, приходящие от звезды, воспринимаются нами, как свет. Но все лучи, видимые и невидимые, поглощаются черной поверхностью и выражают свое действие в нагревании ее. Поэтому самый лучший способ измерять излучение звезды состоит в оценке тепла, которое она посылает, так как это точнее отражает процессы, происходящее на светиле, чем это может сделать видимый свет. К несчастью, тепловое действие лучей звезды настолько мало, что не может быть измерено даже современными приборами. Пока что мы должны оставить надежду определить полное лучеиспускание звезды и ограничиться только той его частью, которая называется светом.
Следовательно, если мы стремимся к точности, то мы должны сказать, что свет, как мы его понимаем, может, в сущности, измеряться лишь по своему действию на зрительный нерв, и нет другого пути измерить его эффект, кроме оценки глазом. Все фотометры, которые служат для измерения света звезд, построены так, что дают возможность увеличивать или уменьшать свет одной звезды и визуально приравнивать ее к свету другой звезды или другого источника и только так оценивать ее.
Что такое звездная величина
Понятие о величинах звезд может быть легко получено каждым случайным созерцателем небес. В любой ясный вечер видны несколько звезд 1-ой величины. Примерами звезд 2-ой величины могут служить 6 наиболее ярких звезд Ковша (Большая Медведица), Полярная Звезда, яркие звезды Кассиопеи. Все эти звезды можно видеть под нашими широтами каждую ночь в течение целого года. Звезд 3-ей величины так много, что трудно выбрать для них примеры. Наиболее яркие звезды в Плеядах именно этой величины. Впрочем, их окружают 5 других звезд, что влияет на оценку их яркости. На расстоянии 15 градусов от Полярной Звезды находится Бета Малой Медведицы: она всегда видна и отличается от Полярной Звезды красноватым оттенком; она находится между двумя другими звездами, из которых одна — 3-ей величины, а другая — 4-ой.
Пять ясно-видимых более слабых звезд Плеяд тоже все около 4-ой величины, пятой величины звезды еще свободно видимы невооруженным глазом; 6-я величина заключает в себе звезды, едва заметные для хорошего зрения.
Современные астрономы, принимая в общих чертах систему, которая дошла до них от древности, постарались придать ей большую определенность. Тщательные исследования показали, что действительное количество света, соответствующее различным величинам, меняется от одной величины до другой почти в геометрической прогрессии; это заключение согласуется с хорошо известным психологическим законом, что ощущение меняется в арифметической прогрессии, если причина, производящая его, меняется в прогрессия геометрической.
Найдено, что средняя звезда 5-ой величины дает от 2 до 3 раз больше света, чем средняя звезда 6-ой величины, звезда 4-ой величины дает от 2 до 3 раз больше света, чем звезда 5-й, и т. д., до 2-ой величины. Для первой величины различие так велико, что едва ли можно указать какое-либо среднее отношение. Сириус, например, в 6 раз ярче, чем Альтаир, который обыкновенно считается типичной звездой первой величины. Чтобы придать точность своим оценкам, современные астрономы постарались свести разницы между различными величинами к одной и той же мерке, а именно приняли, что отношение яркости звезд двух последовательных классов равно двум с половиной.
Если бы прием деления видимых звезд только на 6 отдельных величин был принят без всяких изменений, то мы бы встретили затруднение в том, что в один и тот же класс пришлось бы отнести звезды, весьма различные по яркости. В одном и том же классе оказались бы звезды, превосходящие одна другую в два раза по яркости. Поэтому, чтобы придать результатам точность, пришлось рассматривать класс, величину звезд, как такое количество, которое меняется непрерывно — ввести десятые и даже сотые доли величины. Так, мы имеем звезды 5,0, 5,1, 5,2 величины и т. д., или даже мы можем делить еще мельче и говорить о звездах, имеющих величины 5,11, 5,12 и т. д.
Определение
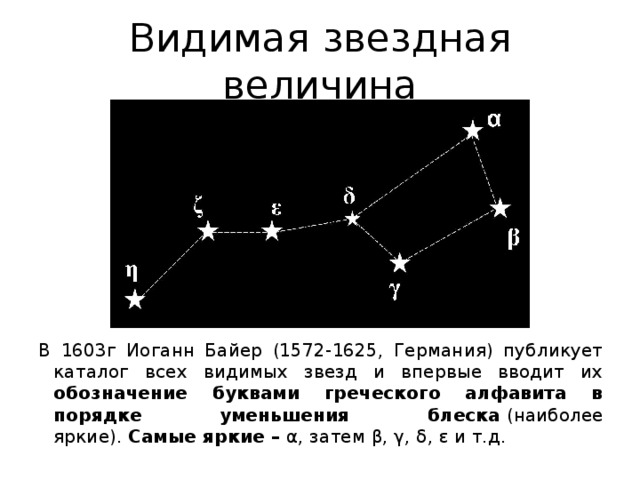
Ещё во II веке до н. э. древнегреческий астроном Гиппарх разделил все звёзды на шесть величин. Самые яркие он назвал звёздами первой величины, самые тусклые — звёздами шестой величины, а остальные равномерно распределил по промежуточным величинам.
Как выяснилось позже, связь такой шкалы с реальными физическими величинами логарифмическая, поскольку изменение яркости в одинаковое число раз воспринимается глазом как изменение на одинаковую величину (закон Вебера — Фехнера). Поэтому в 1856 году Норман Погсон предложил следующую формализацию шкалы звёздных величин, ставшую общепринятой:
- m1−m2=−2,5lg(L1L2){\displaystyle m_{1}-m_{2}=-2{,}5\,\lg \left({\frac {L_{1}}{L_{2}}}\right)}
где m — звёздные величины объектов, L — освещённости от объектов. Такое определение соответствует падению светового потока в 100 раз при увеличении звёздной величины на 5 единиц.
Данная формула даёт возможность определить только разницу звёздных величин, но не сами величины. Чтобы с её помощью построить абсолютную шкалу, необходимо задать нуль-пункт — блеск, которому соответствует нулевая звездная величина (0m). Сначала в качестве 0m был принят блеск Веги. Потом нуль-пункт был переопределён, но для визуальных наблюдений Вега до сих пор может служить эталоном нулевой видимой звёздной величины (по современной системе, в полосе V системы UBV её блеск равен +0,03m, что на глаз неотличимо от нуля).
По современным измерениям, звезда нулевой видимой величины за пределами земной атмосферы создаёт освещённость в 2,54 × 10−6 люкс. Световой поток от такой звезды примерно равен 103 квантов/(см²·с·Å) в зелёном свете (полоса V системы UBV) или 106 квантов/(см²·с) во всём видимом диапазоне света.
Следующие свойства помогают пользоваться видимыми звёздными величинами на практике:
- Увеличению светового потока в 100 раз соответствует уменьшение видимой звёздной величины ровно на 5 единиц.
- Уменьшение звёздной величины на одну единицу означает увеличение светового потока в 1001/5 ≈ 2,512 раза.
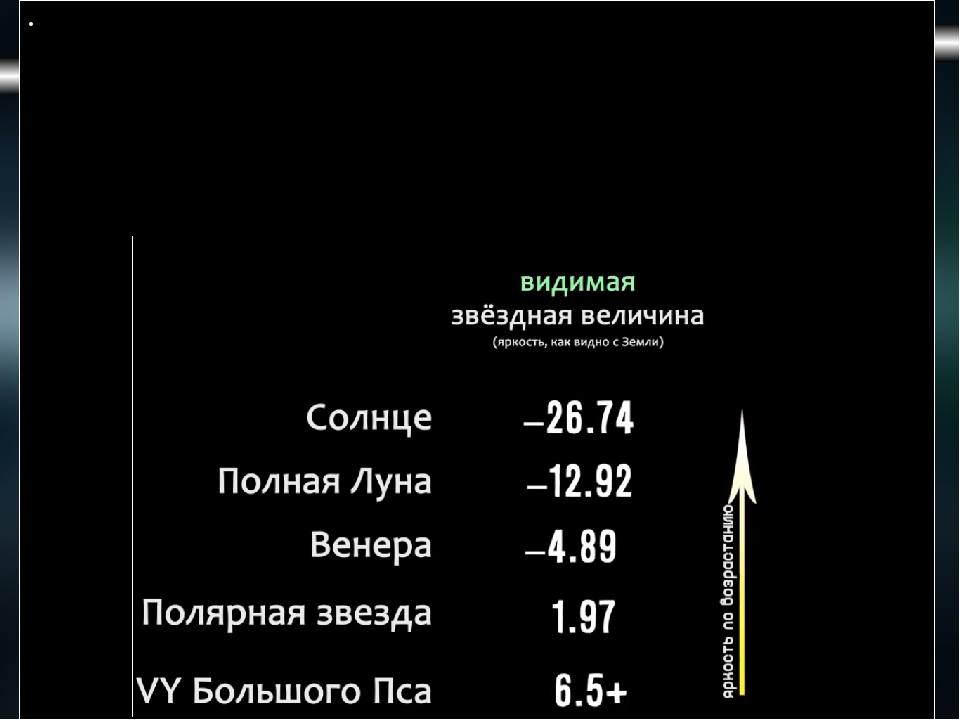
В наши дни понятие звёздной величины используется не только для звёзд, но и для других объектов, например, для Луны и планет. Звёздная величина самых ярких объектов отрицательна. Например, блеск Луны в полной фазе достигает −12,7m, а блеск Солнца равен −26,7m.
История
Понятие звездной величины ввел древнегреческий астроном Гиппарх во II веке до нашей эры. Он распределил все доступные невооруженному глазу звезды на шесть величин: яркие он назвал звездами первой величины, найтьмяниши — шестой. Для промежуточных величин считалось, что, скажем, звезды третьей величины, столь же тусклее звезды второй, насколько они ярче звезды четвертой. Этот способ измерения блеска получил распространение благодаря «Альмагесту» — звездном каталога Клавдия Птолемея.
Такая классификационная шкала почти без изменений применялась до середины 19 века. Первым, кто отнесся к звездной величины как в количественной, а не качественной характеристики, был Фридрих Аргеландер. Именно он начал уверенно применять десятичные доли звездных величин.
1856 Норман Погсон формализовал шкалу звездных величин, установив, что звезда первой величины ровно в 100 раз ярче звезду шестой величины. Поскольку в соответствии с закон Вебера — Фехнера изменение освещенности в одинаковое количество раз воспринимается глазом как изменение на одинаковую величину, то разница в одну звездную величину соответствует изменению интенсивности света в ≈ 2,512 раз. Это иррациональное число, которое называют числом Погсон.
Итак, шкала звездных величин является логарифмической: разница звездных величин двух объектов определяется уравнением:
- ,
где:
- , — Звездные величины объектов,
- , — Освещенности, создаваемые ими.
Эта формула дает возможность определить лишь разницу звездных величин, но не сами величины. Чтобы с ее помощью построить абсолютную шкалу, необходимо задать нуль-пункт — освещенность, которой соответствует нулевая звездная величина (0 m). Сначала Погсон применял как эталон Полярную звезду, положив, что она имеет ровно второй величины. После того, как выяснилось, что Полярная является переменной звездой, шкалу начали привязывать к Веге (которой приписывали нулевую величину), а затем (когда в Веги тоже заподозрили изменчивость) нуль-пункт шкалы переопределили с помощью нескольких других звезд. Впрочем, для визуальных наблюдений Вега может служить эталоном нулевой звездной величины и дальше, поскольку ее звездная величина в видимом свете равен 0,03 m, что на глаз не отличается от нуля.
Современная шкала звездных величин не ограничивается шестью величинами или только видимым светом. Звездная величина очень ярких объектов является отрицательной. Например, Сириус, самая яркая звезда ночного неба, имеет видимую звездную величину -1,47 m. Современная техника позволяет также измерить блеск Луны и Солнца: полная Луна имеет видимую звездную величину -12,6 m, а Солнце -26,8 m. Орбитальный телескоп «Хаббл» может наблюдать звезды до 31,5 m в видимом диапазоне.
Звездная величина и спектр
Трудность получения точных результатов увеличивается еще тем, что звезды различаются по их цвету. С гораздо большой точностью мы можем убеждаться в равенстве двух источников света, когда они имеют один и тот же цветовой оттенок, чем когда цвета их различны. Еще один источник неопределенности происходит от того, что называется явлением Пуркинье (Purkinje), по имени физика, который первый описал его. Он нашел, что если мы имеем два источника светя одной и той же яркости, но один красный, а другой зеленый, то при увеличении или уменьшении в одной и той же пропорции эти источники перестанут казаться одинаковыми по яркости. Другими словами, математическая аксиома о том, что половины или четверти равных величин тоже равны между собой, неприменима к действию света на глаз. Когда яркость уменьшается, зеленое пятно начинает казаться ярче, чем красное. Если мы увеличиваем яркость обоих источников, то красный начинает казаться ярче зеленого. Иначе говоря, красные лучи для нашего зрения быстрее усиливаются и ослабляются, чем лучи зеленые, при одном и том же изменении действительной яркости.
Также выяснено, что этот закон изменения кажущейся яркости не распространяется последовательно на все цвета спектра. Верно, что когда мы переходим от красного к фиолетовому концу спектра, желтый цвет гаснет менее быстро, чем красный, при данном уменьшении яркости, а зеленый — еще менее быстро, чем желтый. Но если мы переходим от зеленого к синему, то уже можно сказать, что последний не пропадает так быстро, как зеленый. Очевидно, из всего этого следует, что две звезды различного цвета, кажущиеся одинаково яркими для невооруженного глаза, уже не будут казаться равными в телескоп. Красные или желтые звезды кажутся сравнительно ярче в телескопе, зеленые и синеватые — сравнительно ярче для невооруженного глаза.
Таким образом можно сделать вывод, что, несмотря на значительное совершенствование средств измерения, развитие микроэлектроники и компьютеров, визуальные наблюдения все еще играют самую важную роль в астрономии, и вряд ли эта роль снизится в обозримом будущем.
Шкала звездных величин
Такое определение дал в XIX астроном Норман Погсон. Он заметил, что разница в одну звездную величину соответствует изменению светового потока примерно в 2,5 раза. То есть звезда 0m освещает наши глаза в 2,5 раза сильнее, чем звезда 1m. Получается, что звезда 1-й величины в 100 раз ярче, чем звезда 6-й.
Для кого-то этот момент может показаться странным. Субъективное ощущение подсказывает, что звезды звезды 6-й величины всего в 6-10 раз слабее, чем звезды 1-й. Руководствуясь этим ощущением, Гиппарх, собственно, и разработал шкалу звездных величин.
Но наше зрение, как и слух, устроены по-другому. Когда сила источника света изменяется в геометрической прогрессии, мы принимаем ее за прогрессию арифметическую! Нам кажется, что две звезды 6-й величины дадут нам звезду 3m, а две звезды 3m дадут звезду 1m. Но если мы в реальности приблизим две звезды одинакового блеска друг к другу (в их роли могут выступить фонарики), то это отношение работать не будет!
Погсон предложил логарифмическую шкалу величин — разница в 5 единиц по шкале звездных величин точно соответствует 100-кратному различию светового потока. То есть звезда 1-й величины ровно в 100 раз ярче звезды 6-й величины и в 100 × 100 = 10000 раз ярче звезды 11-й величины. Это правило в точности соответствует действительности.
Осталось определить стандарт, по отношению к которому можно измерять звездные величины всех других звезд. Таким стандартом долгое время считалась звезда Вега, блеск которой был взят за нуль-пункт звездных величин (0m).
На практике блеск звезд измеряются фотоэлектрическим способом при помощи фотометров. Следовательно, звездные величины неплохо бы привязать к общепринятой физической величине потока излучения. В физике освещенность измеряется в люксах. Связь между звездной величиной (m) и люксом (J) выражается формулой: m = -14 — 2,5lgJ. Так, Солнце имеет звездную величину -26,75m или 125000 люкс. Блеск полной Луны -12,74m, что соответствует 0,3 люкса.

Ясной темной ночью в северном полушарии Земли невооруженным глазом видно около 3000 звезд. В сумме их блеск составляет -4 зв. величине, что примерно равно блеску Венеры. Фото: Mikaest
Абсолютная звёздная величина для звёзд
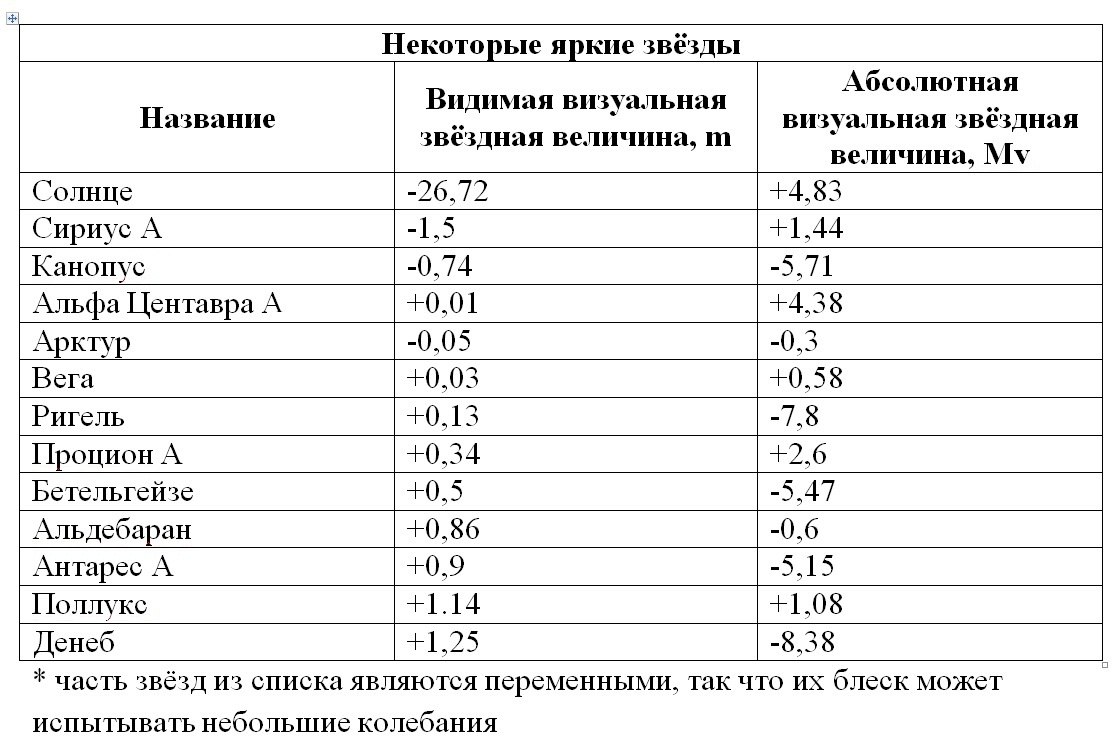
Абсолютная звёздная величина (M) для звёзд определяется как видимая звёздная величина объекта, если бы он был расположен на расстоянии 10 парсек от наблюдателя и не испытывал бы ни межзвёздного, ни атмосферного поглощения. Абсолютная визуальная звёздная величина Солнца (в диапазоне V) равна +4,8m, абсолютная болометрическая (во всех длинах волн) — +4,7m. Разность между вторым и первым значением для одного объекта называется болометрической поправкой и она всегда отрицательна.
Галактики, некоторые звёздные скопления и туманности имеют размеры больше 10 парсек, поэтому для них абсолютная звёздная величина измеряется немного другим образом: они рассматриваются как точечный объект со светимостью, равной полной светимости всей галактики, скопления или туманности, и уже для такого объекта обычным образом измеряется абсолютная звёздная величина. Так, например, Галактика Андромеды имеет абсолютную звёздную величину −20,5m.
Из определения, если известна видимая звёздная величина m{\displaystyle m} и расстояние до объекта d{\displaystyle d}, можно вычислить абсолютную звёздную величину по формуле:
- M=m−5lgdd,{\displaystyle M=m-5\lg {\frac {d}{d_{0}}},}
где d{\displaystyle d_{0}} = 10 пк ≈ 32,616 световых лет. Этой формуле эквивалентны M=m+5−5lgr{\displaystyle M=m+5-5\lg r} и M=m+5+5lgπ′′{\displaystyle M=m+5+5\lg \pi \prime \prime }, где r{\displaystyle r} и π′′{\displaystyle \pi \prime \prime } — расстояние до звезды в парсеках и годичный параллакс в секундах соответственно).
Соответственно, если известны видимая и абсолютная звёздные величины, можно вычислить расстояние по формуле:
- d=d10m−M5.{\displaystyle d=d_{0}10^{\frac {m-M}{5}}.}
Разность между видимой и абсолютной звёздными величинами называется модулем расстояния, причём, если видимая величина приведена с поправкой на поглощение — модуль расстояния называется истинным, а если без поправки — видимым.
Наконец, абсолютная звёздная величина связана со светимостью следующим соотношением:
- lgLL⊙=,4(M⊙−M),{\displaystyle \lg {\frac {L}{L_{\odot }}}=0,4(M_{\odot }-M),}
где L⊙{\displaystyle L_{\odot }} и M⊙{\displaystyle M_{\odot }} — светимость и абсолютная звёздная величина Солнца.
Использование светимости в астрономии

Диаграмма Герцшпрунга — Рассела
Таким образом, светимость достаточно точно отражает как и энергию звезды, так и площадь ее поверхности — поэтому она задействована во многих классификационных диаграммах, используемых астрономами для сравнения звезд. Среди них стоить выделить диаграмму Герцшпрунга-Рассела, отображающую интересные закономерности в распределении звезд во Вселенной — например, по ней легко определить возраст звезды. Также на светимости базируется йеркская спектральная классификация звезд — именно в ней фигурируют такие термины «белые карлики» или «сверхгиганты».
Абзацем выше упоминалось о том, как температура звезды влияет на светимость. Эту зависимость астрономы используют для выяснения параметров звезды — особенно тогда, когда цвет, самый точный индикатор нагрева объекта, искажается гравитацией. Также яркость звезды косвенно связана с ее составом. Чем меньше в веществе светила элементов, тяжелее гелия и водорода, тем больше она может набрать массы — критической характеристики в определении яркости звезды.
https://youtube.com/watch?v=ai7unNTFjms
Абсолютная звёздная величина для звёзд
Абсолютная звёздная величина (M) для звёзд определяется как видимая звёздная величина объекта, если бы он был расположен на расстоянии 10 парсек от наблюдателя. Абсолютная болометрическая (учитывающая полное излучение во всех диапазонах электромагнитных волн) звёздная величина Солнца +4,7.
Если известна видимая звёздная величина m{\displaystyle m} и расстояние до объекта d{\displaystyle d}, можно вычислить абсолютную звёздную величину по формуле:
- M=m−5lgdd{\displaystyle M=m-5\lg {\frac {d}{d_{0}}}}
где d{\displaystyle d_{0}} = 10 пк ≈ 32,616 световых лет
(Также можно воспользоваться формулами: M=m+5−5lgr{\displaystyle M=m+5-5\lg r} и M=m+5+5lgπ′′{\displaystyle M=m+5+5\lg \pi \prime \prime }, где r{\displaystyle r} и π′′{\displaystyle \pi \prime \prime } — расстояние до звезды в парсеках и годичный параллакс в секундах соответственно).
Соответственно, если известны видимая и абсолютная звёздные величины, можно вычислить расстояние по формуле
- d=d10m−M5{\displaystyle d=d_{0}10^{\frac {m-M}{5}}}
Абсолютная звёздная величина связана со светимостью следующим соотношением:
- lgLL⊙=,4(M⊙−M){\displaystyle \lg {\frac {L}{L_{\odot }}}=0,4(M_{\odot }-M)}
где L⊙{\displaystyle L_{\odot }} и M⊙{\displaystyle M_{\odot }} — светимость и абсолютная звёздная величина Солнца.
Абсолютная звездная величина и светимость
Для того чтобы была возможность сравнить истинную яркость космических тел, была разработана такая характеристика как абсолютная звездная величина. Согласно ней вычисляется значение видимой звездной величины объекта, если бы этот объект располагался на за 10 парсек (32,62 световых лет) от Земли. В таком случае отсутствуют зависимость от расстояния до наблюдателя при сравнении различных звезд.
Абсолютная звездная величина для космических объектов в Солнечной системе использует иное расстояние от тела к наблюдателю. А именно 1 астрономическую единицу, при этом, в теории, наблюдатель должен находиться в центре Солнца.
Более современной и полезной величиной в астрономии стала «светимость». Эта характеристика определяет полную энергию, которую излучает космическое тело за определенный отрезок времени. Для ее вычисления как раз и служит абсолютная звездная величина.
Спектральная зависимость
Как уже говорилось ранее, звездная величина может быть измерена для различных видов электромагнитного излучения, а потому имеет разные значения для каждого диапазона спектра. Для получения картинки какого-либо космического объекта астрономы могут использовать фотопластинки, которые более чувствительны к высокочастотной части видимого света, и на изображении звезды получаются голубыми. Такая звездная величина называется «фотографической», mPv. Чтобы получилось значение близкое к визуальному («фотовизуальное», mP), фотопластинку покрывают специальной ортохроматической эмульсией и используют желтый светофильтр.
Снимок Солнца через темный светофильтр
Учеными была составлена так называемая фотометрическая система диапазонов, благодаря которой можно определять основные характеристики космических тел, такие как: температура поверхности, степень отражения света (альбедо, не для звезд), степень межзвездного поглощения света и прочие. Для этого производится фотографирование светила в разных спектрах электромагнитного излучения и последующие сравнение результатов. Для фотографии наиболее популярны следующие фильтры: ультрафиолетовый, синий (фотографическая звездная величина) и желтый (близкий к фотовизуальному диапазону).
Фотография с запечатленными энергиями всех диапазонов электромагнитных волн определяет так называемую болометрическую звездную величину (mb). С ее помощью, зная расстояние и степень межзвездного поглощения, астрономы вычисляют светимость космического тела.
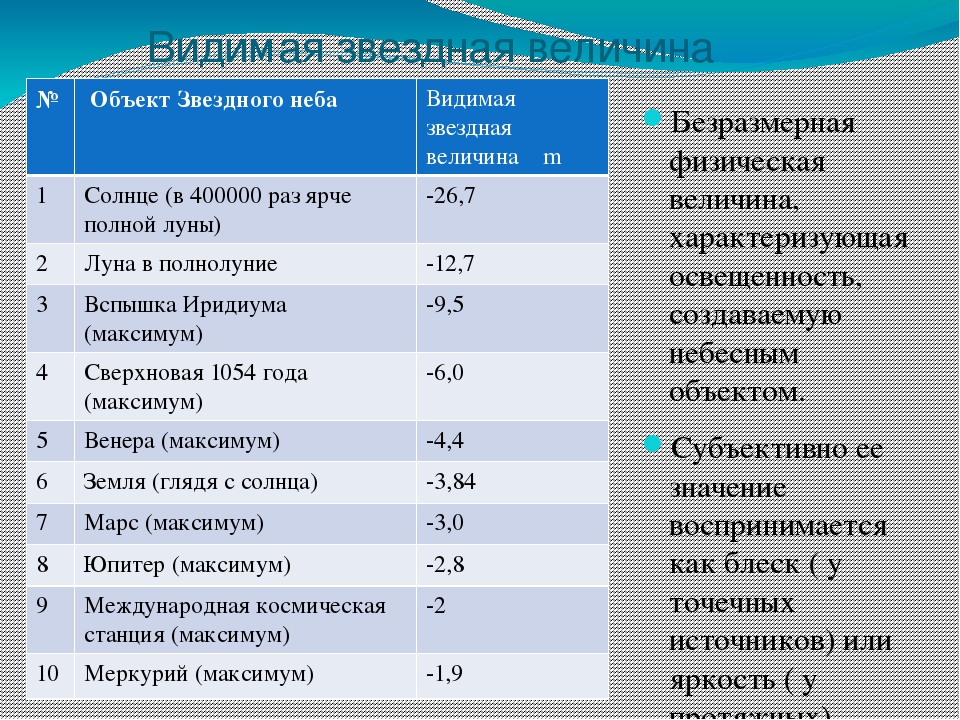
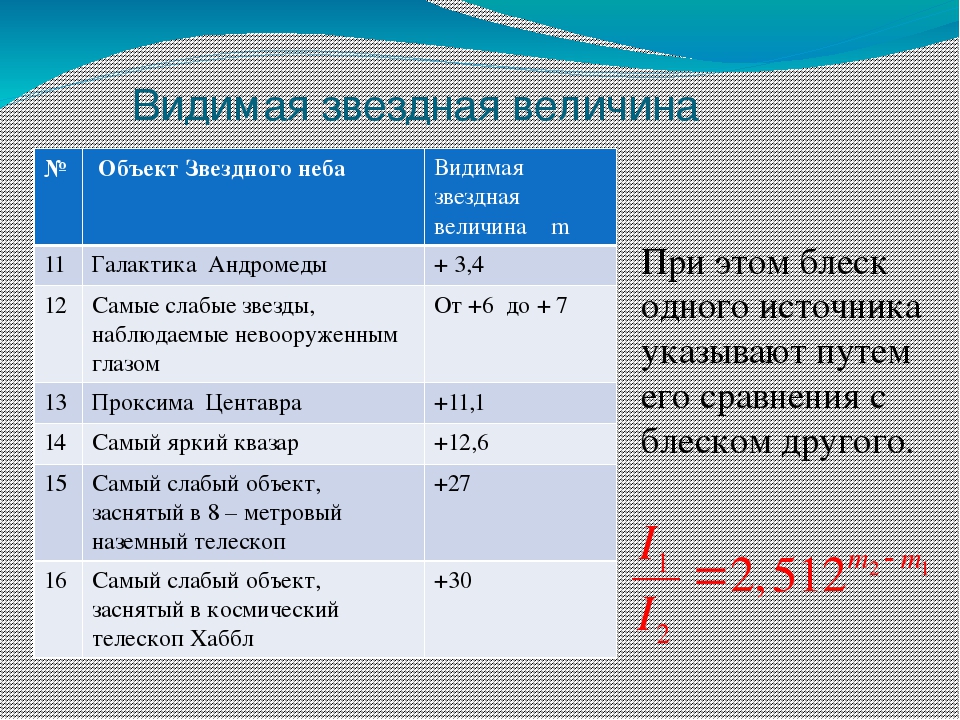
Звездные величины некоторых объектов
- Солнце = −26,7m
- Полная Луна = −12,7m
- Вспышка Иридиума = −9,5 m. Iridium – это система из 66 спутников, которых движутся по орбите Земли и служат для передачи голоса и прочих данных. Периодически поверхность каждого из трех главных аппаратов отсвечивает солнечный свет в сторону Земли, создавая ярчайшую плавную вспышку на небосводе до 10 секунд.
Вспышка Иридиума
- Ярчайший взрыв сверхновой, в 1054-м году, вследствие которого, как считается, образовалась Крабовидная туманность = −6,0 m. Если верить записям китайских и арабских астрономов, сверхновую можно было наблюдать целых 23 дня, даже в дневное время невооруженным глазом.
- Венера во время максимума = −4,4 m
- Земля, для наблюдателя на Солнце = −3,84 m
- Марс во (макс.) = −3,0 m
- Юпитер (макс.) = −2,8 m
- МКС (макс.) = −2 m
Трасса Международной космической станции на фоне созвездия Большой Медведицы
- α Центавра = −0,27 m
- Вега = +0,03 m
- Галактика Андромеды = +3,4 m
- Тусклые звезды, которые еще может уловить человеческий глаз = +6 m — +7 m
- Проксима Центавра = +11,1 m
- Ярчайший квазар = +12,6 m
- Объекты, улавливаемые наземными телескопами (8-миметровыми) = +27 m
- Объекты, улавливаемые космическим телескопом Хаббл = +30 m