Оптические линзы (физика): определение, описание, формула и решение

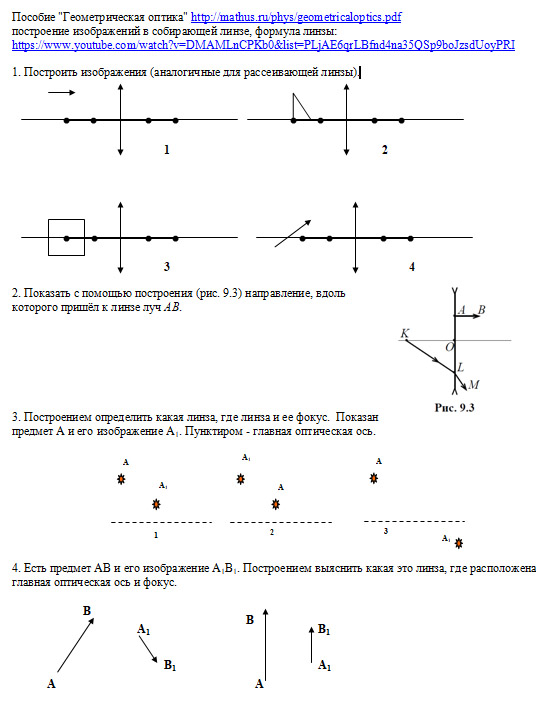
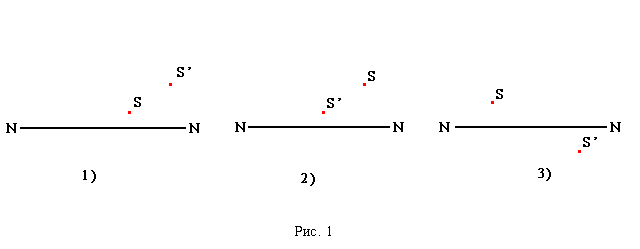Построение изображений в линзах

Для построения изображения в линзах следует помнить:

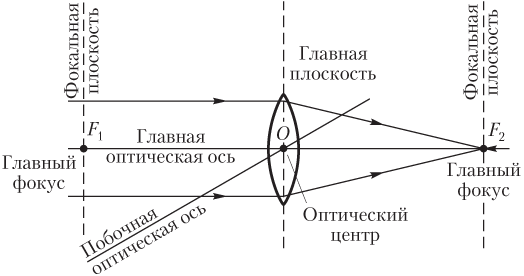
1. луч, идущий вдоль главной оптической оси линзы, не преломляется;
2. луч, проходящий через оптический центр линзы, не преломляется;
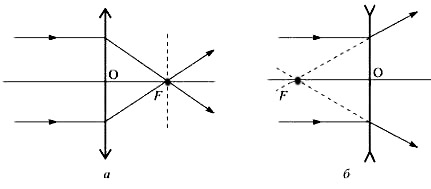
3. луч, падающий на собирающую линзу параллельно главной оптической оси, после преломления пройдет через фокус линзы;
4. луч, падающий на рассеивающую линзу параллельно главной оптической оси, преломится так, что его мнимое продолжение пройдет через фокус линзы, а сам луч – противоположно мнимому продолжению;
5. луч, падающий на собирающую линзу через фокус, после преломления пройдет параллельно главной оптической оси линзы;
6. произвольный луч после преломления в собирающей линзе пойдет через побочный фокус (точку фокальной плоскости, в которой ее пересечет параллельная произвольному лучу побочная оптическая ось);
7. произвольный луч, падающий на рассеивающую линзу, преломится так, что его мнимое продолжение пройдет через точку, в которой пересечет фокальную плоскость линзы побочная оптическая ось, параллельная произвольному лучу.

Изображение, даваемое тонкой линзой, может быть действительным или мнимым.

Действительное изображение получается в результате пересечения преломленных в линзе лучей, исходящих из данной точки.

Мнимое изображение получается в результате пересечения продолжений преломленных в линзе лучей, исходящих из данной точки.

Построение изображений точки, даваемых собирающей линзой

Если точка находится за двойным фокусом линзы, то ее действительное изображение получается между фокусом и двойным фокусом по другую сторону от линзы.

Если точка находится в двойном фокусе линзы, то его действительное изображение получается в двойном фокусе по другую сторону от линзы.

Если точка находится между фокусом и двойным фокусом линзы, то его действительное изображение получается за двойным фокусом по другую сторону от линзы.

Если точка находится в фокусе линзы, то его изображение находится в бесконечности.

Если точка находится между линзой и фокусом, то его мнимое изображение получается по ту же сторону от линзы.

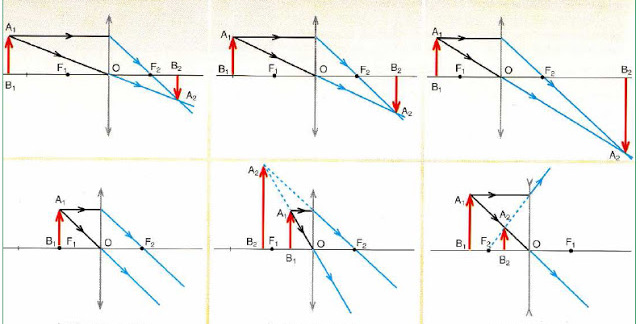
Построение изображений предмета, даваемых собирающей линзой

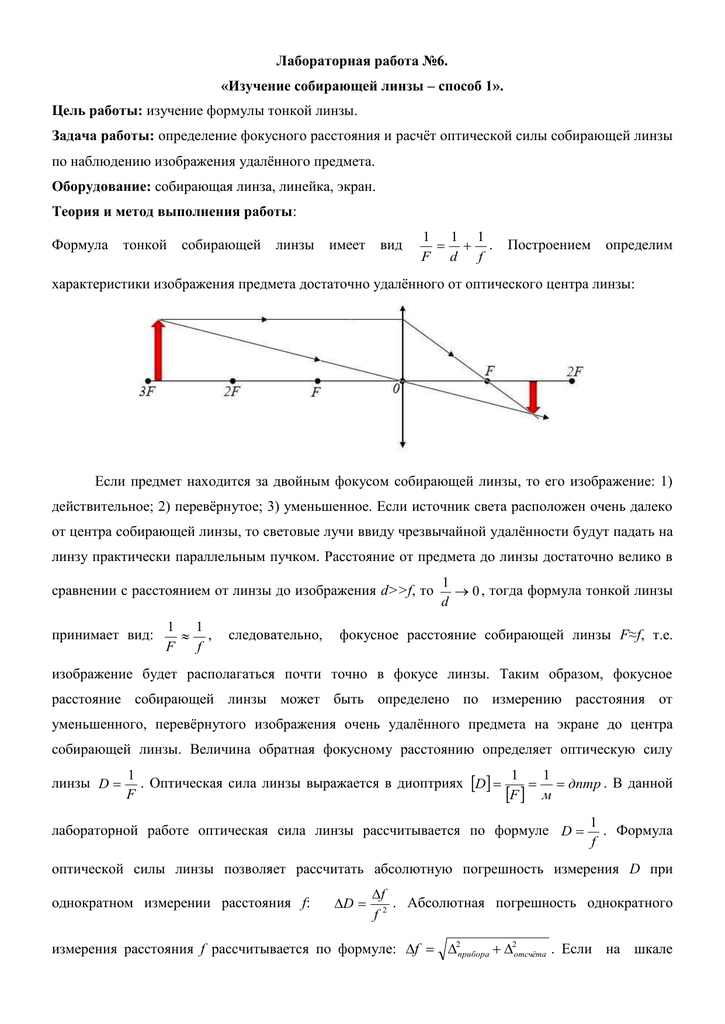
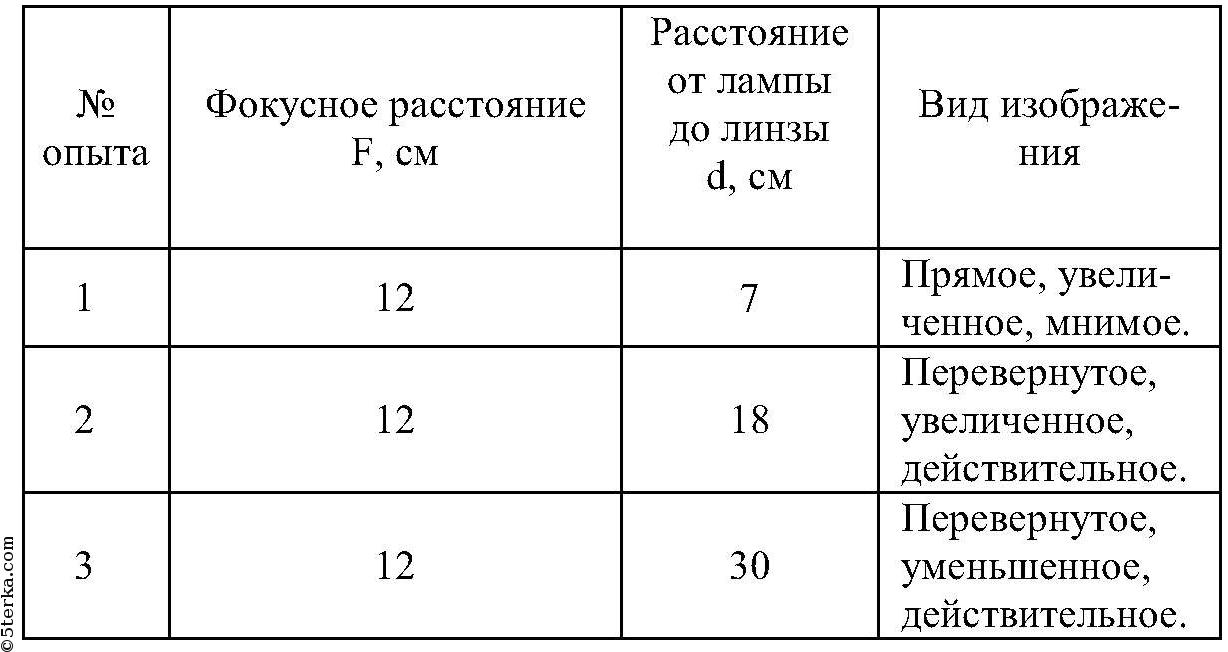
Если предмет находится за двойным фокусом линзы, то его изображение получается действительным, перевернутым, уменьшенным, по другую сторону от линзы.

Если предмет находится в двойном фокусе линзы, то его изображение получается действительным, перевернутым, равным по размерам предмету, в двойном фокусе по другую сторону от линзы.

Если предмет находится между фокусом и двойным фокусом линзы, то его изображение получается действительным, перевернутым, увеличенным, по другую сторону от линзы.

Если предмет находится в фокусе линзы, то его изображение находится в бесконечности.

Если предмет находится между линзой и фокусом, то его изображение получается мнимым, прямым, увеличенным, по ту же сторону от линзы.

Построение изображений точки, даваемых рассеивающей линзой

В рассеивающей линзе изображение точки всегда получается мнимым, по ту же сторону от линзы.

Построение изображений предмета, даваемых рассеивающей линзой

Изображение предмета в рассеивающей линзе всегда получается мнимым, прямым, уменьшенным, по ту же сторону от линзы.

Важно!
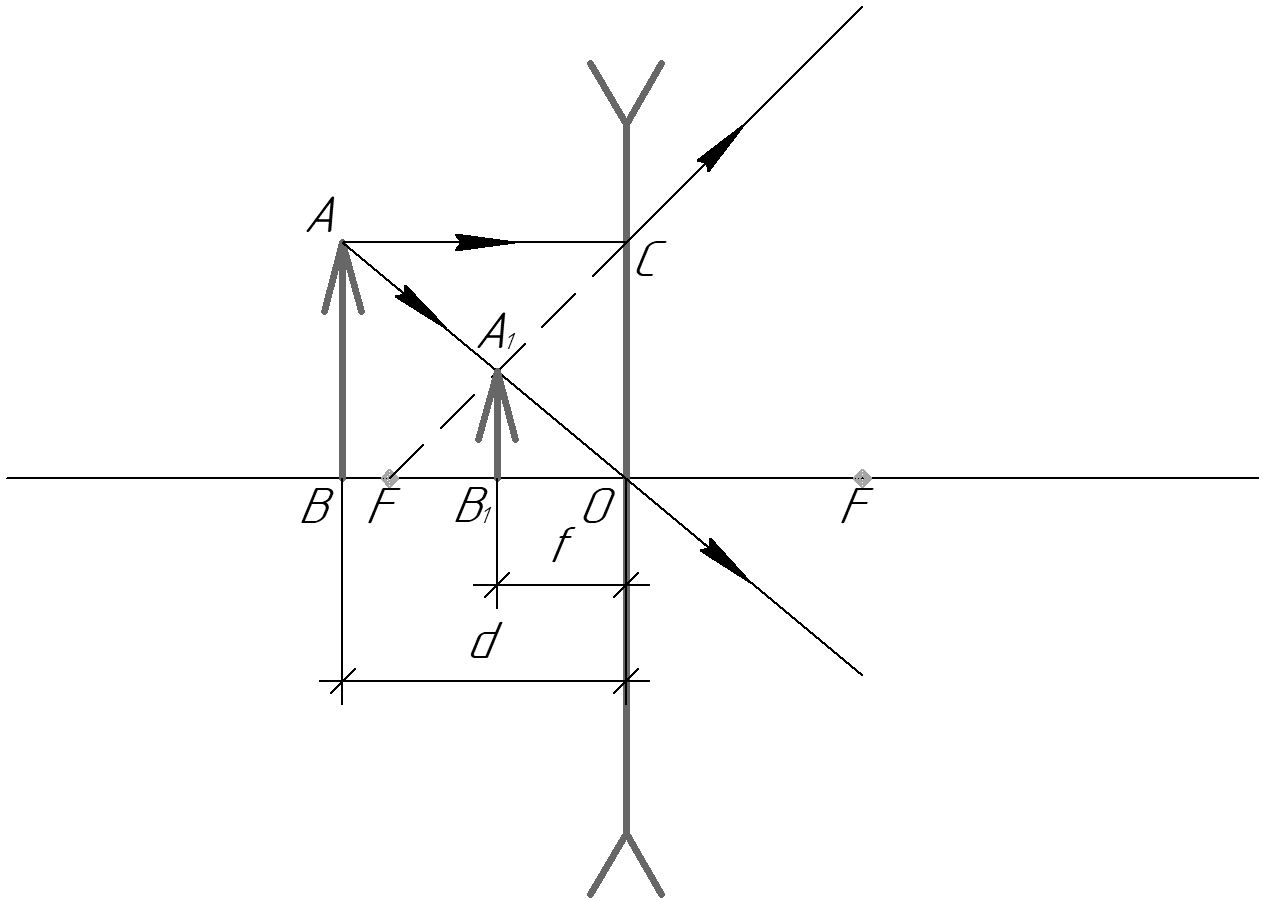
При решении задач на прохождение световых лучей сквозь линзы и получение изображений в них прежде всего выясните, о какой линзе идет речь: собирающей или рассеивающей. Обязательно сделайте чертеж, на котором соответствующими буквами укажите все основные расстояния: расстояние от предмета до линзы, расстояние от линзы до изображения, фокусное расстояние

Также обязательно укажите оптический центр линзы и оба фокуса по разные стороны от линзы.

При построении изображения следует заранее выучить, каким оно должно быть при соответствующем расположении предмета относительно линзы и где находиться (действительным или мнимым, увеличенным или уменьшенным, прямым или обратным). В противном случае при неверном построении, когда вы чуть-чуть искривите луч или он пойдет неточно через фокус или центр, изображение может оказаться не там, где надо, или вместо увеличенного уменьшенным, и тогда в решении появится ошибка.

Краткая история

Любопытно привести этимологию слова «линза». Оно ведет происхождение от латинских слов lens и lentis, что означает «чечевица», поскольку оптические объекты по своей форме действительно похожи на плод этого растения.

Преломляющая способность сферических прозрачных тел была известна еще древним римлянам. Для этой цели они применяли круглые стеклянные сосуды, наполненные водой. Сами же стеклянные линзы начали изготавливаться только в XIII веке в Европе. Использовались они в качестве инструмента для чтения (современные очки или лупа).

Активное использование оптических объектов при изготовлении телескопов и микроскопов относится к XVII (в начале этого века Галилей изобрел первый телескоп). Отметим, что математическая формулировка закона преломления Стелла, без знания которой невозможно изготавливать линзы с заданными свойствами, была опубликована голландским ученым в начале того же XVII века.

Ход лучей в системе линз

Ход лучей в системе линз строится теми же методами, что и для одиночной линзы.

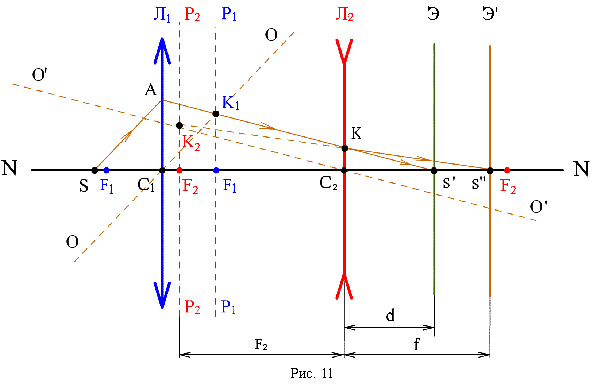
Рассмотрим систему из двух линз, одна из которых имеет фокусное расстояние OF, а вторая O₂F₂. Строим путь SAB для первой линзы и продолжаем отрезок AB до вхождения во вторую линзу в точке C.

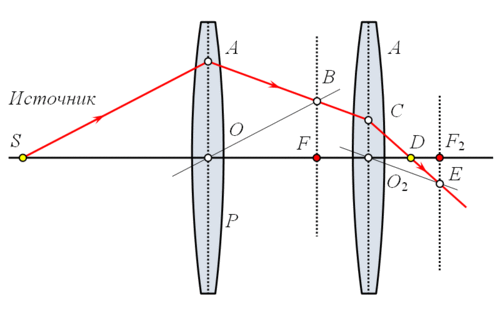
Из точки O₂ строим луч O₂E, параллельный AB. При пересечении с фокальной плоскостью второй линзы этот луч даст точку E. Согласно второму свойству тонкой линзы луч AB после прохождения через вторую линзу пойдёт по пути CE. Пересечение этой линии с оптической осью второй линзы даст точку D, где сфокусируются все лучи, вышедшие из источника S и прошедшие через обе линзы.

Линзы по материалу

Если не вдаваться в химические и технологические подробности, то по материалу очковые линзы можно разделить на:

• пластиковые (полимерные, органические);
• стеклянные (минеральные).

Пластиковые, в свою очередь делятся на:

• собственно полимерные;
• поликарбонатные;
• новые материалы под разными торговыми названиями (например, trivex 1,53).

У пластиковых линз удельный вес в 2 и более раз меньше, чем у минеральных стекол. Это и стало главной причиной завоевания мирового рынка очковых линз органическими полимерами.

Существуют поликарбонатные органические линзы. Поликарбонат является самым ударопрочным. Даже если его разбить, он не разлетаются на мелкие кусочки с острыми опасными для глаза краями, как это происходит с минеральными очковыми линзами. Поликарбонатные очковые линзы считаются самыми безопасными из имеющихся на рынке очковых линз. Особенно они рекомендованы детям и спортсменам.

Закон преломления света

Преломление света – это изменение направления распространения светового луча на границе раздела двух сред.

Угол преломления – это угол между преломленным лучом и перпендикуляром к границе раздела двух сред.

​\( \gamma \)​ – угол преломления

Законы преломления света

• Лучи падающий и преломленный лежат в одной плоскости с перпендикуляром, восстановленным в точку падения луча к преломляющей поверхности.
• Отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных двух сред и равная относительному показателю преломления двух сред:

где ​\( n_{21} \)​ – относительный показатель преломления.

Первой является среда, в которой распространяется падающий луч, второй является среда, в которой распространяется преломленный луч.

Относительный показатель преломления равен отношению абсолютного показателя преломления второй среды к абсолютному показателю преломления первой среды:

где ​\( n_1 \)​ – абсолютный показатель преломления первой среды; ​\( n_2 \)​ – абсолютный показатель преломления второй среды.

Абсолютный показатель преломления показывает, во сколько раз скорость света в вакууме больше, чем в данной среде:

где ​\( c \)​ – скорость света в вакууме, ​\( v \)​ – скорость распространения света в данной среде.

Относительный показатель преломления показывает, во сколько раз скорость распространения света в первой среде больше, чем во второй:

Среда, у которой абсолютный показатель преломления больше, является оптически более плотной средой.

Среда, у которой абсолютный показатель преломления меньше, является оптически менее плотной средой.

Следствия закона преломления света

Если свет падает из оптически менее плотной среды в оптически более плотную, то угол падения больше угла преломления:

Если свет падает из оптически более плотной среды в оптически менее плотную, то угол падения меньше угла преломления:

Если луч падает на плоско параллельную пластину, изготовленную из оптически более плотного вещества, чем окружающая среда, то луч не изменяет своего направления, а лишь смещается на некоторое расстояние.

​\( x \)​ – смещение луча от первоначального направления:

где ​\( d \)​ – толщина пластины.

Важно!
Если в условии задачи говорится, что «кажется, что луч падает под углом ​\( \varphi_1 \)​ к поверхности воды», то имеют в виду не кажущийся угол падения ​\( \alpha_1 \)​, а угол между кажущимся падающим лучом и поверхностью воды \( \varphi_1 \)

Предыстория создания

Первое упоминание о контактных линзах было в 1508 году. Леонардо да Винчи в своих трудах высказал теорию о том, что сфера, заполненная жидкостью, может откорректировать зрение людей, которые плохо видят окружающие предметы

На самом деле он не считал данное изобретение контактными линзы, он первый обратил внимание о возможности преломления света, который проходит через глаза человека

Его труды решил продолжить Рене Декарт. В 1632 году он впервые поместил в глаза емкость, заполненную водой. В первые несколько минут человек действительно мог видеть окружающие предметы. Но такое строение линзы быстро запотевало, человеку неудобно и больно. При этом отсутствовала возможность моргания, роговица глаз сушилась, поэтому образовывать острая боль.

Наиболее приемлемую модель создал Джон Гершель. Именно этот ученый описал в своих трудах контактную линзу, которая должна повторять форму глаза. Нынешнему поколению это понятно, но у ученых в те времена не было возможности рассмотреть данный вопрос правильно.

Линзы по типу

По типу очковые линзы можно разделить на:

• однофокальные – то есть имеющие один фокус (одну диоптрию);
• мультифокальные – сложные по форме линзы, имеющие несколько фокусов (три и два соответственно).

Если у Вас близорукость (миопия) или дальнозоркость (гиперметропия), с астигматизмом или без – не важно, то Вам нужны обычные монофокальные линзы. Если у Вас пресбиопия (в основном это имеет место после 40 лет), то есть ухудшение Вашего зрения связано с возрастом (аккомодация глаза уменьшается и связано это с уменьшением эластичности хрусталика), то Вам могут понадобиться мультифокальные линзы, которые, в свою очередь подразделяются на:

Если у Вас пресбиопия (в основном это имеет место после 40 лет), то есть ухудшение Вашего зрения связано с возрастом (аккомодация глаза уменьшается и связано это с уменьшением эластичности хрусталика), то Вам могут понадобиться мультифокальные линзы, которые, в свою очередь подразделяются на:

• бифокальные;
• прогрессивные;
• офисные.

Бифокальные линзы

Бифокальные линзы позволяют скомпенсировать сразу два дефекта зрения. Такие линзы предназначены для чёткого видения на больших расстояниях и одновременно, позволяют различать близко расположенные предметы благодаря специальному сектору в нижней части линзы. Это позволяет заменить двое очков: «для дали» и «для чтения»

Важной особенностью является то, что правая и левая линза не взаимозаменяемы

Прогрессивные линзы

Прогрессивные линзы (ещё их называют вариофокальными) — это более современные и совершенные линзы, во многом аналогичные бифокальным, но не имеющие чётко выраженных зон для разных расстояний. За счёт этого внешне они ничем не отличаются от обычных линз. Позволяют заменить двое очков: «для дали» и «для чтения». Кроме этого, имеют переходную зону оптического действия (коридор прогрессии). В результате такой сложный дизайн линзы помогает обеспечить чёткое видение во всём диапазоне необходимых расстояний даже для глаз с ослабленной аккомодацией (когда пациент не способен чётко различать предметы и вблизи и вдали)

Важной особенностью является то, что правая и левая линза не взаимозаменяемы

В периферийных зонах, расположенных справа и слева от коридора прогрессии пациент может наблюдать искажения, избавиться от которых невозможно. Однако в современных прогрессивных линзах эти искажения настолько минимизированы, что замечаются, обычно, только в начальный период адаптации к новой линзе.

Офисные линзы

Офисные линзы являются частным случаем прогрессивных линз, но предназначены для коррекции зрения на ближних (чтение, работа с документами) и средних расстояниях (компьютер, офис). От прогрессивных линз они отличаются тем, что не содержат зону для дали (предполагается, что зрение вдаль в подобных случаях не нуждается в коррекции). За счёт этого зоны, обеспечивающие чёткое видение, по сравнению с прогрессивными линзами существенно расширены.

При этом они обладают важным преимуществом перед обычными линзами для близи (для чтения). Дело в том, что линзы для близи предназначены для расстояний около 40 см. Однако в реальной жизни гораздо чаще приходится постоянно переводить взгляд с одних расстояний на другие. Прежде всего, это работа на компьютере, когда взгляд должен фокусироваться то на документах, то на клавиатуре, то на экране монитора и так десятки и сотни раз в течение дня. Добавьте сюда необходимость периодически отвлекаться на собеседника, и станет понятно, что нагрузка для глаз получается запредельной.

Врачи-офтальмологи давно заметили, что у пациентов с пресбиопией, раньше перешедших на мультифокальные линзы (офисные или прогрессивные), естественные процессы ослабления зрения, связанные с возрастом, протекают ощутимо медленнее.

Офисные линзы также относятся к классу мультифокальных, однако, в силу того, что они предназначены для коррекции зрения на ближних и средних расстояниях, основной рефракцией в них принято считать оптическую силу для близи, а уменьшение рефракции в зоне, для средних расстояний обозначать через дегрессию (или уменьшение).

Как следует из названия, очки с такими линзами предназначены для помещений (офиса или дома). Использовать их вне помещений (на улице, за рулём автомобиля) не рекомендуется, поскольку они не предусматривают чёткого видения предметов на больших расстояниях.

Расчёт фокусного расстояния и оптической силы линзы

Значение фокусного расстояния для линзы может быть рассчитано по следующей формуле:

nf=(n−n){1R1−1R2+(n−n)dnR1R2}{\displaystyle {\frac {n_{0}}{f}}=(n-n_{0})\left\{{\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}+{\frac {(n-n_{0})d}{nR_{1}R_{2}}}\right\}}, где

n{\displaystyle n} — показатель преломления материала линзы, n{\displaystyle n_{0}} — показатель преломления среды, окружающей линзу,

d{\displaystyle d} — расстояние между сферическими поверхностями линзы вдоль оптической оси, также известное как толщина линзы,

R1{\displaystyle R_{1}} — радиус кривизны поверхности, которая ближе к источнику света (дальше от фокальной плоскости),

R2{\displaystyle R_{2}} — радиус кривизны поверхности, которая дальше от источника света (ближе к фокальной плоскости),

Для R1{\displaystyle R_{1}} в этой формуле, знак радиуса положителен, если поверхность выпуклая, и отрицателен, если вогнутая. Для R2{\displaystyle R_{2}} наоборот — положителен, если линза вогнутая, и отрицателен, если выпуклая. Если d{\displaystyle d} пренебрежительно мало, относительно её фокусного расстояния, то такая линза называется тонкой, и её фокусное расстояние можно найти как:

nf=(n−n){1R1−1R2}.{\displaystyle {\frac {n_{0}}{f}}=(n-n_{0})\left\{{\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}\right\}.}

(Эту формулу также называют формулой тонкой линзы.) Величина фокусного расстояния положительна для собирающих линз, и отрицательна для рассеивающих. Величина nf{\displaystyle {\frac {n_{0}}{f}}} называется оптической силой линзы. Оптическая сила линзы измеряется в диоптриях, единицами измерения которых являются м−1. Оптическая сила также зависит от показателя преломления окружающей среды n{\displaystyle n_{0}}.

Указанные формулы могут быть получены аккуратным рассмотрением процесса построения изображения в линзе с использованием закона Снелла, если перейти от общих тригонометрических формул к параксиальному приближению. Кроме того, для вывода формулы тонкой линзы удобно заменить её треугольной призмой и затем использовать формулу угла отклонения этой призмы.

Линзы симметричны, то есть они имеют одинаковое фокусное расстояние независимо от направления света — слева или справа, что, однако, не относится к другим характеристикам, например, аберрациям, величина которых зависит от того, какой стороной линза повёрнута к свету.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. При попадании солнечного света на капли дождя иногда образуется радуга. Появление в радуге полос различного цвета обусловлено явлением

1) преломления света
2) поглощения света
3) дисперсии света
4) многократного отражения света

2. На линзу падает луч, показанный на рисунке. Ходу луча после преломления в линзе соответствует линия

1) 1
2) 2
3) 3
4) 4

3. На рисунке изображён ход падающего на линзу луча. Ходу прошедшего через линзу луча соответствует пунктирная линия

1) 1
2) 2
3) 3
4) 4

4. Предмет находится от собирающей линзы на расстоянии, равном ​\( 2F \)​. На каком расстоянии от линзы находится изображение предмета?

1) меньшем ​\( F \)​
2) между ​\( F \)​ и ​\( 2F \)​
3) большем \( 2F \)
4) равном \( 2F \)

5. Предмет находится от собирающей линзы на расстоянии, меньшем \( 2F \) и большем \( F \). На каком расстоянии от линзы находится изображение предмета?

1) большем \( 2F \)
2) между \( F \) и \( 2F \)
3) меньшем \( F \)
4) равном \( 2F \)

6. Линза, фокусное расстояние которой \( F \), дает действительное уменьшенное изображение предмета. На каком расстоянии от линзы находится предмет?

1) меньше \( F \)
2) больше \( F \) и меньше \( 2F \)
3) равном \( 2F \)
4) большем \( 2F \)

7. На рисунке изображены три предмета: А, Б и В. Изображение какого(-их) предмета(-ов) в тонкой собирающей линзе с фокусным расстоянием \( F \) будет увеличенным, прямым и мнимым?

1) только А
2) только Б
3) только В
4) всех трёх предметов

8. На рисунке показаны положения главной оптической оси линзы (прямая ​\( a \)​), предмета ​\( S \)​ и его изображения ​\( S_1 \)​. Согласно рисунку

1) линза является собирающей
2) линза является рассеивающей
3) линза может быть как собирающей, так и рассеивающей
4) изображение не может быть получено с помощью линзы

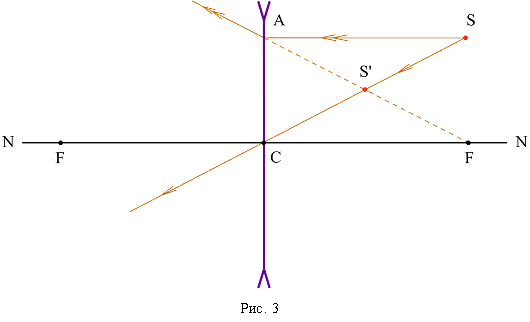
9. На рисунке показаны положения главной оптической оси ​\( OO \)​ линзы, источника ​\( S \)​ и его изображения ​\( S_1 \)​ в линзе. Согласно рисунку

1) линза является рассеивающей
2) линза является собирающей
3) линза может быть как собирающей, так и рассеивающей
4) изображение не может быть получено с помощью линзы

10. На сетчатке глаза изображение предмета

1) действительное уменьшенное перевёрнутое
2) мнимое уменьшенное прямое
3) мнимое увеличенное перевёрнутое
4) действительное увеличенное прямое

11. Установите соответствие между световым явлением (в левом столбце таблицы) и его применением (в правом столбце таблицы). В таблице под номером положения предмета левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.

ПОЛОЖЕНИЕ ПРЕДМЕТА
A) отражение света от гладкой поверхности
Б) преломление света рассеивающей линзой
B) преломление света собирающей линзой

ПОЛОЖЕНИЕ ИЗОБРАЖЕНИЯ
1) очки для дальнозорких людей
2) зеркало
3) очки для близоруких людей

12. Установите соответствие между положением предмета (в левом столбце таблицы) и положением изображения в линзе (в правом столбце таблицы). В таблице под номером положения предмета левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.

ПОЛОЖЕНИЕ ПРЕДМЕТА
A) на расстоянии, большем ​\( 2F \)​
Б) между \( F \) и \( 2F \)
B) между \( F \) и линзой

ПОЛОЖЕНИЕ ИЗОБРАЖЕНИЯ
1) перевернутое на расстоянии, большем \( 2F \)
2) уменьшенное между \( F \) и \( 2F \)
3) увеличенное прямое мнимое
4) действительное на расстоянии \( 2F \) от линзы
5) уменьшенное на расстоянии, большем \( 2F \)

Часть 2

13. После прохождения оптического прибора, закрытого на рисунке ширмой, ход лучей 1 и 2 изменился на 1 и 2. Какое оптическое стекло: собирающая линза, рассеивающая линза, плоское зеркало или плоскопараллельная стеклянная пластина находится за ширмой?

Нахождение расстояния до изображения

Чтобы определять, на каком расстоянии появится изображение, зная положение самого предмета, приведем формулу линзы в физике: 1/f = 1/d_o + 1/d_i, где d_o и d_i — расстояние до предмета и до его изображения от оптического центра, соответственно, f — главный фокус. Если речь идет о собирающем оптическом стекле, тогда число f будет положительным. Наоборот, для рассеивающей линзы f — отрицательное.

Воспользуемся этой формулой и решим простую задачу: пусть предмет находится на расстоянии d_o = 2*f от центра собирающего оптического стекла. Где появится его изображение?

Из условия задачи имеем: 1/f = 1/(2*f)+1/d_i. Откуда: 1/d_i = 1/f — 1/(2*f) = 1/(2*f), то есть d_i = 2*f. Таким образом, изображение появится на расстоянии двух фокусов от линзы, но уже с другой стороны, чем сам предмет (об этом говорит положительный знак величины d_i).

Виды собирающих и рассеивающих линз.

Мы рассмотрели две линзы: двояковыпуклую линзу, которая является собирающей, и двояковогнутую линзу, которая является рассеивающей. Существуют и другие примеры собирающих и рассеивающих линз.

Полный набор собирающих линз представлен на рис. 7.

Помимо известной нам двояковыпуклой линзы, здесь изображены:плосковыпуклая линза, у которой одна из поверхностей плоская, и вогнуто-выпуклая линза, сочетающая вогнутую и выпуклую граничные поверхности

Обратите внимание, что у вогнуто-выпуклой линзы выпуклая поверхность в большей степени искривлена (радиус её кривизны меньше); поэтому собирающее действие выпуклой преломляющей поверхности перевешивает рассеивающее действие вогнутой поверхности, и линза в целом оказывается собирающей

Все возможные рассеивающие линзы изображены на рис. 8.

Наряду с двояковогнутой линзой мы видим плосковогнутую (одна из поверхностей которой плоская) и выпукло-вогнутую линзу. Вогнутая поверхность выпукло-вогнутой линзы искривлена в большей степени, так что рассеивающее действие вогнутой границы преобладает над собирающим действием выпуклой границы, и в целом линза оказывается рассеивающей.

Рис. 7. Собирающие линзы

Рис. 8. Рассеивающие линзы

Попробуйте самостоятельно построить ход лучей в тех видах линз, которые мы не рассмотрели, и убедиться, что они действительно являются собирающими или рассеивающими. Это отличное упражнение, и в нём нет ничего сложного — ровно те же самые построения, которые мы проделали выше!

Линейное увеличение

Линейным увеличением m=a2b2ab{\displaystyle m={{a_{2}b_{2}} \over {ab}}} (для рисунка из предыдущего раздела) называется отношение размеров изображения к соответствующим размерам предмета. Это отношение может быть также выражено дробью m=a2b2ab=vu{\displaystyle m={{a_{2}b_{2}} \over {ab}}={v \over u}}, где v{\displaystyle v} — расстояние от линзы до изображения; u{\displaystyle u} — расстояние от линзы до предмета.

Здесь m{\displaystyle m} есть коэффициент линейного увеличения, то есть число, показывающее во сколько раз линейные размеры изображения меньше (больше) действительных линейных размеров предмета.

В практике вычислений гораздо удобнее это соотношение выражать в значениях u{\displaystyle u} или f{\displaystyle f}, где f{\displaystyle f} — фокусное расстояние линзы.

m=fu−f; m=v−ff{\displaystyle m={f \over {u-f}};\ m={{v-f} \over f}}.

Ход лучей в тонкой линзе

Линза, для которой толщина принята равной нулю, в оптике называется «тонкой». Для такой линзы показывают не две главных плоскости, а одну, в которой как бы сливаются вместе передняя и задняя.

Рассмотрим построение хода луча произвольного направления в тонкой собирающей линзе. Для этого воспользуемся двумя свойствами тонкой линзы:

1. — Луч, прошедший через оптический центр линзы, не меняет своего направления;
2. — Параллельные лучи, проходящие через линзу, сходятся в фокальной плоскости.

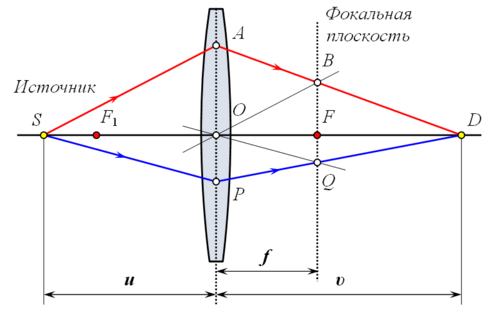
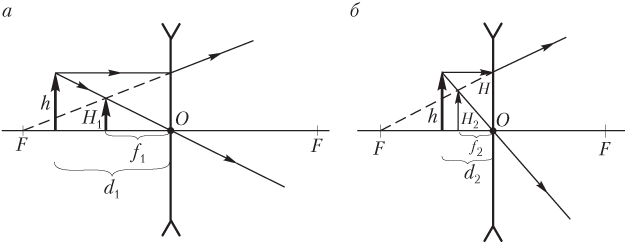
Рассмотрим луч SA произвольного направления, падающий на линзу в точке A. Построим линию его распространения после преломления в линзе. Для этого построим луч OB, параллельный SA и проходящий через оптический центр O линзы. По первому свойству линзы луч OB не изменит своего направления и пересечёт фокальную плоскость в точке B. По второму свойству линзы параллельный ему луч SA после преломления должен пересечь фокальную плоскость в той же точке. Таким образом, после прохождения через линзу луч SA пойдёт по пути AB.

Аналогичным образом можно построить другие лучи, например луч SPQ.

Обозначим расстояние SO от линзы до источника света через u, расстояние OD от линзы до точки фокусировки лучей через v, фокусное расстояние OF через f. Выведем формулу, связывающую эти величины.

Рассмотрим две пары подобных треугольников: △SOA{\displaystyle \triangle SOA} и △OFB{\displaystyle \triangle OFB}, △DOA{\displaystyle \triangle DOA} и △DFB{\displaystyle \triangle DFB}. Запишем пропорции

OAu=BFf;OAv=BFv−f.{\displaystyle {\frac {OA}{u}}={\frac {BF}{f}};\qquad {\frac {OA}{v}}={\frac {BF}{v-f}}.}

Разделив первую пропорцию на вторую, получим

vu=v−ff;vu=vf−1.{\displaystyle {\frac {v}{u}}={\frac {v-f}{f}};\qquad {\frac {v}{u}}={\frac {v}{f}}-1.}

После деления обеих частей выражения на v и перегруппировки членов, приходим к окончательной формуле

1u+1v=1f{\displaystyle {\frac {1}{u}}+{\frac {1}{v}}={\frac {1}{f}}}

где f{\displaystyle f{\frac {}{}}} — фокусное расстояние тонкой линзы.