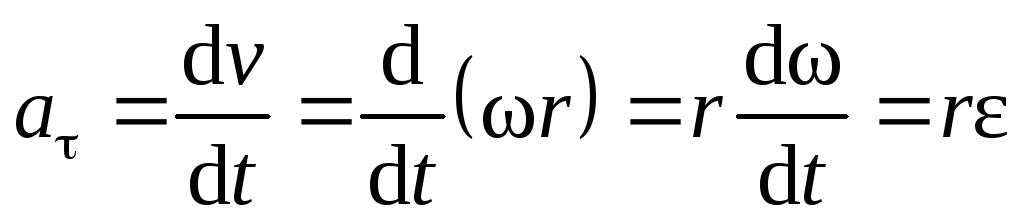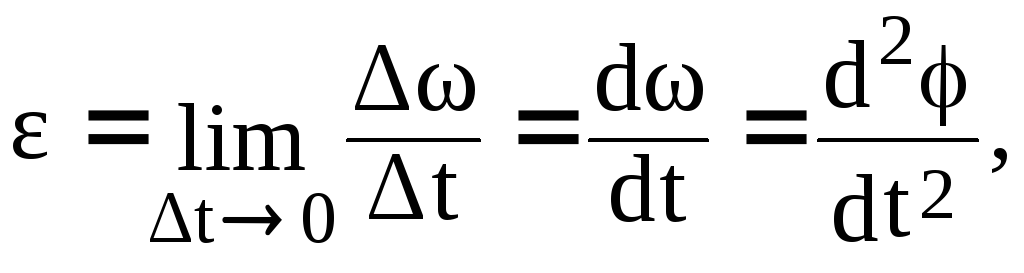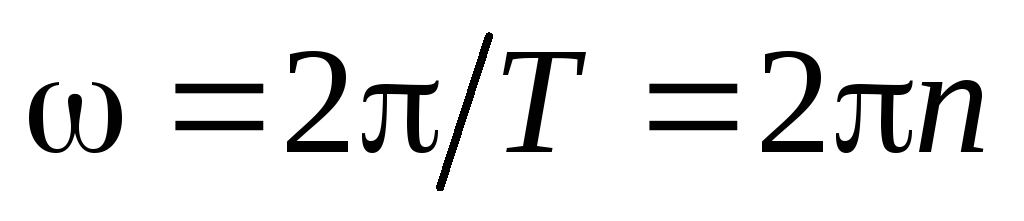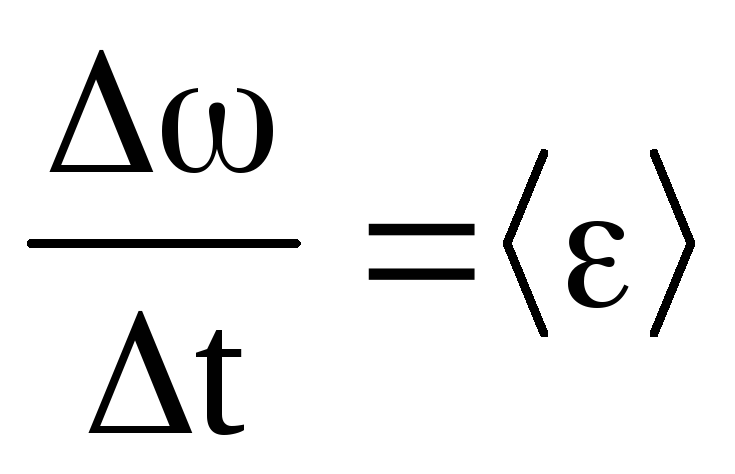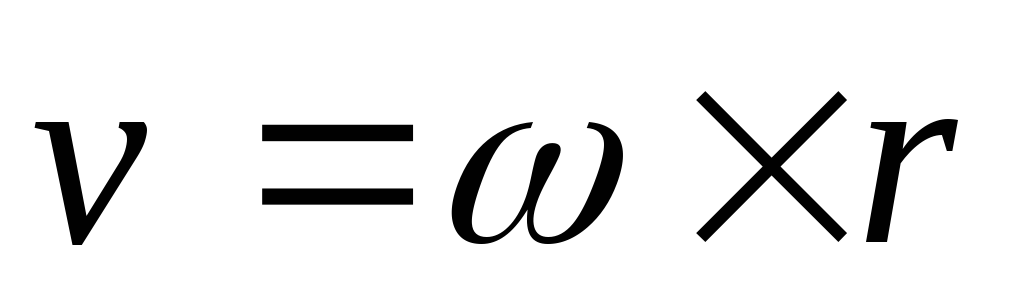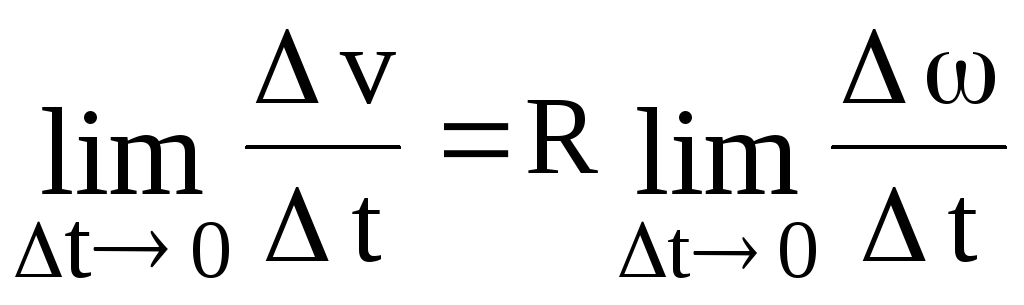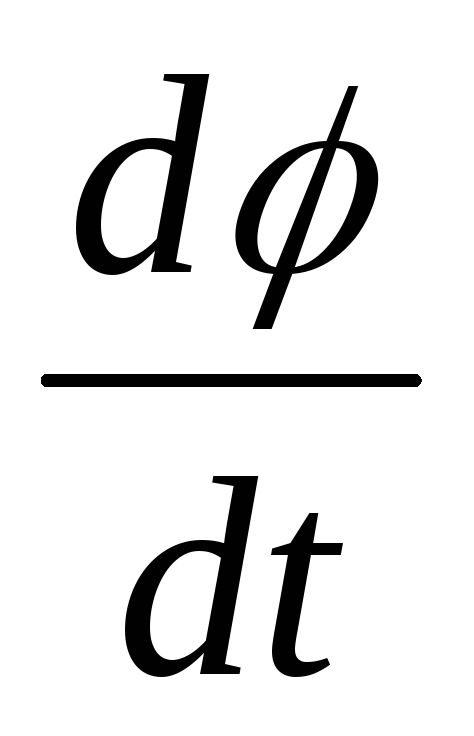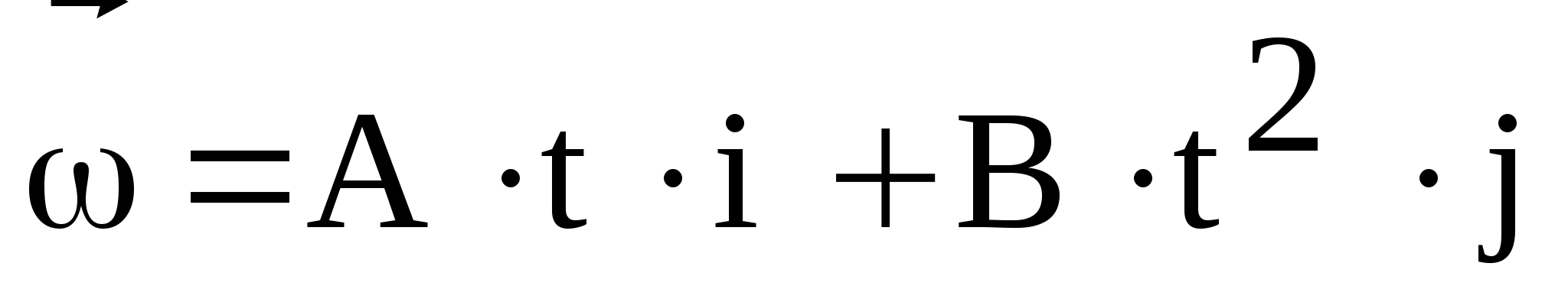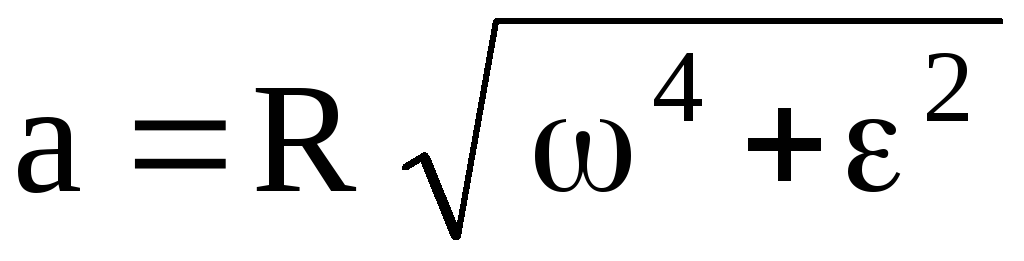§ 1.28. угловая скорость и угловое ускорение

Свойства

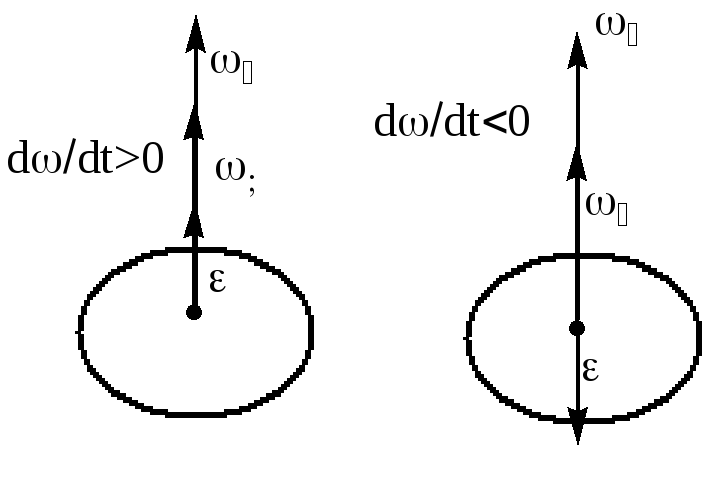
Угловая скорость (синяя стрелка) в одну единицу по часовой стрелке

Угловая скорость (синяя стрелка) в полторы единицы по часовой стрелке

Угловая скорость (синяя стрелка) в одну единицу против часовой стрелки (вектор угловой скорости направлен навстречу направлению взгляда наблюдателя)

Вектор мгновенной скорости любой точки абсолютно твёрдого тела, вращающегося с угловой скоростью ω→{\displaystyle {\vec {\omega }}}, определяется формулой:

v→= ω→,r→ ,{\displaystyle {\vec {v}}=,}

где r→{\displaystyle {\vec {r}}} — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определённом расстоянии (радиусе) r{\displaystyle r} от оси вращения можно считать так: v=ωr.{\displaystyle v=\omega r.} Если вместо радианов применять другие единицы измерения углов, то в двух последних формулах появится множитель, не равный единице.

В случае плоского вращения, то есть когда все векторы скоростей точек тела всегда лежат в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось вращения, то есть на прямую, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается. Однако в общем случае угловая скорость может менять со временем направление в трёхмерном пространстве, и такая упрощенная картина не работает.
Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю). Равномерное вращение является частным случаем плоского вращения.
Производная угловой скорости по времени есть угловое ускорение.
Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчёта, отличающихся положением начала отсчёта и скоростью его движения, но двигающихся равномерно прямолинейно и поступательно друг относительно друга. Однако в этих инерциальных системах отсчёта может различаться положение оси или центра вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
В случае движения точки в трёхмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:

ω→=r→×v→(r→,r→),{\displaystyle {\vec {\omega }}={\frac {{\vec {r}}\times {\vec {v}}}{({\vec {r}},{\vec {r}})}},} где r→{\displaystyle {\vec {r}}} — радиус-вектор точки (из начала координат), v→{\displaystyle {\vec {v}}} — скорость этой точки, r→×v→{\displaystyle {\vec {r}}\times {\vec {v}}} — векторное произведение, (r→,r→){\displaystyle ({\vec {r}},{\vec {r}})} — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы ω→,{\displaystyle {\vec {\omega }},} подходящие по определению, по-другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как даёт разные ω→{\displaystyle {\vec {\omega }}} для каждой точки, а при вращении абсолютно твёрдого тела вектора угловой скорости вращения всех его точек совпадают). Однако в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.

В случае равномерного вращательного движения (то есть движения с постоянным вектором угловой скорости) абсолютно твёрдого тела декартовы координаты точек вращающегося так тела совершают гармонические колебания с угловой (циклической) частотой, равной модулю вектора угловой скорости.

При измерении угловой скорости в оборотах в секунду (об/с) модуль угловой скорости равномерного вращательного движения совпадает с частотой вращения f, измеренной в герцах (Гц), то есть в таких единицах ω=f.{\displaystyle \omega =f.} В случае использования обычной физической единицы угловой скорости — радианов в секунду — модуль угловой скорости численно связан с частотой вращения так: ω=2πf.{\displaystyle \omega ={2\pi f}.} Наконец, при использовании градусов в секунду численная связь с частотой вращения будет: ω=360∘f.{\displaystyle \omega ={360^{\circ }f}.}

Вращение нашей планеты вокруг оси

Каждый человек знает, что планета, на которой он живет, вращается вокруг своей оси, причем экваториальная плоскость Земли наклонена под углом 23˚ к плоскости эклиптики.

Как рассчитать угловую скорость вращения вокруг своей оси Земли? Для этого можно воспользоваться совершенно любой из формул, которые приведены были выше. Поскольку мы знаем, что один оборот вокруг оси происходит за 24 часа, то для расчета следует использовать выражение с периодом T. Получаем:

Здесь значение периода T было переведено в секунды. Полученное значение является небольшим.

Представляет интерес рассчитать, с какой линейной скоростью движутся точки на поверхности планеты на широте 0˚ (экватор). Экваториальный радиус Земли равен 6 378 000 м. Подставляя это значение в формулу для скорости, получим:

Полученное значение является большим в сравнении со скоростями, которые мы наблюдаем в жизни. Человек эту скорость не ощущает, поскольку вращается вместе с воздухом и почвой под ногами с одной скоростью, то есть он покоится относительно них.

Рассмотренное вращение Земли приводит не только к возникновению явления дня и ночи, но и к появлению так называемой силы Кориолиса, которая оказывает влияние на некоторые земные процессы, например, изменяет направление ветров.

Переход от угловой к линейной скорости

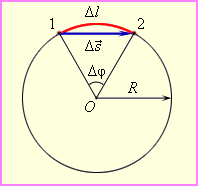
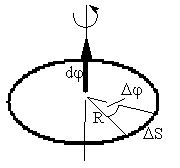
Существует различие между линейной скоростью точки и угловой скоростью. При сравнении величин в выражениях, описывающих правила вращения, можно увидеть общее между этими двумя понятиями. Любая точка В, принадлежащая окружности с радиусом R, совершает путь, равный 2*π*R. При этом она делает один оборот. Учитывая, что время, необходимое для этого, есть период Т, модульное значение линейной скорости точки В находится следующим действием:

ν = 2*π*R / Т = 2*π*R* ν.

Так как ω = 2*π*ν, то получается:

ν = ω* R.

Следовательно, линейная скорость точки В тем больше, чем дальше от центра вращения находится точка.

К сведению. Если рассматривать в качестве такой точки города на широте Санкт-Петербурга, их линейная скорость относительно земной оси равна 233 м/с. Для объектов на экваторе – 465 м/с.

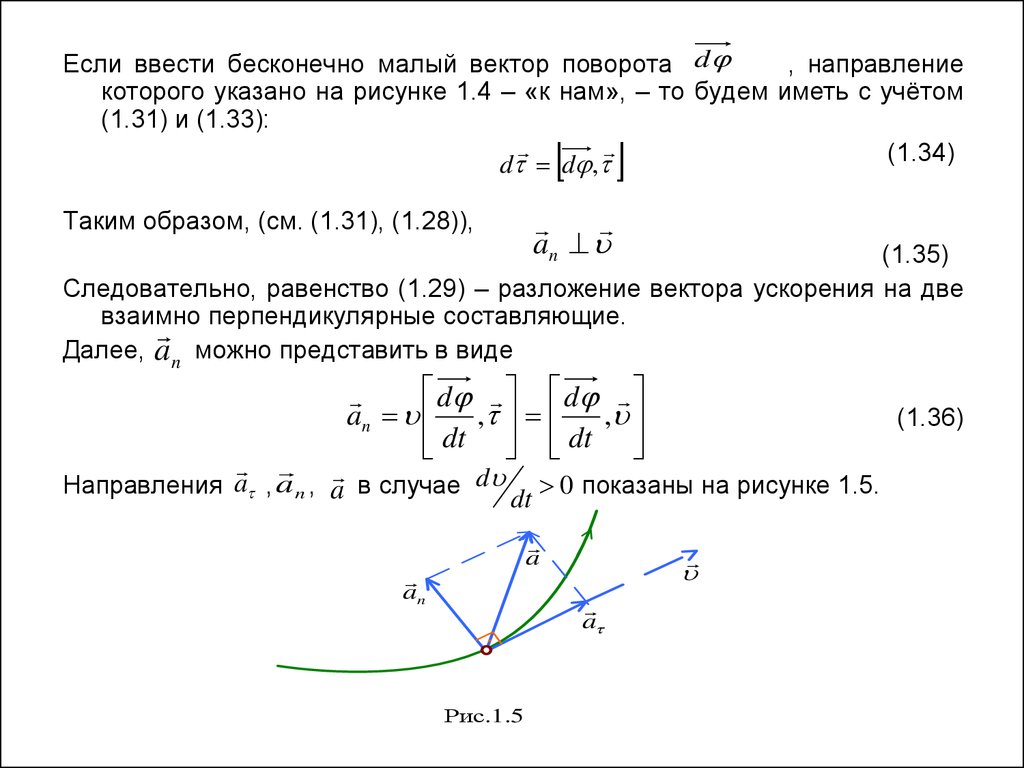
Числовое значение вектора ускорения точки В, движущейся равномерно, выражается через R и угловую скорость, таким образом:

а = ν2/ R, подставляя сюда ν = ω* R, получим: а = ν2/ R = ω2* R.

Это значит, чем больше радиус окружности, по которой движется точка В, тем больше значение её ускорения по модулю. Чем дальше расположена точка твердого тела от оси вращения, тем большее ускорение она имеет.

Поэтому можно вычислять ускорения, модули скоростей необходимых точек тел и их положений в любой момент времени.

Связь между угловой и линейной скоростями

Понимание и умение пользоваться расчётами и не путаться в определениях помогут на практике вычислениям линейной и угловой скоростей, а также свободно переходить при расчётах от одной величины к другой.

Угловая скорость. Формула угловой скорости

Расстояние и время, которое уходит на преодоление этого расстояния, связывает физическое понятие – скорость. И у человека, как правило, не вызывает вопросов определение этой величины. Все понимают, что двигаться на автомобиле со скоростью 100 км/ч — значит за один час проехать 100 километров.

А как быть, если тело вращается? Например, обычный бытовой вентилятор делает с десяток оборотов в секунду. И в то же время скорость вращения лопастей такова, что их запросто можно остановить рукой без вреда для себя. Земля вокруг своей звезды – Солнца — делает один оборот за целый год, а это более 30 миллионов секунд, но скорость её движения по околозвёздной орбите составляет около 30 километров за одну секунду!

Как же связать привычную скорость с быстротой вращения, как выглядит формула угловой скорости?

Понятие угловой скорости

Понятие угловой скорости используется в изучении законов вращения. Оно применяется ко всем вращающимся телам. Будь то вращение некоторой массы вокруг другой, как в случае с Землёй и Солнцем, или же вращение самого тела вокруг полярной оси (суточное вращение нашей планеты).

Отличие угловой скорости от линейной в том, что она фиксирует изменение угла, а не расстояния в единицу времени. В физике угловую скорость принято обозначать буквой греческого алфавита «омега» — ω.

Классическая формула угловой скорости вращения рассматривается так.

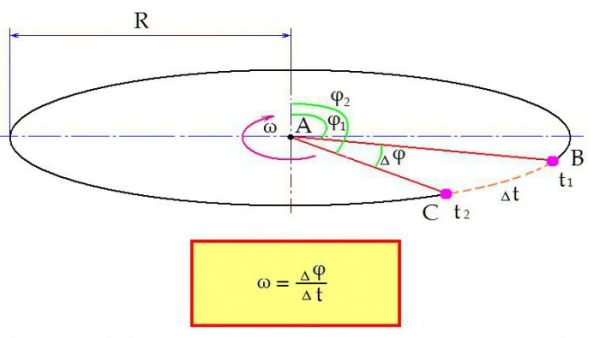
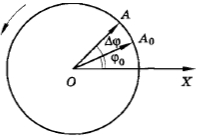
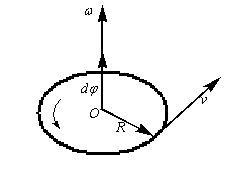
Представим, что вокруг некоторого центра А вращается физическое тело с постоянной скоростью. Его положение в пространстве относительно центра определяется углом φ. В некоторый момент времени t1 рассматриваемое тело находится в точке В. Угол отклонения тела от начального φ1.

Затем тело перемещается в точку С. Оно находится там в момент времени t2. Время, понадобившееся для данного перемещения:

∆t = t2 – t1.

Меняется и положение тела в пространстве. Теперь угол отклонения равен φ2. Изменение угла за период времени ∆t составило:

∆φ = φ2 – φ1.

Теперь формула угловой скорости формулируется следующим образом: угловая скорость определяется как отношение изменения угла ∆φ за время ∆t.

Единицы измерения угловой скорости

Скорость движения тела линейная измеряется в разных величинах. Движение автотранспорта по дорогам привычно указывают в километрах в час, морские суда делают узлы – морские мили в час. Если же рассматривать движение космических тел, то тут чаще всего фигурируют километры в секунду.

Угловая скорость в зависимости от величины и от предмета, который вращается, также измеряется в разных единицах.

Радианы в секунду (рад/с) – классическое мерило скорости в международной системе единиц (СИ). Показывают – на сколько радиан (в одном полном обороте 2 ∙ 3,14 радиан) успевает повернуться тело за одну секунду.

Обороты в минуту (об/мин) – самая распространённая единица для обозначения скоростей вращения в технике. Валы двигателей как электрических, так и автомобильных выдают именно (достаточно посмотреть на тахометр в своём автомобиле) обороты в минуту.

Обороты в секунду (об/с) – используется реже, прежде всего в образовательных целях.

Период обращения

Иногда для определения скорости вращения удобнее пользоваться другим понятием. Периодом обращения принято называть время, за которое некое тело делает оборот 360° (полный круг) вокруг центра вращения. Формула угловой скорости, выраженная через период обращения, принимает вид:

ω = 2П / Т.

Выражать периодом обращения быстроту вращения тел оправдано в случаях, когда тело вращается относительно медленно. Вернёмся к рассмотрению движения нашей планеты вокруг светила.

Формула угловой скорости позволяет вычислить её, зная период обращения:

ω = 2П/31536000 = 0,000000199238499086111 рад/с.

Глядя на полученный результат, можно понять, почему, рассматривая вращение небесных тел, удобнее пользоваться именно периодом обращения. Человек видит перед собой понятные цифры и наглядно представляет себе их масштаб.

Связь угловой и линейной скоростей

В некоторых задачах должны быть определены линейная и угловая скорость. Формула трансформации проста: линейная скорость тела равняется произведению угловой скорости на радиус вращения. Как это показано на рисунке.

«Работает» выражение и в обратном порядке, с его помощью определяется и угловая скорость. Формула через скорость линейную получается путём несложных арифметических манипуляций.

syl.ru

Свойства

Угловая скорость (синяя стрелка) в одну единицу по часовой стрелке

Угловая скорость (синяя стрелка) в полторы единицы по часовой стрелке

v→= ω→,r→ ,{\displaystyle {\vec {v}}=,}

где r→{\displaystyle {\vec {r}}} — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определённом расстоянии (радиусе) r{\displaystyle r} от оси вращения можно считать так: v=rω.{\displaystyle v=r\omega .} Если вместо радианов применять другие единицы измерения углов, то в двух последних формулах появится множитель, не равный единице.

В случае плоского вращения, то есть когда все векторы скоростей точек тела всегда лежат в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось вращения, то есть на прямую, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается. Однако в общем случае угловая скорость может менять со временем направление в трёхмерном пространстве, и такая упрощенная картина не работает.
Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю). Равномерное вращение является частным случаем плоского вращения.
Производная угловой скорости по времени есть угловое ускорение.
Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчёта, отличающихся положением начала отсчёта и скоростью его движения, но двигающихся равномерно прямолинейно и поступательно друг относительно друга. Однако в этих инерциальных системах отсчёта может различаться положение оси или центра вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
В случае движения точки в трёхмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:

1.2 Законы Ньютона и законы сохранения

При
рассмотрении кинематики использовалась
неподвижная система отсчета. В природе
не существует абсолютного движения,
всякое движение имеет относительный
характер: либо одного тела относительно
другого, либо относительно выбранной
системы отсчета. Возникает вопрос, все
ли системы отсчета являются равноправными,
а если нет, то какие являются
предпочтительными. Единственное и
естественное требование к системе
отсчета состоит в том, что ее выбор не
должен вносить усложнения в описание
движения тел, т.е. законы движения в
выбранной системе отсчета должны иметь
наиболее простой вид. В частности, в
такой системе должны оставаться
неизменными свойства пространства и
времени: пространство должно быть
однородным и изотропным, а время
однородным.

Однородностьпространства и времени означает, что
наблюдаемые физические свойства и
явления должны быть одинаковы в любой
точке пространства и в любой момент
времени. Не существует выделенных в
каком-либо отношении точек пространства
и моментов времени.

Изотропностьпространства означает, что все направления
в пространстве равнозначны. Физические
явления в замкнутой системе не должны
изменяться при ее повороте в пространстве.

Система
отсчета, которая использовалась до сих
пор, отвечала этим требованиям, но
возникает вопрос, как ее реализовать,
т.е. с какими объектами, реально
существующими в природе, можно ее
связать. Оказывается, что выбор подобной
системы отсчета является непростым
делом, так как требуемым условиям
отвечает специальный класс физических
объектов. Если «привязать» неподвижную
систему координат к какому-либо
произвольно движущемуся объекту,
например к вагону поезда, можно заметить,
что в данной системе отсчета сразу
произойдут странные явления, например
груз, подвешенный на нити, будет время
от времени отклоняться от вертикали
(что связано с действием различных
ускорений вагона: при торможении или
ускорении и при поворотах). В результате
для описания этих явлений в данной
системе координат придется прибегнуть
к представлениям о взаимодействиях,
внешних по отношению к системе, и включить
их в рассмотрение. В то же время ясно,
что в другой системе координат, не
испытывающей указанных ускорений,
описание механических явлений будет
гораздо проще.

Другой
пример не очень подходящей системы
отсчета — неподвижная система, связанная
с Землей. В этой системе можно, например,
обнаружить вращение плоскости колебаний
физического маятника (на самом деле
связанное с вращением Земли вокруг
своей оси), для объяснения которого нам
также придется привлекать физические
причины, являющиеся посторонними по
отношению к данной системе отсчета.
Вместе с тем, как показывает опыт, по
отношению к Солнцу и звездам маятник
будет вести себя стабильно, т.е. Солнце
и звезды являются подходящими физическими
объектами для выбора указанной системы
отсчета.

Как
показывает опыт, нужным требованиям
удовлетворяют системы отсчета, которые
связаны с физическими объектами, не
испытывающими внешних воздействий,
т.е. не подвергающимися каким-либо
ускорениям. В таких системах отсчета
тела находятся в состоянии покоя или
равномерного прямолинейного движения
до тех пор, пока на них не действуют
другие тела. Свойство тела сохранять
такое состояние называется инерцией,
и поэтому системы отсчета, о которых
«идет речь, носят название инерциальных.
Если наряду с выбранной инерциальной
системой, рассмотреть другую, движущуюся
относительно первой прямолинейно и
равномерно, то свободное движение тела
в новой системе будет также происходить
с постоянной скоростью. Таким образом,
существует бесконечное множество
инерциальных систем отсчета. Во всех
этих системах свойства пространства и
времени одинаковы и одинаковы законы
механики. Не существует никакой абсолютной
системы отсчета, которую можно было бы
предпочесть другим системам. В этом
состоит принцип относительности Галилея.
Его можно сформулировать и так: никакими
механическими опытами невозможно
установить, движется ли данная инерциальная
система или покоится: оба состояния
эквивалентны. Координаты точки в двух
системах отсчета, одна из которыхK’
движется равномерно и прямолинейно
относительно другой (K) со скоростьюV, связаны соотношением (рис.)

. (1.22)

При
этом считается, что время абсолютно,
т.е. течет одинаково в обеих системах:
t’ =t.
Скорость точки в системе К связана со
скоростью в системе К’ формулой:

. (1.23)

Математически
принцип относительности Галилея можно
сформулировать как требование
инвариантности (неизменности) уравнений
механики по отношению к преобразованию
(1.23)

Вектор угловой скорости спина рамы

Учитывая вращающуюся систему координат из трех единичных векторов координат, все три должны иметь одинаковую угловую скорость в каждый момент времени. В такой системе отсчета каждый вектор можно рассматривать как движущуюся частицу с постоянным скалярным радиусом.

Вращающаяся рамка появляется в контексте твердых тел , и для нее были разработаны специальные инструменты: угловая скорость вращения может быть описана как вектор или, что эквивалентно, как тензор .

В соответствии с общим определением, угловая скорость вращения кадра определяется как орбитальная угловая скорость любого из трех векторов (одинаковых для всех) относительно его собственного центра вращения. Сложение векторов угловой скорости для кадров также определяется обычным сложением векторов (композиция линейных перемещений) и может быть полезно для разложения вращения, как в карданном подвесе . Все компоненты вектора могут быть вычислены как производные от параметров, определяющих подвижные системы отсчета (углы Эйлера или матрицы вращения). Как и в общем случае, добавление коммутативности: .
ω1+ω2знак равноω2+ω1{\ displaystyle \ omega _ {1} + \ omega _ {2} = \ omega _ {2} + \ omega _ {1}}

Согласно теореме Эйлера о вращении , любая вращающаяся система отсчета обладает мгновенной осью вращения , которая является направлением вектора угловой скорости, а величина угловой скорости согласуется с двумерным случаем.

Компоненты из векторов кадра

Рассматривая вектор координат системы отсчета как частицу, при , получаем вектор орбитальной угловой скорости:
рзнак равноея{\ Displaystyle \ mathbf {r} = \ mathbf {e} _ {я}}|ея|знак равно1{\ displaystyle | \ mathbf {e} _ {i} | = 1}

ωзнак равнор×vр2знак равное1×е˙1знак равное2×е˙2знак равное3×е˙3.{\ displaystyle {\ boldsymbol {\ omega}} = {\ frac {\ mathbf {r} \ times \ mathbf {v}} {r ^ {2}}} = \ mathbf {e} _ {1} \ times { \ dot {\ mathbf {e}}} _ {1} = \ mathbf {e} _ {2} \ times {\ dot {\ mathbf {e}}} _ {2} = \ mathbf {e} _ {3 } \ times {\ dot {\ mathbf {e}}} _ {3}.}

Вот столбцы матрицы кадра и их производные по времени.
ея{\ Displaystyle \ mathbf {е} _ {я}}е˙я{\ displaystyle {\ dot {\ mathbf {e}}} _ {i}}

Компоненты из углов Эйлера

Диаграмма, показывающая фрейм Эйлера зеленым цветом

Компоненты псевдовектора спиновой угловой скорости были впервые вычислены Леонардом Эйлером с использованием его углов Эйлера и использования промежуточной системы отсчета:

Одна ось системы отсчета (ось прецессии)
Линия узлов подвижной системы отсчета относительно системы отсчета (ось нутации)
Одна ось подвижной рамы (собственная ось вращения)

Эйлер доказал, что проекции псевдовектора угловой скорости на каждую из этих трех осей являются производной соответствующего угла (что эквивалентно разложению мгновенного вращения на три мгновенных вращения Эйлера ). Следовательно:

ωзнак равноα˙ты1+β˙ты2+γ˙ты3{\ displaystyle {\ boldsymbol {\ omega}} = {\ dot {\ alpha}} \ mathbf {u} _ {1} + {\ dot {\ beta}} \ mathbf {u} _ {2} + {\ точка {\ gamma}} \ mathbf {u} _ {3}}

Этот базис не является ортонормированным и его сложно использовать, но теперь вектор скорости можно изменить на фиксированную систему отсчета или на подвижную систему отсчета, просто изменив основы. Например, переход на мобильный фрейм:

ωзнак равно(α˙грех⁡βгрех⁡γ+β˙потому что⁡γ)я+(α˙грех⁡βпотому что⁡γ-β˙грех⁡γ)j+(α˙потому что⁡β+γ˙)k{\ displaystyle {\ boldsymbol {\ omega}} = ({\ dot {\ alpha}} \ sin \ beta \ sin \ gamma + {\ dot {\ beta}} \ cos \ gamma) \ mathbf {i} + ( {\ dot {\ alpha}} \ sin \ beta \ cos \ gamma — {\ dot {\ beta}} \ sin \ gamma) \ mathbf {j} + ({\ dot {\ alpha}} \ cos \ beta + {\ точка {\ gamma}}) \ mathbf {k}}

где — орты для системы отсчета, закрепленной в движущемся теле. Этот пример был сделан с использованием соглашения ZXZ для углов Эйлера.
я,j,k{\ Displaystyle \ mathbf {я}, \ mathbf {j}, \ mathbf {k}}

Связь с конечным поворотом в пространстве[править | править код]

ω→=n→θ˙+n→˙sin⁡θ+n→×n→˙(1−cos⁡θ).{\displaystyle {\vec {\omega }}={\vec {n}}{\dot {\theta }}+{\dot {\vec {n}}}\sin \theta +{\vec {n}}\times {\dot {\vec {n}}}(1-\cos \theta ).}

Если поворот задан матрицей поворота Tij=ninj+(δij−ninj)cos⁡θ−nkεijksin⁡θ,{\displaystyle T_{ij}=n_{i}n_{j}+(\delta _{ij}-n_{i}n_{j})\cos \theta -n_{k}\varepsilon _{ijk}\sin \theta ,} где δij{\displaystyle \;\delta _{ij}} — символ Кронекера, εijk{\displaystyle \varepsilon _{ijk}} — символ Леви-Чивиты (суммирование ведётся по правилу Эйнштейна от 1 до 3), выражение для элементов которой через θ{\displaystyle \;\theta } и n→{\displaystyle {\vec {n}}} могут быть получены, например, с помощью формулы Родрига, то угловая скорость равна

ωi=12εijkTjnT˙kn.{\displaystyle \omega _{i}={\frac {1}{2}}\varepsilon _{ijk}T_{jn}{\dot {T}}_{kn}.}

Если для описания поворота используется кватернион, выражаемый через угол θ{\displaystyle \;\theta } и орт оси поворота n→{\displaystyle {\vec {n}}} как q=(cos⁡(θ/2),n→sin⁡(θ/2)),{\displaystyle q={\bigl (}\cos(\theta /2),{\vec {n}}\sin(\theta /2){\bigr )},} то угловая скорость находится из выражения (0,ω→)=2q˙q¯.{\displaystyle \left(0,{\vec {\omega }}\right)=2\,{\dot {q}}\,{\overline {q}}.}

В случае, когда поворот описывается с помощью вектора V→=n→tg⁡(θ/4),{\displaystyle {\vec {V}}={\vec {n}}\operatorname {tg} (\theta /4),} изменяющегося во времени, обозначим W→=dV→/dt (Wi=dVi/dt),{\displaystyle {\vec {W}}=d{\vec {V}}/dt\ {\bigl (}W_{i}=dV_{i}/dt{\bigr )},} а также Tij1/2=ninj+(δij−ninj)cos⁡(θ/2)−nkεijksin⁡(θ/2){\displaystyle T_{ij}^{1/2}=n_{i}n_{j}+(\delta _{ij}-n_{i}n_{j})\cos(\theta /2)-n_{k}\varepsilon _{ijk}\sin(\theta /2)} — матрица половинного поворота (Tij1/2Tjk1/2=Tik),{\displaystyle \;{\bigl (}T_{ij}^{1/2}T_{jk}^{1/2}=T_{ik}{\bigr )},} V2{\displaystyle \;V^{2}} — квадрат модуля вектора V→.{\displaystyle {\vec {V}}.} Тогда угловая скорость:

ωi=4Tij12Wj1+V2.{\displaystyle \omega _{i}={\frac {4T_{ij}^{1/2}W_{j}}{1+V^{2}}}.}

Циклическая частота вращения (обращения)

Скалярная величина, измеряющая частоту вращательного движения, называется циклической частотой вращения. Это угловая частота, равная не самому вектору угловой скорости, а его модулю. Ещё её именуют радиальной или круговой частотой.

Циклическая частота вращения – это количество оборотов тела за 2*π секунды.

У электрических двигателей переменного тока это частота асинхронная. У них частота вращения ротора отстаёт от частоты вращения магнитного поля статора. Величина, определяющая это отставание, носит название скольжения – S. В процессе скольжения вал вращается, потому что в роторе возникает электроток. Скольжение допустимо до определённой величины, превышение которой приводит к перегреву асинхронной машины, и её обмотки могут сгореть.

Устройство этого типа двигателей отличается от устройства машин постоянного тока, где токопроводящая рамка вращается в поле постоянных магнитов. Большое количество рамок вместил в себя якорь, множество электромагнитов составили основу статора. В трёхфазных машинах переменного тока всё наоборот.

При работе асинхронного двигателя статор имеет вращающееся магнитное поле. Оно всегда зависит от параметров:

частоты питающей сети;
количества пар полюсов.

Скорость вращения ротора состоит в прямом соотношении со скоростью магнитного поля статора. Поле создаётся тремя обмотками, которые расположены под углом 120 градусов относительно друг друга.