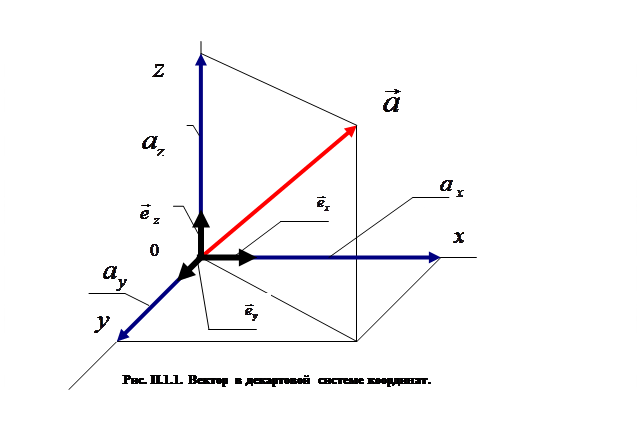
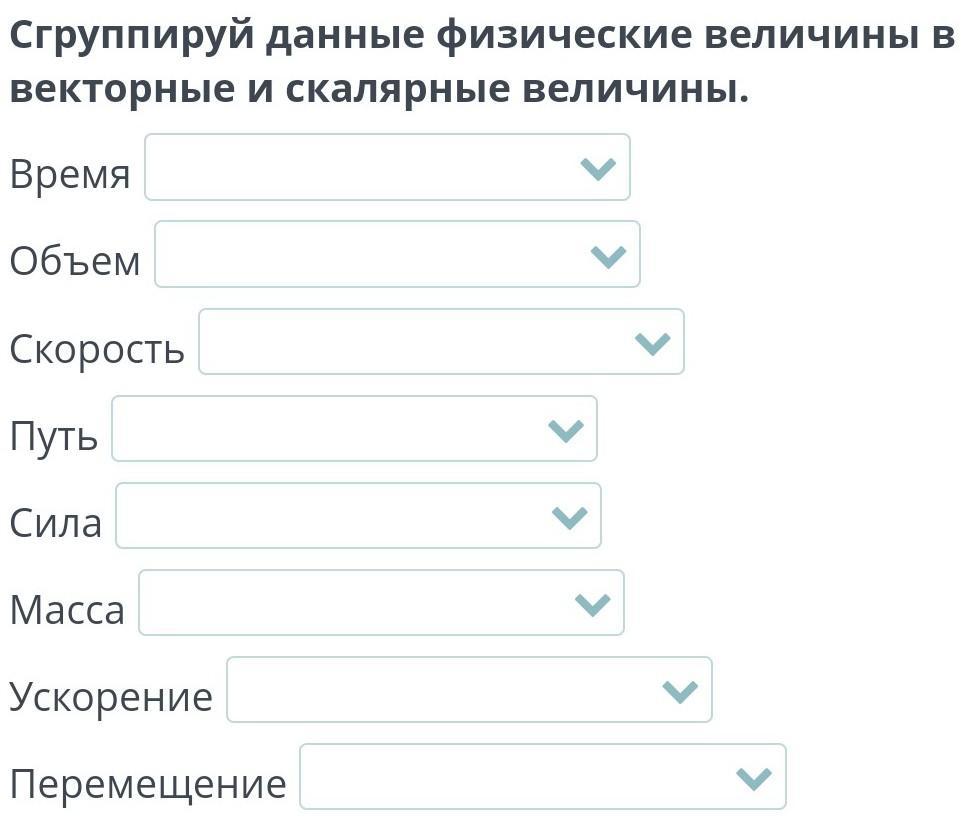
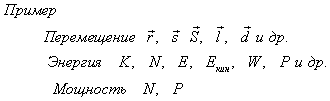Примеры векторов. Как они обозначаются
Что подразумевается под вектором? То, что характеризует движение
Не важно, в пространстве или на плоскости. Какая величина является векторной вообще? Например, летит самолет с определенной скоростью на какой-то высоте, имеет конкретную массу, начал движение из аэропорта с нужным ускорением
Что относится к движению самолета? Что заставило его лететь? Конечно, ускорение, скорость. Векторные величины из курса физики являются наглядными примерами. Говоря прямо, векторная величина связана с движением, перемещением.

Вода тоже движется с определенной скоростью с высоты горы. Видите? Движение осуществляется за счет не объема или массы, а именно скорости. Теннисист дает возможность мячику двигаться при помощи ракетки. Он задает ускорение. К слову сказать, приложенная в данном случае сила также является векторной величиной. Потому что она получается вследствие заданных скоростей и ускорений. Сила способна также меняться, осуществлять конкретные действия. Ветер, который колышет листья на деревьях, тоже можно считать примером. Так как имеется скорость.
Положительные и отрицательные величины
Векторной величиной называется величина, которая имеет направление в окружающем пространстве и модуль. Снова появилось пугающее слово, на этот раз модуль. Представьте, что нужно решить задачку, где будет фиксироваться отрицательное значение ускорения. В природе отрицательных значений, казалось бы, не существует. Как скорость может быть отрицательной?

У вектора есть такое понятие. Это касается, например, сил, которые приложены к телу, но имеют разные направления. Вспомните третий закон Ньютона, где действие равно противодействию. Ребята перетягивают канат. Одна команда в синих футболках, вторая — в желтых. Вторые оказываются сильнее. Допустим, что вектор их силы направлен положительно. В то же время у первых не получается натянуть канат, но пытаются. Возникает противодействующая сила.
Свойства векторов
Вектор — математический элемент, представляющий собой прямой отрезок с направлением. Он обозначается либо 2 заглавными латинскими буквами, либо одной прописной. Длиной вектора является его модуль. Если длина вектора равняется 0, то он называется нулевым. Вектор, имеющий длину 1 см, именуется единичным. Длина ненулевого вектора выражается в виде расстояния между началом и концом направленного отрезка. Проекцией вектора на ось является строго положительный отрезок, сонаправленный с исходной осью. Свойства проекции:

- Произведение вектора на косинус между осью и направленным отрезком равен проекции вектора.
- Проекция на ось принимает значения меньше 0, если отрезок с осью образует тупой угол.
- Проекция на ось принимает значение больше 0, если отрезок с осью образует острый угол.
Коллинеарные векторы — отрезки, располагающиеся либо на одной прямой, либо на параллельных прямых. Нулевой вектор коллинеарен всегда. Если коллинеарные векторы направлены в одну сторону, то они называются сонаправленными. Если отрезки направлены в диаметрально противоположные стороны, то они называются противоположно направленными. Коллинеарные векторы являются равными, если они одинаковы по модулю и направлению.

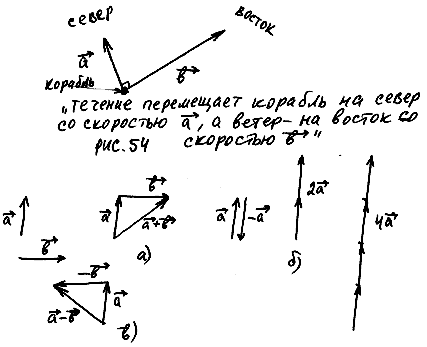
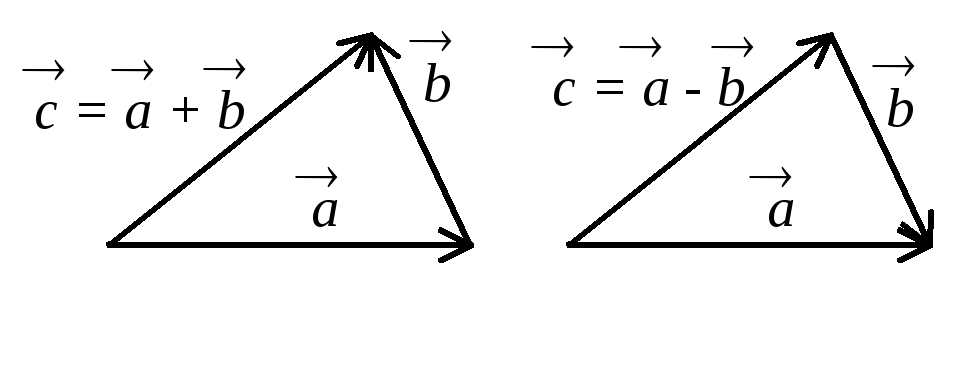
С векторами также можно производить операции сложения, деления, вычитания и умножения. Чтобы сложить два вектора, необходимо от произвольной точки на плоскости отложить первый направленный отрезок и от него отложить второй вектор. Отрезок, соединяющий начало первого вектора и конец второго, будет считаться их суммой. Этот способ сложения именуется методом треугольника.
Вторым способом нахождения суммы векторов является метод параллелограмма. От произвольной точки откладываются оба направленных отрезка. Полученный рисунок нужно достроить до параллелограмма. Диагональ фигуры будет являться суммой векторов.
Для осуществления вычитания необходимо отложить от произвольной точки первый вектор. От полученного отрезка откладывается следующий вектор. Второй отрезок нужно направить в противоположную сторону. Линия, соединяющая отрезки, будет являться разностью векторов.
С векторами также можно проводить операцию умножения. Произведение длин направленных отрезков на косинус угла между ними называется скалярным. В результате вычислений получается число — скаляр. Скалярное произведение равно 0 в случае, когда отрезки пересекаются под углом 90°. Зная скалярное произведение, человек сможет найти косинус угла между построенными векторами.
Полученные в результате выполнения алгебраических операций выражения применяются для исследования перемещения тел вокруг оси вращения и изучения элементов высшей математики. Также направленные отрезки нашли широкое применение в геометрии и астрономии.
Предыдущая
ФизикаПружинный маятник — формулы и уравнения нахождения величин
Следующая
ФизикаМатематический маятник — определение, формулы и принцип действия
Что такое физическая величина?
Нас окружает много различных материальных предметов. Материальных, потому что их возможно потрогать, понюхать, увидеть, услышать и еще много чего можно сделать. То, какие эти предметы, что с ними происходит, или будет происходить, если что-нибудь сделать: кинуть, разогнуть, засунуть в печь. То, почему с ними происходит что-либо и как именно происходит? Все это изучает физика. Поиграйте в игру: загадайте предмет в комнате, опишите его несколькими словами, друг должен угадать что это. Указываю характеристики задуманного предмета. Прилагательные: белый, большой, тяжелый, холодный. Догадались? Это холодильник. Названные характеристики — это не научные измерения вашего холодильника. Измерять у холодильника можно разное. Если длину, то он большой. Если цвет, то он белый. Если температуру, то холодный. А если его массу, то выйдет, что он тяжелый. Представляем, что один холодильник можно исследовать с разных сторон. Масса, длина, температура — это и есть физическая величина.
Но это лишь та небольшая характеристика холодильника, которая приходит на ум мгновенно. Перед покупкой нового холодильника можно ознакомиться еще с рядом физических величин, которые позволяют судить о том, какой он, лучше или хуже, и почему он стоит дороже. Представь масштабы того, на сколько все окружающее нас разнообразно. И на сколько разнообразны характеристики.
Особенности скалярных величин
Скалярные величины характеризуются только одним параметром — числовым значением. Они разделяются на 2 вида:
- Чистые скаляры. Характеризуются числовым значением, не находящимся в зависимости от осей отсчета — линий пересечения плоских поверхностей в единой системе координат.
- Псевдоскаляры. Находятся при помощи расчета числа, знак которого зависит от положительного направления осей в системе координат.
В физике в список скалярных величин входят:

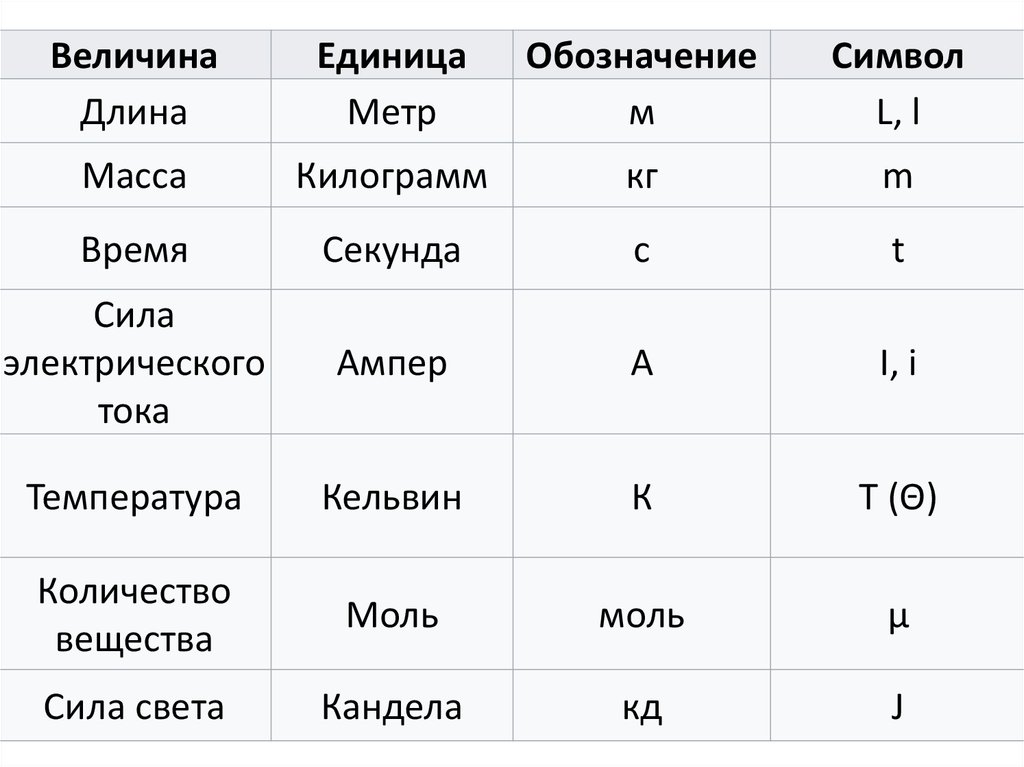
- Масса — определяет величину материи и ее гравитационные свойства. Измеряется в килограммах и обозначается буквой латинского алфавита m.
- Температура — средняя кинетическая энергия физического тела. Выражается в кельвинах или градусах Цельсия.
- Работа — мера действия силы на физическое тело или систему тел. Измеряется в Джоулях и обозначается латинской буквой A.
- Длина — величина, определяющая дистанцию между 2 концами тела в продольном направлении. Исчисляется в метрах. Особым видом длины является путь — скаляр, выражающий расстояние между начальным и конечным положением объекта, осуществляющего перемещение по заданной траектории.
- Время — продолжительность действия или события. Рассчитывается в секундах.
- Период — время совершения 1 полного колебания. Обозначается символом T и измеряется в секундах.
- Частота — величина, обратная периоду. Определяет количество полных колебаний в единицу времени. Рассчитывается в Герцах.
- Объем — скаляр, обозначающий размер пространства, ограниченного поверхностями со всех сторон. Измеряется в м3.
- Напряжение — измеряет изменение потенциальной энергии тела, приходящейся на единицу заряда. Обозначается буквой U и рассчитывается в Вольтах.
- Сила тока — скаляр, показывающий число электрических зарядов, проходящих через сечение проводника в единицу времени. Обозначается символом I и рассчитывается в Амперах.
- Энергия — обозначает способность тела осуществлять работу.
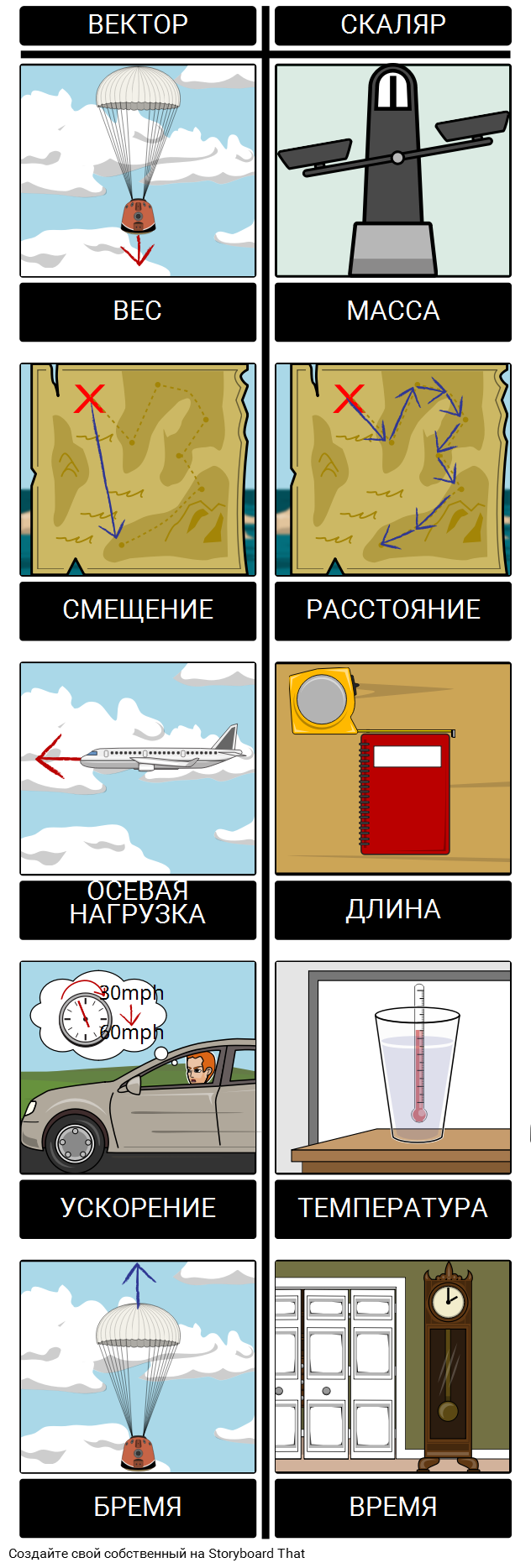
Основные отличия между скалярными и векторными величинами
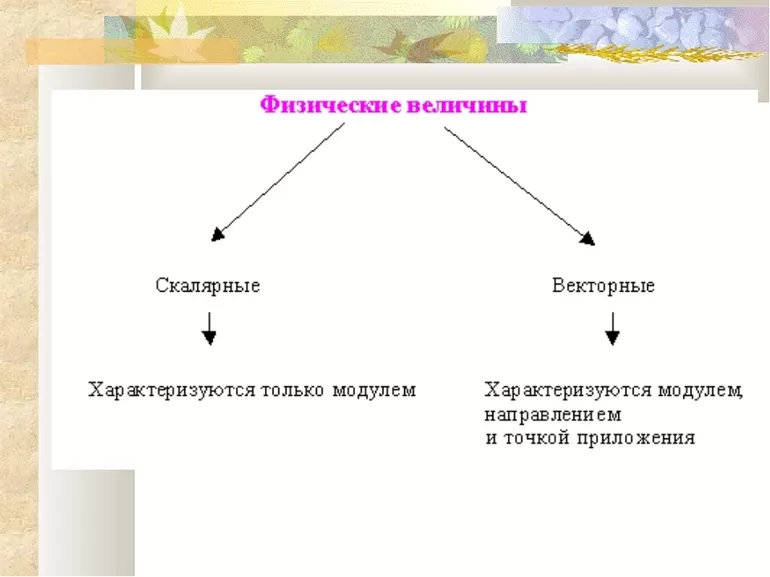
Из описаний, приведенных выше, видно, что главное отличие векторных величин от скалярных заключается в их характеристиках. У векторной величины есть направление и модуль, а у скалярной только численное значение. Безусловно, векторную величину, как и скалярную, можно измерить, но такая характеристика не будет полной, так как отсутствует направление.
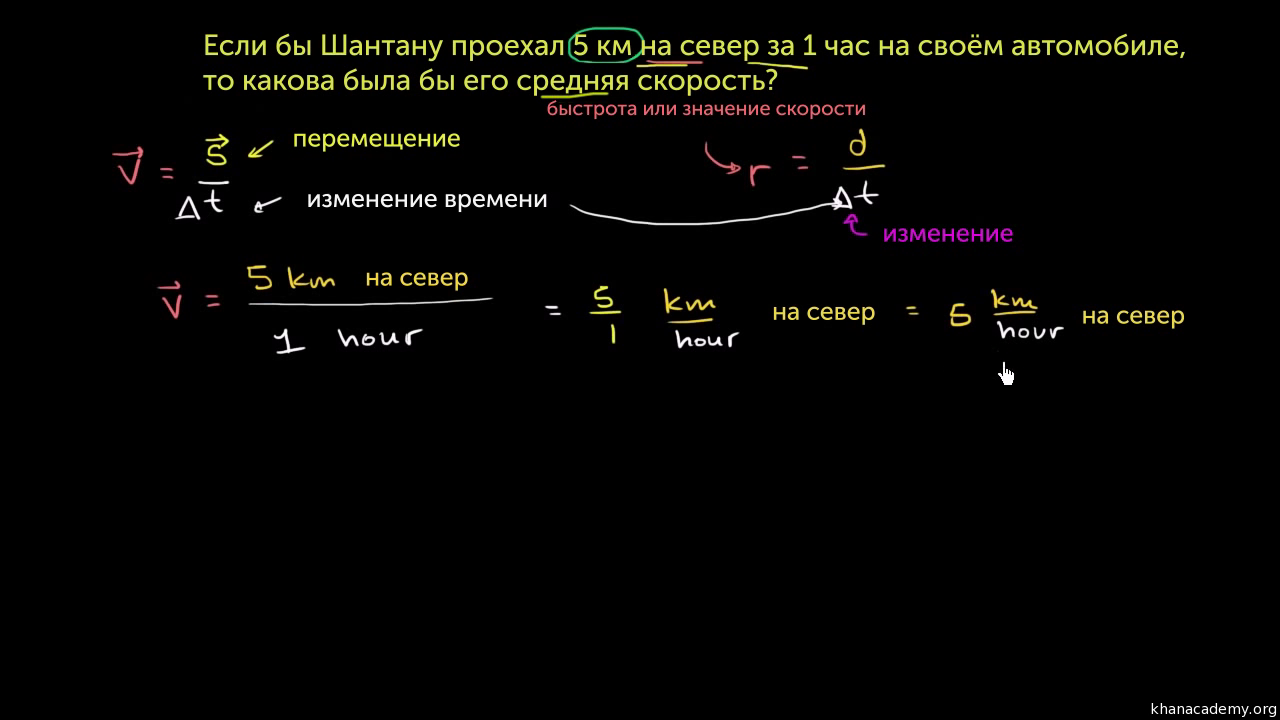
Для того, чтобы более четко представить отличие скалярной величины от векторной, следует привести пример. Для этого возьмем такую область знаний, как климатология. Если сказать, что ветер дует со скоростью 8 метров в секунду, то будет введена скалярная величина. Но, если сказать, что северный ветер дует со скоростью 8 метров в секунду, то речь пойдет о векторном значении.
Векторы играют огромную роль в современной математике, а также во многих сферах механики и физики. Большинство физических величин может быть представлено в виде векторов. Это позволяет обобщить и существенно упростить используемые формулы и результаты. Часто векторные значения и векторы отождествляются друг с другом. Например, в физике можно услышать, что скорость или сила является вектором.
Некоторые формулы векторной алгебры используются в таких областях науки, как:
- Сопромат.
- Кинематика.
- Облучение и электрическое освещение.
- Прикладная механика.
- Гидравлика.
- Электрические машины.
- Теоретическая механика.
- Физика.
Четкое осознание разницы между векторной и скалярной величиной позволит специалистам решать сложные задачи и более подробно характеризовать используемые данные.
https://youtube.com/watch?v=t1mELdfyNYE
Нерелятивистские скаляры
Температура
Примером скалярной величины является температура : температура в данной точке представляет собой одно число. С другой стороны, скорость — это векторная величина.
Другие примеры
Некоторыми примерами скалярных величин в физике являются масса , заряд , объем , время , скорость и электрический потенциал в точке внутри среды. Расстояние между двумя точками в трехмерном пространстве является скаляром, а направление от одной из этих точек на другой нет, поскольку описание направления требует два физических величин , таких как угол в горизонтальной плоскости и под угол в стороне от самолет. Силу нельзя описать с помощью скаляра, поскольку сила имеет как направление, так и величину ; однако только величина силы может быть описана скаляром, например гравитационная сила, действующая на частицу, не является скаляром, но ее величина есть. Скорость объекта является скалярной (например, 180 км / ч), а его скорость — нет (например, 108 км / ч в северном направлении и 144 км / ч в западном). Некоторые другие примеры скалярных величин в механике Ньютона — это электрический заряд и плотность заряда .
Ссылки[править | править код]
|
Выделить Скаляр и найти в:
|
|
|
- Страница — краткая статья
- Страница — энциклопедическая статья
- Разное — на страницах: , , ,
Определение положительного скаляра и его измерения
Понятие положительной скалярной величины и ее измерения позволяет сравнивать между собой однородные скаляры. Положительная скалярная величина способна принимать значения строго выше 0. Она обозначается знаком «+”. Если величина может принимать значения меньше 0, то она называется отрицательной и обозначается символом «-“. Большинство скаляров могут быть только положительными. Для их расчета используют единицы измерения — фиксированного размера объекта.
Чтобы получить скалярную величину, достаточно умножить ее числовое значение на ее единицу измерения. Для структуризации и стандартизации вычислений физических параметров тела была разработана Международная система СИ. Она устанавливает единицы измерения для каждой величины. Во время проведения расчетов скалярных величин применяют алгебраические действия — сложение, вычитание, деление и умножение (отдельный подвид — возведение в степень).

Развитие понятия в физике
Примерами скаляров являются длина, площадь, время, масса, плотность, температура, поток и т. п.
Важно заметить, что понятие скаляра довольно сильно связано с контекстом. Так, в общепринятом контексте современной физики часть приведённых величин скалярными не являются
В современной физике, подразумевающей пространственно-временной подход, под скаляром обычно имеется в виду скалярное поле, то есть пространственно-временной скаляр, лоренц-инвариантная величина, не меняющаяся при переходе от одной инерциальной системы отсчёта к другой (а в общей теории относительности и других метрических теориях гравитации — скаляр остается неизменным также и при переходе к неинерциальным системам отсчёта). В этом отличие от ньютоновской физики, где под скаляром понимается обычный скаляр обычного трёхмерного пространства (так, энергия в ньютоновском смысле — скаляр, а в пространственно-временном — лишь компонента четырёхмерного вектора).
Примечания
- ↑ Среди приведённых величин большинство являются скалярами лишь в весьма ограниченных контекстах. Так, хотя длина или площадь, понимаемые как длина и площадь, определённые для основного пространства рассматриваемой теории, несомненно, являются хорошими примерами скаляров, тем не менее, обычные (то есть рассматриваемые в рамках обычного трёхмерного пространства) длина и площадь, а также время — являются скалярами только в классической (ньютоновской) физике (см. замечание о современной физике), так как основное пространство современных физических теорий по умолчанию обычно включает как минимум четырёхмерное пространство-время. В общеупотребительном современном понимании скалярами из перечисленного являются масса, 4-мерная длина — интервал (а трёхмерная длина — нет!), 4-мерная (но не трёхмерная!) площадь, также — «инварианты» электромагнитного поля: E2 − H2, E⋅H. А время и энергия, например, являются не скалярами, первое — компонентой вектора 4-мерного перемещения, вторая — компонентой 4-вектора энергии-импульса. Вообще же говоря, если идёт речь о физике, чтобы не ошибиться в понимании применения термина скаляр надо выяснить контекст: идёт ли речь об «обычном» трёхмерном пространстве или о пространственно-временной формулировке.
- Речь идёт именно о координате в произвольном базисе, который можно менять. Тем не менее, координата определённого вектора в определённом фиксированном базисе — скаляр. Это внешне немного напоминает казуистику, но на самом деле просто подчёркивает тот факт, что настоящий скаляр остаётся инвариантным при любом изменении базиса (иногда класс преобразований базиса, для которых требуется инвариантность скаляра, ограничивают, но всё же этот класс остаётся достаточно широким; строго же говоря, даже если этот класс широк, если речь идёт об инварианте ограниченного класса преобразований, обычно его именно так и называют, не употребляя термина «скаляр».
Релятивистские скаляры
В теории относительности рассматриваются изменения систем координат, которые меняют пространство на время. Как следствие, несколько физических величин, которые являются скалярами в «классической» (нерелятивистской) физике, необходимо комбинировать с другими величинами и рассматривать как четырехвекторы или тензоры. Например, плотность заряда в точке среды, которая является скаляром в классической физике, должна быть объединена с локальной плотностью тока (3-вектор), чтобы образовать релятивистский 4-вектор. Точно так же плотность энергии должна быть объединена с плотностью импульса и давлением в тензор энергии-импульса .
Примеры скалярных величин в теории относительности включают электрический заряд , (например, собственное время и собственную длину ) и инвариантную массу .
Векторные и скалярные величины
В физике существует два вида физических величин: векторные и скалярные. Основное их отличие в том, что векторные физические величины имеют направление. Что значит физическая величина имеет направление? Например, число картофелин в мешке, мы будем называть обыкновенными числами, или скалярами. Еще одним примером такой величины может служить температура. Другие очень важные в физике величины имеют направление, это, например, скорость; мы должны задать не только быстроту перемещения тела, но и путь, по которому оно движется. Импульс и сила тоже имеют направление, как и смещение: когда кто-нибудь делает шаг, можно сказать не только, как далеко он шагнул, но и куда он шагает, то есть определить направление его движения. Векторные величины лучше запомнить.