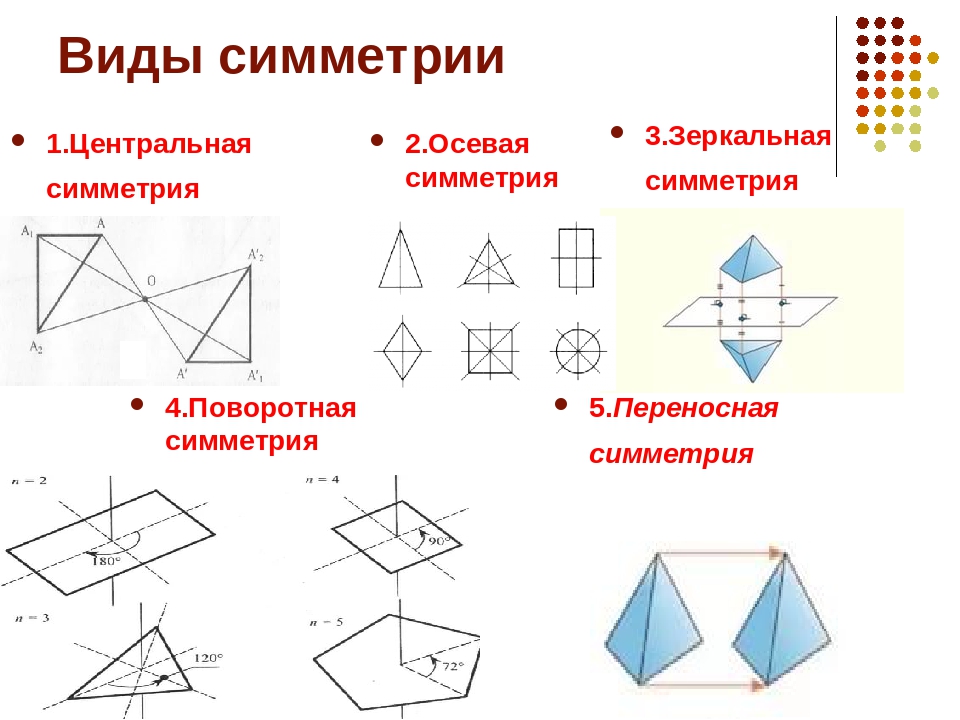
Симметрия

Симметрия дифференциальных уравнений

Симметрия дифференциальных уравнений — это преобразование, которое оставляет дифференциальное уравнение неизменным. Знание таких симметрий может помочь решить дифференциальное уравнение.

Симметрия Ли системы дифференциальных уравнений — это непрерывная симметрия дифференциальных уравнений. Знание симметрии Ли может помочь в упрощении обыкновенных дифференциальных уравнений путём .

Для обыкновенных дифференциальных уравнений знание подходящего набора симметрий Ли позволяет явно получить первые интегралы, что сразу даёт решение без интегрирования уравнения.

Симметрии можно найти путём решения связанного множества обыкновенных дифференциальных уравнений. Получить решение этих уравнений зачастую много проще, чем решить исходную систему дифференциальных уравнений.

Симметрии в физике

Основная статья: Симметрия (физика)

Симметрия в физике
Преобразование	Соответствующаяинвариантность	Соответствующийзаконсохранения
Трансляции времени	Однородностьвремени	…энергии
⊠ C, P, CP и T-симметрии	Изотропностьвремени	…чётности
Трансляции пространства	Однородностьпространства	…импульса
↺ Вращения пространства	Изотропностьпространства	…моментаимпульса
⇆ Группа Лоренца (бусты)	ОтносительностьЛоренц-ковариантность	…движенияцентра масс
~ Калибровочное преобразование	Калибровочная инвариантность	…заряда

В теоретической физике поведение физической системы описывается некоторыми уравнениями. Если эти уравнения обладают какими-либо симметриями, то часто удаётся упростить их решение путём нахождения сохраняющихся величин (интегралов движения). Так, уже в классической механике формулируется теорема Нётер, которая каждому типу непрерывной симметрии сопоставляет сохраняющуюся величину. Из неё, например, следует, что инвариантность уравнений движения тела с течением времени приводит к закону сохранения энергии; инвариантность относительно сдвигов в пространстве — к закону сохранения импульса; инвариантность относительно вращений — к закону сохранения момента импульса.

Суперсимметрия

Суперсимме́трия или симме́трия Ферми́ — Бозе́ — гипотетическая симметрия, связывающая бозоны и фермионы в природе. Абстрактное преобразование суперсимметрии связывает бозонное и фермионное квантовые поля, так что они могут превращаться друг в друга. Образно можно сказать, что преобразование суперсимметрии может переводить вещество во взаимодействие (или в излучение), и наоборот.

По состоянию на начало 2009 года суперсимметрия является физической гипотезой, не подтверждённой экспериментально. Совершенно точно установлено, что наш мир не является суперсимметричным в смысле точной симметрии, так как в любой суперсимметричной модели фермионы и бозоны, связанные суперсимметричным преобразованием, должны обладать одинаковыми массой, зарядом и другими квантовыми числами (за исключением спина). Данное требование не выполняется для известных в природе частиц. Предполагается, тем не менее, что существует энергетический лимит, за пределами которого поля подчиняются суперсимметричным преобразованиям, а в рамках лимита — нет. В таком случае частицы-суперпартнёры обычных частиц оказываются очень тяжёлыми по сравнению с обычными частицами. Поиск суперпартнёров обычных частиц — одна из основных задач современной физики высоких энергий. Ожидается, что Большой адронный коллайдер сможет открыть и исследовать суперсимметричные частицы, если они существуют, или поставить под большое сомнение суперсимметричные теории, если ничего не будет обнаружено.

Трансляционная симметрия

Трансляционная симметрия — тип симметрии, при которой свойства рассматриваемой системы не изменяются при сдвиге на определённый вектор, который называется вектором трансляции. Например, однородная среда совмещается сама с собой при сдвиге на любой вектор, поэтому для неё свойственна трансляционная симметрия.

Трансляционная симметрия свойственна также для кристаллов. В этом случае векторы трансляции не произвольны, хотя их существует бесконечное число. Среди всех векторов трансляций кристаллической решётки можно выбрать 3 таким образом, что любой другой вектор трансляции был бы целочисленно-линейной комбинацией этих трёх векторов. Эти три вектора составляют базис кристаллической решётки.

Теория групп показывает, что трансляционная симметрия в кристаллах совместима только с поворотами на углы θ=2π/n, где n может принимать значения 1, 2, 3, 4, 6.

При повороте на углы 180, 120, 90, 60 градусов положение атомов в кристалле не меняется. Говорят, что кристаллы имеют ось вращения n-го порядка.[уточнить]

Перенос в плоском четырёхмерном пространстве-времени не меняет физических законов. В теории поля трансляционная симметрии, согласно теореме Нётер, соответствует сохранению тензора энергии-импульса. В частности, чисто временные трансляции соответствуют закону сохранения энергии, а чисто пространственные сдвиги — закону сохранения импульса.

Симметрия в геометрии

Симметрии элементарной геометрии (такие как отражение и поворот) описаны в основной статье о .

Точка зрения Клейна

С каждой геометрией Феликс Клейн связывал лежащую в основе групп симметрии. Иерархия геометрий тогда представляется иерархией этих групп и иерархией их инвариантов. Например, длины, углы и площади сохраняются в евклидовой группе симметрий, в то время как только структура инцидентности и двойное отношение сохраняется в более общих проективных преобразованиях. Понятие параллельности, которое сохраняется в аффинной геометрии, не имеет смысла в проективной геометрии. Таким образом, отделяя группы симметрий от геометрий, связи между симметриями можно установить на уровне групп. Поскольку группа аффинной геометрии является подгруппой проективной геометрии, любое понятие инварианта в проективной геометрии априори имеет смысл в аффинной геометрии, что неверно в обратном направлении. Если добавить требуемые симметрии, получите более сильную теорию, но меньше понятий и теорем (которые будут глубже и более общими).

Точка зрения Тёрстона

Уильям Тёрстон ввёл похожую версию симметрий в геометрии. Модель геометрии — это односвязное гладкое многообразие X вместе с транзитивной операцией группы Ли G на X с компактными стабилизаторами. Группу Ли можно рассматривать как группу симметрий геометрии.

Модель геометрии называется максимальной, если G максимальна среди групп, действующих гладко и транзитивно на X с компактными стабилизаторами, то есть, если она является максимальной группой симметрий. Иногда это определение включают в определение модели геометрии.

Геометрическая структура на многообразии M — это дифференцируемый морфизм из M в X/Γ для некоторой модели геометрии X, где Γ — это дискретная подгруппа G, действующая свободно на X. Если данное многообразие допускает геометрическую структуру, то оно допускает структуру, модель которой максимальна.

Трёхмерная модель геометрии X относится к теореме геометризации, если она максимальна и если существует по меньшей мере одно многообразие с геометрической структурой на X. Тёрстон классифицировал 8 моделей геометрий, удовлетворяющих этим условиям. Эти симметрии называются иногда геометриями Тёрстона. (Существует также бесконечно много моделей геометрий компактных стабилизаторов.)

Симметрия в теории вероятности

В случае конечного числа возможных событий симметрия, учитывающая перестановки (перенумерации), даёт дискретное равномерное распределение.

В случае, когда события представляют собой интервал вещественных чисел, симметрия, учитывающая перестановки подинтервалов равной длины, соответствует непрерывному равномерному распределению.

В других случаях, таких как «выбор случайного целого» или «выбор случайного вещественного», нет симметрии вероятностного распределения, учитывающего перестановки чисел или интервалов равной длины. Другие приемлемые симметрии не приводят к конкретному распределению, или, другими словами, нет уникального распределения вероятности, обеспечивающего максимальную симметрию.

Существует один тип , который может сохранять распределение вероятностей неизменным, это отражение относительно точки, например, нуля.

Возможная симметрия для случайных значений с положительной вероятностью — это та, что применима к логарифмам, то есть когда событие и его обратная величина имеют одинаковое распределение. Однако эта симметрия не приводит к определённому вероятностному распределению.

Для «случайной точки» на плоскости или в пространстве можно выбрать центр и рассматривать симметрию распределения вероятностей относительно окружности или сферы.

Симметрия в теории представлений

Симметрия в квантовой механике: бозоны и фермионы

В квантовой механике бозоны имеют представления, симметричные относительно перестановки операторов, а фермионы имеют антисимметричные представления.

Из этого следует принцип исключения Паули для фермионов. Фактически принцип исключения Паули с однозначной волновой функцией многих частиц эквивалентен требованию антисимметричности волновой функции. Антисимметрия состояния двух частиц представляется как сумма состояний, в котором одна частица находится в состоянии |x⟩{\displaystyle \scriptstyle |x\rangle }, а другая — в состоянии |y⟩{\displaystyle \scriptstyle |y\rangle }:

|ψ⟩=∑x,yA(x,y)|x,y⟩{\displaystyle |\psi \rangle =\sum _{x,y}A(x,y)|x,y\rangle }

и антисимметрия при обмене переменных означает, что A(x,y) = −A(y,x). Из этого следует, что A(x,x) = 0, что является исключением Паули. Утверждение остаётся верным в любом базисе, поскольку единичные изменения базиса сохраняют антисимметричные матрицы антисиметричными, хотя и, строго говоря, величина A(x,y) не является матрицей, а является антисимметричным тензором второго порядка.

Обратно, если диагональные элементы A(x,x) нулевые в любом базисе, то составляющая волновой функции

A(x,y)=⟨ψ|x,y⟩=⟨ψ|(|x⟩⊗|y⟩){\displaystyle A(x,y)=\langle \psi |x,y\rangle =\langle \psi |(|x\rangle \otimes |y\rangle )}

обязательно антисимметрична. Чтобы это проверить, рассмотрим элемент матрицы

⟨ψ|((|x⟩+|y⟩)⊗(|x⟩+|y⟩)){\displaystyle \langle \psi |((|x\rangle +|y\rangle )\otimes (|x\rangle +|y\rangle ))}

Он равен нулю, поскольку две частицы имеют нулевую вероятность одновременно оказаться в состоянии |x⟩+|y⟩{\displaystyle \scriptstyle |x\rangle +|y\rangle }. Но это эквивалентно

⟨ψ|x,x⟩+⟨ψ|x,y⟩+⟨ψ|y,x⟩+⟨ψ|y,y⟩{\displaystyle \langle \psi |x,x\rangle +\langle \psi |x,y\rangle +\langle \psi |y,x\rangle +\langle \psi |y,y\rangle }

Первый и последний член в правой части являются диагональными элементами и равны нулю, и полная сумма равна нулю. Таким образом, для элементов матрицы волновой функции выполняется

⟨ψ|x,y⟩+⟨ψ|y,x⟩={\displaystyle \langle \psi |x,y\rangle +\langle \psi |y,x\rangle =0}.

или

A(x,y)=−A(y,x){\displaystyle A(x,y)=-A(y,x)}

Симметрия в религии и культуре

Симметрия в религиозных символах

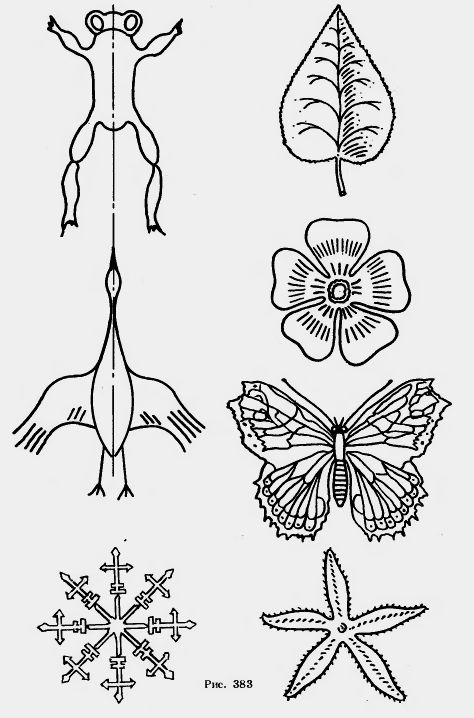
Симметрия в религиозных символах: ряд 1. христианском, иудейском, даосийском; ряд 2. исламском, буддийском, синтоистском; ряд 3. сикхском, в вере Бахаи, индуистском.

Предполагается, что тенденция людей видеть цель в симметрии, является одной из причин, почему симметрия часто является неотъемлемой частью символов мировых религий. Вот лишь некоторые из многих примеров, изображённые на рисунке справа.

Симметрия в социальных взаимодействиях

Люди наблюдают симметричную природу (также включающую асимметричный баланс) социального взаимодействия в различных контекстах. Они включают оценки взаимности, эмпатии, извинения, диалога, уважения, справедливости и мести. Симметричные взаимодействия посылают сигналы «мы одинаковые», а асимметричные взаимодействия выражают мысль «я особый, лучше, чем ты». Взаимоотношения со сверстниками строятся на основе симметрии, а властные отношения — на асимметрии.

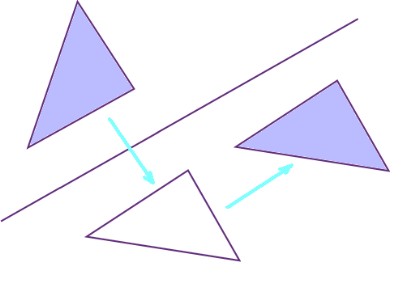
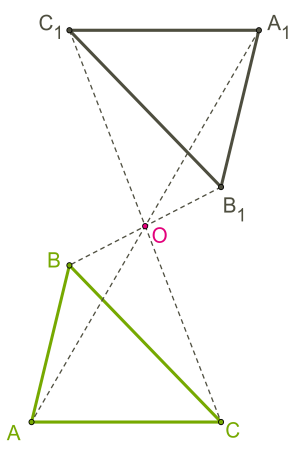
Симметрия в геометрии

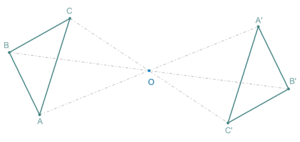
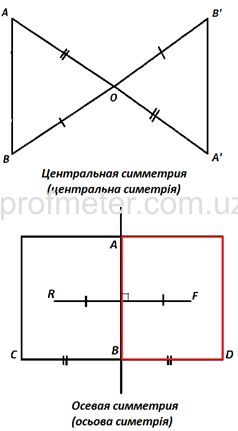
Два треугольника с точечной симметрией отражения в плоскости. Треугольник А’В’С может быть получен из треугольника ABC поворотом на 180 ° вокруг точки O.

Геометрическая симметрия — это наиболее известный тип симметрии для многих людей. Геометрический объект называется симметричным, если после того как он был преобразован геометрически, он сохраняет некоторые исходные свойства. Например, круг повёрнутый вокруг своего центра будет иметь ту же форму и размер, что и исходный круг. Поэтому круг называется симметричным относительно вращения (имеет осевую симметрию).
Виды симметрий, возможных для геометрического объекта, зависят от множества доступных геометрических преобразований и того, какие свойства объекта должны оставаться неизменными после преобразования.

Виды геометрических симметрий:

Зеркальная симметрия
Осевая симметрия
Вращательная симметрия
Центральная симметрия
Скользящая симметрия
Винтовая симметрия

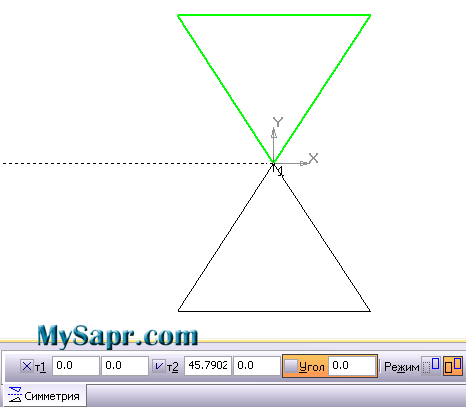
Зеркальная симметрия

Зеркальная симметрия или отражение — движение евклидова пространства, множество неподвижных точек которого является гиперплоскостью (в случае трехмерного пространства — просто плоскостью). Термин зеркальная симметрия употребляется также для описания соответствующего типа симметрии объекта, то есть, когда объект при операции отражения переходит в себя. Это математическое понятие в оптике описывает соотношение объектов и их (мнимых) изображений при отражении в плоском зеркале. Проявляется во многих законах природы (в кристаллографии, химии, физике, биологии и т. д., а также в искусстве и искусствоведении).

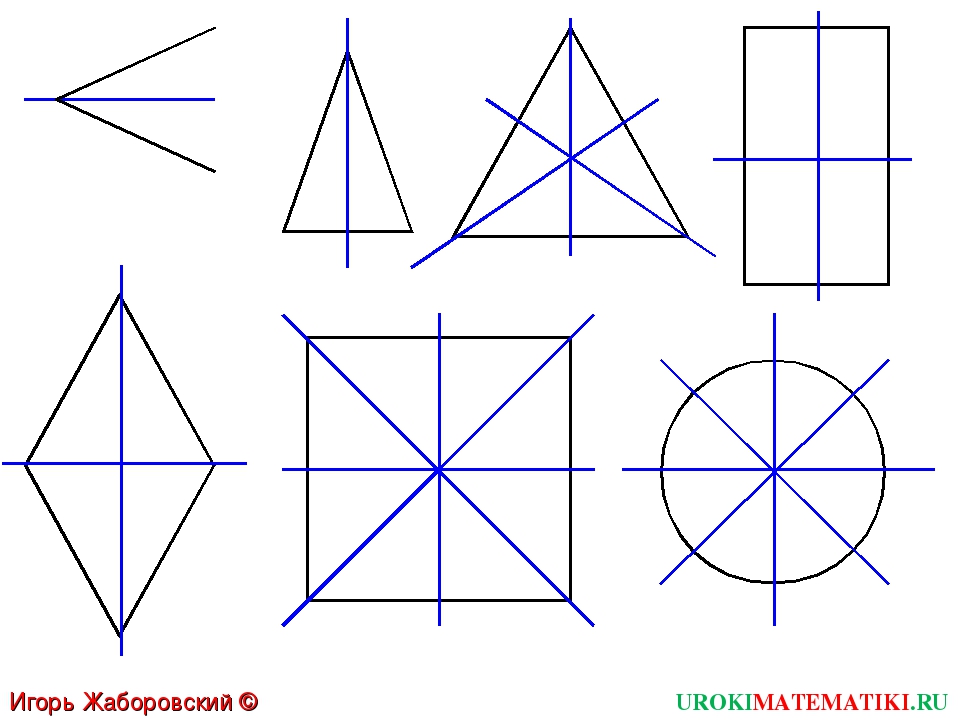
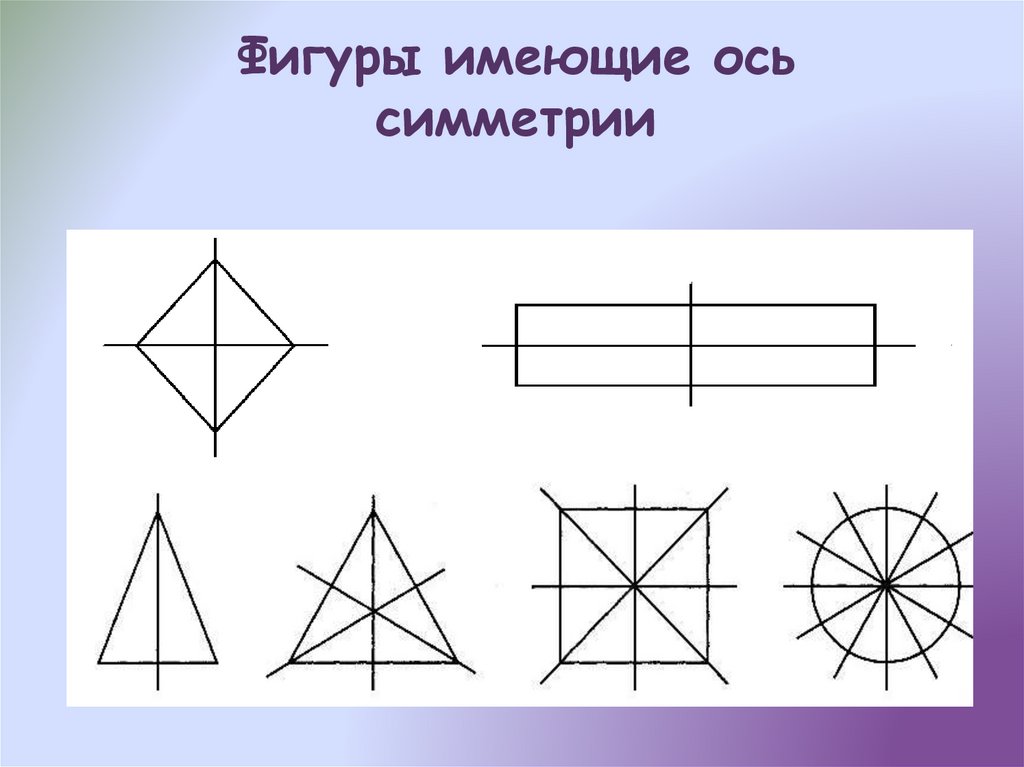
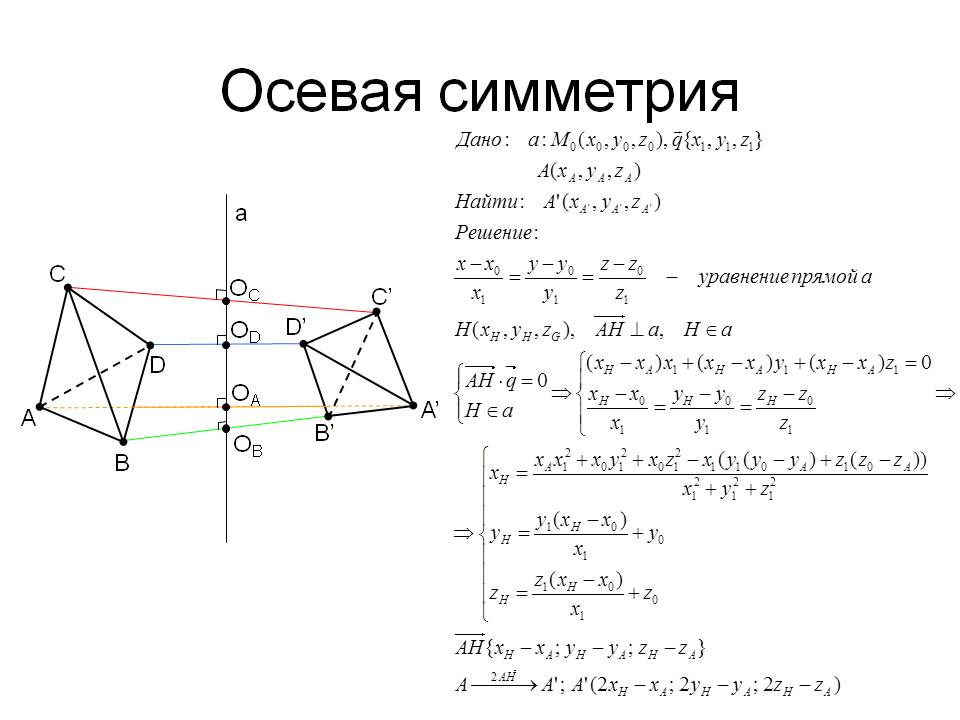
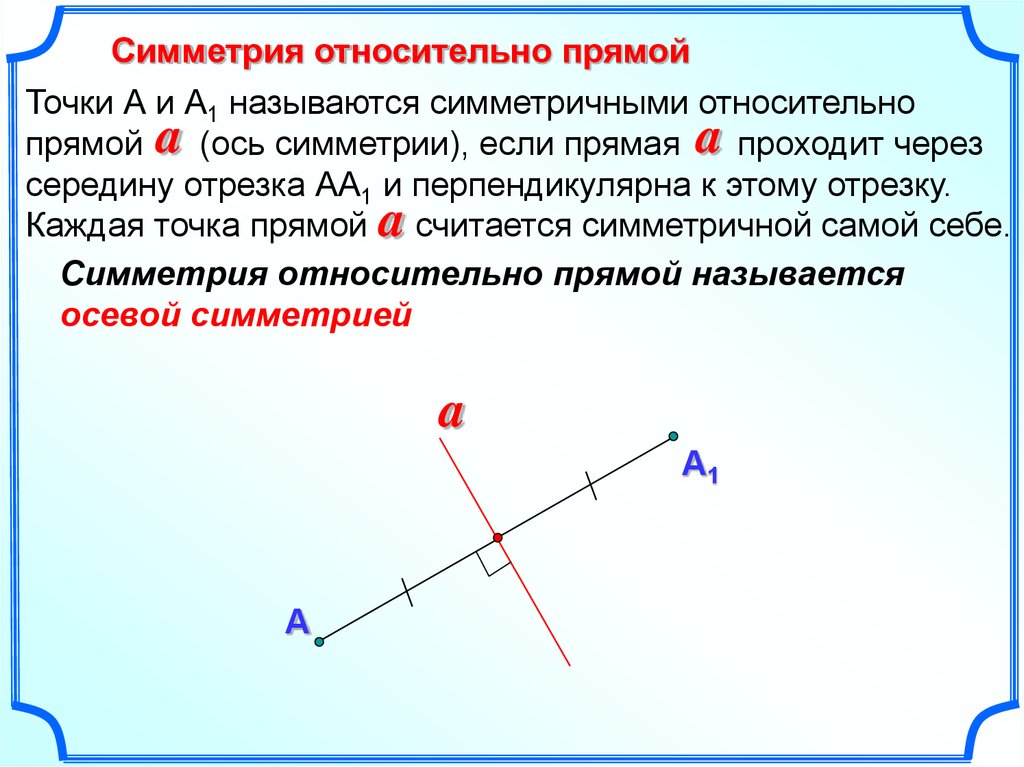
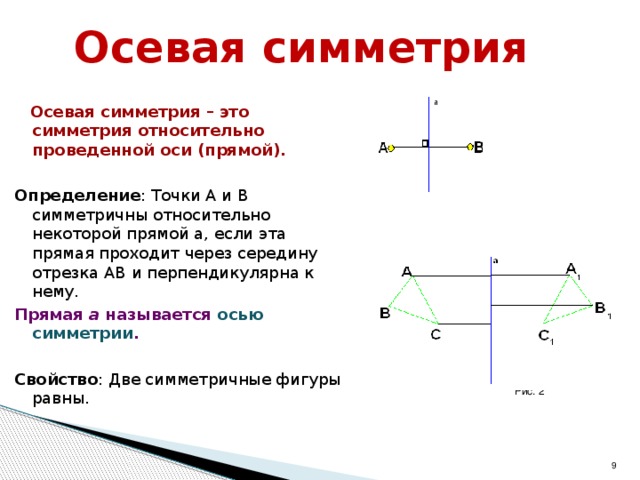
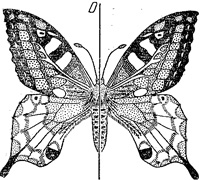
Осевая симметрия

Фигура называется симметричной относительно прямой А, если для каждой точки фигуры симметричная ей точка относительно прямой А также принадлежит этой фигуре.

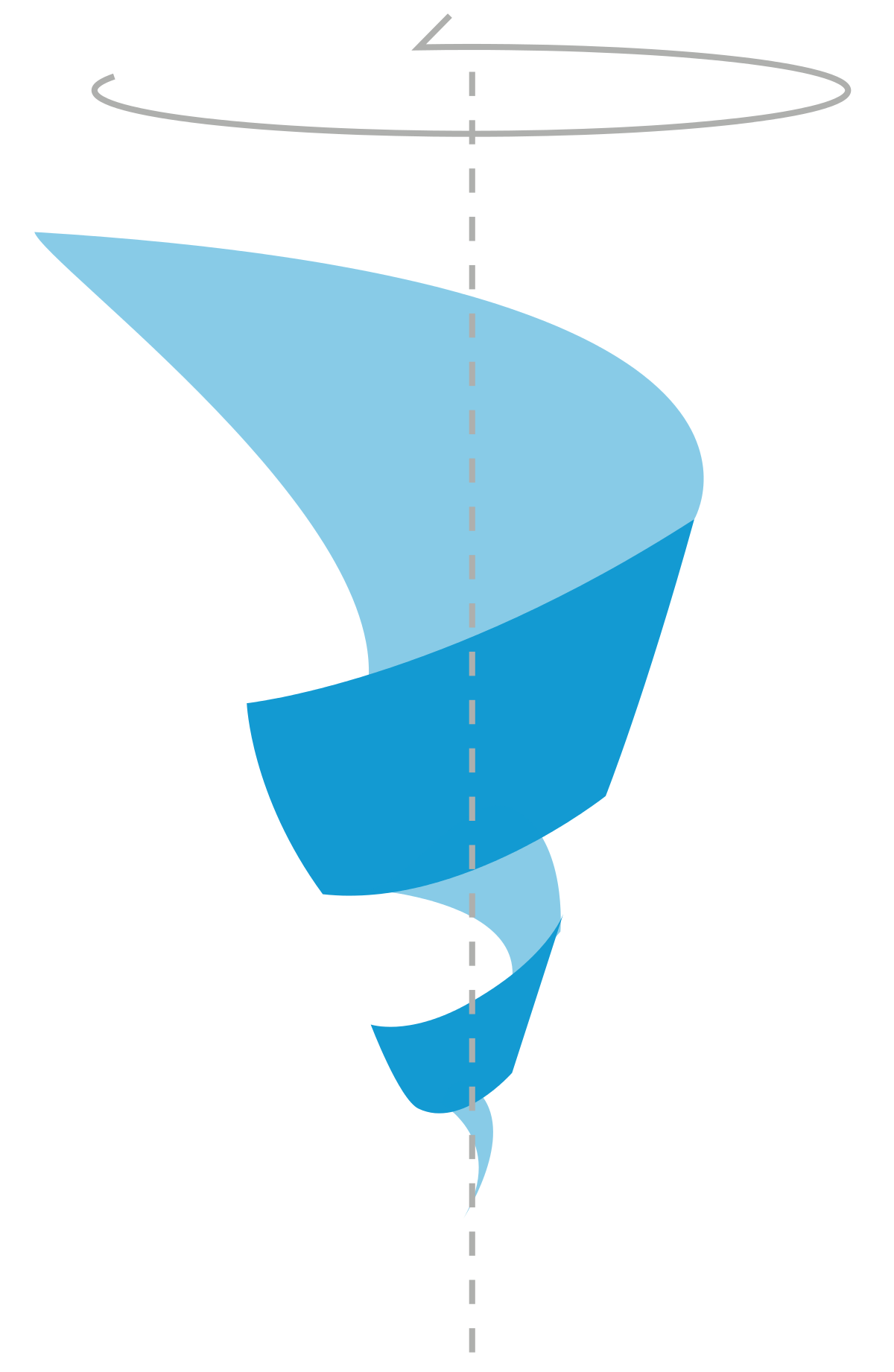
Вращательная симметрия

Вращательная симметрия — термин, означающий симметрию объекта относительно всех или некоторых собственных вращений m-мерного евклидова пространства. Собственными вращениями называются разновидности изометрии, сохраняющие ориентацию. Таким образом, группа симметрии, отвечающая вращениям, есть подгруппа группы E+(m) (см. Евклидова группа).

Трансляционная симметрия может рассматриваться как частный случай вращательной — вращение вокруг бесконечно-удалённой точки. При таком обобщении группа вращательной симметрии совпадает с полной E+(m). Такого рода симметрия неприменима к конечным объектам, поскольку делает всё пространство однородным, однако она используется в формулировке физических закономерностей.

Совокупность собственных вращений вокруг фиксированной точки пространства образуют специальную ортогональную группу SO(m) — группу ортогональных матриц m×m с определителем, равным 1. Для частного случая m = 3 группа носит специальное название — группа вращений.

В физике инвариантность относительно группы вращений называется изотропностью пространства (все направления в пространстве равноправны) и выражается в инвариантности физических законов, в частности, уравнений движения, относительно вращений. Теорема Нётер связывает эту инвариантность с наличием сохраняющейся величины (интеграла движения) — углового момента.

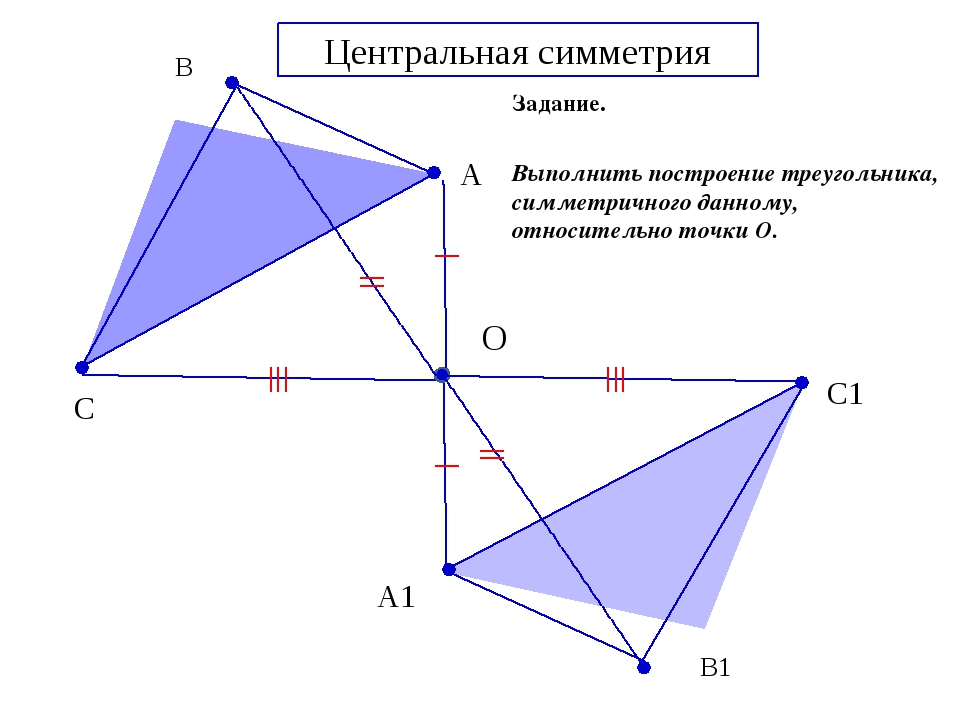
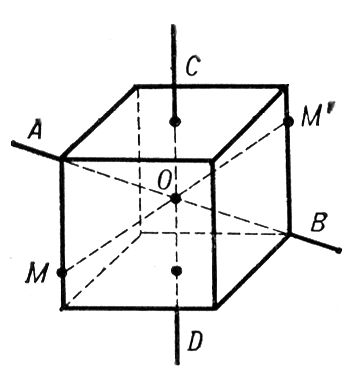
Центральная симметрия

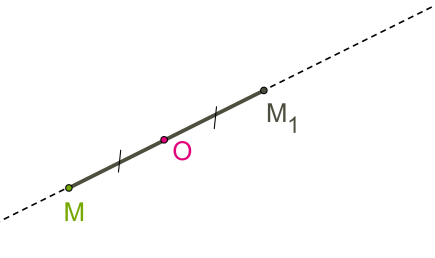
Симметрия относительно точки

Центра́льной симме́трией (иногда центра́льной инве́рсией) относительно точки A называют преобразование пространства, переводящее точку X в такую точку X′, что A — середина отрезка XX′. Центральная симметрия с центром в точке A обычно обозначается через ZA{\displaystyle Z_{A}}, в то время как обозначение SA{\displaystyle S_{A}} можно перепутать с осевой симметрией. Фигура называется симметричной относительно точки A, если для каждой точки фигуры симметричная ей точка относительно точки A также принадлежит этой фигуре. Точка A называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией. Другие названия этого преобразования — симметрия с центром A. Центральная симметрия в планиметрии является частным случаем поворота, точнее, является поворотом на 180 градусов.

Скользящая симметрия

Скользящая симметрия — изометрия евклидовой плоскости.
Скользящей симметрией называют композицию симметрии относительно некоторой прямой l{\displaystyle l} и переноса на вектор, параллельный l{\displaystyle l} (этот вектор может быть и нулевым). Скользящую симметрию можно представить в виде композиции 3 осевых симметрий (теорема Шаля).

Симметрия в линейной алгебре

Симметрия матриц

В линейной алгебре симметричная матрица — это квадратная матрица, которая не меняется при транспонировании. Формально матрица A симметрична, если

A=A⊤{\displaystyle A=A^{\top }}

и, по определению равенства матриц, размеры матриц должны совпадать, так что только квадратная матрица может быть симметричной.

Элементы симметричной матрицы симметричны относительно главной диагонали. Таким образом, если элементы матрицы равны A = (a_ij), то a_ij = a_ji для всех индексов i и j.

Следующая матрица 3×3 симметрична:

17374−53−56.{\displaystyle {\begin{bmatrix}1&7&3\\7&4&-5\\3&-5&6\end{bmatrix}}.}

Любая квадратная диагональная матрица симметрична, поскольку все её недиагональные элементы равны нулю. Все диагональные элементы кососимметричной матрицы должны быть нулевыми, поскольку должны равняться своему отрицательному значению.

В линейной алгебре вещественная симметричная матрица представляет самосопряжённый оператор над вещественным унитарным пространством. Соответствующий объект для комплексного унитарного пространства — Эрмитова матрица с комплексными элементами, которая равна своей Эрмитово-сопряжённой матрице. Таким образом, в линейной алгебре над комплексными числами часто под симметричной матрицей подразумевается матрица с вещественными элементами. Симметричные матрицы появляются естественным образом в различных приложениях и, как правило, пакеты линейной алгебры для них имеют выделенные процедуры.

Симметрия в геометрии

Основная статья:

Симметрии элементарной геометрии (такие как отражение и поворот) описаны в основной статье о .

Точка зрения Клейна

Точка зрения Тёрстона

Симметрии графиков функций

Чётные и нечётные функции

Чётные функции

ƒ(x) = x2 является примером чётной функции.

Пусть f(x) — функция вещественной переменной с вещественными значениями. f является чётной, если в области определения f

f(x)=f(−x){\displaystyle f(x)=f(-x)}

Говоря геометрически, график чётной функции симметричен относительно оси y, что означает, что он не изменится при отражении относительно оси y.

Примерами чётных функций могут служить |x|, x2, x4, cos(x) и cosh(x).

Нечётные функции

ƒ(x) = x3 является примером нечётной функции.

Снова пусть f(x) — функция вещественной переменной с вещественными значениями. f является нечётной, если в области определения f

−f(x)=f(−x),{\displaystyle -f(x)=f(-x)\,,}

или

f(x)+f(−x)=.{\displaystyle f(x)+f(-x)=0\,.}

Геометрически граф нечётной функции имеет симметрию вращения относительно начала координат, в том смысле, что график функции не изменится, если его повернуть на 180 градусов относительно начала координат.

Нечётными функциями являются x, x3, sin(x), sinh(x) и erf(x).

Интегралы

Интеграл нечётной функции от −A до +A равен нулю (где A конечно и функция не имеет вертикальных асимптот между −A и A).

Интеграл чётной функции от −A до +A равен удвоенному интегралу от 0 до +A (где A конечно и функция не имеет вертикальных асимптот между −A и A. Это верно и для бесконечого A, но только в том случае, когда интеграл сходится).