Закон архимеда

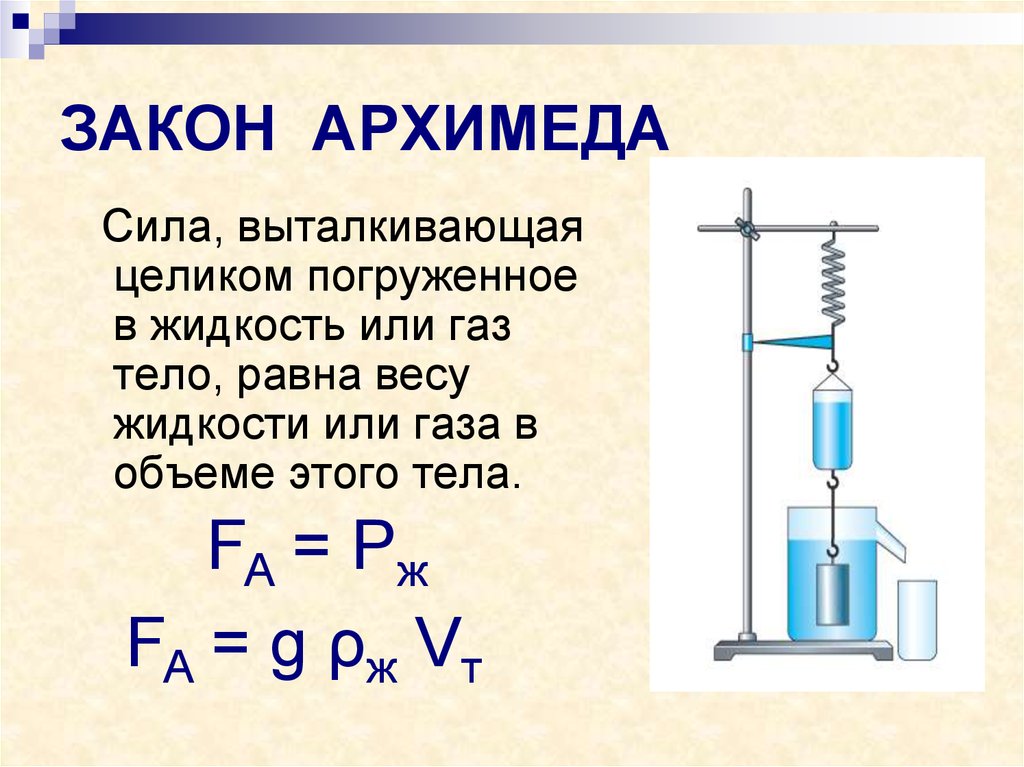
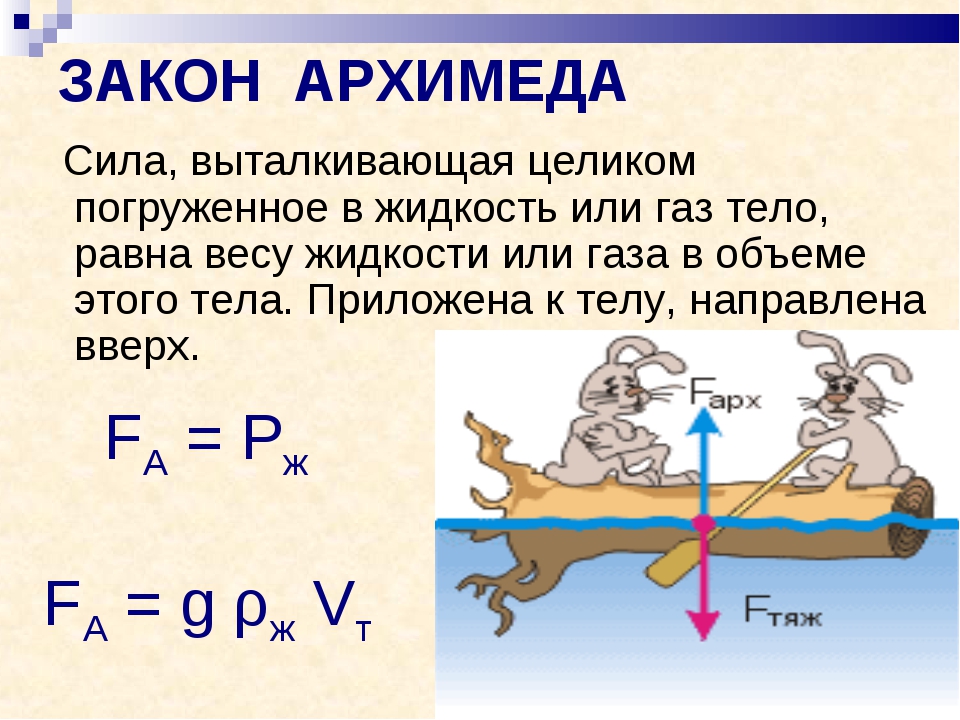
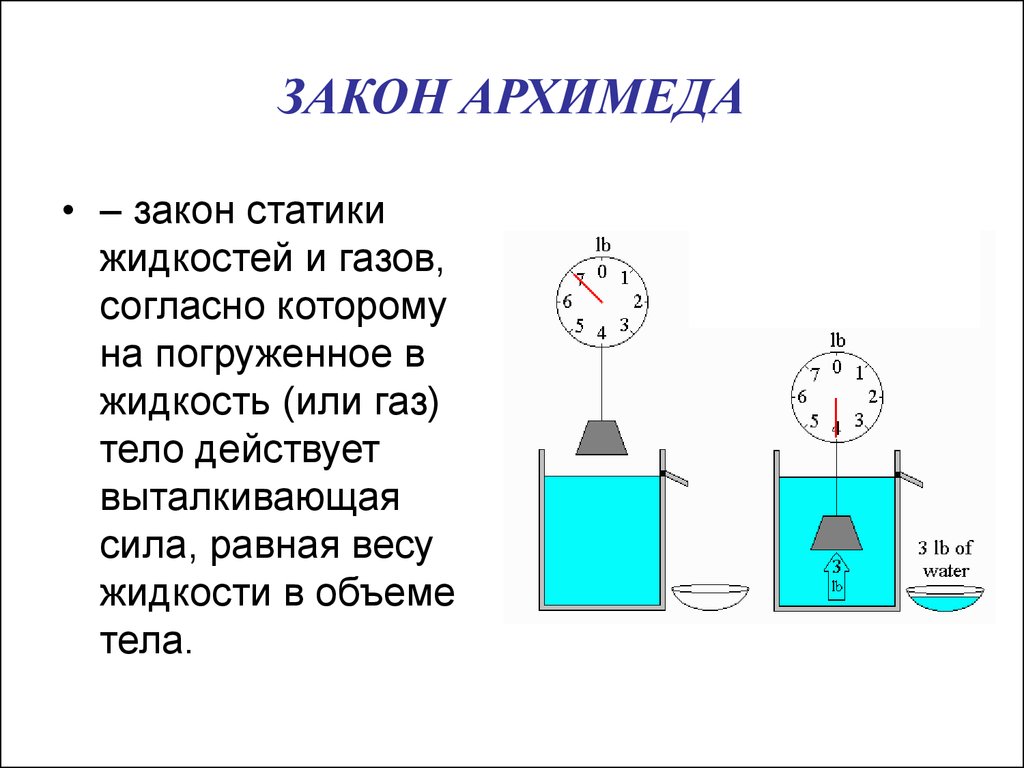
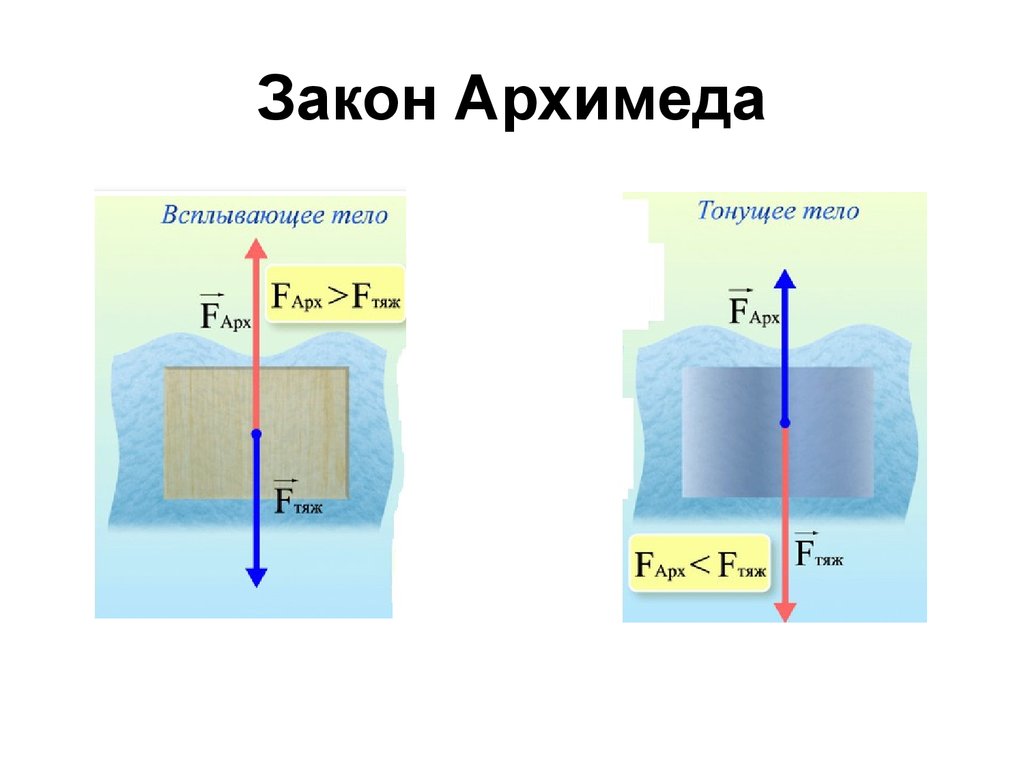
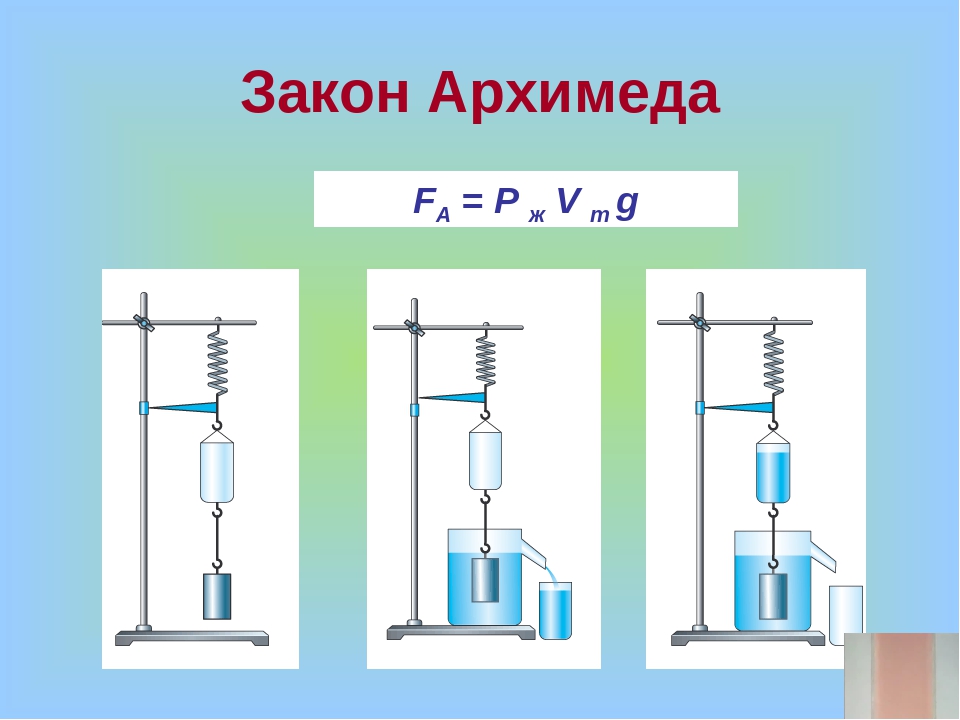
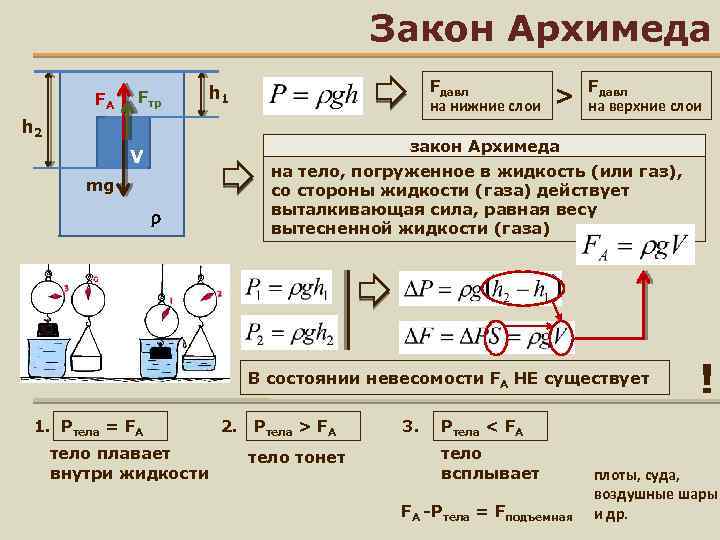
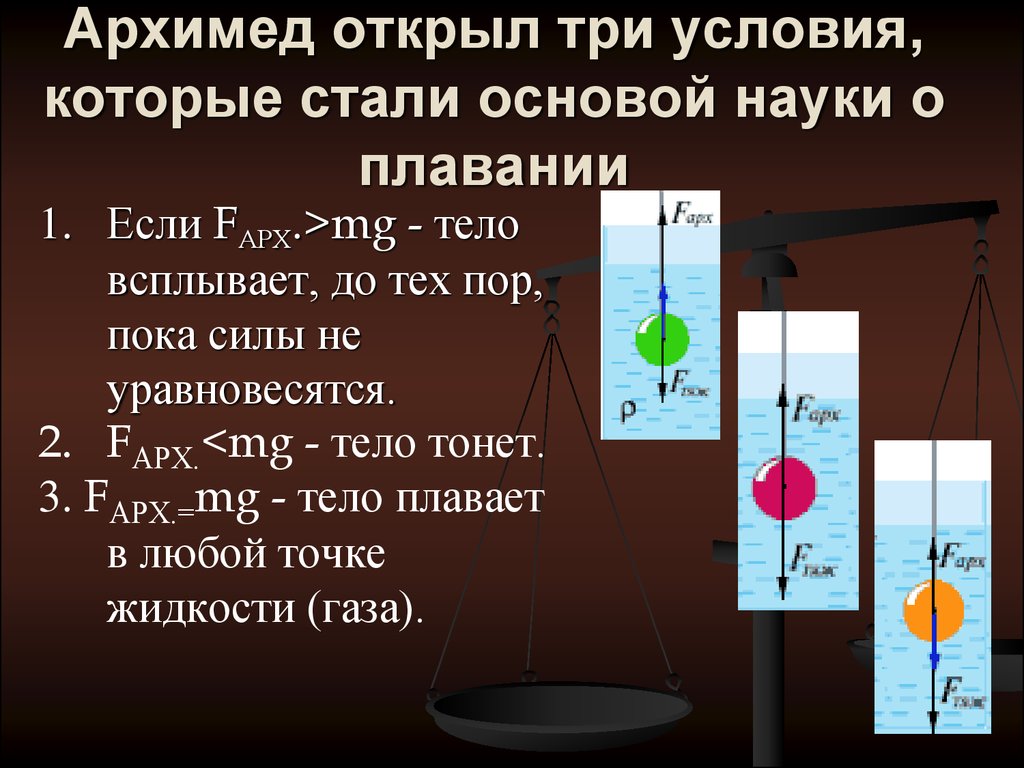
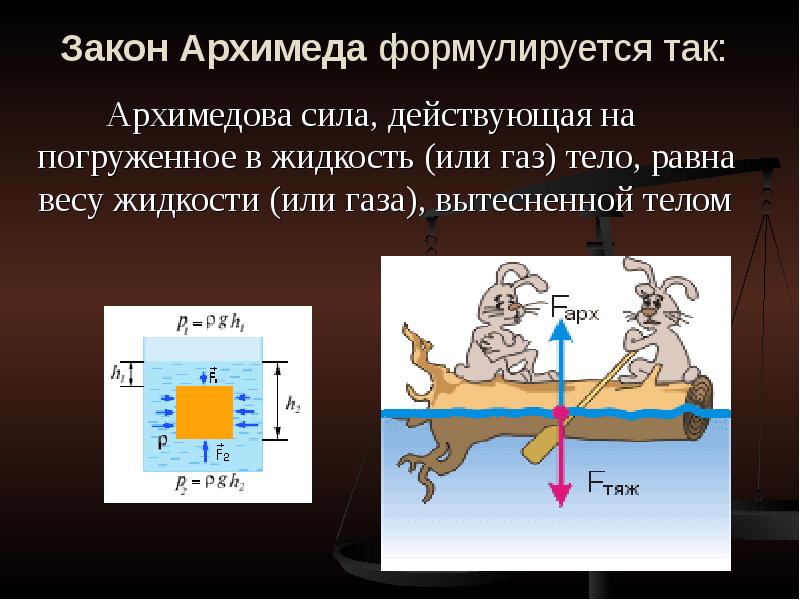
Давление в объеме текучей субстанции

Чтобы понять причину появления архимедовой силы, следует рассмотреть особенности существования давления внутри текучих субстанций. Такими субстанциями считаются газы и жидкости, поскольку любая минимальная сдвиговая сила, приложенная к ним, приводит к смещению в них одних слоев относительно других, то есть появляется течение.

Для примера рассмотрим жидкость (вода, спирт, бензин и т.д.). Во-первых, жидкость является несжимаемым веществом. Во-вторых, все элементарные частицы, которые ее составляют, движутся хаотически в разных направлениях. Это движение приводит к тому, что на любой объем внутри жидкости действует давление со всех сторон. Поскольку каждой компоненте давления соответствует аналогичная, которая направлена в противоположную сторону, то общее давление на рассматриваемый объем равно нулю.

Если жидкость находится в поле гравитационных сил (например, в поле земного тяготения), то верхние слои начинают своим весом давить на нижние. Оказываемое ими давление получило название гидростатического. Оно определяется по формуле:

Где ρ — жидкости плотность, h — расстояние от поверхности жидкости, то есть глубина.

Архимедова сила появляется за счет гидростатического давления. Рассмотрим в следующем пункте подробнее причину ее появления.

Задача на применение закона Архимеда

Предположим, что воздушный шар имеет объем 1000 м3. Плотность воздуха, окружающего шар, равна 1,225 кг/м3. Необходимо определить, какой груз сможет поднять шар, если плотность горячего воздуха в его объеме составляет 1 кг/м3.

Запишем выражение равенства сил:

Где P_g — вес груза, который поднимает шар, P_s — вес самого шара. Будем считать, что средняя плотность шара равна плотности горячего воздуха в нем, тогда приведенное выражение можно переписать так:

Где V — объем шара, ρ_s — его плотность, ρ_a — плотность воздуха, m_g — масса поднимаемого груза. Тогда m_g будет равна:

Таким образом, данный шар сможет поднять 3 человека массой 70 кг каждый.

Почему не тонут корабли?

Теперь следует объяснить плавание судов. Понятно, что корабли, изготовленные из строительного деревянного материала, плавают по волнам, так как плотность дерева меньше плотности воды. Условие плавания здесь срабатывает безоговорочно. Современные корабли изготовлены преимущественно из металлов, у которых большая плотность. Почему металлический гвоздь тонет, а корабль нет?

Кораблю придают специальную форму, чтобы он как можно больше вытеснял воды, вес которой превосходит силу тяжести судна. Этот вес равен выталкивающей (архимедовой) силе, и значит, она больше силы тяжести. Из металла делают основной корпус судна, а остальной его объем заполнен воздухом. Корпусом корабль вытесняет значительное количество воды, достаточно глубоко погружаясь в нее.

Глубину погружения судна моряки называют осадкой. После загрузки корабля его осадка увеличивается. Перегружать корабль нельзя, иначе нарушится условие плавания, корабль может затонуть. Рассчитывается максимальная осадка, на судне проводится красная линия, которую называют ватерлинией, ниже ее корабль оседать не должен.

Вес корабля с максимально взятым грузом называется водоизмещением.

Мореплавание и судостроение неразрывно связаны с историей человечества. От плотов и лодок глубокой древности к каравеллам Колумба и Магеллана, Васко де Гамы и первому российскому военному кораблю «Орел» (1665г.), от первого парохода «Клермонт», построенного Р. Фультоном в США в 1807 году, до ледокола «Арктика», созданного в России в 1975 году.

Суда используются в различных целях: для пассажирских и грузовых перевозок, для научно-исследовательских работ, для охраны границ государства.

К сожалению, с кораблями происходят и неприятности. Во время шторма или других катастроф они могут затонуть. Опять приходит на помощь закон Архимеда.

Со спасательного судна на прочных стропах опускают полые цилиндры большого объема. Чтобы они затонули, их заполняют водой. Водолазы закрепляют эти цилиндры на корпусе корабля. Сжатым воздухом под большим давлением, подаваемым по шлангам, вода из цилиндров вытесняется, заменяется воздухом. Вес цилиндров резко уменьшается. Они начинают выталкиваться из воды и вместе с кораблем всплывают на поверхность.

Спасение затонувшего корабля

В судоходстве, мореплавании, спасении судов помогает закон Архимеда, как один из самых важных законов природы.

Чему равно давление в газах и жидкостях

Напомним определение давления. Давлением p называют физическую величину, равную отношению силы F, направленной перпендикулярно поверхности с площадью S:

$p={F\over S}$ (1)

Французский исследователь Блез Паскаль открыл закон, названный в последствии его именем, который звучит так: жидкости и газы передают производимое на них давление во все стороны одинаково.

На основании закона Паскаля и формулы (1) можно вычислить давление столба жидкости:

$p={F\over S}={m*g\over S}$ (2)

где: m — масса жидкости, g = 9,8 Н/кг — ускорение свободного падения.

Тогда, если выразить массу жидкости через плотность ρ и объем V, получим:

$p={ρ*V*g\over S}$ (3)

Выразив объем V через площадь S и высоту h, получим окончательную формулу для давления:

$p={ρ*g*h}$ (4)

В физике всегда необходимо знать в чем измеряется физическая величина. В честь Паскаля назван не только закон, но и единица измерения давления. Так как сила измеряется в ньютонах, а площадь в метрах квадратных, то:

$$={ \over }$$

Часто используются кратные единицы давления: килопаскаль (кПа) и мегапаскаль (МПа).

Как был открыт Закон Архимеда

Согласно легенде, Архимеду удалось выполнить поручение царя Гиерона. Дело в том, что царь засомневался, сделана ли его корона из чистого золота или из сплава с другими металлами. Архимед должен был проверить честность ювелира. Задача усложнялась еще и тем, что корону ни в коем случае нельзя было ломать. Архимед долго не находил ответа. Но однажды, принимая ванну, он заметил, что из ванны вытекает вода. И тут его осенило! Ведь можно точно так же погрузить корону в воду и измерить объем воды, вытесненной короной. Ученый выскочил из ванны с криком «Эврика!», что в переводе с древнегреческого означает «Нашел!».

Сначала Архимед взвесил слиток чистого золота и корону в воздухе, затем он провел такое же взвешивание в воде. Ученый поочередно погрузил корону и слиток в воду, а затем измерил количество жидкости, вытесненное обоими телами. Оно оказалось разным. Это было явным свидетельством того, что корона кроме золота содержит другие металлы. Таким образом Архимеду удалось уличить мастера в воровстве.

Открытие Архимедом своего закона

Согласно исторической справке свой закон Архимед открыл интересным образом. Витрувий в своих трудах описывает, что сиракузский тиран Гиерон Второй поручил одному из мастеров отлить ему золотую корону. После того как корона была готова, он решил проверить, не обманул ли его мастер, и не добавил ли в золото более дешевое серебро, которое имеет меньшую плотность, чем царь металлов. Эту задачу он задал решить Архимеду. Ученому нельзя было нарушать целостность короны.

Однажды принимая ванну, Архимед обратил внимание, что уровень воды в ней поднимается. Этот эффект он решил использовать для вычисления объема короны, знание которого, а также массы короны, позволяло ему вычислить плотность предмета

Это открытие сильно поразило Архимеда. Витрувий описал его состояние так: он бежал по улице абсолютно раздетым, и кричал «Эврика!», что с древнегреческого переводится «Я нашел!». В итоге плотность короны оказалась меньше, чем чистого золота, и мастер был казнен.

Архимед создал труд, который называется «О плавающих телах», где впервые подробно описывает открытый им закон. Отметим, что формулировка закона Архимеда, которую сделал сам ученый, практически не изменилась.

Воздушный шар как транспортное средство

Воздушный шар — это довольно простой летательный аппарат, который используется для перемещения из одного места в другое. Знание и применение законов физики позволяет путешествовать в корзине, прикрепленной к шару, и наслаждаться прекрасными пейзажами. Согласись, подобные впечатления действительно можно получить только из корзины воздушного шара, ведь самолеты летают гораздо быстрее и выше. Да и вид, открывающийся из иллюминатора воздушного лайнера, несколько иной: пейзажами можно любоваться только на взлете и при посадке.

Купол воздушного шара наполняется воздухом, нагреваемым при помощи горелки. А так как горячий воздух легче холодного, то шар, наполненный таким воздухом, взлетает

Описание

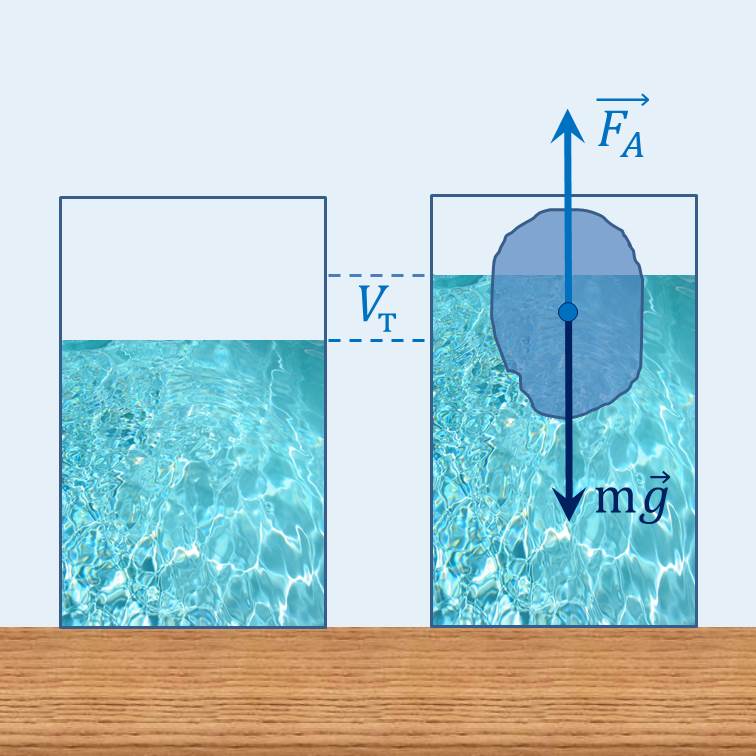
Выталкивающая или подъёмная сила по направлению противоположна силе тяжести, прикладывается к центру тяжести объёма, вытесняемого телом из жидкости или газа.

Если тело плавает (см. плавание тел) или равномерно движется вверх или вниз, то выталкивающая или подъёмная сила по модулю равна силе тяжести, действующей на вытесненный телом объём жидкости или газа.

Плавание тела. Сила Архимеда (FA{\displaystyle F_{A}}) уравновешивает вес тела (Fp{\displaystyle F_{p}}):

FA=Fp;{\displaystyle F_{A}=F_{p};} ρ_жg V_ж = ρ_тg V_т

Например, воздушный шарик объёмом V{\displaystyle V}, наполненный гелием, летит вверх из-за того, что плотность гелия (ρH{\displaystyle \rho _{H}}) меньше плотности воздуха (ρO{\displaystyle \rho _{O}}):

FA>Fp;{\displaystyle F_{A}>F_{p};}
ρOgV>ρHgV.{\displaystyle \rho _{O}gV>\rho _{H}gV.}

Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела, погруженного в жидкость или газ. В силу симметрии прямоугольного тела, силы давления, действующие на боковые грани тела, уравновешиваются. Давление (PA{\displaystyle P_{A}}) и сила давления (FA{\displaystyle F_{A}}), действующие на верхнюю грань тела, равны:

PA=ρghA;{\displaystyle P_{A}=\rho gh_{A};}

FA=ρghAS,{\displaystyle F_{A}=\rho gh_{A}S,}

где:

• PA{\displaystyle P_{A}} — давление, оказываемое жидкостью или газом на верхнюю грань тела, Па;
• FA{\displaystyle F_{A}} — сила давления, действующая на верхнюю грань тела и направленная вниз, Н;
• ρ{\displaystyle \rho } — плотность жидкости или газа, кг/м3;
• hA{\displaystyle h_{A}} — расстояние между поверхностью жидкости или газа и верхней гранью тела, м;
• S{\displaystyle S} — площадь горизонтального поперечного сечения тела, м2.

Давление (PB{\displaystyle P_{B}}) и сила давления (FB{\displaystyle F_{B}}), действующие на нижнюю грань тела, равны:

PB=ρghB;{\displaystyle P_{B}=\rho gh_{B};}

FB=ρghBS,{\displaystyle F_{B}=\rho gh_{B}S,}

где:

• PB{\displaystyle P_{B}} — давление, оказываемое жидкостью или газом на нижнюю грань тела, Па;
• FB{\displaystyle F_{B}} — сила давления, действующая на нижнюю грань тела и направленная вверх, Н;
• hB{\displaystyle h_{B}} — расстояние между поверхностью жидкости или газа и нижней гранью тела, м.

Сила давления жидкости или газа на тело определяется разностью сил FB{\displaystyle F_{B}} и FA{\displaystyle F_{A}}:

FB−FA=ρghBS−ρghAS=ρg(hB−hA)S=ρghS=ρgV,{\displaystyle F_{B}-F_{A}=\rho gh_{B}S-\rho gh_{A}S=\rho g\left(h_{B}-h_{A}\right)S=\rho ghS=\rho gV,}

где:

• h=hB−hA{\displaystyle h=h_{B}-h_{A}} — расстояние между верхней и нижней гранями тела (в случае частичного погружения высота части тела, погружённой в жидкость или газ), м;
• V{\displaystyle V} — объём тела, погружённого в жидкость или газ (в случае частичного погружения объём части тела, погружённой в жидкость или газ), м3.

Разница давлений:

PB−PA=ρghB−ρghA=ρgh.{\displaystyle P_{B}-P_{A}=\rho gh_{B}-\rho gh_{A}=\rho gh.}

В отсутствие гравитационного поля, то есть, в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции, поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов необходимо производить принудительно вентиляторами.

Греческий ученый Архимед

Архимед вырос в семье, которая была связана с наукой, поскольку его отец, Фидий, был великим астрономом своего времени. С раннего детства Архимед стал проявлять интерес к наукам. Учился он в Александрии, где завел дружбу с Эратосфеном из Кирены. Вместе с ним Архимед впервые измерил окружность земного шара. Благодаря влиянию Эратосфена, в юном Архимеде также появился интерес к астрономии.

После возвращения в свой родной город Сиракузы ученый посвящает большое количество времени изучению математики, физики, геометрии, механики, оптики и астрономии. Во всех этих областях науки Архимед совершил различные открытия, понимание которых оказывается трудным даже для современного образованного человека.

Объем жидкости, находящийся в равновесии с остальной жидкостью

В школе в 7 классе закон Архимеда начинают изучать. Чтобы понять смысл этого закона, следует сначала рассмотреть силы, которые действуют на определенный объем жидкости, находящейся в равновесии в толще остальной жидкости.

Сила, действующая на какую-либо поверхность рассматриваемого объема жидкости, равна p*dS, где p — давление, которое зависит только от глубины, dS — площадь этой поверхности.

Поскольку выделенный объем жидкости находится в равновесии, значит результирующая сила, действующая на поверхности этого объема, и связанная с давлением, должна уравновешиваться весом этого объема жидкости. Эта результирующая сила называется силой выталкивания. Точка приложения ее находится в центре тяжести этого объема жидкости.

Поскольку давление в жидкости вычисляется по формуле p =ro*g*h, где ro — плотность жидкости, g — ускорение свободного падения, h — глубина, то равновесие рассматриваемого объема жидкости определяется уравнением: вес тела = ro*g*V, где V — объем рассматриваемой части жидкости.

Плавание различных объектов

Пожалуй, самым известным примером является плавание судов. Так, любой корабль имеет среднюю плотность меньше, чем плотность воды (1 г/см3), поэтому он не тонет, несмотря на то, что сделан из гораздо более плотных металлических материалов.

В случае подводной лодки, следует отметить, что ее плавучесть регулируется с помощью балласта. Так, набирая морскую воду в специально предусмотренные емкости, лодка увеличивает свою среднюю плотность и начинает погружаться. Наоборот, откачивание воды из названных емкостей уменьшает ее среднюю плотность, что приводит к всплытию подводной лодки. В соответствии с этим же принципом рыбы, имеющие плавательный пузырь, с легкостью изменяют глубину своего погружения.

Принцип воздухоплавания аэростатов и воздушных шаров ничем не отличается от плавания судов в воде. Например, воздушный шар использует во время своего полета горячий воздух. Как известно из физики, при нагревании плотность воздуха уменьшается за счет его расширения. В результате воздушный шар получает возможность поднимать некоторый груз в воздухе, используя выталкивающую архимедову силу.

Задачи

Задача 1. Груз массой 3 кг, подвешенный на тонкой нити, целиком по-гружен в воду и не касается дна сосуда (рис. 1). Модуль силы натяжения нити 10 Н. Найдите объём груза (в литрах).

Решение. На груз в воде действуют сила тяжести (), архимедова сила (F_A) и сила натяжения нити (Т). Ось OY направим вверх (рис. 2). Запишем второй закон Ньютона:

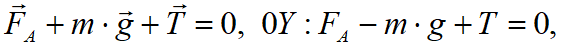
где — плотность воды, которую находим из таблицы «Плотность» (см. «Справочные данные»). Тогда

Задача 2. Предмет из алюминия объемом 100 см3 подвесили к пружине и опустили в бензин. Определите силу натяжения пружины.

Решение. На тело в керосине действуют сила тяжести (), архимедова сила (F_A) и сила упругости (F_упр) пружины. Ось OY направим вверх (рис. 3). Запишем второй закон Ньютона:

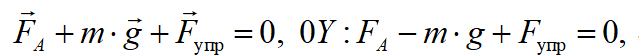
где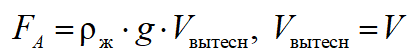 — объем тела, — масса тела,

=700 кг/м3 — плотность бензина, ρ = 2700 кг/м3 — плотность алюминия, которые находим из таблицы «Плотность» (см. «Справочные данные»). Тогда

Задача 3. Стальной шарик висит на нити, привязанной к штативу. Шарик целиком погружен в керосин (рис. 4). Затем стакан с керосином заменили на стакан с водой, и шарик оказался целиком в воде (рис. 5). Как изменились при этом сила натяжения нити и сила Архимеда, действующая на шарик?

Для каждой величины определите соответствующий характер изменения:

1) увеличилась; 2) уменьшилась; 3) не изменилась.

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Сила натяжения нити	Сила Архимеда, действующая на шарик

Решение. На тело в жидкости действуют сила тяжести (), архимедова сила (F_A) и сила натяжения нити (T). Ось OY направим вверх (рис. 6). Запишем второй закон Ньютона:

Архимедова сила равна

где — объем тела. Тогда

Масса бруска m и его объем V не меняются, плотность жидкости ρ_ж увеличивается (ρ_1ж = 800 кг/м3 — плотность керосина, ρ_2ж = 1000 кг/м3 — плотность воды, которые находим из таблицы «Плотность» (см. «Справочные данные»)).

Из уравнения (2) следует, что так как масса бруска m не меняется, а плотность жидкости ρ_ж увеличивается, то сила натяжения нити уменьшается. Это соответствует изменению № 2.

Из уравнения (1) следует, что так как масса бруска m и его объем V не меняются, а плотность жидкости ρ_ж увеличивается, то сила Архимеда так же увеличивается. Это соответствует изменению № 1.

Ответ: 21.

Задача 4. К динамометру подвесили тело. Показания динамометра в воздухе 12 Н, в воде — 7 Н. Определите плотность тела.

Решение. Показания динамометра — это значение силы упругости F_упр его пружины. На тело в воздухе действуют сила тяжести () и сила упругости (F_упр1) (рис. 7, а). На тело в воде действуют сила тяжести (), архимедова сила (F_A) и сила упругости (F_упр2) (рис. 7, б). Ось 0Y направим вверх. Запишем второй закон Ньютона для двух случаев:

где  — объем тела, ρ_ж = 1000 кг/м3 — плотность воды, которую находим из таблицы «Плотность» (см. «Справочные данные»), ρ — плотность тела. Тогда

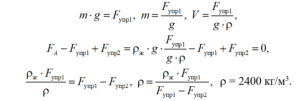
Вывод закона Архимеда для тела произвольной формы

Гидростатическое давление p{\displaystyle p} на глубине h{\displaystyle h}, оказываемое жидкостью плотностью ρ{\displaystyle \rho } на тело, есть p=ρgh{\displaystyle p=\rho gh}. Пусть плотность жидкости (ρ{\displaystyle \rho }) и напряжённость гравитационного поля (g{\displaystyle g}) — постоянные величины, а h{\displaystyle h} — параметр. Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат Oxyz{\displaystyle Oxyz}, причём выберем направление оси z совпадающим с направлением вектора g→{\displaystyle {\vec {g}}}. Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку dS{\displaystyle dS}. На неё будет действовать сила давления жидкости направленная внутрь тела, dF→A=−pdS→{\displaystyle d{\vec {F}}_{A}=-pd{\vec {S}}}. Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:

F→A=−∫SpdS→=−∫SρghdS→=−ρg∫ShdS→=∗−ρg∫Vgrad(h)dV=∗∗−ρg∫Ve→zdV=−ρge→z∫VdV=(ρgV)(−e→z).{\displaystyle {\vec {F}}_{A}=-\int \limits _{S}{p\,d{\vec {S}}}=-\int \limits _{S}{\rho gh\,d{\vec {S}}}=-\rho g\int \limits _{S}{h\,d{\vec {S}}}=^{*}-\rho g\int \limits _{V}{grad(h)\,dV}=^{**}-\rho g\int \limits _{V}{{\vec {e}}_{z}dV}=-\rho g{\vec {e}}_{z}\int \limits _{V}{dV}=(\rho gV)(-{\vec {e}}_{z}).}

При переходе от интеграла по поверхности к интегралу по объёму пользуемся обобщённой теоремой Остроградского-Гаусса.

∗h(x,y,z)=z;{\displaystyle {}^{*}h(x,y,z)=z;}

∗∗grad(h)=∇h=e→z.{\displaystyle ^{**}grad(h)=\nabla h={\vec {e}}_{z}.}

Получаем, что модуль силы Архимеда равен ρgV{\displaystyle \rho gV}, и направлена сила Архимеда в сторону, противоположную направлению вектора напряжённости гравитационного поля.