Серединный перпендикуляр к отрезку
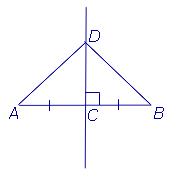
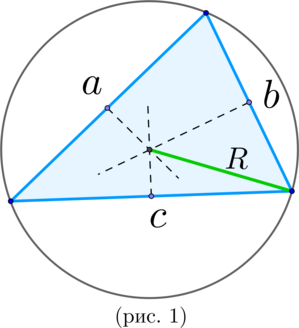
Определение 1. Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).
Рис.1
Теорема 1. Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.
Доказательство. Рассмотрим произвольную точку D, лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что .
Рис.2
Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB. Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1). Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
Доказательство. Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D.
Рис.3
Докажем, что отрезок AE длиннее отрезка EB. Действительно,

Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.
Рис.4
Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE. Действительно,
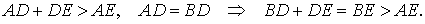
Полученное противоречие и завершает доказательство теоремы 2
Свойства описанной около треугольника окружности. Теорема синусов
| Фигура | Рисунок | Свойство |
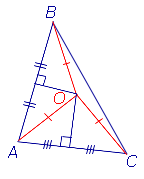
| Серединные перпендикулярык сторонам треугольника | Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. | |
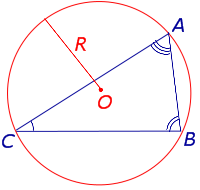
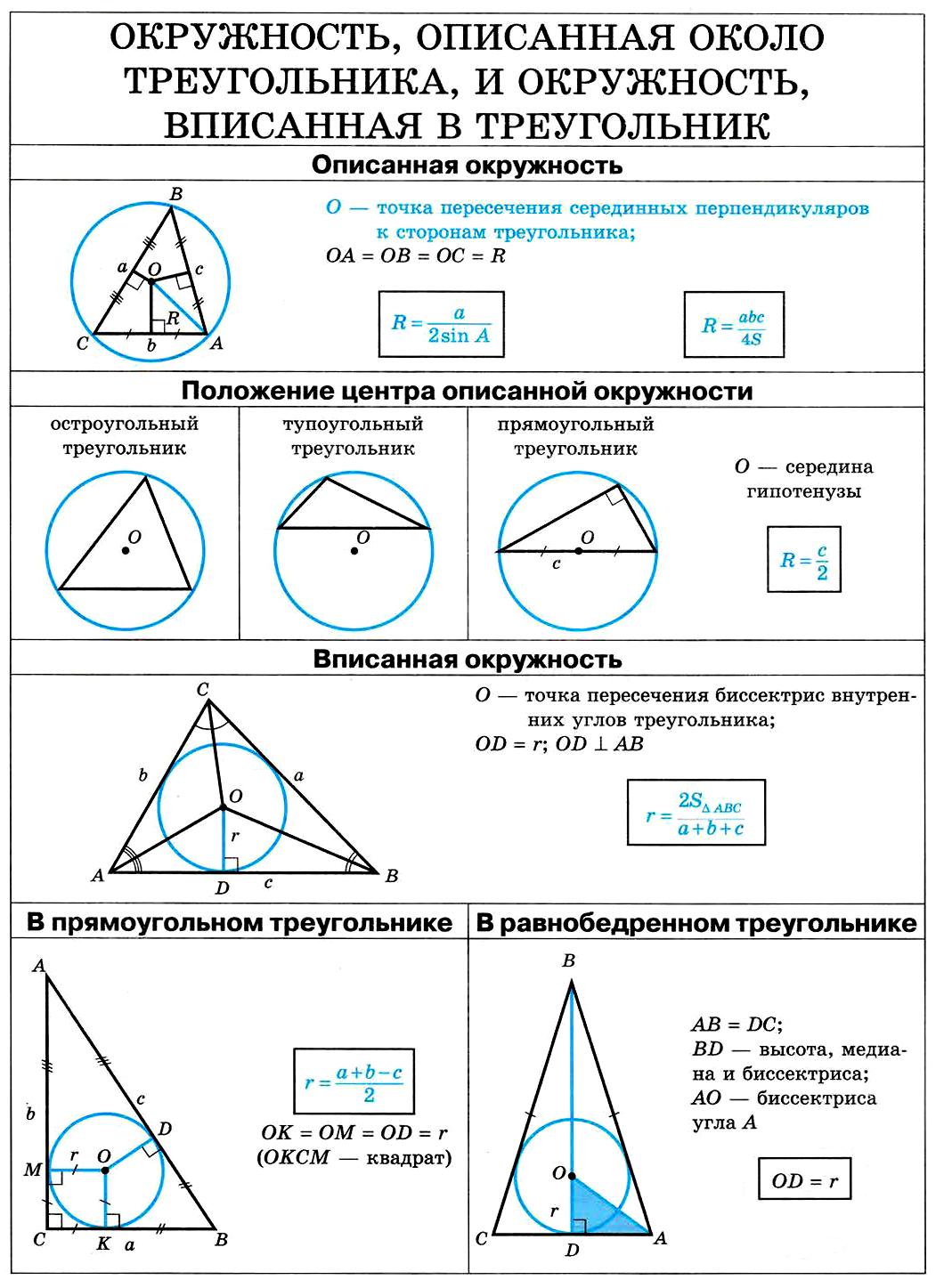
| Окружность, описанная около треугольника | Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. | |
| Центр описанной около остроугольного треугольника окружности | Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. | |
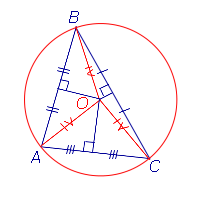
| Центр описанной около прямоугольного треугольника окружности | Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. | |
| Центр описанной около тупоугольного треугольника окружности | Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. | |
| Теорема синусов |
Для любого треугольника справедливы равенства (теорема синусов): , где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности. |
|
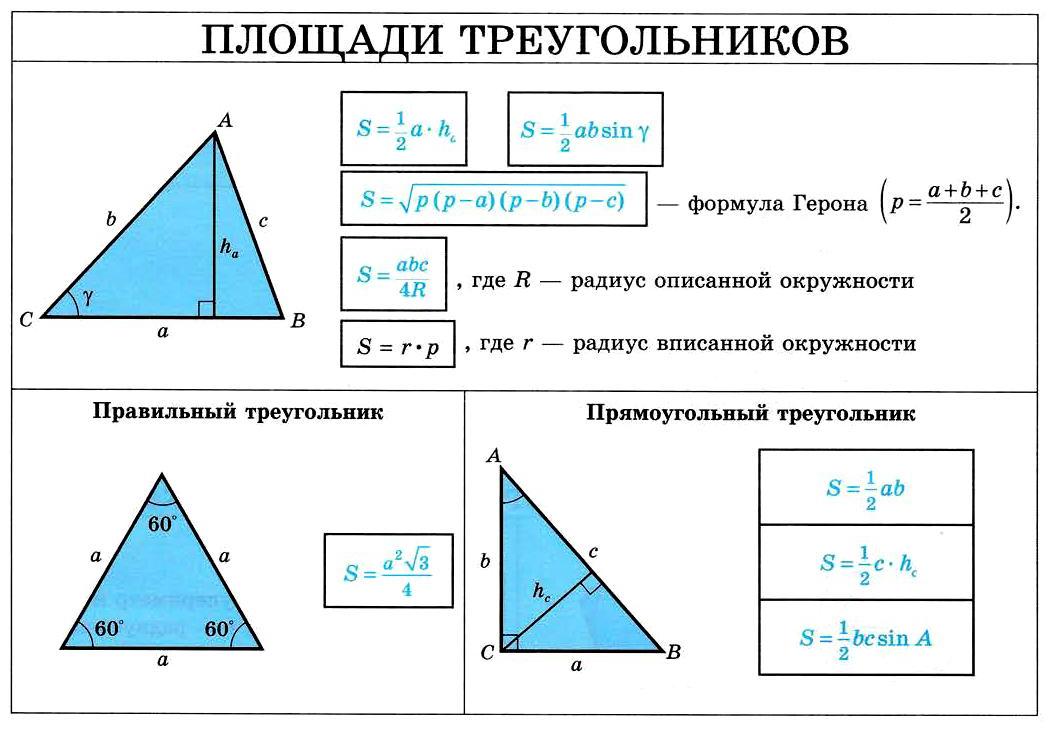
| Площадь треугольника |
Для любого треугольника справедливо равенство: S = 2R2 sin A sin B sin C , где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности. |
|
| Радиус описанной окружности |
Для любого треугольника справедливо равенство: где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности. |
| Серединные перпендикуляры к сторонам треугольника |
|
Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. |
| Окружность, описанная около треугольника |
|
Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. |
| Центр описанной около остроугольного треугольника окружности |
|
Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. |
| Центр описанной около прямоугольного треугольника окружности |
|
Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. |
| Центр описанной около тупоугольного треугольника окружности |
|
Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. |
| Теорема синусов |
|
Для любого треугольника справедливы равенства (теорема синусов): , где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности. |
| Площадь треугольника |
|
Для любого треугольника справедливо равенство: S = 2R2 sin A sin B sin C , где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности. |
| Радиус описанной окружности |
|
Для любого треугольника справедливо равенство: где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности. |
На плоскости
Перпендикулярные прямые на плоскости
Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.
Про прямую m{\displaystyle m} перпендикулярную к прямой ℓ{\displaystyle \ell } проведённую через точку P{\displaystyle P} вне прямой ℓ{\displaystyle \ell }, говорят, что m{\displaystyle m} есть перпендикуляр опущенный из P{\displaystyle P} на ℓ{\displaystyle \ell }.
Если же точка P{\displaystyle P} лежит на прямой ℓ{\displaystyle \ell }, то говорят, что m{\displaystyle m} есть перпендикуляр к восстановленный из P{\displaystyle P} к ℓ{\displaystyle \ell } (устаревший термин восставленный).
В координатах
В аналитическом выражении прямые, заданные линейными функциями
- y=a⋅x+b{\displaystyle y=a\cdot x+b}
и
- y=k⋅x+m{\displaystyle y=k\cdot x+m}
будут перпендикулярны, если выполнено следующее условие на их угловые коэффициенты
- a⋅k=−1.{\displaystyle a\cdot k=-1.}
Построение перпендикуляра
Построение перпендикуляра
‘Шаг 1: (красный) С помощью циркуля проведём полуокружность с центром в точке P, получив точки А’ и В.
‘Шаг 2: (зелёный) Не меняя радиуса, построим две полуокружности с центром в точках A’ и В соответственно, проходящими через точку P. Кроме точки P есть ещё одна точка пересечения этих полуокружностей, назовём её Q.
Шаг 3: (синий) Соединяем точки P и Q. PQ и есть перпендикуляр к прямой AB.
Координаты точки основания перпендикуляра к прямой
A(xa,ya){\displaystyle A(x_{a},y_{a})} и B(xb,yb){\displaystyle B(x_{b},y_{b})} — прямая, O(xo,yo){\displaystyle O(x_{o},y_{o})} — основание перпендикуляра, опущенного из точки P(xp,yp){\displaystyle P(x_{p},y_{p})}.
Если xa=xb{\displaystyle x_{a}=x_{b}} (вертикаль), то xo=xa{\displaystyle x_{o}=x_{a}} и yo=yp{\displaystyle y_{o}=y_{p}}.
Если ya=yb{\displaystyle y_{a}=y_{b}} (горизонталь), то xo=xp{\displaystyle x_{o}=x_{p}} и yo=ya{\displaystyle y_{o}=y_{a}}.
Во всех остальных случаях:
- xo=xa⋅(yb−ya)2+xp⋅(xb−xa)2+(xb−xa)⋅(yb−ya)⋅(yp−ya)(yb−ya)2+(xb−xa)2{\displaystyle x_{o}={\frac {x_{a}\cdot (y_{b}-y_{a})^{2}+x_{p}\cdot (x_{b}-x_{a})^{2}+(x_{b}-x_{a})\cdot (y_{b}-y_{a})\cdot (y_{p}-y_{a})}{(y_{b}-y_{a})^{2}+(x_{b}-x_{a})^{2}}}};
- yo=(xb−xa)⋅(xp−xo)(yb−ya)+yp{\displaystyle y_{o}={\frac {(x_{b}-x_{a})\cdot (x_{p}-x_{o})}{(y_{b}-y_{a})}}+y_{p}}.
Пример решения задачи
В интернете попадаются примеры решения простых задач, а сложные приходится решать самостоятельно, просить помощи у кого-нибудь или покупать на сайтах готовое решение. Для примера нужно решить задание с такими данными:

Прямоугольник, изображенный на рисунке 1 с диагональю равной d.
Серединный перпендикуляр, проведенный к диагонали прямоугольника.
Точка Е делит сторону на отрезки а и 2а.
Нужно найти: углы, указанные на рисунке, стороны и ОЕ. Кроме того, дополнительные данные можно узнать из чертежа, который используется для решения задачи (рис. 1). К любому заданию нужно делать графическое представление, поскольку оно позволяет избежать ошибок при вычислении
Рисунок 1. Чертеж для решения задачи.
Числовых значений нет, тогда необходимо решать в общем виде. Углы можно найти по такому алгоритму:
Нужно рассмотреть треугольник ВДЕ. Он является равнобедренным, поскольку ОЕ — СП, а диагональ — отрезок. Следовательно, ВЕ = ДЕ = 2а.
Необходимо найти угол ЕВО. Сделать это проблемно. Рекомендуется обратить внимание на треугольник АВЕ.
При помощи тригонометрической функции синуса можно вычислить значение угла АBE: sin(АBE) = a/2а = 0,5. Следовательно, arcsin(0,5) = 30 (градусов).
Угол СВЕ вычисляется следующим образом: 90 – 30 = 60 (градусов).
Следовательно, искомый угол равен 30, поскольку 90 – 30 – 30 = 30.
В равнобедренном треугольнике углы при основании равны между собой: ЕДО = ЕВО = 30 (градусов).
Для нахождения сторон нужно составить уравнение в общем виде, обозначив неизвестную величину АВ литерой “х”. Рассмотрев прямоугольный треугольник АВЕ, по теореме Пифагора можно вычислить АВ: x = ^(1/2) = a * ^(1/2). Следовательно, АВ = a * ^(1/2) и ВС = 3а. ОЕ находится по формуле: ОЕ = (2 * 2 * а * S) / (8 * a^2 – d^2). Можно править соотношение таким образом через прямоугольный треугольник ДОЕ: ОЕ = [4 * a^2 – (d^2) / 4]^(1/2).
Предыдущая
ГеометрияЦентральные и вписанные углы — примеры и правила построения
Следующая
ГеометрияПлощадь пирамиды — определение, свойства и формулы
Шаги
Метод 1 из 2:
Сбор данных
-
1
Найдите середину отрезка, ограниченного двумя данными точками. Для этого подставьте координаты точек в формулу: [(x1 + x2)/2,( y1 + y2)/2]. Эта формула вычислит среднее значение координат х и у двух данных точек. Например, даны следующие координаты двух точек: (x1,y1)=(2,5) и (x2,y2)=(8,3).
X
Источник информации- [(2+8)/2, (5 +3)/2] =
- (10/2, 8/2) =
- (5, 4)
- Координаты середины отрезка, ограниченного точками с координатами (2,5) и (8,3), есть (5,4).
-
2
Найдите наклон прямой (угловой коэффициент). Чтобы найти угловой коэффициент по двум точкам, подставьте их координаты в формулу: (y2 — y1) / (x2 — x1). Угловой коэффициент равен тангенсу угла между положительным направлением оси абсцисс и данной прямой. Вот как найти угловой коэффициент прямой, которая проходит через точки (2,5) и (8,3):
X
Источник информации- (3-5)/(8-2) =
- -2/6 =
- -1/3
-
3
Найдите угловой коэффициент перпендикуляра. Для этого найдите обратную величину углового коэффициента прямой и измените знак. Для получения обратной величины разделите единицу на данную величину.
X
Источник информацииОбратная отрицательная величина -1/3 есть 3, потому что 1/(1/3)=3, а знак был изменен с отрицательного на положительный.
Метод 2 из 2:
Вычисление уравнения серединного перпендикуляра
-
1
Линейное уравнение записывается в виде: y = mx + b, где х и у — координаты, m – угловой коэффициент, b – смещение прямой по оси Y.
X
Источник информации -
2
Подставьте в уравнение найденный угловой коэффициент перпендикуляра. Подставьте 3 вместо m:
- 3 —> y = mx + b =
- y = 3x + b
-
3
Подставьте координаты середины отрезка. Это точка с координатами (5,4). Поскольку перпендикуляр проходит через эту точку, подставьте ее координаты в линейное уравнение. Просто подставьте (5,4) вместо х и у.
- (5, 4) —> y = 3x + b =
- 4 = 3(5) + b =
- 4 = 15 + b
-
4
Найдите смещение по оси Y. Для этого обособьте «b» на одной стороне уравнения.
- 4 = 15 + b =
- -11 = b
- b = -11
-
5
Напишите уравнение, описывающее серединный перпендикуляр. Для этого подставьте значения углового коэффициента (3) и смещения по оси Y (-11) в линейное уравнение. Вы не должны подставлять никаких значений вместо х и у, так как это уравнение позволит вам найти координаты любой точки, лежащей на перпендикуляре.
- y = mx + b
- y = 3x — 11
- Уравнение, описывающее серединный перпендикуляр, проходящий через отрезок, ограниченный точками с координатами (2,5) и (8,3), записывается как у=3x-11.
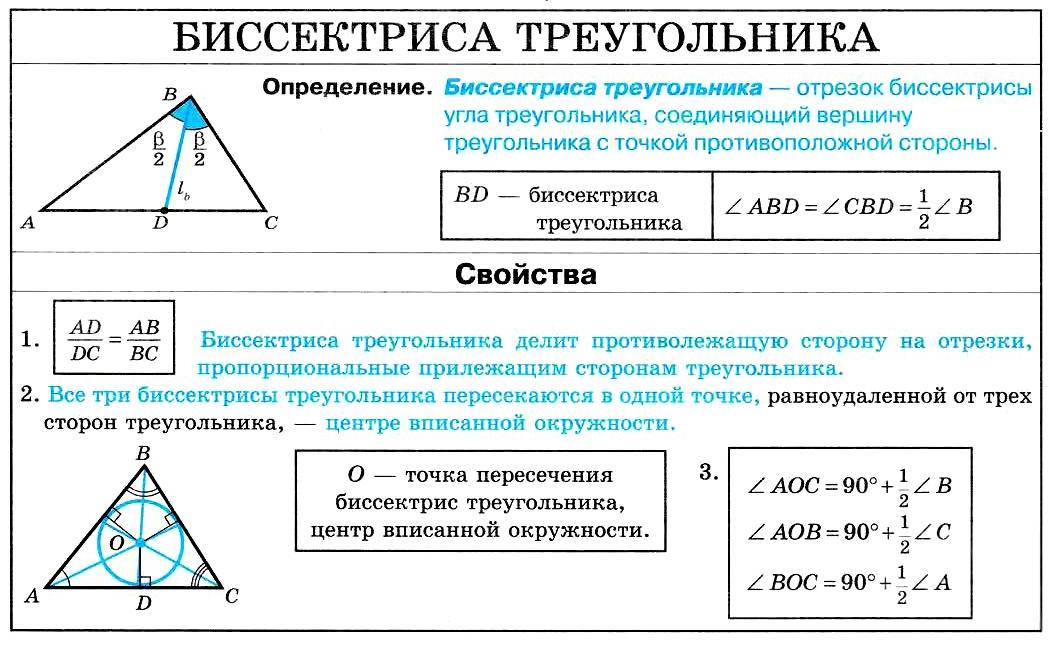
Теорема о биссектрисе, как ГМТ
Биссектриса неразвернутого угла – это геометрическое место точек,
равноудаленных от его сторон.
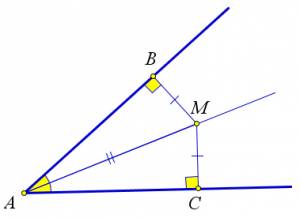
Доказательство
Рассмотрим угол $\angle A$.
Докажем, что любая точка, принадлежащая биссектрисе равноудалена от сторон этого угла.
Возьмём произвольную точку $M$ на биссектрисе угла $A$ и опустим из неё перпендикуляры
$MB$ и $MC$ на стороны данного угла.
Треугольники $AMB$ и $AMC$ равны по гипотенузе и острому углу, поэтому $MB=MC$, и
следовательно, точка $M$ равноудалена от сторон угла.
Обратно: докажем, что если точка равноудалена от сторон угла, то она лежит на
биссектрисе.
Возьмём произвольную точку $M$, из которой опущены перпендикуляры $MB$ и $MC$ на стороны угла и при этом $MB=MC$.
Докажем, что точка $M$ принадлежит биссектрисе.
Треугольники $AMB$ и $AMC$ равны по гипотенузе и катету, следовательно, $\angle BAM=\angle CAM$,
то есть $AM$ – биссектриса угла $\angle A$.
Теорема
Высоты треугольника (или их продолжения) пересекаются в одной точке.
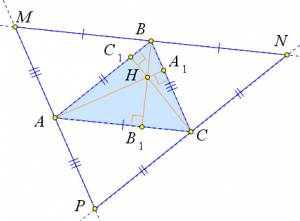
Доказательство
Рассмотрим произвольный треугольник $ABC$, в котором проведены
высоты $AA_1, BB_1, CC_1$.
Докажем, что все высоты пересекаются в одной точке.
Проведем через точку $B$ прямую, параллельную $AC$, через точку $C$ – прямую, параллельную
$AB$, а через точку $A$ – прямую, параллельную $BC$.
Эти прямые, пересекаясь, образуют треугольник $MNP$.
Четырёхугольник $AMBC$ является параллелограммом ($MB\parallel AC$, $MA\parallel BC$).
Аналогично, $ABNC$ – параллелограмм.
Тогда $MB=AC=BN$, как противоположные стороны параллелограмма.
Следовательно, $B$ – середина $MN$, а $BB_1$ – серединный перпендикуляр к отрезку $MN$.
Аналогично, $AA_1$ – серединный перпендикуляр к отрезку $MP$, $CC_1$ – серединный перпендикуляр к отрезку $PN$.
Получается, что $AA_1, BB_1$ и $CC_1$ пересекаются в одной точке, как серединные перпендикуляры треугольника $MNP$.
По отношению к параллельным линиям
Знаки стрелки указывают, что линии a и b , пересеченные поперечной линией c , параллельны.
Если две прямые ( a и b ) перпендикулярны третьей линии ( c ), все углы, образованные вдоль третьей линии, являются прямыми углами. Следовательно, в евклидовой геометрии любые две прямые, перпендикулярные третьей прямой, параллельны друг другу из-за постулата параллельности . И наоборот, если одна линия перпендикулярна второй линии, она также перпендикулярна любой линии, параллельной этой второй линии.
На рисунке справа все углы, заштрихованные оранжевым, конгруэнтны друг другу, а все углы, заштрихованные зеленым, конгруэнтны друг другу, потому что вертикальные углы конгруэнтны, а чередующиеся внутренние углы, образованные поперечными параллельными линиями сечения, равны конгруэнтный. Следовательно, если прямые a и b параллельны, любой из следующих выводов приводит ко всем остальным:
- Один из углов на схеме — прямой.
- Один из углов, закрашенных оранжевым, соответствует одному из углов, закрашенных зеленым.
- Линия c перпендикулярна линии a .
- Линия c перпендикулярна линии b .
Теорема о серединном перпендикуляре, как ГМТ
Серединный перпендикуляр к отрезку – это геометрическое место
точек, равноудаленных от концов отрезка.
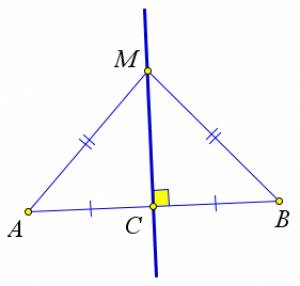
Доказательство
Рассмотрим отрезок $AB$.
Середину отрезка обозначим $C$.
Докажем, что любая точка, принадлежащая серединному перпендикуляру,
равноудалена от сторон.
Действительно, возьмём произвольную точку $M$ на серединном перпендикуляре.
Если $M=C$, то очевидно, что $MA=MB$.
Если $M\neq C$, то треугольники $AMC$ и $BMC$ равны по двум
катетам, следовательно $AM=MB$.
Обратно, докажем, что любая точка равноудалённая от сторон, принадлежит серединному
перпендикуляру.
Возьмём произвольную точку $M$, для которой $MA=MB$.
Если $M=C$, то очевидно, $M$ принадлежит серединному перпендикуляру.
Если $M C$, то треугольник $AMB$ – равнобедренный, и, следовательно, медиана $MC$ является высотой, то есть $MC$ – серединный перпендикуляр.
Об этой статье
wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 19 человек(а). Количество просмотров этой статьи: 21 841.
Категории: Геометрия
English:Find the Perpendicular Bisector of Two Points
Italiano:Trovare l’Equazione dell’Asse del Segmento
Español:encontrar el bisector perpendicular de dos puntos
Português:Encontrar o Bissetor Perpendicular de Dois Pontos
Deutsch:Die Mittelsenkrechte zwischen zwei Punkten bestimmen
Français:trouver l’équation de la médiatrice d’un segment
Nederlands:De middelloodlijn van twee punten bepalen
العربية:إيجاد المستقيم المنصف العمودي لنقطتين
中文:求出两点间的垂直平分线
ไทย:หาเส้นแบ่งครึ่งตั้งฉากของจุดสองจุด
日本語:2つの点の垂直二等分線を求める
हिन्दी:दो बिंदुओं का लंबवत द्विभाजक (Perpendicular Bisector) निकालें
Печать
В кругах и других кониках
Круги
Каждый диаметр из круга перпендикулярно к касательной к этой окружности в точке , где диаметр пересекает окружность.
Отрезок, проходящий через центр окружности, разделяющий хорду пополам , перпендикулярен хорде.
Если пересечение любых двух перпендикулярных хорд делит одну хорду на длины a и b и делит другую хорду на длины c и d , то a 2 + b 2 + c 2 + d 2 равно квадрату диаметра.
Сумма квадратов длин любых двух перпендикулярных хорд, пересекающихся в данной точке, такая же, как и у любых других двух перпендикулярных хорд, пересекающихся в той же точке, и равна 8 r 2 — 4 p 2 (где r — длина окружности радиус, а p — расстояние от центральной точки до точки пересечения).
Теорема Фалеса утверждает, что две прямые, проходящие через одну и ту же точку на окружности, но проходящие через противоположные концы диаметра, перпендикулярны. Это эквивалентно тому, что любой диаметр окружности образует прямой угол в любой точке окружности, кроме двух конечных точек диаметра.
Эллипсы
Большие и малые оси самолета Ан эллипса перпендикулярны друг друг и касательные к эллипсу в точках , где оси пересекаются эллипс.
Большая ось эллипса перпендикулярна направляющей и каждой прямой кишке .
Параболы
В параболе ось симметрии перпендикулярна каждой прямой прямой кишке, директрисе и касательной в точке, где ось пересекает параболу.
От точки на касательной к вершине параболы перпендикулярна прямой, идущей от этой точки через фокус параболы .
параболы является то , что если две касательные к параболе перпендикулярны друг к другу, то они пересекаются на директрисе. И наоборот, две касательные, пересекающиеся на директрисе, перпендикулярны. Это означает, что если смотреть из любой точки на своей директрисе, любая парабола имеет прямой угол.
Гиперболы
из гиперболы перпендикулярна к сопряженной оси и к каждому директрисы.
Произведение расстояний по перпендикулярам от точки P на гиперболе или на ее сопряженной гиперболе до асимптот является постоянной, не зависящей от положения P.
У есть асимптоты , перпендикулярные друг другу. Его эксцентриситет равен2.{\ displaystyle {\ sqrt {2}}.}
Построение перпендикуляра
Построение перпендикуляра (синий) к прямой AB через точку P.
Построение перпендикуляра к полупрямой h из точки P (применимо не только в конечной точке A, M выбирается произвольно), анимация в конце с паузой 10 с
Чтобы провести перпендикуляр к линии AB через точку P с помощью построения циркуля и линейки , действуйте следующим образом (см. Рисунок слева):
- Шаг 1 (красный): постройте круг с центром в точке P, чтобы создать точки A ‘и B’ на линии AB, которые равноудалены от P.
- Шаг 2 (зеленый): построить круги с центрами A ‘и B’ равного радиуса. Пусть Q и P — точки пересечения этих двух окружностей.
- Шаг 3 (синий): соедините Q и P, чтобы построить желаемый перпендикуляр PQ.
Чтобы доказать, что точка PQ перпендикулярна AB, используйте для ‘и QPB’, чтобы заключить, что углы OPA ‘и OPB’ равны. Затем используйте для треугольников OPA ‘и OPB’, чтобы заключить, что углы POA и POB равны.
Чтобы сделать перпендикуляр к линии g в точке P или через нее, используя теорему Фалеса , см. Анимацию справа.
Теорема Пифагора может быть использована как основа методов построения прямых углов. Например, посчитав звенья, можно сделать три отрезка цепи с длинами в соотношении 3: 4: 5. Их можно выложить в виде треугольника, у которого будет прямой угол напротив его самой длинной стороны. Этот метод полезен для разбивки садов и полей, где размеры велики и не требуется большой точности. При необходимости цепи можно использовать повторно.


![Math-public:chetyre_zamechatelnye_tochki_v_treugolnike [президентский фмл №239]](https://rusinfo.info/wp-content/uploads/8/b/f/8bfa8fae6ab3706e086c717c7a967f5b.jpg)






![Math-public:chetyre_zamechatelnye_tochki_v_treugolnike [президентский фмл №239]](https://rusinfo.info/wp-content/uploads/9/f/d/9fd37fb7105d8b2982a4cfa7a0d3938d.png)

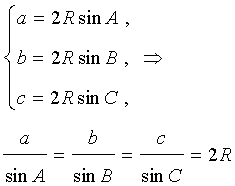

![Math-public:chetyre_zamechatelnye_tochki_v_treugolnike [президентский фмл №239]](https://rusinfo.info/wp-content/uploads/3/8/3/3836e87c736152cef47f47b4e5d6b814.png)