Перпендикуляр к прямой / треугольники / справочник по геометрии 7-9 класс

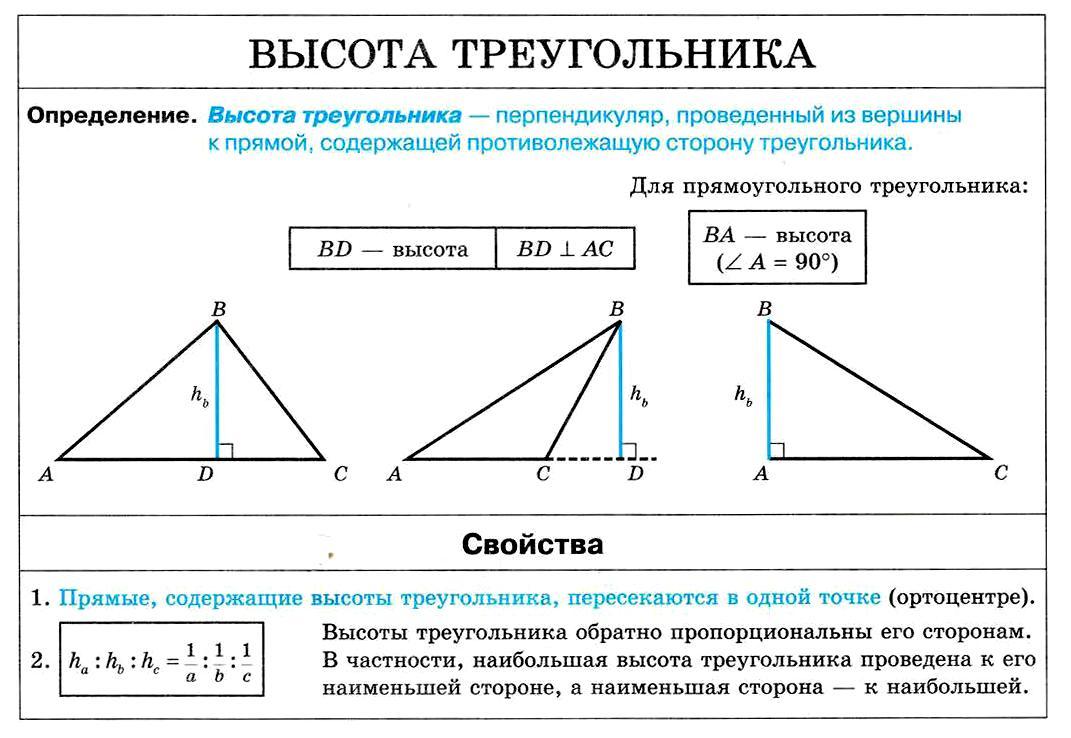
Доказательство взаимного расположения

Рассматриваемый термин получил широкое распространение, он фигурирует практически в каждой геометрической задаче. В некоторых случаях о взаимном расположении известно, в других это нужно доказать. Задача доказательства заключается в определении прямого угла между двумя прямыми или плоскостями. Необходимое и достаточное условие перпендикулярности заключается в теореме:

Прямые взаимно перпендикулярны в случае, если направляющие векторы прямых перпендикулярны.
Доказательство связано с определением направления векторов, любой должен быть перпендикулярен.

Для определения расположения плоскостей или отрезков относительно друг друга следует провести геометрическое построение. Проходить отрезки должны в одной точке.

В многомерных пространствах

Перпендикулярность плоскостей в 4-мерном пространстве

Перпендикулярность плоскостей в четырёхмерном пространстве имеет два смысла: плоскости могут быть перпендикулярны в 3-мерном смысле, если они пересекаются по прямой (а следовательно, лежат в одной гиперплоскости), и двугранный угол между ними равен 90°.

Плоскости могут быть также перпендикулярны в 4-мерном смысле, если они пересекаются в точке (а следовательно, не лежат в одной гиперплоскости), и любые 2 прямые, проведённые в этих плоскостях через точку их пересечения (каждая прямая в своей плоскости), перпендикулярны.

В 4-мерном пространстве через данную точку можно провести ровно 2 взаимно перпендикулярные плоскости в 4-мерном смысле (поэтому 4-мерное евклидово пространство можно представить как декартово произведение двух плоскостей). Если же объединить оба вида перпендикулярности, то через данную точку можно провести 6 взаимно перпендикулярных плоскостей (перпендикулярных в любом из двух вышеупомянутых значений).

Существование шести взаимно перпендикулярных плоскостей можно пояснить таким примером. Пусть дана система декартовых координат x y z t. Для каждой пары координатных прямых существует плоскость, включающая эти две прямые. Количество таких пар равно (42)=6{\displaystyle {\tbinom {4}{2}}=6}: xy, xz, xt, yz, yt, zt, и им соответствуют 6 плоскостей. Те из этих плоскостей, которые включают одноимённую ось, перпендикулярны в 3-мерном смысле и пересекаются по прямой (например, xy и xz, yz и zt), а те, которые не включают одноимённых осей, перпендикулярны в 4-мерном смысле и пересекаются в точке (например, xy и zt, yz и xt).

Перпендикулярность прямой и гиперплоскости

Пусть задано n-мерное евклидово пространство Rn{\displaystyle \mathbb {R} ^{n}}(n>2) и ассоциированное с ним векторное пространство Wn{\displaystyle W^{n}}, а прямая l с направляющим векторным пространством L1{\displaystyle L^{1}} и гиперплоскость Πk{\displaystyle \Pi _{k}} с направляющим векторным пространством Lk{\displaystyle L^{k}} (где L1⊂Wn{\displaystyle L_{1}\subset W^{n}}, Lk⊂Wn, k<n{\displaystyle L^{k}\subset W^{n},\ k<n}) принадлежат пространству Rn{\displaystyle \mathbb {R} ^{n}}.

Прямая l называется перпендикулярной гиперплоскости Πk{\displaystyle \Pi _{k}}, если подпространство L1{\displaystyle L_{1}} ортогонально подпространству Lk{\displaystyle L^{k}}, то есть (∀a→∈L1) (∀b→∈Lk) a→b→={\displaystyle (\forall {\vec {a}}\in L_{1})\ (\forall {\vec {b}}\in L_{k})\ {\vec {a}}{\vec {b}}=0}

Построение перпендикуляра

Выдержать угловой коэффициент можно различным образом. В большинстве случаев для этого нужно иметь при себе циркуль. Построить перпендикуляр можно следующим образом:

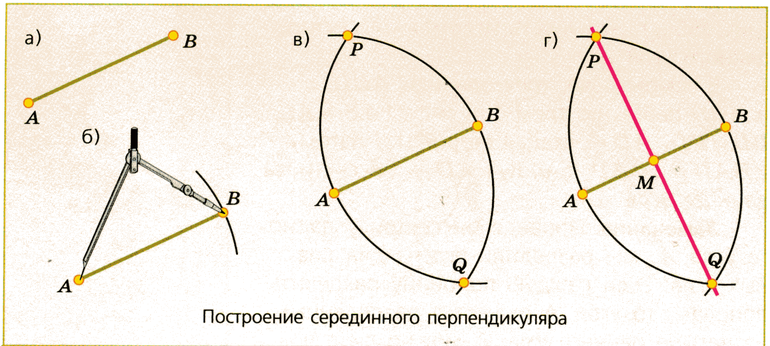
С помощью циркуля проводится построение полуокружности с центром в точке Х. На основном отрезке в результате этого получается две точки А и В. Для отображения полуокружности применяется другой цвет, полученная линия вспомогательная, поэтому не выделяется жирным.
С точки А и В проводится откладывание двух полуокружностей, пересекающихся в двух местах по касательной. Данные точки (P и Q) используются для откладывания линии, которая может пересечь их и основной отрезок с ранее отложенными точками А и В.

Существенно упростить задачу можно путем применения специального чертежного инструмента, к примеру, любого прямоугольного треугольника. Он может называться угольником, основной его признак заключается в наличии двух перпендикулярных плоскостей. Построение проводится следующим образом:

Одна из сторон, смежная с прямым углом, прикладывается к проведенному отрезку. На этом этапе главное — правильно совместить поверхность инструмента с ранее отложенной линией. Незначительное отклонение может привести к изменению угла.
Проводится откладывание вертикального отрезка.

В геометрии чаще всего применяется именно второй способ. Однако первый урок позволяет начертить два взаимно перпендикулярных отрезка с высокой точностью. Недостаток применения циркуля заключается в наличии вспомогательных линий, которые стереть сложно. Написать о взаимном расположении линий можно в описательной записке.

https://youtube.com/watch?v=dV3Gm8VQ5Oc

Применение термина

Как ранее было отмечено, встречается большое количество примеров применения рассматриваемого термина. На основе теоремы и доказательства были созданы различные формулы, позволяющие определить протяженность одного из сторон геометрической фигуры.

В средних и старших классах встречается большое количество задач, связанных с определением угла и протяженности сторон построенной фигуры. В некоторых случаях проводится построение диагонали, которая делит 90° на две равные части.

В жизни взаимное перпендикулярное расположение плоскостей встречается крайне часто. Примером служат несущие элементы различных сооружений. Подобное расположение позволяет правильно распределить оказываемую нагрузку. Править наклон можно путем применения специальных измерительных инструментов.

Многие геометрические фигуры построены на основе перпендикулярного расположения отрезков. Наиболее распространен параллелограмм или квадрат, треугольник. За счет выдерживания правильного угла обеспечивается также взаимное параллельное расположение сторон.

Предыдущая
МатематикаНаименьшее общее кратное (НОК) — алгоритмы и примеры определения
Следующая
МатематикаПлощадь прямоугольника — основные способы, правила и формулы вычислений

Правило встречается в следующих упражнениях:

7 класс

Задание 113,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 178,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 17,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 19,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 379,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 668,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 17,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 22,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 854,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 5,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Трехмерное пространство

В начертательной геометрии линии всегда находятся в двухмерном пространстве. В специальных программах можно начертить отрезки в трехмерном пространстве. Подобное взаимное расположение может выглядеть следующим образом:

Два отрезка перпендикулярны относительно друг друга в случае, если они параллельны другим взаимно перпендикулярным линиям, лежащим в одной плоскости.
Показать правильное взаимное расположение можно путем обозначения угла. Для этого применяются различные способы.
Если две линии лежат в одной плоскости, то они взаимно перпендикулярны при образовании четырех прямых углов.

Определение перпендикулярности прямой и плоскости

Рассматривая определение перпендикулярных прямых следует учитывать, что подобное свойство применимо к плоскости. Основной признак заключается в перпендикулярности отрезка к любому другому, который находится в плоскости. Перпендикулярность прямых в пространстве указывается определенным знаком.

Доказать перпендикулярность можно проведя геометрические построения. Признаки расположения плоскости и прямой под углом 90° заключаются в следующем:

Если прямая перпендикулярна плоскости, то в ней можно отложить другую прямую, лежащую под углом 90°.
В одной точке под прямым углом может пересекаться только две линии, значит, будет лежать только одна плоскость.

Отрезки могут быть также параллельными. В этом случае нет точки, в которой будут они пересекаться.

В вычислении расстояний

Расстояние от точки до линии расстояние до ближайшей точки на этой линии. Это точка, в которой отрезок от нее до данной точки перпендикулярен прямой.

Точно так же расстояние от точки до кривой измеряется отрезком линии, перпендикулярным касательной к кривой в ближайшей точке кривой.

Перпендикулярная регрессия подгоняет линию к точкам данных путем минимизации суммы квадратов перпендикулярных расстояний от точек данных до линии.

Расстояние от точки до плоскости измеряются как длина от точки вдоль отрезка, перпендикулярной к плоскости, а это означает , что она перпендикулярна все линии в плоскости , которые проходят через ближайшую точку на плоскости в данной точку .

В трёхмерном пространстве

Перпендикулярные прямые

Две прямые в пространстве перпендикулярны друг другу, если они соответственно параллельны некоторым двум другим взаимно перпендикулярным прямым, лежащим в одной плоскости. Две прямые, лежащие в одной плоскости, называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла.

Перпендикулярность прямой к плоскости

Определение: Прямая называется перпендикулярной к плоскости, если она перпендикулярна всем прямым, лежащим в этой плоскости.

Признак: Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна этой плоскости.

Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

Перпендикулярные плоскости

Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90°.

Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то этот перпендикуляр полностью лежит в первой плоскости.
Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости.
Плоскость, перпендикулярная двум пересекающимся плоскостям, перпендикулярна их линии пересечения.

На плоскости

Перпендикулярные прямые на плоскости

Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.

Про прямую m{\displaystyle m} перпендикулярную к прямой ℓ{\displaystyle \ell } проведённую через точку P{\displaystyle P} вне прямой ℓ{\displaystyle \ell }, говорят, что m{\displaystyle m} есть перпендикуляр опущенный из P{\displaystyle P} на ℓ{\displaystyle \ell }.
Если же точка P{\displaystyle P} лежит на прямой ℓ{\displaystyle \ell }, то говорят, что m{\displaystyle m} есть перпендикуляр к восстановленный из P{\displaystyle P} к ℓ{\displaystyle \ell } (устаревший термин восставленный).

В координатах

В аналитическом выражении прямые, заданные линейными функциями

y=a⋅x+b{\displaystyle y=a\cdot x+b}

y=k⋅x+m{\displaystyle y=k\cdot x+m}

будут перпендикулярны, если выполнено следующее условие на их угловые коэффициенты

a⋅k=−1.{\displaystyle a\cdot k=-1.}

Построение перпендикуляра

‘Шаг 1: (красный) С помощью циркуля проведём полуокружность с центром в точке P, получив точки А’ и В.

‘Шаг 2: (зелёный) Не меняя радиуса, построим две полуокружности с центром в точках A’ и В соответственно, проходящими через точку P. Кроме точки P есть ещё одна точка пересечения этих полуокружностей, назовём её Q.

Шаг 3: (синий) Соединяем точки P и Q. PQ и есть перпендикуляр к прямой AB.

Координаты точки основания перпендикуляра к прямой

A(xa,ya){\displaystyle A(x_{a},y_{a})} и B(xb,yb){\displaystyle B(x_{b},y_{b})} — прямая, O(xo,yo){\displaystyle O(x_{o},y_{o})} — основание перпендикуляра, опущенного из точки P(xp,yp){\displaystyle P(x_{p},y_{p})}.

Если xa=xb{\displaystyle x_{a}=x_{b}} (вертикаль), то xo=xa{\displaystyle x_{o}=x_{a}} и yo=yp{\displaystyle y_{o}=y_{p}}.
Если ya=yb{\displaystyle y_{a}=y_{b}} (горизонталь), то xo=xp{\displaystyle x_{o}=x_{p}} и yo=ya{\displaystyle y_{o}=y_{a}}.

Во всех остальных случаях:

xo=xa⋅(yb−ya)2+xp⋅(xb−xa)2+(xb−xa)⋅(yb−ya)⋅(yp−ya)(yb−ya)2+(xb−xa)2{\displaystyle x_{o}={\frac {x_{a}\cdot (y_{b}-y_{a})^{2}+x_{p}\cdot (x_{b}-x_{a})^{2}+(x_{b}-x_{a})\cdot (y_{b}-y_{a})\cdot (y_{p}-y_{a})}{(y_{b}-y_{a})^{2}+(x_{b}-x_{a})^{2}}}};

yo=(xb−xa)⋅(xp−xo)(yb−ya)+yp{\displaystyle y_{o}={\frac {(x_{b}-x_{a})\cdot (x_{p}-x_{o})}{(y_{b}-y_{a})}}+y_{p}}.

Построение перпендикуляра

Построение перпендикуляра (синий) к прямой AB через точку P.

Построение перпендикуляра к полупрямой h из точки P (применимо не только в конечной точке A, M выбирается произвольно), анимация в конце с паузой 10 с

Чтобы провести перпендикуляр к линии AB через точку P с помощью построения циркуля и линейки , действуйте следующим образом (см. Рисунок слева):

Шаг 1 (красный): постройте круг с центром в точке P, чтобы создать точки A ‘и B’ на линии AB, которые равноудалены от P.
Шаг 2 (зеленый): построить круги с центрами A ‘и B’ равного радиуса. Пусть Q и P — точки пересечения этих двух окружностей.
Шаг 3 (синий): соедините Q и P, чтобы построить желаемый перпендикуляр PQ.

Чтобы доказать, что точка PQ перпендикулярна AB, используйте для ‘и QPB’, чтобы заключить, что углы OPA ‘и OPB’ равны. Затем используйте для треугольников OPA ‘и OPB’, чтобы заключить, что углы POA и POB равны.

Чтобы сделать перпендикуляр к линии g в точке P или через нее, используя теорему Фалеса , см. Анимацию справа.

Теорема Пифагора может быть использована как основа методов построения прямых углов. Например, посчитав звенья, можно сделать три отрезка цепи с длинами в соотношении 3: 4: 5. Их можно выложить в виде треугольника, у которого будет прямой угол напротив его самой длинной стороны. Этот метод полезен для разбивки садов и полей, где размеры велики и не требуется большой точности. При необходимости цепи можно использовать повторно.

Четырехмерная система координат и лемма

Некоторые программы работают с четырехмерным пространством. Взаимное расположение плоскостей под прямым углом в этом случае имеет два смысла: они могут быть перпендикулярны в трехмерном смысле при образовании двугранного угла 90°.

Рассматриваться взаимное расположение плоскостей может и в 4-мерном смысле. Условия выглядят следующим образом:

Они должны пересекаться в точке.
Любые две линии, проведенные в плоскостях через точку пересечения также могут быть перпендикулярными.

Условия четырехмерного пространства определяют то, что через одну точку можно провести 6 взаимно перпендикулярных плоскостей. Определять их взаимное расположение можно несколькими различными способами.

Лемма, касающаяся перпендикулярности, связана с определением параллельности. Если одна из параллельных линий расположена под прямым углом относительно плоскости или отрезка, то вторая также перпендикулярна. Ответ на многие задачи связан с доказательством леммы:

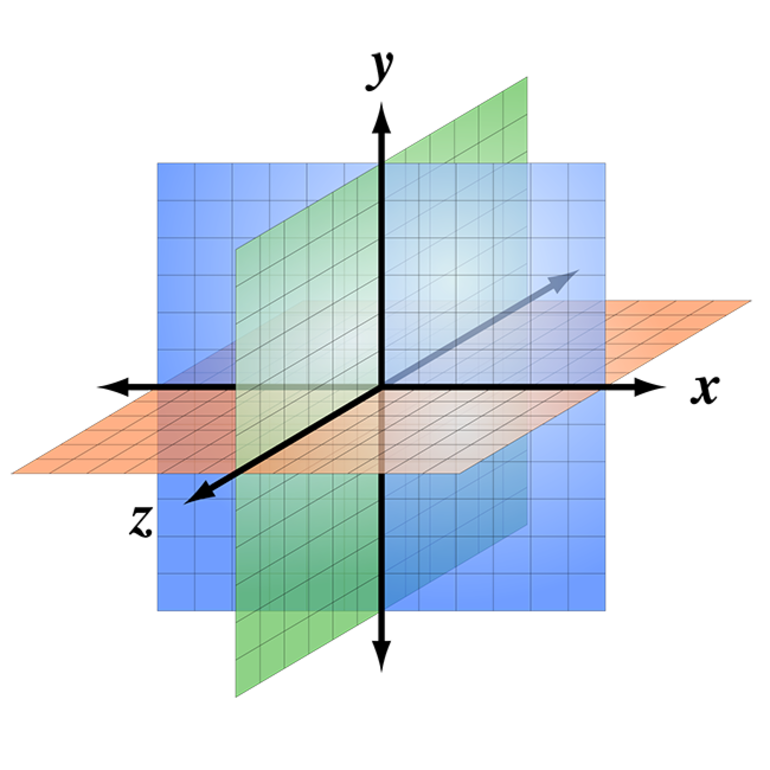
Даны два параллельных отрезка а и b, а также с. Задача заключается в доказательстве b ⊥ c при условии, что a ⊥ c.
Через произвольную точку М проводится третий и четвертый отрезок, которые параллельны прямой а и с. Образующийся угол АМС равен 90°.
Параллельны b и a при условии, что третий дополнительный отрезок параллелен отрезку а. В этом случае он будет параллелен и b.

При соблюдении условий полученный угол будет являться прямым. С учетом проведенных построений можно сформулировать определение перпендикулярности параллельных отрезков.

В кругах и других кониках

Круги

Каждый диаметр из круга перпендикулярно к касательной к этой окружности в точке , где диаметр пересекает окружность.

Отрезок, проходящий через центр окружности, разделяющий хорду пополам , перпендикулярен хорде.

Если пересечение любых двух перпендикулярных хорд делит одну хорду на длины a и b и делит другую хорду на длины c и d , то a 2 + b 2 + c 2 + d 2 равно квадрату диаметра.

Сумма квадратов длин любых двух перпендикулярных хорд, пересекающихся в данной точке, такая же, как и у любых других двух перпендикулярных хорд, пересекающихся в той же точке, и равна 8 r 2 — 4 p 2 (где r — длина окружности радиус, а p — расстояние от центральной точки до точки пересечения).

Теорема Фалеса утверждает, что две прямые, проходящие через одну и ту же точку на окружности, но проходящие через противоположные концы диаметра, перпендикулярны. Это эквивалентно тому, что любой диаметр окружности образует прямой угол в любой точке окружности, кроме двух конечных точек диаметра.

Эллипсы

Большие и малые оси самолета Ан эллипса перпендикулярны друг друг и касательные к эллипсу в точках , где оси пересекаются эллипс.

Большая ось эллипса перпендикулярна направляющей и каждой прямой кишке .

Параболы

В параболе ось симметрии перпендикулярна каждой прямой прямой кишке, директрисе и касательной в точке, где ось пересекает параболу.

От точки на касательной к вершине параболы перпендикулярна прямой, идущей от этой точки через фокус параболы .

параболы является то , что если две касательные к параболе перпендикулярны друг к другу, то они пересекаются на директрисе. И наоборот, две касательные, пересекающиеся на директрисе, перпендикулярны. Это означает, что если смотреть из любой точки на своей директрисе, любая парабола имеет прямой угол.

Гиперболы

из гиперболы перпендикулярна к сопряженной оси и к каждому директрисы.

Произведение расстояний по перпендикулярам от точки P на гиперболе или на ее сопряженной гиперболе до асимптот является постоянной, не зависящей от положения P.

У есть асимптоты , перпендикулярные друг другу. Его эксцентриситет равен2.{\ displaystyle {\ sqrt {2}}.}

В многомерных пространствах

Перпендикулярность плоскостей в 4-мерном пространстве

Перпендикулярность прямой и гиперплоскости

Проведение перпендикуляра из точки к прямой

Для проведения перпендикуляра из точки к прямой, используют чертежный угольник (Рис.5). Чертежный угольник прикладывают так, чтобы одна из его сторон, образующих прямой угол угольника, располагалась вдоль прямой, к которой нужно провести перпендикуляр. Вдоль второй стороны, образующей прямой угол угольника, проводим прямую так, чтобы она проходила через точку, из которой нужно провести перпендикуляр к прямой. Отрезок, соединяющий точку на прямой, к которой нужно провести перпендикуляр, и точку, из которой нужно провести перпендикуляр, и есть перпендикуляр проведенный из данной точки к данной прямой. На Рис.5 АН.

Фигуры с перпендикулярными прямыми

Одной из первых фигур, с которыми знакомится человек, являются квадрат и прямоугольник.

Прямые углы приятны человеческому взгляду, поэтому очень часто квадрат или прямоугольник используют как форму для столешниц, стульев, тумбочек и других предметов. Весь окружающий человека мир составлен из параллельных и перпендикулярных линий.

Рис. 2. Квадрат.

Еще со времен Древней Греции известен прямоугольный треугольник. Форму прямоугольного треугольника принимали различные приборы для навигации, кроме того много времени изучению свойств прямоугольного треугольника уделил Пифагор. Именно его авторству принадлежит Теорема Пифагора, которая крайне востребована в решениях задач.

Существует прямоугольная трапеция, у которой одна из сторон прямоугольна обоим основанием. А планометрия и вовсе пестрит перпендикулярами в пространстве: правильная призма, прямоугольная пирамида и самый обычный куб.

К тому же, в любом треугольнике можно провести высоту, что необходимо для нахождения площади фигуры. Перпендикуляр для нахождения площади пригодится и в параллелограмме, а прямоугольный треугольник и квадрат имеют высоту в составе своих сторон, из-за чего площадь этих фигур гораздо проще найти.

Рис. 3. Высота.

Что мы узнали?

Мы разобрали, что такое перпендикулярные прямые, поговорили о свойствах перпендикуляров и описали фигуры, для построения которых необходимы перпендикулярные прямые. Разобрались в теме для полного понимания при первой встрече с данным вопросом в 6 классе.

Тест по теме

Вопрос 1 из 5

Чтобы отрезки назывались перпендикулярными, так же должно выполняться два условия:
- отрезки должны пересекаться, а угол пересечения между ними должен равняться 90 градусов.
- отрезки должны быть параллельными, а угол между ними должен равняться 90 градусов.
- отрезки должны пересекаться, а угол пересечения между ними должен равняться 180 градусов.
- отрезки должны параллельны, а односторонние углы между ними должны равняться 180 градусов.

Начать тест(новая вкладка)

Теорема

Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

Доказательство:

1. Существование перпендикуляра.

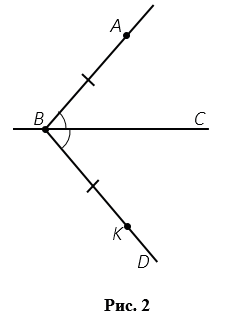
Пусть точка А не лежит на прямой ВС. Проведем луч ВА. Затем от луча ВС отложим угол СВD, равный углу АВС. На луче ВD отложим отрезок ВК, равный отрезку ВА (Рис.2).

Проведем прямую АК, пусть Н — точка пересечения прямых ВС и АК (Рис.3).

АВН = КВН по первому признаку равенства треугольников: ВН — общая сторона, ВА = ВК, АВН =КBН (по построению), ВНА =ВНD. Но ВНА и ВНD — смежные углы, тогда по свойству смежных углов ВНА +ВНD = 180, следовательно, каждый из смежных улов прямой, т.е. ВНА =ВНD = 90, а значит АНВС.

2. Единственность перпендикуляра.

Предположим, что через точку А можно провести еще один перпендикуляр АН₁ к прямой ВС, тогда получим, что две прямые АН и АН₁, перпендикулярные к прямой ВС пересекаются в точке А (Рис.4). Но по свойству перпендикулярных прямых, прямые АН и АН₁ пересекаться не могут, значит, наше предположение неверно и через точку А можно провести только один перпендикуляр к прямой ВС. Теорема доказана.

По отношению к параллельным линиям

Знаки стрелки указывают, что линии a и b , пересеченные поперечной линией c , параллельны.

Если две прямые ( a и b ) перпендикулярны третьей линии ( c ), все углы, образованные вдоль третьей линии, являются прямыми углами. Следовательно, в евклидовой геометрии любые две прямые, перпендикулярные третьей прямой, параллельны друг другу из-за постулата параллельности . И наоборот, если одна линия перпендикулярна второй линии, она также перпендикулярна любой линии, параллельной этой второй линии.

На рисунке справа все углы, заштрихованные оранжевым, конгруэнтны друг другу, а все углы, заштрихованные зеленым, конгруэнтны друг другу, потому что вертикальные углы конгруэнтны, а чередующиеся внутренние углы, образованные поперечными параллельными линиями сечения, равны конгруэнтный. Следовательно, если прямые a и b параллельны, любой из следующих выводов приводит ко всем остальным:

Один из углов на схеме — прямой.
Один из углов, закрашенных оранжевым, соответствует одному из углов, закрашенных зеленым.
Линия c перпендикулярна линии a .
Линия c перпендикулярна линии b .