Средняя скорость движения
При изучении задач на движение мы определяли скорость движения следующим образом: делили пройденное расстояние на время. Но тогда подразумевалось, что тело движется с постоянной скоростью, которая не менялась на протяжении всего пути.
В реальности, это происходит довольно редко или не происходит совсем. Тело, как правило, движется с различной скоростью.
Когда мы ездим на автомобиле или велосипеде, наша скорость часто меняется. Когда впереди нас помехи, нам приходиться сбавлять скорость. Когда же трасса свободна, мы ускоряемся. При этом за время нашего ускорения скорость изменяется несколько раз.
Речь идет о средней скорости движения. Чтобы её определить нужно сложить скорости движения, которые были в каждом часе/минуте/секунде и результат разделить на время движения.
Задача 1. Автомобиль первые 3 часа двигался со скоростью 66,2 км/ч, а следующие 2 часа — со скоростью 78,4 км/ч. С какой средней скоростью он ехал?

Сложим скорости, которые были у автомобиля в каждом часе и разделим на время движения (5ч)

Значит автомобиль ехал со средней скоростью 71,08 км/ч.
Определять среднюю скорость можно и по другому — сначала найти расстояния, пройденные с одной скоростью, затем сложить эти расстояния и результат разделить на время. На рисунке видно, что первые три часа скорость у автомобиля не менялась. Тогда можно найти расстояние, пройденное за три часа:
66,2 × 3 = 198,6 км.
Аналогично можно определить расстояние, которое было пройдено со скоростью 78,4 км/ч. В задаче сказано, что с такой скоростью автомобиль двигался 2 часа:
78,4 × 2 = 156,8 км.
Сложим эти расстояния и результат разделим на 5

Задача 2. Велосипедист за первый час проехал 12,6 км, а в следующие 2 часа он ехал со скоростью 13,5 км/ч. Определить среднюю скорость велосипедиста.

Скорость велосипедиста в первый час составляла 12,6 км/ч. Во второй и третий час он ехал со скоростью 13,5. Определим среднюю скорость движения велосипедиста:

Дисперсия
Один из способов измерения рассеяния данных заключается в том, чтобы определить степень отклонения каждого наблюдения от средней арифметической. Очевидно, что чем больше отклонение, тем больше изменчивость, вариабельность наблюдений.
Однако мы не можем использовать среднее этих отклонений как меру рассеяния, потому что положительные отклонения компенсируют отрицательные отклонения (их сумма равна нулю). Чтобы решить эту проблему, мы возводим в квадрат каждое отклонение и находим среднее возведенных в квадрат отклонений; эта величина называется вариацией, или дисперсией.
Возьмем n наблюдений x1, x2, х3, …, xn, среднее которых равняется .
Вычисляем дисперсию:
В случае, если мы имеем дело не с генеральной совокупностью, а с выборкой, то вычисляется выборочная дисперсия:
n(n-1).
Единицы измерения (размерность) вариации — это квадрат единиц измерения первоначальных наблюдений.
Например, если измерения производятся в килограммах, то единица измерения вариации будет килограмм в квадрате.
Вариация в пределах субъектов и между субъектами
Если провести повторные измерения непрерывной переменной у исследуемого объекта, то можно увидеть ее изменения (внутрисубъектные изменения). Это можно объяснить тем, что объект не всегда может дать точные и те же самые ответы, и/или ошибкой, погрешностью измерения. Однако при измерениях у одного объекта вариация обычно меньше, чем вариация единичного измерения в группе (межсубъектные изменения).
Например, вместимость легкого 17-летнего мальчика составляет от 3,60 до 3,87 л, когда измерения повторяются не менее 10 раз; если провести однократное измерение у 10 мальчиков того же возраста, то объем будет между 2,98 и 4,33 л. Эти концепции важны в плане исследования.
Связанные определения:Выборочное среднее, среднее значение выборкиВыбросДисперсия (рассеяние, разброс)Дисперсия выборки (выборочная дисперсия)Коэффициент вариацииМаксимумМатематическое ожидание дискретной случайной величиныМатематическое ожидание непрерывной случайной величиныМедианаМеры дисперсии, меры разбросаМинимумМодаОписательные статистикиОписательный анализПараметры рассеянияПараметры центральной тенденцииСреднее значениеСреднеквадратичное отклонение популяцииСтандартная ошибка среднегоСтандартное отклонение
Частота
Частота это число, которое показывает сколько раз в выборке встречается тот или иной элемент.
Предположим, что в школе проходят соревнования по подтягиваниям. В соревнованиях участвует 36 школьников. Составим таблицу в которую будем заносить число подтягиваний, а также число участников, которые выполнили столько подтягиваний.

По таблице можно узнать сколько человек выполнило 5, 10 или 15 подтягиваний. Так, 5 подтягиваний выполнили четыре человека, 10 подтягиваний выполнили восемь человек, 15 подтягиваний выполнили три человека.
Количество человек, повторяющих одно и то же число подтягиваний в данном случае являются частотой. Поэтому вторую строку таблицы переименуем в название «частота»:

Такие таблицы называют таблицами частот.
Частота обладает следующим свойством: сумма частот равна общему числу данных в выборке.
Это означает, что сумма частот равна общему числу школьников, участвующих в соревнованиях, то есть тридцати шести. Проверим так ли это. Сложим частоты, приведенные в таблице:
4 + 5 + 10 + 8 + 6 + 3 = 36
Относительная частота
Относительная частота это в принципе та же самая частота, которая была рассмотрена ранее, но только выраженная в процентах.
Относительная частота равна отношению частоты на общее число элементов выборки.
Вернемся к нашей таблице:

Пять подтягиваний выполнили 4 человека из 36. Шесть подтягиваний выполнили 5 человек из 36. Восемь подтягиваний выполнили 10 человек из 36 и так далее. Давайте заполним таблицу с помощью таких отношений:

Выполним деление в этих дробях:

Выразим эти частоты в процентах. Для этого умножим их на 100. Умножение на 100 удобно выполнить передвижением запятой на две цифры вправо:

Теперь можно сказать, что пять подтягиваний выполнили 11% участников, 6 подтягиваний выполнили 14% участников, 8 подтягиваний выполнили 28% участников и так далее.
Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Размах, полученный из процентилей
Что такое процентили
Предположим, что мы расположим наши данные упорядоченно от самой маленькой величины переменной X и до самой большой величины. Величина X, до которой расположен 1% наблюдений (и выше которой расположены 99% наблюдений), называется первым процентилем.
Величина X, до которой находится 2% наблюдений, называется 2-м процентилем, и т. д.
Величины X, которые делят упорядоченный набор значений на 10 равных групп, т. е. 10-й, 20-й, 30-й,…, 90 и процентили, называются децилями. Величины X, которые делят упорядоченный набор значений на 4 равные группы, т.е. 25-й, 50-й и 75-й процентили, называются квартилями. 50-й процентиль — это медиана.
Применение процентилей
Мы можем добиться такой формы описания рассеяния, на которую не повлияет выброс (аномальное значение), исключая экстремальные величины и определяя размах остающихся наблюдений.
Межквартильный размах — это разница между 1-м и 3-м квартилями, т.е. между 25-м и 75-м процентилями. В него входят центральные 50% наблюдений в упорядоченном наборе, где 25% наблюдений находятся ниже центральной точки и 25% — выше.
Интердецильный размах содержит в себе центральные 80% наблюдений, т. е. те наблюдения, которые располагаются между 10-м и 90-м процентилями.
Мы часто используем размах, который содержит 95% наблюдений, т.е. он исключает 2,5% наблюдений снизу и 2,5% сверху. Указание такого интервала актуально, например, для осуществления диагностики болезни. Такой интервал называется референтный интервал, референтный размах или нормальный размах.
Среднее геометрическое
При несимметричном распределении данных среднее арифметическое не будет обобщающим показателем распределения.
Если данные скошены вправо, то можно создать более симметричное распределение, если взять логарифм (по основанию 10 или по основанию е) каждого значения переменной в наборе данных. Среднее арифметическое значений этих логарифмов — характеристика распределения для преобразованных данных.
Чтобы получить меру с теми же единицами измерения, что и первоначальные наблюдения, нужно осуществить обратное преобразование — потенцирование (т. е. взять антилогарифм) средней логарифмированных данных; мы называем такую величину среднее геометрическое.
Если распределение данных логарифма приблизительно симметричное, то среднее геометрическое подобно медиане и меньше, чем среднее необработанных данных.
Среднее арифметическое
Вероятно, большинство из вас использовало такую важную описательную статистику, как среднее.
Среднее — очень информативная мера «центрального положения» наблюдаемой переменной, особенно если сообщается ее доверительный интервал. Исследователю нужны такие статистики, которые позволяют сделать вывод относительно популяции в целом. Одной из таких статистик является среднее.
Доверительный интервал для среднего представляет интервал значений вокруг оценки, где с данным уровнем доверия, находится «истинное» (неизвестное) среднее популяции.
Например, если среднее выборки равно 23, а нижняя и верхняя границы доверительного интервала с уровнем p=.95 равны 19 и 27 соответственно, то можно заключить, что с вероятностью 95% интервал с границами 19 и 27 накрывает среднее популяции.
Если вы установите больший уровень доверия, то интервал станет шире, поэтому возрастает вероятность, с которой он «накрывает» неизвестное среднее популяции, и наоборот.
Хорошо известно, например, что чем «неопределенней» прогноз погоды (т.е. шире доверительный интервал), тем вероятнее он будет верным. Заметим, что ширина доверительного интервала зависит от объема или размера выборки, а также от разброса (изменчивости) данных. Увеличение размера выборки делает оценку среднего более надежной. Увеличение разброса наблюдаемых значений уменьшает надежность оценки.
Вычисление доверительных интервалов основывается на предположении нормальности наблюдаемых величин. Если это предположение не выполнено, то оценка может оказаться плохой, особенно для малых выборок.
При увеличении объема выборки, скажем, до 100 или более, качество оценки улучшается и без предположения нормальности выборки.
Довольно трудно «ощутить» числовые измерения, пока данные не будут содержательно обобщены. Диаграмма часто полезна в качестве отправной точки. Мы можем также сжать информацию, используя важные характеристики данных. В частности, если бы мы знали, из чего состоит представленная величина, или если бы мы знали, насколько широко рассеяны наблюдения, то мы бы смогли сформировать образ этих данных.
Среднее арифметическое, которое очень часто называют просто «среднее», получают путем сложения всех значений и деления этой суммы на число значений в наборе.
Это можно показать с помощью алгебраической формулы. Набор n наблюдений переменной X можно изобразить как X1, X2, X3, …, Xn. Например, за X можно обозначить рост индивидуума (см), X1 обозначит рост 1-го индивидуума, а Xi — рост i-го индивидуума. Формула для определения среднего арифметического наблюдений (произносится «икс с чертой»):
= (Х1 + Х2 + … + Xn) / n
Можно сократить это выражение:
где (греческая буква «сигма») означает «суммирование», а индексы внизу и вверху этой буквы означают, что суммирование производится от i = 1 до i = n. Это выражение часто сокращают еще больше:
или
Мода и медиана
Модой называют элемент, который встречается в выборке чаще других.
Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров

Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.
Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат

Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.
Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.
Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:

Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:

Выпишем рост спортсменов отдельно:
180, 182, 183, 184, 185, 188, 190
В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.
Медианой упорядоченной выборки называют элемент, располагающийся посередине.
Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.
В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану

Но возможны случаи, когда количество элементов выборки чётно.
К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:

Построим этих шестерых спортсменов по росту:

Выпишем рост спортсменов отдельно:
180, 182, 184, 186, 188, 190
В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.
В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.
Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186

Найдем среднее арифметическое элементов 184 и 186
Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.
Поэтому более точное определение медианы зависит от количества элементов в выборке.
Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.
Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.
Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190

Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:
Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:
0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1
Определим среднее арифметическое для данной выборки — получим значение 2,2
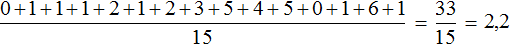
По данному значению можно сказать, что в среднем у спортсменов 2,2 очка
Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:
0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 3, 4, 5, 5, 6
В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.
Взвешенное среднее
Взвешенное среднее используют тогда, когда некоторые значения интересующей нас переменной x более важны, чем другие
Мы присоединяем вес wi к каждому из значений xi в нашей выборке для того, чтобы учесть эту важность
Если значения x1, x2 … xn имеют соответствующий вес w1, w2 … wn, то взвешенное арифметическое среднее выглядит следующим образом:
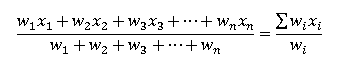
Например, предположим, что мы заинтересованы в определении средней продолжительности госпитализации в каком-либо районе и знаем средний реабилитационный период больных в каждой больнице. Учитываем количество информации, в первом приближении принимая за вес каждого наблюдения число больных в больнице.
Взвешенное среднее и среднее арифметическое идентичны, если каждый вес равен единице.