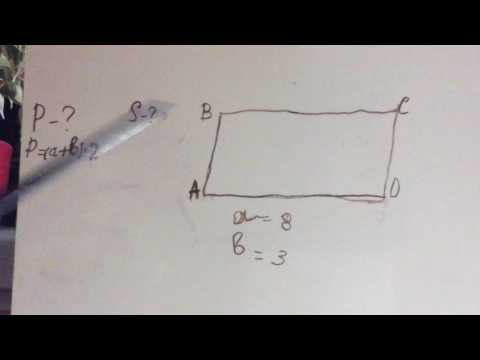
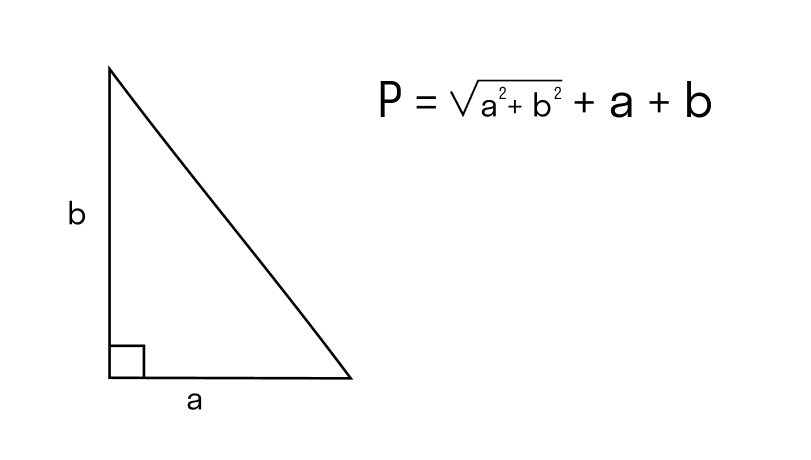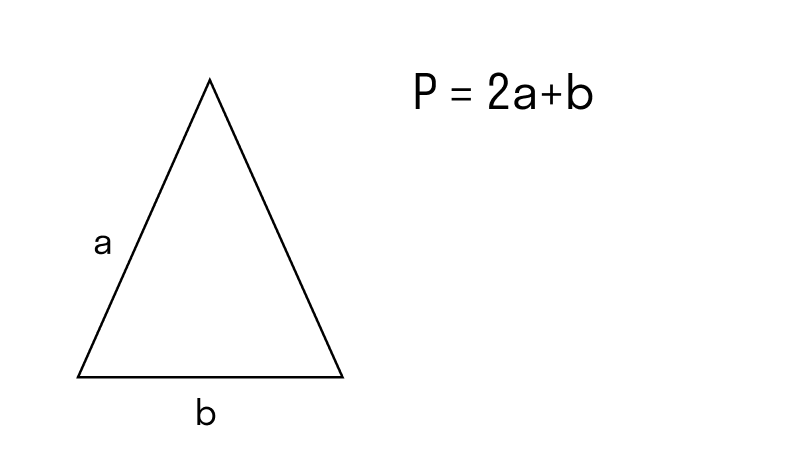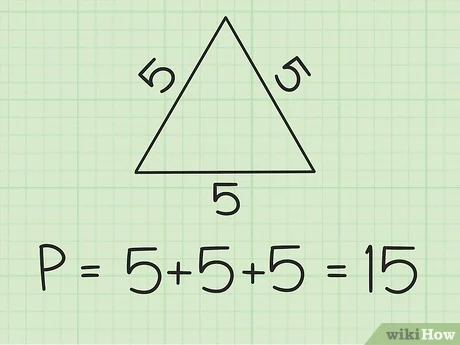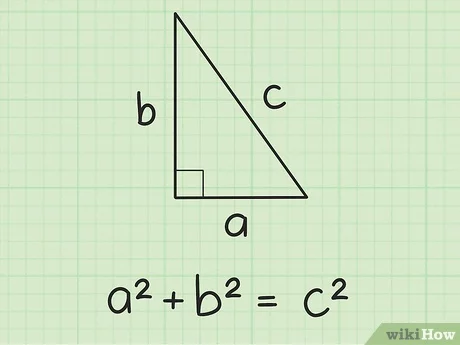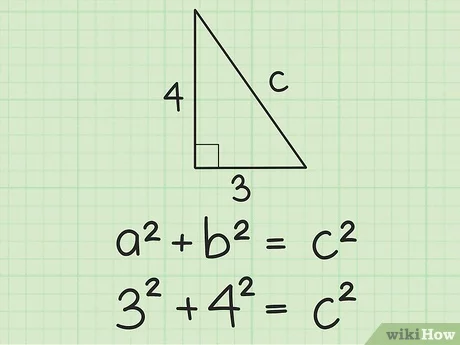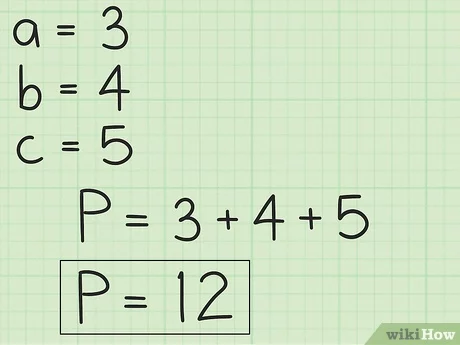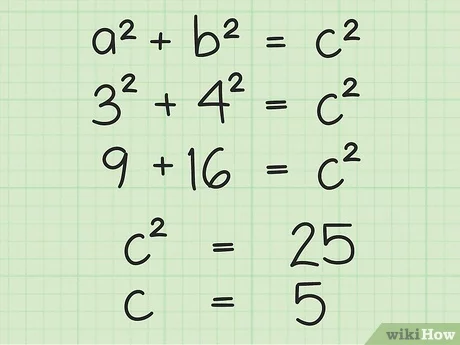Задача 2
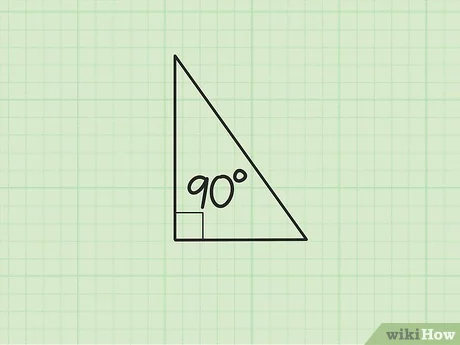
Если в задаче дается острый угол прямоугольного треугольника, значит в любом случае в решении нужно использовать тригонометрические функции. Иначе для нахождения результата просто не хватит данных.
В этой задаче есть два возможных варианта. Острый угол может быть расположен у известного катета, а может противолежать ему. В любом случае придется использовать тригонометрические функции, но результаты могут разница. Обычно в задаче этот момент прописывается, но иногда от решающего требуется предоставить оба варианта решения. Это ясно из условия, в котором не говорится, какой из острых углов дан.
Рассмотрим вариант, при котором дан острый угол при известном катете. Тогда воспользуемся функцией косинуса:
$$Cos(BAC)={AB\over AC}={\sqrt{3}\over2}$$
$$AC={AB\over {cos(BAC)}}$$
$$AC={8\over{\sqrt{3}\over 2}}={16\over\sqrt{3}}=9,24$$ – значение округлим до сотых
BC найдем через значение тангенса.
$$tg(BAC)={BC\over AB}={1\over\sqrt{3}}$$
$$BC=AB*{1\over\sqrt{3}}={AB\over\sqrt{3}}$$
$$BC={8\over\sqrt{3}}=4,62$$
Вычисление периметра произведем по общей формуле:
P=8+9,24+4,62=21,86
Если острый угол противолежит известному катету, то решение будет выглядеть немного иначе.
Найдем BC через значение тангенса.
$$tg(ACB)={AB\over BC}={1\over\sqrt{3}}$$
$$BC={AB\over {1\over\sqrt{3}}}=AB*\sqrt{3}=8*\sqrt{3}=13,86$$
Гипотенузу найдем через значение синуса.
$$sin(ACB)={AB\over AC}={1\over 2}$$
$$AC={AB\over sin(ACB)}={AB\over {1\over 2}}=2*AB=2*8=16$$
Если в расчетах присутствуют округления, то лучше округленный результат не использовать в дальнейших вычислениях. То есть, если мы посчитали BC, то AC лучше найти через синус, а не через косинус или теорему Пифагора, если есть такая возможность. Использование точных значений избавляет от больших погрешностей в результатах.
Что мы узнали?
Мы узнали, что отличия между формулой периметра для прямоугольного и произвольного треугольника нет. Разница в пути решения. Найти периметр прямоугольного треугольника можно через теорему Пифагора, площадь или тригонометрические функции, можно комбинировать различные методы между собой. Главное, это возможность решения задачи без дополнительных построений.
Тест по теме
-
Вопрос 1 из 5
Начать тест(новая вкладка)
2Измерение периметра
Для того, чтобы измерить периметр многоугольника, к которым относятся простые и привычные всем фигуры, такие как треугольник, прямоугольник, квадрат, а также более сложные – куб, пирамида, тетраэдр и другие, потребуется линейка. Нужно измерить каждую грань фигуры, а затем сложить полученные значения.
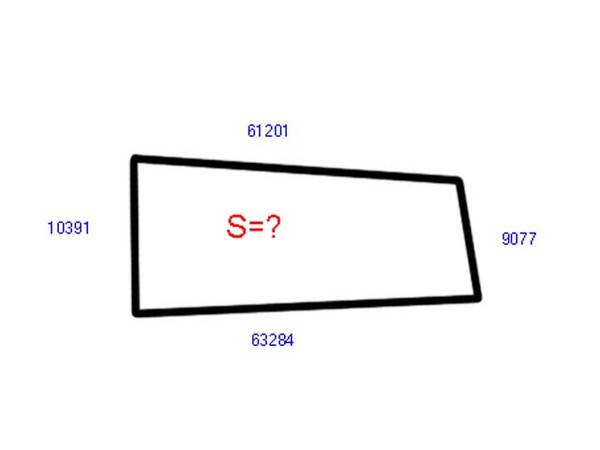
В том случае, если фигура обладает изогнутыми гранями и имеет нестандартный внешний вид, прибегают к помощи нити. Сначала длина грани измеряется при помощи гибкого подручного материала, а затем измеряется с помощью линейки и также значения складываются.
К тому же существуют различные специальные приборы, например роликовый дальномер, при помощи которого периметр можно узнать, находясь от фигуры на расстоянии. Ниже будут рассмотрен ряд примеров.

Пример
Сложную задачу на нахождение периметра правильного треугольника придумать нелегко. Поэтому решим интересную, но простую задачу на заданную тематику. В процессе решения рассмотрим применение теоремы Пифагора для решения задач с правильным треугольником.
Площадь правильного треугольника АВС равняется $9\sqrt{3}$

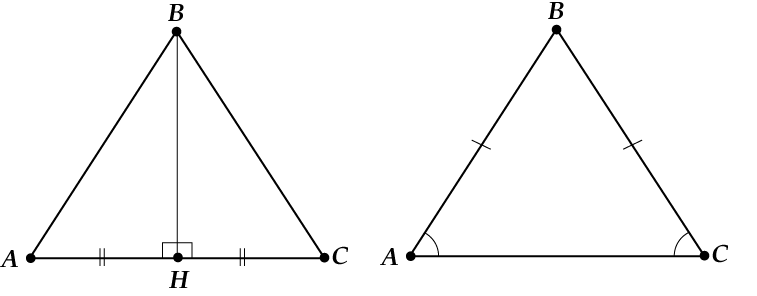
Рис. 2. Рисунок к задаче.
Любую характеристику правильного треугольника можно найти, если есть хотя бы одна из длин
Неважно, будет это сторона, площадь, периметр, медиана или биссектриса. Любой длины будет достаточно для решения задачи
Вспомним формулу площади треугольника и упростим ее для правильного треугольника.
Площадь треугольника находится как половина произведения основания на высоту, проведенную к этому основанию.
В правильном треугольнике АВС проведем медиану АМ, которая совпадет с высотой и биссектрисой. Тогда треугольник АВМ будет прямоугольным. По теореме Пифагора найдем АМ.

Рис. 3. Сумма углов треугольника.
$$АМ=\sqrt{AB^2-BM^2}= \sqrt{а^2-{а\over{2}}^2}= \sqrt{а^2-{{а^2}\over{4}}}=\sqrt{{3a^2}\over{4}}$$
Подставим значение АМ в формулу площади:
$$S={1\over{2}}*a*h={1\over{2}}*a*a*{\sqrt{3}\over{2}}=a^2*{\sqrt{3}\over{4}}$$
Из этой формулы выразим значение стороны:
$$a=\sqrt{4S\over{\sqrt{3}}}=\sqrt{{4*{9\over{\sqrt{3}}}}\over{\sqrt{3}}}=6$$
Теперь найти периметр не составит проблем.
$$P=3a=3*6=18$$
Что мы узнали?
Мы привели формулу периметра правильного треугольника. На примере показали, как можно найти площадь правильного треугольника через площадь. На том же примере показали примерный ход решения любой задачи на решение правильного треугольника.
Тест по теме
-
Вопрос 1 из 5
Начать тест(новая вкладка)
Задача 2
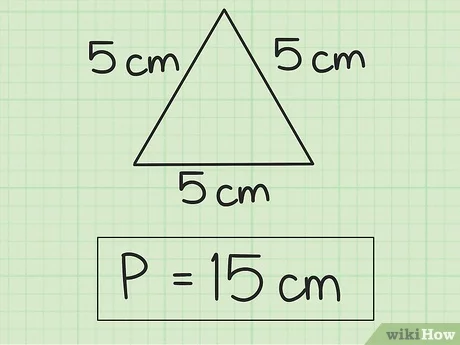
Особое внимание нужно обращать на вид фигуры, который указан в условии задачи. В данной задаче дан равнобедренный треугольник
Чтобы воспользоваться общей формулой, необходимо доказать, что этот равнобедренный треугольник является еще и равносторонним
В данной задаче дан равнобедренный треугольник. Чтобы воспользоваться общей формулой, необходимо доказать, что этот равнобедренный треугольник является еще и равносторонним.
Обратим внимание на величину угла. Угол при основании равен 60
При этом углы у основания равнобедренного треугольника равны, а сумма углов любого треугольника равна 180 градусов. Значит у основания два угла по 60 градусов. Рассчитаем угол при вершине:
180-60-60=60 – угол при вершине так же равен 60 градусам.
Значит, данный треугольник будет равносторонним, так как все углы равны 60 градусам.
Углы по 60 градусов характерны только для равностороннего треугольника. Именно сочетание 3 равных сторон образует 3 равных угла. В любых других ситуациях, хотя бы один угол будет отличаться.
Для площади равностороннего треугольника имеется отдельная формула:
$$S=a^2*{\sqrt{3}\over 4}={64\over\sqrt{3}}$$ – где а значение стороны, которое нам и нужно выразить из этой формулы.
$$а^2={S\over{\sqrt{3}\over 4}}$$
$$a^2={4S\over\sqrt{3}}$$
$$a=\sqrt{4S\over\sqrt{3}}$$
$$a={\sqrt{4*{64\over\sqrt{3}^2}}\over\sqrt{3}}=\sqrt{4*64}=16$$
Подставим полученное значение в формулу:
P=3*a=3*16=48