Виды величин
Под величиной имеется в виду то, что выражает свойства определенного предмета, вещества или явления. К примеру, температура воздуха, масса животного, процентное содержание витаминов в таблетке — это все величины, числовые значения которых можно вычислить.
Для каждой величины есть свои единицы измерения, которые все вместе образуют систему. Ее называют системой исчисления (СИ).
Что такое переменные и постоянные величины? Рассмотрим их на конкретных примерах.
Возьмем прямолинейное равномерное движение. Точка в пространстве движется с одинаковой скоростью на каждом промежутке времени. То есть изменяются время и расстояние, а скорость остается одинаковой. В данном примере время и расстояние — переменные величины, а скорость — постоянная.
Или, например, “пи”. Это иррациональное число, которое продолжается без повторяющейся последовательности цифр и не может быть записано полностью, поэтому в математике оно выражается общепринятым символом, который принимает только значение данной бесконечной дроби. То есть “пи” — это постоянная величина.
История
История обозначения переменных начинается в семнадцатом веке с ученого Рене Декарта.

Известные величины он обозначил первыми буквами алфавита: a, b и так далее, а для неизвестных предложил использовать последние буквы: x, y, z. Примечательным является то, что такие переменные Декарт считал неотрицательными числами, а при столкновении с отрицательными параметрами ставил знак минус перед переменной или, если было неизвестно, каким по знаку является число, многоточие. Но со временем наименованиями переменных стали обозначать числа любого знака, и началось это с математика Иоганна Худде.
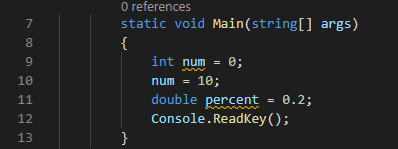
С переменными вычисления в математике решаются проще, ведь как, например, сейчас мы решаем биквадратные уравнения? Вводим переменную. Например:
x4 + 15×2 + 7 = 0
За x2 принимаем некое k, и уравнение приобретает понятный вид:
x2 = k, при k ≥ 0
k2 + 15k + 7 = 0
Вот какую пользу в математику несет введение переменных.
Классификация
Статическая и динамическая типизация переменных
Если тип данных определяется на этапе компиляции, имеет место статическая типизация, а если на этапе выполнения программы — динамическая. В последнем случае иногда говорят, что переменная не имеет типа, хотя данные, содержащиеся в ней, безусловно, относятся к определённому типу данных, но выясняется это уже во время выполнения программы.
В большинстве случаев статическая типизация позволяет уменьшить затраты ресурсов при выполнении программы, поскольку для динамической типизации требуются затраты ресурсов на выяснение типов данных и их приведение в выражениях со смешанными типами. Статическая типизация позволяет проводить проверку типов на этапе компиляции программы. Это также упрощает обнаружение ошибок ещё на этапе разработки, когда их исправление обходится менее дорого.
Тем не менее, во многих случаях необходимо применение динамической типизации. Например, необходимость поддержания совместимости при переходе на новый формат представления данных (например, старая часть проекта посылает процедуре дату символьной строкой, а новые объекты используют более современный числовой тип).
Статические и динамические переменные
Адрес поименованной ячейки памяти также может определяться как на этапе компиляции, так и во время выполнения программы. По времени создания переменные бывают статическими и динамическими. Первые создаются в момент запуска программы или подпрограммы, а вторые создаются в процессе выполнения программы.
Динамическая адресация нужна только тогда, когда количество поступающих на хранение данных заранее точно не известно. Такие данные размещают в специальных динамических структурах, тип которой выбирается в соответствии со спецификой задачи и с возможностями выбранной системы программирования. Это может быть стек, куча, очередь и т. п. Даже файл, в том смысле, который заложил Н.Вирт в Паскаль, является динамической структурой.
Локальные и глобальные переменные. Области видимости
По зоне видимости различают локальные и глобальные переменные. Первые доступны только конкретной подпрограмме, вторые — всей программе. С распространением модульного и объектного программирования, появились ещё и общие переменные (доступные для определённых уровней иерархии подпрограмм). Область видимости иногда задаётся классом памяти. Ограничение видимости может производиться путём введения пространств имён.
Ограничение зоны видимости придумали как для возможности использовать одинаковые имена переменных (что разумно, когда в разных подпрограммах переменные выполняют похожую функцию), так и для защиты от ошибок, связанных с неправомерным использованием переменных (правда, для этого программист должен владеть и пользоваться соответствующей логикой при структуризации данных).
Простые и сложные переменные
По наличию внутренней структуры, переменные могут быть простыми или сложными (составными).
- Простые переменные не имеют внутренней структуры, доступной для адресации. Последняя оговорка важна потому, что для компилятора или процессора переменная может быть сколь угодно сложной, но конкретная система (язык) программирования скрывает от программиста её внутреннюю структуру, позволяя адресоваться только «в целом».
- Сложные переменные программист создаёт для хранения данных, имеющих внутреннюю структуру. Соответственно, есть возможность обратиться напрямую к любому элементу.
Самыми характерными примерами сложных типов являются массив (все элементы однотипные) и запись (элементы могут иметь разный тип).
Следует подчеркнуть относительность такого деления: для разных программ одна и та же переменная может иметь разную структуру.
Например, компилятор различает в переменной вещественного типа 4 поля: знаки мантиссы и порядка, плюс их значения, но для программиста, компилирующего свою программу, вещественная переменная — единая ячейка памяти, хранящая вещественное число.
Алгебраический метод

Чтобы решить систему, изображенную на картинке, данным методом, необходимо сначала помножить одну из ее частей на такое число, чтобы потом иметь возможность взаимно уничтожить одну переменную из обеих частей уравнения. Здесь мы умножаем на три, подводим черту под системой и складываем ее части. В итоге иксы становятся одинаковы по модулю, но противоположны по знаку, и мы их сокращаем. Далее получаем линейное уравнение с одной переменной и решаем его.
Игрек мы нашли, но на этом мы не можем остановиться, ведь мы еще не нашли икс. Подставляем игрек в ту часть, из которой удобно будет вывести икс, например:
-x + 5y = 8 , при y = 1
-x + 5 = 8
Решаем получившееся уравнение и находим икс.
-x = -5 + 8
-x = 3
x = -3
Главное в решении системы — правильно записать ответ. Многие школьники делают ошибку и пишут:
Ответ: -3, 1.
Но это неверная запись. Ведь, как уже писалось выше, решая систему уравнений, мы ищем общее решение для его частей. Правильным будет ответ:
(-3; 1)
Наглядный пример
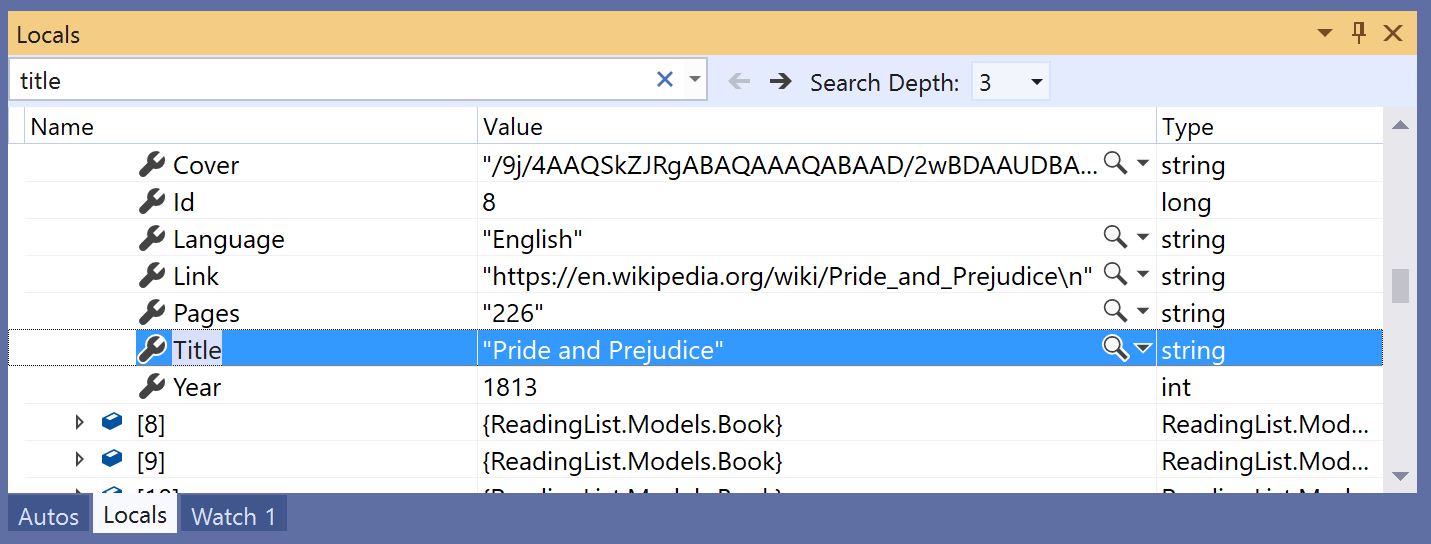
В следующем определении полиморфного типа «список» на языке Standard ML, идентификатор (читается «альфа») является переменной типа:
datatype 'a list = nil | :: of 'a * 'a list
При использовании этого полиморфного типа, в ти́повую переменную подставляется конкретный тип, так что в программе формируется множество мономорфных типов: , , и т. д. При такой подстановке, вместо каждого упоминания переменной типа подставляется один и тот же тип. Полученная информация о типах используется для верификации и оптимизации программы, после чего обычно стирается, так что один и тот же целевой код обрабатывает объекты изначально разных типов (но существуют и исключения из этого правила — см. MLton).
Если полиморфный тип параметризован несколькими переменными типа, то подставляемые в них типы могут быть как разными, так и идентичными, но правило подстановки соблюдается. Например, если такой тип:
datatype ('a,'b) t = Single of 'a | Double of 'a * 'a | Pair of 'a * 'b
инстанцировать следующим образом:
type t_ir = (int, real) t
то , и будут допустимыми значениями типа , а попытка построить значение приведёт к ошибке типизации, поскольку параметр получил значение «».
Переменные в программировании
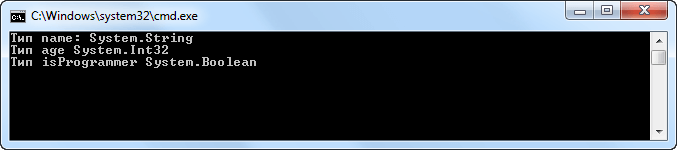
В программировании переменная — это идентификатор, определяющий данные. Обычно это имя, скрывающее за собой область памяти, куда могут помещаться данные, хранящиеся в другой области памяти. Переменная может иметь тип значений, которые она может принимать. В программировании, переменные, как правило, обозначаются одним или несколькими словами или символами, такими, как «time», «x», «foo».
Такое понятие переменной в некотором смысле схоже с математическим. Математики в XVII веке уже использовали переменную, чтобы «забронировать» в формуле место, на которое можно подставлять конкретные значения. Буквенные обозначения резервируют и именуют области этой памяти. Если формула в математике является алгоритмом вычисления, то понятие переменной совпадает с понятием переменной в программировании.
Если формула используется только для выражения отношения между элементами множеств, то нет необходимости в понятии переменных как ячеек памяти.
Понятие переменной

Для начала узнаем, что такое переменная? Это численная величина, которая может принимать множество значений. Она не может быть постоянной, так как в разных задачах и уравнениях для удобства решения мы принимаем за переменную разные числа, то есть, например, z — это общее обозначение для каждой из величин, за которые ее принимают. Обычно их обозначают буквами латинского или греческого алфавита (x, y, a, b и так далее).
Есть разные виды переменных. Ими задаются как некоторые физические величины — путь (S), время (t), так и просто неизвестные значения в уравнениях, функциях и других выражениях.
Например, есть формула: S = Vt. Здесь переменными обозначаются определенные величины, имеющие отношение к реальному миру — путь, скорость и время.
А есть уравнение вида: 3x — 16 = 12x. Здесь уже за x принимается абстрактное число, которое имеет смысл в данной записи.
Неравенства, примеры решения
Неравенство представляет собой запись, в которой два математических выражения или два числа связаны знаками сравнения: <, >, ≤, ≥. Они бывают строгими и обозначаются знаками < и > или нестрогими со знаками ≤, ≥.
Впервые эти знаки ввел Томас Гарриот. После смерти Томаса вышла его книга с этими обозначениями, математикам они понравились, и со временем их стали повсеместно употреблять в математических вычислениях.
Существует несколько правил, которые нужно соблюдать при решении неравенств с одной переменной:
- При переносе числа из одной части неравенства в другую меняем его знак на противоположный.
- При умножении или делении частей неравенства на отрицательное число их знаки меняются на противоположные.
- Если умножить или разделить обе части неравенства на положительное число, то получится неравенство, равное исходному.
Решить неравенство — значит найти все допустимые значения переменной.
Пример с одной переменной:
10x — 50 > 150
Решаем, как обычное линейное уравнение — переносим слагаемые с переменной влево, без переменной — вправо и приводим подобные члены:
10x > 200
Делим обе части неравенства на 10 и получаем:
x > 20
Для наглядности в примере решения неравенства с одной переменной изображаем числовую прямую, отмечаем на ней проколотую точку 20, так как неравенство строгое, и данное число не входит в множество его решений.

Решением этого неравенства будет промежуток (20; +∞).
Решение нестрогого неравенства осуществляется так же, как и строгого:
6x — 12 ≥ 18
6x ≥ 30
x ≥ 5
Но есть одно исключение. Запись вида x ≥ 5 нужно понимать так: икс больше или равно пяти, значит число пять входит во множество всех решений неравенства, то есть, записывая ответ, мы ставим квадратную скобку перед числом пять.
x ∈ [5; +∞)
Калькуляторы дружат с константами
Например, возьмем калькулятор. Что он может делать? Достаточно много: выполнять ряд арифметических и даже более сложных действий.
- Вводим на калькуляторе первое число, например, «2»,
- нажимаем на знак «плюс»,
- вводим второе число, скажем, «3» (см. рис. 1),
- и затем нажимаем знак «=».
Что получим? Очевидно, значение «5». Арифметика. Но с использованием компьютерной техники – калькулятора.
Рис. 1. Суммирование констант 2+3 на калькуляторе (Windows 7)
Не будем дальше углубляться в возможности калькуляторов. Например, можно было бы рассмотреть более сложные калькуляторы: для инженеров, для программистов, для обработки статистических данных и пр. (см. рис. 2).

Рис. 2. Некоторые виды калькуляторов, имеющихся в Windows 7
Но даже сложные калькуляторы так и останутся калькуляторами, то есть, будут делать арифметические операции той или иной степени сложности. Потому что это один уровень абстракции, самый низкий, на уровне чисел. Ничем другим, кроме как обработкой числовых выражений, калькуляторы заниматься не могут.
Переменные в математике
В математике переменной может быть как реальная физическая величина, так и некая абстрактная величина, не отражающая процессов реального мира.
В математическом анализе и большинстве смежных разделов математики под переменной x{\displaystyle x} понимают каждый элемент некоторого множества, состоящего, например, из вещественных чисел. Фиксированный элемент этого множества — число называется значением переменной. Само множество называется областью изменения переменной.
Задание области изменения переменной эквивалентно заданию самой переменной.
- Переменные обозначаются малыми буквами латинского или греческого алфавита (возможно, с индексами): x, y, ε{\displaystyle x,~y,~\varepsilon }.
- Области изменения соответствующих переменных обозначаются обычно теми же символами, взятыми в фигурные скобки: {x}, {y}, {ε}{\displaystyle \left\{x\right\},~\left\{y\right\},~\left\{\varepsilon \right\}}.
При моделировании процессов переменные необходимо отличать от параметров, несмотря на то, что переменная в одном контексте может быть параметром в другом.
В прикладной статистике переменная — оценочный фактор или характеристика, индивидуальный или системный атрибут, изменение которых ожидается с течением времени или между отдельными лицами, например переменная возраст.
Переменная и неизвестное
Нужно отметить, что аналогично переменным обозначаются неизвестные в уравнениях, неравенствах и других подобных задачах, например в уравнении 2x=6{\displaystyle 2x=6}, где буквой x{\displaystyle x} обозначено неизвестное, а не переменная, хотя эти понятия весьма схожи и зависят от контекста.
Суть различия между этими понятиями можно пояснить так.
Запись 2x=6{\displaystyle 2x=6} можно, с одной стороны, трактовать как утверждение о возможности найти значение неизвестного x{\displaystyle x}. В этом случае x{\displaystyle x} — обозначение неизвестного числа.
С другой стороны запись 2x=6{\displaystyle 2x=6} можно трактовать как предикат, принимающий значение «истина» при одних значениях x{\displaystyle x}, и значение «ложь» при других. В этом случае x{\displaystyle x} — переменная. На её место в выражении могут подставляться различные значения с целью определения логического (булева) значения записанного предиката.
История
В середине XVII века у Рене Декарт предложил использовать для известных параметров начальные буквы алфавита: a,b,c…,{\displaystyle a,b,c\dots ,} а для неизвестных — последние буквы: x,y,z.{\displaystyle x,y,z.}
Декарт не объяснял свой выбор. Некоторые историки пытались объяснить выбор буквы x{\displaystyle x} в качестве неизвестной. Так, например, словарь Уэбстера (1909-1916) утверждал, что переменная x{\displaystyle x} появилась как транскрипция арабской буквы ش — первой буквой в слове شيء, которое переводится на русский языка как «что-то», «нечто». Тем не менее эта и другие подобные версии не находят подтверждений и игнорируют тот факт, что Декарт использовал наряду с x{\displaystyle x} еще y{\displaystyle y} и z{\displaystyle z}.
Декарт считал значения переменных всегда неотрицательными, а отрицательные величины выражал знаком отражал знаком «минус» перед переменной. Если знак коэффициента был неизвестен, Декарт ставил многоточие. Нидерландский математик Иоганн Худде уже в 1657 году позволил буквенным переменным принимать значения любого знака.
Ф. Кэджори характеризует декартовскую запись степеней как самую удачную и гибкую символику во всей алгебре — она не только облегчает преобразования, но стимулировала расширение понятия возведения в степень на отрицательные, дробные и даже комплексные показатели, а также появление в математике степенной и показательной функции; все эти достижения трудно было бы осуществить при использовании обозначений XVI века
Что такое переменная?
Определение переменной звучит примерно следующим образом:
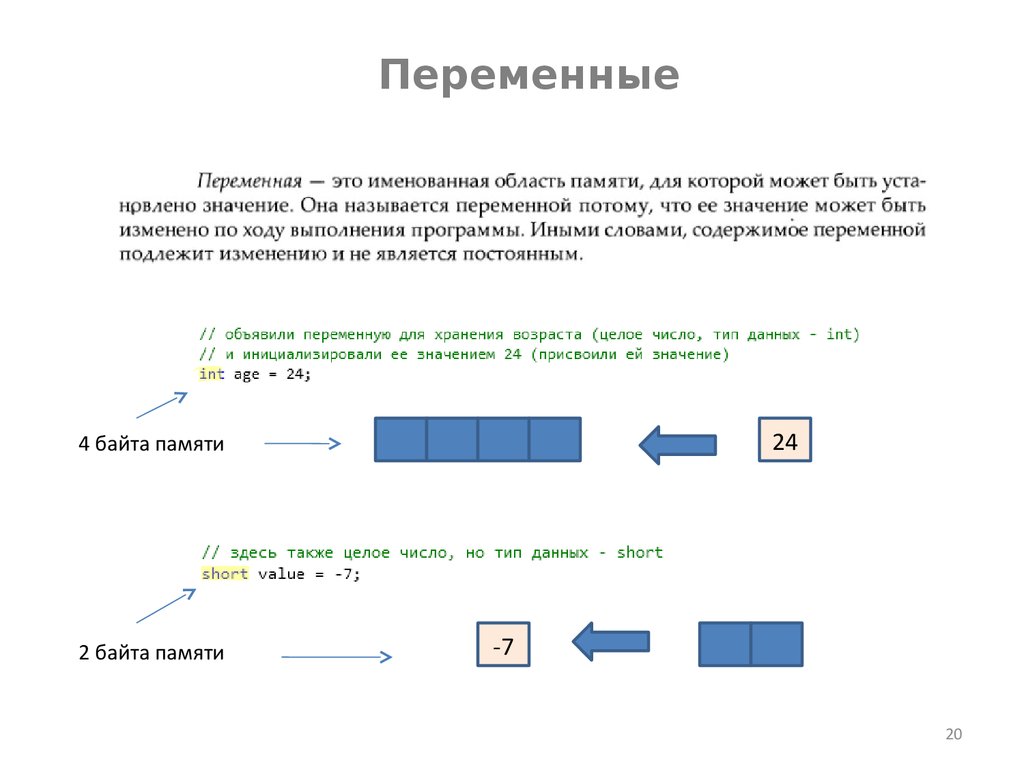
Переменная – это именованная область памяти.
Но что это означает для нас. Давайте разбираться на примере.
Я думаю, что каждый из вас уже знаком с понятием переменной в алгебре. Это тот самый X, который приходиться искать в уравнении. В программировании переменная имеет схожие функции. Это своеобразный псевдоним, что-то неопределенное, неизвестное, под которым может скрываться кто угодно
Представь себе коробочку. На этой коробочке написано «Подарок» и это делает эту коробочку уникальной. Ты всегда сможешь найти именно эту коробку по этому имени (при условии, что не может существовать ни одной другой коробочки с таким именем).
А вот положить в эту коробочку ты можешь все что угодно. Это может быть и новенький IPhone, и миленький котеночек, и что-нибудь куда менее приятное (как в фильме «Семь»). Кстати, если не смотрел этот фильм, очень рекомендую, но только если у тебя крепкая психика и тебе больше 18 лет.
И в дальнейшем ты можешь как угодно работать с этой коробочкой. В любой момент ты можешь положить туда что-нибудь (предварительно выкинув оттуда то, что там лежало раньше), посмотреть, что там лежит, или вообще взять и выкинуть эту коробочку со всем содержимым.
При этом важно понимать, что концепция переменных это очень сложный механизм работы с памятью, который просто скрыт от программиста современными операционными системами и высокоуровневыми языками программирования
Методы
Умное именование функций и методов — это то, что приходит только с опытом проектирования API, и потому достаточно часто можно встретить случаи, когда методы ведут себя не так, как мы ожидаем.
Рассмотрим пример с методом:
В коде мы выразили весьма однозначный вопрос: «Имеются ли у этого человека публикации?», но какой ответ мы получили?
Мы не спрашивали, какие у человека есть публикаций. Название этого метода подразумевает, что возвращаемое значение должно иметь булевый тип, а именно или :
А для получения постов вы можете использовать более подходящее название:
или
Мы часто любим называть программирование творческой деятельностью, и таковой оно в действительности и является. Однако, если вы пишете код, который можете прочитать только вы, и затем оправдываете это «творчеством», то у меня для вас плохие новости.
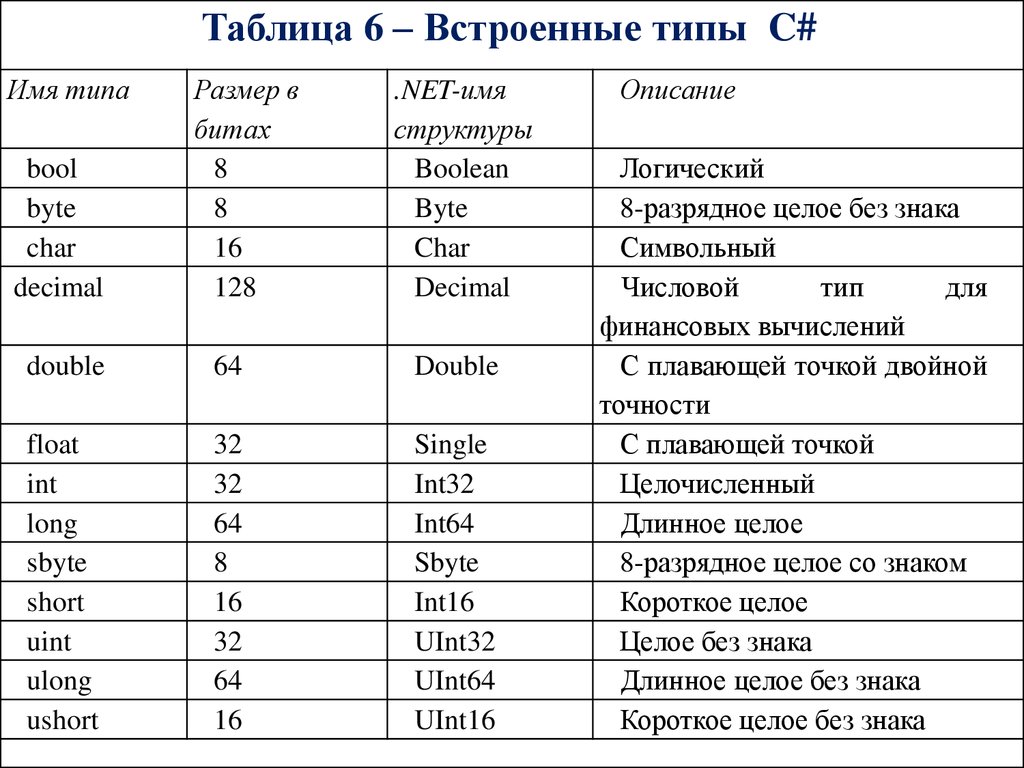
Типизация переменных
Именно так работали бы переменные, если бы в не существовало типизации. Типизация – это возможность разделить коробочки по возможному содержимому. То есть, когда мы создаем коробочку, мы кроме имени указываем, что в ней может располагаться. И тогда, в коробочку для IPhone котеночка ты уже не засунешь.
Это позволяет дополнительно защититься от ошибок, потому что ты будешь заранее знать, что будет в коробочке, и будешь готов к тому, как тебе нужно будет себя вести с содержимым.
Языки программирования условно можно разделить на два больших типа:
Сильнотипизированные – те, где вся ответственность за указание типа переменных ложится на программиста
Слаботипизированные – те, где компьютер сам решает, какой тип используется в конкретном случае.
Язык C# относится к первым. Возможно, это лишает его такой гибкости как тот же самый JavaScript (который относится ко вторым), но при этом дает большую защищенность от ошибок.
Связывание и квантификация переменных типа
Область действия всякой ти́повой переменной привязывается к определённому контексту. В следующем примере идентификатор используется в двух сигнатурах независимо, то есть не означает требование равенства фактически подставляемых типов между определениями:
val foo 'a -> 'a val bar 'a -> 'a
Это становится наглядным при использовании явного связывания (explicit scoping или explicit bounding) ти́повой переменной:
val foo 'a 'a -> 'a val bar 'a 'a -> 'a
Связывание ограничивает область действия данной переменной типа.
В классических диалектах ML явное связывание ти́повых переменных является опциональной возможностью и большинством реализаций не поддерживается за ненадобностью — связывание в них осуществляется неявно при выведении типов, что становится возможным за счёт ограничений ранних версий Хиндли—Милнера. В полной Системе F это объявление записывается как «Λα. λxα. x{\displaystyle \Lambda \alpha .~\lambda x^{\alpha }.~x}». Такая запись называется . Заглавная лямбда в этой записи означает функцию слоя типов (type-level function), параметром которой и является переменная типа. После подстановки в эту переменную конкретного типа, эта функция возвращает мономорфную функцию слоя значений (value-level function). Пренексом называется вынесенное в качестве префикса к сигнатуре типа явное связывание переменной типа. Ранние версии Хиндли—Милнера разрешают только пренексную форму, то есть требуют, чтобы инстанцирование ти́повой переменной конкретным значением было произведено до необходимости обращения к функции. Это ограничение называется — оно не только существенно упрощает механизм проверки согласования типов, но и делает возможным выведение всех или почти всех (в зависимости от диалекта) типов в программе.
Простейшее связывание ти́повых переменных называется их квантификацией. Выделяются два случая:
Действие переменной типа распространяется на всё определение типа: ‘a -> ‘b -> ‘aМатематически такой тип записывается через универсальный квантор — «∀a. ∀b. a→b→a{\displaystyle \forall a.~\forall b.~a\rightarrow b\rightarrow a}» — поэтому такая переменная типа называется «универсально квантифицированной», а весь тип — «универсально полиморфным».
На практике, универсально полиморфные типы дают обобщённость типа данных, а экзистенциальные — абстрактность типа данных.
В языке Хаскел различают несколько режимов (доступных в виде расширений языка): режим Rank2Types разрешает лишь некоторые формы экзистенциальных типов, открывающие полиморфизм не выше 2-го ранга, для которого выведение типов ещё разрешимо; режим RankNTypes разрешает перемещать универсальный квантор () внутрь функциональных типов, входящих в состав более сложных сигнатур, режим ImpredicativeTypes разрешает произвольные экзистенциальные типы.
OCaml реализует поддержку экзистенциальной квантификации посредством решения, названного «локально-абстрактными типами» (locally abstract types).
В спецификации Standard ML для некоторых встроенных операций определена особая квантификация. Её синтаксис не регламентирован и различается в реализациях языка (чаще всего просто скрывается). Например, сигнатура встроенной операции сложения может упрощённо выглядеть примерно следующим образом:
val + int, word, real 'a * 'a -> 'a
Эта семантика реализует примитивную форму ad hoc полиморфизма — объединение нескольких физически различных операций сложения под единым идентификатором «». Разработчики OCaml отказались от такого решения, полностью убрав ad hoc полиморфизм из языка (в более поздних версиях появились обобщённые алгебраические типы данных).
В конце 1980-х появилось расширение Хиндли—Милнера, предоставляющее возможность ограничивать по необходимости диапазон значений для всякой ти́повой переменной во вновь определяемых типах — классы типов. Класс типов строже ограничивает допустимые , разрешая инстанцирование ти́повой переменной лишь типами, принадлежащими явно указанному классу.
Впервые это расширение было реализовано в основе языка Haskell. Например, операция сравнения на равенство имеет в Хаскеле следующую :
(==) :: (Eq a) => a -> a -> Bool
Проект языка следующего поколения — successor ML — отказывается от необходимости выведения типов, опираясь на (в том числе явное связывание переменных типа), что обеспечивает непосредственную поддержку полной Системы F с полиморфизмом первого класса и рядом расширений, в том числе и экзистенциальных типов.