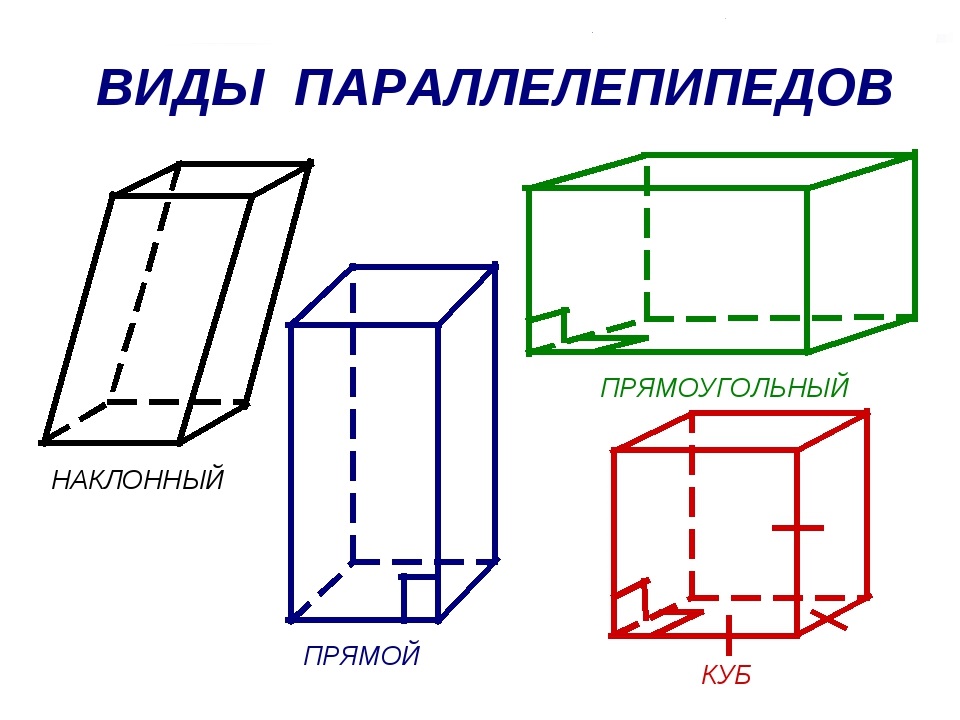
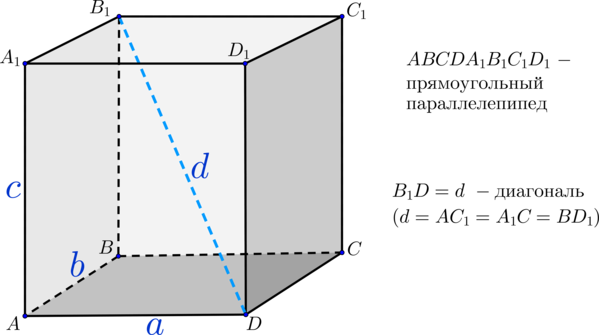
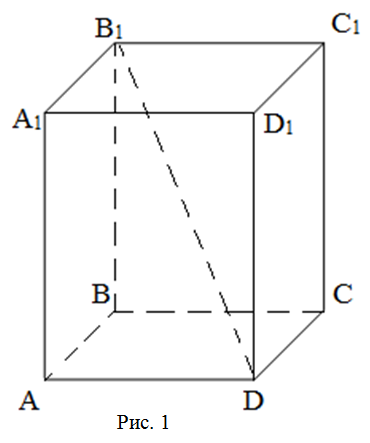
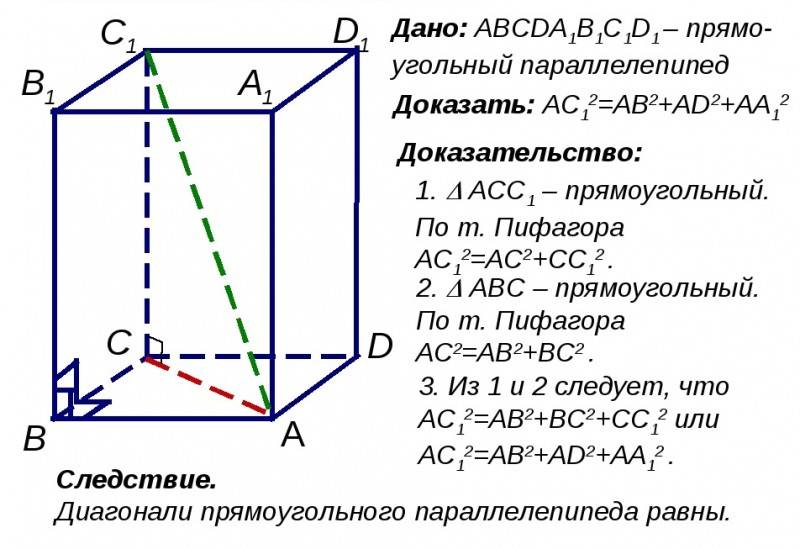
Лексикография
Это слово появляется как parallelipipedon в переводе сэра Генри Биллингсли « Элементов» Евклида , датированного 1570 годом. В издании Cursus mathematicus 1644 года Пьер Эригон использовал правописание « параллелепипед» . Оксфордский словарь английского языка приводит современный параллелепипед , как первое появление в Уолтер Чарлтон в хорея gigantum (1663).
Словарь Чарльза Хаттона (1795 г.) показывает параллелепипед и параллелепипед , показывая влияние объединяющей формы параллело- , как если бы второй элемент был трубопроводом, а не эпипедоном . Ной Вебстер (1806 г.) включает орфографический параллелепипед . Оксфордский словарь английского языка издания 1989 г. описывает параллелепипед (и параллелепипед ) явно как неправильные формы, но они перечислены без комментариев в издании 2004 г., и даны только произношения с акцентом на пятый слог пи ( / paɪ / ).
Отказ от традиционного произношения скрыл различное разделение, предложенное греческими корнями, с epi- («он») и pedon («земля»), объединяющимися, чтобы дать epiped , плоскую «плоскость». Таким образом, грани параллелепипеда плоские, а противоположные грани параллельны.
Свойства параллелепипеда
Теорема 1
Противоположные грани параллелепипеда равны между собой и параллельны.
Доказательство.
Параллельность противоположных граней сразу исходит из определения 1.
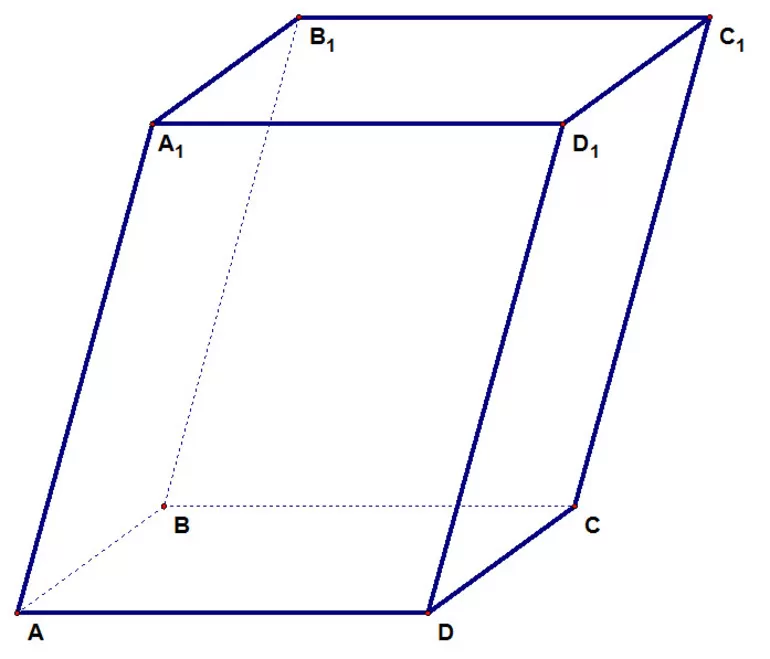
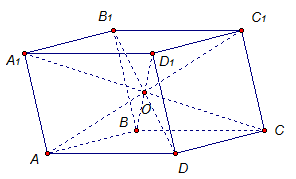
Докажем равенство противоположных граней. Для этого рассмотрим рисунок 2.
Рисунок 2.
Рассмотрим грани ${AA}_1B_1B$ и ${DD}_1C_1C$. Так как, по определению 1, грани параллелепипеда — параллелограммы, то ${AA}_1={DD}_1$ и $AB=DC.$ Так же ${AA}_1||{DD}_1$ и $AB||DC$, следовательно, $\overrightarrow{{AA}_1}\uparrow \uparrow \overrightarrow{{DD}_1}$ и $\overrightarrow{AB}\uparrow \uparrow \overrightarrow{DC}$, то есть $\angle A_1AB=\angle D_1DC$. Значит, по I признаку равенства треугольников$\triangle A_1AB=\triangle D_1DC$. Аналогично доказывается, что $\triangle D_1C_1C=\triangle A_1B_1B$, следовательно, $D_1C_1CD=A_1B_1BA$. Аналогично доказывается равенство других противоположных граней.
Теорема доказана.
Теорема 2
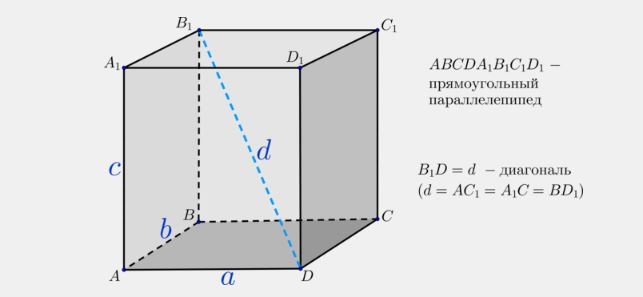
Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Доказательство.
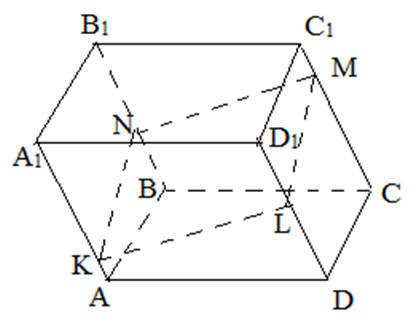
Рассмотрим рисунок 3.
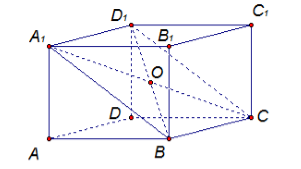 Рисунок 3.
Рисунок 3.
Докажем вначале, что диагонали $A_1C$ и $D_1B$ делятся точкой пересечения $O$ пополам. По теореме 1, имеем $A_1D_1=BC$ и $A_1D_1||BC$. Следовательно, $A_1D_1CB$ — параллелограмм. Тогда, по свойству параллелограмма, получим, что диагонали $A_1C$ и $D_1B$ делятся точкой пересечения $O$ пополам. Аналогично доказывается, что диагонали ${AC}_1$ и $D_1B$ и $A_1C$ и ${DB}_1$ делятся точками их пересечения пополам. Но, так как $O$ центр диагоналей $A_1C$ и $D_1B$, то все диагонали пересекаются в этой точке.
Теорема доказана.
Происхождение Зальцбургского параллелепипеда
Зальцбургский параллелепипед
Впервые научное сообщество узнало о Зальцбургском параллелепипеде 7 июня 1886 года на заседании естественноисторического общества Рейнской области и Вестфалии, где горный инженер Фридрих Гуральт выступил с докладом об артефакте, обнаруженном в угле. В докладе он заявил, что предмет состоит из железа с незначительной примесью никеля и по твердости соответствует стали. Инженер предположил артефакт является метеоритом и попал в угольный пласт в период его формирования.
На этом же заседании несколько ученных обратили внимание на странную форму артефакта, которая выглядит рукотворной. Однако возраст находки отвергает любую возможность обработки ее руками человека
Однако, у многих возникли сомнения в метеоритном происхождении Зальцбургского параллелепипеда. Особенно странной была его правильная форма. Гурльт объяснял ее особыми условиями пролета метеорита через слои атмосферы, однако это предположение не было подтверждено никакими расчетами или убедительными фактами. Помимо этого на артефакте отсутствуют фигуры Видманштеттена, который характерен для железных метеоритов.
В 1966-1967 годах учеными Геро Куратом из Венского музея естественной истории и Рудольфом Гриллем из Геологической службы Австрии был проведен электронно-лучевой микроанализ артефакта. Результаты показали отсутствие в нем никеля, что говорит против его метеоритного происхождения. Не является артефакт и конкрецией, образующейся в угле, так как в нем отсутствовала сера. Согласно исследованиям артефакт состоит из железа и углерода в характерных для доменного чугуна пропорциях. В 1973 году Хуберт Маттлайнер также подтвердил, что он отлит из чугуна.
Идеальный параллелепипед
Идеально параллелепипед представляет собой параллелепипед с целым числом длиной ребер, гранями диагоналями и пространственными диагоналями . В 2009 году было показано, что существуют десятки идеальных параллелепипедов, что явилось ответом на открытый вопрос Ричарда Гая . В одном примере есть края 271, 106 и 103, второстепенные диагонали лица 101, 266 и 255, диагонали основной грани 183, 312 и 323 и диагонали пространства 374, 300, 278 и 272.
Известны идеальные параллелепипеды с двумя прямоугольными гранями. Но неизвестно, существуют ли такие, у которых все грани прямоугольные; такой случай можно было бы назвать идеальным кубоидом .
Свойства параллелепипеда
Особенности фигуры предопределяют ее свойства. К ним относят 4 следующих утверждений:
- Противолежащие ребра и грани фигуры параллельны и равны между собой.
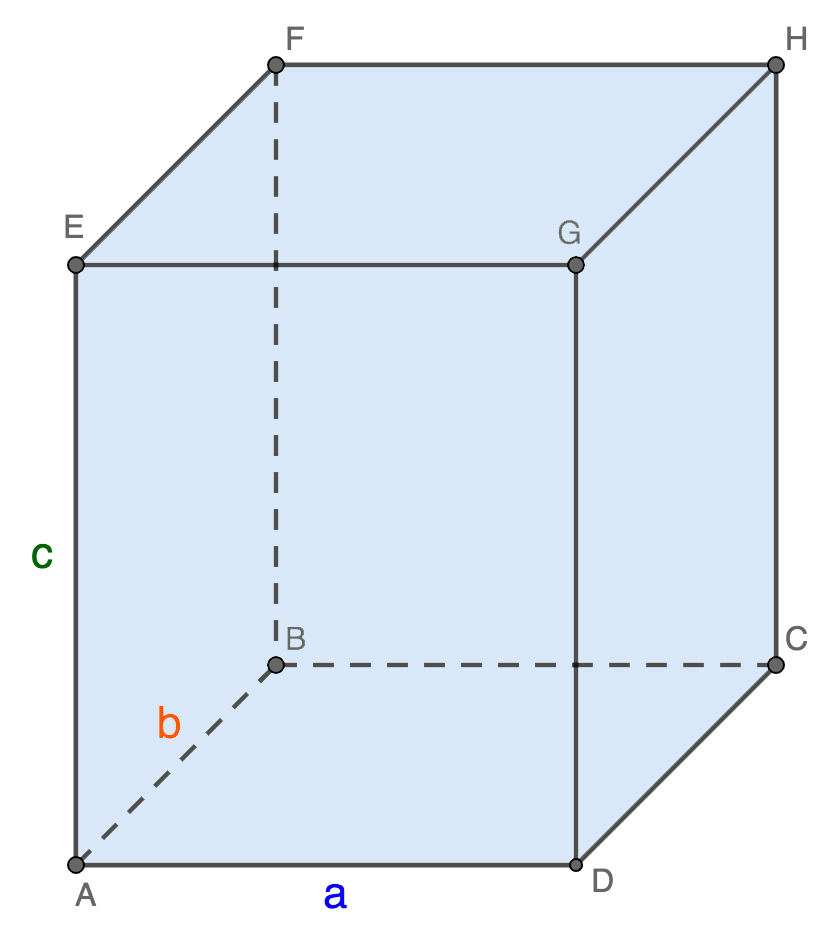
- Углы сонаправленных сторон равны между собой. На фотографии ниже представлено графическое изображение сонапрвленных лучей OA и O1А1. Прямая рассекает пространство на две плоскости. Если лучи расположены в одной полуплоскости и параллельны друг другу, то их называют сонаправленными.
- 4 главные диагонали параллелепипеда пересекаются в одной точке внутри фигуры. Любой отрезок, проведенный между двумя плоскостями граней, через данную точку будет поделен ею пополам. Следствием данного свойства можно сформулировать следующим образом: плоскости, в которых лежат главные диагонали параллелепипеда, симметрично делят геометрическое тело.
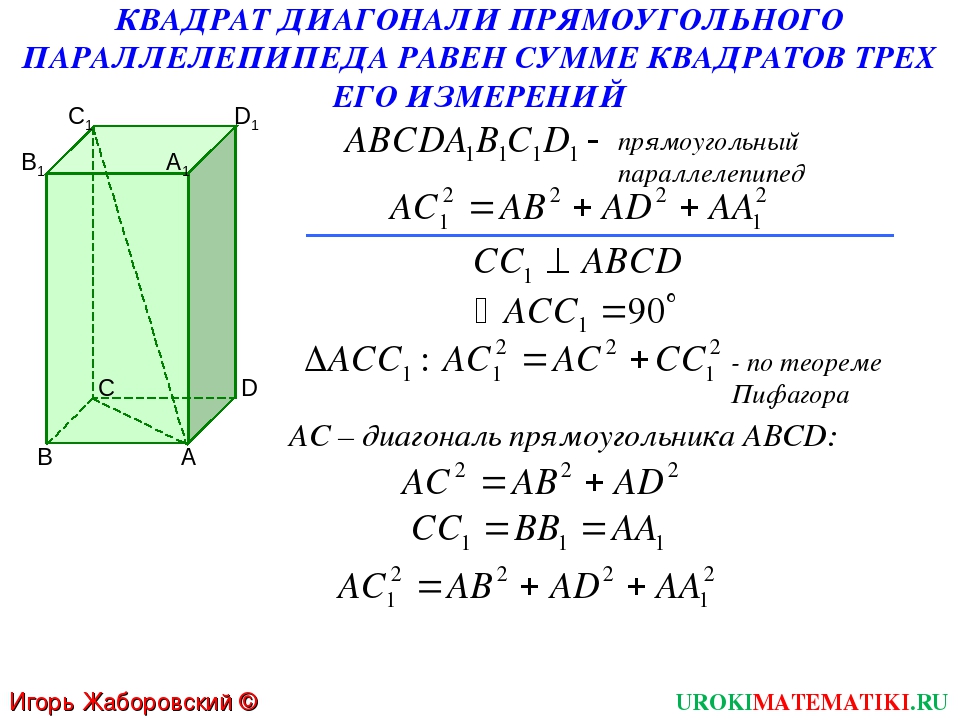
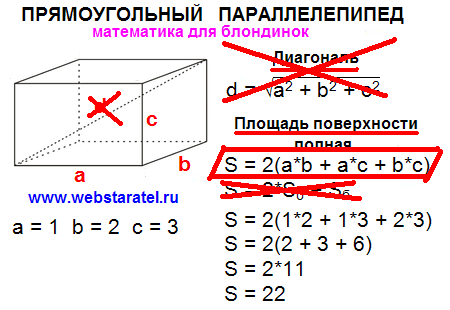
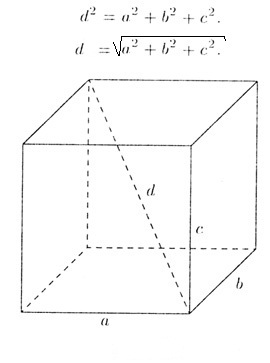
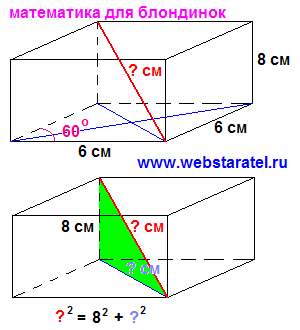
- Согласно теореме Пифагора, квадрат диагонали параллелепипеда равен сумме квадратов ее измерений.
Запомнить все приведенные свойства просто, они легки для понимания и выводятся логически исходя из вида и особенностей геометрического тела. Однако, незамысловатые утверждения могут быть невероятно полезны при решении типовых заданий ЕГЭ и позволят сэкономить время необходимое для прохождения теста.
Вред скандинавской ходьбы с палками
Вред может быть нанесен только в 2 случаях: если не соблюдать правильную технику (приведет к неверному распределению нагрузки) или заниматься при наличии медицинских ограничений. Этот любительский спорт имеет свои противопоказания:
- сердечная недостаточность с выраженной гипоксией;
- до 30 дней с момента перенесенного инфаркта и до 2 месяцев после инсульта;
- выраженный варикоз нижних конечностей, тромбофлебит;
- болезни легких с тяжелым течением, которые сопровождаются симптомами дыхательной недостаточности, либо объем легких снижен до 50%;
- острые вирусные и инфекционные заболевания;
- артериальная гипертензия;
- стенокардия;
- аритмия, сопровождающаяся учащенным сердечным ритмом.
При наличии данных заболеваний занятия финской ходьбой запрещены, т. к. они могут ухудшить состояние человека. Неправильная техника может привести к:
- повреждению связочного аппарата и суставов;
- чрезмерному перенапряжению мышц, после чего они еще долго будут болеть, могут появиться судороги и спазмы;
- нарушениям сердца и сосудистой системы вплоть до появления аритмии и усугубления сердечной ишемии;
- приступам головокружения, сильной усталости.
Чтобы не подвергать позвоночник и суставы чрезмерной нагрузке, необходимо постоянно следить за техникой выполнения
Особенно это важно делать новичкам, пока правильная поза и ритмичность движений не дойдут до автоматизма
Особые случаи по симметрии
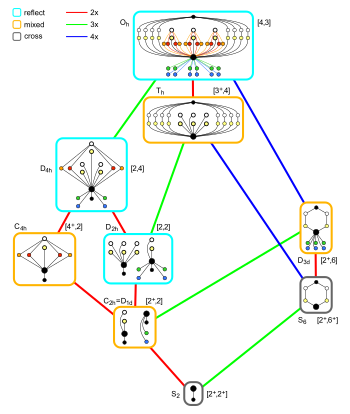 Отношения подгруппы октаэдрической симметрии с центром инверсии Отношения подгруппы октаэдрической симметрии с центром инверсии
|
 Частные случаи параллелепипеда Частные случаи параллелепипеда
|
| Форма | Куб | Квадратный кубоид | Тригональный трапецоэдр | Прямоугольный кубоид | Правая ромбическая призма | Правая параллелограммная призма | Косая ромбическая призма |
|---|---|---|---|---|---|---|---|
| Ограничения | азнак равнобзнак равноc{\ displaystyle a = b = c}αзнак равноβзнак равноγзнак равно90∘{\ Displaystyle \ альфа = \ бета = \ гамма = 90 ^ {\ circ}} | азнак равноб{\ displaystyle a = b}αзнак равноβзнак равноγзнак равно90∘{\ Displaystyle \ альфа = \ бета = \ гамма = 90 ^ {\ circ}} | азнак равнобзнак равноc{\ displaystyle a = b = c}αзнак равноβзнак равноγ{\ Displaystyle \ альфа = \ бета = \ гамма} | αзнак равноβзнак равноγзнак равно90∘{\ Displaystyle \ альфа = \ бета = \ гамма = 90 ^ {\ circ}} | азнак равноб{\ displaystyle a = b}αзнак равноβзнак равно90∘{\ Displaystyle \ альфа = \ бета = 90 ^ {\ circ}} | αзнак равноβзнак равно90∘{\ Displaystyle \ альфа = \ бета = 90 ^ {\ circ}} | азнак равноб{\ displaystyle a = b}αзнак равноβ{\ Displaystyle \ альфа = \ бета} |
| Симметрия | О ч порядка 48 | D 4ч порядка 16 | D 3d заказ 12 | D 2h порядка 8 | C 2h порядка 4 | ||
| Образ | |||||||
| Лица | 6 квадратов | 2 квадрата, 4 прямоугольника | 6 ромбов | 6 прямоугольников | 4 прямоугольника, 2 ромба | 4 прямоугольника, 2 параллелограмма | 2 ромба, 4 параллелограмма |
- Параллелепипед с симметрией O h известен как куб , имеющий шесть одинаковых квадратных граней.
- Параллелепипед с симметрией D 4h известен как квадратный кубоид , который имеет две квадратные грани и четыре совпадающие прямоугольные грани.
- Параллелепипед с симметрией D 3d известен как тригональный трапецоэдр , который имеет шесть конгруэнтных ромбических граней (также называемых изоэдральным ромбоэдром ).
- Для параллелепипедов с симметрией D 2h возможны два случая:
- Прямоугольный кубоид : у него шесть прямоугольных граней (также называемых прямоугольным параллелепипедом или иногда просто кубоидом ).
- Правая ромбическая призма : у нее две ромбические грани и четыре конгруэнтных прямоугольных грани.
-
-
- Примечание: частный случай полностью ромбической формы с двумя ромбическими гранями и четырьмя конгруэнтными квадратными гранями имеет то же имя и одну и ту же группу симметрии (D 2h , порядок 8).(азнак равнобзнак равноc){\ Displaystyle (а = Ь = с)}
-
- Для параллелепипедов с симметрией C 2h возможны два случая:
- Правая параллелограммная призма : у нее четыре прямоугольных грани и две параллелограммные грани.
- Косая ромбическая призма : у нее две ромбические грани, а из остальных граней две соседние равны, а две другие тоже (две пары являются зеркальным отображением друг друга).
Находка в куске угля
Зальцбургский параллелепипед был обнаружен 1 ноября 1885 года в Австрии в городе Шендорфе, когда истопник Рейдль фабрики Исидора Брауна расколол большой кусок угля и оттуда выпал странный металлический предмет. Находка напоминала по форме куб, который делила пополам глубокая бороздка. Найденный предмет владельцем фабрики был подарен музею Каролины Августы в Зальцбурге для подробного изучения.
Было выяснено, что бурый уголь для фабрики Брауна добывали на шахте Вольфзегге. Возраст пластов угля данной шахты составляет от 25 до 65 миллионов лет, следовательно, и возраст найденного артефакта не менее 25 миллионов лет.
Горный инженер Фридрих Адольф Гурльт заинтересовался находкой и выяснил, что его размеры составляли 67х62-47 мм и вес 785 грамм. Вся его поверхность была покрыта «чашечками», но особенно заинтересовала инженера бороздка по центру. Гурльт решил, что Зальцбургский параллелепипед является метеоритом, упавшем на Землю миллионы лет назад.
Объем
Параллелепипед, образованный тремя векторами
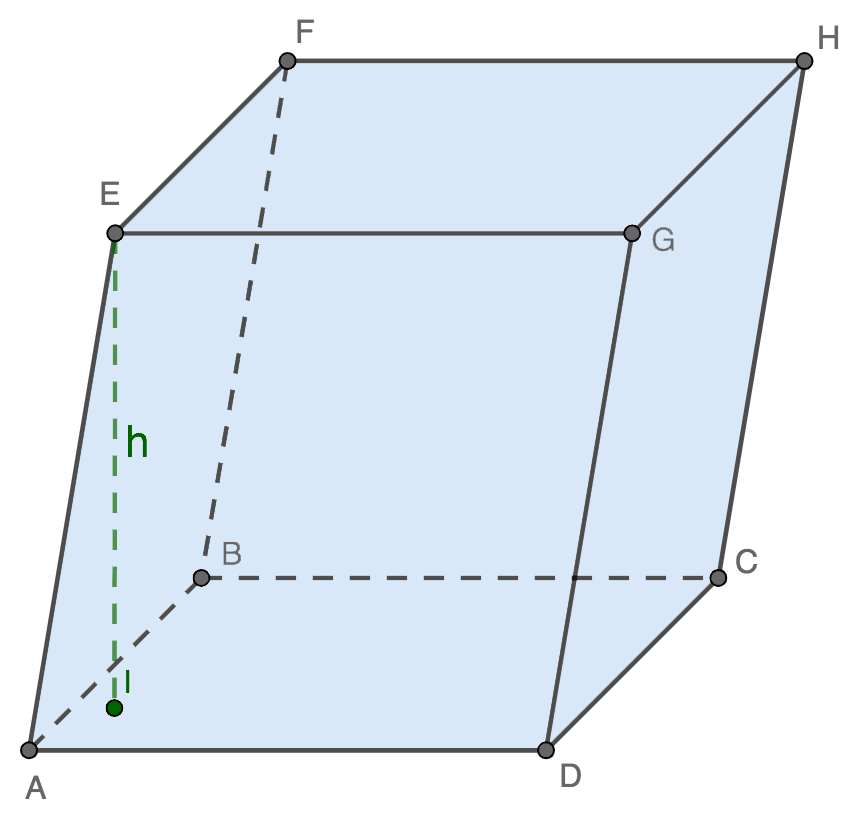
Параллелепипед можно рассматривать как наклонную призму с параллелограммом в качестве основания. Следовательно, объем параллелепипеда — это произведение площади основания и высоты (см. Диаграмму). С участием
V{\ displaystyle V}B{\ displaystyle B}час{\ displaystyle h}
- Bзнак равно|а→|⋅|б→|⋅грехγзнак равно|а→×б→| {\ displaystyle B = | {\ vec {a}} | \ cdot | {\ vec {b}} | \ cdot \ sin \ gamma = | {\ vec {a}} \ times {\ vec {b}} | ~}(где — угол между векторами и ), иγ{\ displaystyle \ gamma}а→{\ displaystyle {\ vec {a}}}б→{\ displaystyle {\ vec {b}}}
- часзнак равно|c→|⋅|потому чтоθ | {\ displaystyle h = | {\ vec {c}} | \ cdot | \ cos \ theta ~ | ~}(где угол между вектором и нормалью к основанию), получаем:θ{\ displaystyle \ theta}c→{\ displaystyle {\ vec {c}}}
- Vзнак равноB⋅часзнак равно(|а→||б→|грехγ)⋅|c→||потому чтоθ |знак равно|а→×б→| |c→| |потому чтоθ |знак равно|(а→×б→)⋅c→| .{\ displaystyle V = B \ cdot h = (| {\ vec {a}} || {\ vec {b}} | \ sin \ gamma) \ cdot | {\ vec {c}} || \ cos \ theta ~ | = | {\ vec {a}} \ times {\ vec {b}} | ~ | {\ vec {c}} | ~ | \ cos \ theta ~ | = | ({\ vec {a}} \ раз {\ vec {b}}) \ cdot {\ vec {c}} | ~.}
Смешанное произведение трех векторов называется тройным произведением . Это можно описать определителем . Следовательно, объем равен:
а→знак равно(а1,а2,а3)Т, б→знак равно(б1,б2,б3)Т, c→знак равно(c1,c2,c3)Т,{\ displaystyle {\ vec {a}} = (a_ {1}, a_ {2}, a_ {3}) ^ {T}, ~ {\ vec {b}} = (b_ {1}, b_ {2 }, b_ {3}) ^ {T}, ~ {\ vec {c}} = (c_ {1}, c_ {2}, c_ {3}) ^ {T},}
- (V1) .Vзнак равно|Detа1б1c1а2б2c2а3б3c3|{\ displaystyle \ quad V = \ left | \ det {\ begin {bmatrix} a_ {1} & b_ {1} & c_ {1} \\ a_ {2} & b_ {2} & c_ {2} \\ a_ {3} & b_ {3} & c_ {3} \ end {bmatrix}} \; \ right |}
Альтернативное представление объема использует только геометрические свойства (углы и длины кромок):
- (V2) ,Vзнак равноабc1+2потому что(α)потому что(β)потому что(γ)-потому что2(α)-потому что2(β)-потому что2(γ){\ displaystyle \ quad V = abc {\ sqrt {1 + 2 \ cos (\ alpha) \ cos (\ beta) \ cos (\ gamma) — \ cos ^ {2} (\ alpha) — \ cos ^ {2 } (\ beta) — \ cos ^ {2} (\ gamma)}}}
где и — длины ребер.
αзнак равно∠(б→,c→),βзнак равно∠(а→,c→),γзнак равно∠(а→,б→), {\ displaystyle \ \ alpha = \ angle ({\ vec {b}}, {\ vec {c}}), \; \ beta = \ angle ({\ vec {a}}, {\ vec {c}} ), \; \ gamma = \ angle ({\ vec {a}}, {\ vec {b}}), \}а,б,c{\ displaystyle a, b, c}
- Доказательство (V2)
Доказательство (V2) использует и :
Позвольте быть 3×3-матрицей, столбцы которой — векторы (см. Выше). Тогда верно следующее:
M{\ displaystyle M}а→,б→,c→{\ displaystyle {\ vec {a}}, {\ vec {b}}, {\ vec {c}}}
-
V2знак равно(DetM)2знак равноDetMDetMзнак равноDetMТDetMзнак равноDet(MТM){\ Displaystyle V ^ {2} = (\ Det M) ^ {2} = \ Det M \ Det M = \ Det M ^ {T} \ Det M = \ Det (M ^ {T} M)}
- знак равноDetа→⋅а→а→⋅б→а→⋅c→б→⋅а→б→⋅б→б→⋅c→c→⋅а→c→⋅б→c→⋅c→знак равно а2б2c2(1+2потому что(α)потому что(β)потому что(γ)-потому что2(α)-потому что2(β)-потому что2(γ)).{\ displaystyle = \ det {\ begin {bmatrix} {\ vec {a}} \ cdot {\ vec {a}} и {\ vec {a}} \ cdot {\ vec {b}} и {\ vec { a}} \ cdot {\ vec {c}} \\ {\ vec {b}} \ cdot {\ vec {a}} & {\ vec {b}} \ cdot {\ vec {b}} & {\ vec {b}} \ cdot {\ vec {c}} \\ {\ vec {c}} \ cdot {\ vec {a}} и {\ vec {c}} \ cdot {\ vec {b}} & {\ vec {c}} \ cdot {\ vec {c}} \ end {bmatrix}} = \ a ^ {2} b ^ {2} c ^ {2} \; \ left (1 + 2 \ cos ( \ alpha) \ cos (\ beta) \ cos (\ gamma) — \ cos ^ {2} (\ alpha) — \ cos ^ {2} (\ beta) — \ cos ^ {2} (\ gamma) \ right ).}
(Используется последний шаг )
а→⋅а→знак равноа2,…,а→⋅б→знак равноабпотому чтоγ,а→⋅c→знак равноаcпотому чтоβ,б→⋅c→знак равнобcпотому чтоα,…{\ displaystyle \ {\ vec {a}} \ cdot {\ vec {a}} = a ^ {2}, …, \; {\ vec {a}} \ cdot {\ vec {b}} = ab \ cos \ gamma, \; {\ vec {a}} \ cdot {\ vec {c}} = ac \ cos \ beta, \; {\ vec {b}} \ cdot {\ vec {c}} = bc \ cos \ alpha, …}
- Соответствующий тетраэдр
Объем любого тетраэдра, который имеет три сходящихся ребра параллелепипеда, равен одной шестой объема этого параллелепипеда (см. ).
Параллелотоп
Коксетер назвал обобщение параллелепипеда в высших измерениях параллелоэдром .
В частности, в n -мерном пространстве он называется n -мерным параллелоэдром или просто n -параллелоэдром. Таким образом, параллелограмм — это 2-параллелоэдр, а параллелепипед — это 3-параллелоэдр.
В более общем смысле параллелоэдр или параллелоэдр Вороного имеет параллельные и конгруэнтные противоположные грани. Итак, 2-параллелоэдр — это параллелогон, который также может включать в себя определенные шестиугольники, а 3-параллелоэдр — это параллелоэдр , включающий 5 типов многогранников.
В диагоналями из в п -parallelotope пересекаются в одной точке и делятся пополам этим пунктом. Инверсия в этой точке не меняет n -параллелоэдр. См. Также неподвижные точки групп изометрий в евклидовом пространстве .
Ребра, исходящие из одной вершины k -параллелоэдра, образуют k- каркас векторного пространства, и параллелоэдр можно восстановить из этих векторов, взяв линейные комбинации векторов с весами от 0 до 1.
(v1,…,vп){\ displaystyle (v_ {1}, \ ldots, v_ {n})}
П -VOLUME из п -parallelotope встроенное в котором может быть вычислено с помощью определителя Грама . В качестве альтернативы объем — это норма внешнего произведения векторов:
рм{\ Displaystyle \ mathbb {R} ^ {m}}м≥п{\ Displaystyle м \ geq п}
- Vзнак равно‖v1∧⋯∧vп‖.{\ Displaystyle V = \ left \ | v_ {1} \ wedge \ cdots \ wedge v_ {n} \ right \ |.}
Если m = n , это составляет абсолютное значение определителя n векторов.
Еще одна формула для вычисления объема с п -parallelotope Р в , которого п + 1 вершины , является
рп{\ Displaystyle \ mathbb {R} ^ {п}}V,V1,…,Vп{\ Displaystyle V_ {0}, V_ {1}, \ ldots, V_ {n}}
- Vол(п)знак равно|dет (V 1Т,V1 1Т,…,Vп 1Т)|,{\ Displaystyle {\ rm {Vol}} (P) = | {\ rm {det}} \ ( ^ {\ rm {T}}, ^ {\ rm {T}}, \ ldots, ^ {\ rm {T}}) |,}
где — вектор-строка, образованный конкатенацией и 1. Действительно, определитель не изменяется, если вычитается из ( i > 0 ), а размещение в последней позиции меняет только его знак.
Vя 1{\ displaystyle }Vя{\ displaystyle V_ {i}}V 1{\ displaystyle }Vя 1{\ displaystyle }V 1{\ displaystyle }
Кроме того , объем любого п — симплекс , который разделяет п сходящиеся ребра параллелепипеда имеет объем , равный единице 1 / п ! объема этого параллелоэдра.