Инерция и момент инерции: базовые сведения

Инерция, кинетическая энергия, работа

Приведем другой пример. Представь тяжелоатлета… Даже двух, которые решили поставить мировой рекорд и сдвинуть самолет. Им придется приложить немало сил, чтобы вначале разогнать самолет от нуля до некоторой скорости, а потом поддерживать эту скорость, преодолевая силу трения, направленную назад. Конечно, проще сдвинуть с места (преодолеть инерцию покоя) и разогнать до большой скорости тело меньшей массы, например, футбольный мяч. Инертность самолета во много раз больше инертности футбольного мяча.

Силачи тянут Ил-76

А к какому трюку прибегает фокусник, чтобы в случае со скатертью все предметы остались на столе? Правильно, нужно выдернуть скатерть за наименьшее время. Чем меньше время, тем меньше энергии перейдет с силой трения на предметы и они просто не успеют разогнаться.

Трюк со скатертью

Энергия движущегося тела называется кинетической энергией и измеряется в Джоулях. Если тело неподвижно, кинетическая энергия равна нулю.

Чтобы разогнать тело массой m до нужной скорости V из состояния покоя (например, самолет), нужно выполнить работу, равную кинетической энергии разогнанного тела (без учета разных потерь):

Работа по изменению кинетической энергии тела совершается за счет приложения к нему некоторой силы – силы тяжести, силы трения, силы воздействия на него другого тела (тяжелоатлета-силача, дующего ветра, реактивной тяги ракетного двигателя и пр.).

Пусть силач разогнал до 0.1 м/с (10 сантиметров в секунду) легковую машину массой 1200 кг и самолет Ил-76 массой 88 500 кг в космосе (не будем учитывать силу трения). Тогда для преодоления инерции этих тел ему пришлось сжечь мышечной энергии на 6 Дж и 442,5 Дж соответсвенно. Т.е. на преодоление инерции покоя у самолета у спортсмена уйдет в 74 раза больше энергии, чем на автомобиль.

Чтобы остановить тело массой m, движущееся со скоростью V, нужно совершить обратную работу, равную отрицательному значению кинетической энергии этого тела:

Т.е. чем больше скорость тела и его масса, тем больше энергии на преодоление инерции движения надо затратить.

Если выключить мотор, машина под действием силы трения ее движущихся частей друг о друга, силы трения о воздух корпуса и силы трения колес об асфальт остановится сама. Но остановить машину можно и быстрее, увеличив силу трения с помощью тормозных дисков, т.е. выжав педаль тормоза.

При равной скорости масса грузовика намного больше, а значит больше его кинетическая энергия. Двигаясь накатом грузовик остановится дальше, чем легковой автомобиль – его инертность выше. Кстати, можно ли остановить грузовик быстрее легкового автомобиля и при каких условиях?

Другие понятия об инерции

Хотелось бы завершить статью несколькими словами о других «инерциях», отличных от рассмотренного явления.

В той же физике существует понятие о температурной инерции, которая характеризует, насколько «трудно» нагреть или охладить данное тело. Температурная инерция прямо пропорциональна теплоемкости.

В более широком философском смысле инерция описывает сложность изменения какого-либо состояния. Так, инертным людям сложно начинать делать что-то новое из-за лени, привычки к рутинному образу жизни и удобству. Кажется, лучше оставить вещи такими, какие они есть, поскольку так жить гораздо проще…

Открытие инерции

Такое свойство тел открыл итальянский ученый Галилео Галилей. На основе своих экспериментов и рассуждений он утверждал: ежели тело не взаимодействует с иными телами, то оно либо пребывает в состоянии спокойствия, либо движется прямолинейно и равномерно. Его открытия вошли в науку как Закон инерции, однако более детально сформулировал его Рене Декарт, а уж Исаак Ньютон внедрил в свою систему законов.

Интересный факт: инерция, определение которой привел нам Галилей, рассматривалась еще в Древней Греции Аристотелем, но из-за недостаточного развития науки, точной формулировки приведено не было. Первый закон Ньютона гласит: существуют такие системы отсчета, относительно которых тело, которое движется поступательно, сохраняет свою скорость постоянной, если на него не действуют иные тела. Формула инерции в едином и обобщенном виде отсутствует, но ниже мы приведем множество иных формул, раскрывающих ее особенности.

Момент инерции в плоском движении твердого тела

Если механическая система вынуждена переместиться параллельный фиксированному самолету, то вращение тела в системе происходит вокруг перпендикуляра оси с этим самолетом. В этом случае момент инерции массы в этой системе — скаляр, известный как полярный момент инерции. Определение полярного момента инерции может быть получено, рассмотрев импульс, кинетическую энергию и законы Ньютона для плоского движения твердой системы частиц.

Если система частиц, собрана в твердое тело, то импульс системы может быть написан с точки зрения положений относительно ориентира R и абсолютных скоростей

где ω — угловая скорость системы и является скоростью.

Для плоского движения угловой скоростной вектор направлен вдоль вектора единицы, который перпендикулярен самолету движения. Введите векторы единицы от ориентира до пункта и вектор единицы так

Это определяет относительный вектор положения и скоростной вектор для твердой системы частиц, перемещающихся в самолет.

Примечание по взаимному продукту: Когда тело перемещается параллельный измельченному самолету, траектории всех пунктов в теле лежат в самолетах, параллельных этому измельченному самолету. Это означает, что любое вращение, которому подвергается тело, должно быть вокруг перпендикуляра оси к этому самолету. Плоское движение часто представляется, как спроектировано на этот измельченный самолет так, чтобы ось вращения появилась как пункт. В этом случае угловая скорость и угловое ускорение тела — скаляры и факт, что они — векторы вдоль оси вращения, проигнорирован. Это обычно предпочитается для введений в тему. Но в случае момента инерции, комбинация массы и геометрии извлекает выгоду из геометрических свойств взаимного продукта. Поэтому в этой секции в плоском движении угловая скорость и ускорение тела — векторный перпендикуляр к измельченному самолету, и взаимные операции по продукту совпадают с используемый для исследования пространственного движения твердого тела.

Угловой момент в плоском движении

Вектор углового момента для плоского движения твердой системы частиц дан

& = \sum_ {i=1} ^n \left (m_i\Delta r_i\mathbf {e} _i \times (\omega \Delta r_i\mathbf {t} _i + \mathbf {V}) \right) \\

& = \left (\sum_ {i=1} ^n m_i \Delta r_i^2\right) \omega \vec {k} + \left (\sum_ {i=1} ^n \left (m_i\Delta r_i\mathbf {e} _i\right) \right) \times\mathbf {V}. \\

Используйте центр массы C как ориентир так

и определите момент инерции относительно центра массы I как

тогда уравнение для углового момента упрощает до

Момент инерции о перпендикуляре оси к движению твердой системы и через центр массы известен как полярный момент инерции.

Для данной суммы углового момента уменьшение в момент инерции приводит к увеличению угловой скорости. Фигуристы могут изменить свой момент инерции, таща в их руках. Таким образом угловая скорость, достигнутая конькобежцем протянутыми руками, приводит к большей угловой скорости, когда руки втянуты из-за уменьшенного момента инерции.

Кинетическая энергия в плоском движении

Кинетическая энергия твердой системы частиц, перемещающихся в самолет, дана

Это уравнение расширяется, чтобы привести к трем условиям

Позвольте ориентиру быть центром массы C системы, таким образом, второй срок становится нолем, и введите момент инерции I, таким образом, кинетическая энергия дана

Момент инерции я — полярный момент инерции тела.

Законы Ньютона для плоского движения

Законы Ньютона для твердой системы частиц N, могут быть написаны с точки зрения проистекающей силы и вращающего момента в ориентире, чтобы привести

где обозначает траекторию каждой частицы.

Синематика твердого тела приводит к формуле для ускорения частицы с точки зрения положения и ускорения справочной частицы, а также углового скоростного вектора и углового вектора ускорения твердой системы частиц как,

Для систем, которые ограничены к плоскому движению, угловая скорость и угловые векторы ускорения направлены вдоль перпендикуляра к самолету движения, которое упрощает это уравнение ускорения. В этом случае векторы ускорения могут быть упрощены, введя векторы единицы от ориентира до пункта и векторы единицы, таким образом

Это приводит к проистекающему вращающему моменту на системе как

где, и векторный перпендикуляр единицы к самолету для всех частиц.

Используйте центр массы как ориентир и определите момент инерции относительно центра массы, тогда уравнение для проистекающего вращающего момента упрощает до

Параметр — полярный момент инерции движущегося тела.

Составной маятник

Составной маятник — тело, сформированное из собрания частиц или непрерывных форм, который вращается твердо вокруг центра. Его моменты инерции — сумма моменты инерции каждой из частиц, которая составлена из.

Естественная частота составного маятника зависит от его момента инерции,

где масса объекта, местное ускорение силы тяжести и расстояние от точки опоры до центра массы объекта. Измерение этой частоты колебания по маленьким угловым смещениям обеспечивает эффективный способ измерить момент инерции тела.

Таким образом, чтобы определить момент инерции тела, просто приостановите его от удобной точки опоры так, чтобы это качалось свободно в перпендикуляре самолета к направлению желаемого момента инерции, затем измерьте ее естественную частоту или период колебания , чтобы получить

где период (продолжительность) колебания (обычно усредняемый за многократные периоды).

Момент инерции тела о его центре массы, тогда вычислен, используя параллельную теорему оси, чтобы быть

где масса тела и расстояние от точки опоры до центра массы.

Момент инерции тела часто определяется с точки зрения его радиуса циркуляции, которая является радиусом кольца равной массы вокруг центра массы тела, у которого есть тот же самый момент инерции. Радиус циркуляции вычислен с момента тела инерции и массы как длина,

Центр колебания

Простой маятник, у которого есть та же самая естественная частота как составной маятник, определяет длину от центра до пункта, названного центром колебания составного маятника. Этот пункт также соответствует центру удара. Длина определена от формулы,

или

Маятник секунд, который предоставляет «тиканью» и «tock» высоких часов с маятником, занимает одну секунду, чтобы качаться поперек. Это — период двух секунд или естественная частота π радианов/секунда для маятника. В этом случае расстояние до центра колебания, может быть вычислено, чтобы быть

Заметьте, что расстояние до центра колебания маятника секунд должно быть приспособлено, чтобы приспособить различные ценности для местного ускорения силы тяжести. Маятник Кейтера, составной маятник, который использует эту собственность измерить местное ускорение силы тяжести и назван gravimeter.

Список трехмерных тензоров инерции

Этот список дан для главных осей каждого объекта.

Чтобы получить скалярные моменты инерции I, указанные выше, тензорный момент инерции I проецируется вдоль некоторой оси, определяемой единичным вектором n, в соответствии с формулой:

п⋅я⋅п≡пяяяjпj,{\ Displaystyle \ mathbf {n} \ cdot \ mathbf {I} \ cdot \ mathbf {n} \ Equiv n_ {i} I_ {ij} n_ {j} \ ,,}

где точки обозначают тензорное сжатие и используется соглашение Эйнштейна о суммировании . В приведенной выше таблице n будет единичным e _x , e _y , e _z для получения I _x , I _y , I _z соответственно.

Описание	Рисунок	Момент тензора инерции
Твердая сфера радиуса r и массы m		язнак равно25мр225мр225мр2{\ displaystyle I = {\ begin {bmatrix} {\ frac {2} {5}} mr ^ {2} & 0 & 0 \\ 0 & {\ frac {2} {5}} mr ^ {2} & 0 \\ 0 & 0 & { \ frac {2} {5}} мистер ^ {2} \ end {bmatrix}}}
Полая сфера радиуса r и массы m		язнак равно23мр223мр223мр2{\ displaystyle I = {\ begin {bmatrix} {\ frac {2} {3}} mr ^ {2} & 0 & 0 \\ 0 & {\ frac {2} {3}} mr ^ {2} & 0 \\ 0 & 0 & { \ frac {2} {3}} мистер ^ {2} \ end {bmatrix}}}
Твердый эллипсоид полуосей a , b , c и массы m		язнак равно15м(б2+c2)15м(а2+c2)15м(а2+б2){\ displaystyle I = {\ begin {bmatrix} {\ frac {1} {5}} m (b ^ {2} + c ^ {2}) & 0 & 0 \\ 0 & {\ frac {1} {5}} m (a ^ {2} + c ^ {2}) & 0 \\ 0 & 0 & {\ frac {1} {5}} m (a ^ {2} + b ^ {2}) \ end {bmatrix}}}
Правый круговой конус радиусом r , высотой h и массой m около вершины		язнак равно35мчас2+320мр235мчас2+320мр2310мр2{\ displaystyle I = {\ begin {bmatrix} {\ frac {3} {5}} mh ^ {2} + {\ frac {3} {20}} mr ^ {2} & 0 & 0 \\ 0 & {\ frac { 3} {5}} mh ^ {2} + {\ frac {3} {20}} mr ^ {2} & 0 \\ 0 & 0 & {\ frac {3} {10}} mr ^ {2} \ end {bmatrix }}}
Сплошной кубоид шириной w , высотой h , глубиной d и массой m		язнак равно112м(час2+d2)112м(ш2+d2)112м(ш2+час2){\ displaystyle I = {\ begin {bmatrix} {\ frac {1} {12}} m (h ^ {2} + d ^ {2}) & 0 & 0 \\ 0 & {\ frac {1} {12}} m (w ^ {2} + d ^ {2}) & 0 \\ 0 & 0 & {\ frac {1} {12}} m (w ^ {2} + h ^ {2}) \ end {bmatrix}}}
Тонкий стержень по оси y длиной l и массой m на конце		язнак равно13мл213мл2{\ displaystyle I = {\ begin {bmatrix} {\ frac {1} {3}} ml ^ {2} & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & {\ frac {1} {3}} ml ^ {2} \ end {bmatrix}}}
Тонкий стержень по оси y длиной l и массой m относительно центра		язнак равно112мл2112мл2{\ displaystyle I = {\ begin {bmatrix} {\ frac {1} {12}} ml ^ {2} & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & {\ frac {1} {12}} ml ^ {2} \ end {bmatrix}}}
Сплошной цилиндр радиуса r , высоты h и массы m		язнак равно112м(3р2+час2)112м(3р2+час2)12мр2{\ displaystyle I = {\ begin {bmatrix} {\ frac {1} {12}} m (3r ^ {2} + h ^ {2}) & 0 & 0 \\ 0 & {\ frac {1} {12}} m (3r ^ {2} + h ^ {2}) & 0 \\ 0 & 0 & {\ frac {1} {2}} г-н ^ {2} \ end {bmatrix}}}
Толстостенная цилиндрическая труба с открытыми концами, внутренним радиусом r ₁ , внешним радиусом r ₂ , длиной h и массой m		язнак равно112м(3(р22+р12)+час2)112м(3(р22+р12)+час2)12м(р22+р12){\ displaystyle I = {\ begin {bmatrix} {\ frac {1} {12}} m (3 (r_ {2} ^ {2} + r_ {1} ^ {2}) + h ^ {2}) & 0 & 0 \\ 0 & {\ frac {1} {12}} m (3 (r_ {2} ^ {2} + r_ {1} ^ {2}) + h ^ {2}) & 0 \\ 0 & 0 & {\ frac {1} {2}} m (r_ {2} ^ {2} + r_ {1} ^ {2}) \ end {bmatrix}}}

Аналогия с линейным импульсом

Теперь перейдем к тому же выводу, что был озвучен в конце предыдущего пункта, проведя аналогию между вращательным и поступательным движениями в физике. Как известно, последнее описывается следующей формулой:

Это простое выражение определяет импульс системы. Сравним его форму с таковой для момента импульса (см. верхнее выражение в предыдущем пункте). Мы видим, что величины v и ω имеют одинаковый смысл: первая характеризует скорость изменения линейных координат объекта, вторая — угловых координат. Поскольку обе формулы описывают процесс равномерного (равноуглового) движения, то величины m и I также должны иметь одинаковый смысл.

Теперь рассмотрим 2-й закон Ньютона, который выражается формулой:

Обращая внимание на форму записи нижнего равенства в предыдущем пункте, имеем подобную рассмотренной ситуацию. Момент силы M в его линейной представлении — это сила F, а линейное ускорение a полностью аналогично угловому dω/dt

И снова мы приходим к эквивалентности массы и момента инерции.

Какой смысл несет масса в классической механике? Она является мерой инерции: чем больше m, тем труднее сдвинуть предмет с места, а тем более придать ему ускорение. То же самое можно сказать и о моменте инерции применительно к движению вращения.

Что представляет собой инерция?

Под инерцией в физике понимают способность всех тел, обладающий массой, сохранять покоящееся состояние либо двигаться с одинаковой скоростью в одном и том же направлении. Если необходимо изменить механическое состояние тела, то приходится прикладывать некоторую внешнюю силу к нему.

В данном определении следует обратить внимание на два момента:

Во-первых, это вопрос состояния покоя. В общем случае такого состояния не существует в природе. Все в ней находится в постоянном движении. Тем не менее, когда мы едем в автобусе, то нам кажется, что водитель не двигается со своего места. В таком случае идет речь об относительности движения, то есть относительно пассажиров водитель находится в покое. Отличие между состояниями покоя и равномерного движения заключается лишь в системе отсчета. В примере выше пассажир в состоянии покоя относительно автобуса, в котором едет, но движется относительно остановки, которую проезжает.
Во-вторых, инерция тела пропорциональна его массе. Наблюдаемые нами объекты в жизни все имеют ту или иную массу, поэтому все они характеризуются некоторой инертностью.

Таким образом, инерция характеризует степень трудности изменения состояния движения (покоя) тела.

Не можем остановиться: момент импульса

Допустим, нам нужно остановить космический корабль с массой 40 т, который находится на околоземной орбите. Для этого потребуется затратить немалые усилия. Почему? Все дело во вращательном импульсе космического корабля.

В главе 9 подробно описывается понятие импульс материальной точки, который выражается следующей формулой:

где \( m \) — это масса, a \( v \) — скорость материальной точки.

По аналогии, при описании вращательного движения физики используют понятие вращательный импульс (который в русскоязычной научной литературе чаще называют моментом импульса материальной точки. — Примеч. ред.):

где \( l \) — это момент инерции, а \( \omega \) — угловая скорость материальной точки.

Момент импульса в системе СИ измеряется в кг·м2·с-1 (более подробно системы единиц измерения описываются в главе 2). Одним из наиболее важных свойств момента импульса является закон сохранения момента импульса.

Сохраняем момент импульса

Закон сохранения момента импульса гласит: момент импульса сохраняется, если равна нулю сумма всех моментов внешних сил. Этот закон проявляется во многих обыденных ситуациях. Например часто приходится видеть, как мастера фигурного катания на льду вращаются с широко разведенными в стороны руками, а затем резко приближают их к своему телу и сильно ускоряют свое вращение. Дело в том, что таким образом они уменьшают свой момент инерции и, согласно закону сохранения момента импульса, увеличивают свою угловую скорость. Зная начальную угловую скорость вращения фигуриста \( \omega_0 \) и его моменты инерции в позе с разведенными руками \( I_0 \) и в позе с сомкнутыми руками \( I_1 \), легко найти конечную угловую скорость \( \omega_1 \) по формуле:

Однако этот закон удобно использовать не только в таких простых ситуациях. Возвращаясь к примеру с космическим кораблем на околоземной орбите, следует отметить, что его орбита далеко не всегда является строго круглой. Чаще всего орбиты спутников Земли и других планет имеют эллиптическую форму. Поэтому без закона сохранения момента импульса было бы гораздо сложнее определять параметры их орбитального движения.

Пример закона сохранения момента импульса: вычисляем скорость спутника

Предположим, что космический корабль вращается на эллиптической орбите вокруг Плутона. Причем в самой близкой к Плутону точке орбиты спутник находится на расстоянии 6·106 м от центра Плутона и имеет скорость 9·103 м/с. Вопрос: какой будет скорость спутника в самой далекой точке эллиптической орбиты на расстоянии 2·107 м от центра Плутона?

Для ответа на этот вопрос нужно воспользоваться законом сохранения момента импульса, поскольку на спутник не действуют никакие внешние моменты сил (сила гравитационного притяжения направлена параллельно радиусу и не создает момента). Однако закон сохранения момента импульса нужно преобразовать так, чтобы вместо угловых скоростей в его формулировке фигурировали тангенциальные скорости.

Итак, рассмотрим формулу закона сохранения момента импульса:

где \( I_{бл} \) — это момент инерции спутника в самой близкой точке, \( I_{дал} \) — это момент инерции спутника в самой далекой точке, \( \omega_{бл} \) — угловая скорость спутника в самой близкой точке, а \( \omega_{дал} \) — угловая скорость спутника в самой далекой точке.

Предположим, что размеры спутника гораздо меньше расстояния до центра Плутона и спутник можно считать материальной точкой. Тогда его моменты инерции равны:

где \( r_{бл} \) — это расстояние от спутника до центра Плутона в самой близкой точке эллиптической орбиты, а \( r_{дал} \) — это расстояние от спутника до центра Плутона в самой далекой точке эллиптической орбиты.

Кроме того:

Подставляя все перечисленные соотношения в формулу закона сохранения момента импульса

получим:

Отсюда путем несложных алгебраических преобразований, получим:

Подставляя значения, получим:

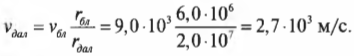
Итак, в ближайшей к Плутону точке орбиты спутник будет иметь скорость 9000 м/с, а в самой дальней — 2700 м/с. Этот результат мы легко получили только благодаря знанию закона сохранения момента импульса.

Вращательное движение

Приведенные выше примеры рассматривают явление инерции с точки зрения прямолинейного перемещения тела в пространстве. Однако существует еще один тип движения, который распространен в природе и Вселенной — это вращение вокруг точки или оси.

Масса тела характеризует его инерционные свойства поступательного движения. Для описания же аналогичного свойства, которое проявляет себя при вращении, вводят понятие момента инерции. Но перед тем как рассматривать эту характеристику, следует познакомиться с самим вращением.

Круговое перемещение тела вокруг оси или точки описывается двумя важными формулами. Ниже они приводятся:

В первой формуле L — это момент импульса, I — момент инерции, ω — угловая скорость. Во втором выражении α — это ускорение угловое, которое равно производной по времени от угловой скорости ω, M — момент силы системы. Он рассчитывается как произведение результирующей внешней силы на плечо, к которому она приложена.

Первая формула описывает вращательное движение, вторая — его изменение во времени. Как видно, в обеих этих формулах присутствует момент инерции I.

Тензор инерции и эллипсоид инерции

Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором s→=‖sx,sy,sz‖T,|s→|=1{\displaystyle {\vec {s}}=\left\Vert s_{x},s_{y},s_{z}\right\Vert ^{T},\left\vert {\vec {s}}\right\vert =1}, можно представить в виде квадратичной (билинейной) формы:

Is=s→T⋅J^⋅s→,{\displaystyle I_{s}={\vec {s}}^{T}\cdot {\hat {J}}\cdot {\vec {s}},\qquad } (1)

где J^{\displaystyle {\hat {J}}} — тензор инерции. Матрица тензора инерции симметрична, имеет размеры 3×3{\displaystyle 3\times 3} и состоит из компонент центробежных моментов:

J^=‖Jxx−Jxy−Jxz−JyxJyy−Jyz−Jzx−JzyJzz‖,{\displaystyle {\hat {J}}=\left\Vert {\begin{array}{ccc}J_{xx}&-J_{xy}&-J_{xz}\\-J_{yx}&J_{yy}&-J_{yz}\\-J_{zx}&-J_{zy}&J_{zz}\end{array}}\right\Vert ,}

Jxy=Jyx,Jxz=Jzx,Jzy=Jyz,{\displaystyle J_{xy}=J_{yx},\quad J_{xz}=J_{zx},\quad J_{zy}=J_{yz},\quad }Jxx=∫(m)(y2+z2)dm,Jyy=∫(m)(x2+z2)dm,Jzz=∫(m)(x2+y2)dm.{\displaystyle J_{xx}=\int \limits _{(m)}(y^{2}+z^{2})dm,\quad J_{yy}=\int \limits _{(m)}(x^{2}+z^{2})dm,\quad J_{zz}=\int \limits _{(m)}(x^{2}+y^{2})dm.}

Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора J^{\displaystyle {\hat {J}}}:

J^d=Q^T⋅J^⋅Q^,{\displaystyle {\hat {J}}_{d}={\hat {Q}}^{T}\cdot {\hat {J}}\cdot {\hat {Q}},}

J^d=‖JXJYJZ‖,{\displaystyle {\hat {J}}_{d}=\left\Vert {\begin{array}{ccc}J_{X}&0&0\\0&J_{Y}&0\\0&0&J_{Z}\end{array}}\right\Vert ,}

где Q^{\displaystyle {\hat {Q}}} — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины JX,JY,JZ{\displaystyle J_{X},J_{Y},J_{Z}} — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:

Is=JX⋅sx2+JY⋅sy2+JZ⋅sz2,{\displaystyle I_{s}=J_{X}\cdot s_{x}^{2}+J_{Y}\cdot s_{y}^{2}+J_{Z}\cdot s_{z}^{2},}

откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на Is{\displaystyle I_{s}}

(sxIs)2⋅JX+(syIs)2⋅JY+(szIs)2⋅JZ=1{\displaystyle \left({s_{x} \over {\sqrt {I_{s}}}}\right)^{2}\cdot J_{X}+\left({s_{y} \over {\sqrt {I_{s}}}}\right)^{2}\cdot J_{Y}+\left({s_{z} \over {\sqrt {I_{s}}}}\right)^{2}\cdot J_{Z}=1}

и произведя замены:

ξ=sxIs,η=syIs,ζ=szIs,{\displaystyle \xi ={s_{x} \over {\sqrt {I_{s}}}},\eta ={s_{y} \over {\sqrt {I_{s}}}},\zeta ={s_{z} \over {\sqrt {I_{s}}}},}

получаем канонический вид уравнения эллипсоида в координатах ξηζ{\displaystyle \xi \eta \zeta }:

ξ2⋅JX+η2⋅JY+ζ2⋅JZ=1.{\displaystyle \xi ^{2}\cdot J_{X}+\eta ^{2}\cdot J_{Y}+\zeta ^{2}\cdot J_{Z}=1.}

Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:

r2=ξ2+η2+ζ2=(sxIs)2+(syIs)2+(szIs)2=1Is.{\displaystyle r^{2}=\xi ^{2}+\eta ^{2}+\zeta ^{2}=\left({s_{x} \over {\sqrt {I_{s}}}}\right)^{2}+\left({s_{y} \over {\sqrt {I_{s}}}}\right)^{2}+\left({s_{z} \over {\sqrt {I_{s}}}}\right)^{2}={1 \over I_{s}}.}

Вычисляем момент инерции протяженного объекта

Момент инерции легко вычисляется для очень маленького (точечного) объекта, если все точки объекта расположены на одинаковом расстоянии от точки вращения. Например в предыдущем примере, если считать, что мячик для игры в гольф гораздо меньше длины нити, то все его точки находятся на одинаковом расстоянии от точки вращения, равном радиусу окружности вращения \( r \). В таком случае момент инерции имеет знакомый вид:

где \( r \) — это расстояние, на котором сосредоточена вся масса мячика \( m \).

Однако такая идеальная ситуация имеет место далеко не всегда. А чему равен момент инерции протяженного объекта, например стержня, вращающегося относительно одного из своих концов? Ведь его масса сосредоточена не в одной точке, а распределена по всей длине. Вообще говоря, для определения момента инерции протяженного объекта нужно просуммировать моменты инерции всех материальных точек объекта:

Например, момент инерции \( l \) системы из двух “точечных” мячиков для игры в гольф с одинаковой массой \( m \) на расстояниях \( r_1 \) и \( r_2 \) равен сумме их отдельных моментов инерции \( l_1=mr_1^2 \) и \( l_2=mr_2^2 \):

А как определить момент инерции диска, вращающегося относительно своего центра? Нужно мысленно разбить диск на множество материальных точек, вычислить момент инерции каждой такой точки и просуммировать полученные моменты инерции. Физики научились вычислять моменты инерции для многих объектов со стандартной формой. Некоторые из них приведены в табл. 11.1.

Попробуем вычислить моменты инерции нескольких предметов с простой геометрией.

Пример: замедление вращения компакт-диска

Компакт-диски могут вращаться с разными угловыми скоростями. Это необходимо для обеспечения одинаковой линейной скорости считывания информации на участках, находящихся на разных расстояниях от центра вращения. Пусть диск массой 30 г и диаметром 12 см сначала вращается со скоростью 700 оборотов в секунду, а спустя 50 минут — со скоростью 200 оборотов в секунду. Какой средний момент сил действует на компакт-диск при таком уменьшении скорости? Связь момента сил и углового ускорения имеет вид:

Момент инерции диска с радиусом \( r \), вращающегося относительно своего центра в плоскости диска, выражается формулой:

Подставляя значения, получим:

Теперь нужно определить угловое ускорение, которое определяется следующей формулой:

Изменение угловой скорости \( \Delta\omega \) произошло за промежуток времени:

В данном примере изменение угловой скорости:

где \( \omega_1 \) — конечная, а \( \omega_0 \) — начальная угловая скорость компакт-диска.

Чему они равны? Начальная скорость 700 оборотов в секунду означает, что диск за секунду 700 раз проходит \( 2\pi \) радиан:

Аналогично, конечная скорость 200 оборотов в секунду означает, что диск за секунду 200 раз проходит \( 2\pi \) радиан:

Подставляя значения в формулу углового ускорения, получим:

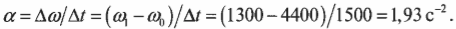
Подставляя значения момента инерции и углового ускорения в итоговую формулу момента силы, получим:

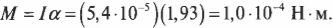
Итак, средний момент равен 10-4 Н·м, а чему будет равна сила для создания такого момента, если она приложена к краю диска? Ее величину легко вычислить по следующей формуле:

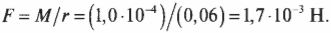
Оказывается, для такого замедления компакт-диска нужно приложить не такую уж и большую силу.

Еще один пример: поднимаем груз

Вращательное движение порой внешне выглядит не так очевидно, как вращение ком- пакт-диска. Например подъем груза с помощью блока также является примером вращательного движения. Хотя канат и груз движутся поступательно, но сам блок вращается (рис. 11.2). Пусть радиус блока равен 10 см, его масса равна 1 кг, масса груза равна 16 кг, а к веревке прилагается сила 200 Н. Попробуем вычислить угловое ускорение блока.

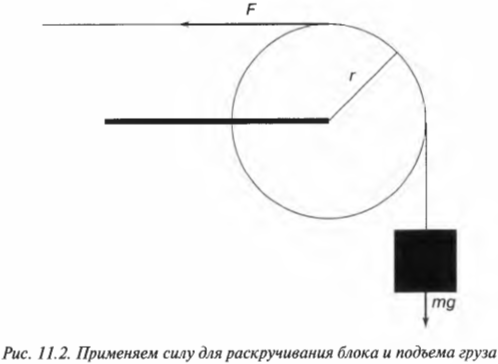
В данном примере нужно вычислить сумму всех моментов сил \( \mathbf{\sum\! M} \), которые действуют на веревку:

В данном примере на веревку действует два момента сил: один \( M_1 \) со стороны груза весом \( mg \), а другой \( M_2 \) — со стороны горизонтальной силы \( F \):

Отсюда получаем формулу для углового ускорения:

Эти моменты \( M_1 \) и \( M_2 \) имеют одинаковое плечо, равное радиусу блока \( r \), поэтому:

Поскольку блок имеет форму диска, то из табл. 11.1 находим его момент инерции:

Подставляя выражения для \( l \), \( M_1 \) и \( M_2 \) в формулу для углового ускорения, получим:

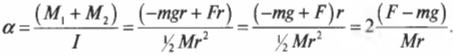
Подставляя значения, получим:

Момент инерции

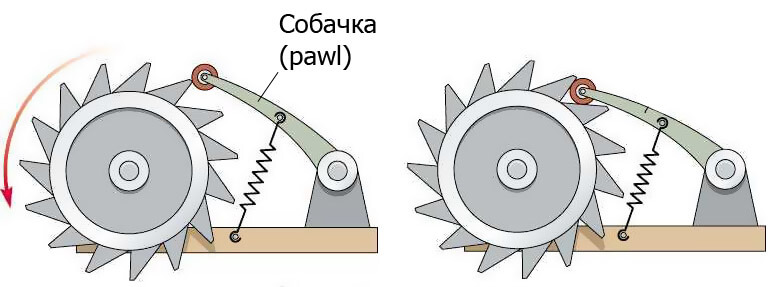
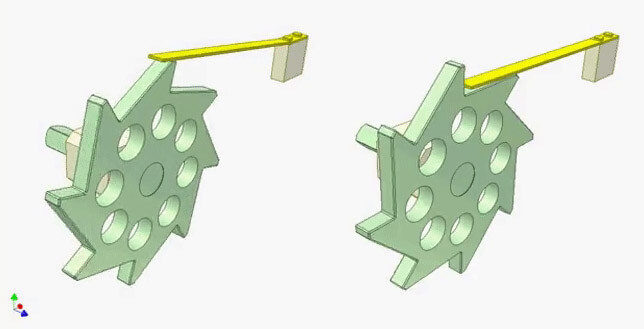
Инерция проявляется не только для прямолинейного движения, но и при вращении тел. В двигателе есть специальное устройство – маховик (на рисунке справа маховик покрашен темно-серым цветом и имеет зубчики). Инерция его вращения помогает работать двигателю нормально. Энергия расширяющихся газов при воспламенении топлива толкает поршень вниз, а затем ему нужно идти вверх, выталкивая продукты сгорания. Без маховика поршень не смог бы провернуть коленвал без рывков. Двигатель без маховика заглохнет.

Ну а со спинерами и волчками знакомы многие.

Вот только в приведенных примерах форма тела не меняется. А изменится ли инертность тела при изменении его формы?

Вращение на фигурном катании

Многие могут вспомнить фигурное катание. Масса тела фигуриста за выступление не меняется. Но его скорость вращения мгновенно увеличивается, стоит прижать руки и ноги, и вытянуться в струнку. Т.е. при уменьшении радиуса тела скорость вращения увеличивается. Т.е. инертность тела должна уменьшиться? Давайте разбираться.

Вернемся к формулам. Скорость вращающегося тела описывается как произведение угловой скорости (омега) на радиус:

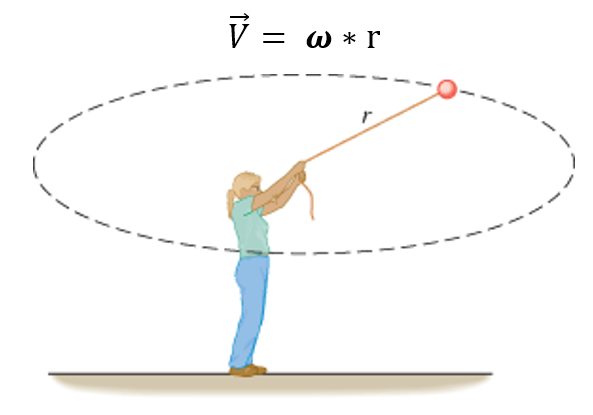Скорость вращающегося тела

При этом кинетическая энергия вращающегося тела примет вид:

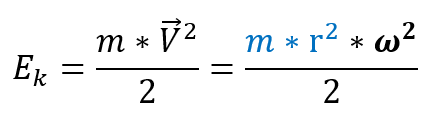
Синим цветом выделено произведение массы тела на радиус в квадрате. Эта величина называется моментом инерции вращающегося тела и обозначается латинской буквой I (и).

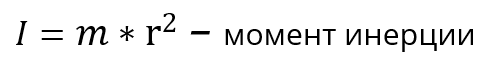
Мерой инертности вращающего тела выступает момент инерции, который зависит от массы тела и расстояния этой массы от центра вращения.

Представим, что девочка не только вращает груз над собой, но и идет. Тогда полная кинетическая энергия девочки с грузом примет вид:

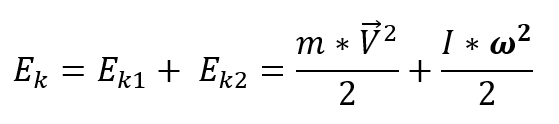
Первая часть описывает кинетическую энергию двигающейся прямолинейно с некоторой скоростью девочки с грузом, а вторая – кинетическую энергию вращающегося груза. Полная кинетическая энергия — это сумма энергии прямолинейно движущегося тела и энергии вращающегося тела. Точно так же кинетическая энергия будет рассчитываться для движущегося по столу раскрученного волчка или съезжающего с наклонной плоскости цилиндра.

Так как вращающееся тело может иметь форму, отличную от точки или маленького шарика, то и формула момента инерции для более точных расчетов может принимать разный вид.

Некоторые формулы для расчета момента инерции для тел разной формы

Пример.

Цилиндры одинаковой массы (m1 = m2), но разного радиуса (r₁ < r₂), скатываются с горки высотой h. Какой цилиндр скатится быстрее? Какое из тел обладает меньшей инертностью?

Цилиндры одинаковой массы, но разного радиуса, скатываются с горки высотой h

В верхней точке кинетическая энергия обоих цилиндров будет равна нулю, так как скорость равна нулю. Потенциальная энергия будет одинаковой и максимальной.

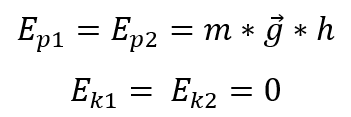Потенциальная и кинетическая энергия 1 и 2 цилиндра верхней точке

При скатывании цилиндров по закону сохранения энергии потенциальная энергия переходит в кинетическую и в самой нижней точке будет равна нулю, так как высота равна нулю. А кинетическая энергия в нижней точке будет складываться из поступательной кинетической энергии и кинетической энергии вращающегося тела и у обоих тел также будет одинаковой, так как их потенциальные энергии были равны.

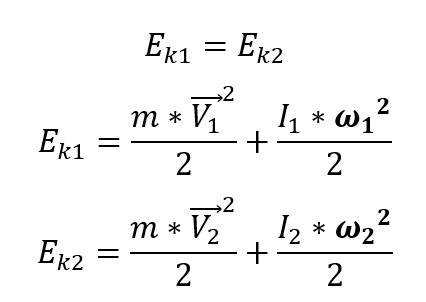Кинетическая энергия первого и второго цилиндра в нижней точке

Но так как радиус первого тела меньше второго, то и момент инерции первого тела меньше второго и будет справедливо:

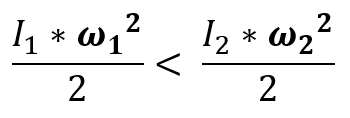
Тогда для кинетической энергии поступательного движения будет справедливо отношение:

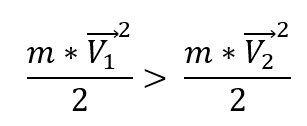
Следовательно, скорость первого цилиндра должна быть выше скорости второго, и он скатится быстрее. Так как мерой инертности вращающегося тела является момент инерции, то первое тело с меньшим радиусом и меньшим моментом инерции будет обладать меньшей инертностью, чем второе. Разогнаться под действием каких-либо сил (силы тяжести) такому телу проще.

Момент инерции диска однородного

Полученные в предыдущем пункте знания применимы для расчета момента инерции однородного цилиндра, который в случае h<r принято называть диском (h — высота цилиндра).

Для решения поставленной задачи достаточно рассчитать интеграл по объему этого тела. Выпишем исходную формулу:

Если ось вращения проходит перпендикулярно плоскости диска через его центр, тогда можно представить этот диск в виде нарезанных мелких колечек, толщина каждого из них является очень малой величиной dr. В этом случае объем такого колечка можно рассчитать так:

Это равенство позволяет интеграл по объему заменить на интегрирование по радиусу диска. Имеем:

Вычисляя первообразную подынтегрального выражения, а также учитывая, что интегрирование проводится по радиусу, который изменяется от 0 до r, получаем:

Поскольку масса рассматриваемого диска (цилиндра) равна:

то получаем конечное равенство:

Эта формула момента инерции диска справедлива для абсолютно любого цилиндрического однородного тела произвольной толщины (высоты), ось вращения которого проходит через его центр.

Инерция и момент инерции: базовые сведения

Инерция, кинетическая энергия, работа

Другие понятия об инерции

Открытие инерции

Момент инерции в плоском движении твердого тела

Угловой момент в плоском движении

Кинетическая энергия в плоском движении

Законы Ньютона для плоского движения

Составной маятник

Центр колебания

Список трехмерных тензоров инерции

Аналогия с линейным импульсом

Что представляет собой инерция?

Не можем остановиться: момент импульса

Сохраняем момент импульса

Пример закона сохранения момента импульса: вычисляем скорость спутника

Вращательное движение

Тензор инерции и эллипсоид инерции

Вычисляем момент инерции протяженного объекта

Пример: замедление вращения компакт-диска

Еще один пример: поднимаем груз

Момент инерции

Рекомендованная литература и полезные ссылки

Момент инерции диска однородного