Ось абсцисс

Системы координат

Название оси абсцисс относится к системам координат. На самом деле в мире используется две системы, хотя привычной для нас является декартова система координат.

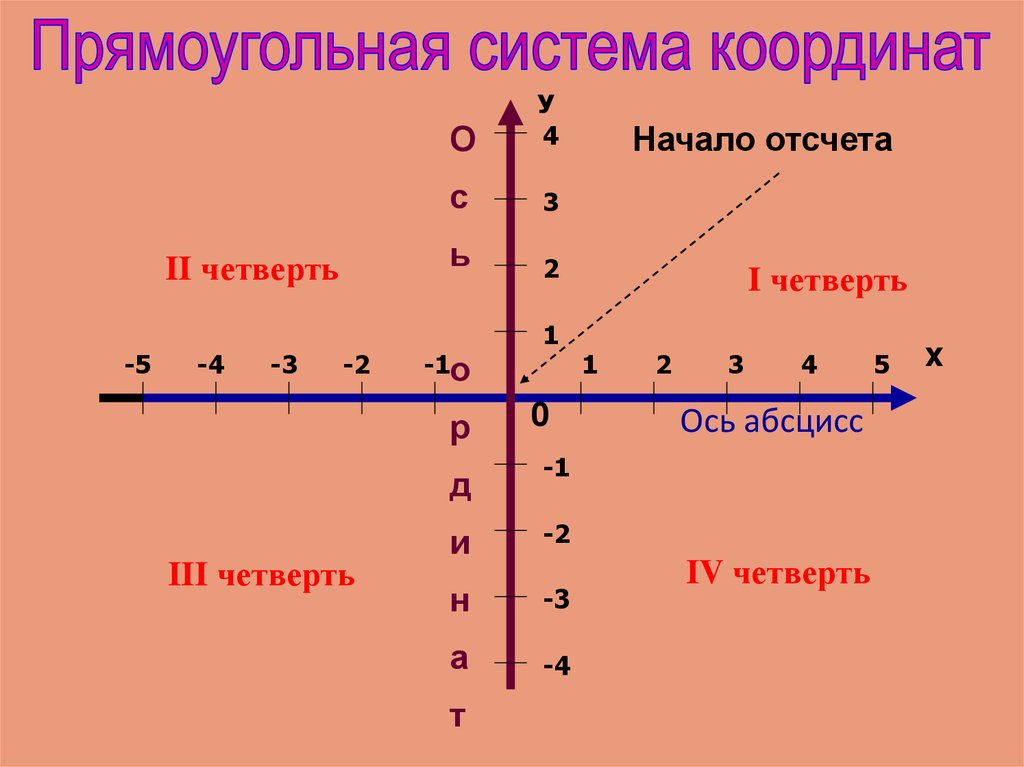
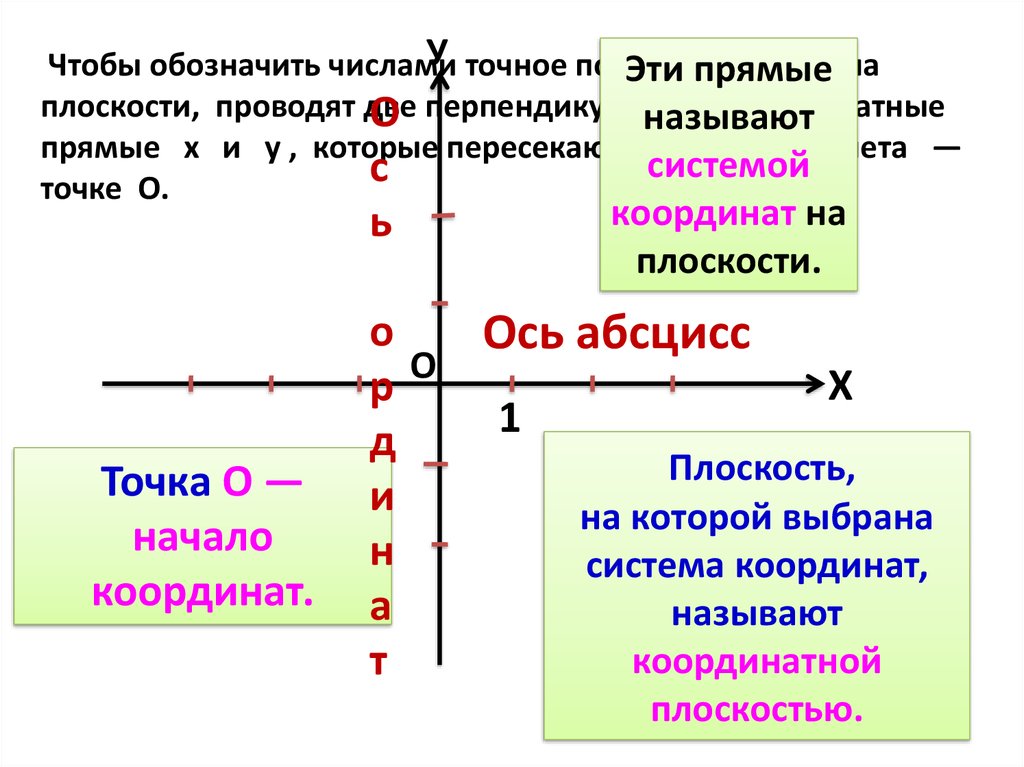
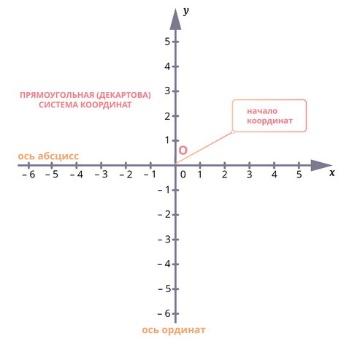
Плоская декартова система координат состоит из двух взаимно перпендикулярных отрезков. Точка пересечения отрезков считается началом отчета. На каждом из отрезков обозначается единичный отрезок и направление движения.

Каждый из перпендикулярных отрезков называется осью. Единичный отрезок у каждой из осей может быть разным. Направления задаются, как правило, традиционно: вверх и вправо. Но иногда составители задач пытаются подловить учеников на этом и делают другие направления в системе. Поэтому, нужно быть крайне внимательным при работе с чужой системой координат.

Еще одной системой координат называется полярной. Если в декартовой системе для того, чтобы определить местоположение точки нужно знать две ее координаты, то в полярной системе нужно знать координату и угол подъема. Этой системой пользовались в древность, сегодня от нее почти отказались из-за излишней сложности.

Отрывок, характеризующий Абсцисса

абсцисса это x
абсцисса это хордината у
Я эту тему прохожу в 6-ом классе и ты наверное тоже, но судя по тому, что этот вопрос решн 5 лет назад я сделал вывод что в 11 классе. Спасибо за такой простой и понятный ответ (лучший)!

В прямоугольной системе координат ось YY называется осью ординат.

При построении графиков функций, ось ординат обычно используется как область значений функции.

Рисунок тут

Легко запомнить, если трудно: «Ах» и «Оу»
Коротко и ясно и не надо читать, а просто смотри и слушай! Что такое ордината? https://www.youtube.com/watch?v=M9v-9dwIUuY Что такое абсцисса? https://www.youtube.com/watch?v=dPZ6QUtveH8

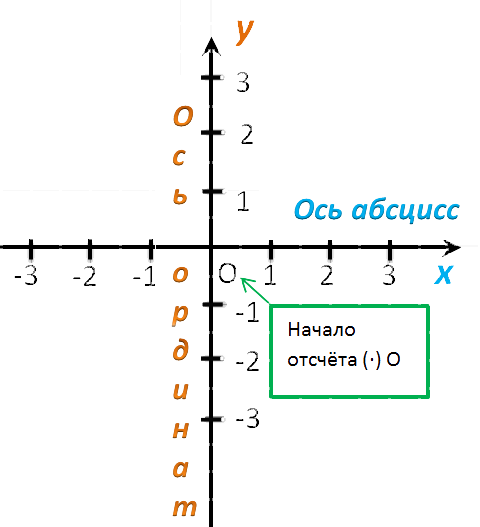
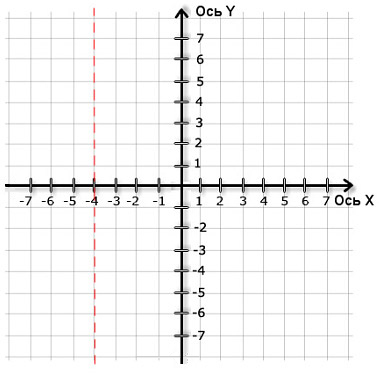
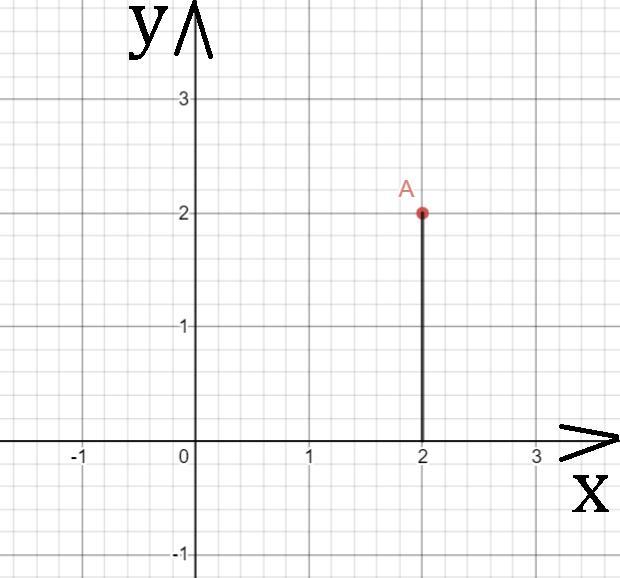
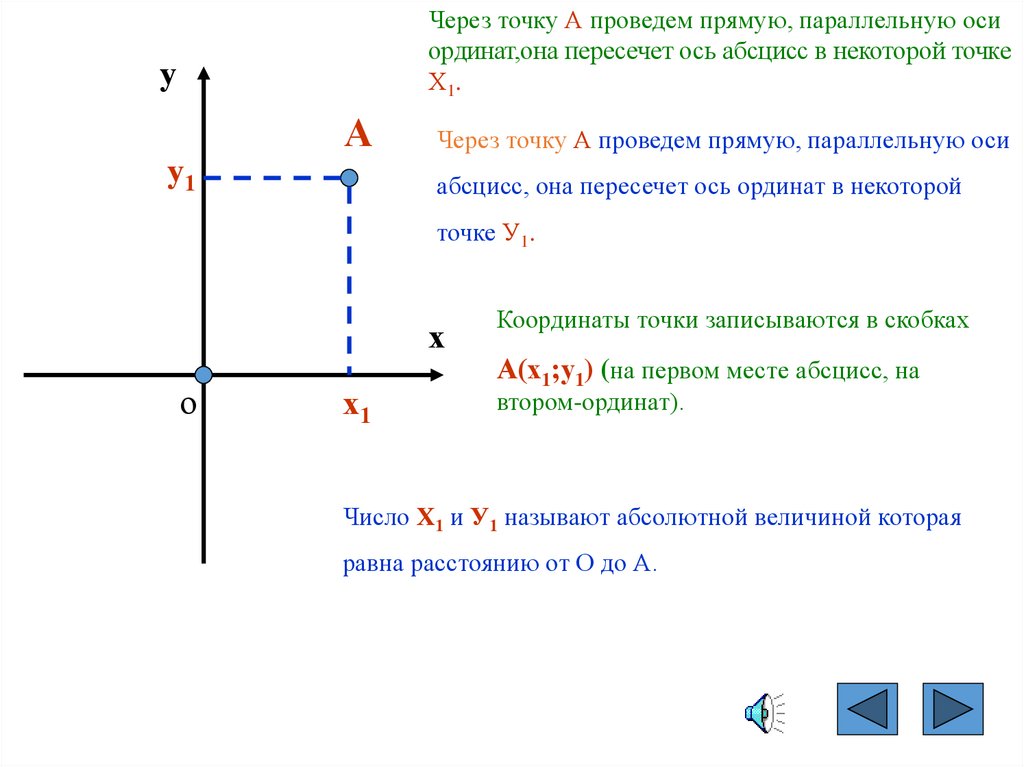
Абсциссой (лат. abscissa отрезок) точки A называется координата этой точки на оси XX в прямоугольной системе координат. Величина абсциссы точки A равна длине отрезка OB (см. рис. 1). Если точка B принадлежит положительной полуоси OX, то абсцисса имеет положительное значение. Если точка B принадлежит отрицательной полуоси XO, то абсцисса имеет отрицательное значение. Если точка A лежит на оси YY, то е абсцисса равна нулю.

В прямоугольной системе координат ось XX называется осью абсцисс.

При построении графиков функций, ось абсцисс обычно используется как область определения функции.

Ординатой (от лат. ordinatus — расположенный в порядке) точки A называется координата этой точки на оси YY в прямоугольной системе координат. Величина ординаты точки A равна длине отрезка OC (см. рис. 1). Если точка C принадлежит положительной полуоси OY, то ордината имеет положительное значение. Если точка C принадлежит отрицательной полуоси YO, то ордината имеет отрицательное значение. Если точка A лежит на оси XX, то е ордината равна нулю.

Оси декартовой системы

Вот мы и подошли к главному вопросу. Ось х имеет название оси абсцисс. Название это происходит от латинского «отрезок». Ось названа так потому, что отслеживает движение точки по горизонтали.

Вторая ось называется осью ординат, от латинского «порядок, движение по порядку». Имеется в виду, что эта координата отслеживает порядок движения вверх. Такая уж была логика у математиков древности.

Секрет в том, что названия осей можно менять как угодно, но оси все равно будут зваться осью абсцисс и осью ординат. Вне зависимости от буквенного обозначения осей, единичных отрезков и начала отсчета.

Что мы узнали?

Мы поговорили о системах координат. Выделили полярную и декартову систему. Отдельно обсудили декартову систему. Поговорили об обязательных характеристиках системы координат: единичный отрезок, направление осей, начало отсчета. Выяснили, что такое ось абсцисс. Поговорили о том, почему именно такое название получила каждая из осей.

Вопрос 1 из 5

Начать тест(новая вкладка)

Оси координат

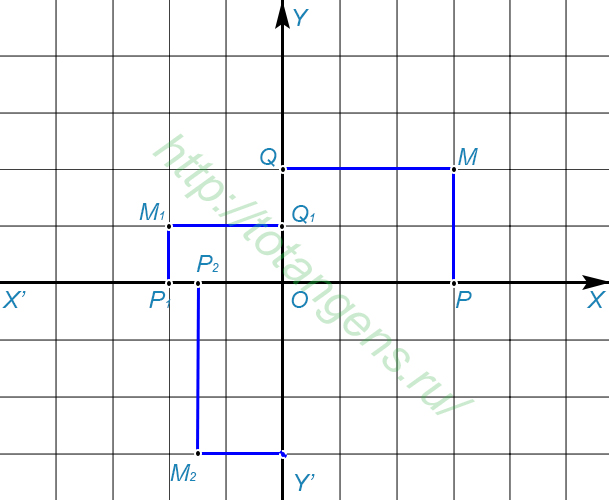
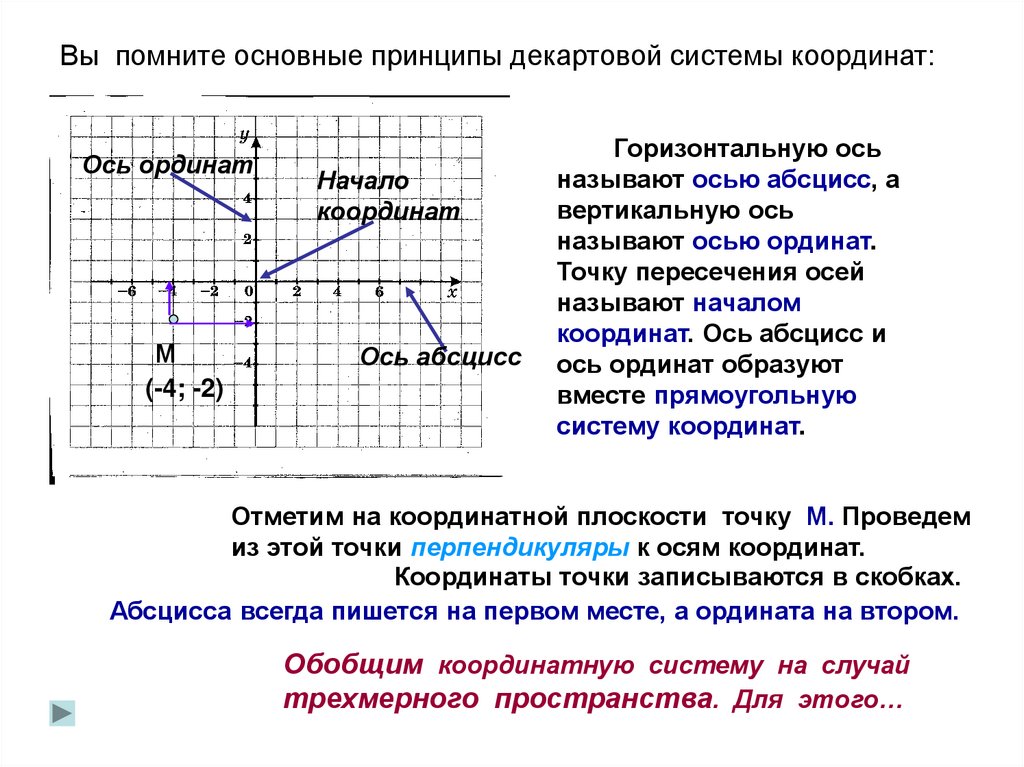
Оси координат это основа системы. Чтобы узнать координаты какой-либо точки, нужно опустить перпендикуляры на каждую из осей. Отрезки, заключенные между точкой отчета и точкой пересечения оси с перпендикуляром зовутся проекциями точки на оси. Размер этих проекций, выраженный в единичных отрезках, и есть координаты точки.

Традиционно оси называют переменными х и у. Это связано с традиционной записью функций, которые часто в виде графиков переносятся на ось координат. Например, функция у=х+3 – прямая линия. При этом сразу понятно, что если подставить любое число вместо х, то можно получить соответствующее значение у. Так высчитывают координаты точки в составе графика.

По факту оси можно называть как угодно. Это зависит только от ученика, решающего задачу. А названия абсцисс и ординат сохраняется всегда.

Осью абсцисс зовется ось х. Она отвечает за отслеживание горизонтальных перемещений точки. В переводе с латинского языка «абсцисса» переводится как «отрезок».

Если говорить кратко о оси ординат, то так зовется ось у. Эта ось отвечает за перемещения по вертикали. Если точка поднимается или опускается, это можно отследить по изменению ординаты. Ордината переводится как порядок.

Если воспользоваться переводом, то можно сказать так: чтобы отметить точку в системе координат, нужно отложить отрезок по горизонтали, равный абсциссе и поднять точку на несколько порядков вверх по ординате. Так проще запомнить правильные названия осей.

Что мы узнали?

Мы поговорили о Декартовой системе координат. Узнали, зачем нужно использовать правильные названия осей. Поговорили о том, что такое абсцисса и ордината. Выяснили, почему чаще всего оси обозначаются х и у. Сказали о том, что традиционное обозначение может быть заменено в любой момент.

Тест по теме

Вопрос 1 из 5

Начать тест(новая вкладка)

Системы координат

Ось — абсцисса

Ось абсцисс разделена на 100 равных частей.

Ось абсцисс разбивают на некоторое число шагов с равными или неравными интервалами. В пределах каждого шага функцию считают постоянной. Осреднение проводят по равенству площадей трапеции и прямоугольника для каждого шага. Среднее значение ординаты на каждом шаге проецируют на ось ординат и полученные точки соединяют с левым концом выбранного отрезка интегрирования, расположенного вдоль оси абсцисс влево от начала координат.

Ось абсцисс разбивает плоскость на две полуплоскости. Принято полуплоскость у 0 называть верхней полуплоскостью, а полуплоскость у С 0 — нижней полуплоскостью.

Оси абсцисс и ординат ( рис. 6.1.2) являются осями наработки г. По оси абсцисс откладывается наработка электрооборудования так, если бы оно работало в нормативных условиях эксплуатации, а по оси ординат скорректированное значение наработки с учетом условий эксплуатации.

Ось абсцисс ( концентрационная) на этом рисунке двойная: содержание углерода и содержание цементита.

Оси абсцисс смещены таким образом, что линии, соответствующие однородной прецессии, на всех пяти записях находятся на одной вертикали.

Кривая результирующей м. д. с. обмотки. а — расположение про.

Ось абсцисс должна быть проведена так, чтобы площади кривой по обе стороны оси были равны, так как поток полюса одной полярности должен быть равен потоку полюса другой полярности.

Ось абсцисс разбивают на некоторое число шагов с равными или неравными интервалами. В пределах каждого шага функцию считают постоянной. Осреднение проводят по равенству площадей трапеций и прямоугольника для каждого шага. Среднее значение ординаты на каждом шаге проецируют на ось ординат и полученные точки соединяют с левым концом выбранного отрезка интегрирования, расположенного вдоль оси абсцисс влево от начала координат.

Ось абсцисс разбивают на некоторое число шагов с равными или неравными интервалами. В пределах каждого шага функцию считают постоянной. Осреднение проводят по равенству площадей трапеции и прямоугольника для каждого шага. Среднее значение ардинаты на каждом шаге проецируют на ось ординат и полученные точки соединяют с левым концом выбранного отрезка интегрирования, расположенного вдоль оси абсцисс влево от начала координат.

Ось абсцисс, на которой откладывается суммарный объем поглощенного в процессе восстановления водорода, разбивается на три равных участка, на которых изображена кинетика восстановления нитробензола; на втором и третьем участках — кинетика восстановления нитрозобензола и на третьем участке — кинетика восстановления фенилгидроксиламина. Аналогично расположены кривые эдс.

Ось абсцисс — число эквивалентов основания, приходящееся на 1 моль фосфорной кислоты.

Ось абсцисс, на которой откладываются молярные доли компонентов смеси, ограничена отрезком ОО, равным 1, и дает состав и жидкои и паровой фазы.

Оси абсцисс и ординат графика вычерчиваются сплошными линиями без стрелок на концах. Иногда, когда это необходимо, графики снабжаются координатной сеткой, соответствующей целесообразно выбранному масштабу. Вместо сетки можно просто нанести масштаб короткими штрихами на оси координат. Исключение составляют графики, ось абсцисс или ось ординат которых служит общей шкалой для двух величин. Следует избегать дробных значений масштабных делений по осям координат.

Ось абсцисс ( частот) представлена в логарифмическом масштабе, а ось ординат, после соответствующего пересчета амплитуда сигнала ( дБ) — давление ( Па), в реальных единицах давления.

Отрывок, характеризующий Абсцисса

Если вы находитесь в некоторой нулевой точке и размышляете над тем, сколько единиц расстояния
нужно пройти строго вперёд, а затем — строго вправо, чтобы оказаться в некоторой другой точке, то вы
уже пользуетесь прямоугольной декартовой системой координат на плоскости. А если точка находится выше
плоскости, на которой вы стоите, и к вашим расчётам добавляется подъём к точке по лестнице строго вверх
также на определённое число единиц расстояния, то вы уже пользуетесь прямоугольной декартовой системой
координат в пространстве.

Упорядоченная система двух или трёх
пересекающихся перпендикулярных друг другу осей с общим началом отсчёта (началом координат) и общей единицей длины называется
прямоугольной декартовой системой координат

.

С именем французского математика Рене Декарта
(1596-1662) связывают прежде всего такую систему координат, в которой на всех осях отсчитывается
общая единица длины и оси являются прямыми. Помимо прямоугольной существует общая декартова система координат

(аффинная система координат
). Она может включать и
не обязательно перпендикулярные оси. Если же оси перпендикулярны, то система координат является
прямоугольной.

Прямоугольная декартова система координат на плоскости

имеет
две оси, а прямоугольная декартова система координат в пространстве

— три оси.
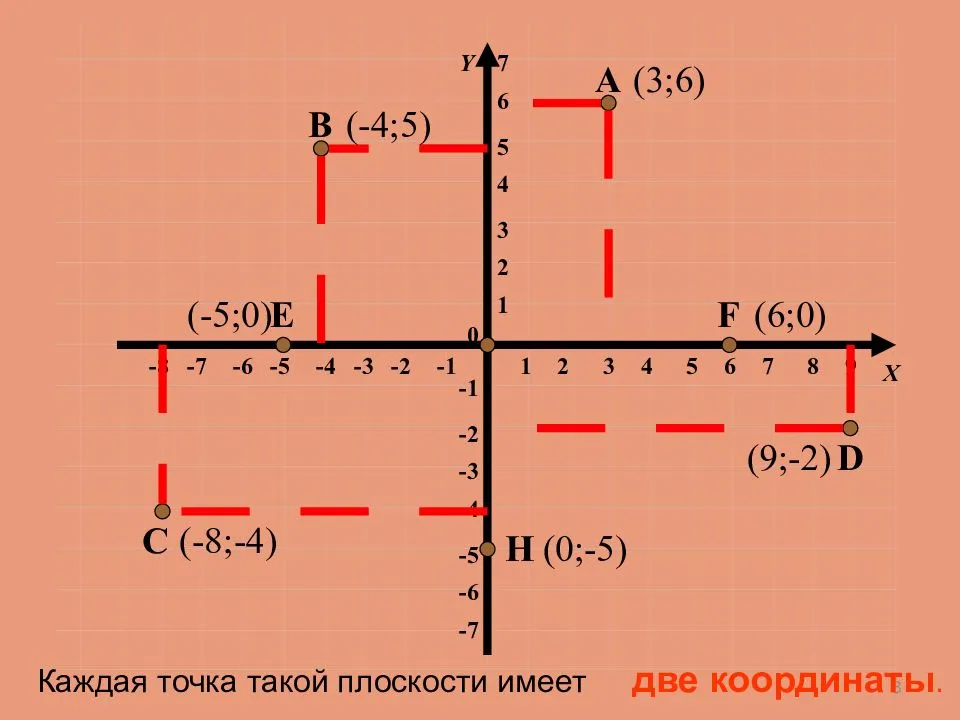
Каждая точка на плоскости или в пространстве определяется упорядоченным набором координат — чисел в
соответствии единице длины системы координат.

Заметим, что, как следует из определения, существует декартова система координат и
на прямой, то есть в одном измерении. Введение декартовых координат на прямой представляет собой один
из способов, с помощью которого любой точке прямой ставится в соответствие вполне определённое вещественное
число, то есть координата.

Метод координат, возникший в работах Рене Декарта, ознаменовал собой революционную
перестройку всей математики. Появилась возможность истолковывать алгебраические уравнения (или неравенства)
в виде геометрических образов (графиков) и, наоборот, искать решение геометрических задач с помощью
аналитических формул, систем уравнений. Так, неравенство z
xOy
и находящейся выше этой плоскости на 3 единицы.

С помощью декартовой системы координат принадлежность точки заданной кривой
соответствует тому, что числа x
и y
удовлетворяют некоторому уравнению. Так, координаты
точки окружности с центром в заданной точке (a
; b
)

удовлетворяют уравнению (x
— a
)² + (y
— b
)² = R
²
.

Абсцисса, ордината и аппликата

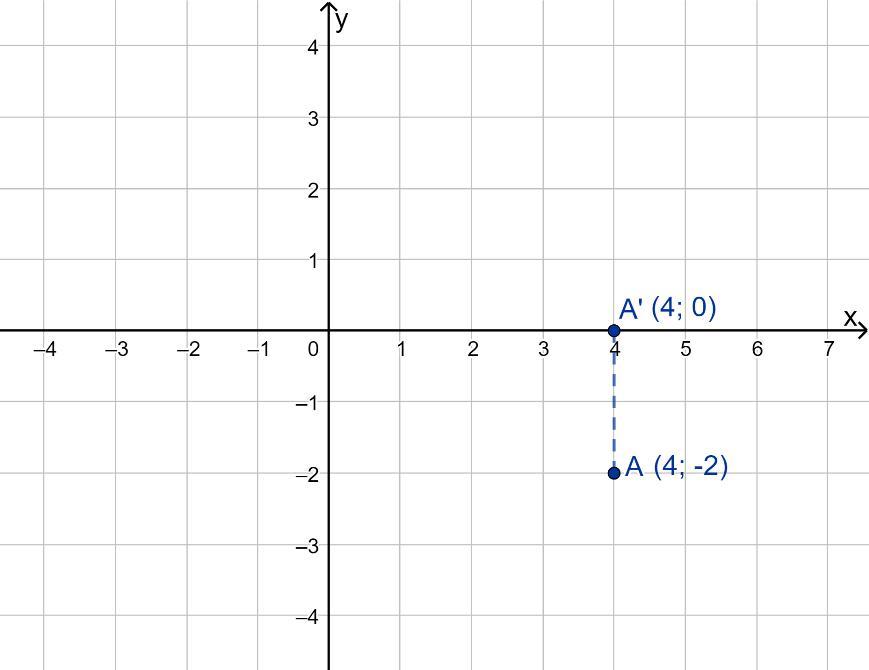
В прямоугольной двумерной системе координат для точного определения координат той или иной точки или отрезка используется абсцисса и ордината. Абсцисса — это координата точки по оси OX, ордината — координата по оси OY. Чтобы определить значение абсциссы и ординаты интересующей точки в прямоугольной системе координат необходимо провести перпендикуляры от данной точки к осям OX и OY соответственно. Значение на осях и будут значениями абсциссы и ординаты точки.

Если точка располагается в трехмерной системе координат, добавляется также понятие «аппликата» — это значение точки по оси OZ.

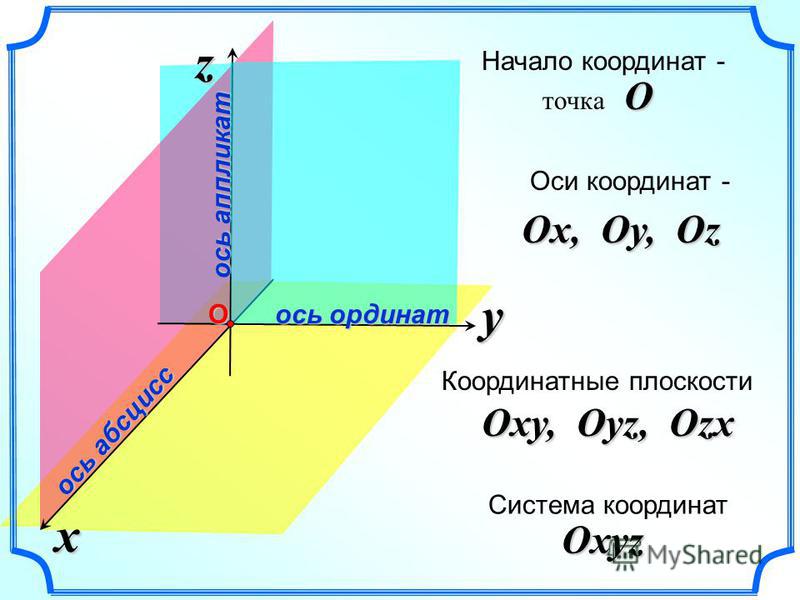
Прямоугольная декартова система координат в пространстве

Декартовы координаты в пространстве вводятся в полной аналогии с декартовыми
координатами на плоскости.

Три взаимно перпендикулярные оси в пространстве (координатные оси) с общим началом
O

и одинаковой масштабной единицей образуют декартову
прямоугольную систему координат в пространстве

.

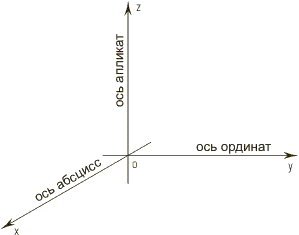
Одну из указанных осей называют осью Ox

, или осью абсцисс

,
другую — осью Oy

, или осью ординат

,
третью — осью Oz

, или осью аппликат

.
Пусть M
x

, M
y

M
z

— проекции произвольной точки
М

пространства на оси Ox

,
Oy

и Oz

соответственно.

Проведём через точку М
Ox
Ox

в точке M
x

.
Проведём через точку М

плоскость, перпендикулярную оси Oy

. Эта плоскость пересекает ось
Oy

в точке M
y

.
Проведём через точку М

плоскость, перпендикулярную оси Oz

. Эта плоскость пересекает ось
Oz

в точке M
z

Декартовыми прямоугольными координатами x

,
y

и z

точки М

будем называть соответственно величины направленных отрезков OM
x

,
OM
y

и OM
z

.
Величины этих направленных отрезков рассчитываются соответственно как
x
= x
0
— 0
,
y
= y
0
— 0
и
z
= z
0
— 0
.

Декартовы координаты x

,
y

и z

точки М

называются соответственно
её абсциссой

, ординатой

и аппликатой

.

Попарно взятые координатные оси располагаются в координатных плоскостях
xOy

, yOz

и zOx

.

Декартова система координат

Принцип работы с декартовой системой основан на понимании понятия проекции. Проекция в системе это перпендикуляр, опущенный на оси. Оси обозначаются как х и у. Ось х направлена вправо. Ось у направлена влево.

Представим себе точку на плоскости. Если нам нужно узнать ее координаты, то необходимо опустить два перпендикуляра: по одному на оси.

Так мы получим проекцию точки на ось х, это отрезок от начала отчета до точки пересечения оси с перпендикуляром. И проекцию отрезка на ось у: это расстояние на оси у от начала координат до точки пересечения оси с перпендикуляром.

Значение каждой из проекции и будет являться координатами точки на плоскости. По этим же координатам можно получить точку заново. Для этого нужно отложить требуемые значения на осях, после чего провести через отложенные точки прямые, перпендикулярные осям. Точка пересечения перпендикуляров и будет искомой прямой.

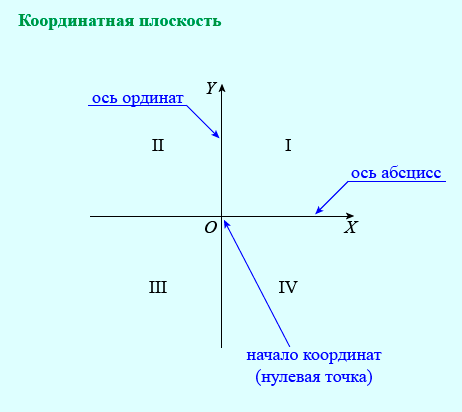
Прямоугольная декартова система координат на плоскости

Две перпендикулярные оси на плоскости с общим началом и одинаковой масштабной единицей
образуют декартову прямоугольную систему координат на плоскости

. Одна из этих
осей называется осью Ox

, или осью абсцисс

,
другую — осью Oy

, или осью ординат

.
Эти оси называются также координатными осями. Обозначим через M
x

и
M
y

соответственно проекции произвольной
точки М

на оси Ox

и
Oy

. Как получить проекции? Проведём через точку М
Ox

. Эта прямая пересекает ось
Ox

в точке M
x

.
Проведём через точку М

прямую, перпендикулярную оси Oy

. Эта прямая пересекает ось
Oy

в точке M
y

.
Это показано на рисунке ниже.

x

и
y

точки М

будем называть
соответственно величины направленных отрезков OM
x

и OM
y

. Величины этих направленных
отрезков рассчитываются соответственно как x
= x
0
— 0
и
y
= y
0
— 0
. Декартовы координаты x

и
y

точки М
абсциссой

и ординатой

. Тот факт, что точка
М

имеет координаты x

и
y

, обозначается так: M
(x
, y
)
.

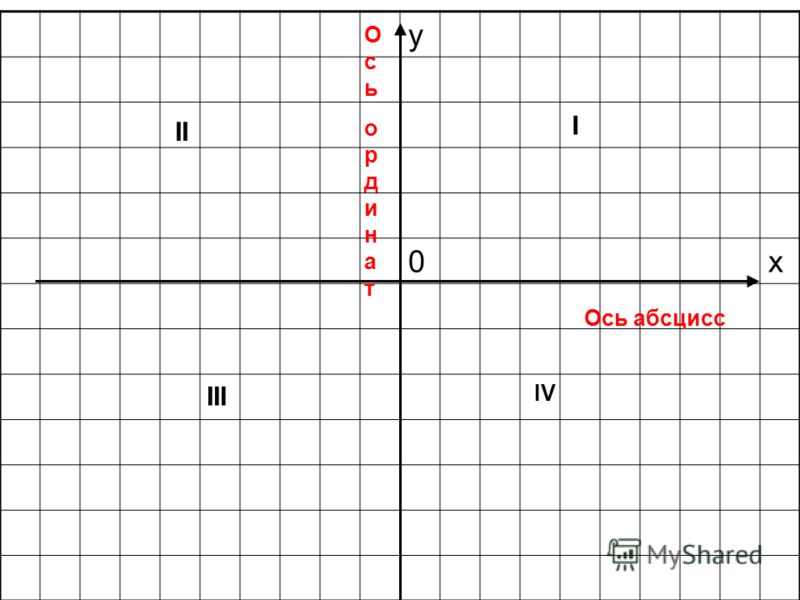
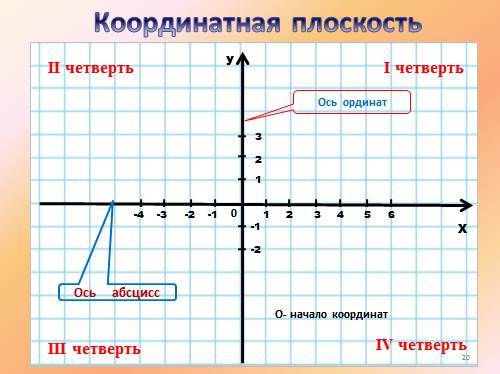
Координатные оси разбивают плоскость на четыре квадранта

, нумерация которых показана
на рисунке ниже. На нём же указана расстановка знаков координат точек в зависимости от их расположения
в том или ином квадранте.

Помимо декартовых прямоугольных координат на плоскости часто рассматривается также
полярная система координат. О способе перехода от одной системы координат к другой — в уроке
полярная система координат
.

Декартова система координат

Рене Декарт прославился многими открытиями в науке, несмотря на всяческие гонения со стороны бушевавшей инквизиции. Но в умах многих и многих поколений потомков он остался как изобретатель декартовой или прямоугольной системы координат.

Прямоугольная система координат сегодня используется везде: в радарах, для настройки светового оборудования, в оптике – практически любая отрасль не может обойтись без использования столь удобной системы.

Система Декарта состоит из двух взаимно перпендикулярных прямых. В любой системе координат обязательно должны быть:

Начало отсчета.
Единичные отрезки.
Направление осей.

Единичные отрезки на разных осях могут быть различны. Размер отрезка выбирают в соответствии с отметками, которые нужно нанести.