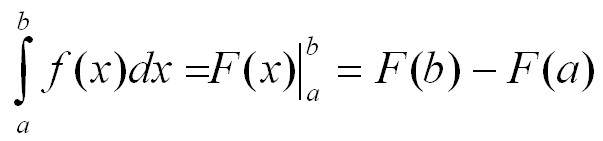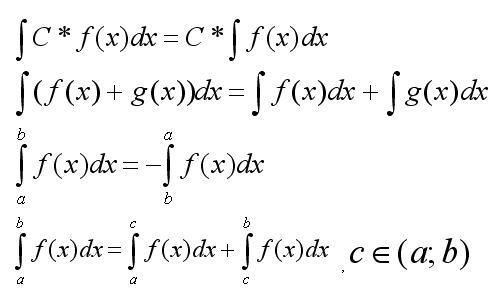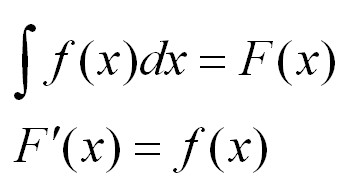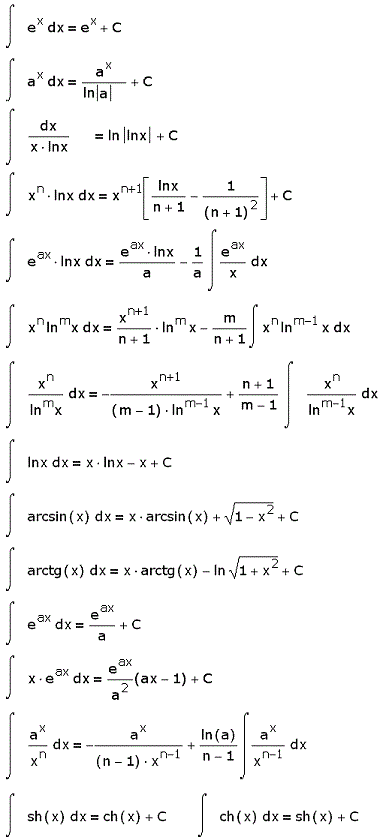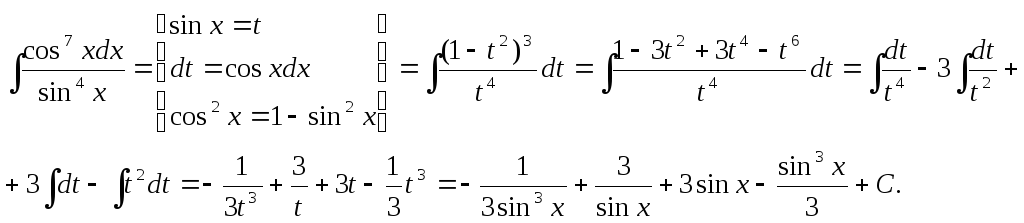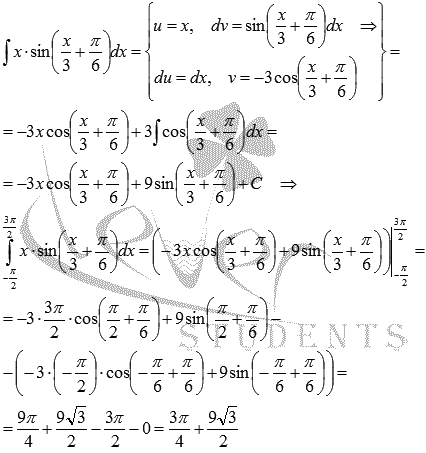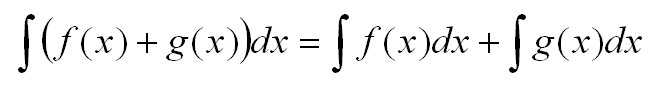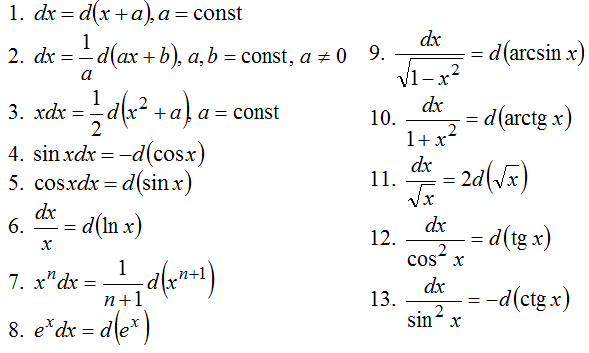Интегралы

Метод интегрирования по частям.

Пусть функции \(u(x)\) и \(v(x)\) имеют непрерывные производные на промежутке \(\Delta\). Тогда функция \(uv\) также имеет непрерывную производную на \(\Delta\) и согласно правилу дифференцирования произведения выполняется равенство
$$
uv’=(uv)’-vu’.\nonumber
$$

Интегрируя это равенство и учитывая, что
$$
\int (uv)’dx=uv + C,\nonumber
$$
получаем
$$
\int uv’dx = uv + C — \int vu’ dx.\nonumber
$$

Относя произвольную постоянную \(C\) к интегралу \(\displaystyle \int vu’dx\), находим
$$
\int uv’dx = uv-\int vu’dx,\label{ref21}
$$
или
$$
\int udv = uv-\int vdu,\label{ref22}
$$

Формула \eqref{ref21} или \eqref{ref22} называется формулой интегрирования по частям. Она сводит вычисление интеграла \(\displaystyle udv\) к вычислению интеграла \(\displaystyle vdu\).

Пример 15.

$$
\int x\cos x dx=\int x d(\sin x)=x\sin x-\int \sin xdx=x\sin x-\cos x+C.\ \blacktriangle\nonumber
$$

Пример 16.

Вычислить интеграл
$$
J=\int \sqrt{x^2+a}dx.\nonumber
$$

\(\triangle\) Полагая \(u=\displaystyle\sqrt{x^2+a},\ v=x\), по формуле \eqref{ref21} находим
$$
J=x\sqrt{x^2+a}-\int \frac{x^2}{\sqrt{x^2+a}}dx,\nonumber
$$
где
$$
\int \frac{x^2}{\sqrt{x^2+a}}dx=\int \frac{x^2+a-a}{\sqrt{x^2+a}}dx=J-a\int \frac{dx}{\sqrt{x^2+a}}.\nonumber
$$

Отсюда получаем уравнение относительно \(J\):
$$
J=x\sqrt{x^2+a}-J+a\int \frac{dx}{\sqrt{x^2+a}}.\nonumber
$$

Используя результат , находим
$$
\int \sqrt{x^2+a}dx=\frac{x}{2}\sqrt{x^2+a}+\frac{a}{2}\operatorname{ln}|x+\sqrt{x^2+a}|+C.\ \blacktriangle\nonumber
$$

Пример 17.

Пусть
$$
J_n=\int \frac{dx}{(x^2+a^2)^n},\quad n\in\mathbb{N},\quad a\neq 0.\nonumber
$$
Выведем рекуррентную формулу для вычисления интеграла \(J_n\).

\(\triangle\) Пусть \(u=(x^2+a^2)^{-n},\ v=x\). Тогда \(u’=-2nx(x^2 + a^2)^{-n-1},\ v’=1\) и по формуле \eqref{ref21} получаем
$$
J_n=\frac{x}{(x^2+a^2)^n}+2n\int \frac{x^2}{(x^2+a^2)^{n+1}}dx,\nonumber
$$
где
$$
\int \frac{x^2}{(x^2+a^2)^{n+1}}dx=\int \frac{(x^2+a^2)-a^2}{(x^2+a^2)^{n+1}}dx=J_n-a^2J_{n+1}.\nonumber
$$
Следовательно,
$$
J_n=\frac{x}{(x^2+a^2)^n}+2nJ_n-2na^2J_{n+1},\nonumber
$$
откуда
$$
J_{n+1}=\frac{x}{2na^2(x^2+a^2)^n}+\frac{2n-1}{2na^2}J_n.\ \blacktriangle\label{ref23}
$$

Замечание 7.

Так как
$$
J_1=\int \frac{dx}{x^2+a^2}=\frac{1}{a}\operatorname{arctg}\frac{x}{a}+C,\nonumber
$$
то из формулы \eqref{ref23} находим
$$
J_2=\int \frac{dx}{(x^2+a^2)^2}=\frac{x}{2a^2(x^2+a^2)}+\frac{1}{2a^3}\operatorname{arctg}\frac{x}{a}+C.\nonumber
$$

Замечание 8.

Повторное применение формулы \eqref{ref21} позволяет получить обобщенную формулу интегрирования по частям
$$
\int uv^{(n+1)}dx=\\=uv^{(n)}-u’v^{(n-1)}+u″v^{(n-2)}+…+(-1)^n u^{(n)}v+(-1)^{n+1}\int u^{(n+1)}vdx\label{ref24}
$$
в предположении, что существуют непрерывные производные \(u^{(n+1)},\ v^{(n+1)}\) на рассматриваемом промежутке. При \(n=1\) формула \eqref{ref24} принимает вид
$$
\int uv″dx=uv’-u’v+\int u″vdx.\label{ref25}
$$

Пример 18.

Вычислить интеграл
$$
J = \int x^2 e^x dx.\nonumber
$$

\(\triangle\) Полагая \(u=x^2,\ v = e^x\) и учитывая, что \(u’=2x,\ u″ = 2,\ v’=v″=e^x\), получаем по формуле \eqref{ref25}
$$
J = x^2 e^x-2x e^x+2\int e^x dx,\nonumber
$$
откуда
$$
\int x^2 e^x dx=(x^2-2x+2)e^x+C.\ \blacktriangle\nonumber
$$

Пример 19.

Вычислить интеграл
$$
J=\int e^{\alpha x}\cos \beta x dx,\quad \alpha\beta\neq 0.\nonumber
$$

\(\triangle\) Положим \(u= \cos \beta x,\ v=\displaystyle\frac{e^{\alpha x}}{\alpha^2}\). Тогда \(u’=-\beta \sin\beta x,\ u″=-\beta^2\cos\beta x,\ v’=\displaystyle\frac{e^{\alpha x}}{\alpha},\ v″=e^{\alpha x}\). По формуле \eqref{ref25} находим
$$
J =\frac{e^{\alpha x}}{\alpha}\cos\beta x+\frac{\beta}{\alpha^2}e^{\alpha x}\sin \beta x-\frac{\beta^2}{\alpha^2}J + C,
$$
откуда
$$
J=\frac{\alpha \cos\beta x+\beta\sin \beta x}{\alpha^2+\beta^2}e^{\alpha x}+C_1.\ \blacktriangle\nonumber
$$

Понятие двойного интеграла

Двойной интеграл в общем виде записывается следующим образом:

Разбираемся в терминах и обозначениях:– значок двойного интеграла; – область интегрирования (плоская фигура); – подынтегральная функция двух переменных, часто она довольно простая; – значки дифференциалов.

Что значит вычислить двойной интеграл?

Вычислить двойной интеграл – это значит найти ЧИСЛО. Самое обычное число:
И крайне желательно найти его правильно =)

Результат (число ) может быть отрицательным. И ноль тоже запросто может получиться. Специально остановился на данном моменте, поскольку немало студентов испытывают беспокойство, когда ответ получается «шото вроде как странный».

Многие помнят, что «обычный» определённый интеграл – тоже число. Здесь всё так же. У двойного интеграла существует и отличный геометрический смысл, но об этом позже, всему своё время.

Как вычислить двойной интеграл?

Для того чтобы вычислить двойной интеграл, его необходимо свести к так называемым повторным интегралам. Сделать это можно двумя способами. Наиболее распространён следующий способ:

Вместо знаков вопроса необходимо расставить пределы интегрирования. Причём одиночные знаки вопроса  у внешнего интеграла – это числа, а двойные знаки вопроса  у внутреннего интеграла – это функции одной переменной , зависящие от «икс».

Откуда взять пределы интегрирования? Они зависят от того, какая в условии задачи дана область . Область  представляет собой обычную плоскую фигуру, с которой вы неоднократно сталкивались, например, при вычислении площади плоской фигуры или вычислении объема тела вращения. Очень скоро вы узнаете, как правильно расставлять пределы интегрирования.

После того, как переход к повторным интегралам осуществлён, следуют непосредственно вычисления: сначала берётся внутренний интеграл , а потом – внешний. Друг за другом. Отсюда и название – повторные интегралы.

Грубо говоря, задача сводится к вычислению двух определённых интегралов. Как видите всё не так сложно и страшно, и если вы совладали с «обыкновенным» определённым интегралом, что мешает разобраться с двумя интегралами?!

Второй способ перехода к повторным интегралам встречается несколько реже:
Что поменялось? Поменялся порядок интегрирования: теперь внутренний интеграл берётся по «икс», а внешний – по «игрек». Пределы интегрирования, обозначенные звёздочками – будут другими! Одиночные звёздочки внешнего интеграла – это числа, а двойные звёздочки внутреннего интеграла – это обратные функции , зависящие от «игрек».

Какой бы мы ни выбрали способ перехода к повторным интегралам, окончательный ответ обязательно получится один и тот же:

Пожалуйста, запомните это важное свойство, которое можно использовать, в том числе, для проверки решения

Алгоритм решения двойного интеграла:

Систематизируем информацию: в каком порядке нужно решать рассматриваемую задачу?

1) Необходимо выполнить чертёж. Без чертежа задачу не решить. Точнее, решать-то она решается, но это будет похоже на игру в шахматы вслепую. На чертеже следует изобразить область , которая представляет собой плоскую фигуру. Чаще всего фигура незамысловата и ограничена какими-нибудь прямыми, параболами, гиперболами и т.д. Грамотную и быструю технику построения чертежей можно освоить на уроках Графики и основные свойства элементарных функций, Геометрические преобразования графиков. Итак, этап первый – выполнить чертёж.

2) Расставить пределы интегрирования и перейти к повторным интегралам.

3) Взять внутренний интеграл

4) Взять внешний интеграл и получить ответ (число).

Как же вычислить определенный интеграл

Оказывается, сделать это, умея интегрировать, т. е. находить неопределенные интегралы, очень просто. И помогает в этом формула основателей интегро-дифференциального исчисления Ньютона и Лейбница

Согласно ей, вычисление искомого интеграла состоит на первом этапе в нахождении неопределенного, последующем вычислении значения найденной первообразной F(x) при подстановке x, равного сначала верхнему пределу, затем нижнему и, наконец, в определении разности этих значений. При этом константу С можно не записывать. т.к. она пропадает при выполнении вычитания.

Рассмотрим некоторые интегралы с подробным решением.

Найдем площадь участка под одной полуволной синусоидой.

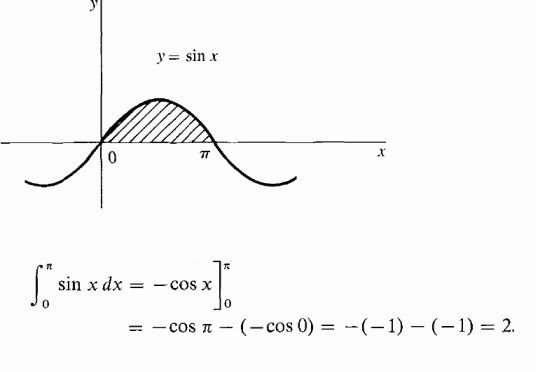
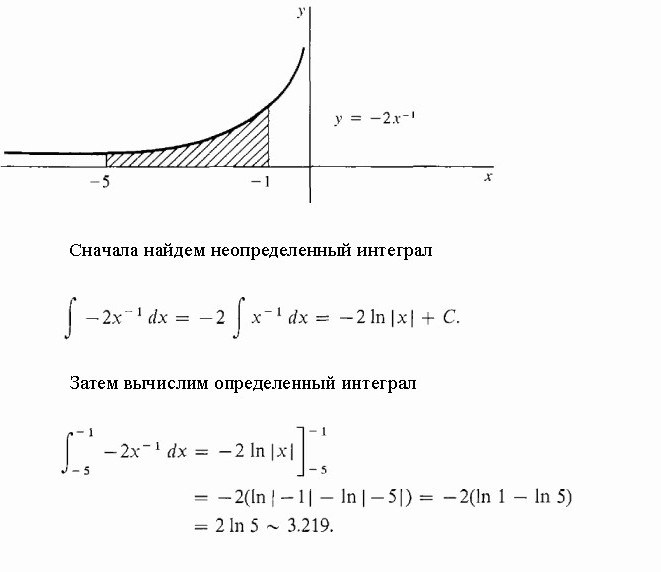
Рассмотрим теперь интегралы с подробным решением, использующим в первом примере свойство аддитивности, а во втором — подстановку промежуточной переменной интегрирования. Вычислим определенный интеграл от дробно-рациональной функции:

y=(1+t)/t3 от t=1 до t=2.

Теперь покажем, как можно упростить взятие интеграла введением промежуточной переменной. Пусть нужно вычислить интеграл от (x+1)2.

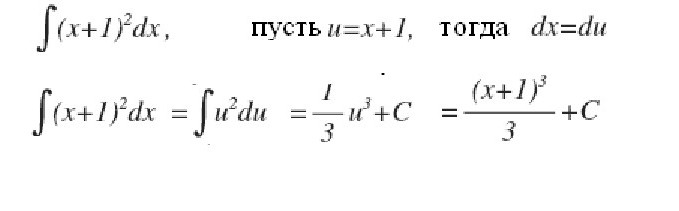
Простейшие дифференциальные уравнения.

Дифференциальные уравнения первого порядка.

Задачу о нахождении первообразной для непрерывной на интервале \((a, b)\) функции \(f(x)\) можно сформулировать так: найти функцию \(y(x)\), которая на интервале \((a, b)\) является решением уравнения
$$
y'(x) = f(x).\label{ref25}
$$

Уравнение такого вида является обыкновенным дифференциальным уравнением первого порядка. Все решения уравнения \eqref{ref25} можно записать в виде
$$
y(x) = \int\limits_{x_{0}}^x f(t)\ dt + C,\label{ref26}
$$
где \(x_{0} \in (a, b),\ C\) — произвольная постоянная.

Чтобы выделить единственное решение уравнения \eqref{ref25}, достаточно задать значение функции \(y(x)\) в какой-либо точке, например в точке \(x_{0}\). Если \(y(x_{0}) = y_{0}\), то из формулы \eqref{ref26} получаем
$$
y(x) = y_{0} + \int\limits_{x_{0}}^x f(t)\ dt.\nonumber
$$

В приложениях часто встречаются дифференциальные уравнения первого порядка, имеющие вид
$$
y'(x) = ky(x),\label{ref27}
$$
где \(k\) — постоянная. Уравнением \eqref{ref27} описывается, например, закон размножения бактерий, так как скорость роста числа бактерий пропорциональна их количеству.

Решениями уравнения \eqref{ref27} являются функции \(y = C e^{kx}\), где \(C\) — произвольная постоянная. Можно показать, что других решений уравнение \eqref{ref27} не имеет. Если известно, что \(y(x_{0}) = y_{0}\), то \(C = y_{0}\), и поэтому
$$
y=y_0 e^{k(x-x_0)}.\nonumber
$$

Дифференциальные уравнения второго порядка.

Рассмотрим уравнение
$$
y″(x) + \omega^{2}y(x) = 0,\label{ref28}
$$
где \(\omega\) — некоторое положительное число. Уравнение \eqref{ref28} называют уравнением гармонических колебаний.

Легко проверить, что функции \(\cos \omega x\) и \(\sin \omega x\) являются решениями уравнения \eqref{ref28}. Отсюда следует, что функции вида
$$
y = C_{1} \cos \omega x + C_{2} \sin \omega x,\label{ref29}
$$

где \(C_{1}\)\ и \(C_{2}\) — произвольные постоянные, удовлетворяют уравнению \eqref{ref28}. Можно показать, что других решений уравнение \eqref{ref28} не имеет. Если известно значение функции \(y(x)\) и значение ее производной при \(x = x_{0}\) (начальные условия), то есть заданы числа \(y_{0} = y(x_{0})\) и \(\tilde{y}_{0} = y'(x_{0})\), то этими условиями определяется единственное решение уравнения \eqref{ref28}. Например, если\(y(0) = 0,\ y'(0) = 1\), то из формулы \eqref{ref29} находим \(C_{1} = 0,\ C_{2} = \displaystyle\frac{1}{\omega}\), и поэтому \(y = \displaystyle\frac{1}{\omega} \sin \omega x\).

Обратимся к уравнению
$$
y″(x)- \omega^{2}y(x) = 0,\label{ref30}
$$
где \(\omega > 0\). Его решениями, как нетрудно проверить, являются функции \(e^{\omega x}\) и \(e^{- \omega x}\), и поэтому функции вида
$$
y = C_{1}e^{\omega x} + C_{2}e^{- \omega x},\label{ref31}
$$
где \(C_{1}\) и \(C_{2}\) — произвольные постоянные, также удовлетворяют уравнению \eqref{ref30}.

Можно показать, что других решений уравнение \eqref{ref30} не имеет. Если заданы числа \(y_{0} = y(x_{0})\) и \(\tilde{y}_{0} = y'(x_{0})\), то из формулы \eqref{ref31} найдем \(C_{1}\) и \(C_{2}\) и тем самым определим единственное решение уравнения \eqref{ref30}. Например, если известно, что \(y(0) = 1,\ y'(0) = 0\), то \(C_{1} + C_{2} = 1,\ \omega C_{1}- \omega C_{2} = 0\), откуда \(C_{1} = C_{2} = \displaystyle\frac{1}{2}\) и поэтому \(y = \displaystyle\frac{1}{2} (e^{\omega x}- e^{- \omega x} = \operatorname{ch} \omega x)\).

Метод решения несобственного интеграла второго родас точками разрыва на обоих концах отрезка

Заключительные пункты этой статьи предназначены для читателей, которые хорошо разобрались с несобственными интегралами второго рода на уроке Несобственные интегралы. Примеры решений. Рассмотрим другие разновидности несобственных интегралов второго рода. Ничего сложного!

Многие выкладки предыдущего параграфа будут справедливы и сейчас.

Сразу конкретная задача:

Пример 12

Вычислить несобственный интеграл или установить его расходимость.

Подынтегральная функция терпит бесконечные разрывы в обоих концах отрезка интегрирования. Изобразим подынтегральную функцию  на чертёже: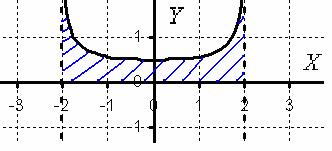

Геометрически данный несобственный интеграл представляет собой площадь бесконечной криволинейной трапеции, которая не ограничена сверху.

Методика решения точно такая же, как и в предыдущем параграфе – разделяй и властвуй:

А уж интегралы правой части рассматривались во втором разделе урока Несобственные интегралы. Примеры решений.

Но, вместо этого замечаем, что подынтегральная функция является чётной. Чётность использовать МОЖНО. В этом легко убедиться и по чертежу. Таким образом, интеграл целесообразно споловинить, а результат удвоить. Решаем наиболее рациональным способом:

Подынтегральная функция терпит бесконечные разрывы в точках . Данная функция является чётной, а интервал интегрирования симметричен относительно нуля.

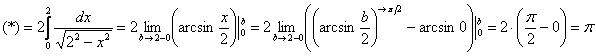
Ответ: , то есть, несобственный интеграл сходится

Пример 13

Исследовать несобственный интеграл на сходимость 😉

Это пример для самостоятельного решения. Всё, как и в предыдущем параграфе – нечетностью функции пользоваться НЕ НУЖНО. Аккуратно делим интеграл на две части и исследуем сходимость по типовому алгоритму. Полное решение и ответ в конце урока.

Не редкость, когда подынтегральная функция не является четной или нечетной, да и отрезок интегрирования не симметричен относительно нуля. Например, рассмотрим несобственный интеграл . Подынтегральная функция опять терпит бесконечные разрывы в обоих концах отрезка интегрирования. Алгоритм такой же, делим интеграл на два интеграла:

Интегралы правой части разобраны на уроке Несобственные интегралы. Примеры решений. В качестве факультатива выясните, существует ли этот интеграл в общем случае, и если существует – то сходится или нет.

Метод решения несобственного интегралас точкой разрыва на отрезке интегрирования

Если честно, такой пример встречался в моей практике всего один раз (по крайне мере, вспомнил лишь один), поэтому я ограничусь только обзором.

Пример опять же будет в известной степени условным, первое, что в голову пришло. Рассмотрим несобственный интеграл . На концах отрезка интегрирования всё хорошо. Но подынтегральная функция терпит бесконечный разрыв прямо на отрезке в точке . Подынтегральная функция является четной, но это не имеет никакого значения, поскольку отрезок интегрирования не симметричен относительно нуля.

Метод уже состарился, как хмм… чешуя динозавра. Представим несобственный интеграл в виде суммы двух несобственных интегралов:

Интегралы правой части вам уже знакомы. А проговаривать алгоритм в третий раз не буду, смотрите предыдущие два параграфа)

Желаю успехов!

Решения и ответы:

Пример 2: Решение: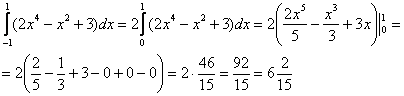

Пример 5: Решение:Проведем замену: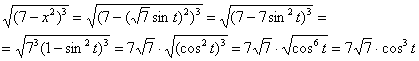Новые пределы интегрирования:

Пример 8: Решение:Подынтегральная функция непрерывна на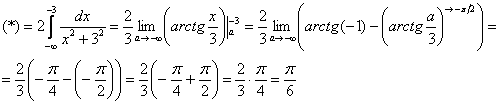

Пример 11: Решение:Подынтегральная функция непрерывна на всей числовой прямой.Представим интеграл в виде суммы двух интегралов:Вычислим первый интеграл: Вычислим второй интеграл: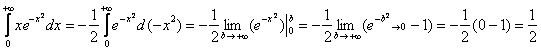 Таким образом: – интеграл сходится и равен нулю.Ответ: Примечание 1: В частности, равно нулю и главное значение интеграла

Примечание 2: Будет серьезной оплошностью сразу записать, что , пользуясь нечетностью подынтегральной функции и симметричностью интервала интегрирования. Стандартный алгоритм обязателен!!!

Пример 13: Решение: Подынтегральная функция терпит бесконечные разрывы в точках . Представим данный интеграл в виде суммы двух интегралов:Вычислим первый интеграл: Вычислим второй интеграл: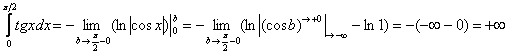Таким образом, интеграла  в общем случае не существует. Исследуем сходимость интеграла по Коши: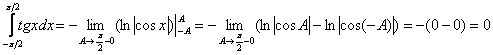

Ответ: интеграл сходится лишь по Коши, главное значение

(Переход на главную страницу)

Фундаментальное соотношение интегрального исчисления

Оно связывает отношения между дифференцированием и интегрированием и показывает, что существует операция, обратная дифференцированию функции, — ее интегрирование. Оно также показывает, что если любая функция f(х) непрерывна, то применением к ней этой математической операции можно найти целый ансамбль (совокупность, множество) функций, первообразных для нее (или иначе, найти неопределенный интеграл от нее).

Пусть функция F(x) является обозначением результата интегрирования функции f(х). Соответствие между этими двумя функциями в результате интегрирования второй из них обозначается следующим образом:

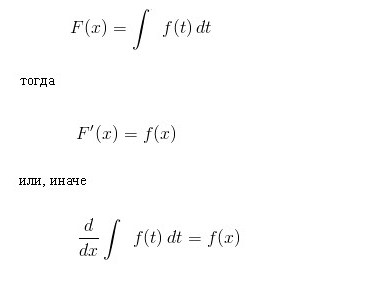
Как видно, при символе интеграла отсутствуют пределы интегрирования. Это означает, что из определенного он преобразован в неопределенный интеграл. Слово «неопределенный» означает, что результатом операции интегрирования в данном случае является не одна, а множество функций. Ведь, кроме собственно функции F(x), последним выражениям удовлетворяет и любая функция F(x)+С, где С = const. При этом подразумевается, что постоянный член в ансамбле первообразных можно задавать по произволу.

Следует подчеркнуть, что, если интеграл, определенный от функции, является числом, то неопределенный есть функция, точнее, их множество. Термин «интегрирование» применяется для определения операции разыскания обоих видов интегралов.

Интегралы от обратных тригонометрических функций. Интегралы от обратных тригонометрических функций, умноженных на многочлен

Общее правило: за  всегда обозначается обратная тригонометрическая функция.

Напоминаю, что к обратным тригонометрическим функциям относятся арксинус, арккосинус, арктангенс и арккотангенс. Для краткости записи я буду называть их «арками»

Пример 11

Найти неопределенный интеграл.

Решаем.

Интегрируем по частям: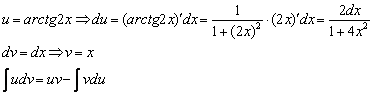

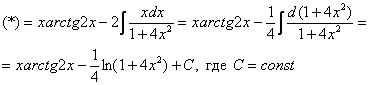
Интеграл  найден методом подведения функции под знак дифференциала, можно использовать и метод замены в «классическом» виде. Аналогичный пример мы разбирали на уроке Метод замены переменной в неопределенном интеграле.

Таким образом, помимо «чистого» интегрирования по частям нередко требуется применять и другие методы, приёмы решения.

Пример 12

Найти неопределенный интеграл.

Это пример для самостоятельного решения

И заключительный пример сегодняшнего урока под счастливым номером тринадцать: «арк», умноженный на многочлен. Он сложнее, и предназначен для маньяков желающих лучше разобраться в методе интегрирования по частям. Пример, пожалуй, будет тоже для самостоятельного решения, поскольку меня немного утомил тот логарифм в квадрате.

Пример 13

Найти неопределенный интеграл.

Что касаемо интегрирования по частям, почти всё разобрали. Рассмотренный метод часто применяется в комбинации с другими приёмами решения интегралов. Читатели с хорошими навыками могут ознакомиться с такими примерами на уроке Сложные интегралы.

А сейчас, как любила говорить моя учительница по математике, пора кончать.

Желаю успехов!

Решения и ответы:

Пример 3: Решение:

Пример 4: Решение:

Интегрируем по частям:

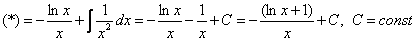
Пример 6: Решение:

Дважды интегрируем по частям:

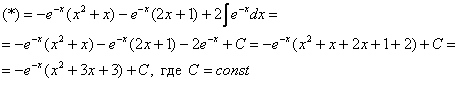
Пример 8: Решение:

Интегрируем по частям:

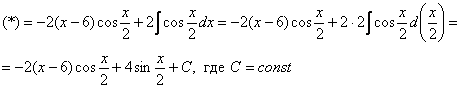
Пример 10: Решение:

Интегрируем по частям:

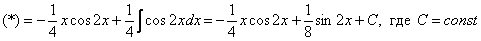
Примечание: Здесь мы использовали известную тригонометрическую формулу двойного угла . Её можно было использовать и сразу: , а  потом интегрировать по частям.

Похожим способом также решаются интегралы вроде ,  – в них необходимо (сразу или в ходе решения) понизить степень синуса (косинуса) с помощью соответствующих формул. Более подробно – см. Интегралы от тригонометрических функций.

Пример 12: Решение:

Интегрируем по частям: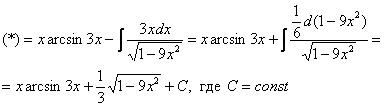

Пример 13: Решение:

Интегрируем по частям:

Примечание: Если возникли трудности с интегралом , то следует посетить урок Интегрирование некоторых дробей. 

Вы выполнили проверку? Может я и ошибся где… 😉

(Переход на главную страницу)

Переход от Римановой суммы к определенному интегралу

В высшей математике доказывается теорема, которая гласит, что если при неограниченном возрастании числа n аппроксимирующих прямоугольников наибольшая их ширина стремится к нулю, то Риманова сумма A_n стремится к некоторому пределу A. Число A – одно и то же при любом способе образования аппроксимирующих прямоугольников и при любом выборе точек x*_i.

Наглядное пояснение теоремы дает рисунок ниже.

Из него видно, что, чем уже прямоугольники, тем ближе площадь ступенчатой фигуры к площади под кривой. При числе прямоугольников n→∞ их ширина Δx_i→0, а предел A суммы A_n численно равен искомой площади. Этот предел и есть определенный интеграл функции f (х):

Символ интеграла, представляющий собой видоизмененную курсивную литеру S, был введен Лейбницем. Ставить сверху и снизу обозначения интеграла его пределы предложил Ж. Б. Фурье. При этом ясно указывается начальное и конечное значение x.

Риманова сумма

Прежде чем погрузиться в подробный ответ на вопрос, что такое интеграл, выделим некоторые основные идеи.

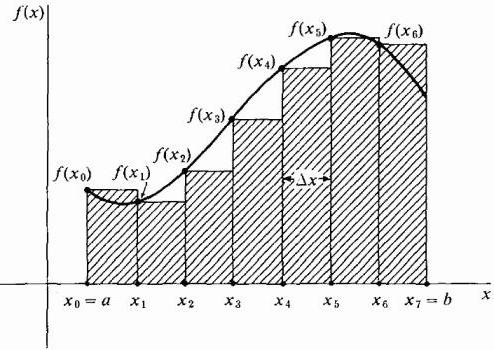
Во-первых, область под кривой делится на некоторое число n вертикальных полос достаточно малой ширины Δx. Далее каждая вертикальная полоса заменяется вертикальным прямоугольником высотой f(х), шириной Δx, и площадью f(х)dx. Следующим шагом является формирование суммы площадей всех этих прямоугольников, называемой Римановой суммой (смотрите рисунки ниже).

Рисуя наши прямоугольники шириной Δx, мы можем брать их высоту, равную значению функции на левом краю каждой полоски, т. е. на кривой будут лежать крайние левые точки их верхних коротких сторон шириной Δx. При этом на участке, где функция растет, и ее кривая является выпуклой, все прямоугольники оказываются ниже этой кривой, т. е. их сумма будет заведомо меньшей точной величины площади под кривой на этом участке (см. рисунок ниже). Такой способ аппроксимации называется левосторонним.

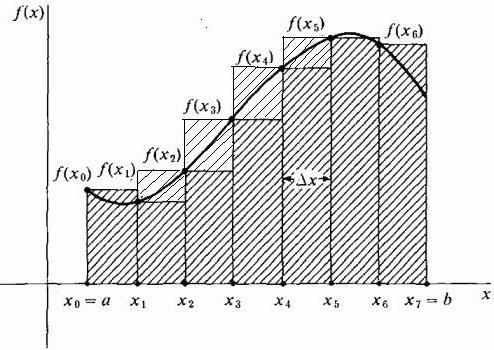
В принципе, можно нарисовать аппроксимирующие прямоугольники таким образом, чтобы на кривой лежали крайние правые точки их верхних коротких сторон шириной Δx. Тогда они будут выше кривой, и приближение площади на этом участке окажется больше ее точной величины, как показано на рисунке ниже. Этот способ носит название правостороннего.

Но мы можем также взять высоту каждого из аппроксимирующих прямоугольников, равной просто некоторому значению функции в произвольной точке x*_i внутри соответствующей полоски Δx_i (смотри рис. ниже). При этом мы даже можем не брать одинаковую ширину всех полосок.

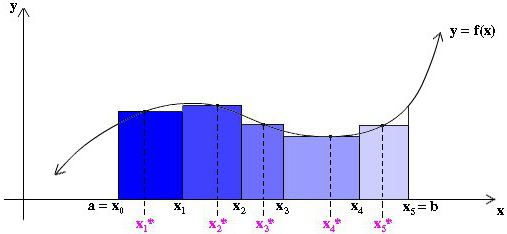
Составим Риманову сумму:

Интеграл – что это?

Предпосылки. Потребность в интегрировании возникла в Древней Греции. В то время Архимед начал применять для нахождения площади окружности методы, похожие по сути на современные интегральные исчисления. Основным подходом для определения площади неровных фигур тогда был «Метод исчерпывания», который достаточно лёгок для понимания.

Суть метода. В данную фигуру вписывается монотонная последовательность других фигур, а затем вычисляется предел последовательности их площадей. Этот предел и принимался за площадь данной фигуры.

Метод исчерпывания для определения площади круга

В этом методе легко прослеживается идея интегрального исчисления, которая заключается в нахождении предела бесконечной суммы. В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.

Современный интеграл. Классическая теория интегрирования была сформулирована в общем виде Ньютоном и Лейбницем. Она опиралась на существовавшие тогда законы дифференциального исчисления. Для её понимания, необходимо иметь некоторые базовые знания, которые помогут математическим языком описать визуальные и интуитивные представления об интегралах.

Метод интегрирования по частям в определенном интеграле

Здесь новизны еще меньше. Все выкладки статьи Интегрирование по частям в неопределенном интеграле в полной мере справедливы и для определенного интеграла.
Плюсом идёт только одна деталь, в формуле интегрирования по частям добавляются пределы интегрирования:

Формулу Ньютона-Лейбница здесь необходимо применить дважды: для произведения   и, после того, как мы возьмем интеграл .

Тип интеграла для примера я опять подобрал такой, который еще нигде не встречался на сайте. Пример не самый простой, но очень и очень познавательный.

Пример 8

Вычислить определенный интеграл

Решаем.

Интегрируем по частям:

У кого возникли трудности с интегралом , загляните на урок Интегралы от тригонометрических функций, там он подробно разобран.

(1) Записываем решение в соответствии с формулой интегрирования по частям.

(2) Для произведения применяем формулу Ньютона-Лейбница. Для оставшегося интеграла используем свойства линейности, разделяя его на два интеграла. Не путаемся в знаках!

(3) Берем два оставшихся интеграла. Интеграл  также разобран на уроке Интегралы от тригонометрических функций

(4) Применяем формулу Ньютона-Лейбница для двух найденных первообразных.

Далее ответ доводится «до ума». Повторюсь, будьте ПРЕДЕЛЬНО ВНИМАТЕЛЬНЫ при подстановках и заключительных вычислениях. Здесь допускают ошибки чаще всего.

Если честно, я недолюбливаю формулу  и, по возможности, … обхожусь вообще без нее! Рассмотрим второй способ решения, с моей точки зрения он более рационален.

Вычислить определенный интеграл

На первом этапе я нахожу неопределенный интеграл:

Интегрируем по частям:

Первообразная функция найдена. Константу  в данном случае добавлять не имеет смысла.

В чём преимущество такого похода? Не нужно «таскать за собой» пределы интегрирования, действительно, замучаться можно десяток раз записывать мелкие значки пределов интегрирования

На втором этапе я провожу проверку (обычно на черновике).

Тоже логично. Если я неправильно нашел первообразную функцию, то неправильно решу и определенный интеграл. Это лучше выяснить немедленно, дифференцируем ответ:

Получена исходная подынтегральная функция, значит, первообразная функция найдена верно.

Третий этап – применение формулы Ньютона-Лейбница:

И здесь есть существенная выгода! В «моём» способе решения гораздо меньший риск запутаться в подстановках и вычислениях – формула Ньютона-Лейбница применяется всего лишь один раз. Если чайник решит подобный интеграл по формуле  (первым способом), то стопудово где-нибудь допустит ошибку.

Рассмотренный алгоритм решения можно применить для любого определенного интеграла.

Уважаемый студент, распечатай и сохрани:

Что делать, если дан определенный интеграл, который кажется сложным или не сразу понятно, как его решать?

1) Сначала находим неопределенный интеграл (первообразную функцию). Если на первом же этапе случился облом, дальше рыпаться с Ньютоном и Лейбницем бессмысленно. Путь только один – повышать свой уровень знаний и навыков в решении неопределенных интегралов.

2) Проверяем найденную первообразную функцию дифференцированием. Если она найдена неверно, третий шаг будет напрасной тратой времени.

3) Используем формулу Ньютона-Лейбница. Все вычисления проводим ПРЕДЕЛЬНО ВНИМАТЕЛЬНО  –  тут самое слабое звено задания.

И, на закуску, интеграл для самостоятельного решения.

Пример 9

Вычислить определенный интеграл

Решение и ответ где-то рядом.

Следующий рекомендуемый урок по теме – Как вычислить площадь фигуры с помощью определенного интеграла? Там речь пойдет о геометрическом смысле определенного интеграла. Дополнительные материалы по определенному интегралу также можно найти в статье Эффективные методы вычисления определенных интегралов. Данный урок содержит ряд очень важных технических приёмов и позволит существенно повысить навыки вычисления определенного интеграла.

Желаю успехов!

Решения и ответы:

Пример 2: Решение:

Пример 4: Решение:

Пример 6: Решение:

Проведем замену переменной: ,Новые переделы интегрирования:

Примечания: В рассмотренном интеграле – как раз тот случай, когда уместно применить свойство определенного интеграла . Если не совсем понятно, почему из арктангенса можно вынести минус, рекомендую обратиться к методическому материалу Графики и свойства элементарных функций.

Пример 7: Решение:Замена: Новые пределы интегрирования:

Пример 9: Решение:Интегрируем по частям:

Вы точно их прорешали и получили такие ответы? 😉 И на старуху бывает порнуха.

(Переход на главную страницу)

Дифференциал определенного интеграла

Если вернуться к его обозначению, то вполне можно предположить, что a = const, а b является конкретным значением некоторой независимой переменной x. Тогда определенный интеграл с верхним пределом x̃ из конкретного числа превращается в функцию от x̃. Такой интеграл равен площади фигуры под кривой, обозначенной точками aABb на рисунке ниже.

Предположим, что мы дали переменной x̃ = b некоторое малое приращение Δx̃. Тогда приращение площади фигуры aABb складывается из площади прямоугольника (заштрихован на рисунке) Bb∙Δx̃ и площади фигуры BDC под кривой. Площадь прямоугольника равна Bb∙Δx̃ = f(x̃)Δx̃, т.е она является линейной функцией приращения независимой переменной. Площадь же фигуры BDC заведомо меньше, чем площадь прямоугольника BDCK = Δx̃∙Δy, и при стремлении Δx̃ →0 она уменьшается еще быстрее него. Значит, f(x̃)Δx̃ = f(x̃)dx̃ есть дифференциал переменной площади aABb, т. е. дифференциал определенного интеграла

Отсюда можно заключить, что вычисление интегралов заключается в разыскании функций по заданным выражениям их дифференциалов. Интегральное исчисление как раз и представляет собой систему способов разыскания таких функций по известным их дифференциалам.

Задачи, приводящие к понятию определенного интеграла.

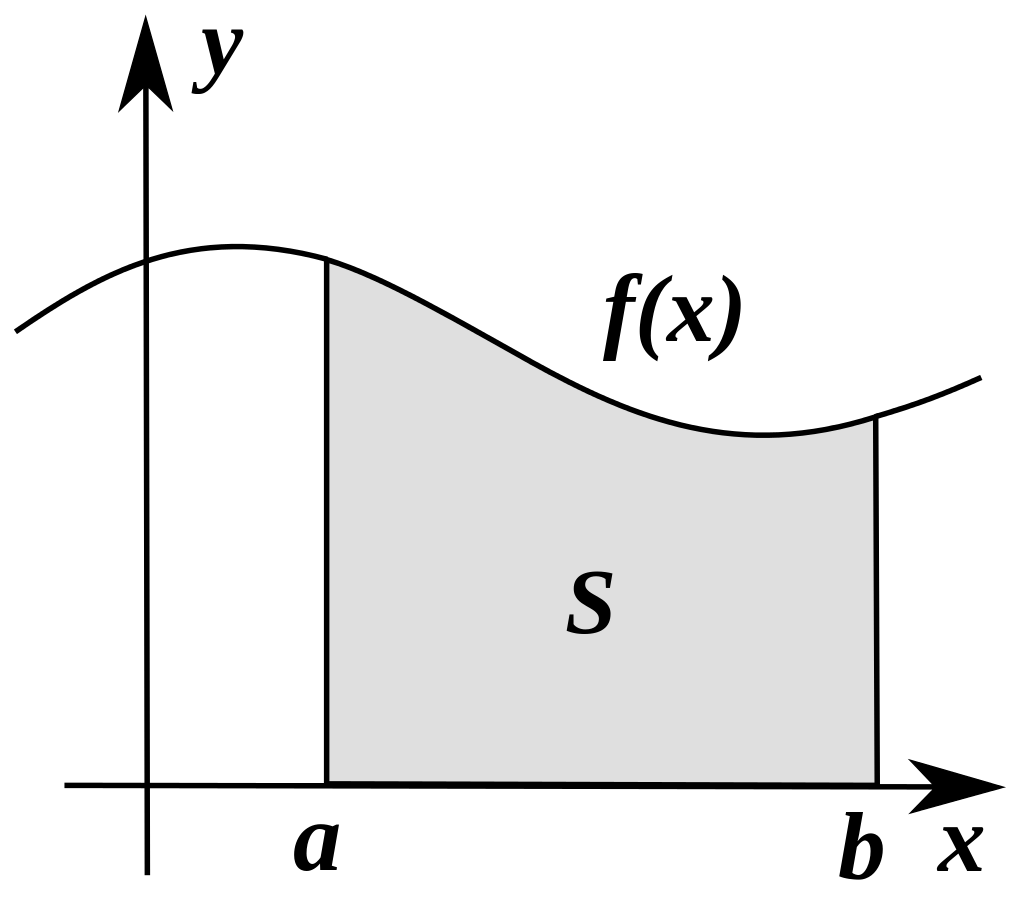
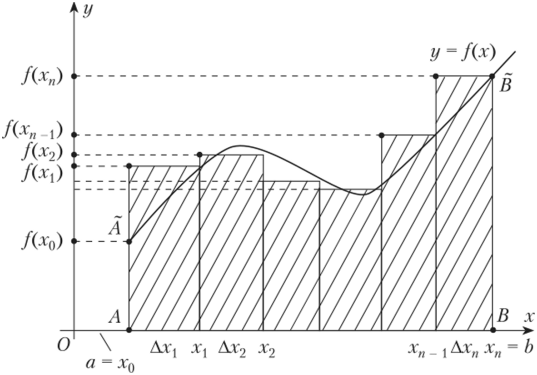
Площадь криволинейной трапеции.

Пусть функция \(f\) непрерывна на отрезке \(\Delta = \) и неотрицательна, то есть \(f(x) \geq 0\) при всех \(x \in \Delta\). Рассмотрим фигуру \(G\) (рис. 34.1), ограниченную отрезками прямых \(x = a,\ x = b,\ y = 0\) и графиком функции \(y = f(x)\), то есть
$$
G = \{(x, y): a \leq x \leq b,\ 0 \leq y \leq f(x)\}.\nonumber
$$

Такую фигуру называют криволинейной трапецией, а отрезок \(\Delta\) — ее основанием.

Рис. 34.1

Разобьем отрезок \(\Delta\) на \(n\) частей точками \(x_{i}(i = \overline{1, n-1})\), где \(x_{1} < x_{2} < \ldots < x_{n-2} < x_{n-1}\), и проведем через эти точки прямые, параллельные оси \(Oy\). Тогда фигура \(G\) разобьется на \(n\) частей, каждая из которых является криволинейной трапецией.

Обозначим \(\Delta x_{i} = x_{i}-x_{i-1},\ x_{0} = a,\ x_{n} = b\), и пусть  \(\xi_{i} \in\ \Delta_{i}\), где \(\Delta_{i} = ,\ i = \overline{1, n}\). Тогда сумма
$$
\sigma = \sum_{i=1}^{n}f(\xi_{i})\Delta x_{i},\nonumber
$$
зависящая от разбиения отрезка \(\Delta\) и выбора точек \(\xi_{i}\), равна площади ступенчатой фигуры (рис. 34.1), составленной из \(n\) прямоугольников, причем основанием \(i\)-го прямоугольника служит отрезок \(\Delta_{i}\), а длина его высоты равна \(f(\xi_{i})\). Интуитивно ясно, что эта ступенчатая фигура будет мало отличаться от исходной фигуры \(G\) при достаточно мелком разбиении.

Будем увеличивать число точек разбиения так, чтобы наибольшая из длин отрезков \(\Delta_{i}\) стремилась к нулю. Если при этом сумма \(\sigma\) будет иметь предел \(S\), не зависящий ни от способа дробления отрезка \(\Delta\), ни от выбора точек то естественно считать, что площадь фигуры \(G\) равна \(S\). Существование этого предела будет доказано ниже в разделе .

Пример 1.

Найти площадь фигуры, ограниченной параболой \(y = x^{2}\) и отрезками прямых \(x = a\), где \(a > 0\), и \(y = 0\) (рис. 34.2).

Рис. 34.1

\(\triangle\) Пользуясь тем, что предел суммы \(\sigma\) для непрерывной функции \(f(x) = x^{2}\) (см. раздел ) не зависит от способа дробления отрезка \(\Delta = \) и выбора точек \(\xi_{i}\) будем считать, что отрезок \(\Delta\) разбит на \(n\) отрезков равной длины, а в качестве точки \(\xi_{i}\ (i = \overline{1, n})\) взят правый конец отрезка \(\Delta_{i}\). Тогда \(\xi_{i} = x_{i} = \displaystyle \frac{a}{n}i,\ \Delta x_{i} = \frac{a}{n},\ \sigma = \sum_{\substack{i=1} }^{\substack{n}}x_{i}^{2}\Delta x_{i} = \frac{a^{3}}{n^{3}}\sum_{\substack{i=1} }^{\substack{n}}i^{2}\).

Так как \(\displaystyle \sum_{i=1}^{n}i^{2} = \frac{n(n + 1)(2n + 1)}{6}\) (доказательство представлено ), то \(\sigma =\displaystyle \frac{a^{3}}{3}\left(1 + \frac{1}{n}\right)\left(1 + \frac{1}{2n}\right)\), откуда \(\displaystyle \lim_{n \rightarrow \infty} \sigma = \frac{a^{3}}{3}\). Поэтому искомая площадь  равна \(\displaystyle \frac{a^{3}}{3}\). \(\blacktriangle\)

Заметим, что этот результат был получен еще Архимедом с помощью предельного перехода. Существует также простой способ нахождения предела для \(\sigma\), основанный на .

Работа переменной силы.

Пусть материальная точка движется вдоль числовой прямой \(Ox\) под действием силы \(P\), причем направление действия силы совпадает с направлением движения материальной точки. Предположим, что сила \(P\) задана как непрерывная функция от координаты \(x\) этой прямой, то есть \(P = P(x)\).

Найдем работу силы \(P\) при перемещении материальной точки от \(x = a\) до \(x = b\). Разобьем отрезок , как и в задаче о площади криволинейной трапеции, точками \(x_{i}\) и выберем  \(\xi_{i} \in \Delta_{i} (i = \overline{1, n})\). Тогда работа силы \(P\) на отрезке \(\Delta_{i}\) приближенно равна \(P(\xi_{i})\Delta x_{i}\), а на отрезке работу этой силы можно считать приближенно равной сумме \(\displaystyle \sum_{i=1}^{n}P(\xi_{i})\Delta x_{i}\). Предел этой суммы (при тех же условиях, что и в задаче о площади) естественно назвать работой переменной силы при перемещении материальной точки из точки \(a\) в точку \(b\).

В рассмотренных задачах речь идет о нахождении предела сумм вида \(\displaystyle \sum_{i=1}^{n}f(\xi_{i})\Delta x_{i}\), которые называют интегральными суммами. К вычислению предела таких сумм сводится решение многих важных задач из геометрии, физики, техники и других дисциплин. Поэтому вопросы, связанные с обоснованием предельного перехода описанного типа, заслуживают всестороннего изучения.