Содержание
Cateau

Cateau – расслабляющий визуальный роман с приятной и стильной рисовкой, предлагающий неспешно прогуляться по улицам Парижа и по-новому взглянуть на дружбу.
А начинается все с того, что в один прекрасный день вы замечаете, что ваша соседка по комнате загрустила, кажется больной, будто в ней пропала искра жизни. Как настоящий друг вы должны найти способ ей помочь, и начать стоит с одного из ее главных интересов – кошек.
Отправляйтесь на очаровательно атмосферные улицы Парижа, знакомьтесь с по-настоящему разными персонажами, общайтесь с кошками, но помните, что каждый ваш выбор влечет за собой последствия и может кардинально изменить исход этого маленького, но такого важного приключения
Зачем создавать ПАО
Если число партнёров по бизнесу растет, и уже превысило 50, а это максимальное для ООО (общества с ограниченной ответственностью) количество участников, или же акции планируется выводить на рынок для привлечения дополнительных инвесторов, где они могут продаваться желающими гражданами.
Тогда создание ПАО оправдано, и грандиозные цели компенсируют сложности его образования.

Что такое ПАО? Прежде всего, это коммерческая организация, созданная, чтобы получать прибыль от деятельности. При этом деятельность может быть любой, разрешённой законами России.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Использую для заработка
Как действует яд «Новичок»?
О химическом составе и, как следствие, действии «Новичка» на организм известно мало. Предполагается Вил Мирзаянов: «Новичок» могли произвести только в России , что яд работает как ингибитор холинэстеразы. По сообщениям Zweites Statement der Charité: Klinische Befunde weisen auf Vergiftung von Alexei Nawalny hin врачей из берлинской клиники Charite, именно этот токсин был обнаружен в организме Алексея Навального.
Ингибиторы холинэстеразы содержатся в ядах природного происхождения (например, некоторых видов змей), а также синтезируются искусственно. Это соединение стимулирует нервную систему. В определённых дозах его используют Роль ингибиторов ацетилхолинэстеразы при лечении психических заболеваний, в том числе болезней Альцгеймера и Паркинсона. Разберёмся, как оно работает.
Холинэстераза — группа ферментов, которые разрушают нейромедиатор ацетилхолин. Ацетилхолин, в свою очередь, — это вещество, благодаря которому происходит передача сигналов от одного нейрона к другому. Он играет важную роль: благодаря ацетилхолину нервные клетки активно «общаются» между собой, стимулируют мышцы
А человек получает возможность быстро и энергично двигаться, концентрировать внимание, учиться, переживать возбуждение
Ингибитор холинэстеразы — это вещество, которое подавляет действие фермента, что ведёт к увеличению количества ацетилхолина в организме. В результате нервные клетки начинают обмениваться сигналами слишком интенсивно. Это вызывает постоянное возбуждение, перенапряжение, спазм мышц, судороги.
Оценка сложности
Сложность алгоритмов обычно оценивают по времени выполнения или по используемой памяти. В обоих случаях сложность зависит от размеров входных данных: массив из 100 элементов будет обработан быстрее, чем аналогичный из 1000. При этом точное время мало кого интересует: оно зависит от процессора, типа данных, языка программирования и множества других параметров. Важна лишь асимптотическая сложность, т. е. сложность при стремлении размера входных данных к бесконечности.
Допустим, некоторому алгоритму нужно выполнить условных операций, чтобы обработать элементов входных данных. При увеличении на итоговое время работы будет значительно больше влиять возведение в куб, чем умножение его на или же прибавление . Тогда говорят, что временная сложность этого алгоритма равна , т. е. зависит от размера входных данных кубически.
Использование заглавной буквы О (или так называемая О-нотация) пришло из математики, где её применяют для сравнения асимптотического поведения функций. Формально означает, что время работы алгоритма (или объём занимаемой памяти) растёт в зависимости от объёма входных данных не быстрее, чем некоторая константа, умноженная на .
2 Актуальность
На официальном сайте всегда представлена актуальная информация. Часы работы организации, адреса офисов, расписание поездов, обновления той или иной программы и другие важные данные всегда следует смотреть на официальных сайтах.
Информация на других неофициальных сайтах может быть поначалу актуальной. Однако впоследствии выложенная на неофициальном сайте информация зачастую не обновляется и поэтому со временем быстро утрачивает актуальность.
Представители официальной компании внимательно следят за актуальностью информации, изложенной на официальном сайте, и вовремя актуализируют ее, обновляют. Изложенные факты оперативно корректируют, устаревшие данные удаляют, новый контент добавляют.
Что такое нотация О большое и почему оно важно
Проще говоря, нотация О большое описывает сложность вашего кода с использованием алгебраических терминов.
Чтобы понять, что такое О большое, мы можем взглянуть на типичный пример O (n²), который обычно произносится как «Большой O в квадрате». Буква «n» здесь представляет размер входных данных, а функция «g (n) = n²» внутри «O ()» дает нам представление о том, насколько сложен алгоритм по отношению к количеству входных данных.
Типичным алгоритмом со сложностью O(n²) будет алгоритм сортировки выбором. Сортировка выбором — это алгоритм сортировки, который выполняет итерацию по списку, чтобы гарантировать, что каждый элемент с индексом i является i-м наименьшим/наибольшим элементом списка. Наглядный пример.
Алгоритм может быть описан следующим кодом. Чтобы убедиться, что i-й элемент является i-м наименьшим элементом в списке, этот алгоритм сначала просматривает список с помощью цикла for. Затем для каждого элемента он использует другой цикл for, чтобы найти наименьший элемент в оставшейся части списка.
SelectionSort(List) {
for(i from 0 to List.Length) {
SmallestElement = List
for(j from i to List.Length) {
if(SmallestElement > List) {
SmallestElement = List
}
}
Swap(List, SmallestElement)
}
}
В этом сценарии мы рассматриваем переменную List как входные данные, поэтому размер ввода n — это количество элементов внутри List. Предположим, что оператор if, а присвоение значения, ограниченное оператором if, занимает постоянное время. Затем мы можем найти О большое для функции SelectionSort, проанализировав, сколько раз выполняются операторы.
Сначала внутренний цикл for выполняет операторы внутри n раз. А затем, после увеличения i, внутренний цикл for выполняется n-1 раз … пока он не будет запущен еще один раз, тогда оба цикла for достигнут своих условий завершения.
 Selection Sort Loops Illustrated
Selection Sort Loops Illustrated
На самом деле это в конечном итоге дает нам геометрическую сумму, и благодаря математики средней школе мы обнаружим, что внутренний цикл будет повторяться 1 + 2… + n раз, что равно n(n-1)/2 раза. Если мы умножим это, мы получим n²/2-n/2.
Когда мы вычисляем О большое, мы заботимся только о доминирующих операторах, и не заботимся о коэффициентах. Таким образом, мы выбираем n² как О большое. Мы записываем его как O(n²), а произносим как «О большое в квадрате».
Теперь вам может быть интересно, что это за «доминирующие операторы»? И почему нас не волнуют коэффициенты? Не волнуйтесь, мы рассмотрим эти вопросы по очереди далее.
Общие понятия
Общество с Ограниченной Ответственностью – это организационная форма, определяющая правила ведения бизнеса и отношений между собственниками компании.
По наблюдениям она является наиболее востребованной среди владельцев малого бизнеса. ООО представляет собой компанию, созданную одним предпринимателем или объединением усилий нескольких партнеров, в число которых могут входить и другие ООО.
Организация является коммерческой, а главная цель ее функционирования – получение дохода. Прибыль делится между участниками, входящими в число организаторов бизнеса, пропорционально размеру их долей, а также иными способами, согласно Уставу сообщества.
Управление деятельностью фирмы передается исполнительному органу, который назначается учредителями. За собственниками сохраняется право влияния на стратегию работы организации за счет регулярного проведения общих собраний участников.
Учредитель, который решить не продолжать работать в рамках
данного ООО, может свою долю выставить на продажу или выйти, потребовав
возмещения стоимости имущества общества, соразмерного его долевому участию.
Причем первоочередное право приобретения имеют другие участники организации.
Сравнение сложности между типичными нотациями Больших O
Когда мы пытаемся выяснить О большое для конкретной функции g(n), мы заботимся только о доминирующем операторе (dominant term) функции. Доминирующий оператор — это такой оператор, который растет быстрее всего.
Например, n² растет быстрее, чем n, поэтому, если у нас есть что-то вроде g(n) = n² + 5n + 6, то О большое будет (n²). Если вы когда нибудь проводили некоторые исчисления, это очень похоже на сокращение пределов для дробных многочленов, когда вам важен только доминирующий оператор для числителей и знаменателей в конце.
 Another way to look at Big O, Image from Stack Overflow
Another way to look at Big O, Image from Stack Overflow
Но какая функция растет быстрее, чем другие? На самом деле существует довольно много правил.
 Complexity Growth Illustration from Big O Cheatsheet
Complexity Growth Illustration from Big O Cheatsheet
1. O(1) имеет наименьшую сложность
Часто называемый «постоянный по времени», если вы можете создать алгоритм для решения проблемы с O(1), то это будет лучший выбор алгоритма. В некоторых сценариях сложность может выходить за пределы O(1), тогда мы можем проанализировать их, найдя ее аналог O(1/g(n)). Например, O(1/n) является более сложным, чем O(1/n²).
2. O (log(n)) является более сложным, чем O(1), но менее сложным, чем полиномы
Поскольку сложность часто связана с алгоритмами «разделяй и властвуй», O (log(n)) — это, как правило, хорошая сложность, которую можно достичь для алгоритмов сортировки. O (log(n)) является менее сложным, чем O (√n), потому что функцию квадратного корня можно считать полиномом, где показатель степени равен 0,5.
5. Факториалы имеют большую сложность, чем степень
Если вам интересны доказательства, посмотрите Гамма-функцию (Gamma function), это аналитическое продолжение факториала. Краткое доказательство состоит в том, что и факториалы, и степень имеют одинаковое количество умножений, но числа, которые умножаются, растут для факториалов, оставаясь неизменными для степени.
6. Умножение
При умножении сложность будет больше, чем оригинал, но не больше, чем эквивалентность умножения чего-то более сложного. Например, O (n*log (n)) является более сложным, чем O (n), но менее сложным, чем O (n²), потому что O (n²) = O (n * n), а n более сложный, чем log (n). ).
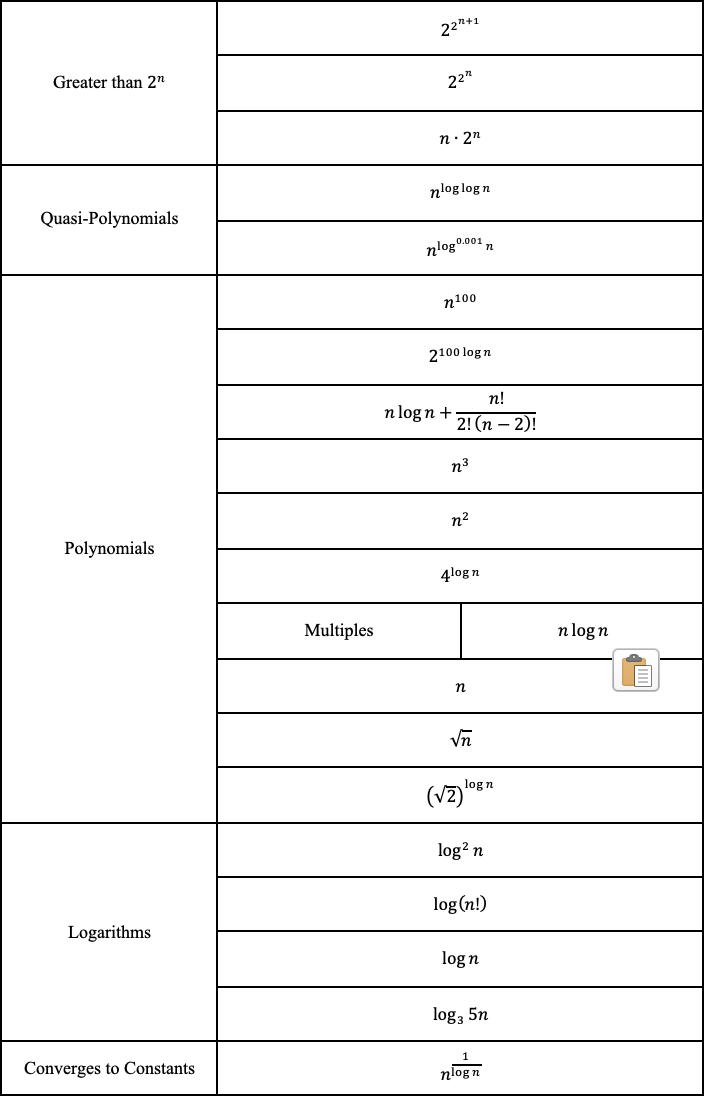
Если хотите можете проверить свое понимание. Попробуйте ранжировать следующие функции от самых сложных до менее. Решения с подробными объяснениями можно будет найти в следующем разделе. Некоторые из них достаточно сложные и могут потребовать более глубокого понимания математики. Когда вы доберетесь до решения, вы узнаете об этом больше.
 Examples taken from Textbook Problems
Examples taken from Textbook Problems
Учредители
Предприниматель или организация, которые участвуют в создании Общества с Ограниченной Ответственностью, называется учредителями. Каждый из них имеет свою долю, влияние на деятельность компании и получение части прибыли от коммерческой деятельности.
С первого дня существования ООО, его учредители заносятся в список, который в последующем хранится 50 лет.
Какая информация фиксируется:
- данные учредителя;
- номер, серия, дата выдачи паспорта, вид и адрес регистрации;
- если совладелец юридическое лицо – его название и юридический адрес;
- величина доли;
- дата и способ ее внесения.

Лучшая, Средняя, Худшая, Ожидаемая Сложность
Сложность также может быть проанализирована как лучший случай, наихудший случай, средний случай и ожидаемый случай.
Для примера давайте рассмотрим сортировку вставками (insertion sort). Сортировка вставками выполняет итерацию по всем элементам в списке. Если элемент больше, чем его предыдущий элемент, он вставляет элемент назад, пока он не станет больше, чем предыдущий элемент.
 Insertion Sort Illustrated, Image from Wikipedia
Insertion Sort Illustrated, Image from Wikipedia
Если массив изначально отсортирован, обмен вообще не будет произведен. Алгоритм будет просто пройдет итерацию по массиву один раз, что приведет к временной сложности O (n). Следовательно, мы бы сказали, что наилучшая временная сложность сортировки вставками — O (n). Сложность O (n) также часто называют линейной сложностью.
Иногда алгоритму может просто не повезти. Например, быстрая сортировка будет должна пройти через список за O (n), если элементы отсортированы в обратном порядке, но в среднем этот алгорит сортирует массив за O (n * log(n)). Как правило, когда мы оцениваем временную сложность алгоритма, мы смотрим на ее худшую производительность. Подробнее об этом и быстрой сортировке мы поговорим в следующем разделе.
Средняя сложность описывает ожидаемую производительность алгоритма. Иногда включает в себя расчет вероятности каждого сценария. Ниже приведена шпаргалка по временной и пространственной сложности типичных алгоритмов.
 Big O Cheatsheet for Common Algorithms
Big O Cheatsheet for Common Algorithms
Решение для вопроса из Раздела 4:
Осматривая функции, мы можем начать с ранжирования следующих полиномов от наиболее сложного до менее по правилу 3. Где корень квадратный из n равен просто n в степени 0,5.

Тогда, применяя правила 2 и 6, мы получим следующее. Логарифм с основанием 3 может быть преобразован в с основанием 2 (log base conversions). Логарифм с основанием 3 по-прежнему растет немного медленнее, чем с основанием 2, и поэтому в рейтинге получает место после него.

Остальные могут показаться немного сложными, но давайте попробуем быть немного повнимательнее и посмотреть, как же все такие их можно расположить.
Прежде всего, 2 в степени 2 в степени n больше 2 в степени n, а +1 еще больше его увеличивает.

Чтобы степень log (n) с основанием 2 была равна n, мы можем преобразовать следующее. Логарифм от 0,001 растет немного больше, чем просто константы, но меньше, чем почти все остальное.

Выражение, у которого n в степени log (log (n)), на самом деле является вариацией квазиполинома (, который больше полинома, но меньше экспоненты. Поскольку log (n) растет медленнее, чем n, его сложность немного меньше. Выражение с обратным логарифмом сходится к константе, поскольку 1 / log (n) расходится к бесконечности.

Факториалы могут быть представлены умножением и, следовательно, могут быть преобразованы в сложения вне логарифмической функции. «N select 2» может быть преобразовано в полином с кубическим членом, являющимся наибольшим.

И, наконец, мы можем ранжировать функции от самых сложных до наименее сложных.
5 Экономия личного времени пользователя
Пользователь интернета в поисках необходимой информации зачастую проводит много времени за компьютером, планшетом, телефоном. Поисковик может «подсовывать» человеку разные сайты-посредники, либо даже мошеннические сайты.
О связи между фейками и официальным сайтом
Фейки являются ложной информацией, которая распространяется в сети весьма быстро. Если пользователь не хочет способствовать распространению фейков в сети, ему нужно проверять по возможности информацию на официальном сайте. Цитировать информацию или давать на нее ссылки также лучше именно с официальных сайтов.
В общем, перепостить информацию с официального сайта – это одно дело. Тут владелец официального сайта с большой долей вероятности отвечает за выложенные в сети сведения. Перепосты с других неофициальных ресурсов – это зачастую распространение непроверенной информации. Обычно пересказывают понравившуюся информацию, а не достоверную, актуальную и надежную.
Какая информация должна быть на официальном сайте
Основные сведения, которые обычно представлены на официальных сайтах, перечислены ниже.
1 Логотип или товарный знак компании;
2 Услуги, товары, цены;
3 Подробное описание предлагаемых услуг, товаров;
4 Обратная связь, чтобы можно было связаться с представителем компании разными способами: телефон (звонки часто бывают бесплатными для клиента по номеру 8-800-…), электронная почта, онлайн-чаты с консультантами;
5 Контактные данные компании, включая ее ИНН, КПП, ОГРН и прочие реквизиты, зарегистрированные в официальных реестрах;
6 Сведения о компании, описание ее деятельности, миссия;
7 Поиск информации на сайте. Этот инструмента называется «поиск по сайту». С его помощью можно искать информацию в пределах данного официального сайта, а не по всему интернету, чтобы случайно в ходе поиска не «выпасть» в общую сеть с возможно недостоверной и непроверенной информацией;
8 Выбор языка, например, русского или английского. Международная поддержка языков необходима, если компания имеет зарубежные представительства или работает с клиентами из других стран.
Видеоформат статьи
Другие материалы:
1. Пять официальных браузеров
2. Ventusky: интерактивный сервис погоды вашего региона и всего мира
3. Как происходит сражение за пользователя между Google и Яндексом?
4. Какие бывают поисковые системы и как они работают?
5. Что такое пиратский контент, как он попадает в сеть и почему иногда исчезает?
ПАО (ОАО) — это публичное акционерное общество
Если компания позиционирует себя как Непубличное АО, она не обязана выводить свои акции на рынок, и может перераспределять доли с согласия своих акционеров.

Переименования АО были приняты законодательно в 2014 г. в связи с необходимостью приблизить российские законодательные нормативы к нормам корпоративного права Европы.

Сегодня в мире бизнеса можно увидеть и обновлённые названия — ПАО и АО (НАО), и те, которые существовали до принятия изменений: ОАО и ЗАО. Согласно новым статьям ГК РФ, все зарегистрированные сегодня организации не обязаны срочно менять свои наименования. Поменяют они в тот момент, когда будут вносить изменения в устав, в рабочем порядке.
Но такие крупные и значимые для Российской экономики организации, как Газпром, Сбербанк, МТС, уже добавили к своему названию аббревиатуру ПАО.
Процедура банкротства юридического лица
Эта процедура состоит из нескольких этапов. Для того, чтобы начать банкротство компании, необходимо, чтобы было соблюдено одно из условий:
- долг на протяжении 3-х месяцев;
- сумма задолженности — не менее 300 тысяч рублей.
Далее подается заявление в Арбитражный суд, и назначается процедура. Некоторые компании предлагают юридическую помощь в подготовке, подаче документов и рассмотрении дела. Далее следуют этапы:
- Наблюдение для того, чтобы постараться максимально сохранить активы; проводится собрание кредиторов.
- Финансовое оздоровление. На этом этапе обязательна реструктуризация долга, составление графика погашение кредитов. Максимальный срок — 2 года.
- Внешнее управление не может длиться больше 1,5 лет. Пени и штрафы по открытым долгам не начисляются.
- Конкурсное производство. Если оздоровление не принесло своих плодов, тогда вводится процедура равномерного покрытия долга.
Процедура сложная и требует внимательной и тщательной подготовки, как и как открытие своего магазина оффлайн или онлайн формы.

Что такое сайт
Рассмотрим подробнее, что такое сайт,и какие функции он имеет. Веб-сайт представляет собой набор взаимосвязанных сетевых веб-ресурсов, таких как веб-страницы, которые обычно отождествляются с общим доменным именем это значит принадлежат одному владельцу или организации. Самым ярким примером можно назвать сайт wikipedia.org.
Самое распространённое деление сайтов происходит на 2 группы. Первые – это те, которые доступны из всей Глобальной сети, а вторые – те, доступ к которым разрешён только из определённой локальной сетки, с помощью URL сайта – это уникальный адрес ресурса. Например, внутри сети какой-то конкретной организации.
Веб-страницы, которые являются строительными блоками веб-сайтов, представляют собой документы, обычно составленные в виде простого текста с добавлением инструкций по форматированию языка разметки гипертекста (HTML, XHTML).

Они могут включать элементы с других веб-сайтов. Доступ к веб-страницам и их передачаосуществляются с помощью протокола передачи гипертекста (HTTP). А так же с дополнительным использованием HTTPS – это протокол, обеспечивающий шифрование данных, для обеспечения безопасности и конфиденциальности пользователя.
Веб-сайты могут иметь много функций и могут использоваться в различных направлениях. Сайт может быть персональным, корпоративным веб-сайтом для компании, правительственным, веб-ресурсом организации и т. д. Они, как правило, посвящены определенной теме или цели — от развлечений и социальных сетей до предоставления новостей и обучения.
Процедура банкротства физических лиц
Законодательная система, как и в случае банкротства ИП предусматривает грамотный юридический подход. Начать процедуру может само лицо, если его единичный или суммарный долг превысил 500 тысяч рублей или просрочка составила 3 месяца.
Подавать заявление можно как самостоятельно, так и его могут подать по отношению к третьим лицам кредиторы и представители налоговой службы.
Для начала законодательной системы должны быть определенные признаки банкротства. Ими могут стать требования кредиторов на сумму свыше пол миллиона рублей, или же добровольная подача документов, в случае, если долг не менее 200 тысяч рублей, но человек объективно понимает, что не сможет его полностью выплатить в уставленное время. Рекомендую наперед оценивать свои финансовые возможности, когда изучаете, что такое ипотека и сколько вам необходимо платить каждый месяц на протяжении всего периода.

Необходимые документы
Список весьма большой, и включает:
- паспорт;
- документы о семейном состоянии, свидетельства о рождении детей;
- копия ИНН;
- выписка по лицевому счету, копия СНИЛС;
- справка, которая подтверждает статус ИП или его отсутствие. Срок действия документа 5 дней;
- пакет документов, который описывает финансовое состояние;
- документы, доказывающие что есть задолженность.
Материалы рассматриваются от 15 дней до 3-х месяцев с момента подачи в суд.
Заявления о банкротстве
Когда вы оценили плюсы и минусы и приняли решение начать процедуру банкротства физического лица, необходимо написать заявление и подать его в Арбитражный суд. В нем указываете в типичной форме желание, чтобы вас признали банкротом, описывается суть дела, его нюансы.
Список кредиторов
Мало просто включить в список документов перечень лиц, кому должны денег, за какой период и сколько составляет просрочка. Необходимо каждый пункт подтвердить соответствующим документом — кредитным договором, расписками, чеками, банковскими выписками. В последствии он может расширяться, когда кредитор узнает о том, что должник начал процедуру и тоже захочет получить назад свои средства. Вполне логичный вопрос: как узнать является ли человек банкротом или находится в процессе получения такого статуса, чтобы успеть вовремя подать документы и стать в очередь. Получить информацию можно из источников:
- федерального реестра;
- сайт картотеки арбитражных дел;
- бюро кредитных историй.
Рекомендую также наперед детально изучить список документов для подачи перед тем, как оформить налог для самозанятых, чтобы в дальнейшем не возникало проблем.
Имущество для реализации
В пакет документов входят все документы, которые подтверждают право собственности — договоры купли-продажи, наследства, депозиты и прочее. В процессе разбирательств его опишут, оценят, выставят на аукцион и за эти средства будут взысканы долги в сторону кредиторов. Зная, чем чревато банкротство, многие лица выбирают технологию фиктивного банкротства.
Перед этим они «переводят» имущество на других лиц, и по сути на руках ничего не остается. Для банкрота это удобный сценарий, а вот для кредиторов возникает вопрос, как и когда он получить свои средства. А о том, что такое финансирование инвестиций, как избежать негативных моментов во время этого процесса можно узнать на www.iqmonitor.ru, где есть готовая тематическая статья.

Оплата госпошлины и заявление в суд
С собранным полным пакетом документов и заявление необходимо отправиться в суд, и приложить чек, который подтверждает оплату на сумму 300 рублей. Сотрудники канцелярии суда проверят весь пакет документов по перечню, который также прилагается к делу. Если чего-то будет не хватать, то процедура растягивается во времени, ведь документы нужно собрать и донести.
[править] Ссылки
- mhkoff
- Обзор на МХК от Badmaestro
| МХК относится к теме «ВКонтакте» | |||||||||||||||||||
|