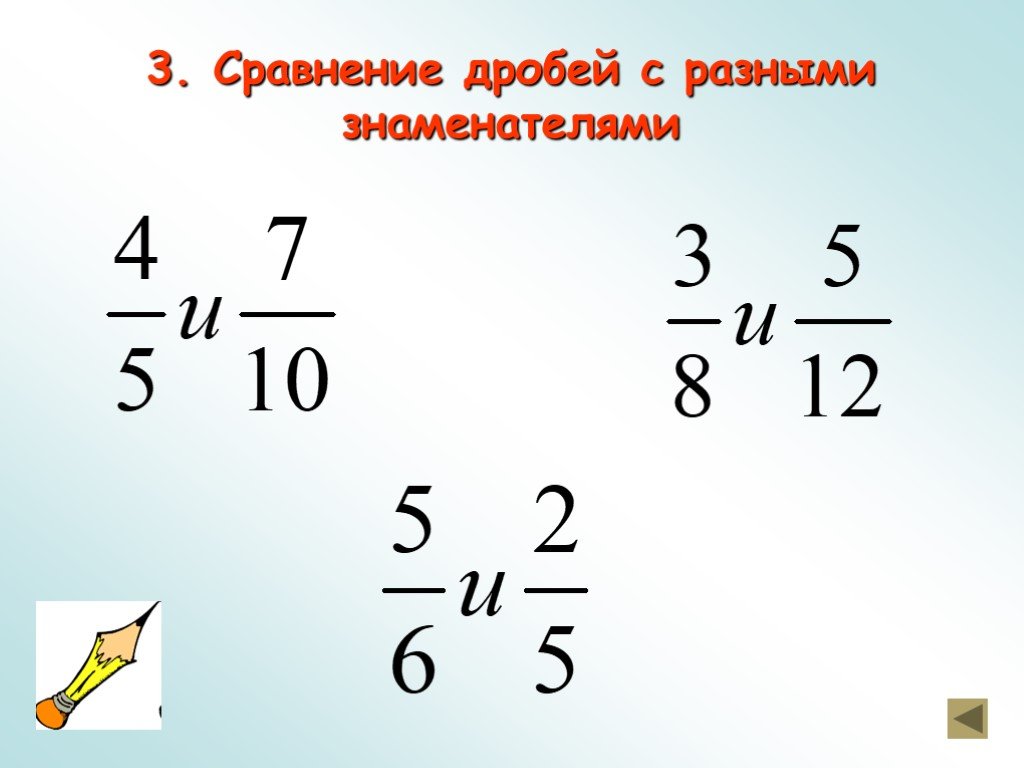
Ошибки
Школьники легко понимают тему неправильных и правильных дробей. Что такого сложного? Если уж ошибки и случаются, то практически всегда по невнимательности – неправильно найден общий знаменатель, например. Есть, конечно, и одна популярная ошибка, и допускается она в уравнениях.
Есть выражение: (3/4)x = 3. Требуется узнать, чему равен «икс». Ошибка может заключаться в том, что ученик осуществляет умножение обеих частей уравнения на ¾, а не деление. И тогда вместо верного ответа (x=4) получается неверный: x = 9/4. От этой проблемы избавиться легко – нужно всего лишь некоторое время не лениться записывать процедуру деления правой и левой части. Тогда ошибка сразу бросается в глаза.
Два подхода к решению заданий с разными числами
В примере требуется вычислить сумму и разность, а также произведение и частное двух чисел: 2 целых 3/5 и 14/11.
В первом подходе смешанное число будет представлено в виде неправильной дроби.
После выполнения действий, описанных выше, получится такое значение: 13/5.
Для того чтобы узнать сумму, нужно привести дроби к одинаковому знаменателю. 13/5 после умножения на 11 станет 143/55. А 14/11 после умножения на 5 примет вид: 70/55. Для вычисления суммы нужно только сложить числители: 143 и 70, а потом записать ответ с одним знаменателем. 213/55 — эта неправильная дробь ответ задачи.
При нахождении разности эти же числа вычитаются: 143 — 70 = 73. Ответом будет дробь: 73/55.
При умножении 13/5 и 14/11 не нужно приводить к общему знаменателю. Достаточно перемножить попарно числители и знаменатели. Получится ответ: 182/55.
Так же и при делении. Для правильного решения нужно заменить деление на умножение и перевернуть делитель: 13/5 : 14/11 = 13/5 х 11/14 = 143/70.
Во втором подходе неправильная дробь обращается в смешанное число.
После выполнения действий алгоритма 14/11 обратится в смешанное число с целой частью 1 и дробной 3/11.
Во время вычисления суммы нужно сложить целые и дробные части по отдельности. 2 + 1 = 3, 3/5 + 3/11 = 33/55 + 15/55 = 48/55. Итоговый ответ получается 3 целых 48/55. В первом подходе была дробь 213/55. Проверить правильность можно, переведя его в смешанное число. После деления 213 на 55 получается частное 3 и остаток 48. Нетрудно заметить, что ответ правильный.
При вычитании знак «+» заменяется на «-». 2 — 1 = 1, 33/55 — 15/55 = 18/55. Для проверки ответ из предыдущего подхода нужно перевести в смешанное число: 73 делится на 55 и получается частное 1 и остаток 18.
Для нахождения произведения и частного пользоваться смешанными числами неудобно. Здесь всегда рекомендуется переходить к неправильным дробям.
Взгляд с разных точек зрения
Прежде чем разбираться, как сделать неправильную дробь правильной, надо разобраться в более фундаментальных вопросах. А именно – о чем вообще идёт речь?
Рассмотрим пример из повседневной жизни. Возьмите пирог, разрежьте на одинаковые куски — каждый из них будет, по сути, правильной дробью, а именно – частью от некоторого целого. Что получится, если мы сложим все полученные фрагменты вместе? Один целый пирог. А что, если частей больше, чем нужно? Мы совместили куски, получив целый пирог, а ещё и лишние остались!
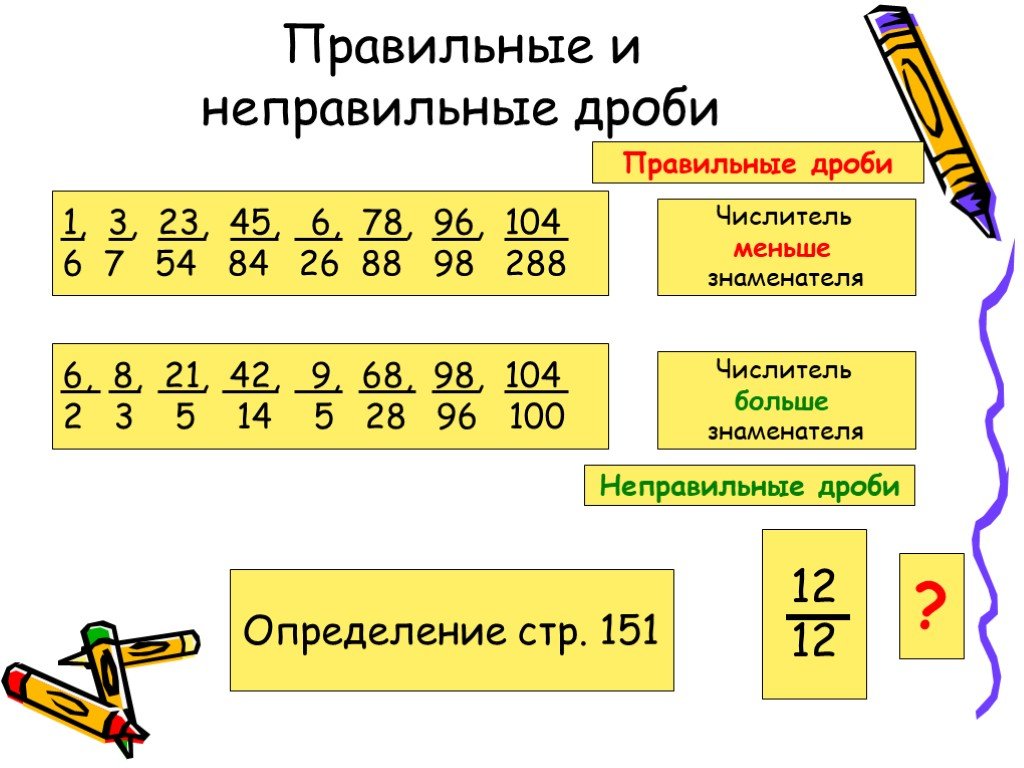
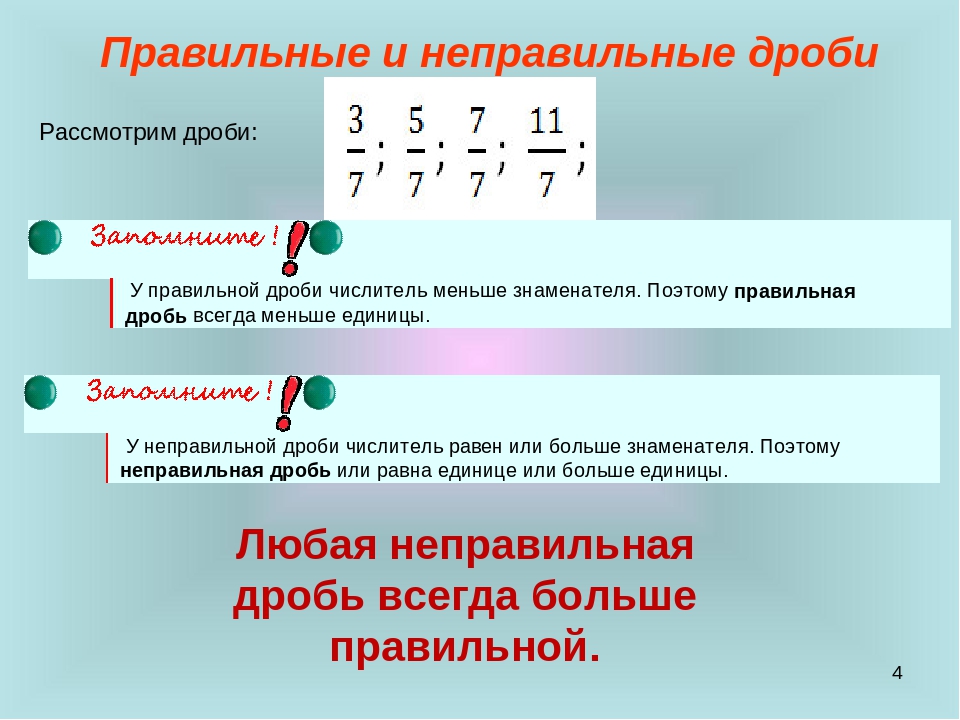
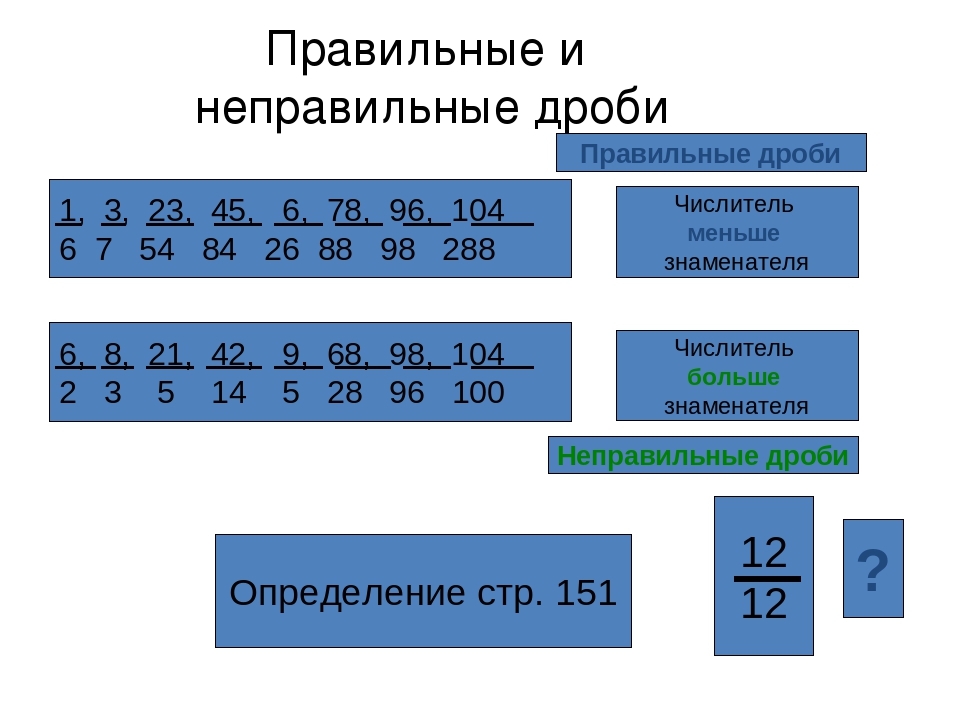
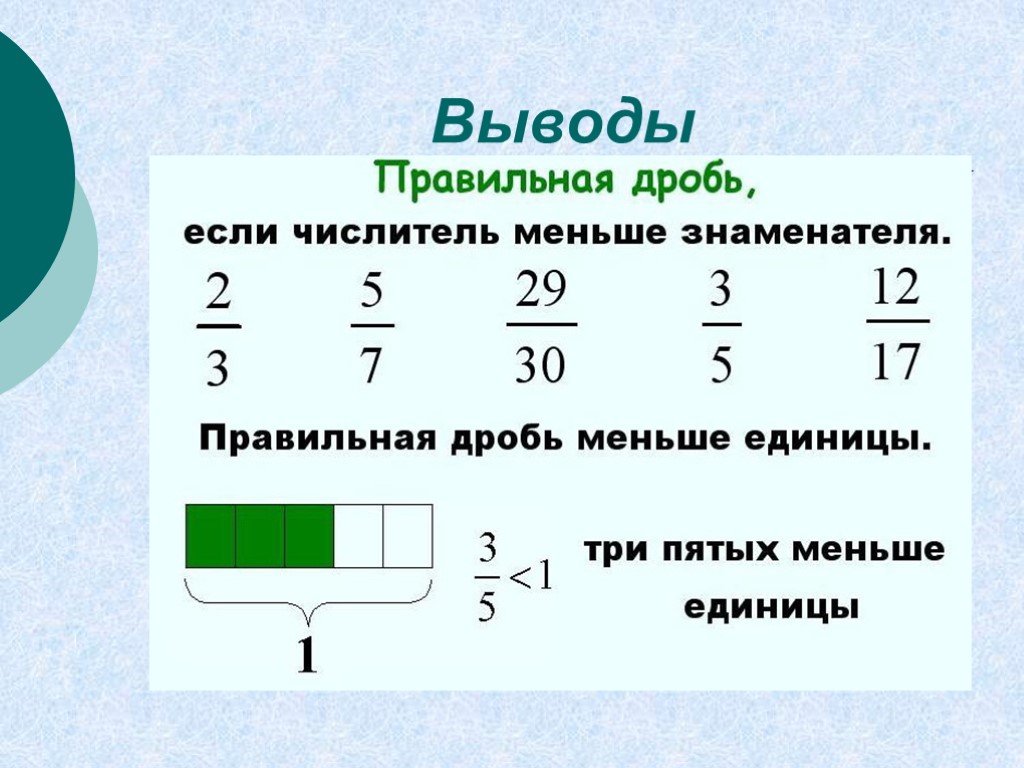
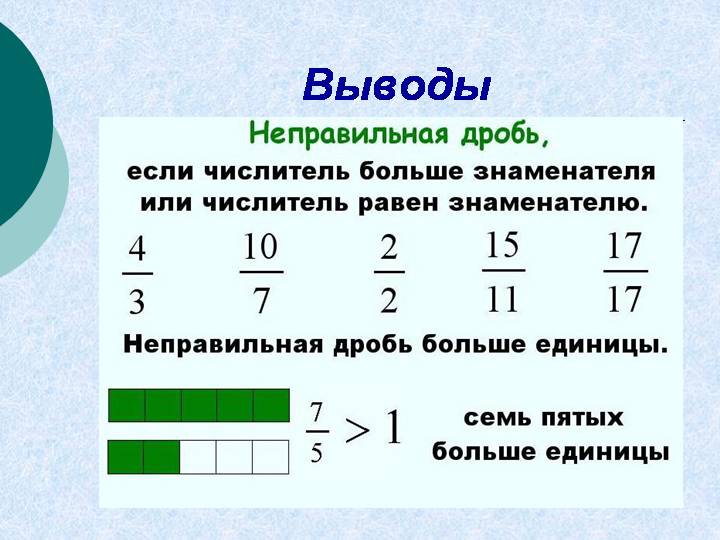
С математической точки зрения мы получили неправильная дробь – это когда части в сумме дают значение больше единицы. Узнать её в задаче или уравнении – легче лёгкого. Нижняя часть — знаменатель — у неё меньше, чем верхняя — числитель. А если нижнее число больше верхнего, то это правильная дробь.
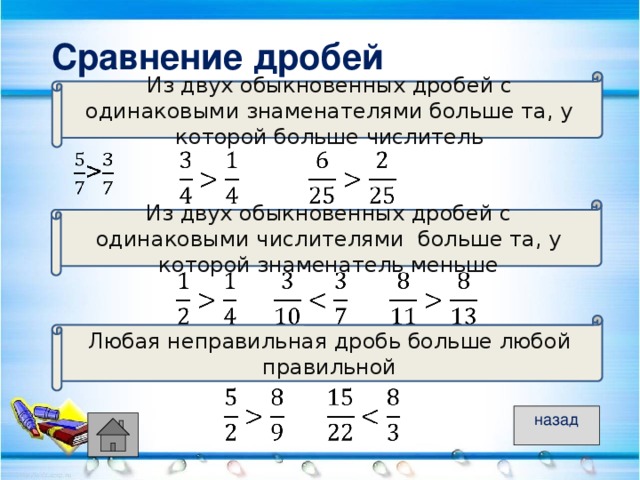
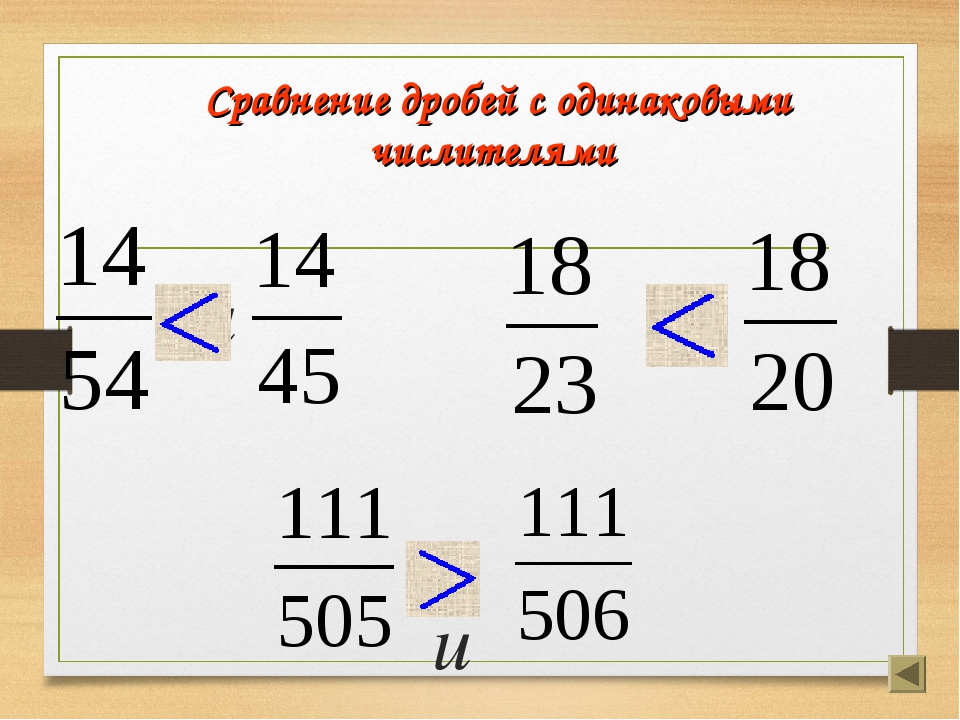
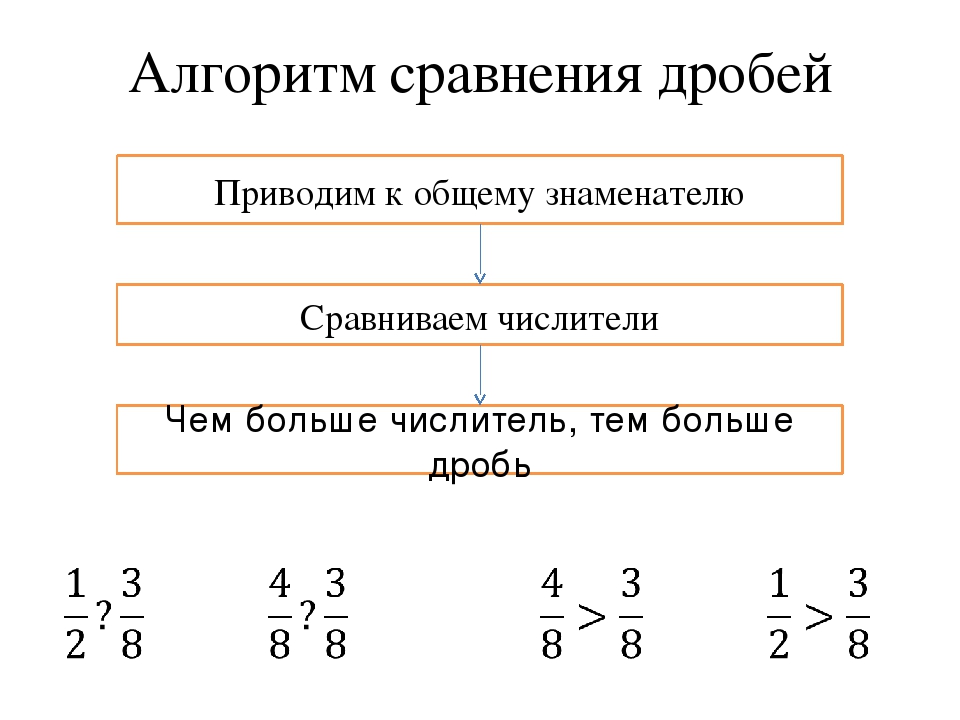
Сравнение неправильных дробей с одинаковыми знаменателями.
Есть несколько правил сравнения неправильных дробей с одинаковыми знаменателями:
- Если у неправильных дробей положительные числители, то та дробь больше у которой числитель больше.
- Если у неправильных дробей отрицательные числители, то та дробь больше у которой числитель меньше.
- Если у неправильных дробей разные знаки, то та дробь больше которая имеет знак “+”.
Рассмотрим пример:
Выполните сравнение неправильных дробей с одинаковыми знаменателями: а) \(\frac{20}{13}\) и \(\frac{15}{13}\) б) \(\frac{-161}{57}\) и \(\frac{-98}{57}\) г) \(\frac{17}{3}\) и \(\frac{-11}{3}\)
Решение:
а) Раз у дробей \(\frac{20}{13}\) и \(\frac{15}{13}\) одинаковые знаменатели переходим к сравнению числителей 20>15,
б) Так как знаменатели у дробей \(\frac{-161}{57}\) и \(\frac{-98}{57}\) одинаковые сравниваем отрицательные числители. Тот отрицательный числитель больше, который по модулю меньше.
|-161|=161
|-98|=98 меньше по модулю, значит это число ближе к нулю на числовой прямой чем -161, поэтому
-161<-98
г) Сравнивать дроби с разными знаками \(\frac{17}{3}\) и \(\frac{-11}{3}\) очень просто, та дробь больше которая имеет знак “+”.
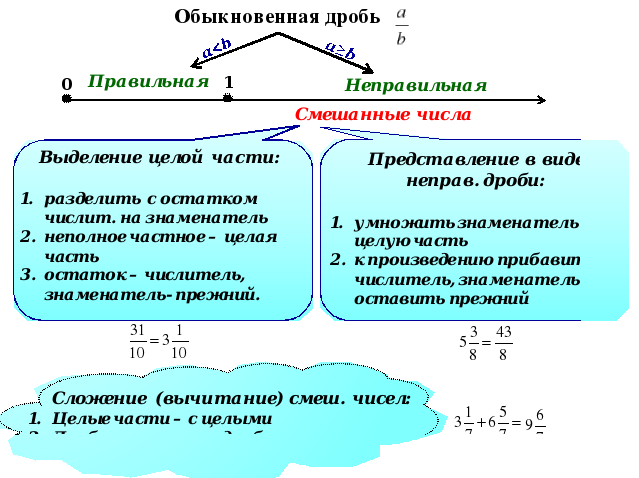
Как смешанную дробь перевести в неправильную дробь?
Чтобы из смешанной дроби сделать неправильную дробь нужно знаменатель умножить на целую часть и сложить с числителем, получим числитель неправильной дроби. А знаменатель остается без изменения. Рассмотрим пример:
Вопросы по теме:Смешанная дробь может быть меньше единицы?
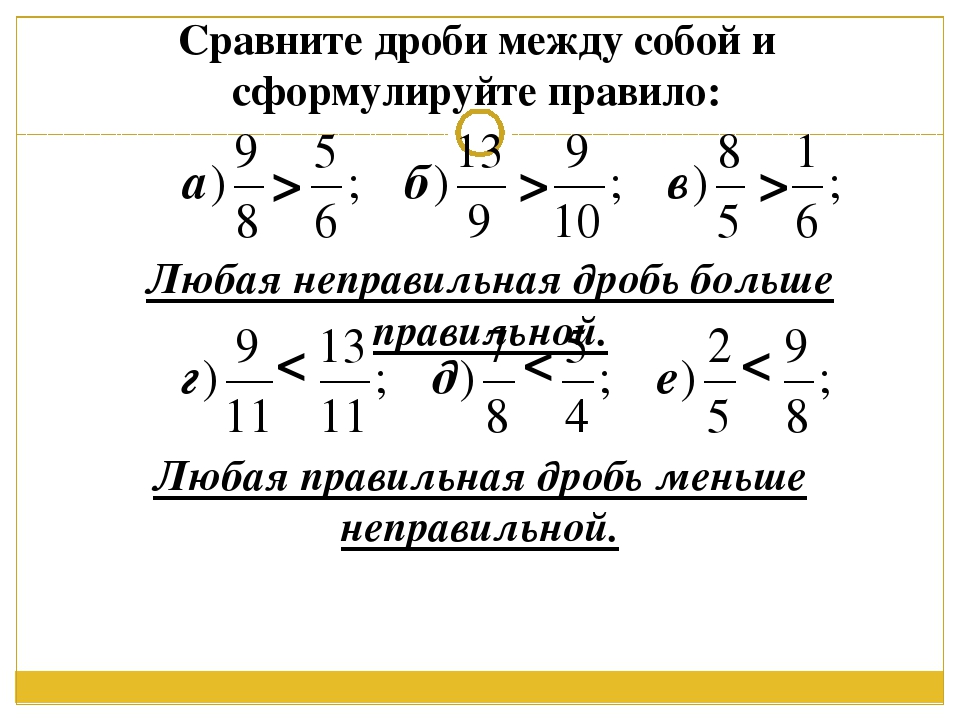
Ответ: нет, потому что смешанную дробь можно представить в виде неправильной дроби, а неправильная дробь всегда больше или равна единицы.
Что показывает целая часть у смешанной дроби?
Ответ: целая часть показывает сколько полных знаменателей содержит дробь.
Как представить смешанное число в виде неправильной дроби?
Ответ: к произведению знаменатели и целой части прибавить числитель получим числитель искомой неправильной дроби, а знаменатель не меняется.
Как перевести неправильную дробь в смешанное число? И как выделить целую часть?
Ответ: делим в столбик числитель на знаменатель, неполное частное – это целое, делитель – это знаменатель, а остаток – это числитель. Смотрите пример выше.
Что такое смешанные дроби или смешанные числа?
Ответ: Смешанные дроби – это числа, которые состоят из целой и дробной части.
Пример №1:
Представьте дробь в виде смешанного числа: \(\frac{508}{17}\)
Решение:
Разделим дробь столбиком:
Ответ: Получили смешанную дробь \(29\frac{15}{17}\)
Пример №2:
Представьте число в виде неправильной дроби: а) \(9\frac{2}{3}\), б) \(1\frac{3}{7}\)
Решение:
а) \(9\frac{2}{3} = \frac{9 \times 3 +2}{3} = \frac{29}{3}\\\\\)
б) \(1\frac{3}{7} = \frac{1 \times 7 +3}{7} = \frac{10}{7}\\\\\)
Задача №1:
Миша готовился к экзамену. За месяц он решил 120 задач. За первую неделю Миша решил \(\frac{2}{5}\) от этого числа. Сколько задач решил Миша за первую неделю?
Решение:
У нас есть дробь \(\frac{2}{5}\), знаменатель равен 5 это значит, что общее число 120 надо разделить на 5 и получим сколько составляет одна часть.
\(120 \div 5 = 24\) задачи это одна часть или \(\frac{1}{5}\)
В числителе стоит 2, значит нам надо взять две части, поэтому 24 умножаем на 2.
\(24 \times 2 = 48\) задач
Ответ: за неделю Миша решил 48 задач.
Недостаточность рациональных чисел
Гипотенуза такого треугольника не выражается никаким рациональным числом
В геометрии следствием так называемой аксиомы Архимеда (в более общем понимании, чем упомянуто выше) является возможность построения сколь угодно малых (то есть, коротких) величин, выражаемых рациональными числами вида 1n{\displaystyle 1/n}. Этот факт создаёт обманчивое впечатление, что рациональными числами можно измерить вообще любые геометрические расстояния. Легко показать, что это не верно.
Из теоремы Пифагора известно, что гипотенуза прямоугольного треугольника выражается как квадратный корень суммы квадратов его катетов. Т. о. длина гипотенузы равнобедренного прямоугольного треугольника с единичным катетом равна 2{\displaystyle {\sqrt {2}}}, то есть числу, квадрат которого равен 2.
Если допустить, что число 2{\displaystyle {\sqrt {2}}} представляется некоторым рациональным числом, то найдётся такое целое число m{\displaystyle m} и такое натуральное число n{\displaystyle n}, что 2=mn{\displaystyle {\sqrt {2}}={\frac {m}{n}}}, причём дробь mn{\displaystyle {\frac {m}{n}}} несократима, то есть числа m{\displaystyle m} и n{\displaystyle n} — взаимно простые.
Если 2=mn{\displaystyle {\sqrt {2}}={\frac {m}{n}}}, то 2=2⋅2=mn⋅mn=m2n2{\displaystyle 2={\sqrt {2}}\cdot {\sqrt {2}}={\frac {m}{n}}\cdot {\frac {m}{n}}={\frac {m^{2}}{n^{2}}}}, то есть m2=2n2{\displaystyle m^{2}=2n^{2}}. Следовательно, число m2{\displaystyle m^{2}} чётно, но произведение двух нечётных чисел нечётно, что означает, что само число m{\displaystyle m} также чётно. А значит найдётся натуральное число k{\displaystyle k}, такое что число m{\displaystyle m} можно представить в виде m=2k{\displaystyle m=2k}. Квадрат числа m{\displaystyle m} в этом смысле m2=4k2{\displaystyle m^{2}=4k^{2}}, но с другой стороны m2=2n2{\displaystyle m^{2}=2n^{2}}, значит 4k2=2n2{\displaystyle 4k^{2}=2n^{2}}, или n2=2k2{\displaystyle n^{2}=2k^{2}}. Как уже показано ранее для числа m{\displaystyle m}, это значит, что число n{\displaystyle n} — чётно, как и m{\displaystyle m}. Но тогда они не являются взаимно простыми, так как оба делятся на . Полученное противоречие доказывает, что 2{\displaystyle {\sqrt {2}}} не есть рациональное число.
Из вышесказанного следует, что существуют отрезки на плоскости, а, значит, и на числовой прямой, которые не могут быть измерены рациональными числами. Это приводит к возможности расширения понятия рациональных чисел до вещественных.
Какие бывают дроби
Знакомство с новой темой в школе начинается с обыкновенных дробей. Их легко узнать по горизонтальной черте, разделяющей два числа – сверху и снизу. Верхнее называется числителем, нижнее – знаменателем. Существует и строчный вариант написания неправильных и правильных обыкновенных дробей – через косую черту, например: ½, 4/9, 384/183. Такой вариант используется, когда высота строки ограничена и нет возможности применить «двухэтажную» форму записи. Почему? Да потому что она удобнее. Чуть позже мы в этом убедимся.
Помимо обыкновенных, существуют также десятичные дроби. Различить их очень просто: если в одном случае используется горизонтальная или наклонная черта, то в другом – запятая, разделяющая последовательности цифр. Посмотрим пример: 2,9; 163,34; 1,953. Мы намеренно воспользовались точкой с запятой в качестве разделителя, чтобы разграничить числа. Первое из них будет читаться так: «две целых, девять десятых».
Распространенные ошибки
При осуществлении действий с дробями учащийся может легко совершить одну из популярных ошибок. Обычно они происходят из-за невнимательности, а иногда – из-за того, что изученный материал ещё не отложился в голове как следует.
Нередко сумма чисел, стоящая в числителе, вызывает желание сократить отдельные её компоненты. Допустим, в примере: (13 + 2) / 13, написанном без скобок (с горизонтальной чертой), многие ученики по неопытности зачеркивают 13 сверху и снизу. Но так делать нельзя ни в коем случае, ведь это грубая ошибка! Если бы вместо сложения стоял знак умножения, мы получили бы в ответе число 2. Но при осуществлении сложения никакие операции с одним из слагаемых не позволительны, только со всей суммой целиком.
Ещё ребята часто ошибаются при делении дробей. Возьмем две правильные несократимые дроби и разделим друг на друга: (5/6) / (25/33). Ученик может перепутать и записать результирующее выражение как ( 25) / (6*33). Но так бы получилось при умножении, а в нашем случае всё будет несколько иначе: ( 33) / (6*25). Сокращаем то, что возможно, и в ответе увидим 11/10. Получившуюся неправильную дробь запишем как десятичную — 1,1.
Сокращение смешанных дробей.
Смешанные дроби по тем же правилам что и обыкновенные дроби. Разница лишь в том, что мы можем целую часть не трогать, а дробную часть сократить или смешанную дробь перевести в неправильную дробь, сократить и перевести обратно в правильную дробь.
Рассмотрим пример:
Сократите смешанную дробь \(2\frac{30}{45}\).
Решение:
Решим двумя способами:Первый способ:
Распишем дробную часть на простые множители, а целую часть не будем трогать.
Второй способ:
Переведем сначала в неправильную дробь, а потом распишем на простые множители и сократим. Полученную неправильную дробь переведем в правильную.
Вопросы по теме:Можно ли сокращать дроби при сложении или вычитании?
Ответ: нет, нужно сначала сложить или вычесть дроби по правилам, а только потом сокращать. Рассмотрим пример:
Вычислите выражение \(\frac{50+20-10}{20}\) .
Решение:
Часто допускают ошибку сокращая одинаковые числа в числителе и знаменателе в нашем случаем число 20, но их сокращать нельзя пока не выполните сложение и вычитание.
На какие числа можно сокращать дробь?
Ответ: можно сокращать дробь на наибольший общий делитель или обычный делитель числителя и знаменателя. Например, дробь \(\frac{100}{150}\).
Распишем на простые множители числа 100 и 150.
100=2⋅2⋅5⋅5
150=2⋅5⋅5⋅3
Наибольшим общим делителем будет число НОД(100, 150)= 2⋅5⋅5=50
Получили несократимую дробь \(\frac{2}{3}\).
Но необязательно всегда делить на НОД не всегда нужна несократимая дробь, можно сократить дробь на простой делитель числителя и знаменателя. Например, у числа 100 и 150 общий делитель 2. Сократим дробь \(\frac{100}{150}\) на 2.
Получили сократимую дробь \(\frac{50}{75}\).
Какие дроби можно сокращать?
Ответ: сокращать можно дроби у которых числитель и знаменатель имеют общий делитель. Например, дробь \(\frac{4}{8}\). У числа 4 и 8 есть число, на которое они оба делятся это число 2. Поэтому такую дробь можно сократить на число 2.
Пример:
Сравните две дроби \(\frac{2}{3}\) и \(\frac{8}{12}\).
Эти две дроби равны. Рассмотрим подробно дробь \(\frac{8}{12}\):
Отсюда получаем, \(\frac{8}{12}=\frac{2}{3}\)
Две дроби равны тогда и только тогда, когда одна из них получена путем сокращения другой дроби на общий множитель числителя и знаменателя.
Пример:
Сократите если возможно следующие дроби: а) \(\frac{90}{65}\) б) \(\frac{27}{63}\) в) \(\frac{17}{100}\) г) \(\frac{100}{250}\)
Решение:
а) \(\frac{90}{65}=\frac{2 \times \color{red} {5} \times 3 \times 3}{\color{red} {5} \times 13}=\frac{2 \times 3 \times 3}{13}=\frac{18}{13}\)
б) \(\frac{27}{63}=\frac{\color{red} {3 \times 3} \times 3}{\color{red} {3 \times 3} \times 7}=\frac{3}{7}\)
в) \(\frac{17}{100}\) несократимая дробь
г) \(\frac{100}{250}=\frac{\color{red} {2 \times 5 \times 5} \times 2}{\color{red} {2 \times 5 \times 5} \times 5}=\frac{2}{5}\)
Как сократить?
Главное правило гласит, что долевую цифру можно сократить поделить ее числитель и знаменатель на одинаковый делитель (отличный от 0) так, чтобы получилась новая цифра с меньшими параметрами, но равная исходной по величине. Исходя из этого правила можно понять, что дроби бывают сократимые и несократимые.
Пример сокращения дробей: 8/24 сократим, поделив ее параметры на 2. Получим: 8:2=4 и 24:2=12. В результате, исходная цифра превратится в 4/12 . Можно повторить операцию, вновь поделив числа: 4:2=2 и 12:2=6. Получим 2/6. Еще раз повторим операцию: 2:2=1 и 6:2=3. В итоге получится несократимая цифра 1/3, поскольку ее параметры уже нельзя разделить на одинаковый делитель. Любое сократимое число можно привести к несократимому.
Важно ! Если делимое или делитель представлены выражением (, вначале каждое из выражений надо умножить на один множитель и дробь превратить в простую, сократив на этот множитель выражение: . Сокращать можно при умножении дробных выражений друг на друга: *
Сами по себе эти числа несократимые, но выполняя операцию умножения, можно сократить их по диагонали: * = =. Сокращать при умножении можно только крест-накрест: числитель первой со знаменателем второй, и наоборот
Сокращать можно при умножении дробных выражений друг на друга: *. Сами по себе эти числа несократимые, но выполняя операцию умножения, можно сократить их по диагонали: * = =. Сокращать при умножении можно только крест-накрест: числитель первой со знаменателем второй, и наоборот.
Сокращать можно и смешанную цифру, т.е. целую часть и правильную дробь представить в виде неправильной. Для этого следует выполнить некоторые действия:
- Имея 5, преобразуем его в неправильную дробь. Для этого знаменатель перемножим с его целой частью и приплюсуем к полученной цифре числитель: 5*9+1=46,
- Сумма станет числителем неправильной доли, а его низ позаимствуем от первоначальной,
- В итоге получаем: .
Справедливо и обратное действие: из неправильной дроби сделать смешанную. Для этого рассмотрим обратное действие с :
- Разделим между собой верх и низ: 46:9=5,111111111111111,
- Целый результат деления станет полной цифрой, а бесконечный остаток – верхом доли,
- Знаменатель при этом останется неизмененным,
- Получаем 5.
Таким способом сокращать дроби при любых операциях возможно. Можно сокращать значения ее делимого и делителя при умножении их на одинаковый множитель, и превращая из смешанного числа в долю, и наоборот.
Сокращение дробей
Счётность множества
Нумерация положительных рациональных чисел
Чтобы оценить количество рациональных чисел, нужно найти мощность их множества. Легко доказать, что множество рациональных чисел счётно. Для этого достаточно привести алгоритм, который нумерует рациональные числа, то есть устанавливает биекцию между множествами рациональных и натуральных чисел.
Примером такого построения может служить следующий простой алгоритм. Составляется бесконечная таблица обыкновенных дробей, на каждой i{\displaystyle i}-ой строке в каждом j{\displaystyle j}-ом столбце которой располагается дробь ij{\displaystyle {\frac {i}{j}}}. Для определённости считается, что строки и столбцы этой таблицы нумеруются с единицы. Ячейки таблицы обозначаются (i,j){\displaystyle \left(i,j\right)}, где i{\displaystyle i} — номер строки таблицы, в которой располагается ячейка, а j{\displaystyle j} — номер столбца.
Полученная таблица обходится «змейкой» по следующему формальному алгоритму.
- Если текущее положение (i,j){\displaystyle \left(i,j\right)} таково, что i{\displaystyle i} — нечётное, а j=1{\displaystyle j=1}, то следующим положением выбирается (i+1,j){\displaystyle \left(i+1,j\right)}.
- Если текущее положение (i,j){\displaystyle \left(i,j\right)} таково, что i=1{\displaystyle i=1}, а j{\displaystyle j} — чётное, то следующим положением выбирается (i,j+1){\displaystyle \left(i,j+1\right)}.
- Если для текущего положения (i,j){\displaystyle \left(i,j\right)} сумма индексов (i+j){\displaystyle \left(i+j\right)} нечётна, то следующее положение — (i−1,j+1){\displaystyle \left(i-1,j+1\right)}.
- Если для текущего положения (i,j){\displaystyle \left(i,j\right)} сумма индексов (i+j){\displaystyle \left(i+j\right)} чётна, то следующее положение — (i+1,j−1){\displaystyle \left(i+1,j-1\right)}.
Эти правила просматриваются сверху вниз и следующее положение выбирается по первому совпадению.
В процессе такого обхода каждому новому рациональному числу ставится в соответствие очередное натуральное число. То есть дроби 11{\displaystyle 1/1} ставится в соответствие число 1, дроби 21{\displaystyle 2/1} — число 2, и т. д. Нужно отметить, что нумеруются только несократимые дроби. Формальным признаком несократимости является равенство единице наибольшего общего делителя числителя и знаменателя дроби.
Следуя этому алгоритму, можно занумеровать все положительные рациональные числа. Это значит, что множество положительных рациональных чисел Q+{\displaystyle \mathbb {Q} _{+}} счётно. Легко установить биекцию между множествами положительных и отрицательных рациональных чисел, просто поставив в соответствие каждому рациональному числу противоположное ему. Т. о. множество отрицательных рациональных чисел Q−{\displaystyle \mathbb {Q} _{-}} тоже счётно. Их объединение Q+∪Q−{\displaystyle \mathbb {Q} _{+}\cup \mathbb {Q} _{-}} также счётно по свойству счётных множеств. Множество же рациональных чисел Q=Q+∪Q−∪{}{\displaystyle \mathbb {Q} =\mathbb {Q} _{+}\cup \mathbb {Q} _{-}\cup \left\{0\right\}} тоже счётно как объединение счётного множества с конечным.
Разумеется, существуют и другие способы занумеровать рациональные числа. Например, для этого можно воспользоваться такими структурами как дерево Калкина — Уилфа, дерево Штерна — Броко или ряд Фарея.
Утверждение о счётности множества рациональных чисел может вызывать некоторое недоумение, так как на первый взгляд складывается впечатление, что оно гораздо обширнее множества натуральных чисел. На самом деле это не так и натуральных чисел хватает, чтобы занумеровать все рациональные.
Как записать дробь на компьютере
Поскольку стандартные средства не всегда позволяют создать дробь, состоящую из двух «ярусов», ученики порой идут на различные ухищрения. Например, копируют числители и знаменатели в графический редактор «Пейнт» и склеивают их воедино, рисуя между ними горизонтальную линию. Конечно, есть более простой вариант, который, кстати, предоставляет и массу дополнительных возможностей, которые станут полезны вам в будущем.
Откройте «Майкрософт Ворд». Одна из панелей в верхней части экрана носит называние «Вставка» — нажмите её. Справа, в той стороне, где расположены значки закрытия и сворачивания окна, есть кнопка «Формула». Это именно то, что нам нужно!
Если вы воспользуетесь данной функцией, на экране появится прямоугольная область, в которой можно использовать любые математические знаки, отсутствующие на клавиатуре, а также писать дроби в классическом виде. То есть разделяя числитель и знаменатель горизонтальной чертой. Вы даже можете удивиться, что такую правильную дробь настолько легко записать.
