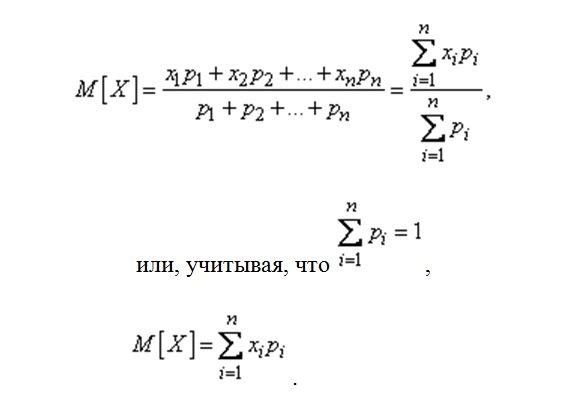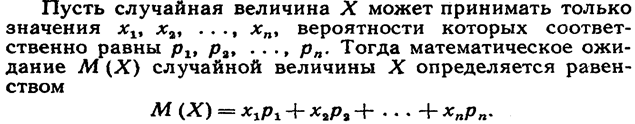Математическое ожидание дискретной случайной величины

Говоря простым языком, это среднеожидаемое значение при многократном повторении испытаний. Пусть случайная величина принимает значения с вероятностями соответственно. Тогда математическое ожидание данной случайной величины равно сумме произведений всех её значений на соответствующие вероятности:

или в свёрнутом виде:

Вычислим, например, математическое ожидание случайной величины – количества выпавших на игральном кубике очков:

очка

В чём состоит вероятностный смысл полученного результата? Если подбросить кубик достаточно много раз, то среднее значение выпавших очков будет близкО к 3,5 – и чем больше провести испытаний, тем ближе. Собственно, об этом эффекте я уже подробно рассказывал на уроке о статистической вероятности.

Теперь вспомним нашу гипотетическую игру:

Возникает вопрос: а выгодно ли вообще играть в эту игру? …у кого какие впечатления? Так ведь «навскидку» и не скажешь! Но на этот вопрос можно легко ответить, вычислив математическое ожидание, по сути – средневзвешенный по вероятностям выигрыш:

, таким образом, математическое ожидание данной игры проигрышно.

Не верь впечатлениям – верь цифрам!

Да, здесь можно выиграть 10 и даже 20-30 раз подряд, но на длинной дистанции нас ждёт неминуемое разорение. И я бы не советовал вам играть в такие игры 🙂 Ну, может, только ради развлечения.

Из всего вышесказанного следует, что математическое ожидание – это уже НЕ СЛУЧАЙНАЯ величина.

Творческое задание для самостоятельного исследования:

Пример 4

Мистер Х играет в европейскую рулетку по следующей системе: постоянно ставит 100 рублей на «красное». Составить закон распределения случайной величины – его выигрыша. Вычислить математическое ожидание выигрыша и округлить его до копеек. Сколько в среднем проигрывает игрок с каждой поставленной сотни?

Справка: европейская рулетка содержит 18 красных, 18 чёрных и 1 зелёный сектор («зеро»). В случае выпадения «красного» игроку выплачивается удвоенная ставка, в противном случае она уходит в доход казино

Существует много других систем игры в рулетку, для которых можно составить свои таблицы вероятностей. Но это тот случай, когда нам не нужны никакие законы распределения и таблицы, ибо доподлинно установлено, что математическое ожидание игрока будет точно таким же. От системы к системе меняется лишь дисперсия, о которой мы узнаем во 2-й части урока.

Но прежде будет полезно размять пальцы на клавишах калькулятора:

Пример 5

Случайная величина задана своим законом распределения вероятностей:

Найти , если известно, что . Выполнить проверку.

Есть?

Тогда переходим к изучению дисперсии дискретной случайной величины, и по возможности, ПРЯМО СЕЙЧАС!! – чтобы не потерять нить темы.

Решения и ответы:

Пример 3. Решение: по условию – вероятность попадания в мишень. Тогда: – вероятность промаха.

Составим – закон распределения попаданий при двух выстрелах:

– ни одного попадания. По теореме умножения вероятностей независимых событий:

– одно попадание. По теоремам сложения вероятностей несовместных и умножения независимых событий:

– два попадания. По теореме умножения вероятностей независимых событий:

Проверка: 0,09 + 0,42 + 0,49 = 1

Ответ

Примечание: можно было использовать обозначения – это не принципиально.

Пример 4. Решение: игрок выигрывает 100 рублей в 18 случаях из 37, и поэтому закон распределения его выигрыша имеет следующий вид: Вычислим математическое ожидание: Таким образом, с каждой поставленной сотни игрок в среднем проигрывает 2,7 рубля.

Пример 5. Решение: по определению математического ожидания: поменяем части местами и проведём упрощения:таким образом:

Выполним проверку:, что и требовалось проверить.

Ответ

(Переход на главную страницу)

ПОЛОЖИТЕЛЬНОЕ МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ – ЭТО ВАЖНО

Если ваша средняя прибыль превышает средний убыток, то вам нечего и париться. Если не верите, то давайте посчитаем! К примеру, вы взяли математическое ожидание 1 к 4. При этом, ваш стоп по сделке 10 пунктов, а тейк, соответственно, 40 пунктов. При этом, у вас только 30% прибыльных сделок, вы не ослышались, только 30%. За выборку возьмем 100 сделок, считаем:

70 сделок х 10 пунктов = – 700 пунктов.

30 сделок х 40 пунктов = + 1200 пунктов.

ИТОГ: + 500 пунктов.

Итого, как вы видите, даже при подавляющем большинстве убыточных сделок при таком математическом ожидании положительном вы бы все равно получали прибыль. Соответственно, как вы видите, в техническом плане все просто! У вас есть четкая система, есть четкие ММ, есть математическое ожидание и все, вы на лошадке.

Определение

Пусть задано вероятностное пространство (Ω,A,P){\displaystyle (\Omega ,{\mathfrak {A}},\mathbb {P} )} и определённая на нём случайная величина X{\displaystyle X}. То есть, по определению, XΩ→R{\displaystyle X\colon \Omega \to \mathbb {R} } — измеримая функция. Если существует интеграл Лебега от X{\displaystyle X} по пространству Ω{\displaystyle \Omega }, то он называется математическим ожиданием, или средним (ожидаемым) значением и обозначается MX{\displaystyle M} или EX{\displaystyle \mathbb {E} }.

MX=∫ΩX(ω)P(dω).{\displaystyle M=\int \limits _{\Omega }\!X(\omega )\,\mathbb {P} (d\omega ).}

Ключевые принципы математического анализа

Игроки разбирают поединки, опираясь на многие факторы. Новички порой игнорируют математический анализ, который разделяется на такие этапы:

сбор информации для определения рейтинга и текущей формы спортсменов и коллективов;
анализ отобранных данных и составляющих, которые сказываются на результате, например, умение организовывать голевые комбинации, пробивать в створ ворот или зарабатывать штрафные удары. Учитывается время на создание или реализацию различных действий;
разбор демотивационных моментов: пропущенные голы, игра в заключительные минуты встречи, тактические ошибки при обороне, действия команды и отдельных игроков в матчах с аутсайдерами/фаворитами и многое другое;
создание математической модели, в которую закладываются факторы, изложены выше;
анализ всех имеющихся данных, подведение итогов и принятие окончательного решения. Прогноз может говорить как о победе команды, так и о том, что она не проиграет.

Проведение математического расчета человеком, который никогда не сталкивался с алгоритмами, вызовет затруднения. Придется упорно поработать и изучить все тонкости способа, чтобы получить положительные результаты.

Еще одна сложность – беспристрастное отношение к командам. Симпатия к одному из соперников не даст трезво оценить вероятность определенного исхода. Преданный фанат будет верить в любимую команду, несмотря на очевидную логику и статистику.

Мат. ожидание в трейдинге

Одну формулу в пример я все-таки приведу, чтобы можно было уловить суть. Это один из вариантов, в котором учитывают показатель мат. ожидания.

При расчете мат. ожидания берется следующая формула: вероятность получения прибыли * на среднюю прибыль от одной сделки минус вероятность получения убытков * средний убыток от одной сделки. И если, к примеру, учесть тот факт, что положительных и отрицательных сделок у нас 50 на 50, при этом средняя прибыль 500 пунктов, а средний убыток 250, то получится формула вида: (0,5*500) – (0,5*250) = 250 – 125 = 125.

В данном идеальном варианте мат. ожидание положительное. И на самом деле, очень странно, когда пытаются взять идеальные условия и доказать что нужно делать так-то и так. Например, что обязательно каждая сделка должна быть не меньше чем 1 к 2 (убыток к прибыли). Или средний профит обязательно выше среднего убытка. Мы никогда не сможем точно определить вероятность прибыльной/убыточной сделки. Все необходимые значения мы сможем оценить лишь постфактум на условии статистики. Торговля не сможет вам гарантировать той или иной вероятности по сделке и по профиту.

Все это я рассказываю к тому, что пытаться рассчитать положительное или отрицательное мат. ожидание постфактум, учитывая только вышеуказанные показатели, не совсем верно. На положительные результаты в торговле влияет очень много факторов. Важнее просто грамотно вести статистику, записывать подробный результат и пытаться выяснить почему получился тот или иной итог. Возможно по текущей торговой формации слишком мало положительных сделок. Либо при увеличении показателя риск к прибыли результат был бы положительным

В этом случае важно учесть тот факт, что нужный нам показатель профита действительно будет оправданным и сделка будет срабатывать. Так как вроде бы с точки зрения мат

ожидания все сошлось, но на деле в реальной торговле инструмент не будет доходить до нашего профита, так как он оказался завышенным, либо мы не учли других факторов.

Также я могу сказать следующее, что даже если совершать сделки 1 к 1, то в некоторых случаях они могут быть абсолютно оправданными, если положительных сделок будет больше чем отрицательных. В некоторых моих формациях есть сделки 1 к 1, при этом результат по данным формациям положительный. Поэтому, в некоторых случаях не нужно доверять всему что написано. И когда я вижу утверждение, что можно зарабатывать на рынке лишь тогда, когда риск к прибыли будет не меньше чем 1 к 2, то для меня это звучит странно.

А теперь, еще один простой пример в каких случаях стоит учитывать мат. ожидание. Например, при использовании такого показателя как ATR. Допустим, инструмент превысил свой показатель ATR более чем на 100 %, то в таком случае глупо заходить в позицию, так как с точки зрения мат. ожидания вероятность разворота выше. Либо заходить в позицию в том случае, когда ATR не позволяет вам закрыть позицию, скажем, 1 к 3. Например, если вы понимаете что инструмент прошел 90 % своего ATR и вы явно не сможете забрать ту прибыль которую планировали, не нарушив мат. ожидание. Это обычная математика против которой идти глупо.

В трейдинге нужно всегда стараться чтобы мат. ожидание было положительным. И когда будете анализировать ваши статистические данные, не забывайте про это и вносите коррективы в вашу торговлю верно.

На этом буду заканчивать. Надеюсь, вы уловили суть из моих размышлений Подписывайтесь на новости сайта, всем пока.

Watch this video on YouTube

Математическое ожидание преобразования случайной величины

Пусть gR→R{\displaystyle g\colon \mathbb {R} \to \mathbb {R} } — борелевская функция, такая что случайная величина Y=g(X){\displaystyle Y=g(X)} имеет конечное математическое ожидание. Тогда для него справедлива формула

Mg(X)=∑i=1∞g(xi)pi,{\displaystyle M\left=\sum \limits _{i=1}^{\infty }g(x_{i})p_{i},}

если X{\displaystyle X} имеет дискретное распределение;

Mg(X)=∫−∞∞g(x)fX(x)dx,{\displaystyle M\left=\int \limits _{-\infty }^{\infty }\!g(x)f_{X}(x)\,dx,}

если X{\displaystyle X} имеет абсолютно непрерывное распределение.

Если распределение PX{\displaystyle \mathbb {P} ^{X}} случайной величины X{\displaystyle X} общего вида, то

Mg(X)=∫−∞∞g(x)PX(dx).{\displaystyle M\left=\int \limits _{-\infty }^{\infty }\!g(x)\,\mathbb {P} ^{X}(dx).}

В специальном случае, когда g(X)=Xk{\displaystyle g(X)=X^{k}}, математическое ожидание Mg(X)=MXk{\displaystyle M=M} называется k{\displaystyle k}-м моментом случайной величины.

Пример расчета математического ожидания ставок на футбол

В ставках на футбол появляется третья величина, о которой нельзя забывать, – ничья. То есть, при расчете математического ожидания необходимо добавлять вероятность ничейного исхода. За примером – в Лигу чемпионов.

Матч «Ливерпуль» – «Атлетико» и котировки известного букмекера.

Победа «Ливерпуля» – 1.59. Вероятность 62,9%;

Ничья – 3.98. Вероятность 25,1%;

Победа «Атлетико» – 6.80. Вероятность 14,7%.

Размер ставки снова составляет 1000 рублей, и мы рассчитываем математическое ожидание победы обеих команд.

Победа «Ливерпуля». (62,9% * 590) – ((25,1% + 14,7%) * 1000) = (-26,89) рублей.
Победа «Атлетико». (14,7% * 5800) – ((62,9% + 25,1%) * 1000) = (-27,4) рубля.

На какой бы исход игрок ни ставил, но в долгосрочной перспективе такие коэффициенты, согласно математическому ожиданию, прибыли не принесут.

УМО для абсолютно непрерывных случайных величин

Пусть X,Y{\displaystyle X,Y} — случайные величины, такие что вектор (X,Y)⊤{\displaystyle (X,Y)^{\top }} абсолютно непрерывен, и его распределение задаётся плотностью вероятности fX,Y(x,y){\displaystyle f_{X,Y}(x,y)}. Введём условную плотность fX∣Y{\displaystyle f_{X\mid Y}}, положив по определению

fX∣Y(x∣y)=fX,Y(x,y)fY(y){\displaystyle f_{X\mid Y}(x\mid y)={\frac {f_{X,Y}(x,y)}{f_{Y}(y)}}},

где fY{\displaystyle f_{Y}} — плотность вероятности случайной величины Y{\displaystyle Y}. Тогда

EX∣Y=h(Y){\displaystyle \mathbb {E} =h(Y)},

где функция h{\displaystyle h} имеет вид

h(y)=∫−∞∞xfX∣Y(x∣y)dx{\displaystyle h(y)=\int \limits _{-\infty }^{\infty }x\,f_{X\mid Y}(x\mid y)\,dx}.

В частности,

EX∣Y=yj=∫−∞∞xfX∣Y(x∣yj)dx{\displaystyle \mathbb {E} =\int \limits _{-\infty }^{\infty }x\,f_{X\mid Y}(x\mid y_{j})\,dx}.

Если математическое ожидание всегда отрицательное, можно ли быть в прибыли на дистанции?

Главный вопрос – если математическое ожидание по ставкам всегда получается отрицательным, то для чего нужна формула его расчета, и как она может помочь в беттинге? И вообще, возможно ли быть в прибыли на длительной дистанции? Ответ кроется в двух понятиях:

Валуй в ставках;
Вилки в ставках.

Валуй – ситуация, когда игрок находит в линии букмекера неверно оцененное событие

Если букмекер по каким-то причинам неверно оценил событие (так предполагает игрок), значит, неверно выставил коэффициент. Произошла недооценка или переоценка события. По расчетам игрока, ставка имеет большую вероятность на проход, чем та, которую указал букмекер в линии. Если пересчитать это в математическое ожидание, оно получится плюсовым.

В примере с матчем «Ливерпуля» и мадридского «Атлетико» достаточно увеличить вероятность победы испанского клуба всего на 0,5%, и математическое ожидание получится плюсовым (+1,6 рубля).

Определение и формула математического ожидания

Мат. ожидание – среднее значение случайной величины.

Ничего не понятно? Давайте перефразируем близко к сфере беттинга.

Математическое ожидание – итоговое значение выигрыша или проигрыша по ставке при регулярном ее размещении с одинаковым коэффициентом.

Иными словами, математическое ожидание показывает, будут ли ставки на дистанции по одной и той же котировке прибыльными, или нет.

Формула мат. ожидания в привязке к беттингу:

(Вероятность выигрыша * сумму выигрыша) – (Вероятность проигрыша * сумму ставки)

Классический пример расчета

Возьмем классический пример с подбрасыванием монетки и ставками – выпадет орел или решка. С точки зрения вероятности, коэффициент на оба события (орел или решка) должен быть 2.0 (вероятность 50%). Но, предположим, вам дико повезло, и одна букмекерская контора готова предложить коэффициент 2.1 на «орел» и 2.0 на «решку», при том, что вероятность выпадения обеих сторон остается прежней. В таком случае при ставке в 100 рублей на котировку 2.1 выигрыш составит 110 рублей, а математическое ожидание будет выглядеть следующим образом:

(50% * 110) – (50% * 100) = 5 рублей.

Математическое ожидание показывает: если все время делать ставки в данном примере на коэффициент 2.1, игрок на длительной дистанции будет в плюсе.

Однако, из статьи о марже букмекера мы уже знаем, что идеальной ситуации (коэффициенты 2.0 / 2.0), а, тем более, выигрышной позиции изначально не бывает. Поэтому от мира гипотетического переходим к реальным примерам.

Ещё один пример

Мы провели 50 испытаний и получили 10 видов исходов – цифры от 0 до 9 — появляющихся в различном процентном отношении. Это, соответственно: 2%, 10%, 4%, 14%, 2%,18%, 6%, 16%, 10%, 18%. Напомним, что для получения вероятностей требуется разделить значения в процентах на 100. Таким образом, получим 0,02; 0,1 и т.д. Представим для дисперсии случайной величины и математического ожидания пример решения задачи.

Среднее арифметическое рассчитаем по формуле, которую помним с младшей школы: 50/10 = 5.

Теперь переведем вероятности в количество исходов «в штуках», чтобы было удобнее считать. Получим 1, 5, 2, 7, 1, 9, 3, 8, 5 и 9. Из каждого полученного значения вычтем среднее арифметическое, после чего каждый из полученных результатов возведем в квадрат. Посмотрите, как это сделать, на примере первого элемента: 1 – 5 = (-4). Далее: (-4) * (-4) = 16. Для остальных значений проделайте эти операции самостоятельно. Если вы всё сделали правильно, то после сложения всех промежуточных результатов вы получите 90.

Продолжим расчёт дисперсии и математического ожидания, разделив 90 на N. Почему мы выбираем N, а не N-1? Правильно, потому что количество проведенных экспериментов превышает 30. Итак: 90/10 = 9. Дисперсию мы получили. Если у вас вышло другое число, не отчаивайтесь. Скорее всего, вы допустили банальную ошибку при расчётах. Перепроверьте написанное, и наверняка всё встанет на свои места.

Наконец, вспомним формулу математического ожидания. Не будем приводить всех расчётов, напишем лишь ответ, с которым вы сможете свериться, закончив все требуемые процедуры. Матожидание будет равно 5,48. Напомним лишь, как осуществлять операции, на примере первых элементов: 0*0,02 + 1*0,1… и так далее. Как видите, мы просто умножаем значение исхода на его вероятность.

Резюме

Математические ставки на спорт эффективны при условии, что вы досконально разбираетесь в спортивной дисциплине и умеете правильно определять вероятность исходов. В противном случае, знания математики в беттинге окажутся бесполезными.

Что такое двойной шанс в ставках на спорт: 1х, х2, 12?

Как рассчитывается система в БК?

Комбинированные ставки

Минута первого гола

Ничья в одном из таймов

Первый тайм больше второго

Результативность таймов

Система 2 из 4

Система 3 из 4

Система 3 из 5

Ставка на автогол

Ставка на Х – что значит?

Сумма минут, на которых забиты голы

Второй тайм больше первого

Забьет в обоих таймах

Как понять «точный счет любой другой»?

Гол в пустые ворота

Гол в обоих таймах – что значит?

Что такое экспресс система ставок?

Что такое экспресс ставки?

Что такое математические ставки на спорт?

Что такое ординар (одиночная ставка) в ставках на спорт?

Что такое ставки с перевесом?

Что значит нп1 в ставках?

Что значит П1 в ставках?

Что значит п1п1 и п1н в ставках?

Что значит П2 в ставках на спорт?

Что значит результативная ничья?

Что значит ставка нн?

Что значит ставка нп2?

Долгосрочные ставки на спорт

Гол в меньшинстве

Забьет в одном из таймов

Виды ставок на спорт

Закон распределения дискретной случайной величины

– это соответствие между возможными значениями этой величины и их вероятностями. Чаще всего закон записывают таблицей:
Довольно часто встречается термин ряд распределения, но в некоторых ситуациях он звучит двусмысленно, и поэтому я буду придерживаться «закона».

А теперь очень важный момент: поскольку случайная величина обязательно примет одно из значений , то соответствующие события образуют полную группу и сумма вероятностей их наступления равна единице:

или, если записать свёрнуто:

Так, например, закон распределения вероятностей выпавших на кубике очков имеет следующий вид:

Без комментариев.

Возможно, у вас сложилось впечатление, что дискретная случайная величина может принимать только «хорошие» целые значения. Развеем иллюзию – они могут быть любыми:

Пример 1

Некоторая игра имеет следующий закон распределения выигрыша:

Найти

…наверное, вы давно мечтали о таких задачах 🙂 Открою секрет – я тоже. В особенности после того, как завершил работу над теорией поля.

Решение: так как случайная величина может принять только одно из трёх значений, то соответствующие события образуют полную группу, а значит, сумма их вероятностей равна единице:

Разоблачаем «партизана»: – таким образом, вероятность выигрыша условных единиц составляет 0,4.

Контроль: , в чём и требовалось убедиться.

Ответ:

Не редкость, когда закон распределения требуется составить самостоятельно. Для этого используют классическое определение вероятности, теоремы умножения / сложения вероятностей событий и другие фишки тервера:

Пример 2

В коробке находятся 50 лотерейных билетов, среди которых 12 выигрышных, причём 2 из них выигрывают по 1000 рублей, а остальные – по 100 рублей. Составить закон распределения случайной величины – размера выигрыша, если из коробки наугад извлекается один билет.

Решение: как вы заметили, значения случайной величины принято располагать в порядке их возрастания. Поэтому мы начинаем с самого маленького выигрыша, и именно рублей.

Всего таковых билетов 50 – 12 = 38, и по классическому определению: – вероятность того, что наудачу извлечённый билет окажется безвыигрышным.

С остальными случаями всё просто. Вероятность выигрыша рублей составляет:

И для :

Проверка: – и это особенно приятный момент таких заданий!

Ответ: искомый закон распределения выигрыша:

Следующее задание для самостоятельного решения:

Пример 3

Вероятность того, что стрелок поразит мишень, равна . Составить закон распределения случайной величины – количества попаданий после 2 выстрелов.

…я знал, что вы по нему соскучились 🙂 Вспоминаем теоремы умножения и сложения. Решение и ответ в конце урока.

Закон распределения полностью описывает случайную величину, однако на практике бывает полезно (а иногда и полезнее) знать лишь некоторые её числовые характеристики.

Математическое ожидание в трейдинге – простыми словами

Если говорить просто, то математическое ожидание – это усреднённый статистический показатель, дающий представление о прибыльности торговой системы или стратегии. Расчёт математического ожидания позволяет трейдеру увидеть, что превалирует в его торговле – убыток или прибыль.

Казалось бы, чтобы это понять, достаточно просто подбить процент прибыльных и убыточных сделок по итогу какого-то периода – недели, месяца и т. п. Но такая статистика не всегда будет объективна, ведь на прибыльность сделок в этот период могли влиять самые разные факторы, не имеющие отношения к эффективности торговой системы.

Для расчёта же математического ожидания берётся как минимум, 100 сделок. Расчёт происходит по простой формуле: От процента успешных сделок торговой системы, умноженного на прибыль в средней прибыльной сделке, отнимается процент убыточных сделок, умноженный на средний убыток в такой сделке. Статистические данные для расчёта можно без труда выгрузить из торгового терминала.

ПОБЕДА И ПОРАЖЕНИЕ – ЭТО СТАТИСТИКА

Но тут как раз в дело вступает та самая пресловутая психология. Понятное дело, что пересиживать убытки морально очень сложно! Если вы думаете, что опытные трейдеры не подвластны этому, то вы ошибаетесь. Но истинный профессионал осознает, что убыток, ровным счетом, как и прибыль – это не конкретная личностная победа или поражение, а это в первую очередь статистика и ничего более.

Не нужно воспринимать убытки и прибыли в качестве побед или поражений. Хотя мыслить нужно положительно! Все это является закономерным исходом вашей работы. При этом, даже убыточная сделка не говорит о том, что вы что-то сделали неправильно. Если сделка оказалась убыточной, но была проведена четко по системе, то это нормально и в этом нет ничего такого плохого и ужасного!

Самое главное, сохраняйте спокойствие, положительный настрой, следуйте своей системе и будет вам счастье

Кроме того, никогда не нужно спешить, и это очень важно! Каждый ваш вход в рынок должен быть четким и обоснованным. Кроме того, не забывайте, что положительное математическое ожидание является тем инструментом, который позволит себя уверенно чувствовать даже в периоды убытков

Каждый сам для себя должен решить, какое математическое ожидания должно быть. Но на мой взгляд, необходимо брать не менее 1 к 2, но тут, опять же, решать вам!

Предыдущая
Ручная торговляПобарный анализ. С чем его едят?
Следующая
Ручная торговляЗоны поддержки и сопротивления. Ориентиры на графике

ИЗУЧИМ КОЛИЧЕСТВО ПРИБЫЛЬНЫХ СДЕЛОК К УБЫТОЧНЫМ 50/50

Вообще, вот представим на секунду, что у вас на долгосрочном отрезке соотношение прибыльным к убыточным сделкам находится на уровне 50 на 50. Давайте рассмотрим такое соотношение на примере небольшой выборки, состоящей из 10 сделок. Вы должны понимать, что в рамках этой выборки ваше соотношение сделок может распределяться различным образом. Посмотрите пример, чтобы понять, к чему я веду:

– – – – – + + + + +
– + – + – + – + – +
– – + – – + + – – +
+ + + – – + – – + +

Грубо говоря, к чему эти наскальные рисунки. А вот это как раз вариации выборки, и таких вариантов может быть очень много. По сути, все эти 4 примера – это возможные варианты выборки в рамках соотношения сделок 50 на 50.

Вы никогда не знаете, насколько длинной будет цепочка прибылей или убытков в рамках этой выборки. Но, что вы можете сделать – это четко следовать своей системе. Давайте будем откровенными, если бы мы получили 5 убытков подряд, вызвало бы это у нас эмоции? Заставило бы это нас начать нарушать свою систему?

Я уверен, что большинстве случаев это было бы так! Ну, одна сделка, ну две сделки воспринимались бы еще как-то. Но вот третья и последующая четвертая убыточная сделка подряд уже выбила бы нас из колеи. А вот этого делать как раз нельзя, у вас есть система и ее надо придерживаться, во что бы то ни стало! Самое главное, чтобы ваше математическое ожидание было положительным!

4.3.5. document.write(‘Математическое ожидание и дисперсия’); window.top.document.title = «4.3.5. Математическое ожидание и дисперсия»;

Пусть мы измеряем случайную величину N раз, например, десять раз измеряем скорость ветра и хотим найти среднее значение. Как связано среднее значение с функцией распределения?

Будем кидать игральный кубик большое количество раз. Количество очков, которое выпадет на кубике при каждом броске, является случайной величиной и может принимать любые натуральные значения от 1 до 6. Среднее арифметическое выпавших очков, подсчитанных за все броски кубика, тоже является случайной величиной, однако при больших N оно стремится ко вполне конкретному числу – математическому ожиданию M_x. В данном случае M_x = 3,5.

Каким образом получилась эта величина? Пусть в N испытаниях раз выпало 1 очко, раз – 2 очка и так далее. Тогда
При N → ∞ количество исходов, в которых выпало одно очко,

Аналогично,
Отсюда

Математическое ожидание дискретной случайной величины

Модель 4.5.
Игральные кости

Предположим теперь, что мы знаем закон распределения случайной величины x, то есть знаем, что случайная величина x может принимать значения x₁, x₂, …, x_k с вероятностями p₁, p₂, …, p_k.

Математическое ожидание M_x случайной величины x равно

Математическое ожидание случайной величины часто обозначается как <x>. Записи <x> и M_x эквивалентны.

Пример 1

Найти математическое ожидание числа очков, которые выбьет первый стрелок в предыдущем примере.

Показать решение

Математическое ожидание не всегда является разумной оценкой какой-нибудь случайной величины. Так, для оценки средней заработной платы разумнее использовать понятие медианы, то есть такой величины, что количество людей, получающих меньшую, чем медиана, зарплату и большую, совпадают.


	Медианой случайной величины называют число x_1/2 такое, что p (x < x_1/2) = 1/2.

Другими словами, вероятность p₁ того, что случайная величина x окажется меньшей x_1/2, и вероятность p₂ того, что случайная величина x окажется большей x_1/2, одинаковы и равны 1/2. Медиана определяется однозначно не для всех распределений.

Вернёмся к случайной величине x, которая может принимать значения x₁, x₂, …, x_k с вероятностями p₁, p₂, …, p_k.

Дисперсией случайной величины x называется среднее значение квадрата отклонения случайной величины от её математического ожидания:

Используя вероятности p_i того, что величина x принимает значения x_i, эту формулу можно переписать следующим образом:

Среднеквадратическим отклонением случайной величины x называется корень квадратный из дисперсии этой величины:

Пример 2

В условиях предыдущего примера вычислить дисперсию и среднеквадратическое отклонение случайной величины x.

Показать решение

Модель 4.6.
Стрельба в мишень

Пример 3

Найти распределение вероятности числа очков, выпавших на кубике с первого броска, медиану, математическое ожидание, дисперсию и среднеквадратичное отклонение.

Показать решение

Свойства математического ожидания

Математическое ожидание суммы независимых случайных величин равно сумме их математических ожиданий:
Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:

Пример 4

Найти математическое ожидание суммы и произведения очков, выпавшей на двух кубиках.

Показать решение

Свойства дисперсии

Пример 5

Найти математическое ожидание и дисперсию суммы очков, выпавших при бросании кубика N раз.

Показать решение

Дисперсия случайной величины связана с математическим ожиданием квадрата этой случайной величины следующим соотношением:

НЕТ ПОВЕСТИ ПЕЧАЛЬНЕЕ НА СВЕТЕ

Вообще, все рассказы о том, что торговать на бинарных опционах невероятно просто – это все иллюзорность и не более того. Эти россказни распространяются только с целью того, чтобы привлечь как можно больше целевой аудитории. Понятное дело, что хомячки, одурманенные крутыми рассказами о легкости этой сферы, идут сюда и, естественно, просаживают тут деньги.

Читайте страницу: Стратегия без Мартингейла на бинарных опционах. Узнайте, как она организуется.

Таких историй просто море, я думаю, что вы и сами слышали о таких историях. Различные форумы просто переполняются душераздирающими рассказами о том, как люди потеряли деньги, что рынок говно, соответственно, нечто не положительное, а совсем наоборот. и прочее. Если говорить про бинарные опционы, то, да, зарабатывать тут можно. Но при этом нельзя забывать, что опционы являются невероятно рискованным инструментом со всеми вытекающими последствиями.