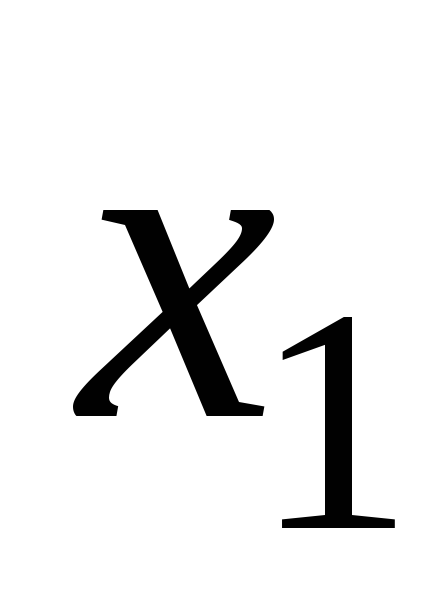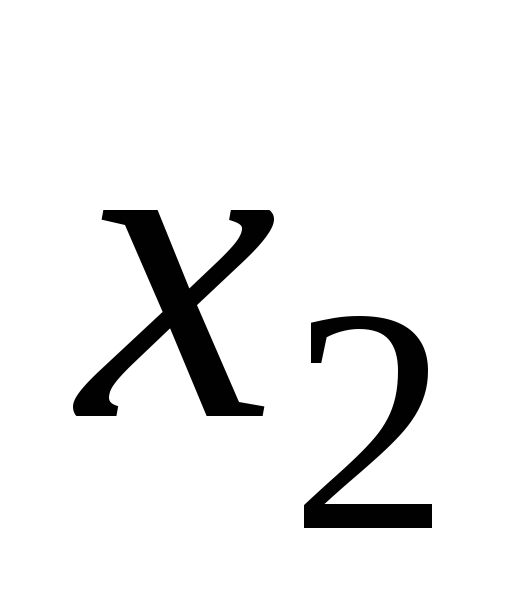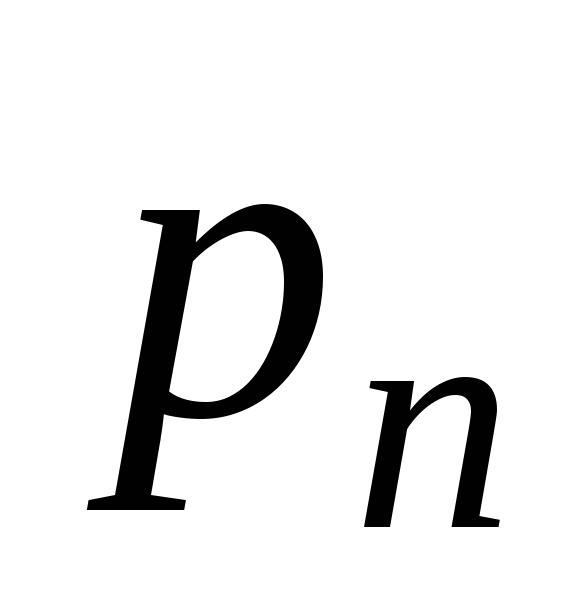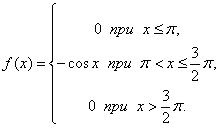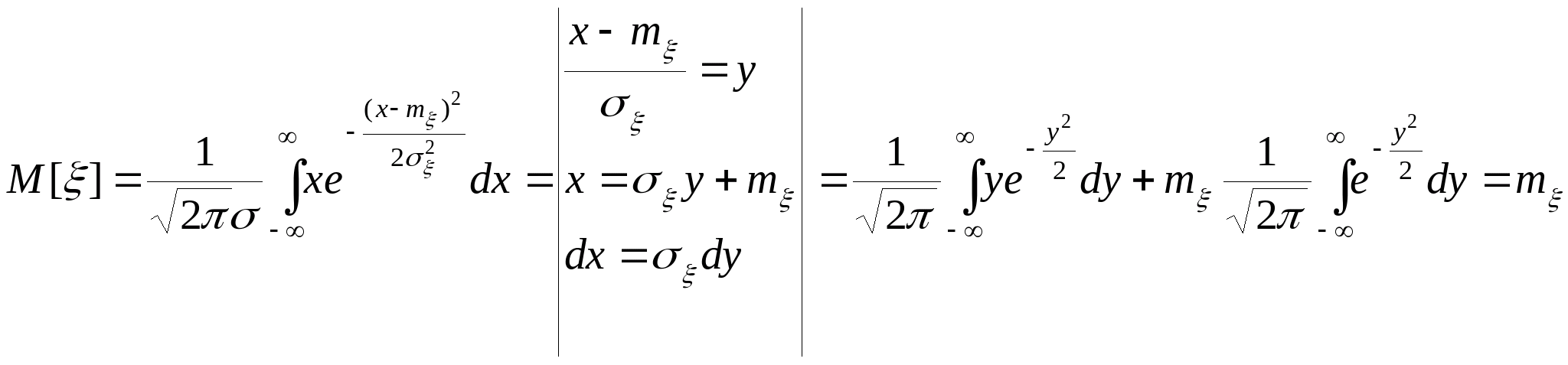Функция плотности распределения вероятностей[править]
| Определение: |
| Функция плотности распределения вероятностей (англ. Probability density function) — функция , определённая на как первая производная функции распределения. |
Свойства функции плотности вероятности:
Интеграл от плотности по всему пространству равен единице:
- .
Плотность вероятности определена почти всюду.
- Иными словами, множество точек, для которых она не определена, имеет меру ноль.
Для примера выше
Для дискретной случайной величины не существует функции плотности распределения вероятностей, так как такая случайная величина не является абсолютно непрерывной функцией.
История
Роль случайной величины, как одного из основных понятий теории вероятностей, впервые была чётко осознана П. Л. Чебышевым, который обосновал общепринятую на сегодня точку зрения на это понятие (1867). Понимание случайной величины как частного случая общего понятия функции, пришло значительно позднее, в первой трети 20 века. Впервые полное формализованное представление основ теории вероятностей на базе теории меры было разработано А. Н. Колмогоровым (1933) , после которого стало ясным, что случайная величина представляет собой измеримую функцию, определённую на вероятностном пространстве. В учебной литературе эта точка зрения впервые последовательно проведена У. Феллером (см. предисловие к , где изложение строится на основе понятия пространства элементарных событий и подчёркивается, что лишь в этом случае представление случайной величины становится содержательным).
Простейшие обобщения
Случайная величина, вообще говоря, может принимать значения в любом измеримом пространстве. Тогда её чаще называют случайным вектором или случайным элементом. Например,
- Измеримая функция называется -мерным случайным вектором (относительно борелевской σ-алгебры на ).
- Измеримая функция называется -мерным комплексным случайным вектором (также относительно соответствующей борелевской σ-алгебры).
- Измеримая функция, отображающая вероятностное пространство в пространство подмножеств некоторого (конечного) множества, называется (конечным) случайным множеством.
Примеры
Дискретная случайная величина
Подбрасывание монеты
Все возможные исходы подбрасывания монеты могут быть описаны пространством элементарных событий Ω={{\displaystyle \Omega =\{}орёл, решка}{\displaystyle \}} или коротко {op,pe}{\displaystyle \{op,pe\}}. Пусть случайная величина X{\displaystyle X} равна выигрышу, который мы получим в результате ставок на результат исхода подбрасывания монеты. Так пусть мы получим 10 руб. каждый раз, когда монетка ω{\displaystyle \omega } выпадает орлом, и -33 руб. при выпадении решки. Математически эту функцию выигрыша или X{\displaystyle X} можно представить так:
- X(ω)={10,if ω=op,−33,if ω=pe.{\displaystyle X(\omega )={\begin{cases}10,&{\text{if }}\omega ={\text{op}},\\-33,&{\text{if }}\omega ={\text{pe}}.\end{cases}}}
Если монетка идеальная, то выигрыш X{\displaystyle X} будет иметь вероятность, заданную как:
-
P(y)={12,if y=10,12,if y=−33,{\displaystyle P(y)={\begin{cases}{\tfrac {1}{2}},&{\text{if }}y=10,\\{\tfrac {1}{2}},&{\text{if }}y=-33,\end{cases}}}
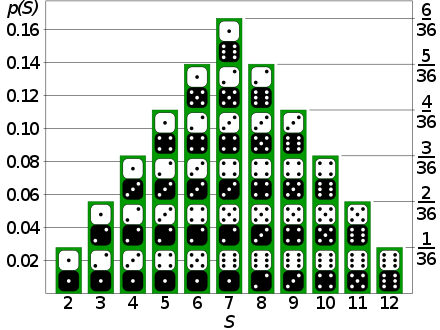
Если пространство исходов равно множеству всех возможных комбинаций очков на двух костях, и случайная величина равна сумме этих очков, тогда S — это дискретная случайная величина, чьё распределение описывается функцией вероятности, значение которой изображено как высота соответствующей колонки. - где P(y){\displaystyle P(y)} — вероятность получения y{\displaystyle y} рублей выигрыша при подбрасывании монетки.
Бросание игральных костей
Случайная величина так же может быть использована для описания процесса бросания игральных костей, а так же для расчёта вероятности конкретного исхода таких бросков. В одном из классических примеров данного эксперимента используются две игральные кости n1 и n2, каждая из которых может принимать значения из множества {1, 2, 3, 4, 5, 6} (количество очков на сторонах костей). Общее количество очков выпавших на костях и будет значением нашей случайной величины X{\displaystyle X}, которая задаётся функцией:
- X((n1,n2))=n1+n2{\displaystyle X((n_{1},n_{2}))=n_{1}+n_{2}}
и (если кости идеальные) функция вероятности для X{\displaystyle X} задаётся через:
- P(S)=min(S−1,13−S)36, for S∈{2,3,4,5,6,7,8,9,10,11,12}{\displaystyle P(S)={\frac {\min(S-1,13-S)}{36}},{\text{ for }}S\in \{2,3,4,5,6,7,8,9,10,11,12\}},
- где S{\displaystyle S} — сумма очков на выпавших костях.
Пусть в одном из экспериментов нужно случайным образом выбрать одного человека (обозначим его как ) из группы испытуемых, пусть тогда случайная величина X{\displaystyle X} выражает рост выбранного нами человека . В этом случае, с математической точки зрения, случайная величина X{\displaystyle X} интерпретируется как функция y=X({\displaystyle y=X(}){\displaystyle )}, которая трансформирует испытуемогов число — его рост y{\displaystyle y}. Для того чтобы рассчитать вероятность того, что рост попадёт в промежуток между 180см и 190см, или вероятность того, что его рост будет выше 150см., нужно знать распределение вероятности, которое в совокупности с X{\displaystyle X} и позволяет рассчитывать вероятности тех или иных исходов случайных экспериментов.
Методы описания
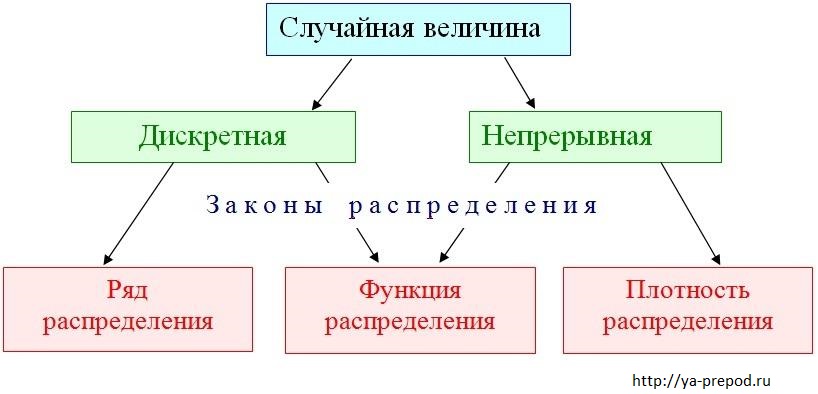
Частично задать случайную величину, описав этим все её вероятностные свойства как отдельной случайной величины, можно с помощью функции распределения, плотности вероятности и характеристической функции, определяя вероятности возможных её значений. Функция распределения F(x) является вероятностью того, что значения случайной величины меньше вещественного числа x. Из этого определения следует, что вероятность попадания значения случайной величины в интервал [a, b) равна F(b)-F(a). Преимущество использования функции распределения заключается в том, что с её помощью удаётся достичь единообразного математического описания дискретных, непрерывных и дискретно-непрерывных случайных величин. Тем не менее, существуют разные случайные величины, имеющие одинаковые функции распределения.
Если случайная величина дискретная, то полное и однозначное математическое описание её распределения определяется указанием вероятностей pk=P(ξ=xk){\displaystyle p_{k}=P(\xi =x_{k})} всех возможных значений этой случайной величины. В качестве примера рассмотрим биномиальный и пуассоновский законы распределения.
Биноминальный закон распределения описывает случайные величины, значения которых определяют количество «успехов» и «неудач» при повторении опыта N раз. В каждом опыте «успех» может наступить с вероятностью p, «неудача» — с вероятностью q=1-p. Закон распределения в этом случае определяется формулой Бернулли:
- Pk,n=Cnk⋅pk⋅qn−k{\displaystyle P_{k,n}=C_{n}^{k}\cdot p^{k}\cdot q^{n-k}}.
Если при стремлении n{\displaystyle n} к бесконечности произведение np{\displaystyle np} остаётся равной константе λ>{\displaystyle \lambda >0}, то биномиальный закон распределения сходится к закону Пуассона, который описывается следующей формулой:
- p(k)≡P(Y=k)=λkk!e−λ{\displaystyle p(k)\equiv \mathbb {P} (Y=k)={\frac {\lambda ^{k}}{k!}}\,e^{-\lambda }},
где
- символ «!{\displaystyle !}» обозначает факториал,
- e=2.718281828…{\displaystyle e=2.718281828\ldots } — основание натурального логарифма.
История
Роль случайной величины, как одного из основных понятий теории вероятностей, впервые была чётко осознана П. Л. Чебышевым, который обосновал общепринятую на сегодня точку зрения на это понятие (1867). Понимание случайной величины как частного случая общего понятия функции, пришло значительно позднее, в первой трети 20 века. Впервые полное формализованное представление основ теории вероятностей на базе теории меры было разработано А. Н. Колмогоровым (1933) , после которого стало ясным, что случайная величина представляет собой измеримую функцию, определённую на вероятностном пространстве. В учебной литературе эта точка зрения впервые последовательно проведена У. Феллером (см. предисловие к , где изложение строится на основе понятия пространства элементарных событий и подчёркивается, что лишь в этом случае представление случайной величины становится содержательным).
Функция распределения[править]
| Определение: |
| Функция распределения случайной величины (англ. cumulative distribution function (CDF)) — функция , определённая на как , т.е. выражающая вероятность того, что примет значение меньшее или равное |
Если случайная величина дискретна, то есть её распределение однозначно задаётся функцией
Функция распределения этой случайной величины кусочно-постоянна и может быть записана как .
Свойства функции распределения дискретной случайной величины:
F(x_1)\leqslant F(x_2) при x_1 \leqslant x_2;
F(x) непрерывна во всех точках x\in \mathbb{R}, таких что \forall i ~ x \ne x_i , и имеет разрыв первого рода в точках, таких что \forall i ~ x = x_i.
\lim\limits_{x \to -\infty} F(x) = 0, \lim\limits_{x \to +\infty} F(x) = 1.
Примерыправить
- Найдем функцию распределения количества попаданий в мишень. Пусть у нас есть выстрелов, вероятность попадания равна . Необходимо найти . Для , так как нельзя попасть в мишень отрицательное число раз. Для
- Аналогичное решение имеет функция распределения числа выпавших орлов при броске монеты, если шанс выпадения орла — .
- Найдем функцию распределения числа очков, выпавших при бросании игральной кости. Пусть у нас есть вероятности выпадения чисел соответственно равны . Для , так как не может выпасть цифра меньше . Для
В отличие от дискретной случайной величины, непрерывная случайная величина может принять любое действительное значение из некоторого промежутка ненулевой длины, что делает невозможным её представление в виде таблицы или перечисления состояний. Поэтому ее часто явно задают через функцию распределения, например
Простейшие обобщения
Случайная величина, вообще говоря, может принимать значения в любом измеримом пространстве. Тогда её чаще называют случайным вектором или случайным элементом. Например,
- Измеримая функция XΩ→Rn{\displaystyle X\colon \Omega \to \mathbb {R} ^{n}} называется n-мерным случайным вектором (относительно борелевской σ{\displaystyle \sigma }-алгебры на Rn{\displaystyle \mathbb {R} ^{n}}).
- Измеримая функция XΩ→Cn{\displaystyle X\colon \Omega \to \mathbb {C} ^{n}} называется n-мерным комплексным случайным вектором (также относительно соответствующей борелевской σ{\displaystyle \sigma }-алгебры).
- Измеримая функция, отображающая вероятностное пространство в пространство подмножеств некоторого (конечного) множества, называется (конечным) случайным множеством.
Определение
Формальное математическое определение следующее: пусть (Ω,F,P){\displaystyle (\Omega ,{\mathcal {F}},\mathbb {P} )} — вероятностное пространство, тогда случайной величиной называется функция XΩ→R{\displaystyle X\colon \Omega \to \mathbb {R} }, измеримая относительно F{\displaystyle {\mathcal {F}}} и борелевской σ-алгебры на R{\displaystyle \mathbb {R} }. Вероятностное поведение отдельной (независимой от других) случайной величины полностью описывается её распределением.
Случайную величину можно определить и другим эквивалентным способом. Функция XΩ→R{\displaystyle X\colon \Omega \to \mathbb {R} } называется случайной величиной, если для любых вещественных чисел a{\displaystyle a} и b{\displaystyle b} множество событий ω{\displaystyle \omega }, таких что X(ω)∈(a,b){\displaystyle X(\omega )\in (a,b)}, принадлежит F{\displaystyle {\mathcal {F}}}.
Методы описания
Частично задать случайную величину, описав этим все её вероятностные свойства как отдельной случайной величины, можно с помощью функции распределения, плотности вероятности и характеристической функции, определяя вероятности возможных её значений. Функция распределения F(x) является вероятностью того, что значения случайной величины меньше вещественного числа x. Из этого определения следует, что вероятность попадания значения случайной величины в интервал [a, b) равна F(b)-F(a). Преимущество использования функции распределения заключается в том, что с её помощью удаётся достичь единообразного математического описания дискретных, непрерывных и дискретно-непрерывных случайных величин. Тем не менее, существуют разные случайные величины, имеющие одинаковые функции распределения.
Если случайная величина дискретная, то полное и однозначное математическое описание её распределения определяется указанием вероятностей pk=P(ξ=xk){\displaystyle p_{k}=P(\xi =x_{k})} всех возможных значений этой случайной величины. В качестве примера рассмотрим биномиальный и пуассоновский законы распределения.
Биноминальный закон распределения описывает случайные величины, значения которых определяют количество «успехов» и «неудач» при повторении опыта N раз. В каждом опыте «успех» может наступить с вероятностью p, «неудача» — с вероятностью q=1-p. Закон распределения в этом случае определяется формулой Бернулли:
- Pk,n=Cnk⋅pk⋅qn−k{\displaystyle P_{k,n}=C_{n}^{k}\cdot p^{k}\cdot q^{n-k}}.
Если при стремлении n{\displaystyle n} к бесконечности произведение np{\displaystyle np} остаётся равной константе λ>{\displaystyle \lambda >0}, то биномиальный закон распределения сходится к закону Пуассона, который описывается следующей формулой:
- p(k)≡P(Y=k)=λkk!e−λ{\displaystyle p(k)\equiv \mathbb {P} (Y=k)={\frac {\lambda ^{k}}{k!}}\,e^{-\lambda }},
где
- символ «!{\displaystyle !}» обозначает факториал,
- e=2.718281828…{\displaystyle e=2.718281828\ldots } — основание натурального логарифма.
Методы описания
Частично задать случайную величину, описав этим все её вероятностные свойства как отдельной случайной величины, можно с помощью функции распределения, плотности вероятности и характеристической функции, определяя вероятности возможных её значений. Функция распределения F(x) является вероятностью того, что значения случайной величины меньше вещественного числа x. Из этого определения следует, что вероятность попадания значения случайной величины в интервал [a, b) равна F(b)-F(a). Преимущество использования функции распределения заключается в том, что с её помощью удаётся достичь единообразного математического описания дискретных, непрерывных и дискретно-непрерывных случайных величин. Тем не менее, существуют разные случайные величины, имеющие одинаковые функции распределения.
Если случайная величина дискретная, то полное и однозначное математическое описание её распределения определяется указанием вероятностей pk=P(ξ=xk){\displaystyle p_{k}=P(\xi =x_{k})} всех возможных значений этой случайной величины. В качестве примера рассмотрим биномиальный и пуассоновский законы распределения.
Биноминальный закон распределения описывает случайные величины, значения которых определяют количество «успехов» и «неудач» при повторении опыта N раз. В каждом опыте «успех» может наступить с вероятностью p, «неудача» — с вероятностью q=1-p. Закон распределения в этом случае определяется формулой Бернулли:
- Pk,n=Cnk⋅pk⋅qn−k{\displaystyle P_{k,n}=C_{n}^{k}\cdot p^{k}\cdot q^{n-k}}.
Если при стремлении n{\displaystyle n} к бесконечности произведение np{\displaystyle np} остаётся равной константе λ>{\displaystyle \lambda >0}, то биномиальный закон распределения сходится к закону Пуассона, который описывается следующей формулой:
- p(k)≡P(Y=k)=λkk!e−λ{\displaystyle p(k)\equiv \mathbb {P} (Y=k)={\frac {\lambda ^{k}}{k!}}\,e^{-\lambda }},
где
- символ «!{\displaystyle !}» обозначает факториал,
- e=2.718281828…{\displaystyle e=2.718281828\ldots } — основание натурального логарифма.
Определение
Формальное математическое определение следующее: пусть (Ω,F,P){\displaystyle (\Omega ,{\mathcal {F}},\mathbb {P} )} — вероятностное пространство, тогда случайной величиной называется функция XΩ→R{\displaystyle X\colon \Omega \to \mathbb {R} }, измеримая относительно F{\displaystyle {\mathcal {F}}} и борелевской σ-алгебры на R{\displaystyle \mathbb {R} }. Вероятностное поведение отдельной (независимой от других) случайной величины полностью описывается её распределением.
Случайную величину можно определить и другим эквивалентным способом. Функция XΩ→R{\displaystyle X\colon \Omega \to \mathbb {R} } называется случайной величиной, если для любых вещественных чисел a{\displaystyle a} и b{\displaystyle b} множество событий ω{\displaystyle \omega }, таких что X(ω)∈(a,b){\displaystyle X(\omega )\in (a,b)}, принадлежит F{\displaystyle {\mathcal {F}}}.
Определение
Формальное математическое определение следующее: пусть (Ω,F,P){\displaystyle (\Omega ,{\mathcal {F}},\mathbb {P} )} — вероятностное пространство, тогда случайной величиной называется функция XΩ→R{\displaystyle X\colon \Omega \to \mathbb {R} }, измеримая относительно F{\displaystyle {\mathcal {F}}} и борелевской σ-алгебры на R{\displaystyle \mathbb {R} }. Вероятностное поведение отдельной (независимой от других) случайной величины полностью описывается её распределением.
Случайную величину можно определить и другим эквивалентным способом. Функция XΩ→R{\displaystyle X\colon \Omega \to \mathbb {R} } называется случайной величиной, если для любых вещественных чисел a{\displaystyle a} и b{\displaystyle b} множество событий ω{\displaystyle \omega }, таких что X(ω)∈(a,b){\displaystyle X(\omega )\in (a,b)}, принадлежит F{\displaystyle {\mathcal {F}}}.
Математическое ожидание дискретной случайной величины
Говоря простым языком, это среднеожидаемое значение при многократном повторении испытаний. Пусть случайная величина принимает значения с вероятностями соответственно. Тогда математическое ожидание данной случайной величины равно сумме произведений всех её значений на соответствующие вероятности:
или в свёрнутом виде:
Вычислим, например, математическое ожидание случайной величины – количества выпавших на игральном кубике очков:
 очка
очка
В чём состоит вероятностный смысл полученного результата? Если подбросить кубик достаточно много раз, то среднее значение выпавших очков будет близкО к 3,5 – и чем больше провести испытаний, тем ближе. Собственно, об этом эффекте я уже подробно рассказывал на уроке о статистической вероятности.
Теперь вспомним нашу гипотетическую игру:
Возникает вопрос: а выгодно ли вообще играть в эту игру? …у кого какие впечатления? Так ведь «навскидку» и не скажешь! Но на этот вопрос можно легко ответить, вычислив математическое ожидание, по сути – средневзвешенный по вероятностям выигрыш:
 , таким образом, математическое ожидание данной игры проигрышно.
, таким образом, математическое ожидание данной игры проигрышно.
Не верь впечатлениям – верь цифрам!
Да, здесь можно выиграть 10 и даже 20-30 раз подряд, но на длинной дистанции нас ждёт неминуемое разорение. И я бы не советовал вам играть в такие игры 🙂 Ну, может, только ради развлечения.
Из всего вышесказанного следует, что математическое ожидание – это уже НЕ СЛУЧАЙНАЯ величина.
Творческое задание для самостоятельного исследования:
Пример 4
Мистер Х играет в европейскую рулетку по следующей системе: постоянно ставит 100 рублей на «красное». Составить закон распределения случайной величины – его выигрыша. Вычислить математическое ожидание выигрыша и округлить его до копеек. Сколько в среднем проигрывает игрок с каждой поставленной сотни?
Справка: европейская рулетка содержит 18 красных, 18 чёрных и 1 зелёный сектор («зеро»). В случае выпадения «красного» игроку выплачивается удвоенная ставка, в противном случае она уходит в доход казино
Существует много других систем игры в рулетку, для которых можно составить свои таблицы вероятностей. Но это тот случай, когда нам не нужны никакие законы распределения и таблицы, ибо доподлинно установлено, что математическое ожидание игрока будет точно таким же. От системы к системе меняется лишь дисперсия, о которой мы узнаем во 2-й части урока.
Но прежде будет полезно размять пальцы на клавишах калькулятора:
Пример 5
Случайная величина задана своим законом распределения вероятностей:
Найти , если известно, что . Выполнить проверку.
Есть?
Тогда переходим к изучению дисперсии дискретной случайной величины, и по возможности, ПРЯМО СЕЙЧАС!! – чтобы не потерять нить темы.
Решения и ответы:
Пример 3. Решение: по условию – вероятность попадания в мишень. Тогда: – вероятность промаха.
Составим – закон распределения попаданий при двух выстрелах:
– ни одного попадания. По теореме умножения вероятностей независимых событий:
– одно попадание. По теоремам сложения вероятностей несовместных и умножения независимых событий:
– два попадания. По теореме умножения вероятностей независимых событий:
Проверка: 0,09 + 0,42 + 0,49 = 1
Ответ
Примечание: можно было использовать обозначения – это не принципиально.
Пример 4. Решение: игрок выигрывает 100 рублей в 18 случаях из 37, и поэтому закон распределения его выигрыша имеет следующий вид: Вычислим математическое ожидание: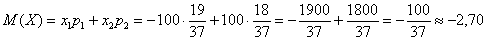 Таким образом, с каждой поставленной сотни игрок в среднем проигрывает 2,7 рубля.
Таким образом, с каждой поставленной сотни игрок в среднем проигрывает 2,7 рубля.
Пример 5. Решение: по определению математического ожидания: поменяем части местами и проведём упрощения:таким образом:
Выполним проверку: , что и требовалось проверить.
, что и требовалось проверить.
Ответ
(Переход на главную страницу)
Примеры
Дискретная случайная величина
Подбрасывание монеты
Все возможные исходы подбрасывания монеты могут быть описаны пространством элементарных событий Ω={{\displaystyle \Omega =\{}орёл, решка}{\displaystyle \}} или коротко {op,pe}{\displaystyle \{op,pe\}}. Пусть случайная величина X{\displaystyle X} равна выигрышу, который мы получим в результате ставок на результат исхода подбрасывания монеты. Так пусть мы получим 10 руб. каждый раз, когда монетка ω{\displaystyle \omega } выпадает орлом, и -33 руб. при выпадении решки. Математически эту функцию выигрыша или X{\displaystyle X} можно представить так:
- X(ω)={10,if ω=op,−33,if ω=pe.{\displaystyle X(\omega )={\begin{cases}10,&{\text{if }}\omega ={\text{op}},\\-33,&{\text{if }}\omega ={\text{pe}}.\end{cases}}}
Если монетка идеальная, то выигрыш X{\displaystyle X} будет иметь вероятность, заданную как:
-
P(y)={12,if y=10,12,if y=−33,{\displaystyle P(y)={\begin{cases}{\tfrac {1}{2}},&{\text{if }}y=10,\\{\tfrac {1}{2}},&{\text{if }}y=-33,\end{cases}}}
Если пространство исходов равно множеству всех возможных комбинаций очков на двух костях, и случайная величина равна сумме этих очков, тогда S — это дискретная случайная величина, чьё распределение описывается функцией вероятности, значение которой изображено как высота соответствующей колонки. - где P(y){\displaystyle P(y)} — вероятность получения y{\displaystyle y} рублей выигрыша при подбрасывании монетки.
Бросание игральных костей
Случайная величина так же может быть использована для описания процесса бросания игральных костей, а так же для расчёта вероятности конкретного исхода таких бросков. В одном из классических примеров данного эксперимента используются две игральные кости n1 и n2, каждая из которых может принимать значения из множества {1, 2, 3, 4, 5, 6} (количество очков на сторонах костей). Общее количество очков выпавших на костях и будет значением нашей случайной величины X{\displaystyle X}, которая задаётся функцией:
- X((n1,n2))=n1+n2{\displaystyle X((n_{1},n_{2}))=n_{1}+n_{2}}
и (если кости идеальные) функция вероятности для X{\displaystyle X} задаётся через:
- P(S)=min(S−1,13−S)36, for S∈{2,3,4,5,6,7,8,9,10,11,12}{\displaystyle P(S)={\frac {\min(S-1,13-S)}{36}},{\text{ for }}S\in \{2,3,4,5,6,7,8,9,10,11,12\}},
- где S{\displaystyle S} — сумма очков на выпавших костях.
Пусть в одном из экспериментов нужно случайным образом выбрать одного человека (обозначим его как ) из группы испытуемых, пусть тогда случайная величина X{\displaystyle X} выражает рост выбранного нами человека . В этом случае, с математической точки зрения, случайная величина X{\displaystyle X} интерпретируется как функция y=X({\displaystyle y=X(}){\displaystyle )}, которая трансформирует испытуемогов число — его рост y{\displaystyle y}. Для того чтобы рассчитать вероятность того, что рост попадёт в промежуток между 180см и 190см, или вероятность того, что его рост будет выше 150см., нужно знать распределение вероятности, которое в совокупности с X{\displaystyle X} и позволяет рассчитывать вероятности тех или иных исходов случайных экспериментов.
Примеры
Дискретная случайная величина
Подбрасывание монеты
Все возможные исходы подбрасывания монеты могут быть описаны пространством элементарных событий Ω={{\displaystyle \Omega =\{}орёл, решка}{\displaystyle \}} или коротко {op,pe}{\displaystyle \{op,pe\}}. Пусть случайная величина X{\displaystyle X} равна выигрышу, который мы получим в результате ставок на результат исхода подбрасывания монеты. Так пусть мы получим 10 руб. каждый раз, когда монетка ω{\displaystyle \omega } выпадает орлом, и -33 руб. при выпадении решки. Математически эту функцию выигрыша или X{\displaystyle X} можно представить так:
- X(ω)={10,if ω=op,−33,if ω=pe.{\displaystyle X(\omega )={\begin{cases}10,&{\text{if }}\omega ={\text{op}},\\-33,&{\text{if }}\omega ={\text{pe}}.\end{cases}}}
Если монетка идеальная, то выигрыш X{\displaystyle X} будет иметь вероятность, заданную как:
-
P(y)={12,if y=10,12,if y=−33,{\displaystyle P(y)={\begin{cases}{\tfrac {1}{2}},&{\text{if }}y=10,\\{\tfrac {1}{2}},&{\text{if }}y=-33,\end{cases}}}
Если пространство исходов равно множеству всех возможных комбинаций очков на двух костях, и случайная величина равна сумме этих очков, тогда S — это дискретная случайная величина, чьё распределение описывается функцией вероятности, значение которой изображено как высота соответствующей колонки. - где P(y){\displaystyle P(y)} — вероятность получения y{\displaystyle y} рублей выигрыша при подбрасывании монетки.
Бросание игральных костей
Случайная величина так же может быть использована для описания процесса бросания игральных костей, а так же для расчёта вероятности конкретного исхода таких бросков. В одном из классических примеров данного эксперимента используются две игральные кости n1 и n2, каждая из которых может принимать значения из множества {1, 2, 3, 4, 5, 6} (количество очков на сторонах костей). Общее количество очков выпавших на костях и будет значением нашей случайной величины X{\displaystyle X}, которая задаётся функцией:
- X((n1,n2))=n1+n2{\displaystyle X((n_{1},n_{2}))=n_{1}+n_{2}}
и (если кости идеальные) функция вероятности для X{\displaystyle X} задаётся через:
- P(S)=min(S−1,13−S)36, for S∈{2,3,4,5,6,7,8,9,10,11,12}{\displaystyle P(S)={\frac {\min(S-1,13-S)}{36}},{\text{ for }}S\in \{2,3,4,5,6,7,8,9,10,11,12\}},
- где S{\displaystyle S} — сумма очков на выпавших костях.
Пусть в одном из экспериментов нужно случайным образом выбрать одного человека (обозначим его как ) из группы испытуемых, пусть тогда случайная величина X{\displaystyle X} выражает рост выбранного нами человека . В этом случае, с математической точки зрения, случайная величина X{\displaystyle X} интерпретируется как функция y=X({\displaystyle y=X(}){\displaystyle )}, которая трансформирует испытуемогов число — его рост y{\displaystyle y}. Для того чтобы рассчитать вероятность того, что рост попадёт в промежуток между 180см и 190см, или вероятность того, что его рост будет выше 150см., нужно знать распределение вероятности, которое в совокупности с X{\displaystyle X} и позволяет рассчитывать вероятности тех или иных исходов случайных экспериментов.
Дискретная случайная величина
Случайной называют величину, которая
в результате испытания примет одно и
только одно из возможных значений,
наперед неизвестное и зависящее от
случайных причин, которые заранее не
могут быть учтены.
Обозначают случайные величины буквами
Х,Y,Z, а их
возможные значения —х,у,z.
Дискретной называют случайную величину,
которая принимает отдельные, изолированные
друг от друга значения с определенными
вероятностями. Число возможных значений
дискретной случайной величины может
быть конечным или бесконечным, но
счетным.
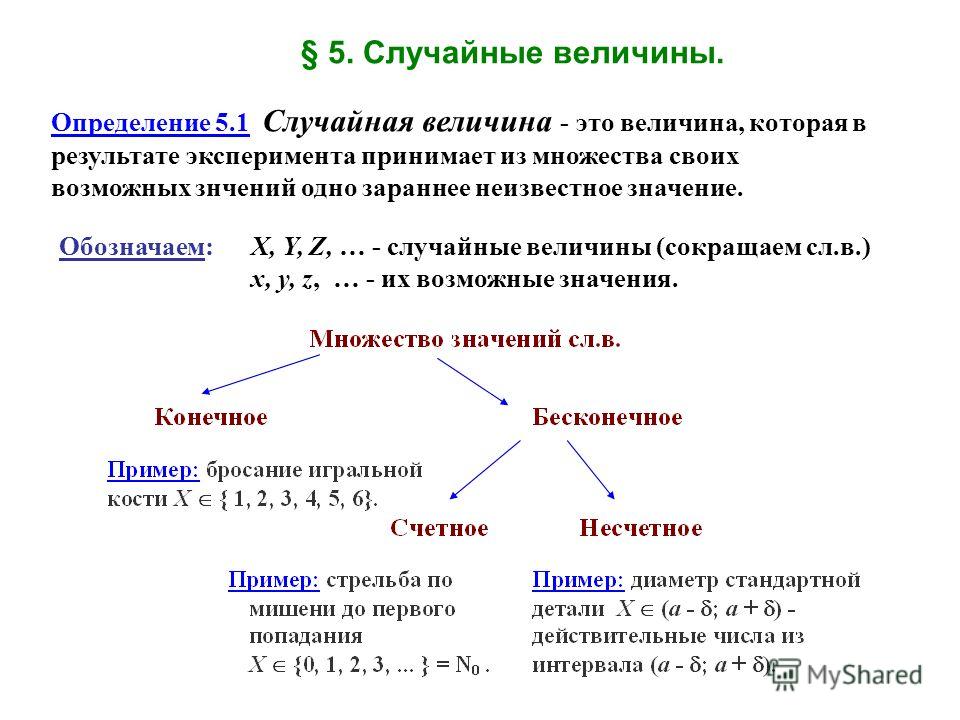
Дискретная случайная величина может
быть задана рядом распределения —
это соответствие между возможными
значениями и их вероятностями:
|
Х |
|
|
… |
|
|
Р |
|
|
… |
|
 ,
, .
.
События
 образуют полную группу, следовательно,
образуют полную группу, следовательно,
сумма вероятностей этих событий равна
единице:
 .
.
Ряд распределения дискретной случайной
величины можно изобразить графически
в виде полигона или многоугольника
распределения вероятностей. Для этого
по горизонтальной оси в выбранном
масштабе нужно отложить значения
случайной величины, а по вертикальной —
вероятности этих значений, тогда точки
с координатами
 будут изображать полигон распределения
будут изображать полигон распределения
вероятностей; соединив же эти точки
отрезками прямой, получиммногоугольник
распределения вероятностей.
Пример 7.1.ПустьХ— дискретная
случайная величина, заданная рядом
распределения
|
Х |
–2 |
–1 |
2 |
4 |
|
|
Р |
0,1 |
0,2 |
0,3 |
0,2 |
0,2 |
Построить полигон и многоугольник
распределения вероятностей.
Р
А4
ешение.
На осиХоткладываем значения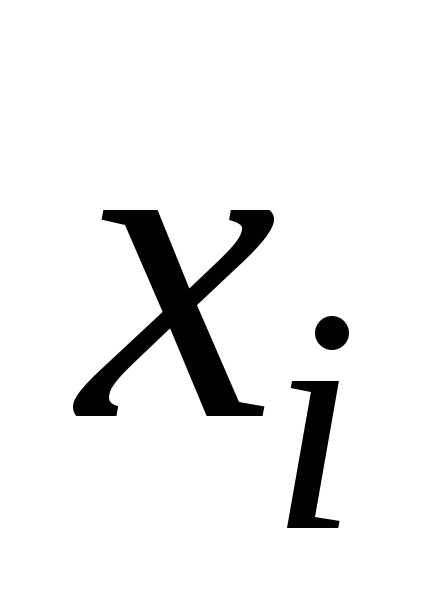 ,
,
равные –2, –1, 0, 2, 4, а по вертикальной
оси вероятности этих значений (рис.
7.1):
Р
А
–1
–2
–3
1
2
3
4
5
А1
А2
А3
А5
y
А6
0,1
0,2
0,3
x
ис.
7.1
Точки
 изображают полигон распределения, а
изображают полигон распределения, а
ломаная —
—
многоугольник распределения вероятностей.
Дискретная случайная величина может
быть задана функцией распределения.
Функцией распределения случайной
величины Хназывается функция ,
,
выражающая для каждогохвероятность
того, что случайная величинаХпримет
значение меньшеех:

Функцию
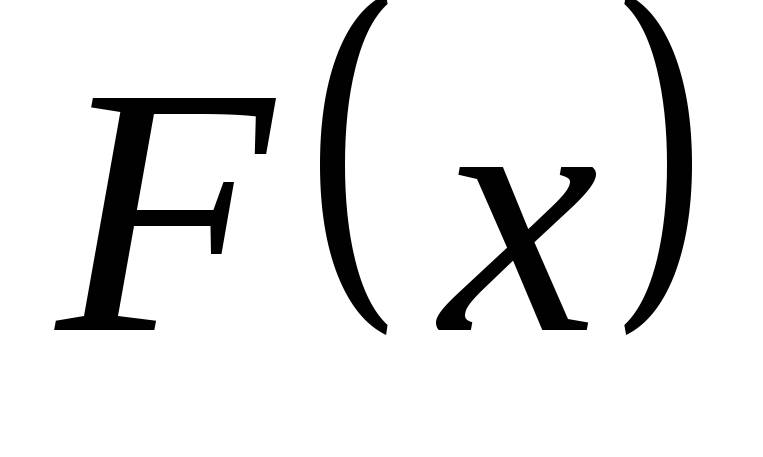 иногда называют интегральной функцией
иногда называют интегральной функцией
распределения.
Если
значения случайной величины — точки
на числовой оси, то геометрически функция
распределения интерпретируется как
вероятность того, что случайная величинаХпопадает левее заданной точких
(рис. 7.2):
Рис. 7.2
F(x)
обладает свойствами:
1. Функция распределения случайной
величины есть неотрицательная функция,
заключенная между нулем и единицей:
 .
.
Утверждение следует из того, что функция
распределения — это вероятность.
2. Функция распределения есть неубывающая
функция на всей числовой оси.
3. На минус бесконечности функция
распределения равна нулю, на плюс
бесконечности равна 1, т.е.
 ;
; .
.
4. Вероятность попадания случайной
величины в интервал
 (включая
(включая )
)
равна приращению ее функции распределения
на этом интервале, т.е.
 .
.
История
Роль случайной величины, как одного из основных понятий теории вероятностей, впервые была чётко осознана П. Л. Чебышевым, который обосновал общепринятую на сегодня точку зрения на это понятие (1867). Понимание случайной величины как частного случая общего понятия функции, пришло значительно позднее, в первой трети 20 века. Впервые полное формализованное представление основ теории вероятностей на базе теории меры было разработано А. Н. Колмогоровым (1933) , после которого стало ясным, что случайная величина представляет собой измеримую функцию, определённую на вероятностном пространстве. В учебной литературе эта точка зрения впервые последовательно проведена У. Феллером (см. предисловие к , где изложение строится на основе понятия пространства элементарных событий и подчёркивается, что лишь в этом случае представление случайной величины становится содержательным).
Дискретная случайная величина[править]
| Определение: |
| Дискретной случайной величиной (англ. discrete random variable) называется случайная величина, множество значений которой не более чем счётно, причём принятие ею каждого из значений есть случайное событие с определённой вероятностью. |
Примерыправить
Проще говоря, дискретные случайные величины — это величины, количество значений которых можно пересчитать. Например:
- Число попаданий в мишень при выстрелах. Принимаемые значения
- Количество выпавших орлов при бросков монетки. Принимаемые значения
- Число очков, выпавших при бросании игральной кости. Случайная величина принимает одно из значений —
Существуют также непрерывные случайные величины. Например, координаты точки попадания при выстреле.