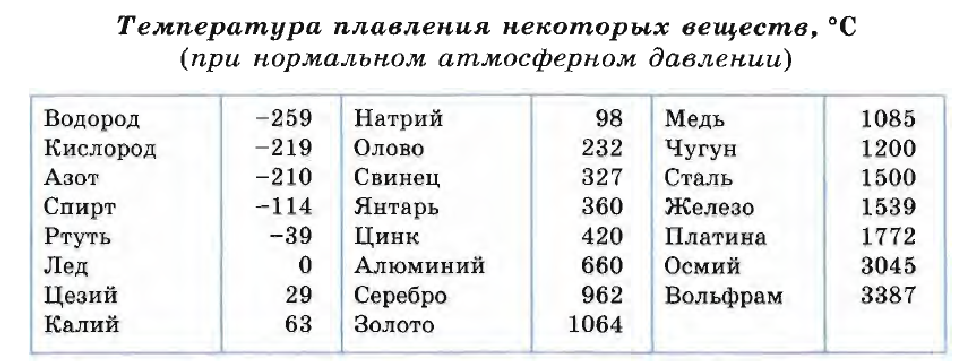
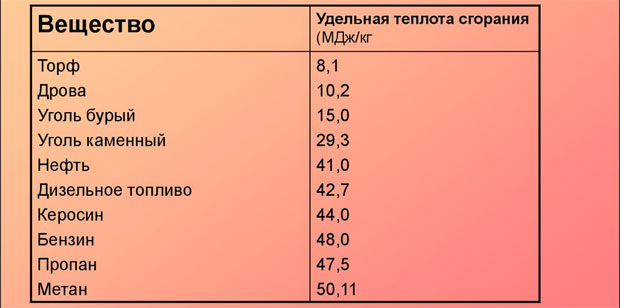
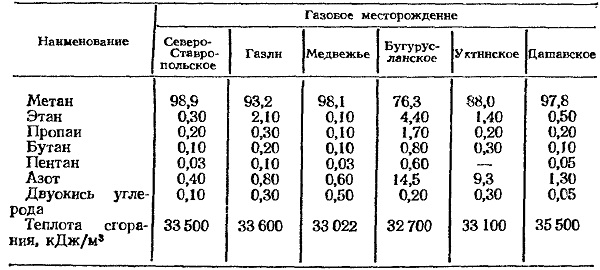
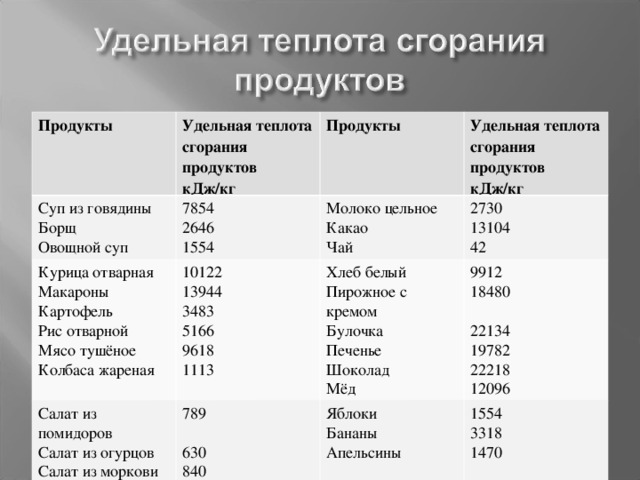
«Количество теплоты. Удельная теплоёмкость»
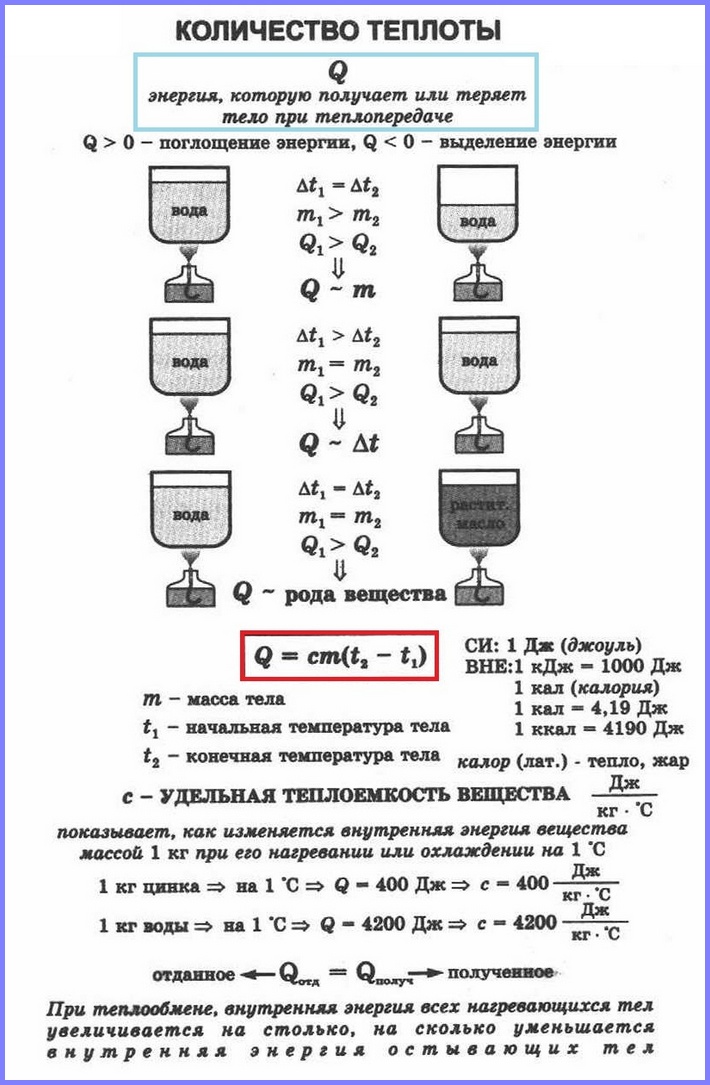
Количество теплоты
Изменение внутренней энергии путём совершения работы характеризуется величиной работы, т.е. работа является мерой изменения внутренней энергии в данном процессе. Изменение внутренней энергии тела при теплопередаче характеризуется величиной, называемой количествоv теплоты.
Количество теплоты – это изменение внутренней энергии тела в процессе теплопередачи без совершения работы. Количество теплоты обозначают буквой Q.
Работа, внутренняя энергия и количество теплоты измеряются в одних и тех же единицах — джоулях (Дж), как и всякий вид энергии.
В тепловых измерениях в качестве единицы количества теплоты раньше использовалась особая единица энергии — калория (кал), равная количеству теплоты, необходимому для нагревания 1 грамма воды на 1 градус Цельсия (точнее, от 19,5 до 20,5 °С). Данную единицу, в частности, используют в настоящее время при расчетах потребления тепла (тепловой энергии) в многоквартирных домах. Опытным путем установлен механический эквивалент теплоты — соотношение между калорией и джоулем: 1 кал = 4,2 Дж.
При передаче телу некоторого количества теплоты без совершения работы его внутренняя энергия увеличивается, если тело отдаёт какое-то количество теплоты, то его внутренняя энергия уменьшается.
Если в два одинаковых сосуда налить в один 100 г воды, а в другой 400 г при одной и той же температуре и поставить их на одинаковые горелки, то раньше закипит вода в первом сосуде. Таким образом, чем больше масса тела, тем большее количество тепла требуется ему для нагревания. То же самое и с охлаждением.
Количество теплоты, необходимое для нагревания тела зависит еще и от рода вещества, из которого это тело сделано. Эта зависимость количества теплоты, необходимого для нагревания тела, от рода вещества характеризуется физической величиной, называемой удельной теплоёмкостью вещества.
Удельная теплоёмкость
Удельная теплоёмкость – это физическая величина, равная количеству теплоты, которое необходимо сообщить 1 кг вещества для нагревания его на 1 °С (или на 1 К). Такое же количество теплоты 1 кг вещества отдаёт при охлаждении на 1 °С.
Удельная теплоёмкость обозначается буквой с. Единицей удельной теплоёмкости является 1 Дж/кг °С или 1 Дж/кг °К.
Значения удельной теплоёмкости веществ определяют экспериментально. Жидкости имеют большую удельную теплоёмкость, чем металлы; самую большую удельную теплоёмкость имеет вода, очень маленькую удельную теплоёмкость имеет золото.
Поскольку кол-во теплоты равно изменению внутренней энергии тела, то можно сказать, что удельная теплоёмкость показывает, на сколько изменяется внутренняя энергия 1 кг вещества при изменении его температуры на 1 °С. В частности, внутренняя энергия 1 кг свинца при его нагревании на 1 °С увеличивается на 140 Дж, а при охлаждении уменьшается на 140 Дж.
Количество теплоты Q, необходимое для нагревания тела массой m от температуры t1°С до температуры t2°С, равно произведению удельной теплоёмкости вещества, массы тела и разности конечной и начальной температур, т.е.
Q = c ∙ m (t2 — t1)
По этой же формуле вычисляется и количество теплоты, которое тело отдаёт при охлаждении. Только в этом случае от начальной температуры следует отнять конечную, т.е. от большего значения температуры отнять меньшее.
Это конспект по теме «Количество теплоты. Удельная теплоёмкость». Выберите дальнейшие действия:
- Перейти к следующему конспекту: «Уравнение теплового баланса»
- Вернуться к списку конспектов по Физике
- Посмотреть решение типовых задач на количество теплоты
Неравенство Клаузиуса. Энтропия
Предположим, что рассматриваемое тело может обмениваться теплотой лишь с N{\displaystyle N} бесконечными тепловыми резервуарами, внутренняя энергия которых столь велика, что при рассматриваемом процессе температура каждого остаётся строго постоянной. Предположим, что над телом был совершён произвольный круговой процесс, то есть по окончании процесса оно находится абсолютно в том же состоянии, что и в начале. Пусть при этом за весь процесс оно заимствовало из i-го резервуара, находящегося при температуре Ti{\displaystyle T_{i}}, количество теплоты Qi{\displaystyle Q_{i}}. Тогда верно следующее неравенство Клаузиуса:
- ∘∑i=1NQiTi⩽{\displaystyle \circ \sum _{i=1}^{N}{\frac {Q_{i}}{T_{i}}}\leqslant 0.}
Здесь ∘{\displaystyle \circ } обозначает круговой процесс. В общем случае теплообмена со средой переменной температуры неравенство принимает вид
- ∮δQ(T)T⩽{\displaystyle \oint {\frac {\delta Q(T)}{T}}\leqslant 0.}
Здесь δQ(T){\displaystyle \delta Q(T)} — количество теплоты, переданное участком среды с (постоянной) температурой T{\displaystyle T}. Это неравенство применимо для любого процесса, совершаемого над телом. В частном случае квазистатического процесса оно переходит в равенство. Математически это означает, что для квазистатических процессов можно ввести функцию состояния, называемую энтропией, для которой
- S=∫δQ(T)T,{\displaystyle S=\int {\frac {\delta Q(T)}{T}},}
- dS=δQT.{\displaystyle dS={\frac {\delta Q}{T}}.}
Здесь T{\displaystyle T} — это абсолютная температура внешнего теплового резервуара. В этом смысле 1T{\displaystyle {\frac {1}{T}}} является интегрирующим множителем для количества теплоты, умножением на который получается полный дифференциал функции состояния.
Для неквазистатических процессов такое определение энтропии не работает. Например, при адиабатическом расширении газа в пустоту
- ∫δQ(T)T=,{\displaystyle \int {\frac {\delta Q(T)}{T}}=0,}
однако энтропия при этом возрастает, в чём легко убедиться, переведя систему в начальное состояние квазистатически и воспользовавшись неравенством Клаузиуса. Кроме того, энтропия (в указанном смысле) не определена для неравновесных состояний системы, хотя во многих случаях систему можно считать локально равновесной и обладающей некоторым распределением энтропии.
Определение
Количество теплоты входит в математическую формулировку первого начала термодинамики, которую можно записать как Q=A+ΔU{\displaystyle Q=A+\Delta U}. Здесь ΔU{\displaystyle \Delta U} — изменение внутренней энергии системы, Q{\displaystyle Q} — количество теплоты, переданное системе, а A{\displaystyle A} — работа, совершённая системой. Однако определение теплоты должно указывать способ её измерения безотносительно к первому началу. Так как теплота — это энергия переданная в ходе теплообмена, для измерения количества теплоты необходимо пробное калориметрическое тело. По изменению внутренней энергии пробного тела можно будет судить о количестве теплоты, переданном от системы пробному телу. Без использования пробного тела первое начало теряет смысл содержательного закона и превращается в бесполезное для расчётов определение количества теплоты.
Пусть в системе, состоящей из двух тел X{\displaystyle X} и Y{\displaystyle Y}, тело Y{\displaystyle Y} (пробное) заключено в жёсткую адиабатическую оболочку. Тогда оно не способно совершать макроскопическую работу, но может обмениваться энергией (то есть теплотой) с телом X{\displaystyle X}. Предположим, что тело X{\displaystyle X} также почти полностью заключено в адиабатическую, но не жёсткую оболочку, так что оно может совершать механическую работу, но обмениваться теплотой может лишь с Y{\displaystyle Y}. Количеством теплоты, переданным телу X{\displaystyle X} в некотором процессе, называется величина QX=−ΔUY{\displaystyle Q_{X}=-\Delta U_{Y}}, где ΔUY{\displaystyle \Delta U_{Y}} — изменение внутренней энергии тела Y{\displaystyle Y}. Согласно закону сохранения энергии, полная работа, выполненная системой, равна убыли полной внутренней энергии системы двух тел: A=−ΔUx−ΔUy{\displaystyle A=-\Delta U_{x}-\Delta U_{y}}, где A{\displaystyle A} — макроскопическая работа, совершенная телом X{\displaystyle X}, что позволяет записать это соотношение в форме первого начала термодинамики:Q=A+ΔUx{\displaystyle Q=A+\Delta U_{x}}.
| Виды энергии: | ||
|---|---|---|
| Механическая | Потенциальная Кинетическая | |
| ‹› | Внутренняя | |
| Электромагнитная | Электрическая Магнитная | |
| Химическая | ||
| Ядерная | ||
| G{\displaystyle G} | Гравитационная | |
| ∅{\displaystyle \emptyset } | Вакуума | |
| Гипотетические: | ||
| Тёмная | ||
| См.также:Закон сохранения энергии |
Таким образом, вводимое в феноменологической термодинамике количество теплоты может быть измерено посредством калориметрического тела (об изменении внутренней энергии которого можно судить по показанию соответствующего макроскопического прибора). Из первого начала термодинамики следует корректность введённого определения количества теплоты, то есть независимость соответствующей величины от выбора пробного тела Y{\displaystyle Y} и способа теплообмена между телами. При таком определении количества теплоты первое начало становится содержательным законом, допускающим экспериментальную проверку, так как все три величины, входящие в выражение для первого начала, могут быть измерены независимо.
Определение и формула количества теплоты
Внутреннюю энергию термодинамической системы можно изменить двумя способами:
- совершая над системой работу,
- при помощи теплового взаимодействия.
Передача тепла телу не связана с совершением над телом макроскопической работы. В данном случае изменение внутренней энергии вызвано тем, что отдельные молекулы тела с большей температурой совершают работу над некоторыми молекулами тела, которое имеет меньшую температуру. В этом случае тепловое взаимодействие реализуется за счет теплопроводности. Передача энергии также возможна при помощи излучения. Система микроскопических процессов (относящихся не ко всему телу, а к отдельным молекулам) называется теплопередачей. Количество энергии, которое передается от одного тела к другому в результате теплопередачи, определяется количеством теплоты, которое предано от одного тела другому.
Определение
Теплотой
называют энергию, которая получается (или отдается) телом в процессе теплообмена с окружающими телами (средой). Обозначается теплота, обычно буквой Q.
Это одна из основных величин в термодинамике. Теплота включена в математические выражения первого и второго начал термодинамики. Говорят, что теплота – это энергия в форме молекулярного движения.
Теплота может сообщаться системе (телу), а может забираться от нее. Считают, что если тепло сообщается системе, то оно положительно.
Почему газ – лучший пример изменения внутренней энергии, и почему из-за этого школьники не любят физику

Выше мы описывали изменения термодинамических параметров металлического шарика. Они без специальных приборов не очень заметны, и читателю остается поверить на слово о происходящих с объектом процессах. Другое дело, если система – газ. Надавите на него – это будет видно, нагрейте – поднимется давление, опустите под землю – и это можно с легкостью зафиксировать. Поэтому в учебниках чаще всего в качестве наглядной термодинамической системы берут именно газ.
Но, увы, в современном образовании реальным опытам уделяется не так много внимания. Ученый, который пишет методическое пособие, отлично понимает, о чем идет речь. Ему кажется, что на примере молекул газа все термодинамические параметры будут нужным образом продемонстрированы. Но ученику, который только открывает для себя этот мир, скучно слушать про идеальную колбу с теоретическим поршнем. Если бы в школе существовали настоящие исследовательские лаборатории и на работу в них выделялись часы, все было бы по-другому. Пока, к сожалению, опыты только на бумаге. И, скорее всего, именно это становится причиной того, что люди считают данный раздел физики чем-то чисто теоретическим, далеким от жизни и ненужным.
Определение
Количество теплоты входит в математическую формулировку первого начала термодинамики, которую можно записать как Q=ΔU+A{\displaystyle Q=\Delta U+A}. Здесь Q{\displaystyle Q} — количество теплоты, переданное системе, ΔU{\displaystyle \Delta U} — изменение внутренней энергии системы и A{\displaystyle A} — работа, совершённая системой. Однако корректное определение теплоты должно указывать способ её экспериментального измерения безотносительно к первому началу. Так как теплота — это энергия, переданная в ходе теплообмена, для измерения количества теплоты необходимо пробное калориметрическое тело. По изменению внутренней энергии пробного тела можно судить о количестве теплоты, переданном от системы пробному телу, и тем самым экспериментально проверить справедливость первого начала, независимо измерив все три входящие в него величины: работу, внутреннюю энергию и теплоту. Если в феноменологической термодинамике не указать способ независимого измерения количества теплоты посредством калориметрического тела, то первое начало теряет смысл содержательного физического закона и превращается в тавтологическое определение количества теплоты.
Такое измерение можно осуществить следующим способом. Пусть в системе, состоящей из двух тел X{\displaystyle X} и Y{\displaystyle Y} и заключённой в адиабатическую оболочку, тело Y{\displaystyle Y} (пробное) отделено от тела X{\displaystyle X} жёсткой, но теплопроводящей оболочкой. Тогда оно не способно совершать макроскопическую работу, но может обмениваться энергией посредством теплообмена с телом X{\displaystyle X}. Предположим, что тело X{\displaystyle X} может совершать механическую работу, но, так как вся система адиабатически изолирована, оно может обмениваться теплотой может лишь с телом Y{\displaystyle Y}. Количеством теплоты, переданным телу X{\displaystyle X} в некотором процессе, называется величина QX=−ΔUY{\displaystyle Q_{X}=-\Delta U_{Y}}, где ΔUY{\displaystyle \Delta U_{Y}} — изменение внутренней энергии тела Y{\displaystyle Y}. Согласно закону сохранения энергии, полная работа, выполненная системой, равна убыли полной внутренней энергии системы двух тел: A=−ΔUx−ΔUy{\displaystyle A=-\Delta U_{x}-\Delta U_{y}}, где A{\displaystyle A} — макроскопическая работа, совершенная телом X{\displaystyle X}, что позволяет записать это соотношение в виде выражения для первого начала термодинамики: Q=A+ΔUx{\displaystyle Q=A+\Delta U_{x}}.
| Виды энергии: | ||
|---|---|---|
| Механическая | Потенциальная Кинетическая | |
| ‹› | Внутренняя | |
| Электромагнитная | Электрическая Магнитная | |
| Химическая | ||
| Ядерная | ||
| G{\displaystyle G} | Гравитационная | |
| ∅{\displaystyle \emptyset } | Вакуума | |
| Гипотетические: | ||
| Тёмная | ||
| См. также: Закон сохранения энергии |
Таким образом, вводимое в феноменологической термодинамике количество теплоты может быть измерено посредством калориметрического тела (об изменении внутренней энергии которого можно судить по показанию соответствующего макроскопического прибора). Из первого начала термодинамики следует корректность введённого определения количества теплоты, то есть независимость соответствующей величины от выбора пробного тела Y{\displaystyle Y} и способа теплообмена между телами. При таком определении количества теплоты первое начало становится содержательным законом, допускающим непосредственную экспериментальную проверку, кроме того, из него можно получить множество следствий, которые также проверяются в эксперименте.
Формула
Перед тем, как приступить к непосредственному расчёту параметра следует ознакомиться с формулой и её компонентами.
Формула для расчёта удельной теплоёмкости имеет следующий вид:
с = Q/(m*∆T)
Знание величин и их символических обозначений, использующихся при расчёте, крайне важно. Однако необходимо не только знать их визуальный вид, но и чётко представлять значение каждого из них
Расчёт удельной теплоёмкости вещества представлен следующими компонентами:
ΔT – символ, означающий постепенное изменение температуры вещества. Символ «Δ» произносится как дельта.
ΔT можно рассчитать по формуле:
ΔT = t2–t1, где
- t1 – первичная температура;
- t2 – конечная температура после изменения.
m – масса вещества используемого при нагреве (гр).
Q – количество теплоты (Дж/J)
На основании Цр можно вывести и другие уравнения:
- Q = m*цp*ΔT – количество теплоты ;
- m = Q/цр*(t2 — t1) – массы вещества;
- t1 = t2–(Q/цp*m) – первичной температуры;
- t2 = t1+(Q/цp*m) – конечной температуры.
Определение
Количество теплоты входит в математическую формулировку первого начала термодинамики, которую можно записать как Q=A+ΔU{\displaystyle Q=A+\Delta U}. Здесь ΔU{\displaystyle \Delta U} — изменение внутренней энергии системы, Q{\displaystyle Q} — количество теплоты, переданное системе, а A{\displaystyle A} — работа, совершённая системой. Однако определение теплоты должно указывать способ её измерения безотносительно к первому началу. Так как теплота — это энергия переданная в ходе теплообмена, для измерения количества теплоты необходимо пробное калориметрическое тело. По изменению внутренней энергии пробного тела можно будет судить о количестве теплоты, переданном от системы пробному телу. Без использования пробного тела первое начало теряет смысл содержательного закона и превращается в бесполезное для расчётов определение количества теплоты.
Пусть в системе, состоящей из двух тел X{\displaystyle X} и Y{\displaystyle Y}, тело Y{\displaystyle Y} (пробное) заключено в жёсткую адиабатическую оболочку. Тогда оно не способно совершать макроскопическую работу, но может обмениваться энергией (то есть теплотой) с телом X{\displaystyle X}. Предположим, что тело X{\displaystyle X} также почти полностью заключено в адиабатическую, но не жёсткую оболочку, так что оно может совершать механическую работу, но обмениваться теплотой может лишь с Y{\displaystyle Y}. Количеством теплоты, переданным телу X{\displaystyle X} в некотором процессе, называется величина QX=−ΔUY{\displaystyle Q_{X}=-\Delta U_{Y}}, где ΔUY{\displaystyle \Delta U_{Y}} — изменение внутренней энергии тела Y{\displaystyle Y}. Согласно закону сохранения энергии, полная работа, выполненная системой, равна убыли полной внутренней энергии системы двух тел: A=−ΔUx−ΔUy{\displaystyle A=-\Delta U_{x}-\Delta U_{y}}, где A{\displaystyle A} — макроскопическая работа, совершенная телом X{\displaystyle X}, что позволяет записать это соотношение в форме первого начала термодинамики:Q=A+ΔUx{\displaystyle Q=A+\Delta U_{x}}.
| Виды энергии: | |
|---|---|
| Механическая | |
| Потенциальная | |
| Кинетическая | |
| ‹› | Внутренняя |
| Гравитационная | |
| Электрическая | |
| Электромагнитная | |
| Химическая | |
| Ядерная | |
| ∅{\displaystyle \emptyset } | Вакуума |
| Гипотетические: | |
| Тёмная |
Таким образом, вводимое в феноменологической термодинамике количество теплоты может быть измерено посредством калориметрического тела (об изменении внутренней энергии которого можно судить по показанию соответствующего макроскопического прибора). Из первого начала термодинамики следует корректность введённого определения количества теплоты, то есть независимость соответствующей величины от выбора пробного тела Y{\displaystyle Y} и способа теплообмена между телами. При таком определении количества теплоты первое начало становится содержательным законом, допускающим экспериментальную проверку, так как все три величины, входящие в выражение для первого начала, могут быть измерены независимо.
Первый закон термодинамики
Закон сохранения и превращения энергии, распространенный на тепловые явления, называется первым законом (началом) термодинамики.
Можно дать формулировку этого закона исходя из способов изменения внутренней энергии.
Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:
Если рассматривать работу самой системы над внешними телами, то закон может быть сформулирован так:
количество теплоты, переданное системе, идет на изменение ее внутренней энергии и совершение системой работы над внешними телами:
Если система изолирована и над ней не совершается работа и нет теплообмена с внешними телами, то в этом случае внутренняя энергия не изменяется. Если к системе не поступает теплота, то работа системой может совершаться только за счет уменьшения внутренней энергии. Это значит, что невозможно создать вечный двигатель – устройство, способное совершать работу без каких-либо затрат топлива.
Первый закон термодинамики для изопроцессов
Изотермический процесс: \( Q=A’\,(T=const, \Delta U=0) \)Физический смысл: все переданное газу тепло идет на совершение работы.
Изобарный процесс: \( Q=\Delta U+A’ \)Физический смысл: подводимое к газу тепло идет на увеличение его внутренней энергии и на совершение газом работы.
Изохорный процесс: \( Q=\Delta U\,(V=const, A’=0) \)Физический смысл: внутренняя энергия газа увеличивается за счет подводимого тепла.
Адиабатный процесс: \( \Delta U=-A’ \) или \( A=\Delta U\,\mathbf{(Q=0)} \)Физический смысл: внутренняя энергия газа уменьшается за счет совершения газом работы. Температура газа при этом понижается.
Задачи об изменении внутренней энергии тел
Такие задачи можно разделить на группы:
- При взаимодействии тел изменяется их внутренняя энергия без совершения работы над внешней средой.
- Рассматриваются явления, связанные с превращением одного вида энергии в другой при взаимодействии двух тел. В результате происходит изменение внутренней энергии одного тела вследствие совершенной им или над ним работы.
При решении задач первой группы:
- установить, у каких тел внутренняя энергия уменьшается, а у каких – возрастает;
- составить уравнение теплового баланса \( (\Delta U=0) \), при записи которого в выражении \( Q =cm(t_2 – t_1) \) для изменения внутренней энергии нужно вычитать из конечной температуры тела начальную и суммировать члены с учетом получающегося знака;
- решить полученное уравнение относительно искомой величины;
- проверить решение.
При решении задач второй группы:
- убедиться, что в процессе взаимодействия тел теплота извне к ним не подводится, т.е. действительно ли \( Q = 0 \);
- установить, у какого из двух взаимодействующих тел изменяется внутренняя энергия и что является причиной этого изменения – работа, совершенная самим телом, или работа, совершенная над телом;
- записать уравнение \( Q = \Delta U + A \) для тела, у которого изменяется внутренняя энергия, учитывая знак перед работой и КПД рассматриваемого процесса;
- если работа совершается за счет уменьшения внутренней энергии одного из тел, то \( А= -\Delta U \), а если внутренняя энергия тела увеличивается за счет работы, совершенной над телом, то \( A=\Delta U \);
- найти выражения для \( \Delta U \) и \( A \);
- подставить в исходное уравнение вместо \( \Delta U \) и \( A \) выражения для них, получить окончательное соотношение для определения искомой величины;
- решить полученное уравнение относительно искомой величины;
- проверить решение.
Теплопередача
Теплопередача – процесс изменения внутренней энергии тела без совершения работы.
Существуют три вида теплопередачи: теплопроводность, конвекция и излучение (лучистый теплообмен). Теплопередача происходит между телами, имеющими разную температуру. Тепло передается от тела с более высокой температурой к телу с более низкой температурой.
Теплопроводность – это процесс переноса энергии от более нагретых тел (частей тела) к менее нагретым в результате движения и взаимодействия частиц тела. Высокую теплопроводность имеют металлы – так, лучшие проводники тепла – медь, золото, серебро. Теплопроводность жидкостей меньше, а газы являются плохими проводниками тепла. Пористые тела плохо проводят тепло, так как в порах содержится воздух. Вещества с низкой теплопроводностью используют в качестве теплоизоляторов. Теплопроводность невозможна в вакууме. При теплопроводности не происходит переноса вещества.
Явление теплопроводности газов аналогично явлению диффузии. Быстрые молекулы из слоя с более высокой температурой перемещаются в более холодный слой, а молекулы из холодного слоя перемещаются в более нагретый. За счет этого средняя кинетическая энергия молекул более теплого слоя уменьшается, и его температура становится ниже.
В жидкостях и твердых телах при повышении температуры какого-либо участка твердого тела или жидкости его частицы начинают колебаться сильнее. Соударяясь с соседними частицами, где температура ниже, эти частицы передают им часть своей энергии, и температура этого участка возрастает.
Конвекция – перенос энергии потоками жидкости или газа.
Объяснить механизм конвекции можно на основе теплового расширения тел и закона Архимеда. При нагревании объем жидкости увеличивается, а плотность уменьшается. Нагретый слой под действием силы Архимеда поднимается вверх, а холодный опускается вниз. Это естественная конвекция. Она возникает при неравномерном нагревании жидкости или газа снизу в поле тяготения.
При вынужденной конвекции перемещение вещества происходит под действием насосов, лопастей вентилятора. Такая конвекция применяется в состоянии невесомости. Интенсивность конвекции зависит от разности температур слоев среды и агрегатного состояния вещества. Конвекционные потоки поднимаются вверх. При конвекции происходит перенос вещества.
В твердых телах конвекция невозможна, так как частицы не могут из-за сильного взаимодействия покидать свои места. В вакууме конвекция также невозможна.
Примером конвективных потоков в природе являются ветры (бризы дневной и ночной, муссоны).
Излучение (лучистый теплообмен) – перенос энергии электромагнитными волнами. Перенос тепла излучением возможен в вакууме. Источником излучения является любое тело, температура которого отлична от нуля К. При поглощении энергия теплового излучения переходит во внутреннюю энергию. Темные тела быстрее нагреваются излучением, чем тела с блестящей поверхностью, но и остывают быстрее. Мощность излучения зависит от температуры тела. С увеличением температуры тела энергия излучения увеличивается. Чем больше площадь поверхности тела, тем интенсивнее излучение.