Что такое дюрация облигации: разбор на примерах

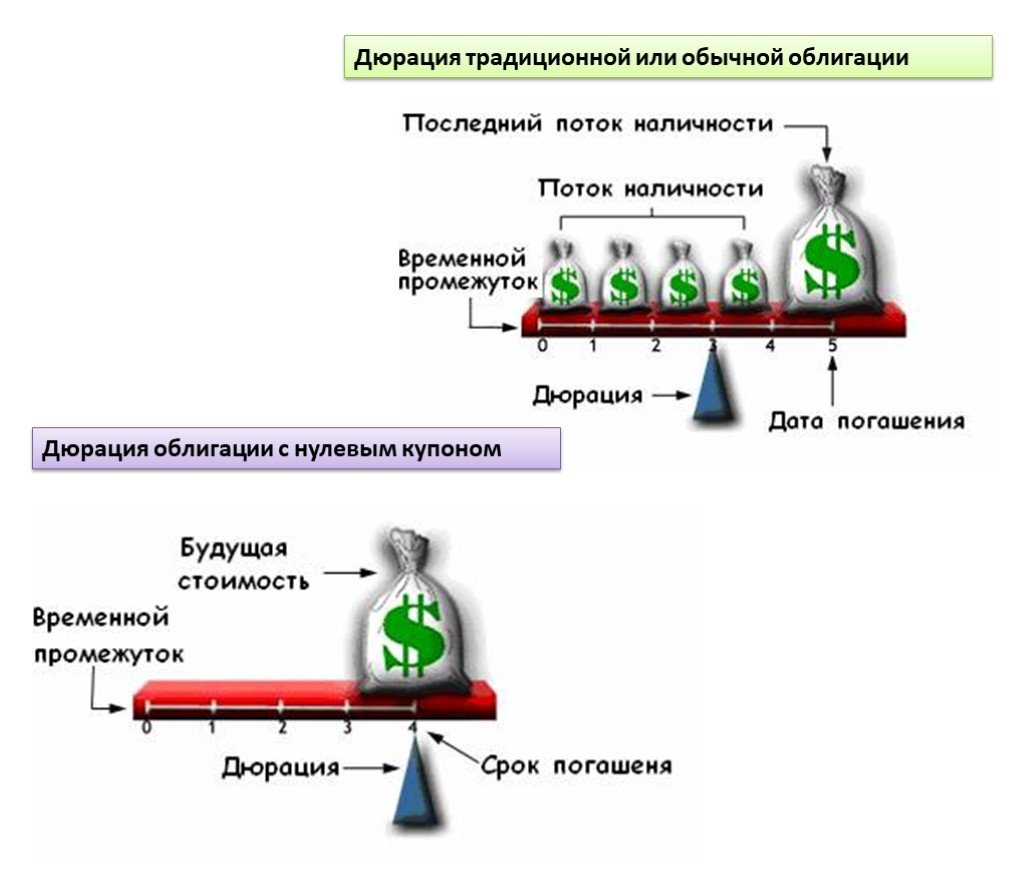
Переменные величины постоянного прибытка

Инвестор пошёл нынче грамотный. Сплошь и рядом дипломы о высшем образовании. Разумные гуманитарии могут обойтись без скучных математических иероглифов, придерживаясь золотого правила: покупай дешевле, продавай дороже. Педантичные технари могут поэкспериментировать с математическими расчётами. Итак, подробнее.

Для читателей, освоивших азы точной науки и желающих применить знания с пользой, предлагается формула дюрации облигации. Математический аппарат для расчета времени возврата инвестиций создал в 1938 году американский учёный Фредерик Макалей. Но современники не оценили практическое значение теории. Открытие предали забвению, а через 15 лет молодая поросль математиков, американских же, повторно открыла явление и успешно внедрила на финансовом поле.

Определить дюрацию облигации с промежуточными выплатами можно по формуле:

D=(PV₁*T₁+…+PV_N*T_N) / Price , где

D – искомый элемент;

N – срок обращения до ликвидации;

T_i – отрезок стрижки очередного талона; i=1…N;

PVi – сумма будущих поступлений: купона и номинала;

Price – рыночная стоимость актива.

Дюрация облигации: расчет, формула

Величина дюрации может быть использована для характеристики многих инвестиционных инструментов, но чаще всего ее применяют для учета рисков при использовании ценных бумаг с установленным сроком обращения.

Наиболее распространенным использованием показателя дюрации является расчет дюрации облигации. Как уже было приведено выше, дюрация облигации идентична общему понятию дюрации, что представляет собой определенное количество лет, необходимое на погашение полной стоимости облигации.

Облигация является эмиссионной долговой ценной бумагой и ее рыночная стоимость может меняться в течение периода ее полного погашения.

Дюрация позволяет инвестору в полной мере оценить финансовую привлекательность облигаций на рынке ценных бумаг, учитывая сразу несколько важных показателей — срок, на который выдана облигация, ставку процента (купон), номинальную стоимость ценной бумаги. Вычисленный показатель дюрации облигации поможет инвесторам принять решение о размещении портфеля ценных бумаг с наибольшей прибылью.

Расчет дюрации ценной бумаги может быть произведен несколькими способами:

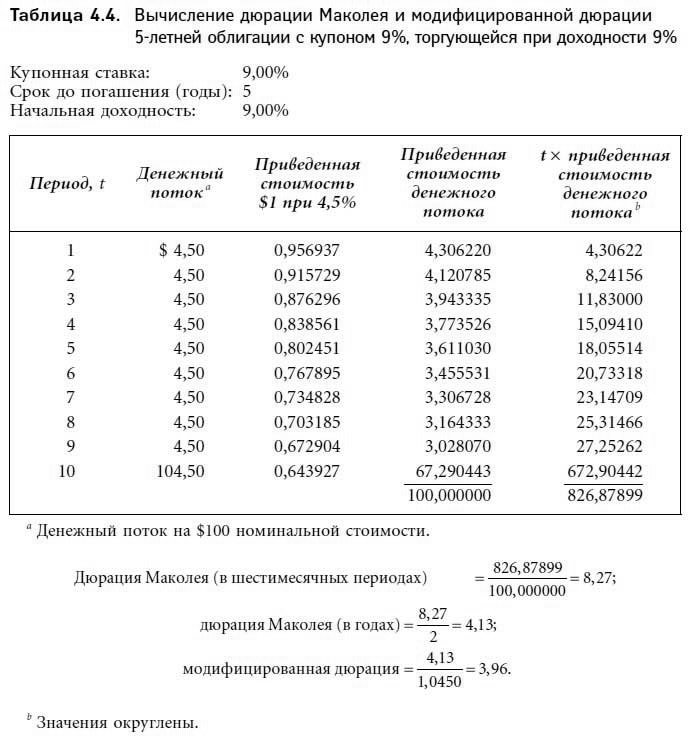
Дюрация Маколея

Фредерик Маколей вывел формулу вычисления дюрации еще в 30-х годах прошлого столетия, однако практическое использование в России ее началось только с 1993 г.

Формула выглядит следующим образом:

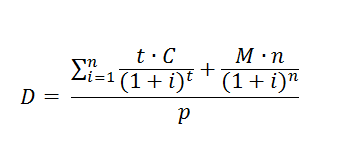
где D – дюрация,
n – количество платежей,
t – время, необходимое для полного погашения,
M – погашение номинальной стоимости ценной бумаги,
С – денежный поток процентных доходов,
i – ставка дисконтирования,
p – рыночная стоимость ценной бумаги

К примеру, инвестор имеет две облигации номинальной стоимостью 5000 рублей каждая, при этом одна из них с нулевым купоном (бескупонная) и сроком погашения 3 года, другая с купоном, равным 5 %, который выплачивается ежегодно, сроком погашения также 3 года.

В первом случае дюрация будет равна сроку погашения облигации, а именно 3 года, так как денежный поток процентных доходов равен 0.

Во втором случае расчет можно произвести следующим образом:

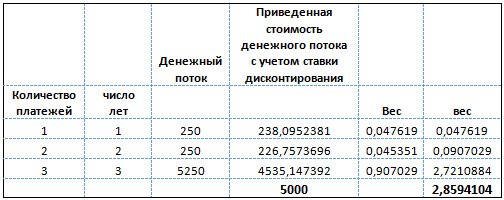
Дюрация облигации с 5 % купоном составит 2,86 года.

Модифицированная дюрация

В случае если процентная ставка доходности меняется в каком-либо временном промежутке до момента полного погашения номинальной стоимости, то необходимо использовать для расчета формулу модифицированной дюрации:

Dm= D/(1+ Cm/n)

где Dm – модифицированная дюрация,
Cm – доходность до погашения,
n – количество выплат по купонам в год

Применяя предыдущий расчет, вычислим Dm= 2.86/((1+0.05/1))=2.86/1.05=2.72

Таким образом, при увеличении дохода по купону, дюрация снижается.

Однако, модифицированная дюрация применима лишь в том случае, если доходные денежные потоки с изменением процентной ставки не меняются, что в практическом применении чаще всего невозможно. Для расчета необходим более чувствительный инструмент к колебаниям ставки процента и, соответственно, доходности, каким и является эффективная дюрация.

Эффективная дюрация

При расчете эффективной дюрации облигации учитываются колебания процентных ставок как в сторону уменьшения, так и в сторону увеличения. Формула для расчета выглядит следующим образом:

Где De – эффективная дюрация,
Pi- — стоимость облигации при уменьшении процентной ставки,
Pi+ — стоимость облигации при увеличении процентной ставки,
Ро – начальная стоимость облигации,
i+ — увеличенная начальная процентная ставка,
i- — уменьшенная начальная процентная ставка.

Расчет эффективной дюрации применим с использование биноминального процентного дерева для исчисления стоимости облигации с учетом колебаний процентных ставок.

Примеры применения на практике

Теперь пришло время поговорить о том, для чего же всё-таки нужно знать такой параметр как ДО, и как его можно применять на практике.

Снижение риска инвестиций

Во-первых, как уже упоминалось выше, дюрация может служить мерой рискованности ваших инвестиций. Чем меньше величина дюрации (читай – срок окупаемости), тем меньше и риск потерять вложенные средства (или часть из них).

Для иллюстрации этого момента давайте рассмотрим простой пример. Представьте себе, что к вам пришли два человека, каждый с просьбой одолжить ему сумму в 1000000 рублей на срок в один год. Каждый из них готов уплачивать проценты в размере 15% годовых, но первый заёмщик готов платить проценты ежемесячно (а размере 15%/12 месяцев = 1,25%), а второй только по истечении года. Кому из них, при прочих равных условиях, вы предпочтёте одолжить деньги?

Ответ очевиден, наиболее выгодным для вас вариантом является одолжить деньги первому заёмщику, который согласен платить проценты ежемесячно. Этот вариант обладает тем неоспоримым преимуществом, что вы начинаете получать возврат инвестированных средств с первого же месяца. А это в свою очередь снижает риск инвестиций (ведь при одинаково неблагоприятном стечении обстоятельств, с первого заёмщика вы получите хоть что-то, в то время как со второго рискуете не получить вообще ничего).

Теперь перейдём к облигациям. Предположим, вы выбираете между двумя облигациями с одинаковыми сроками погашения и стоимостью. Но первая из этих облигаций предполагает выплату купонного дохода раз в месяц, а вторая только раз в год. Соответственно, ДО для первой облигации будет меньше, чем для второй (мы ведь помним, что ДО тем меньше, чем чаще выплачивается купонный доход по ней). И, следовательно, риск инвестиций в первые облигации будет меньшим, чем риск инвестиций во вторые облигации.

Зависимость ДО от процентной ставки

Облигации в целом являются довольно консервативным финансовым инструментом, то есть риск по ним и так минимален (он практически сопоставим с рисками по банковским депозитам). Поэтому дюрацию облигаций чаще рассматривают не в контексте снижения риска, а в контексте зависимости от процентных ставок.

Чтобы проиллюстрировать эту зависимость, давайте рассмотрим простой пример. Предположим, что вы приобрели, на одинаковые суммы денег, два вида облигаций одного и того же эмитента, но с разными сроками погашения. У первых срок погашения через год (ДО меньше), у вторых срок погашения через 10 лет (следовательно, ДО гораздо больше). Купонный доход по обоим видам облигаций составляет 10% годовых.

Теперь предположим, что процентные ставки в стране начали сильно расти и если сегодня выпускали облигации доходностью в 10%, то через некоторое время появляются новые облигации дающие доходность в 12%, а затем и в 15% и в 20%. Как вы думаете, при этом изменится стоимость ваших облигаций дающих 10% годового дохода? Правильно, их стоимость упадет, поскольку спрос на них значительно снизится (зачем людям покупать ваши «десятипроцентные» облигации по прежней цене, если они могут вложить деньги в более доходные бумаги).

Причём стоимость облигаций с большим значением ДО (у которых срок погашения через 10 лет) снизится гораздо больше, чем стоимость облигаций с меньшим значением дюрации (у которых срок погашения через год).

Представим теперь, что события стали развиваться диаметрально противоположным образом и процентные ставки в стране начали падать. То есть если сегодня вложить деньги под 10% годовых можно было относительно легко, то через некоторое время процентная ставка снизится до 5% и вложить деньги под те же 10% (с сохранением того же уровня риска) уже будет попросту невозможно. Очевидно, что при этом варианте развития событий, ваши облигации значительно вырастут в цене, ведь каждый предпочтёт вложить свои деньги под более высокий процент.

Причём, опять же, наиболее вырастут в цене именно облигации с большим значением дюрации (со сроком погашения через 10 лет).

Примеры дюрации

1. Возьмем две облигации: дисконтную и обычную купонную. Первая покупается с дисконтом (например, за 700 рублей), а в конце срока действия облигации возвращается номинал (1000 рублей). До конца срока действия дисконтной бумаги инвестор ничего не получает — поэтому дюрация в этом случае равна сроку, через который будет погашен выпуск.

Обычная же облигация платит купоны, т.е. возвращает инвестору часть вложенной суммы до своего погашения. Если представить, то обе облигации выпущены сроком на 10 лет и через 5 объявляют дефолт, то в случае выпуска с дисконтом инвестор не получит ничего, а во втором случае компенсирует часть вложенных средств купонами. Например, при купоне 10% годовых через 5 лет инвестор вернет половину инвестиций. Другими словами: в случае купонной облигации дюрация всегда меньше срока ее обращения.

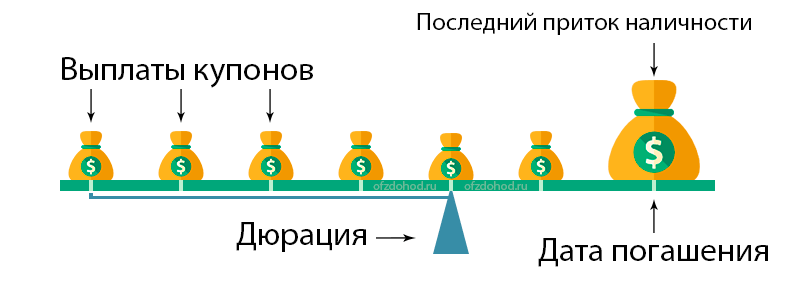
2. Другая ситуация: две купонные облигации с одинаковым купоном, но разным сроком обращения: 3 года и 10 лет. Понятно, что в первом случае инвестор быстрее получит тело депозита назад — так что дюрация в первом случае ниже.

3. Еще один случай: срок действия и доходность к погашению облигаций одинакова, но ставка купонов по ним разная: например 3 и 6%. В этом случае можно ожидать более низкой дюрации от бумаги с более высоким купоном, так как он ускоряет окупаемость.

4. Кроме того, можно рассмотреть случай бессрочной облигации, которая может никогда не вернуть тело депозита, но обещает исправно выплачивать купон. Тут показатель можно вычислить только из купонов — например, при ставке 10% годовых инвестору потребуется 10 лет (3650 дней), чтобы окупить свои инвестиции.

Виды инвестиционных расписок

Облигация – это эмиссионная долговая гарантия, бонд. Эмитент занимает у владельца свободных финансов возвратную сумму. При этом помимо номинала инвестору возвращается бонус в виде процента.

Эмитируют бонды и ноты все, кому требуются средства на развитие бизнеса: корпорации и банки, государство и органы местного самоуправления.

Государство с помощью эмиссии покрывает дефицит бюджета, регулирует денежную массу. А также обеспечивает баланс между секторами финансового рынка. Российские граждане знакомы с эмиссионным творчеством государства: за период существования республики деньги занимались под выигрышный внутренний займ, ГКО, ваучеры, золотые сертификаты, теперь вот добавились ОФЗ.

Классифицируют купонные и бескупонные облигации. Талоны обеспечивают гарантированную фиксированную прибыль раз в год в течение всего времени действия купюры.

Срок возврата инвестиций у «стриженой» бумаги всегда меньше периода к выкупу. Это естественно, так как держатель ежегодно получает талонный приход, и поэтому стоимость находящейся во владении купюры быстрее приближается к номиналу. Нулевой купон гарантирует совпадение сроков погашения и компенсации инвестиций.

Еще один пример

Иван Михайлович и Петя идут к вам и просят дать им взаймы. Они хотят получить от вас 100 тысяч с 10 процентами годовых. Но Иван Михайлович хочет в долг деньги на 3 года. При этом Петя хочет свои деньги на 10 лет. И тот и другой собираются оплачивать проценты по своему долгу.

Для расчета прибыли в таком случае, вам подойдет понимание дюрации по Макколею. Она представляет собой оценку усредненной скорости платежей по облигации. Также учитывается дисконтирование цены отдельных денежных выплат.

Опять вопрос. Кого из них лучше всего прокредитовать?

Одолжив Ивану Михайловичу, вы сможете получить свои деньги назад куда скорее. Поэтому риск потерять деньги по причине ненадежности заемщика куда меньше. За такой временной отрезок вероятность появления разнообразных ситуаций, которые могут оказывать влияние на стоимость денег куда ниже.

Кредитуя же второго человека на такой долгий временной отрезок, вы можете потерять свои деньги с большей вероятностью. Возможно в государстве через 6 лет начнется заметная инфляция и деньги потеряют часть своей ценности.

Таким образом, одолжив свои сбережения на 3 года, вы понесете куда меньшие потери.

Как же тогда используется модифицированная дюрация?

Но если вы захотите выйти раньше (т.е. продать облигацию до даты погашения), то делать это придется по рыночной цене, которая будет иметь место в день предполагаемой продажи. А вот рыночная стоимость в день продажи может быть не 98%, а другой, т.к. она меняется исходя из рыночной доходности (под рыночной доходностью подразумевается ключевая процентная ставка).

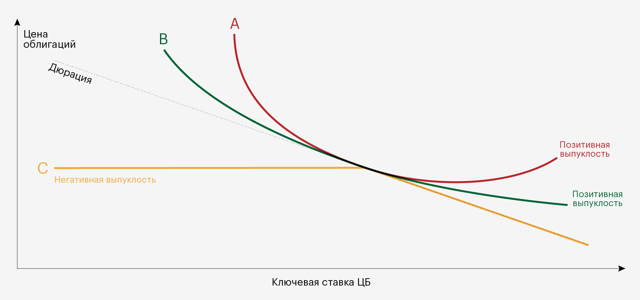
Итак, МД = 5, цена облигации 98%, доходность 12%. На сколько изменится цена в случае снижения доходности с 12% до 10,5% (т.е. на -1,5%). Для точного расчета данного значения будет применяться следующее равенство – смотри рисунок ниже.

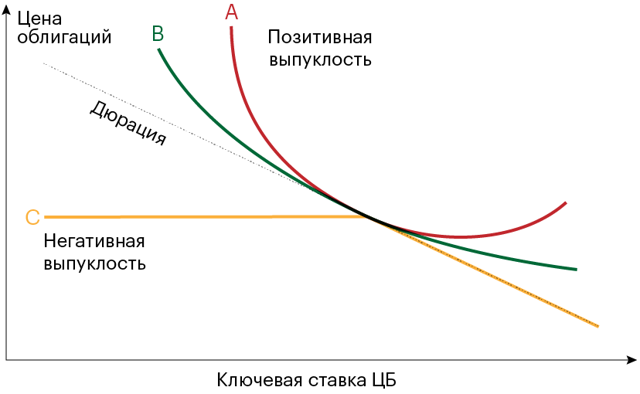
Почему в формуле стоит знак «примерно равно»? Потому что расчет ведется для облигаций с низкой (т.е. позитивной) выпуклостью. Если выпусклость будет высокой (т.е. негативной), то вышеприведенная формула даст значительную погрешность. Негативная выпуклость означает, что при сильном изменении рыночных процентных ставок стоимость облигаций будет сильнее падать и слабее расти. Отсюда следует, что МД не подходит для облигаций с правом выкупа и с высокими ставками.

Получается, при условии снижения среднерыночной доходности на -1,5%, т.е. с 12% до 10,5%, стоимость данной облигации вырастет на +7,35% = (98%*(-5%)*(-1,5%))/100% и составит 105,35% (98%+7,35%). Таким путем вы можете вычислить, насколько изменится стоимость ваших инвестиций по сравнению с их сегодняшней стоимостью, если ключевая процентная ставка вырастет или упадет.

Почему данный показатель называется модифицированной дюрацией? Потому что с математической точки зрения вышеприведенное равенство аналогично формуле дюрации, поэтому его принято называть именно так.

Таким образом, модифицированная дюрация способна учесть изменение рыночной процентной ставки. А поскольку изменение рыночной ставки влечет за собой изменение доходности по облигациям, значит, ее колебания повлияют и на дюрацию. В результате, МД покажет, как изменятся параметры облигации (дюрация и цена) при изменении ключевой ставки на 1%.

Дюрация проекта

Основы расчета дюрации в настоящее время применяются не только для оценки процентных рисков портфеля ценных бумаг, но и для расчета длительности инвестиций в различных инвестиционных проектах. Дюрация проектов, в первую очередь, поможет инвестору сделать выбор между несколькими альтернативными инвестиционными проектами с одинаковым уровнем доходности. Коэффициент дюрации будет отражать тот временной промежуток, через который инвестиционный проект начнет приносить доход.

Формула расчета дюрации проекта идентична основной формуле, выведенной Ф. Маколей. Основными показателями для вычисления будут являться также стоимость доходов и периоды получения доходов.

Коэффициент дюрации является довольно универсальным финансовым показателем, с помощью которого можно характеризовать не только доходные ценные бумаги и инвестиции, но и произвести оценку краткосрочных и долгосрочных кредитных операций.

Часто методика вычисления дюрации кредитного портфеля применяется банками. В данном случае, экономический смысл показателя дюрации активов и обязательств состоит в оценке риска влияния процентных ставок на банковский сектор. Чем ближе показатели дюрации доходности инвестиционных и кредитных операций, тем устойчивее финансовое положение организации и меньше риск негативного влияния вследствие изменения ставок процента на рынке.

В заключении хотелось бы отметить, что величина дюрации для инвестора играет важную роль. С помощью точных и правильных расчетов можно составить стратегию наполнения инвестиционного портфеля ценных бумаг, оценить имеющиеся инвестиционные проекты и избежать рисков колебания процентных ставок с целью увеличения доходности.

Что такое дюрация облигаций

Впервые о дюрации заговорил американский экономист Ф. Маколи в пятидесятых годах XX-го века.

Он считал, что оценивать временной показатель ценных бумаг нужно:

не только по дате погашения,
но также по сроку поступления купонных платежей, для которых создается свой график.

Если биржевой игрок купил облигацию с нулевым купоном, то дюрация равняется дате погашения ценной бумаги.

Если была куплена простая облигация – срок дюрации закончится раньше срока погашения.

Сначала, расчет и самое понятие дюрации облигаций воспринимаются с трудом. Но, если вы хотите всерьез заняться инвестициями, нацелены на хороший результат, то вам нужно хорошо разобраться в этом.

Это значит, что с ростом количества потенциальных выплат, возрастает коэффициент дюрации.

Считается дюрация по формуле, которая подразумевает деление номинального платежа на рыночную цену облигации (уже с процентами). Полученное значение умножается на текущий момент времени.

Конечный показатель дюрации также зависит от количества периодов до окончания действия соглашения и процентной ставки планируемых доходов.

Расчет модифицированной дюрации

Модифицированная дюрация является продолжением дюрации Маколея, которая позволяет инвесторам измерить чувствительность облигаций к изменениям в процентных ставках.

Для расчета модифицированной дюрации, необходимо подсчитать дюрацию Маколея по следующей формуле:

Дюрация Маколея = сумма текущей стоимости купона * Т (время каждого потока в течение года) / рыночную стоимость облигации.

Расчет осуществляется и суммируется для количества периодов до погашения. Например, представим, что бонд имеет срок обращения, равный трем годам.

По нему предлагается купон в 10% и процентная ставка 5%. Соответственно, с учетом всех базовых принципов ценообразования, стоимость облигации составит:

$100 | (1,05) + $100 / (1,05) ^ 2 + $1 100 / (1,05) ^ 3 = $95,24 + $90,70 + $950,22 = $1 136,16

Далее используем формулу Маколея для расчета дюрации, которая равна

($95,24 * 1 / $1 136,16) + ($90,70 * 2 / $1 136,16) + ($950,22 * 3 / $1 136,16) = 2,753

Этот результат показывает, что потребуется 2,753 года для получения настоящей стоимости облигации. С этой цифрой возможно подсчитать модифицированную дюрацию.

Для ее поиска все, что нужно инвестору – это разделить дюрацию Маколея на 1 и прибавить (доходность до срока погашения / количество периодов выплаты купона за год).

В этом примере будет следующий расчет:

2,753 / (1,05 / 1) = 2,621

В этом примере видно, то на каждое изменение в один процент по ставкам, стоимость облигаций будет меняться на 2,621 процент.

Далее предлагаем несколько принципов дюрации, о которых важно помнить

Первое, по мере роста срока обращения, увеличивается дюрация и облигация становится более волатильной.
Второе, по мере роста купона, дюрация снижается, и облигация становится менее волатильной.
Соответственно, снижается и чувствительность ценной бумаги к будущему росту процентных ставок.

Эффективная дюрация

Под этим термином понимается расчет для облигаций с интегрированными опционами принимая во внимание что ожидаемые денежные потоки будут колебаться в зависимости от изменений ставки процента

Чувствительность к процентной ставке

Чувствительность к процентной ставке – это мера того, как цена актива с фиксированной доходностью изменяется в результате изменения процентных ставок.

Стоимость базисного пункта

Этот термин используется для описания того, как изменения базисного пункта в доходности могут повлиять на стоимость облигации.

Дюрация

Этот термин используется для указания того, сколько лет необходимо для получения правильной стоимости облигации путем взвешивания текущей стоимости всех будущих купонных платежей и основной стоимости облигации.

Дюрация облигации: расчет, формула

Расчет дюрации ценной бумаги может быть произведен несколькими способами:

2. Формула дюрации — как подсчитать значение

Дюрация зависит от трех составляющих: цена, процентная ставка и срока до погашения

Где:

De – значение эффективной дюрации облигации
P_i- – рыночная цена при понижении ставки
P_i+ – рыночная цена при возрастании ставки
Pr – номинальная цена ценной бумаги
i₊ – повышенная стартовая ставка
i_— – сниженная стартовая ставка

Считать самостоятельно дюрацию облигации по формуле не нужно. Она уже подсчитана автоматически. Данные можно посмотреть в торговом терминале QUIK или в открытых источниках по облигациям: https://www.rusbonds.ru (например).

Сложность формулы заключается в том, что текущие деньги не равны завтрашним деньгам. Поэтому для точности расчётов их следует дисконтировать.

Есть также другая формула дюрации, которая учитывает еще и ставку дисконтирования:

Где:

n – число платежей
t – период, требуемый для полного погашения
M – погашение номинальной цены облигации
C – денежные поступления процентной прибыли
i – ставка дисконтирования
p – рыночная цена облигации

Дюрация Маколея

Формула выглядит следующим образом:

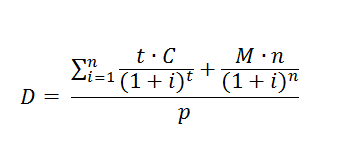
где D – дюрация,
n – количество платежей,
t – время, необходимое для полного погашения,
M – погашение номинальной стоимости ценной бумаги,
С – денежный поток процентных доходов,
i – ставка дисконтирования,
p – рыночная стоимость ценной бумаги

Во втором случае расчет можно произвести следующим образом:

Дюрация облигации с 5 % купоном составит 2,86 года.

Модифицированная дюрация

Dm= D/(1+ Cm/n)

где Dm – модифицированная дюрация,
Cm – доходность до погашения,
n – количество выплат по купонам в год

Применяя предыдущий расчет, вычислим Dm= 2.86/((1+0.05/1))=2.86/1.05=2.72

Таким образом, при увеличении дохода по купону, дюрация снижается.

Эффективная дюрация

Где De – эффективная дюрация,
Pi- — стоимость облигации при уменьшении процентной ставки,
Pi+ — стоимость облигации при увеличении процентной ставки,
Ро – начальная стоимость облигации,
i+ — увеличенная начальная процентная ставка,
i- — уменьшенная начальная процентная ставка.

Как использовать ДО на практике?

Разобравшись в сути и зная данные о ДО, можно осуществлять эффективные операции по покупке и продаже данных финансовых инструментов, основываясь на собственные прогнозы. На этой информации строятся целые стратегии.

Для этого нужно учесть следующие факты:

Меньшая ДО предполагает меньший риск, соответственно, чем она выше, тем выше и риск, так как такая облигация имеет более высокую чувствительность к изменениям цены и процентных ставок;
Высокая процентная ставка говорит о доходной ценной бумаге, быстром возврате вложенных денежных средств и низкой ДО, а чем ниже уровень купона – тем больше ДО будет;
ДО не может превысить время обращения любой ценной бумаги, а если она купонная – то ДО будет меньше, чем срок ее погашения;
Бескупонный актив имеет ДО равную сроку ее обращения;
Дюрация всегда изменяется, так как при сокращении времени до погашения актива, уменьшается и ее величина.

Если инвестор прогнозирует, исходя из роста цен, будущее снижение ставок по процентам, это говорит о том, что цена на финансовый инструмент с большей дюрацией также поднимется. Поэтому, в данном случае, чтобы получить большую прибыль, нужно будет выбрать бумагу с большей ДО.

А если ставки вырастут, то цена на финансовый инструмент с большей ДО снизится сильнее, чем при меньшей величине данного показателя, актив с которой и нужно будет выбрать.

Если у вас имеются активы одного эмитента, но разных выпусков, то и ДО у них будут разные. Большую доходность в этом случае принесет тот инструмент, по которому дюрация будет выше, несмотря на то, что эмитент обладает одинаковым кредитным качеством.

Если же активы имеют одинаковую доходность, то лучше приобрести тот, который будет иметь меньшую ДО.

Поэтому, очень важно владеть информацией о ДО, понимать ее суть, и строить правильные стратегии, позволяющие получить хороший доход, к чему все и стремятся. Итак, мы приближаемся к завершению данной темы

Сегодня мы с вами уяснили суть, рассмотрели примеры и некоторые стратегии, определили, как данный показатель может влиять на получаемый доход. Надеюсь, вам было интересно, и эта информация будет полезной для вас!

Итак, мы приближаемся к завершению данной темы. Сегодня мы с вами уяснили суть, рассмотрели примеры и некоторые стратегии, определили, как данный показатель может влиять на получаемый доход. Надеюсь, вам было интересно, и эта информация будет полезной для вас!

Для закрепления материала посмотрите видео.

На этом я с вами прощаюсь до завтра. Всем хорошего дня!

Заключение

В заключение приведем несколько ключевых моментов:

Дюрация отдельной ценной бумаги не имеет особого значения. Показатели имеет смысл анализировать по совокупности (например, по портфелю) или в сравнении с другими аналогичными инструментами.
Показатель во многом зависит от ключевой ставки. При повышении ставок выбирайте облигации с низкой дюрацией и наоборот.
Если вы все же решили рассчитать дюрацию самостоятельно, помните главное правило: полученное значение всегда должно быть меньше или равно сроку погашения долгового обязательства

Если у вас получилось значение больше, значит, в расчетах есть ошибка.
Расчет дюрации не применяется для облигаций с плавающим купоном.
Значение показателя меняется ежедневно, особое внимание следует обращать на периоды после купонных выплат.

Подведение итога

Дюрация облигации не демонстрирует доходность, получаемую от ценных бумаг. Значение дает представление о сроках, когда расходы на них будут компенсированы. Причем роли не играет, является это возвратом вложения или чистым доходом, важен только факт «расход=доход».

Дюрация – некий конечный фильтр при выборе направления для инвестирования. Если исходить из всех данных и определений, можно подвести итог:

Размер дюрации ежедневно сокращается, так как приближается срок получения дохода.
Дюрация бескупонной долговой бумаги всегда соответствует сроку ее погашения.
Ценные бумаги с низким купонным доходом всегда имеют меньшую дюрацию.
Чем ниже значение дюрации, тем менее рискованны инвестиции.
Облигации с большим значением дюрации более зависимы от ключевой ставки, что в результате влияет на реальную стоимость долговой бумаги.

Дюрация облигации является лишь одним из инструментов трейдера, используемым для выбора инвестиционного направления. Она отражает только один из параметров, которые используют инвесторы – момент возврата вложения. При принятии решенияо покупке стоит обязательно учитывать доходность облигации.

Что такое дюрация облигации?

Переменные величины постоянного прибытка

Дюрация облигации: расчет, формула

Дюрация Маколея

Модифицированная дюрация

Эффективная дюрация

Примеры применения на практике

Снижение риска инвестиций

Зависимость ДО от процентной ставки

Примеры дюрации

Виды инвестиционных расписок

Еще один пример

Как же тогда используется модифицированная дюрация?

Дюрация проекта

Что такое дюрация облигаций

Расчет модифицированной дюрации

Эффективная дюрация

Чувствительность к процентной ставке

Стоимость базисного пункта

Дюрация

Дюрация облигации: расчет, формула

2. Формула дюрации — как подсчитать значение

Дюрация Маколея

Модифицированная дюрация

Эффективная дюрация

Как использовать ДО на практике?

Заключение

Подведение итога