Характеристики сигналов
Формально прописанными в ГОСТ характеристиками сигналов являются ниже следующие.
Характеристики импульсов
- Спектральная функция импульса — комплексная функция, представляющая собой преобразование Фурье от импульса.
- Модуль спектральной функции импульса
- Аргумент спектральной функции импульса
Характеристики периодических сигналов
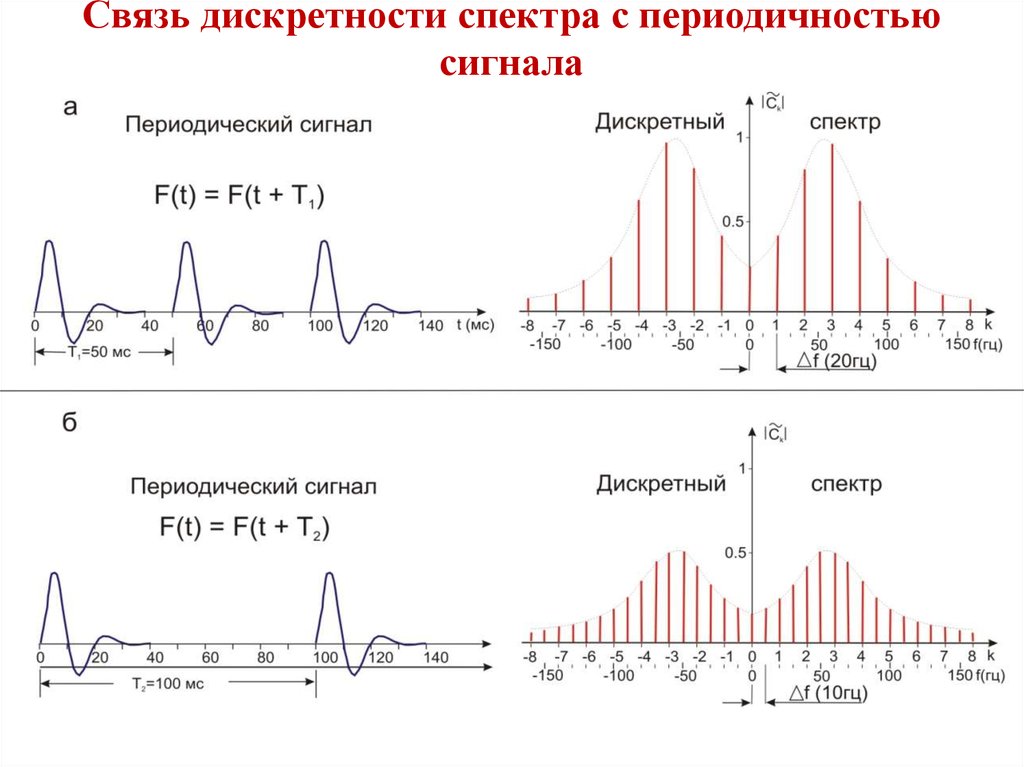
- Период периодического сигнала — параметр, равный наименьшему интервалу времени, через который повторяются мгновенные значения периодического сигнала.
- Частота периодического сигнала — параметр, представляющий собой величину, обратную периоду периодического сигнала.
- Комплексный спектр периодического сигнала — Комплексная функция дискретного аргумента, равного целому числу значений частоты периодического сигнала, представляющая собой значения коэффициентов комплексного ряда Фурье для периодического сигнала.
- Амплитудный спектр периодического сигнала — Функция дискретного аргумента, представляющая собой модуль комплексного спектра периодического сигнала.
- Фазовый спектр периодического сигнала — функция дискретного аргумента, представляющая собой аргумент комплексного спектра периодического сигнала.
- Гармоника — гармонический сигнал с амплитудой и начальной фазой, равными соответственно значениям амплитудного и фазового спектра периодического сигнала при некотором значении аргумента.
Характеристики случайных сигналов
- Одномерная плотность вероятности — функция, равная пределу отношения вероятности пребывания случайного сигнала в некотором интервале значений к ширине этого интервала при стремлении его к нулю, причем ее аргументом является значение, к которому стягивается интервал
- Корреляционная функция — функция, равная среднему значению произведения переменной составляющей случайного сигнала и такой же переменной составляющей, но запаздывающей на заданное время.
- Нормированная корреляционная функция — функция, равная отношению корреляционной функции случайного сигнала к его дисперсии
- Энергетический спектр — функция, представляющая собой преобразование Фурье от корреляционной функции, аргументом которой является частота
Характеристики взаимодействия сигналов
- Отношение сигнал - помеха — отношение величин, характеризующих интенсивности сигнала и помехи.
- Коэффициент модуляции «вверх» — коэффициент, равный отношению пикового отклонения «вверх» закона модуляции к его постоянной составляющей при амплитудной модуляции.
- Коэффициент модуляции «вниз» — коэффициент, равный отношению пикового отклонения «вниз» закона модуляции к его постоянной составляющей при амплитудной модуляции.
- Девиация частоты «вверх» — пиковое отклонение «вверх» закона модуляции при частотной модуляции.
- Девиация частоты «вниз» — пиковое отклонение «вниз» закона модуляции при частотной модуляции.
- Индекс угловой модуляции — пиковое отклонение закона модуляции фазомодулированного сигнала при гармоническом законе модуляции
Характеристики взаимосвязи сигналов
- Взаимокорреляционная функция — функция, равная среднему значению произведения переменной составляющей одного случайного сигнала и запаздывающей на заданное время переменной составляющей другого случайного сигнала.
- Взаимный энергетический спектр — Функция, представляющая собой преобразование Фурье от взаимнокорреляционной функции, аргументом которой является частота
- Время запаздывания — параметр, равный значению временного сдвига одного из сигналов, при котором достигается тождественное равенство его другому сигналу с точностью до постоянного множителя и постоянного слагаемого.
- Фазовый сдвиг — модуль разности начальных фаз двух гармонических сигналов одинаковой частоты.
Характеристики искажений сигналов
- Коэффициент гармоник — коэффициент, характеризующий отличие формы данного периодического сигнала от гармонической, равный отношению среднеквадратического напряжения суммы всех гармоник сигнала, кроме первой, к среднеквадратическому напряжению первой гармоники.
- Относительное отклонение сигнала от линейного закона — коэффициент, равный отношению абсолютного отклонения (40) данного сигнала от прямой линии, соединяющей мгновенные значения сигнала, соответствующие началу и концу заданного интервала времени к максимальному значению сигнала на этом же интервале
- Коэффициент нелинейности сигнала — коэффициент, равный отношению размаха производной сигнала на заданном интервале времени к максимальному значению производной на этом же интервале.
- Абсолютное отклонение сигналов — максимальное значение разности мгновенных значений сигналов, взятых в один и тот же момент времени на протяжении заданного интервала времени.
4.2. Сигналы с непрерывной амплитудной модуляцией
Рассмотрение модулированных сигналов начнем с сигналов, у которых в качестве изменяемого параметра выступает амплитуда несущего колебания. Модулированный сигнал в этом случае является амплитудно-модулированным или сигналом с амплитудной модуляцией (АМ-сигналом).
Как уже было отмечено выше, основное внимание будет уделено сигналам, несущее колебание которых представляет собой гармоническое колебание вида
,
где – амплитуда несущего колебания,
– частота несущего колебания.
Здесь и далее полагается, что начальные фазы гармонических колебаний равны нулю.
В качестве модулирующих сигналов сначала рассмотрим непрерывные сигналы . Тогда модулированные сигналы будут являться сигналами с непрерывной амплитудной модуляцией. Такой сигнал описывается выражением
, (4.2)
где – огибающая АМ-сигнала,
– коэффициент амплитудной модуляции.
Из выражения (4.2) следует, что АМ-сигнал представляет собой произведение огибающей на гармоническую функцию . Коэффициент амплитудной модуляции характеризует глубину модуляции и в общем случае описывается выражением
. (4.3)
Очевидно, при сигнал представляет собой просто несущее колебание.
Для более детального анализа характеристик АМ-сигналов рассмотрим простейший АМ-сигнал, в котором в качестве модулирующего сигнала выступает гармоническое колебание
, (4.4)
где , – соответственно амплитуда и частота модулирующего (управляющего) сигнала, причем . В этом случае сигнал описывается выражением
, (4.5)
и называется сигналом однотональной амплитудной модуляции.
На рис. 4.2 изображены модулирующий сигнал , колебание несущей частоты и сигнал .
Для такого сигнала коэффициент глубины амплитудной модуляции равен
.
Воспользовавшись известным тригонометрическим соотношением
после несложных преобразований получим
(4.6)
Выражение (4.6) устанавливает спектральный состав однотонального АМ-сигнала. Первое слагаемое представляет собой немодулированное колебание (несущее колебание). Второе и третье слагаемые соответствуют новым гармоническим составляющим, появившимся в результате модуляции амплитуды несущего колебания; частоты этих колебаний и называются нижней и верхней боковыми частотами, а сами составляющие – нижней и верхней боковыми составляющими.
Амплитуды этих двух колебаний одинаковы и составляют величину
, ( 4.7)
На рис. 4.3 изображен амплитудный спектр однотонального АМ-сигнала. Из этого рисунка следует, что амплитуды боковых составляющих располагаются симметрично относительно амплитуды и начальной фазы несущего колебания. Очевидно, ширина спектра однотонального АМ-сигнала равна удвоенной частоте управляющего сигнала
.
В общем случае, когда управляющий сигнал характеризуется произвольным спектром, сосредоточенным в полосе частот от до , спектральный характер АМ-сигнала принципиально не отличается от однотонального.
На рис. 4.4 изображены спектры управляющего сигнала и сигнала с амплитудной модуляцией. В отличие от однотонального АМ-сигнала в спектре произвольного АМ-сигнала фигурируют нижняя и верхняя боковые полосы. При этом верхняя боковая полоса является копией спектра управляющего сигнала, сдвинутой по оси частот на
величину , а нижняя боковая полоса представляет собой зекальное отображение верхней. Очевидно, ширина спектра произвольного АМ-сигнала
, (4.8)
т.е. равна удвоенной верхней граничной частоте управляющего сигнала.
Возвратимся к сигналу однотональной амплитудной модуляции и найдем его энергетические характеристики. Средняя мощность АМ-сигнала за период управляющего сигнала определяется по формуле:
. (4.9)
Так как , а , положим , где . Подставляя выражение (4.6) в (4.9), после несложных, но достаточно громоздких преобразований с учетом того, что и с использованием тригонометрических соотношений
и ,
получим
. (4.10)
Здесь первое слагаемое характеризует среднюю мощность несущего колебания, а второе – суммарную среднюю мощность боковых составляющих, т.е.
.
Так как суммарная средняя мощность боковых составляющих делится поровну между нижней и верхней, что вытекает из (4.7), то отсюда следует
. (4.11)
Таким образом, на передачу несущего колебания в АМ-сигнале тратится более половины мощности (с учетом того, что ), чем на передачу боковых составляющих. Так как информация заложена именно в боковых составляющих, передача составляющей несущего колебания нецелесообразна с энергетической точки зрения. Поиск более эффективных методов использования принципа амплитудной модуляции приводит к сигналам балансной и однополосной амплитудной модуляции.
Отличие дискретного сигнала от цифрового
Про Азбуку Морзе наверное слышали все. Придумал художник Самуэль Морзе, другие новаторы усовершенствовали, а использовали все. Это способ передачи текста, где точками и тире закодированы буквы. Упрощенно, кодировка называется морзянкой. Её долго использовали на телеграфе и для передачи информации по радио. Кроме того, сигналить можно с помощью прожектора или фонарика.
Код морзянки зависит только от самого знака. А не от его продолжительности или громкости (силы). Как ни ударь ключом (моргни фонариком), воспринимаются только два варианта– точка и тире. Можно только увеличить скорость передачи. Ни громкость, ни продолжительность в расчёт ни принимаются. Главное, что бы сигнал дошёл.
Так же и цифровой сигнал
Важно закодировать данные с помощью 0 и 1. Получатель должен только разобрать, комбинацию нолей и единиц
Неважно с какой громкостью и какой продолжительностью будет каждый сигнал. Важно получить нолики и единички. Это суть цифровой технологии.
Дискретный сигнал получится если закодировать ещё громкость (яркость) и продолжительность каждой точки и тире, или 0 и 1. В этом случае вариантов кодировки больше, но и путаницы тоже. Громкость и продолжительность можно не разобрать. В этом и разница между цифровым и дискретным сигналами. Цифровой генерируется и воспринимается однозначно, дискретный с вариациями.
Применение цифрового сигнала
Чем же отличается цифровой электрический сигнал от других? Тем, что он способен совершать в ретрансляторе полную регенерацию. Когда в оборудование связи поступает сигнал, имеющий малейшие помехи, он сразу же меняет свою форму на цифровую. Это позволяет, например, телевышке снова сформировать сигнал, но уже без шумового эффекта.
В том случае, если код поступает уже с большими искажениями, то, к сожалению, восстановлению он не подлежит. Если брать в сравнении аналоговую связь, то в аналогичной ситуации ретранслятор может извлечь часть данных, затрачивая много энергии.
Обсуждая сотовую связь разных форматов, при сильном искажении на цифровой линии разговаривать практически невозможно, так как не слышны слова или целые фразы. Аналоговая связь в таком случае более действенна, ведь можно продолжать вести диалог.
Именно из-за подобных неполадок цифровой сигнал ретрансляторы формируют очень часто для того, чтобы сократить разрыв линии связи.
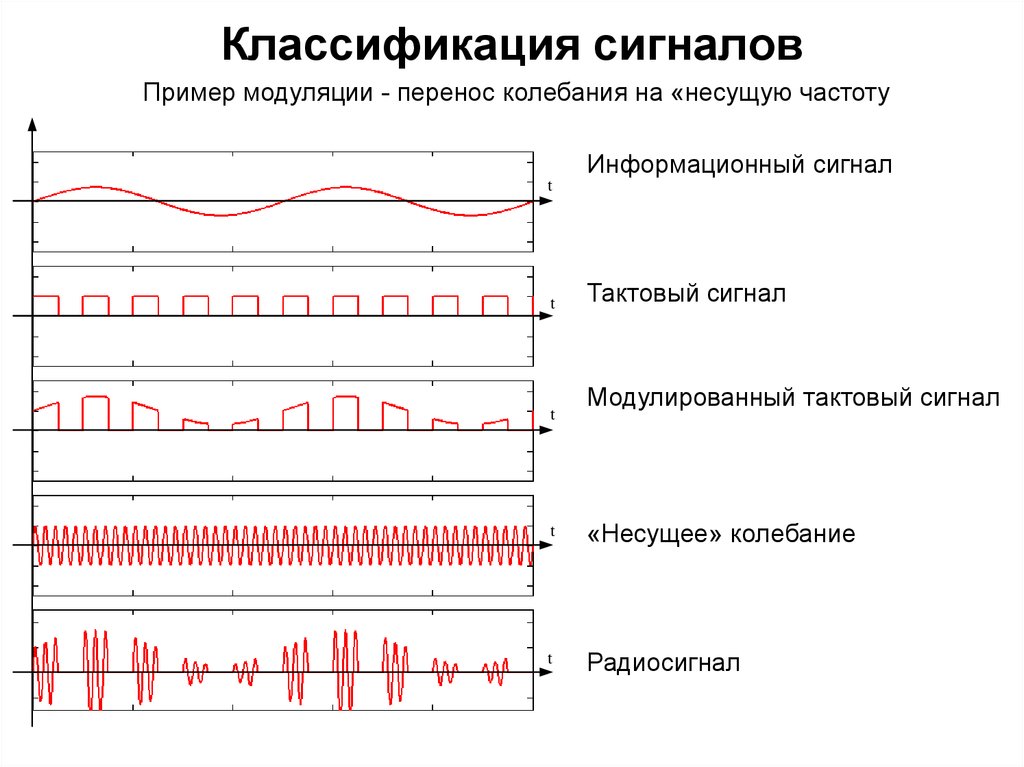
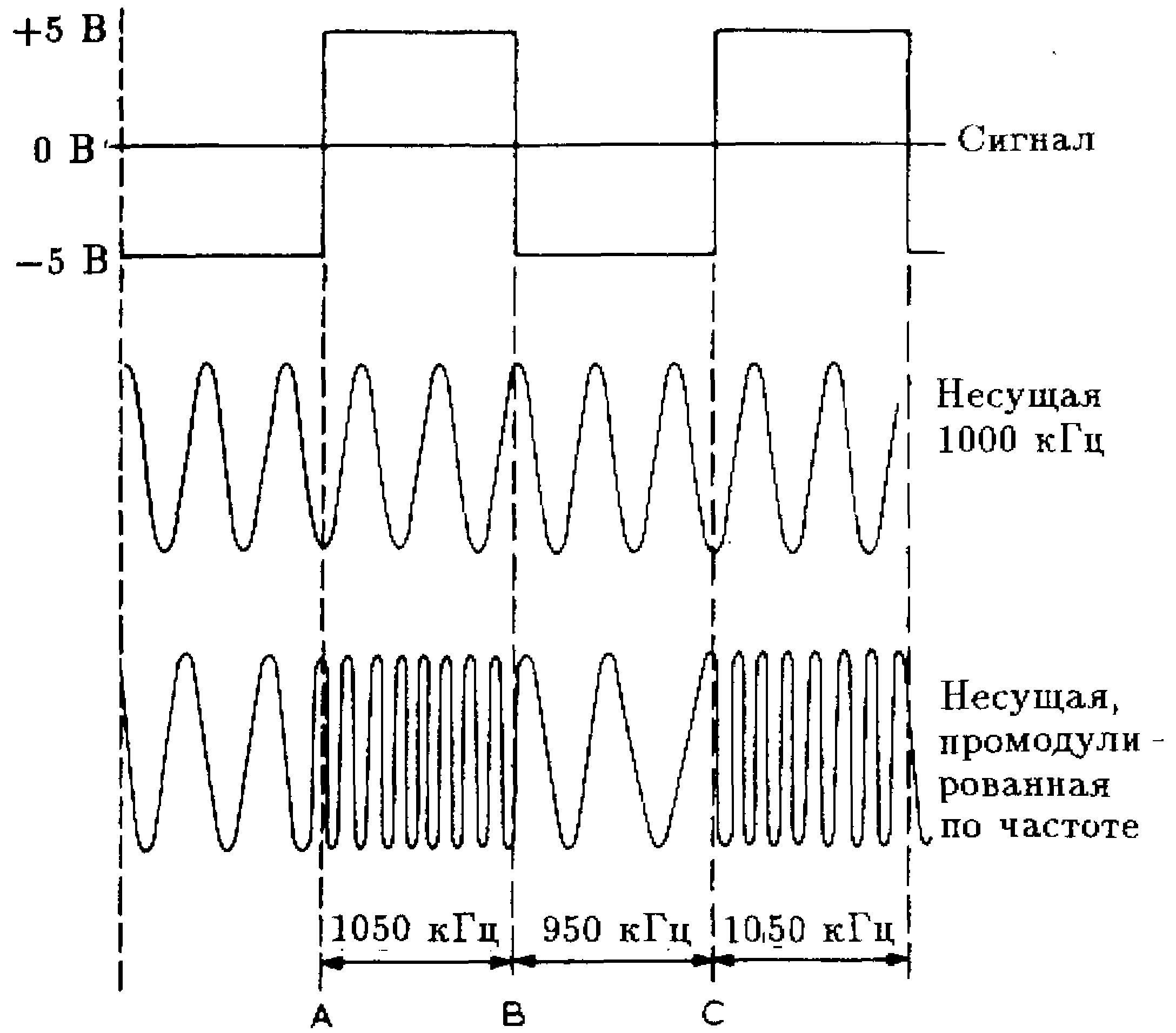
Модуляция сигналов
Все вышеперечисленные способы передачи данных связаны с таким явлением, как модуляция (для цифровых сигналов — манипуляция). Зачем она нужна?
Как известно, электромагнитные волны (с помощью которых переносятся разные виды сигналов) склонны к затуханию, а это существенно уменьшает дальность их передачи. Чтобы этого не произошло, низкочастотные колебания переносятся в область длинных высокочастотных волн. Это явление и называется модуляцией (манипуляцией).
Помимо увеличения расстояния передачи данных, благодаря ей повышается помехоустойчивость сигналов. А также появляется возможность одновременно организовывать сразу несколько независимых каналов передачи информации.
Сам процесс выглядит следующим образом. В прибор, именуемый модулятором, поступают одновременно два сигнала: низкочастотный (несет определенную информацию) и высокочастотный (безинформационный, зато способен передаваться на длинные дистанции). В этом устройстве они преобразуются в один, который одновременно совмещает в себе достоинства их обоих.
Виды выходных сигналов зависят от измененного параметра входного несущего высокочастотного колебания.
Если оно гармоническое – такой процесс модуляции именуется аналоговым.
Если периодическое – импульсным.
Если несущим сигналом является просто постоянный ток – такая разновидность называется шумоподобной.
Первых два вида модуляции сигналов, в свою очередь, делятся на подвиды.
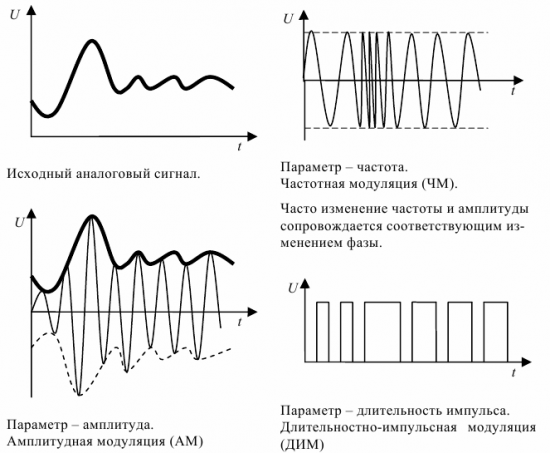
Аналоговая модуляция бывает такой.
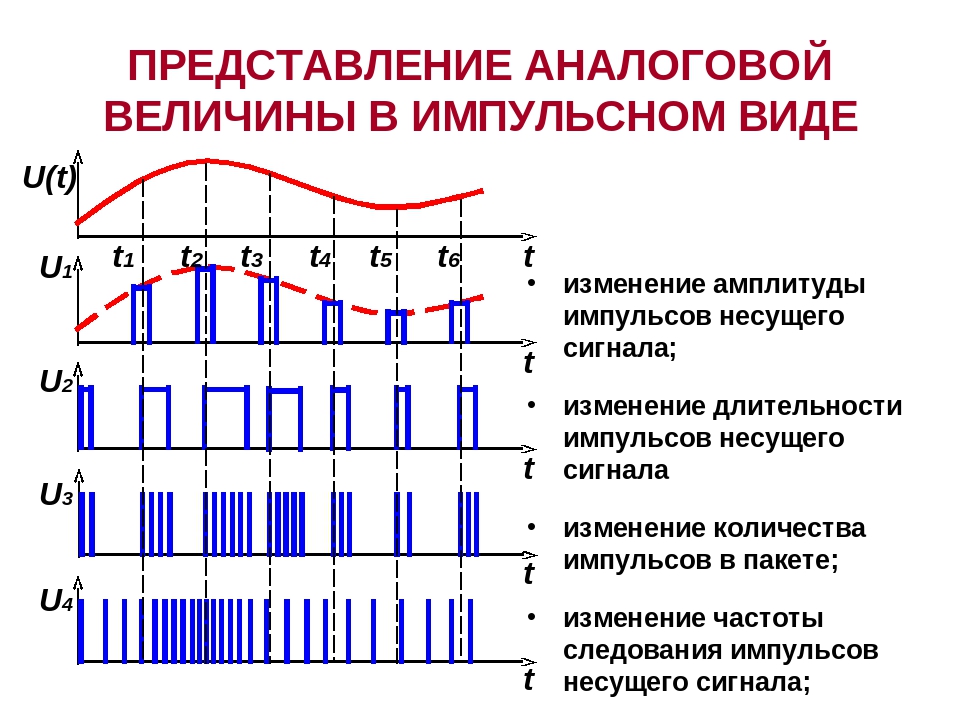
- Амплитудная (АМ) – изменение амплитуды несущего сигнала.
- Фазовая (ФМ) – меняется фаза.
- Частотная – влиянию подвергается только частота.
Виды модуляции сигналов импульсных (дискретных).
- Амплитудно-импульсная (АИМ).
- Частотно-импульсная (ЧИМ).
- Широтно-испульсная (ШИМ).
- Фазо-импульсная (ФИМ).
Рассмотрев, какие существуют способы передачи данных, можно сделать вывод, что, независимо от их вида, все они играют важную роль в жизни человека, помогая ему всесторонне развиваться и защищая от возможных опасностей.
Что касается аналогового и цифрового сигналов (с помощью которых передается информация в современном мире) то, вероятнее всего, в ближайшие двадцать лет в развитых странах первый будет практически полностью вытеснен вторым.
Для чего обрабатывается сигнал?
Сигнал обрабатывается с целью передачи и получения информации, которая в нем зашифрована. Как только она будет извлечена, ее можно использовать различными способами. В отдельных ситуациях ее переформатируют.
Существует и другая причина обработки всех сигналов. Она заключается в небольшом сжатии частот (чтобы не повредить информацию). После этого ее форматируют и передают на медленных скоростях.
В аналоговом и цифровом сигналах используются особенные методы. В частности, фильтрация, свертка, корреляция. Они необходимы для восстановления сигнала, если он поврежден или имеет шум.
Сигнал
Сигнал представляет собой специальный код, который передается в пространство одной или несколькими системами. Эта формулировка является общей.
В сфере информации и связи сигналом назван специальный носитель каких-либо данных, который используется для передачи сообщений. Он может быть создан, но не принят, последнее условие не обязательно. Если же сигнал является сообщением, то его «ловля» считается необходимой.
Описываемый код передачи данных задается математической функцией. Она характеризует все возможные изменения параметров. В радиотехнической теории эта модель считается базовой. В ней же аналогом сигнала был назван шум. Он представляет собой функцию времени, которая свободно взаимодействует с переданным кодом и искажает его.
В статье охарактеризованы виды сигналов: дискретный, аналоговый и цифровой. Также коротко дана основная теория по описываемой теме.
Сигнал и событие
Событие (получение записки, наблюдение сигнальной ракеты, приём символа по телеграфу) является сигналом только в той системе отношений, в которой сообщение опознается значимым (например, в условиях боевых действий сигнальная ракета — событие, значимое только для того наблюдателя, которому оно адресовано). Очевидно, что сигнал, заданный аналитически, событием не является и не несет информацию, если функция сигнала и её параметры известны наблюдателю.
В технике сигнал всегда является событием. Другими словами, событие — изменение состояния любого компонента технической системы, опознаваемое логикой системы как значимое, является сигналом. Событие, неопознаваемое данной системой логических или технических отношений как значимое, сигналом не является.
См. также: Множество и Пространство имён
Аналоговый сигнал
Это природный тип сигналов окружает нас повсеместно и постоянно. Звук, изображение, тактильные ощущения, запах, вкус и команды мозга. Все возникающие, во Вселенной без участия человека, сигналы являются аналоговыми.
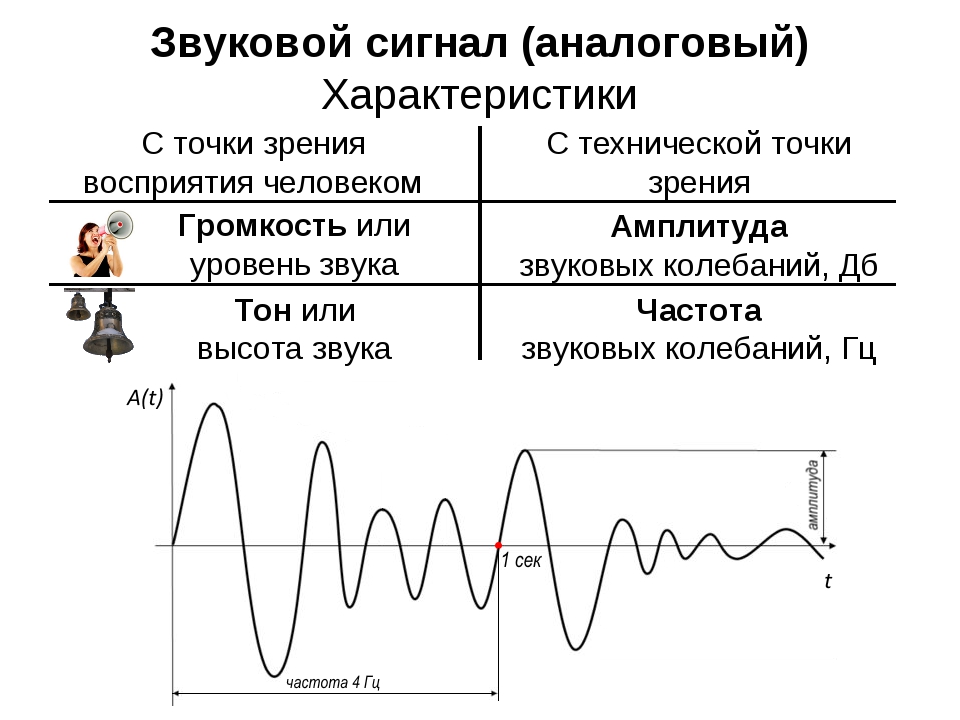
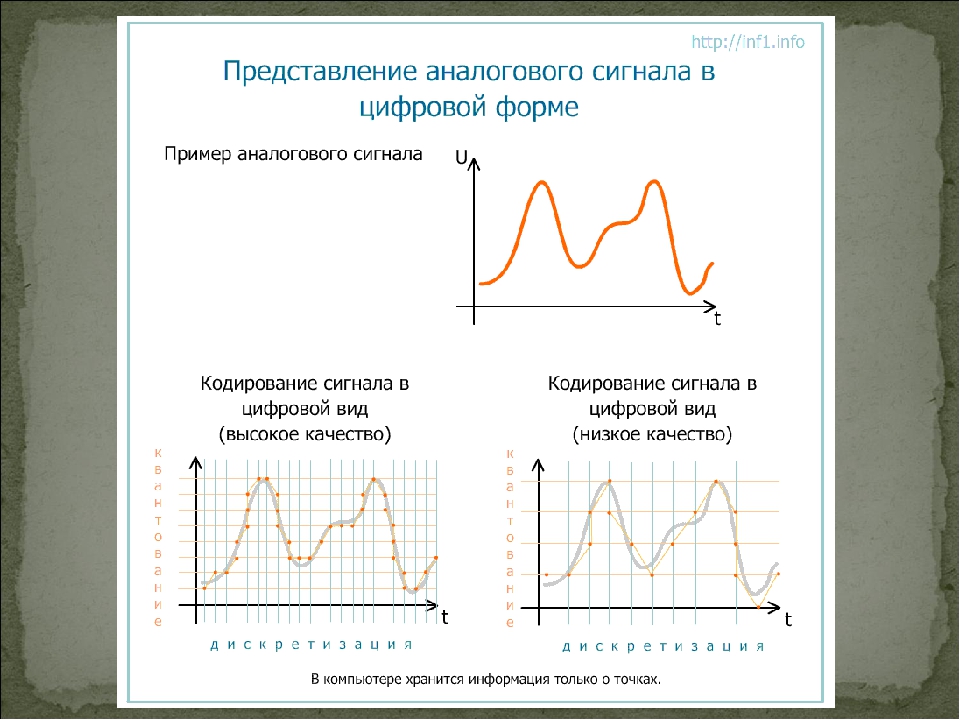
В электронике, электротехнике и системах связи аналоговую передачу данных применяют со времени изобретения электричества. Характерной особенностью является непрерывность и плавность изменения параметров. Графически сеанс аналоговой связи можно описать как непрерывную кривую, соответствующую величине электрического напряжения в определённый момент времени. Линия изменяется плавно, разрывы возникают только при обрыве связи. В природе и электронике аналоговые данные генерируются и распространяются непрерывно. Отсутствие непрерывного сигнала означает тишину или черный экран.
В непрерывных системах связи аналогом звука, изображения и любых других данных является электрические или электромагнитные импульсы. Например, громкость и тембр голоса передаются от микрофона на динамик посредством электрического сигнала. Громкость зависит от величины, а тембр от частоты напряжения. Поэтому при голосовой связи сначала напряжение становится аналогом звука, а потом звук аналогом напряжения. Таким же образом происходит передача любых данных в аналоговых системах связи.
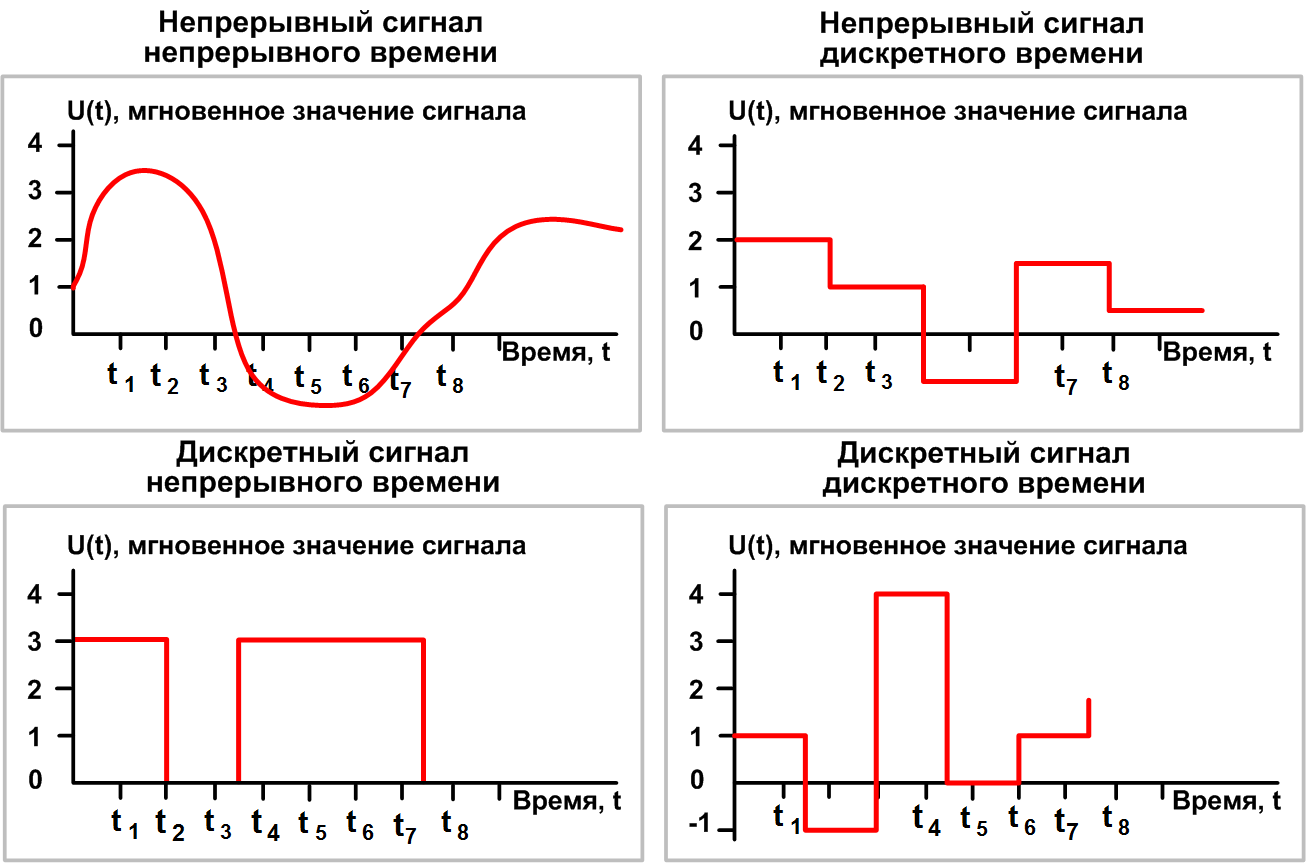
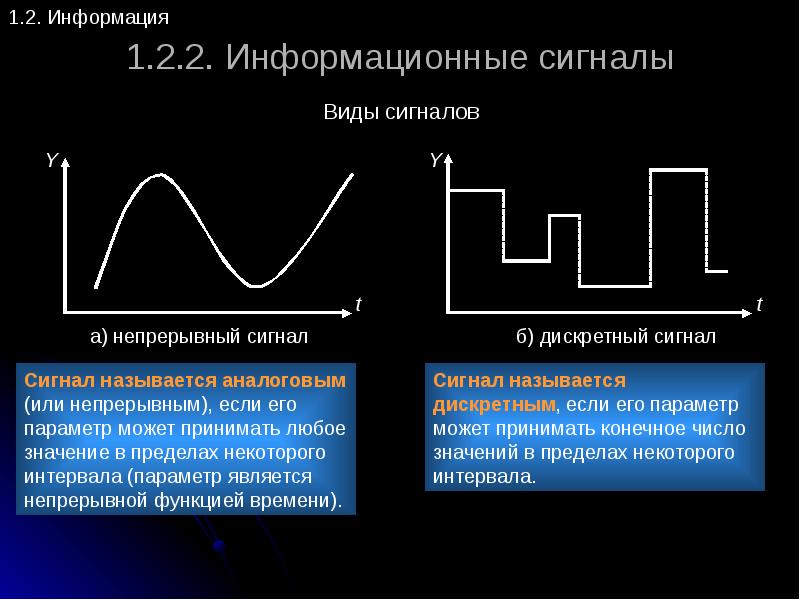
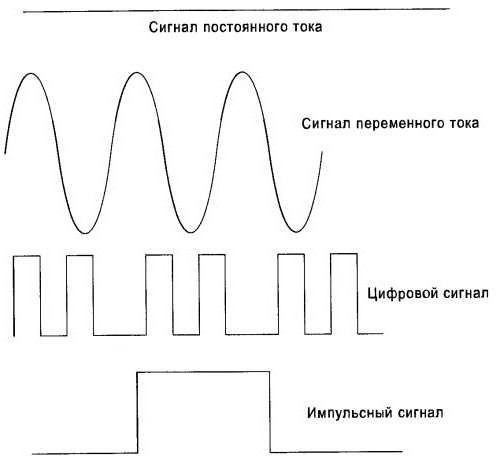
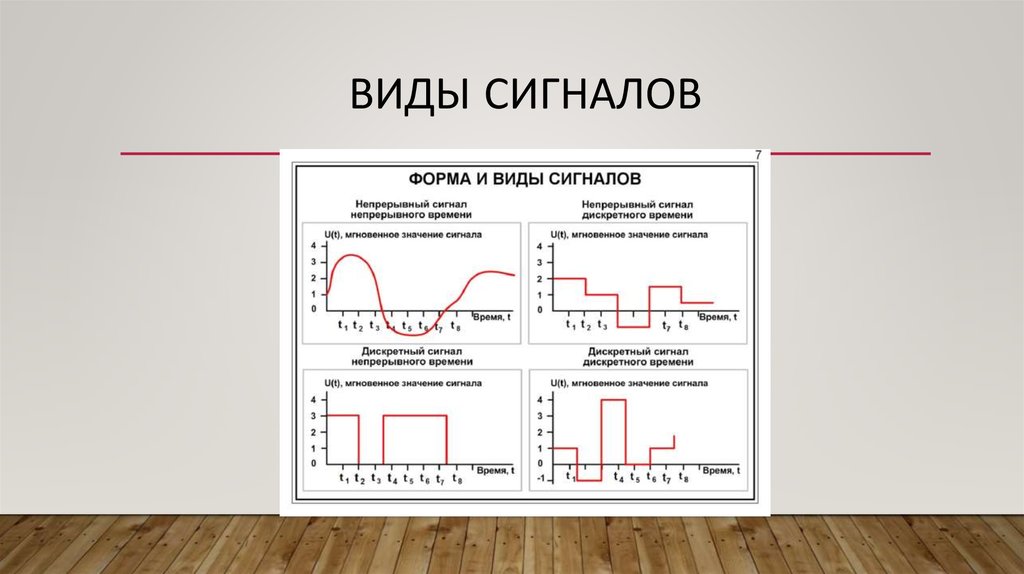
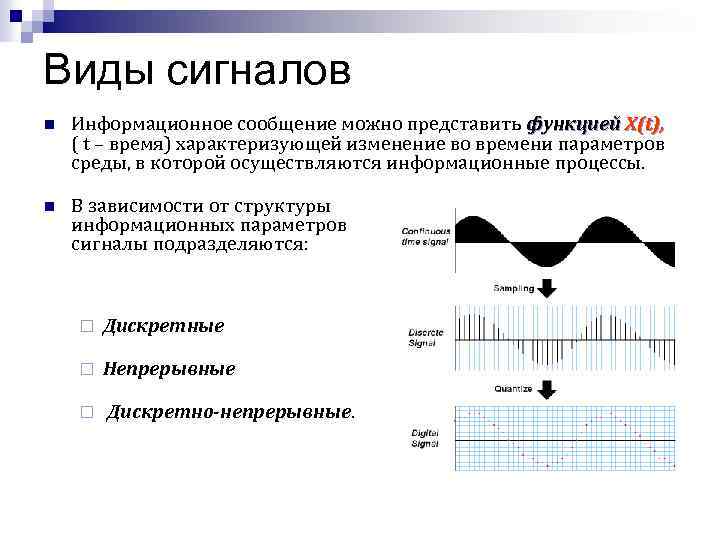
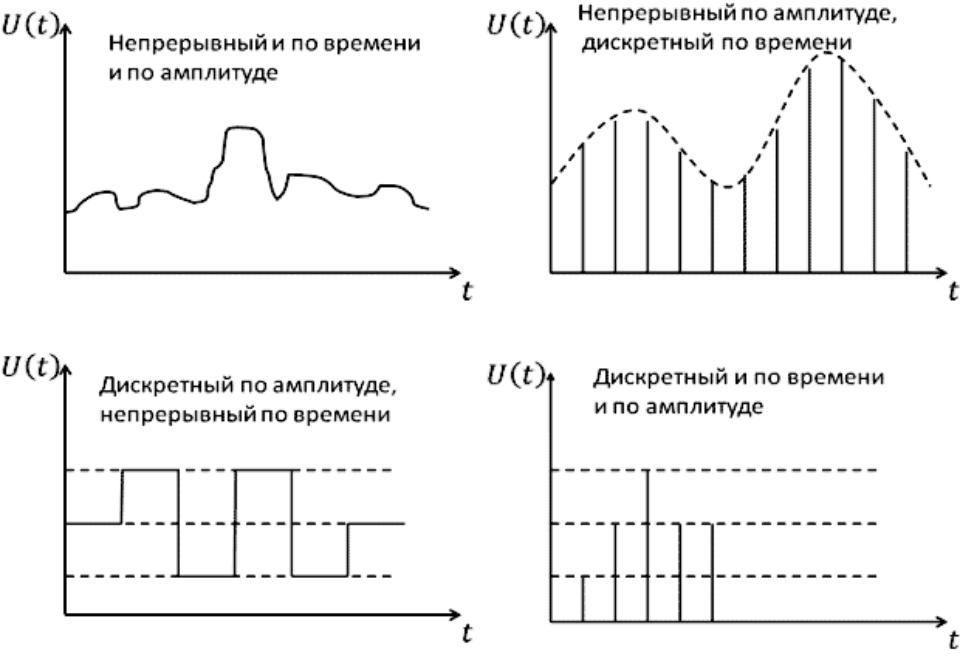
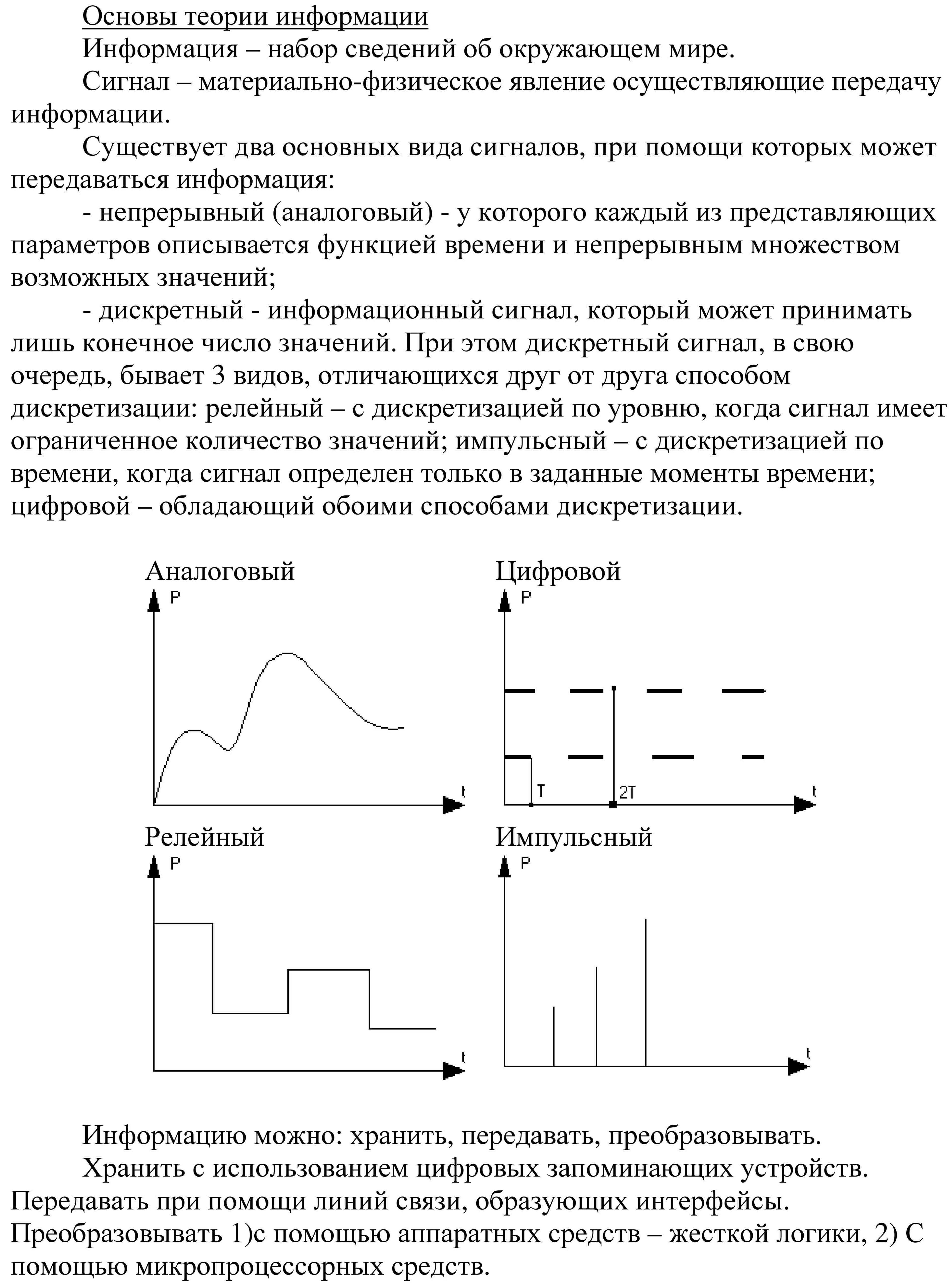
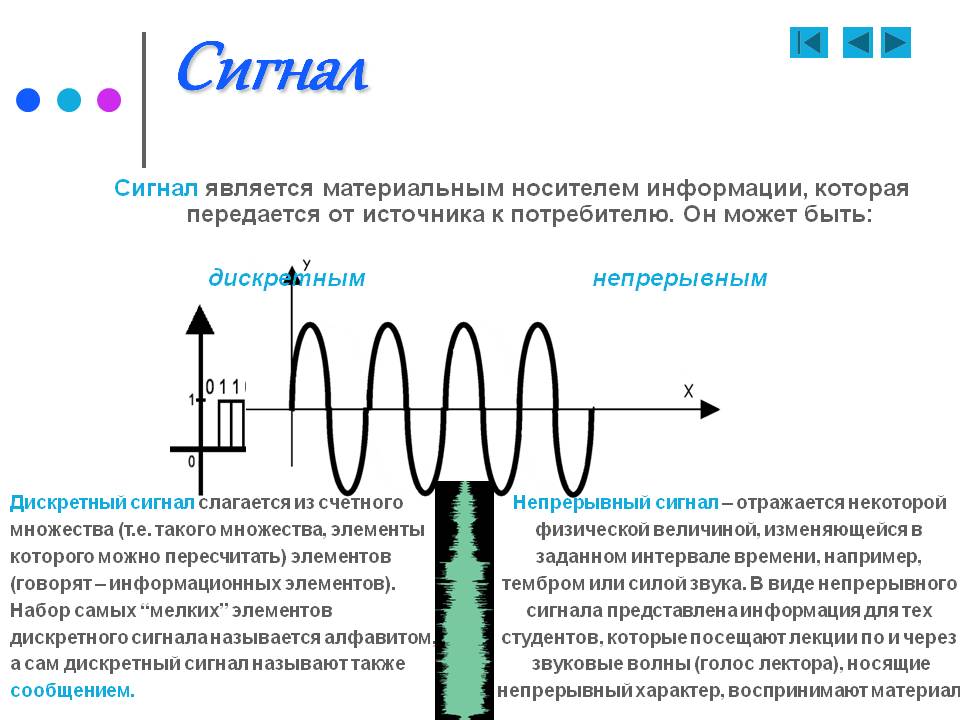
Виды сигналов
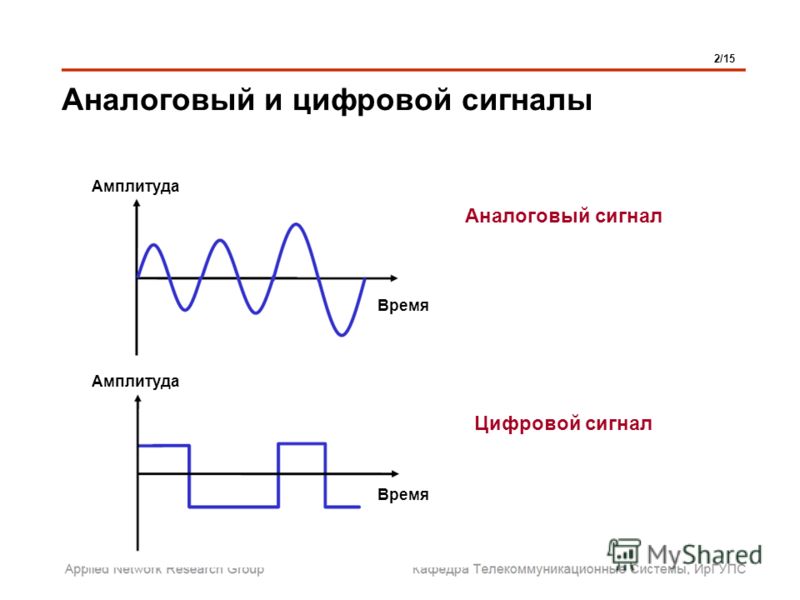
Сигнал это изменение физической величины во времени и пространстве. По сути это коды для обмена данными в информационной и управленческой средах. Графически любой сигнал можно представить в виде функции. По линии на графике можно определить тип и характеристики сигнала. Аналоговый будет выглядеть как непрерывная кривая, цифровой как ломаная прямоугольная линия, скачущая от ноля до единицы. Все, что мы видим глазами и слышим ушами поступает в виде аналогового сигнала.
Аналоговый сигнал
Зрение, слух, вкус, запах и тактильные ощущения поступают нам в виде аналогового сигнала. Мозг командует органами и получает от них информацию в аналоговом виде. В природе вся информация передаётся только так.
В электронике аналоговый сигнал основан на передаче электричества. Определённым величинам напряжения соответствуют частота и амплитуда звука, цвет и яркость света изображения и так далее. То есть цвет, звук или информация являются аналогом электрического напряжения.
При этом неважно идёт сигнал по проводам или радио. Передатчик непрерывно отправляет, а приёмник обрабатывает аналоговый вид информации
Принимая непрерывный электрический сигнал по проводам или радиосигнал через эфир приёмник преобразует напряжение в соответствующий звук или цвет. Изображение появляется на экране или звук транслируется через динамик.
Дискретный сигнал
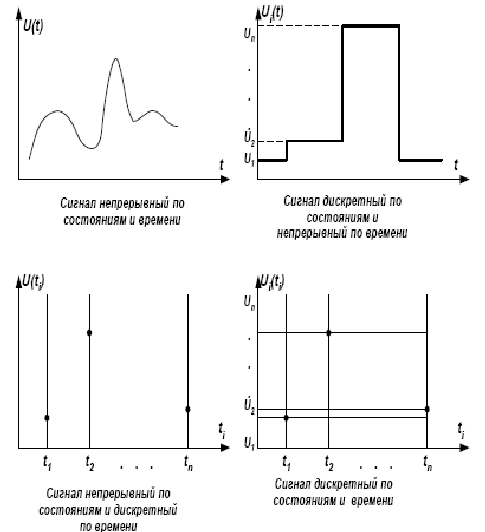
Вся суть кроется в названии. Дискретный от латинского discretus, что означает прерывистый (разделённый). Можно сказать, что дискретный повторяет амплитуду аналогового, но плавная кривая превращается в ступенчатую. Изменяясь либо во времени, оставаясь непрерывной по величине, или по уровню, не прерываясь по времени.
Так, в определенный период времени (например миллисекунду или секунду) дискретный сигнал будет какой-то установленной величины. По окончании этого времени он резко изменится в большую или меньшую сторону и останется таким ещё миллисекунду или секунду. И так беспрерывно. Поэтому дискретный это преобразованный аналоговый. То есть полпути до цифрового.
Цифровой сигнал
После дискретного следующим шагом преобразования аналогового стал цифровой сигнал. Главная особенность – либо он есть, или его нет. Вся информация преобразуется в сигналы ограниченные по времени и по величине. Сигналы цифровой технологии передачи данных кодируются нолем и единицей в разных вариантах. А основой является бит, принимающий одно из этих значений. Бит от английского binarydigit или двоичный разряд.
Но один бит имеет ограниченную возможность для передачи информации, поэтому их объединили в блоки. Чем больше битов в одном блоке, тем больше информации он несёт. В цифровых технологиях используют биты объединенные в блоки кратные 8. Восьмибитовый блок назвали байтом. Один байт небольшая величина, но уже может хранить зашифрованную информацию о всех буквах алфавита. Однако при добавлении всего одного бита число комбинаций ноля и единицы удваивается. И если 8 битов делает возможным 256 вариантов кодировки, то 16 уже 65536. А килобайт или 1024 байт и вовсе немаленькая величина.
В большом количестве объединённых байтов хранится много информации, чем больше комбинаций 1 и 0 тем больше закодировано. Поэтому в 5 – 10 МБ (5000 – 10000 кБ) имеем данные музыкального трека хорошего качества. Идём дальше, и в 1000 МБ закодирован уже фильм.
Но так как вся окружающая людей информация аналоговая, то для её приведения в цифровой вид нужны усилия и какое-либо устройство. Для этих целей был создан DSP (digital signal processor) или ЦПОС (цифровой процессор обработки сигналов). Такой процессор есть в каждом цифровом устройстве. Первые появились еще в 70-е годы прошлого века. Методы и алгоритмы меняются и совершенствуются, но принцип остаётся постоянным – преобразование аналоговых данных в цифровые.
Обработка и передача цифрового сигнала зависит от характеристик процессора — разрядности и скорости. Чем они выше, тем качественней получится сигнал. Скорость указывается в миллионах инструкций в секунду (MIPS), и у хороших процессоров достигает нескольких десятков MIPS. Скорость определяет сколько единиц и нолей сможет устройство «запихнуть» в одну секунду и качественно передать непрерывную кривую аналогового сигнала. От этого зависит реалистичность картинки в телевизоре и звука из динамиков.
Что такое дискретный сигнал
В цифровой системе хранения и передачи данных, отсутствие сигнала, также является формой обмена информацией. В какой-то момент времени он равен нулю, в другой принимает какое-либо значение. Поэтому дискретным называют сигнал прерывный, отсюда и название discretus или разделённый. Аналоговые данные разбиваются на отдельные блоки, обрабатываются и передаются в виде цифрового кода.
Дискретность не подразумевает разрыв связи. В цифровых системах широко используется двоичная система обработки и обмена информацией. Двоичная подразумевает кодировку данных с помощью единицы и нулей. В доли секунды сигнал прерывисто принимает значение 1 или 0. Вместо непрерывной кривой имеем отдельные дискретные значения. Определенный набор нулей и единичек уже несёт в себе какую либо информацию. Примитивный набор это бит или двоичный разряд. Сам по себе он ничего не значит. Данные могут кодироваться только при объединении восьми битов в следующую по сложности комбинацию – байт. Чем больше объединённых байтов, тем больше и точнее можно описать передаваемую информацию.
На качество генерируемых данных влияет не только количество объединённых битов, но и скорость передачи. Непрерывная аналоговая кривая должна быть разбита на как много больше мини участков прерывного сигнала. Полученный таким образом звук и цвет будут соответствовать оригиналу. Качественный дискретный сигнал формирует точную копию аналогового. Например, звуковая дорожка MP3 закодированная со скоростью 320 000 бит в секунду (320 kbps) значительно лучше кодированной в 128 kbps. Дорожки скоростью меньше 128 слушать вообще невозможно.
Что такое сигнал
Сигнал – это некоторый физический процесс, параметры которого изменяются в соответствии с передаваемым сообщением. Пример – электрический сигнал, радиосигнал, как частный случай электромагнитного сигнала, акустический сигнал, оптический и т.д. В зависимости от того, в какой среде идет распространение сигнала. Сигнал – это материальный носитель информации.
Обычно сигнал, независимо от его физической природы, представляют, как некоторую функцию времени x(t). Такое представление есть общепринятая математическая абстракция физического сигнала.
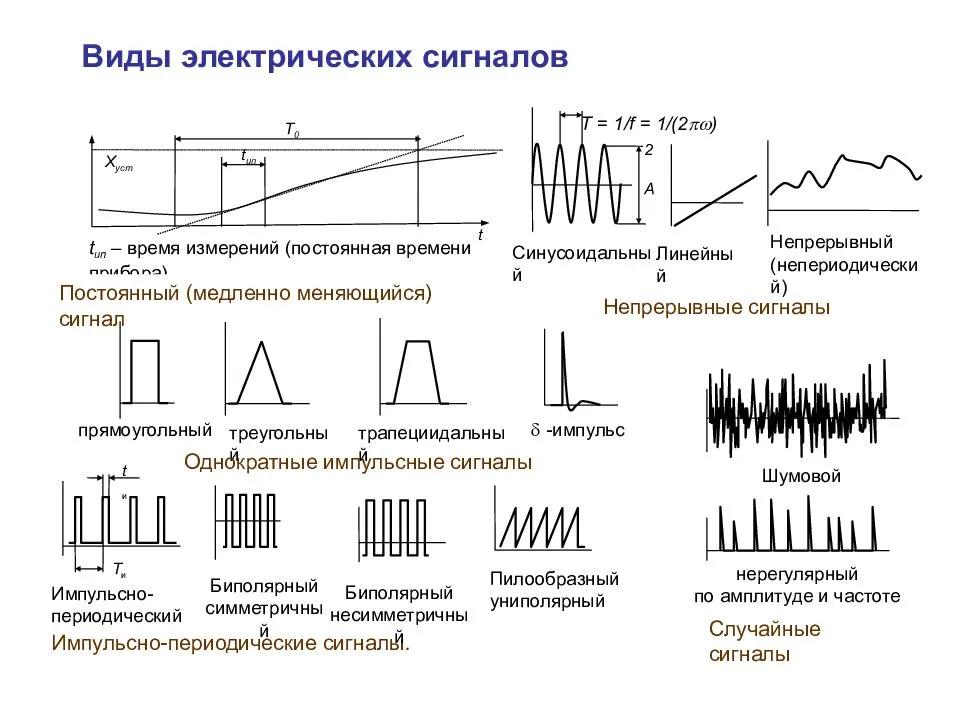
Типы сигналов
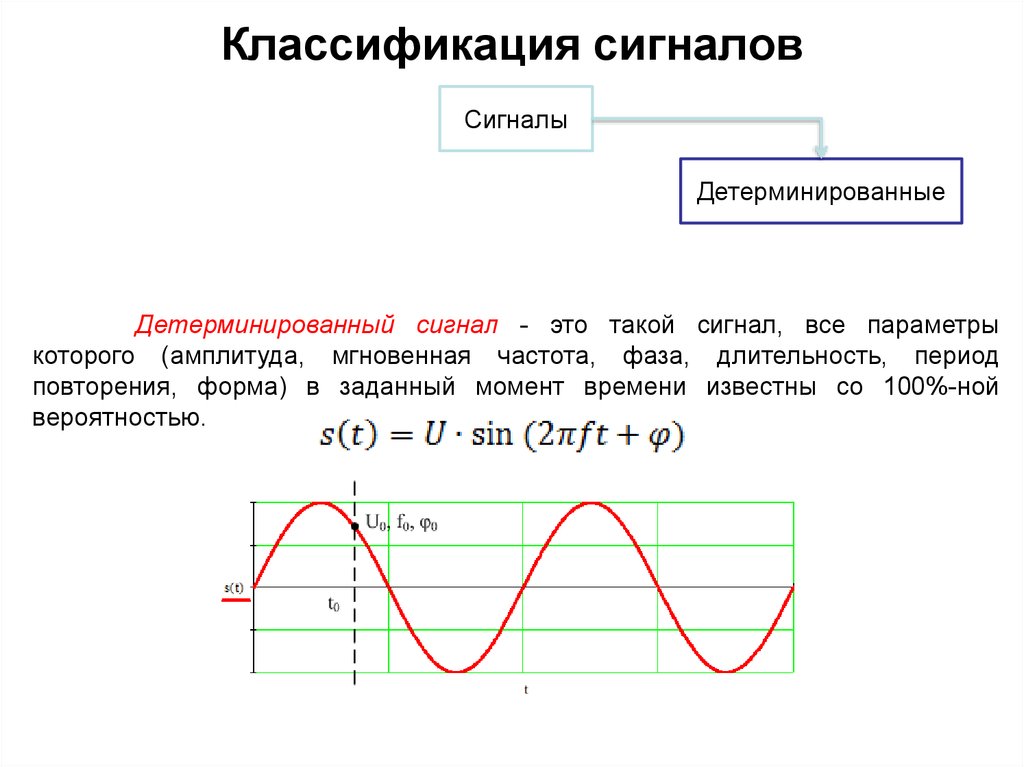
Детерминированный, или регулярный – это сигнал, закон изменения которого известен и известны все его параметры.
Такой сигнал передает информацию? Информация уменьшает неопределенность. В детерминированном сигнале мы знаем все, мы знаем какой он будет через минуту, через год. Детерминированный сигнал информацию в себе никакую не несет. Например, сигнал с гетеродина, мы сами его сформировали, задали частоту, амплитуду, фазу.
Квазидетерминированный — это сигнал, закон изменения которого известен, но один или несколько параметров является случайной величиной.
Пример: x(t)=Asin(wt+j), где амплитуда А и j — случайная величина.
Например, мы знаем его частоту, но не знаем амплитуду и фазу — это квазидетерминированный сигнал, “квази”-почти, почти определенный сигнал. Информация вносит некоторую случайность. Если мы знаем амплитуду, частоту и фазу, значит информации там нет. Квазидетерминированный сигнал передает информацию, передача информации идет в тех параметрах, которые случайны, в нашем примере амплитуда и фаза случайные величины. Именно в этих величинах передается информация. Информация всегда несет в себе хаос, случайность. Все модулированные сигналы, ЧМ, ФМ это квазидетерминированные сигналы.
Случайным называют сигнал, мгновенные значения которого не известны, а могут быть лишь предсказаны с некоторой вероятностью.
Кроме этого все сигналы могут быть непрерывными (аналоговыми) и дискретными (цифровыми или импульсными).
О случайном сигнале мы можем судить о его вероятностных характеристиках. Мы можем знать его плотность вероятности, но какое значение примет сигнал через секунду, минуту мы не знаем. Когда мы работаем со случайным сигналом, мы всегда работаем с вероятностью.
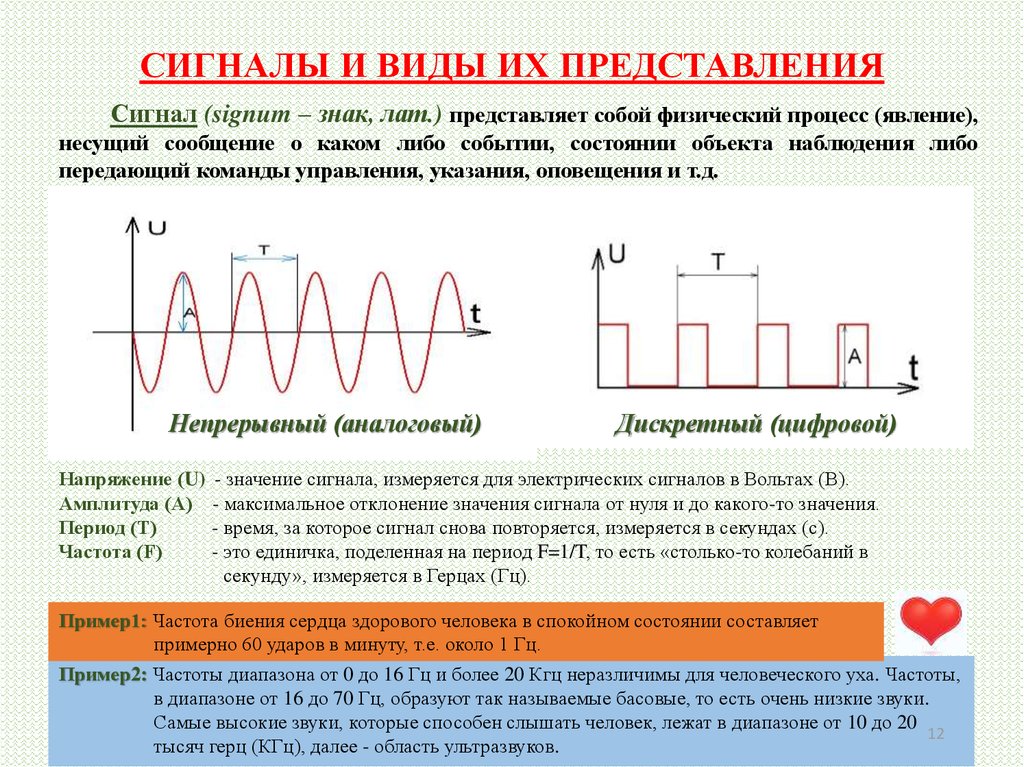
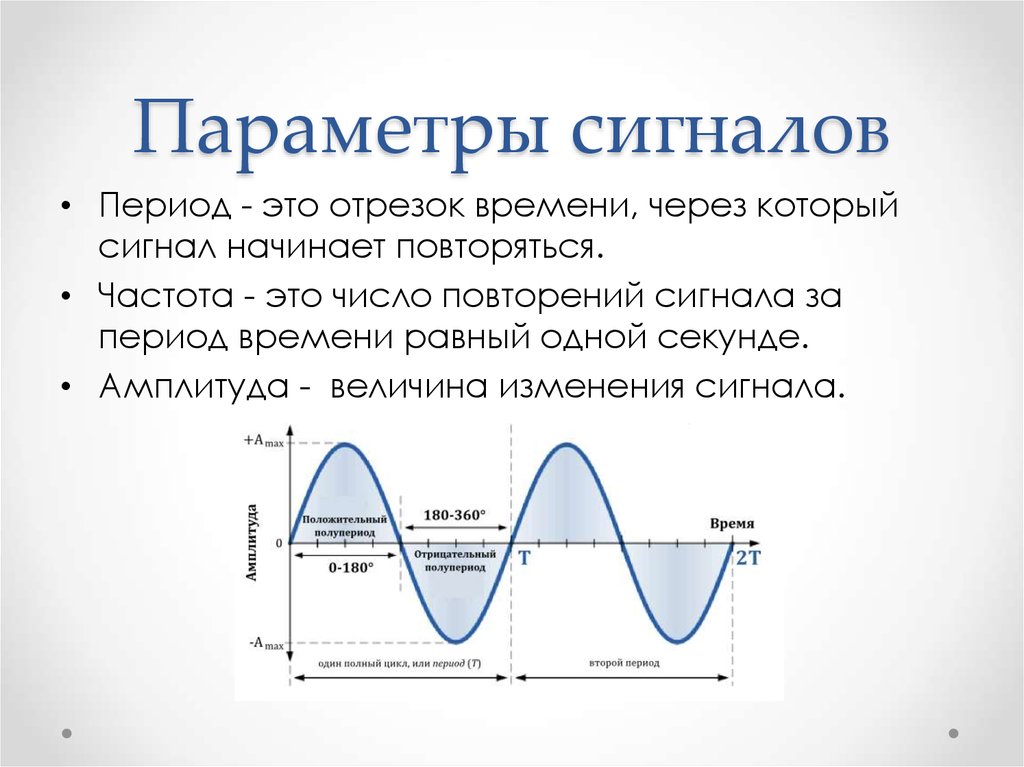
Параметры сигналов
Какие параметры мы будем использовать? Это энергия за некоторый интервал времени T. X(t) это сам сигнал, чтобы определить энергию мы должны взять по модулю, возвести в квадрат, проинтегрировать на некотором промежутке времени и получим энергию.
Средняя мощность за некоторое время t. Это энергия деленная на время.
Мгновенная мощность, если средняя мощность измеряется на некотором участке времени, то мгновенная измеряется в один, конкретный момент времени.
Средняя мощность измеряется на промежутке времени, а мгновенная в точке.
Спектральная плотность энергии и мощности
Спектральная плотность сигнала характеризует распределение энергии или мощности сигнала по диапазону частот. Спектральная плотность энергии, это как у нас энергия распределяется по частотному диапазону. Вычисляется через преобразование Фурье.
И соответственно, СПМ это, как у нас распределяется мощность по частотному диапазону.
В формуле, модуль в квадрате это спектральная плотность энергии, поделили ее на время T и по определению, время T должно стремиться к бесконечности. Но на практике, никто не ждет бесконечности, все оценивают СПМ на некотором интервале времени.
СПМ это некоторая функция зависящая от частоты. По шкале СПМ возьмем 10 Вт/Гц, и окрестности в 1 Гц по частоте. То в полосе 1 Гц будет заключено 10 Вт мощности.
Есть два сигнала и представлены их спектральные плотности мощности. ВОПРОС. Мощность какого сигнала больше?
Мы должны определить площадь под кривой, проинтегрировать. S1=2*10=20 Вт, S2=1*30=30 Вт. В первом случае S1 имеет мощность 20 Вт, а во втором 30 Вт.
СПМ реального сигнала, отображаемая на спектральном анализаторе.
Современные анализаторы спектра могут считать автоматически площадь, вы включаете определение мощности, задаете частотный интервал в котором он должен измерить эту мощность и он сам вычисляет канальную мощность сигнала.