Дипольный момент системы
Эквипотенциальные поверхности электрического диполя
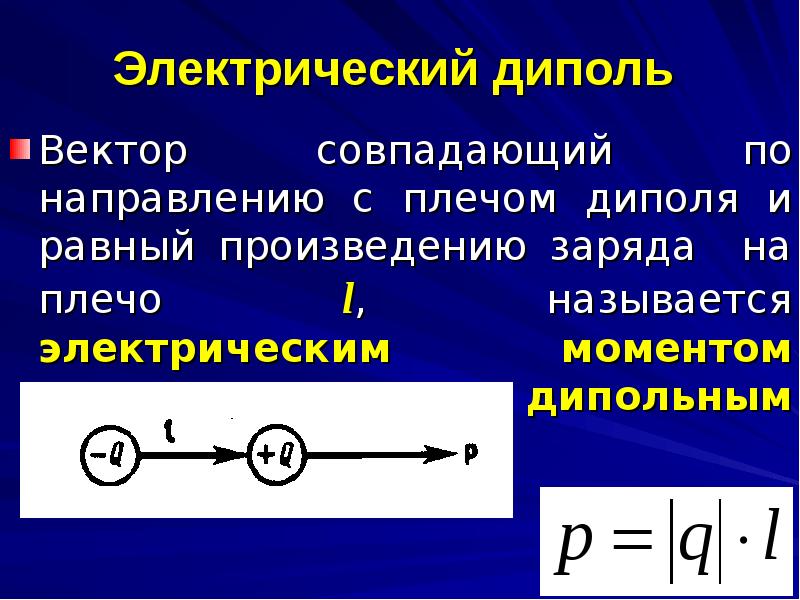
Электрический диполь
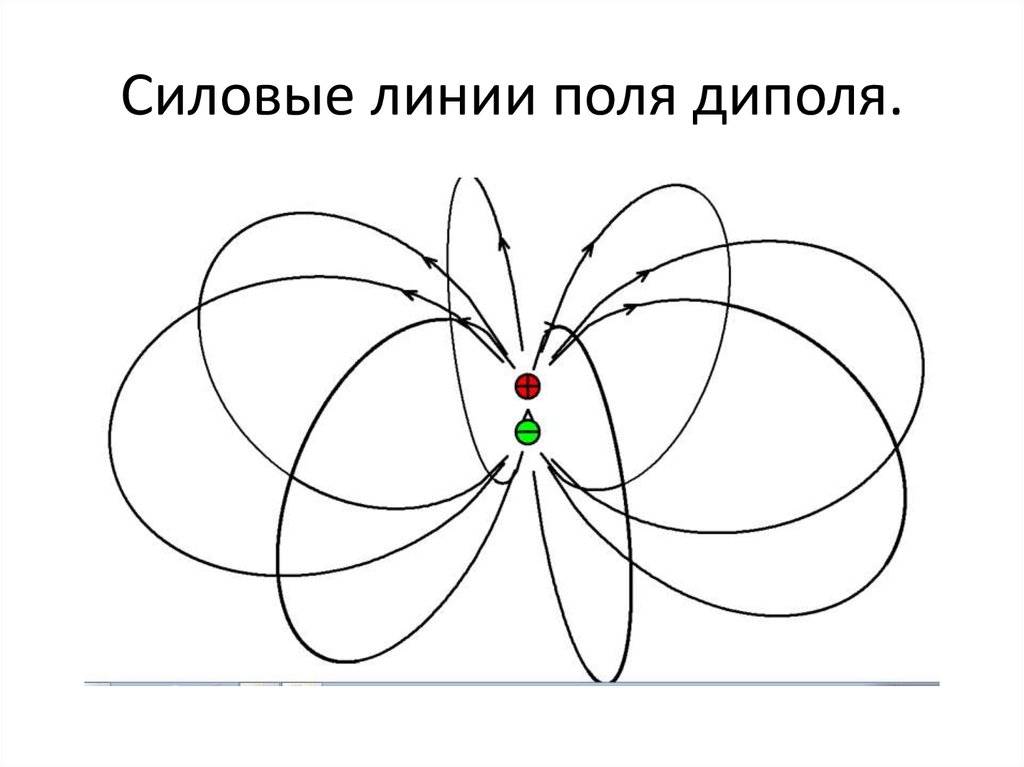
Силовые линии электрического диполя
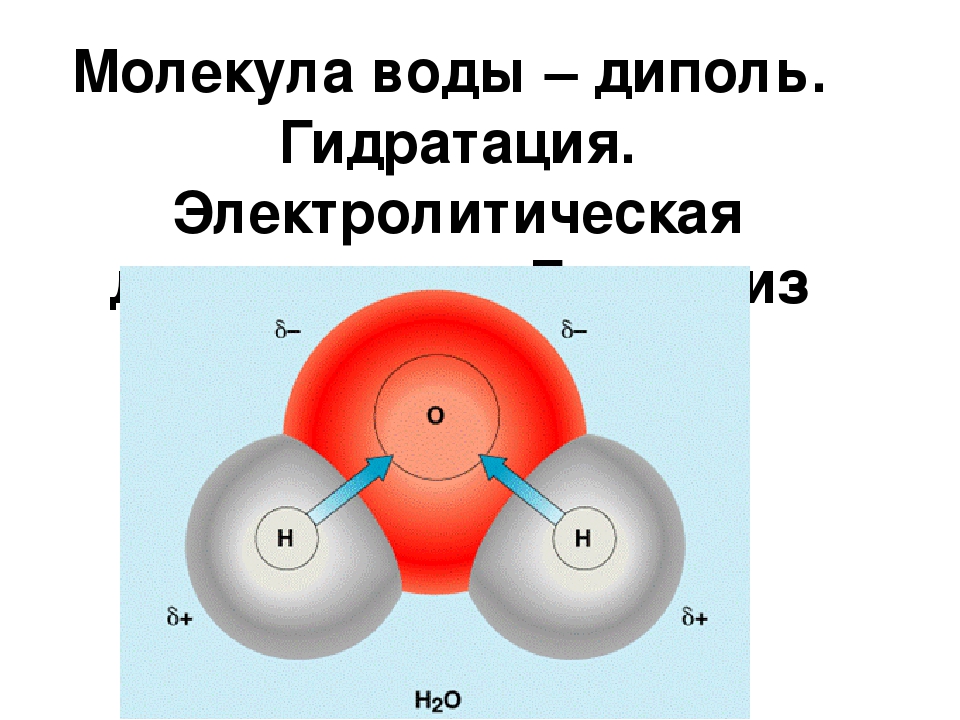
Электрический диполь — идеализированная электронейтральная система, состоящая из точечных и равных по абсолютной величине положительного и отрицательного электрических зарядов.
Другими словами, электрический диполь представляет собой совокупность двух равных по абсолютной величине разноимённых точечных зарядов, находящихся на некотором расстоянии друг от друга.
Произведение вектора l→,{\displaystyle {\vec {l}},} проведённого от отрицательного заряда к положительному, на абсолютную величину зарядов q,{\displaystyle q\,,} называется дипольным моментом: d→=ql→.{\displaystyle {\vec {d}}=q{\vec {l}}.}
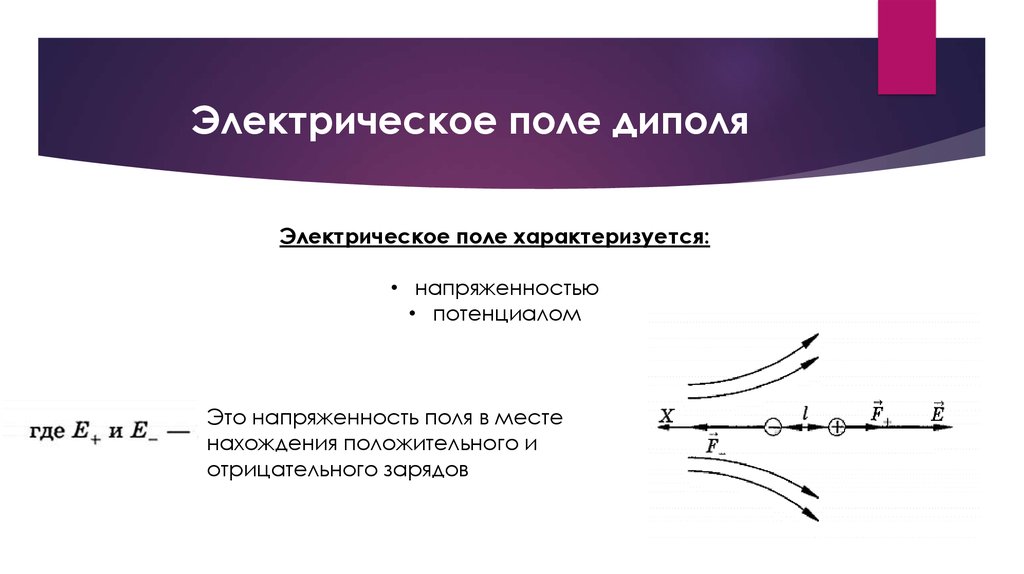
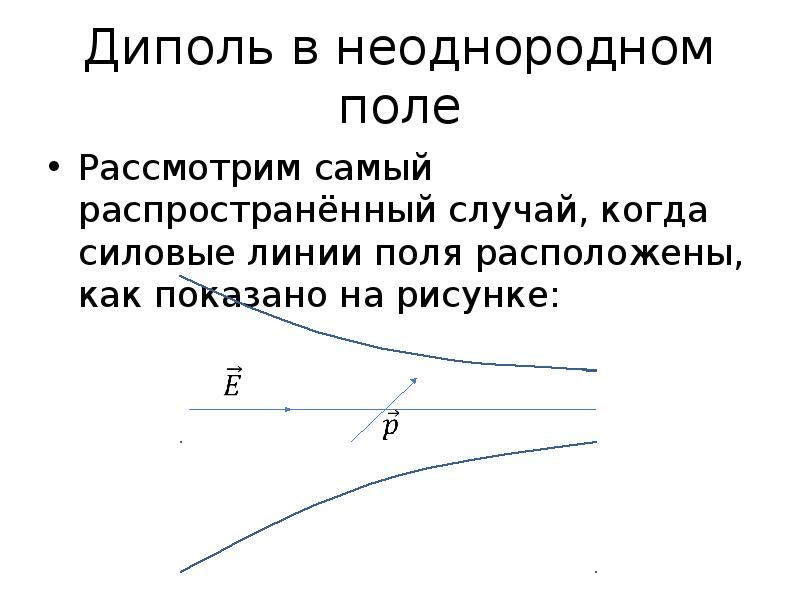
Во внешнем электрическом поле E→{\displaystyle {\vec {E}}} на электрический диполь действует момент сил d→×E→,{\displaystyle {\vec {d}}\times {\vec {E}},} который стремится повернуть его так, чтобы дипольный момент развернулся вдоль направления поля.
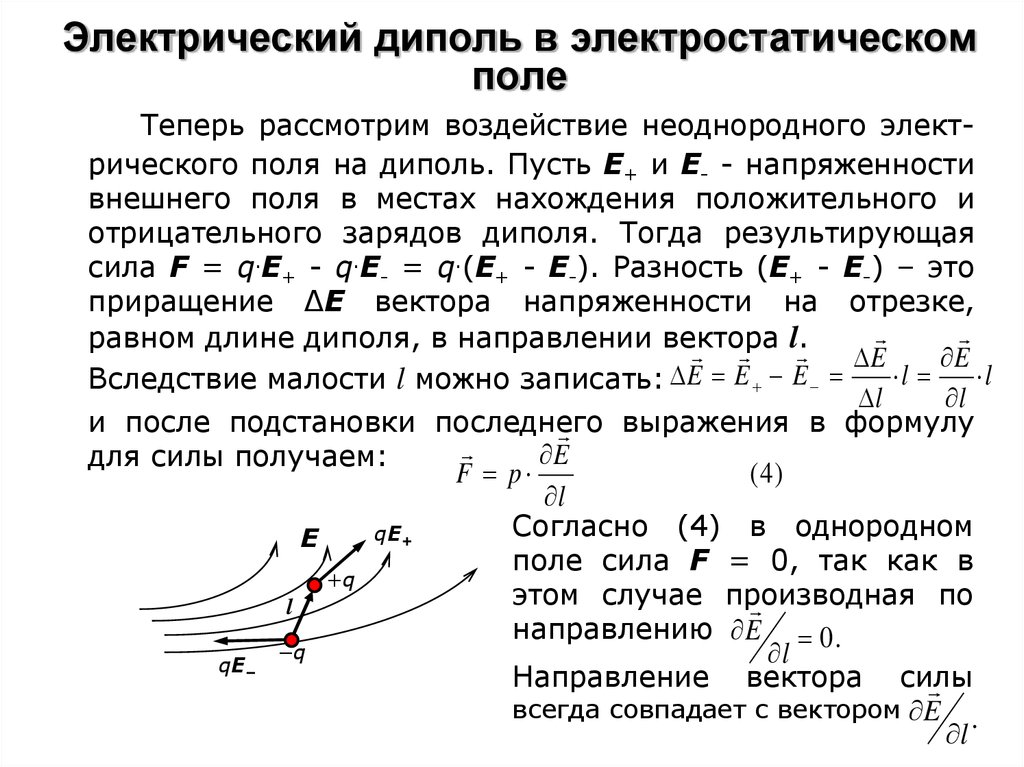
Потенциальная энергия электрического диполя в (постоянном) электрическом поле равна −E→⋅d→.{\displaystyle -{\vec {E}}\cdot {\vec {d}}.} (В случае неоднородного поля это означает зависимость не только от момента диполя — его величины и направления, но и от места, точки нахождения диполя).
Вдали от электрического диполя напряжённость его электрического поля убывает с расстоянием R{\displaystyle R} как R−3,{\displaystyle R^{-3},} то есть быстрее, чем у точечного заряда (E∼R−2{\displaystyle E\sim R^{-2}}).
Любая в целом электронейтральная система, содержащая электрические заряды, в некотором приближении (то есть собственно в дипольном приближении) может рассматриваться как электрический диполь с моментом d→=∑iqir→i,{\displaystyle {\vec {d}}=\sum _{i}q_{i}{\vec {r}}_{i},} где qi{\displaystyle q_{i}} — заряд i{\displaystyle i}-го элемента, r→i{\displaystyle {\vec {r}}_{i}} — его радиус-вектор. При этом дипольное приближение будет корректным, если расстояние, на котором изучается электрическое поле системы, велико по сравнению с её характерными размерами.
Магнитный диполь
Магнитный диполь — аналог электрического, который можно представить себе как систему двух «магнитных зарядов» — магнитных монополей. Эта аналогия условна, так как магнитные заряды не обнаружены. В качестве модели магнитного диполя можно рассматривать небольшую (по сравнению с расстояниями, на которых излучается генерируемое диполем магнитное поле) плоскую замкнутую проводящую рамку площади S,{\displaystyle S\,,} по которой течёт ток I.{\displaystyle I\,.} При этом магнитным моментом диполя (в системе СГСМ) называют величину μ→=ISn→,{\displaystyle {\vec {\mu }}=IS{\vec {n}},} где n→{\displaystyle {\vec {n}}} — единичный вектор, направленный перпендикулярно плоскости рамки в том направлении, при наблюдении в котором ток в рамке представляется текущим по часовой стрелке.
Выражения для вращающего момента M→{\displaystyle {\vec {M}}}, действующего со стороны магнитного поля на магнитный диполь, и потенциальной энергии постоянного магнитного U{\displaystyle U}диполя в магнитном поле, аналогичны соответствующим формулам для взаимодействия электрического диполя с электрическим полем, только входят туда магнитный момент m→{\displaystyle {\vec {m}}} и вектор магнитной индукции B→{\displaystyle {\vec {B}}}:
- M→=m→×B→,{\displaystyle {\vec {M}}={\vec {m}}\times {\vec {B}},}
- U=−m→⋅B→.{\displaystyle U=-{\vec {m}}\cdot {\vec {B}}.}
Поле колеблющегося диполя
В этом разделе рассматривается поле, создаваемое точечным электрическим диполем d(t),{\displaystyle \mathbf {d} (t),} находящимся в заданной точке пространства.
Поле на близких расстояниях (ближняя зона)
Поле точечного диполя, колеблющегося в вакууме, имеет вид
- E=3n(n,d)−dR3+3n(n,d˙)−d˙cR2+n(n,d¨)−d¨c2R{\displaystyle \mathbf {E} ={\frac {3\mathbf {n} (\mathbf {n} ,\mathbf {d} )-\mathbf {d} }{R^{3}}}+{\frac {3\mathbf {n} (\mathbf {n} ,{\dot {\mathbf {d} }})-{\dot {\mathbf {d} }}}{cR^{2}}}+{\frac {\mathbf {n} (\mathbf {n} ,{\ddot {\mathbf {d} }})-{\ddot {\mathbf {d} }}}{c^{2}R}}}
- B=d˙cR2+d¨Rc2,n=n,E+dR3,{\displaystyle \mathbf {B} =\left=\left,}
где n=RR{\displaystyle \mathbf {n} ={\frac {\mathbf {R} }{R}}} — единичный вектор в рассматриваемом направлении, c{\displaystyle c} — скорость света.
Этим выражениям можно придать несколько другую форму, если ввести вектор Герца
- Z=−1R⋅d(t−Rc).{\displaystyle \mathbf {Z} =-{\frac {1}{R}}\cdot \mathbf {d} \left(t-{\frac {R}{c}}\right).}
Напомним, что диполь покоится в начале координат, так что d{\displaystyle \mathbf {d} } является функцией одной переменной. Тогда
- E=−rotrotZ,{\displaystyle \mathbf {E} =-\operatorname {rot} \,\operatorname {rot} \,\mathbf {Z} ,}
- B=−1crotZ˙.{\displaystyle \mathbf {B} =-{\frac {1}{c}}\operatorname {rot} \,{\dot {\mathbf {Z} }}.}
При этом потенциалы поля можно выбрать в виде
- A=−Z˙c, ϕ=divZ.{\displaystyle \mathbf {A} =-{\frac {\dot {\mathbf {Z} }}{c}},~~\phi =\operatorname {div} \,\mathbf {Z} .}
Указанные формулы можно применять всегда, когда применимо дипольное приближение.
Дипольное излучение (излучение в волновой зоне или дальней зоне)
Приведённые формулы существенно упрощаются, если размеры системы много меньше длины излучаемой волны, то есть скорости зарядов много меньше c, а поле рассматривается на расстояниях много больших, чем длина волны. Такую область поля называют волновой зоной. Распространяющуюся волну можно в этой области считать практически плоской. Из всех членов в выражениях для E{\displaystyle \mathbf {E} } и B{\displaystyle \mathbf {B} } существенными оказываются только члены, содержащие вторые производные от d,{\displaystyle \mathbf {d} ,} так как
- d˙c≈dλ,{\displaystyle {\frac {\dot {\mathbf {d} }}{c}}\approx {\frac {d}{\lambda }},}
- d¨c2≈dλ2.{\displaystyle {\frac {\ddot {\mathbf {d} }}{c^{2}}}\approx {\frac {d}{\lambda ^{2}}}.}
Выражения для полей в системе СГС принимают вид
- H=1c2Rd¨,n, H=n,E,{\displaystyle \mathbf {H} ={\frac {1}{c^{2}R}},~~\mathbf {H} =,}
- E=1c2Rd¨,n,n, E=B,n.{\displaystyle \mathbf {E} ={\frac {1}{c^{2}R}}\left,\mathbf {n} \right],~~\mathbf {E} =.}
В плоской волне интенсивность излучения в телесный угол dΩ{\displaystyle d\Omega } равна
- dI=cH24πR2dΩ,{\displaystyle dI=c{\frac {H^{2}}{4\pi }}R^{2}d\Omega ,}
поэтому для дипольного излучения
- dI=14πc3d¨,n2dΩ=d¨24πc3sin2θdΩ.{\displaystyle dI={\frac {1}{4\pi c^{3}}}^{2}d\Omega ={\frac {{\ddot {\mathbf {d} }}^{2}}{4\pi c^{3}}}\sin ^{2}{\theta }d\Omega .}
где θ{\displaystyle \theta } — угол между векторами d¨{\displaystyle {\ddot {\mathbf {d} }}} и n.{\displaystyle \mathbf {n} .} Найдём полную излучаемую энергию. Учитывая, что dΩ=2πsinθdθ,{\displaystyle d\Omega =2\pi \,\sin {\theta }\,d\theta ,} проинтегрируем выражение по dθ{\displaystyle d\theta } от {\displaystyle 0} до π.{\displaystyle \pi .} Полное излучение равно
- I=23c3d¨2.{\displaystyle I={\frac {2}{3c^{3}}}{\ddot {\mathbf {d} }}^{2}.}
Укажем спектральный состав излучения. Он получается заменой вектора d¨{\displaystyle {\ddot {\mathbf {d} }}} на его Фурье-компоненту и одновременным умножением выражения на 2. Таким образом,
- dEω=4ω43c3|dω|2dω2π.{\displaystyle d{\mathcal {E}}_{\omega }={\frac {4\omega ^{4}}{3c^{3}}}\left|\mathbf {d} _{\omega }\right|^{2}{\frac {d\omega }{2\pi }}.}