Числа. целые числа. свойства целых чисел

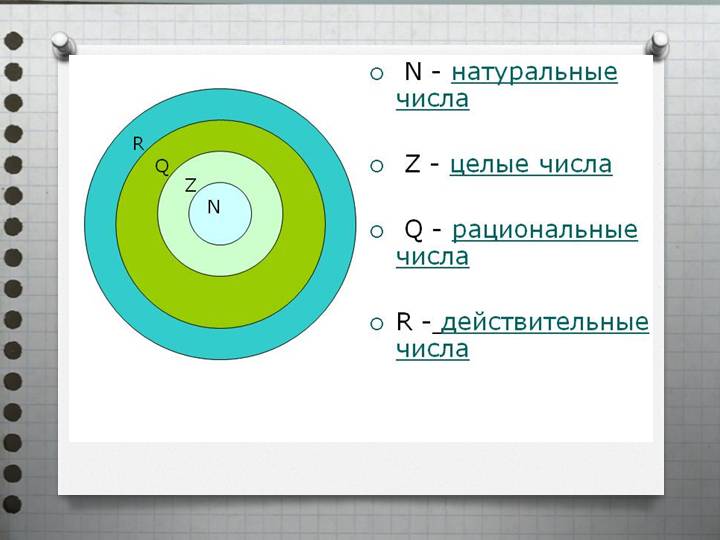
Описание изменения величин при помощи целых чисел

Пришло время поговорить о том, для чего вообще нужны целые числа.

Основное предназначение целых чисел заключается в том, что с их помощью удобно описывать изменение количества каких-либо предметов. Разберемся с этим на примерах.

Пусть на складе находится некоторое количество деталей. Если на склад привезут еще, к примеру, 400 деталей, то количество деталей на складе увеличится, а число 400 выражает это изменение количества в положительную сторону (в сторону увеличения). Если же со склада заберут, например, 100 деталей, то количество деталей на складе уменьшится, а число 100 будет выражать изменение количества в отрицательную сторону (в сторону уменьшения). На склад не будут привозить детали, и не будут увозить детали со склада, то можно говорить о неизменности количестве деталей (то есть можно будет говорить о нулевом изменении количества).

В приведенных примерах изменение количества деталей можно описать при помощи целых чисел 400, −100 и соответственно. Положительное целое число 400 показывает изменение количества в положительную сторону (увеличение). Отрицательное целое число −100 выражает изменение количества в отрицательную сторону (уменьшение). Целое число показывает, что количество осталось без изменения.

Удобство использования целых чисел по сравнению с использованием натуральных чисел заключается в том, что не нужно явно указывать увеличивается количество или уменьшается, — целое число определяет изменение количественно, а знак целого числа указывает направление изменения.

Целые числа также могут выражать не только изменение количества, но и изменение какой-либо величины. Разберемся с этим на примере изменения температуры.

Повышение температуры, скажем, на 4 градуса выражается положительным целым числом 4. Понижение температуры, например, на 12 градусов можно описать отрицательным целым числом −12. А неизменность температуры – это ее изменение, определяемое целым числом .

Отдельно нужно сказать о трактовке отрицательных целых чисел как величины долга. Например, если у нас есть 3 яблока, то целое положительное число 3 показывает количество яблок, которыми мы владеем. С другой стороны, если мы должны кому-либо отдать 5 яблок, а у нас их нет в наличии, то эту ситуацию можно описать при помощи отрицательного целого числа −5. В этом случае мы «обладаем» −5 яблоками, знак минус указывает на долг, а число 5 определяет долг количественно.

Понимание отрицательного целого числа в качестве долга позволяет, например, обосновать . Приведем пример. Если кто-то должен 2 яблока одному человеку и одно яблоко – другому, то общий долг составляет 2+1=3 яблока, поэтому −2+(−1)=−3.

Список литературы.

Некогда разбираться?

Знак у нечисловых объектов[ | код]

Знак угла | код

Положительные и отрицательные углы

Величина угла на плоскости считается положительной, если она измеряется против часовой стрелки, иначе — отрицательной. Аналогично классифицируются два случая вращения:

• вращение на плоскости — например, вращение на (–90°) происходит по часовой стрелке;
• поворот в пространстве вокруг ориентированной оси, как правило, считается положительным, если выполнено «правило буравчика», иначе он считается отрицательным.

Знак направления | код

В аналитической геометрии и физике нередко продвижения вдоль заданной прямой или кривой условно делятся на положительные и отрицательные. Такое деление может зависеть от постановки задачи или от выбранной системы координат. Например, при подсчёте длины дуги кривой часто удобно приписать этой длине на одном из двух возможных направлений знак минус.

Знак в вычислительной технике | код

старший бит
1	1	1	1	1	1	1	=	127
1	1	1	1	1	1	=	126
1	=	2
1	=	1
=
1	1	1	1	1	1	1	1	=	−1
1	1	1	1	1	1	1	=	−2
1	1	=	−127
1	=	−128
Для представления знака целого числа большинство компьютеров используют дополнительный код.

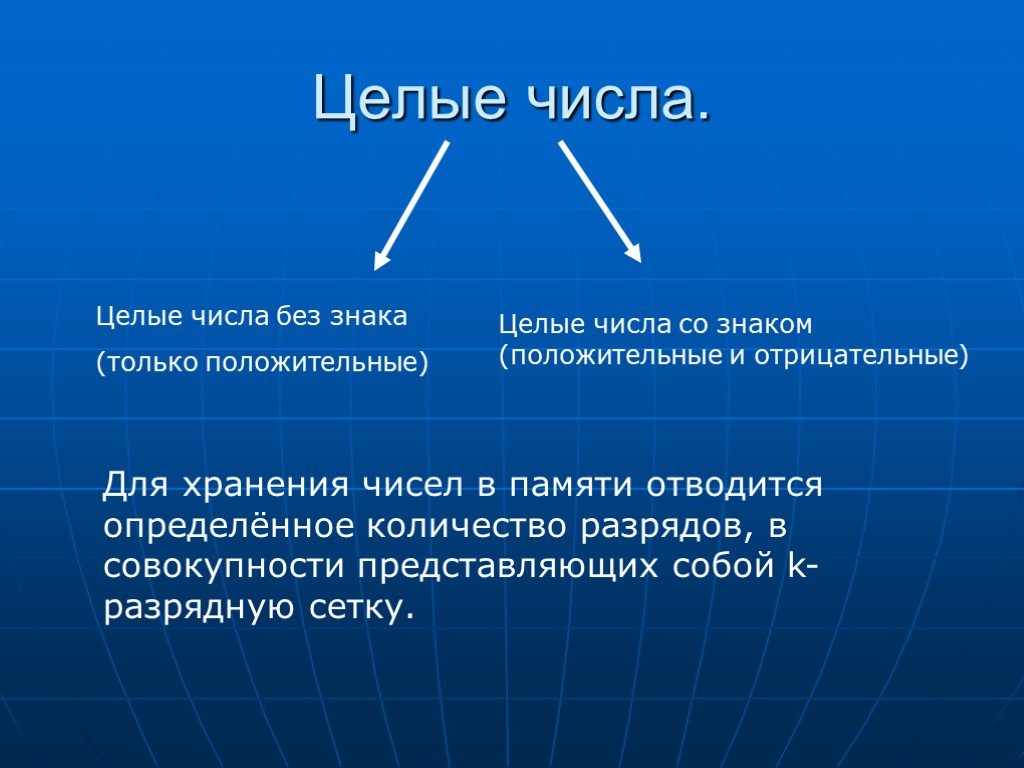
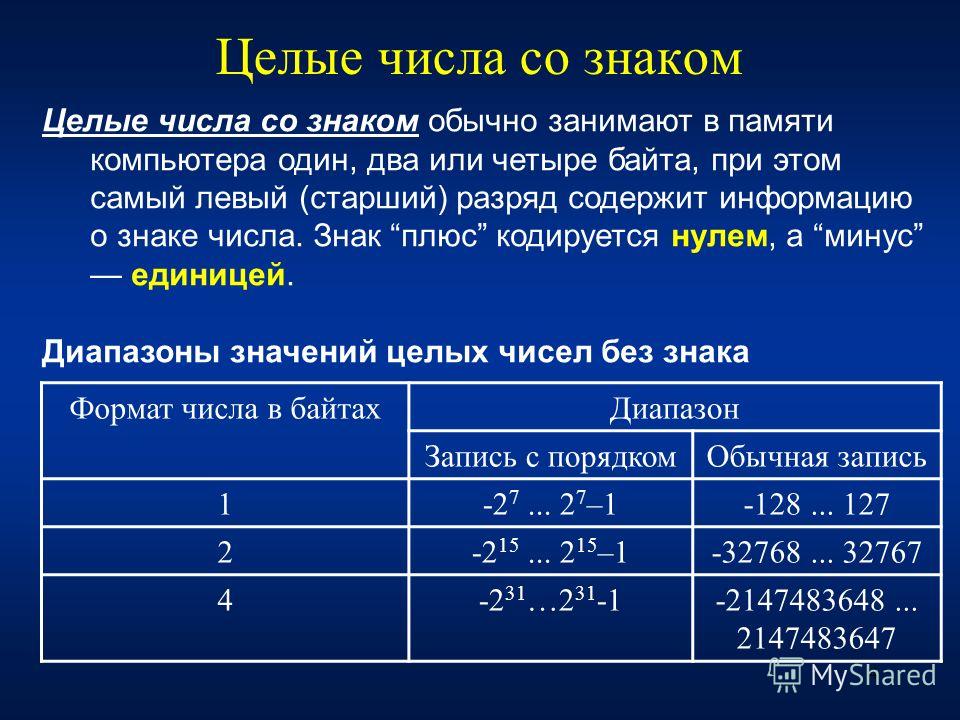
Целое число, хранящееся в памяти компьютера, может быть знаковым или беззнаковым (в последнем случае оно рассматривается как положительное). Знаковые числа используют один из битов как код знака (обычно 0 кодирует положительное число, 1 — отрицательное), у беззнаковых все биты равноправны. Для представления знака и значения целых чисел большинство компьютеров используют дополнительный код, хотя встречается и прямой код.

Вещественные числа хранятся и обрабатываются как числа с плавающей запятой, то есть содержат мантиссу и порядок числа, причём каждая из этих частей снабжена битом своего знака.

Дискретная математика | код

В комбинаторике определяется знак перестановки — положительный, если перестановка чётная, и отрицательный, если перестановка нечётная.

В теории графов рассматриваются ориентированные и , в которых каждому ребру соответствует направление или знак (положительный или отрицательный).

Другие применения знака | код

Электрический заряд может быть положительным или отрицательным.

Существует , в ней каждая цифра числа может иметь положительный или отрицательный знак..

В теории меры определено понятие обобщённой меры со знаком («заряда»), которая может иметь положительные или отрицательные значения.

Знак может быть присвоен бесконечно удалённой точке расширенной числовой оси.

В физике, любой электрический заряд обладает знаком, положительным или отрицательным. По соглашению, положительным считается заряд с тем же знаком, что у протона, а отрицательный заряд — это заряд с тем же знаком, что у электрона. Знак имеют также такие физические величины, как температура, высота над уровнем моря и ряд других.

Знак числа

Положительные и отрицательные числа

Отрицательные и положительные числа на числовой прямой

Вещественное число называется положительным, если оно больше нуля, и отрицательным, если меньше. Положительные числа записываются со знаком плюс или вообще без знака, отрицательные — со знаком минус.

Нулю не присвоен никакой знак, то есть +{\displaystyle +0} и −{\displaystyle -0} — это в арифметике одно и то же число. В математическом анализе смысл символов +{\displaystyle +0} и −{\displaystyle -0} может различаться, см. об этом Отрицательный и положительный ноль; в информатике компьютерная кодировка двух нулей (целого типа) может отличаться, см. Прямой код.

В связи со сказанным вводятся ещё несколько полезных терминов:

• Число неотрицательно, если оно больше или равно нулю.
• Число неположительно, если оно меньше или равно нулю.
• Положительные числа без нуля и отрицательные числа без нуля иногда (чтобы подчеркнуть, что они ненулевые) называют «‘строго положительными» и «строго отрицательными» соответственно.

Та же терминология иногда используется для вещественных функций. Например, функция называется положительной, если все её значения положительны, неотрицательной, если все её значения неотрицательны и т. д. Говорят также, что функция положительна/отрицательна на заданном интервале её определения..

Для комплексных чисел понятия знака числа не существует, потому что для них не определено, как сравнивать числа на больше/меньше.

Обозначения

• Множество положительных действительных чисел обозначается как R>{\displaystyle \mathbb {R} _{>0}}.
• Множество неотрицательных действительных чисел обозначается как R⩾{\displaystyle \mathbb {R} _{\geqslant 0}}.
• Множество отрицательных действительных чисел обозначается как R<{\displaystyle \mathbb {R} _{<0}}.
• Множество неположительных действительных чисел обозначается как R⩽{\displaystyle \mathbb {R} _{\leqslant 0}}.

Функция знака sgn(x)

График функции y=sgn⁡(x){\displaystyle y=\operatorname {sgn}(x)}

Основная статья: sgn

Функция знака y=sgn⁡(x){\displaystyle y=\operatorname {sgn}(x)} (произносится: сигнум от x) часто бывает полезна как индикатор знака числа. Эта функция определяется следующим образом:

sgn⁡(x)={−1(x<),  (x=),  1(x>).{\displaystyle \operatorname {sgn}(x)={\begin{cases}-1\quad (x<0),\\~~\,0\quad (x=0),\\~~\,1\quad (x>0).\end{cases}}}

Другими словами, функция равна 1{\displaystyle 1} для положительного аргумента, −1{\displaystyle -1} для отрицательного и нулю для нулевого аргумента. Функция предусмотрена и в ряде языков программирования.

Пример использования функции см. в статье .

Модуль (абсолютная величина) числа

Основная статья: Абсолютная величина

Если у числа x{\displaystyle x} отбросить знак, полученное значение называется модулем или абсолютной величиной числа x{\displaystyle x}, оно обозначается |x|.{\displaystyle |x|.} Примеры: |3|=3; |−3|=3.{\displaystyle |3|=3;\ |{-3}|=3.}

Для любых вещественных чисел a,b{\displaystyle a,b} имеют место следующие свойства.

• Формула разложения числа на знак и модуль: a=sgn⁡(a)⋅|a|{\displaystyle a=\operatorname {sgn}(a)\cdot |a|}
• Модуль любого числа всегда неотрицателен, причём |a|={\displaystyle |a|=0} тогда и только тогда, когда a={\displaystyle a=0.}
• Модули противоположных чисел совпадают: |−a|=|a|.{\displaystyle |{-a}|=|a|.}
• −|a|⩽a⩽|a|.{\displaystyle -|a|\leqslant a\leqslant |a|.}
• |a+b|⩽|a|+|b|{\displaystyle |a+b|\leqslant |a|+|b|} (неравенство треугольника).

Знак у нечисловых объектов

Знак угла

Положительные и отрицательные углы

Величина угла на плоскости считается положительной, если она измеряется против часовой стрелки, иначе — отрицательной. Аналогично классифицируются два случая вращения:

• вращение на плоскости — например, вращение на (–90°) происходит по часовой стрелке;
• поворот в пространстве вокруг ориентированной оси, как правило, считается положительным, если выполнено «правило буравчика», иначе он считается отрицательным.

Знак направления

В аналитической геометрии и физике нередко продвижения вдоль заданной прямой или кривой условно делятся на положительные и отрицательные. Такое деление может зависеть от постановки задачи или от выбранной системы координат. Например, при подсчёте длины дуги кривой часто удобно приписать этой длине на одном из двух возможных направлений знак минус.

Знак в вычислительной технике

старший бит
1	1	1	1	1	1	1	=	127
1	1	1	1	1	1	=	126
1	=	2
1	=	1
=
1	1	1	1	1	1	1	1	=	−1
1	1	1	1	1	1	1	=	−2
1	1	=	−127
1	=	−128
Для представления знака целого числа большинство компьютеров используют дополнительный код.

Целое число, хранящееся в памяти компьютера, может быть знаковым или беззнаковым (в последнем случае оно рассматривается как положительное). Знаковые числа используют один из битов как код знака (обычно 0 кодирует положительное число, 1 — отрицательное), у беззнаковых все биты равноправны. Для представления знака и значения целых чисел большинство компьютеров используют дополнительный код, хотя встречается и прямой код.

Вещественные числа хранятся и обрабатываются как числа с плавающей запятой, то есть содержат мантиссу и порядок числа, причём каждая из этих частей снабжена битом своего знака.

Дискретная математика

В комбинаторике определяется знак перестановки — положительный, если перестановка чётная, и отрицательный, если перестановка нечётная.

В теории графов рассматриваются ориентированные и , в которых каждому ребру соответствует направление или знак (положительный или отрицательный).

Другие применения знака

Электрический заряд может быть положительным или отрицательным.

Существует , в ней каждая цифра числа может иметь положительный или отрицательный знак..

В теории меры определено понятие обобщённой меры со знаком («заряда»), которая может иметь положительные или отрицательные значения.

Знак может быть присвоен бесконечно удалённой точке расширенной числовой оси.

В физике, любой электрический заряд обладает знаком, положительным или отрицательным. По соглашению, положительным считается заряд с тем же знаком, что у протона, а отрицательный заряд — это заряд с тем же знаком, что у электрона. Знак имеют также такие физические величины, как температура, высота над уровнем моря и ряд других.

Знак числа[ | код]

Положительные и отрицательные числа | код

Отрицательные и положительные числа на числовой прямой

Вещественное число называется положительным, если оно больше нуля, и отрицательным, если меньше. Положительные числа записываются со знаком плюс или вообще без знака, отрицательные — со знаком минус.

Нулю не присвоен никакой знак, то есть +{\displaystyle +0} и −{\displaystyle -0} — это в арифметике одно и то же число. В математическом анализе смысл символов +{\displaystyle +0} и −{\displaystyle -0} может различаться, см. об этом Отрицательный и положительный ноль; в информатике компьютерная кодировка двух нулей (целого типа) может отличаться, см. Прямой код.

В связи со сказанным вводятся ещё несколько полезных терминов:

• Число неотрицательно, если оно больше или равно нулю.
• Число неположительно, если оно меньше или равно нулю.
• Положительные числа без нуля и отрицательные числа без нуля иногда (чтобы подчеркнуть, что они ненулевые) называют «‘строго положительными» и «строго отрицательными» соответственно.

Та же терминология иногда используется для вещественных функций. Например, функция называется положительной, если все её значения положительны, неотрицательной, если все её значения неотрицательны и т. д. Говорят также, что функция положительна/отрицательна на заданном интервале её определения..

Для комплексных чисел понятия знака числа не существует, потому что для них не определено, как сравнивать числа на больше/меньше.

Обозначения | код

• Множество положительных действительных чисел обозначается как R>{\displaystyle \mathbb {R} _{>0}}.
• Множество неотрицательных действительных чисел обозначается как R⩾{\displaystyle \mathbb {R} _{\geqslant 0}}.
• Множество отрицательных действительных чисел обозначается как R<{\displaystyle \mathbb {R} _{<0}}.
• Множество неположительных действительных чисел обозначается как R⩽{\displaystyle \mathbb {R} _{\leqslant 0}}.

Функция знака sgn(x) | код

График функции y=sgn⁡(x){\displaystyle y=\operatorname {sgn}(x)}

Основная статья: sgn

Функция знака y=sgn⁡(x){\displaystyle y=\operatorname {sgn}(x)} (произносится: сигнум от x) часто бывает полезна как индикатор знака числа. Эта функция определяется следующим образом:

sgn⁡(x)={−1(x<),  (x=),  1(x>).{\displaystyle \operatorname {sgn}(x)={\begin{cases}-1\quad (x<0),\\~~\,0\quad (x=0),\\~~\,1\quad (x>0).\end{cases}}}

Другими словами, функция равна 1{\displaystyle 1} для положительного аргумента, −1{\displaystyle -1} для отрицательного и нулю для нулевого аргумента. Функция предусмотрена и в ряде языков программирования.

Пример использования функции см. в статье .

Модуль (абсолютная величина) числа | код

Основная статья: Абсолютная величина

Если у числа x{\displaystyle x} отбросить знак, полученное значение называется модулем или абсолютной величиной числа x{\displaystyle x}, оно обозначается |x|.{\displaystyle |x|.} Примеры: |3|=3; |−3|=3.{\displaystyle |3|=3;\ |{-3}|=3.}

Для любых вещественных чисел a,b{\displaystyle a,b} имеют место следующие свойства.

• Формула разложения числа на знак и модуль: a=sgn⁡(a)⋅|a|{\displaystyle a=\operatorname {sgn}(a)\cdot |a|}
• Модуль любого числа всегда неотрицателен, причём |a|={\displaystyle |a|=0} тогда и только тогда, когда a={\displaystyle a=0.}
• Модули противоположных чисел совпадают: |−a|=|a|.{\displaystyle |{-a}|=|a|.}
• −|a|⩽a⩽|a|.{\displaystyle -|a|\leqslant a\leqslant |a|.}
• |a+b|⩽|a|+|b|{\displaystyle |a+b|\leqslant |a|+|b|} (неравенство треугольника).

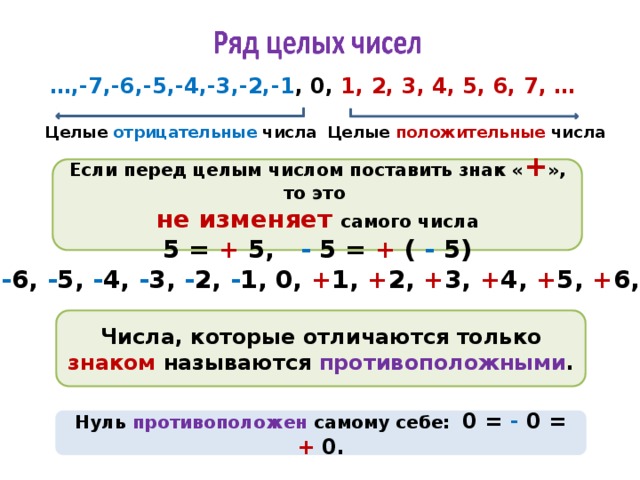
Целые положительные и целые отрицательные числа

Изучив материал статьи положительные и отрицательные числа, мы из всех целых чисел можем выделить целые положительные и целые отрицательные числа.

Определение.

Целые положительные числа — это целые числа со знаком плюс.

Например, число 5 – это целое положительное число. Другими примерами целых положительных чисел являются числа 11, 501, 40 000 003.

Определение.

Целые отрицательные числа – это целые числа со знаком минус.

Приведем несколько примеров целых отрицательных чисел. Числа −6, −5 555, −12 121 – целые отрицательные.

Число нуль (число ) не является ни целым положительным, ни целым отрицательным числом. Нуль как бы отделяет целые отрицательные числа от целых положительных.

Вообще, в силу определения противоположных чисел, любое число, противоположное целому положительному числу, есть целое отрицательное число. И наоборот, любое число, противоположное целому отрицательному числу, есть целое положительное. Это утверждение позволяет дать определения целых положительных и целых отрицательных чисел на основе их сравнения с нулем (здесь нужно владеть материалом статьи сравнение целых чисел).

Определение.

Целые положительные числа – это целые числа, которые больше нуля.

Определение.

Целые отрицательные числа – это целые числа, которые меньше нуля.

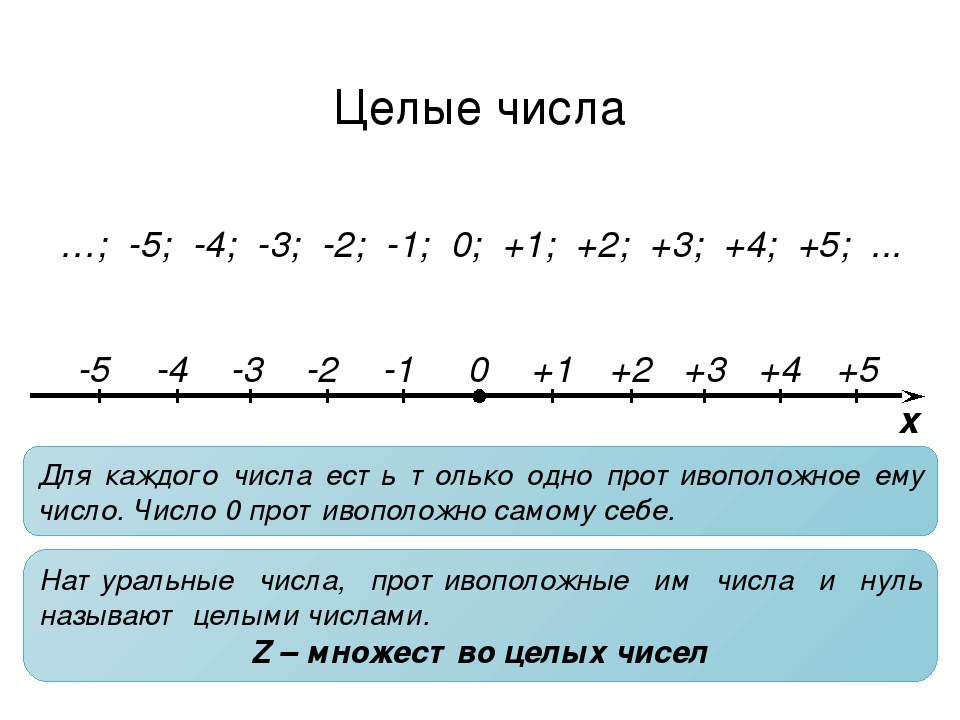
Целые положительные и отрицательные числа можно также определить по их положению на координатной прямой. На горизонтальной координатной прямой точки, координатами которых являются целые положительные числа, лежат правее начала отсчета. В свою очередь точки с целыми отрицательными координатами располагаются левее точки O.

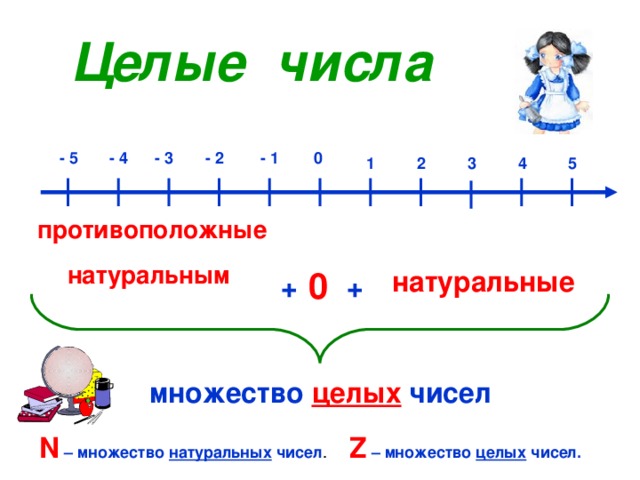
Понятно, что множество всех целых положительных чисел представляет собой множество натуральных чисел. В свою очередь множество всех целых отрицательных чисел – это множество всех чисел, противоположных натуральным числам.

Отдельно обратим Ваше внимание на то, что любое натуральное число мы можем смело назвать целым, а любое целое число мы НЕ можем назвать натуральным. Натуральным мы можем назвать лишь любое целое положительное число, так как целые отрицательные числа и нуль не являются натуральными.

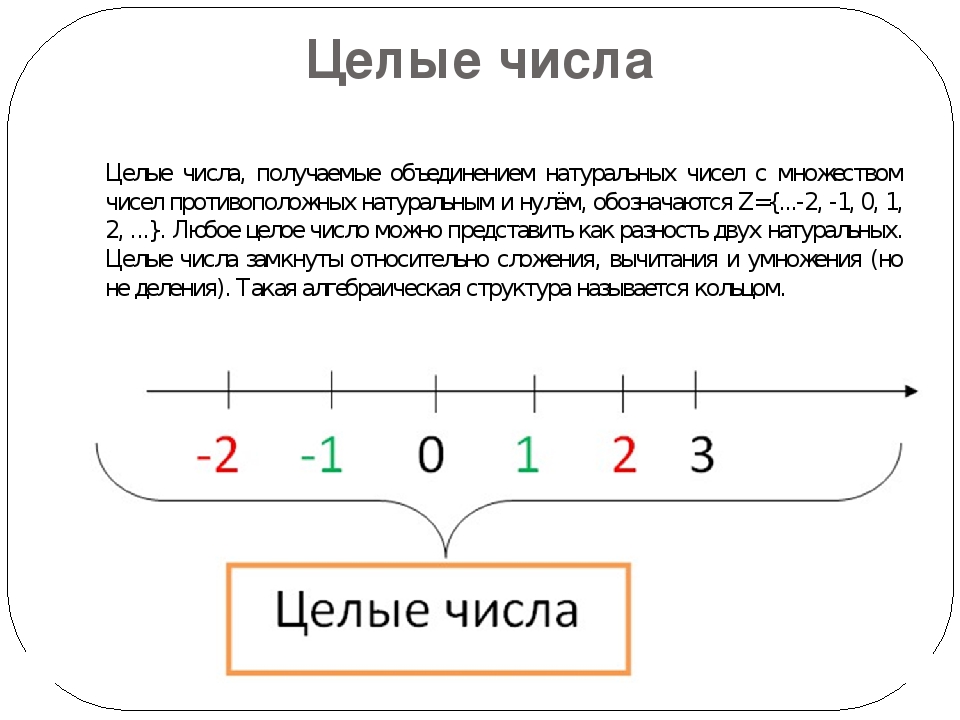
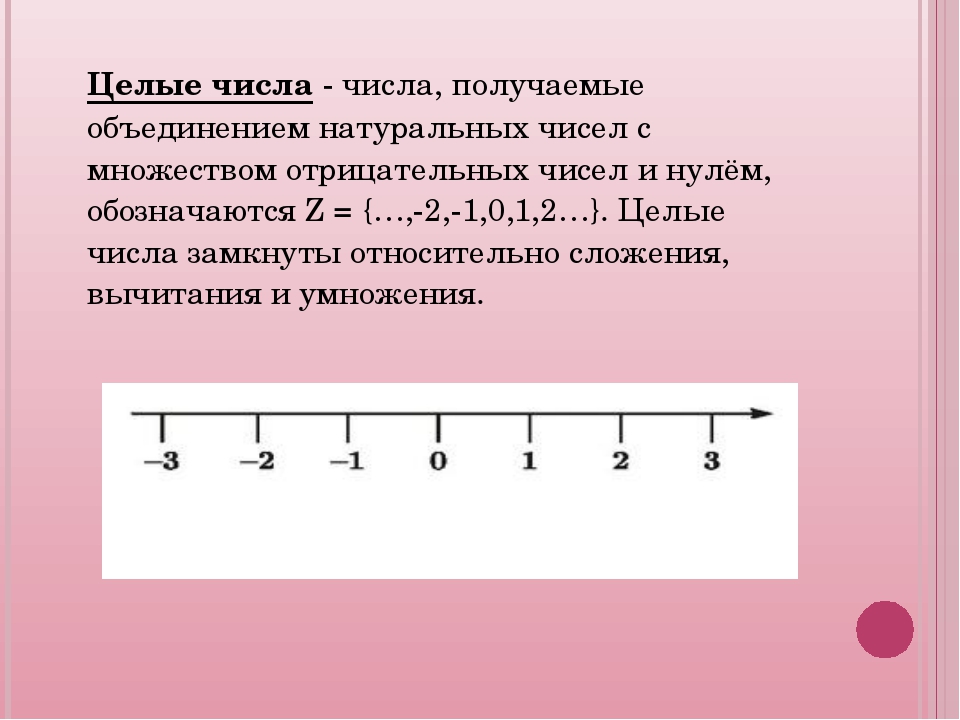
Целые числа на координатной прямой

Давайте взглянем на координатную прямую, чтобы увидеть точки, соответствующие целым числам. Будем считать, что координатная прямая проведена горизонтально и направлена вправо.

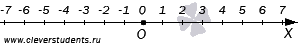
Из построения координатной прямой следует, что началу отсчета и точкам, отмеченным штрихами, взаимно однозначно соответствуют целые числа. То есть, каждой из указанных точек соответствует единственное целое число, следовательно, несовпадающим точкам отвечают разные целые числа. Началу отсчета (точке O) соответствует целое число нуль, а точкам, которые отмечены штрихами, соответствуют другие целые числа. Никаким другим точкам координатной прямой целые числа не соответствуют, и никакому целому числу не отвечает точка координатной прямой, отличная от указанных выше.

В любую точку, отмеченную штрихом (координатами этих точек являются целые числа), мы можем попасть, если от начала отсчета последовательно отложим некоторое количество единичных отрезков.

Знак числа

Положительные и отрицательные числа

Отрицательные и положительные числа на числовой прямой

Вещественное число называется положительным, если оно больше нуля, и отрицательным, если меньше. Положительные числа записываются со знаком плюс или вообще без знака, отрицательные — со знаком минус.

Нулю не присвоен никакой знак, то есть +{\displaystyle +0} и −{\displaystyle -0} — это в арифметике одно и то же число. В математическом анализе смысл символов +{\displaystyle +0} и −{\displaystyle -0} может различаться, см. об этом Отрицательный и положительный ноль; в информатике компьютерная кодировка двух нулей (целого типа) может отличаться, см. Прямой код.

В связи со сказанным вводятся ещё несколько полезных терминов:

• Число неотрицательно, если оно больше или равно нулю.
• Число неположительно, если оно меньше или равно нулю.
• Положительные числа без нуля и отрицательные числа без нуля иногда (чтобы подчеркнуть, что они ненулевые) называют «‘строго положительными» и «строго отрицательными» соответственно.

Та же терминология иногда используется для вещественных функций. Например, функция называется положительной, если все её значения положительны, неотрицательной, если все её значения неотрицательны и т. д. Говорят также, что функция положительна/отрицательна на заданном интервале её определения..

Для комплексных чисел понятия знака числа не существует, потому что для них не определено, как сравнивать числа на больше/меньше.

Обозначения

• Множество положительных действительных чисел обозначается как R>{\displaystyle \mathbb {R} _{>0}}.
• Множество неотрицательных действительных чисел обозначается как R⩾{\displaystyle \mathbb {R} _{\geqslant 0}}.
• Множество отрицательных действительных чисел обозначается как R<{\displaystyle \mathbb {R} _{<0}}.
• Множество неположительных действительных чисел обозначается как R⩽{\displaystyle \mathbb {R} _{\leqslant 0}}.

Функция знака sgn(x)

График функции y=sgn⁡(x){\displaystyle y=\operatorname {sgn}(x)}

Основная статья: sgn

Функция знака y=sgn⁡(x){\displaystyle y=\operatorname {sgn}(x)} (произносится: сигнум от x) часто бывает полезна как индикатор знака числа. Эта функция определяется следующим образом:

sgn⁡(x)={−1(x<),  (x=),  1(x>).{\displaystyle \operatorname {sgn}(x)={\begin{cases}-1\quad (x<0),\\~~\,0\quad (x=0),\\~~\,1\quad (x>0).\end{cases}}}

Другими словами, функция равна 1{\displaystyle 1} для положительного аргумента, −1{\displaystyle -1} для отрицательного и нулю для нулевого аргумента. Функция предусмотрена и в ряде языков программирования.

Пример использования функции см. в статье .

Модуль (абсолютная величина) числа

Основная статья: Абсолютная величина

Если у числа x{\displaystyle x} отбросить знак, полученное значение называется модулем или абсолютной величиной числа x{\displaystyle x}, оно обозначается |x|.{\displaystyle |x|.} Примеры: |3|=3; |−3|=3.{\displaystyle |3|=3;\ |{-3}|=3.}

Для любых вещественных чисел a,b{\displaystyle a,b} имеют место следующие свойства.

• Формула разложения числа на знак и модуль: a=sgn⁡(a)⋅|a|{\displaystyle a=\operatorname {sgn}(a)\cdot |a|}
• Модуль любого числа всегда неотрицателен, причём |a|={\displaystyle |a|=0} тогда и только тогда, когда a={\displaystyle a=0.}
• Модули противоположных чисел совпадают: |−a|=|a|.{\displaystyle |{-a}|=|a|.}
• −|a|⩽a⩽|a|.{\displaystyle -|a|\leqslant a\leqslant |a|.}
• |a+b|⩽|a|+|b|{\displaystyle |a+b|\leqslant |a|+|b|} (неравенство треугольника).

Знак числа

Положительные и отрицательные числа

Отрицательные и положительные числа на числовой прямой

Вещественное число называется положительным, если оно больше нуля, и отрицательным, если меньше. Положительные числа записываются со знаком плюс или вообще без знака, отрицательные — со знаком минус.

Нулю не присвоен никакой знак, то есть +{\displaystyle +0} и −{\displaystyle -0} — это в арифметике одно и то же число. В математическом анализе смысл символов +{\displaystyle +0} и −{\displaystyle -0} может различаться, см. об этом Отрицательный и положительный ноль; в информатике компьютерная кодировка двух нулей (целого типа) может отличаться, см. Прямой код.

В связи со сказанным вводятся ещё несколько полезных терминов:

• Число неотрицательно, если оно больше или равно нулю.
• Число неположительно, если оно меньше или равно нулю.
• Положительные числа без нуля и отрицательные числа без нуля иногда (чтобы подчеркнуть, что они ненулевые) называют «‘строго положительными» и «строго отрицательными» соответственно.

Та же терминология иногда используется для вещественных функций. Например, функция называется положительной, если все её значения положительны, неотрицательной, если все её значения неотрицательны и т. д. Говорят также, что функция положительна/отрицательна на заданном интервале её определения..

Для комплексных чисел понятия знака числа не существует, потому что для них не определено, как сравнивать числа на больше/меньше.

Обозначения

• Множество положительных действительных чисел обозначается как R>{\displaystyle \mathbb {R} _{>0}}.
• Множество неотрицательных действительных чисел обозначается как R⩾{\displaystyle \mathbb {R} _{\geqslant 0}}.
• Множество отрицательных действительных чисел обозначается как R<{\displaystyle \mathbb {R} _{<0}}.
• Множество неположительных действительных чисел обозначается как R⩽{\displaystyle \mathbb {R} _{\leqslant 0}}.

Функция знака sgn(x)

График функции y=sgn⁡(x){\displaystyle y=\operatorname {sgn}(x)}

Основная статья: sgn

Функция знака y=sgn⁡(x){\displaystyle y=\operatorname {sgn}(x)} (произносится: сигнум от x) часто бывает полезна как индикатор знака числа. Эта функция определяется следующим образом:

sgn⁡(x)={−1(x<),  (x=),  1(x>).{\displaystyle \operatorname {sgn}(x)={\begin{cases}-1\quad (x<0),\\~~\,0\quad (x=0),\\~~\,1\quad (x>0).\end{cases}}}

Другими словами, функция равна 1{\displaystyle 1} для положительного аргумента, −1{\displaystyle -1} для отрицательного и нулю для нулевого аргумента. Функция предусмотрена и в ряде языков программирования.

Пример использования функции см. в статье .

Модуль (абсолютная величина) числа

Основная статья: Абсолютная величина

Если у числа x{\displaystyle x} отбросить знак, полученное значение называется модулем или абсолютной величиной числа x{\displaystyle x}, оно обозначается |x|.{\displaystyle |x|.} Примеры: |3|=3; |−3|=3.{\displaystyle |3|=3;\ |{-3}|=3.}

Для любых вещественных чисел a,b{\displaystyle a,b} имеют место следующие свойства.

• Формула разложения числа на знак и модуль: a=sgn⁡(a)⋅|a|{\displaystyle a=\operatorname {sgn}(a)\cdot |a|}
• Модуль любого числа всегда неотрицателен, причём |a|={\displaystyle |a|=0} тогда и только тогда, когда a={\displaystyle a=0.}
• Модули противоположных чисел совпадают: |−a|=|a|.{\displaystyle |{-a}|=|a|.}
• −|a|⩽a⩽|a|.{\displaystyle -|a|\leqslant a\leqslant |a|.}
• |a+b|⩽|a|+|b|{\displaystyle |a+b|\leqslant |a|+|b|} (неравенство треугольника).

Знак у нечисловых объектов

Знак угла

Положительные и отрицательные углы

Величина угла на плоскости считается положительной, если она измеряется против часовой стрелки, иначе — отрицательной. Аналогично классифицируются два случая вращения:

• вращение на плоскости — например, вращение на (–90°) происходит по часовой стрелке;
• поворот в пространстве вокруг ориентированной оси, как правило, считается положительным, если выполнено «правило буравчика», иначе он считается отрицательным.

Знак направления

В аналитической геометрии и физике нередко продвижения вдоль заданной прямой или кривой условно делятся на положительные и отрицательные. Такое деление может зависеть от постановки задачи или от выбранной системы координат. Например, при подсчёте длины дуги кривой часто удобно приписать этой длине на одном из двух возможных направлений знак минус.

Знак в вычислительной технике

старший бит
1	1	1	1	1	1	1	=	127
1	1	1	1	1	1	=	126
1	=	2
1	=	1
=
1	1	1	1	1	1	1	1	=	−1
1	1	1	1	1	1	1	=	−2
1	1	=	−127
1	=	−128
Для представления знака целого числа большинство компьютеров используют дополнительный код.

Целое число, хранящееся в памяти компьютера, может быть знаковым или беззнаковым (в последнем случае оно рассматривается как положительное). Знаковые числа используют один из битов как код знака (обычно 0 кодирует положительное число, 1 — отрицательное), у беззнаковых все биты равноправны. Для представления знака и значения целых чисел большинство компьютеров используют дополнительный код, хотя встречается и прямой код.

Вещественные числа хранятся и обрабатываются как числа с плавающей запятой, то есть содержат мантиссу и порядок числа, причём каждая из этих частей снабжена битом своего знака.

Дискретная математика

В комбинаторике определяется знак перестановки — положительный, если перестановка чётная, и отрицательный, если перестановка нечётная.

В теории графов рассматриваются ориентированные и , в которых каждому ребру соответствует направление или знак (положительный или отрицательный).

Другие применения знака

Электрический заряд может быть положительным или отрицательным.

Существует , в ней каждая цифра числа может иметь положительный или отрицательный знак..

В теории меры определено понятие обобщённой меры со знаком («заряда»), которая может иметь положительные или отрицательные значения.

Знак может быть присвоен бесконечно удалённой точке расширенной числовой оси.

В физике, любой электрический заряд обладает знаком, положительным или отрицательным. По соглашению, положительным считается заряд с тем же знаком, что у протона, а отрицательный заряд — это заряд с тем же знаком, что у электрона. Знак имеют также такие физические величины, как температура, высота над уровнем моря и ряд других.

Знак у нечисловых объектов

Знак угла

Положительные и отрицательные углы

Величина угла на плоскости считается положительной, если она измеряется против часовой стрелки, иначе — отрицательной. Аналогично классифицируются два случая вращения:

• вращение на плоскости — например, вращение на (–90°) происходит по часовой стрелке;
• поворот в пространстве вокруг ориентированной оси, как правило, считается положительным, если выполнено «правило буравчика», иначе он считается отрицательным.

Знак направления

В аналитической геометрии и физике нередко продвижения вдоль заданной прямой или кривой условно делятся на положительные и отрицательные. Такое деление может зависеть от постановки задачи или от выбранной системы координат. Например, при подсчёте длины дуги кривой часто удобно приписать этой длине на одном из двух возможных направлений знак минус.

Знак в вычислительной технике

старший бит
1	1	1	1	1	1	1	=	127
1	1	1	1	1	1	=	126
1	=	2
1	=	1
=
1	1	1	1	1	1	1	1	=	−1
1	1	1	1	1	1	1	=	−2
1	1	=	−127
1	=	−128
Для представления знака целого числа большинство компьютеров используют дополнительный код.

Целое число, хранящееся в памяти компьютера, может быть знаковым или беззнаковым (в последнем случае оно рассматривается как положительное). Знаковые числа используют один из битов как код знака (обычно 0 кодирует положительное число, 1 — отрицательное), у беззнаковых все биты равноправны. Для представления знака и значения целых чисел большинство компьютеров используют дополнительный код, хотя встречается и прямой код.

Вещественные числа хранятся и обрабатываются как числа с плавающей запятой, то есть содержат мантиссу и порядок числа, причём каждая из этих частей снабжена битом своего знака.

Дискретная математика

В комбинаторике определяется знак перестановки — положительный, если перестановка чётная, и отрицательный, если перестановка нечётная.

В теории графов рассматриваются ориентированные и , в которых каждому ребру соответствует направление или знак (положительный или отрицательный).

Другие применения знака

Электрический заряд может быть положительным или отрицательным.

Существует , в ней каждая цифра числа может иметь положительный или отрицательный знак..

В теории меры определено понятие обобщённой меры со знаком («заряда»), которая может иметь положительные или отрицательные значения.

Знак может быть присвоен бесконечно удалённой точке расширенной числовой оси.

В физике, любой электрический заряд обладает знаком, положительным или отрицательным. По соглашению, положительным считается заряд с тем же знаком, что у протона, а отрицательный заряд — это заряд с тем же знаком, что у электрона. Знак имеют также такие физические величины, как температура, высота над уровнем моря и ряд других.