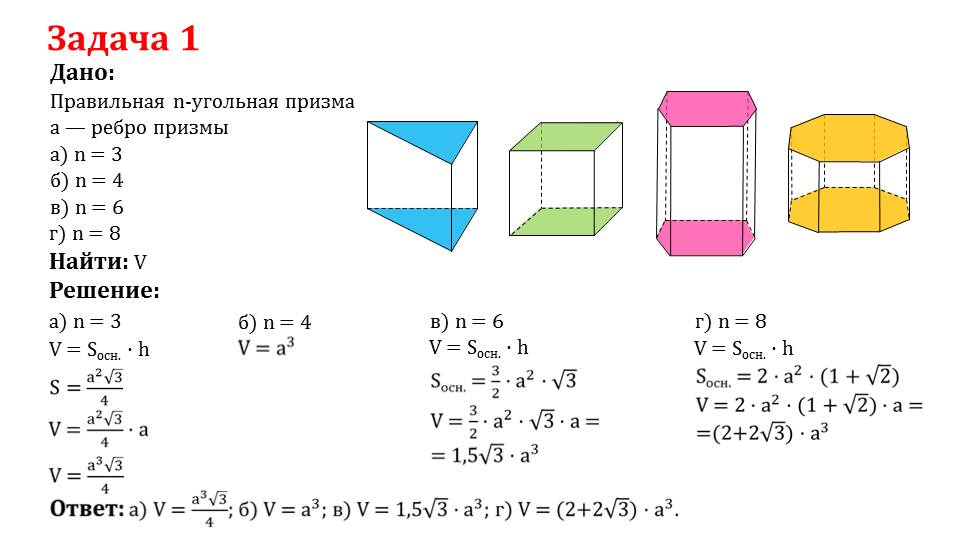
Скрученная призма
Скрученная призма — это невыпуклый призматический многогранник, полученный из однородной q-угольной путём деления боковых граней диагональю и вращения верхнего основания, обычно на угол πq{\displaystyle {\frac {\pi }{q}}} радиан (180q{\displaystyle {\frac {180}{q}}} градусов), в направлении, при котором стороны становятся вогнутыми.
Скрученная призма не может быть разбита на тетраэдры без введения новых вершин. Наименьший случай называется многогранником Шёнхардта.
Скрученная призма топологически идентична антипризме, но имеет половину : Dn, [n,2]+, порядка 2n. Эту призму можно рассматривать как выпуклую антипризму, у которой удалены тетраэдры между парами треугольников.
| Треугольная | Четырёхугольные | 12-угольная | |
|---|---|---|---|
| Многогранник Шёнхардта | Скрученная квадратная призма | Квадратная антипризма | Скрученная двенадцатиугольная призма |
Элементы
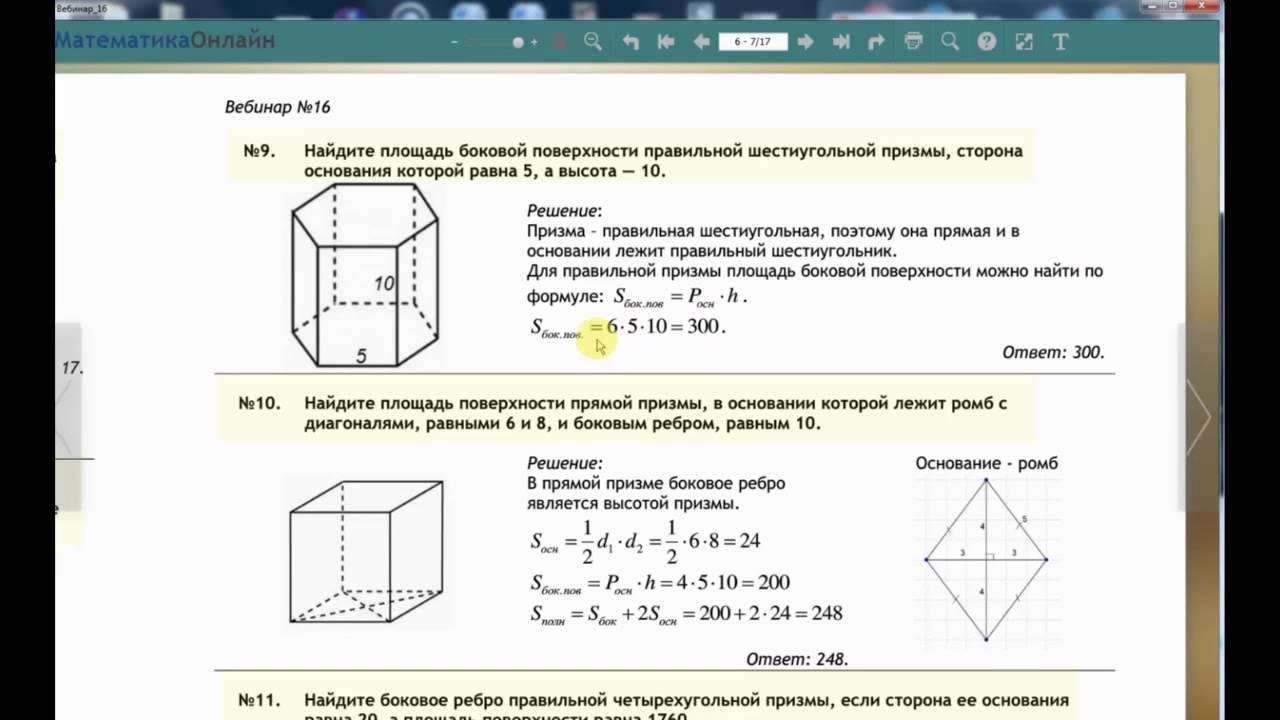
Для любой призмы главными ее элементами являются ребра, грани и вершины. Шестиугольная призма не является исключением. Приведенный выше рисунок позволяет посчитать количество этих элементов. Так, граней или сторон мы получаем 8 (два основания и шесть боковых параллелограммов), число вершин составляет 12 (по 6 вершин для каждого основания), количество ребер шестиугольной призмы равно 18 (шесть боковых и 12 для оснований).
В 1750-е годы Леонард Эйлер (швейцарский математик) установил для всех полиэдров, к которым относится призма, математическую связь между числами указанных элементов. Эта связь имеет вид:
Указанные выше цифры удовлетворяют этой формуле.
Длина диагонали прямоугольного параллелепипеда
Диагональ параллелепипеда — это отрезок, который соединяет две вершины, не имеющие общих сторон, которые их образуют. В любой четырехугольной призме диагоналей всего четыре. Для прямоугольного параллелепипеда, в основании которого расположен прямоугольник, длины всех диагоналей равны друг другу.
Ниже на рисунке приведена соответствующая фигура. Красный отрезок является ее диагональю.

Рассчитать ее длину очень просто, если вспомнить о теореме Пифагора. Каждый школьник может получить искомую формулу. Она имеет следующую форму:
Здесь D — длина диагонали. Остальные символы — это длины сторон параллелепипеда.
Многие путают диагональ параллелепипеда с диагоналями его сторон. Ниже приводится рисунок, где цветными отрезками изображены диагонали сторон фигуры.
Длина каждой из них также определяется по теореме Пифагора и равна квадратному корню из суммы квадратов соответствующих длин сторон.
Какие элементы характеризуют призму?
Элементами фигуры называют составные части, которые ее образуют. Конкретно для призмы можно выделить три главных типа элементов:
- вершины;
- грани или стороны;
- ребра.
Гранями считаются основания и боковые плоскости, представляющие параллелограммы в общем случае. В призме всегда каждая сторона относится к одному из двух типов: либо это многоугольник, либо параллелограмм.
Ребра призмы — это те отрезки, которые ограничивают каждую сторону фигуры. Как и грани, ребра также бывают двух типов: принадлежащие основанию и боковой поверхности или относящиеся только к боковой поверхности. Первых всегда в два раза больше, чем вторых, независимо от вида призмы.
Вершины — это точки пересечения трех ребер призмы, два из которых лежат в плоскости основания, а третье — принадлежит двум боковым граням. Все вершины призмы находятся в плоскостях оснований фигуры.
Числа описанных элементов связаны в единое равенство, имеющее следующий вид:
Р = В + С — 2.
Здесь Р — количество ребер, В — вершин, С — сторон. Это равенство называется теоремой Эйлера для полиэдра.
На рисунке показана треугольная правильная призма. Каждый может посчитать, что она имеет 6 вершин, 5 сторон и 9 ребер. Эти цифры согласуются с теоремой Эйлера.
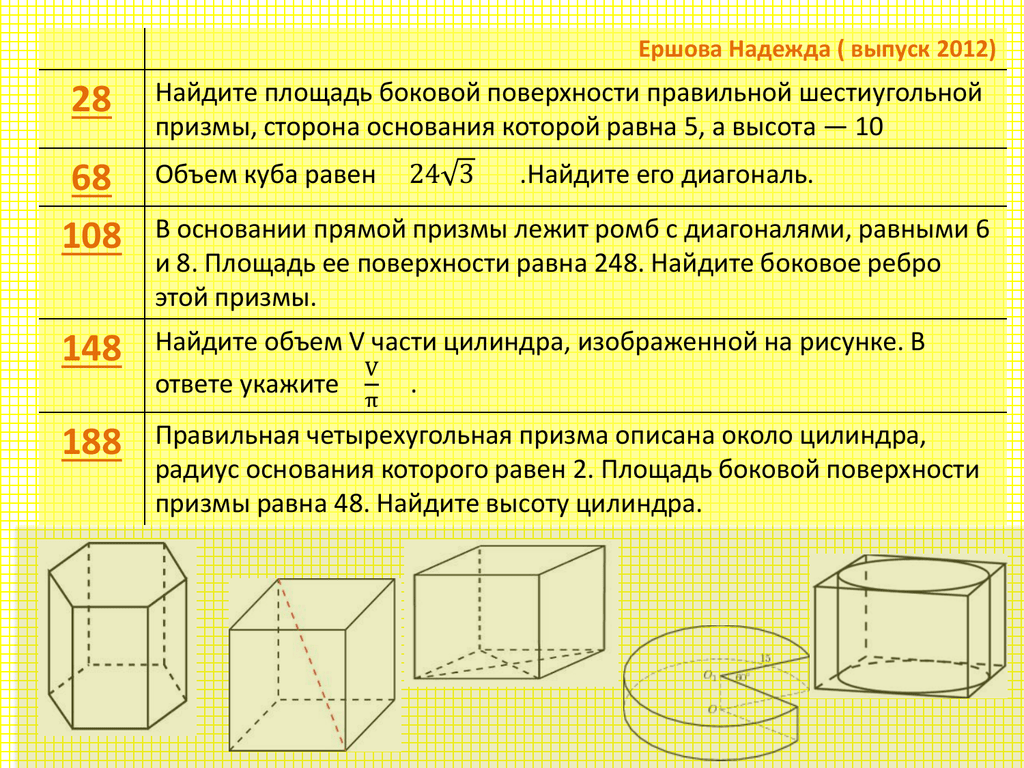
Задачи на расчет треугольной призмы
Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:
V = 1/2 · 6 · 8 · 5 = 120.
Задача 2.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.

Решение:
Объём призмы равен произведению площади основания на высоту: V = Sосн ·h.
Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S2 = S1k2 = S122 = 4S1.
Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.
Таким образом, искомый объём равен 20.
Формулы по математике для ЕГЭ и ОГЭ
Как перевести погонный метр в метры
Шар и сфера, объем шара, площадь сферы, формулы
Как решать экономические задачи егэ по математике профильный уровень
Задачи ЕГЭ по кодированию генетического кода
Диагонали призмы и ее линейные параметры
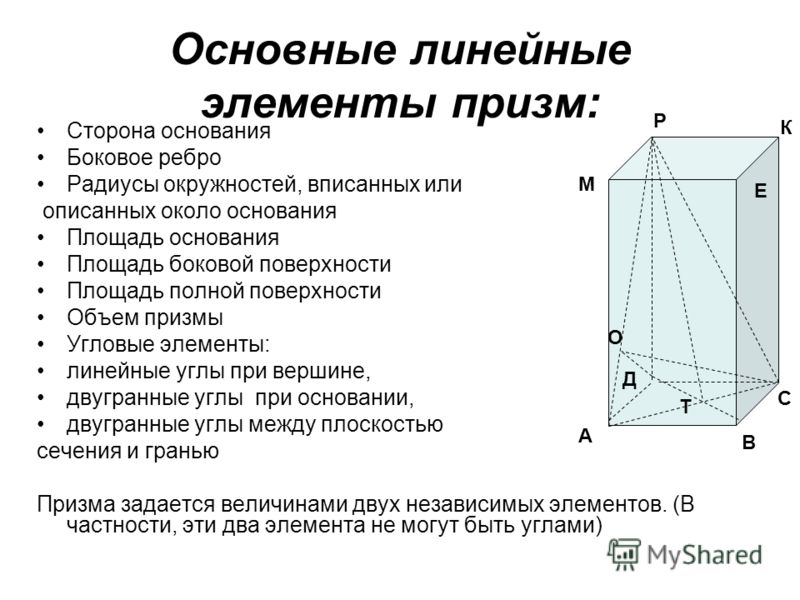
Основными линейными характеристиками любой призмы являются ее высота h и длины сторон ее основания ai, где i = 1, …, n. Если основание является многоугольником правильным, тогда для описания его свойств достаточно знать длину a одной стороны. Знание отмеченных линейных параметров позволяет однозначно определить такие свойства фигуры, как ее объем или поверхность.
Диагонали прямой призмы представляют собой отрезки, которые соединяют любые две несмежные вершины. Такие диагонали могут быть трех типов:
- лежащие в плоскостях основания;
- находящиеся в плоскостях боковых прямоугольников;
- принадлежащие объему фигуры.
Длины тех диагоналей, что относятся к основанию, следует определять в зависимости от типа n-угольника.
Диагонали боковых прямоугольников рассчитываются по следующей формуле:
Для определения объемных диагоналей необходимо знать значение длины соответствующей диагонали основания и высоты. Если некоторую диагональ основания обозначить буквой d0i, тогда объемная диагональ d2i вычисляется так:
Например, в случае правильной четырехугольной призмы длина объемной диагонали будет равна:
Отметим, что прямая треугольная призма обладает лишь одним из трех названных типов диагоналей: диагональю боковой стороны.
Диагонали сторон четырехугольной прямой призмы
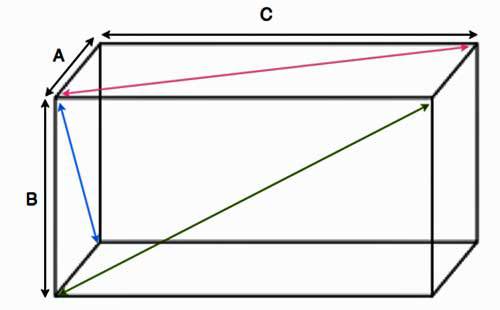
На рисунке выше изображены четыре одинаковые прямые призмы, и даны параметры их ребер. На призмах Diagonal A, Diagonal B и Diagonal C штриховой красной линией изображены диагонали трех разных граней. Поскольку призма является прямой с высотой 5 см, а ее основание представлено прямоугольником со сторонами 3 см и 2 см, то отыскать отмеченные диагонали не представляет никакого труда. Для этого необходимо воспользоваться теоремой Пифагора.
Длина диагонали основания призмы (Diagonal A) равна:
DA = √(32+22) = √13 ≈ 3,606 см.
Для боковой грани призмы диагональ равна (см. Diagonal B):
DB = √(32+52) = √34 ≈ 5,831 см.
Наконец, длина еще одной боковой диагонали равна (см. Diagonal C):
DС = √(22+52) = √29 ≈ 5,385 см.
Элементы фигуры
Речь идет о геометрических элементах, из которых состоит рассматриваемая призма. Первое, что бросается в глаза при первом взгляде на фигуру — это ее грани. Как было отмечено, у нее их шесть. Две одинаковые грани образуют основания прямоугольной призмы, четыре оставшиеся составляют ее боковую поверхность. Все грани являются или прямоугольниками, либо квадратами.

Следующий важный элемент фигуры — это ребра. Призма имеет 12 ребер, причем 8 из них принадлежат основаниям. Оставшиеся четыре ребра являются боковыми. Их длина равна высоте фигуры.
Наконец, третьим важным элементом изучаемой призмы являются ее вершины. В отличие от пирамиды или конуса, призма не имеет выделенной вершины. Все они у нее являются равноправными. Их количество равно восьми.
Как видно из представленной количественной характеристики элементов прямой прямоугольной призмы, для их чисел справедлива теорема Эйлера:
Что такое призма?
Когда школьников просят назвать определение призмы, то они отвечают, что данная фигура представляет собой два одинаковых параллельных многоугольника, стороны которых соединены параллелограммами. Это определение является максимально общим, поскольку оно не накладывает условия на форму многоугольников, на их взаимное расположение в параллельных плоскостях. Кроме того, оно предполагает наличие соединяющих параллелограммов, к классу которых также относятся квадрат, ромб и прямоугольник. Ниже можно посмотреть, что собой представляет четырехугольная призма.

Мы видим что призма — это многогранник (полиэдр), состоящий из n + 2 сторон, 2 × n вершин и 3 × n ребер, где n — количество сторон (вершин) одного из многоугольников.
Оба многоугольника принято называть основаниями фигуры, остальные грани — это боковые стороны призмы.
Примеры призм. Треугольные призмы. Четырехугольные призмы.Параллелепипеды
| Призма | Рисунок | Свойства |
| Наклонная треугольная призма |
AA1, BB1, CC1 не ABС и A1B1C1. ABС – произвольный треугольник. |
|
| Прямая треугольная призма |
AA1, BB1, CC1 ABС и A1B1C1. ABС – произвольный треугольник. прямой треугольной призмы – . равна длине . |
|
| Правильная треугольная призма |
AA1, BB1, CC1 ABС и A1B1C1. ABС – . правильной треугольной призмы – . равна длине . |
|
| Наклонная четырехугольная призма |
AA1, BB1, CC1,DD1 не ABСD и A1B1C1D1. ABСD – произвольный четырехугольник. |
|
| Прямая четырехугольная призма |
AA1, BB1, CC1, DD1 ABСD и A1B1C1D1. ABСD – произвольный четырехугольник. прямой четырехугольной призмы – . равна длине . |
|
| Правильная четырехугольная призма |
AA1, BB1, CC1, DD1 ABСD и A1B1C1D1. ABСD – . правильной четырехугольной призмы – . равна длине . |
|
| Параллелепипед |
все которой . Противоположные параллелепипеда равны. |
|
| Прямой параллелепипед | 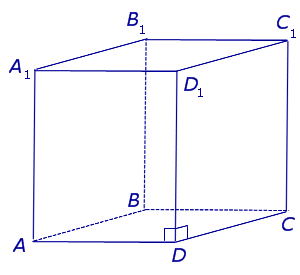 |
, ABСD и A1B1C1D1 которой – . равна длине . |
| Прямоугольный параллелепипед |
, ABСD и A1B1C1D1 которой – . Все прямоугольного параллелепипеда являются . |
|
| Правильный параллелепипед |
Синоним термина ABСD и A1B1C1D1 – равные , – равные . равна длине . |
|
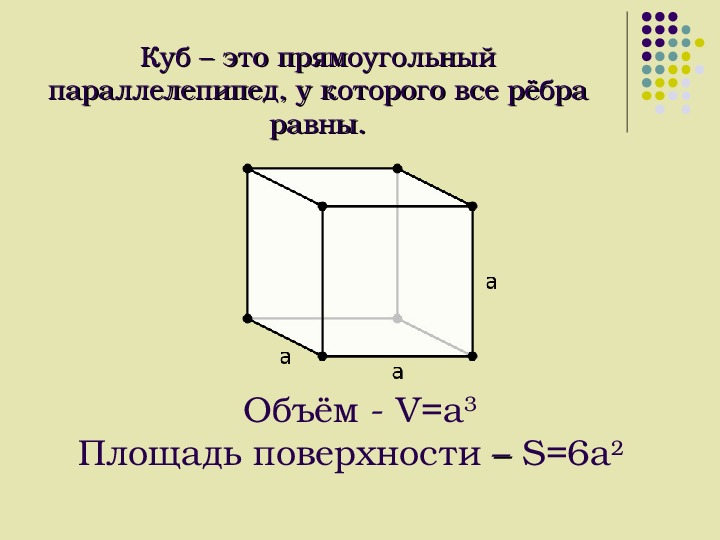
| Куб |
Правильный параллелепипед, у которого все равные . У куба все равны и попарно перпендикулярны. равна длине . |
| Наклонная треугольная призма |
|
Свойства: AA1, BB1, CC1 не ABС и A1B1C1.ABС – произвольный треугольник. |
| Прямая треугольная призма |
|
Свойства: AA1, BB1, CC1 ABС и A1B1C1.ABС – произвольный треугольник. прямой треугольной призмы – . равна длине . |
| Правильная треугольная призма |
|
Свойства: AA1, BB1, CC1 ABС и A1B1C1.ABС – . правильной треугольной призмы – . равна длине . |
| Наклонная четырехугольная призма |
|
Свойства: AA1, BB1, CC1, DD1 не ABСD и A1B1C1D1.ABСD – произвольный четырехугольник. |
| Прямая четырехугольная призма |
|
Свойства: AA1, BB1, CC1, DD1 ABСD и A1B1C1D1.ABСD – произвольный четырехугольник. прямой четырехугольной призмы – . равна длине . |
| Правильная четырехугольная призма |
|
Свойства: AA1, BB1, CC1, DD1 ABСD и A1B1C1D1.ABСD – . правильной четырехугольной призмы – . равна длине . |
| Параллелепипед |
|
Свойства:все которой .Противоположные параллелепипеда равны. |
| Прямой параллелепипед |
|
Свойства:, ABСD и A1B1C1D1 которой – . равна длине . |
| Прямоугольный параллелепипед |
|
Свойства:, ABСD и A1B1C1D1 которой – .Все прямоугольного параллелепипеда являются . |
| Правильный параллелепипед |
|
Свойства:Синоним термина ABСD и A1B1C1D1 – равные , – равные . равна длине . |
| Куб |
|
Свойства:Правильный параллелепипед, у которого все равные .У куба все равны и попарно перпендикулярны. равна длине . |

Домашнее задание
А теперь давайте попробуем закрепить изученную тему с помощью решения задач.
Давайте нарисуем наклонную треугольную призму, у которой расстояние между ее ребрами будет равно: 3 см, 4 см и 5 см, а боковая поверхность этой призмы будет равна 60 см2. Имея такие параметры, найдите боковое ребро данной призмы.
А вы знаете, что геометрические фигуры постоянно окружают нас не только на уроках геометрии, но и в повседневной жизни встречаются предметы, которые напоминают ту или иную геометрическую фигуру.

У каждого дома, в школе или на работе имеется компьютер, системный блок которого имеет форму прямой призмы.
Если вы возьмете в руки простой карандаш, то вы увидите, что основной частью карандаша, является призма.
Идя по центральной улице города, мы видим, что у нас под ногами лежит плитка, которая имеет форму шестиугольной призмы.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Определение.
Призма
— это многогранник, все вершины которого расположены в двух параллельных плоскостях, причем в этих же двух плоскостях лежат две грани призмы, представляющие собой равные многоугольники с соответственно параллельными сторонами, а все ребра, не лежащие в этих плоскостях, параллельны.
Две равные грани называются основаниями призмы
(ABCDE, A 1 B 1 C 1 D 1 E 1)
.
Все остальные грани призмы называются боковыми гранями
(AA 1 B 1 B, BB 1 C 1 C, CC 1 D 1 D, DD 1 E 1 E, EE 1 A 1 A).
Все боковые грани образуют боковую поверхность призмы
.
Все боковые грани призмы являются параллелограммами.
Ребра, не лежащие в основаниях, называются боковыми ребрами призмы(AA 1
, BB 1
, CC 1
, DD 1
, EE 1
).
Диагональю призмы
называется отрезок, концами которого служат две вершины призмы, не лежащие на одной ее грани (АD 1).
Длина отрезка, соединяющего основания призмы и перпендикулярного одновременно обоим основаниям,называется высотой призмы
.
Обозначение:
ABCDE A 1 B 1 C 1 D 1 E 1
. (Сначала в порядке обхода указывают вершины одного основания, а затем в том же порядке — вершины другого; концы каждого бокового ребра обозначают одинаковыми буквами, только вершины, лежащие в одном основании, обозначаются буквами без индекса, а в другом — с индексом)
Название призмы связывают с числом углов в фигуре, лежащей в ее основании, например, на рисунке 1 в основании лежит пятиугольник, поэтому призму называют пятиугольной призмой
. Но т.к. у такой призмы 7 граней, то она семигранник
(2 грани — основания призмы, 5 граней — параллелограммы, — ее боковые грани)
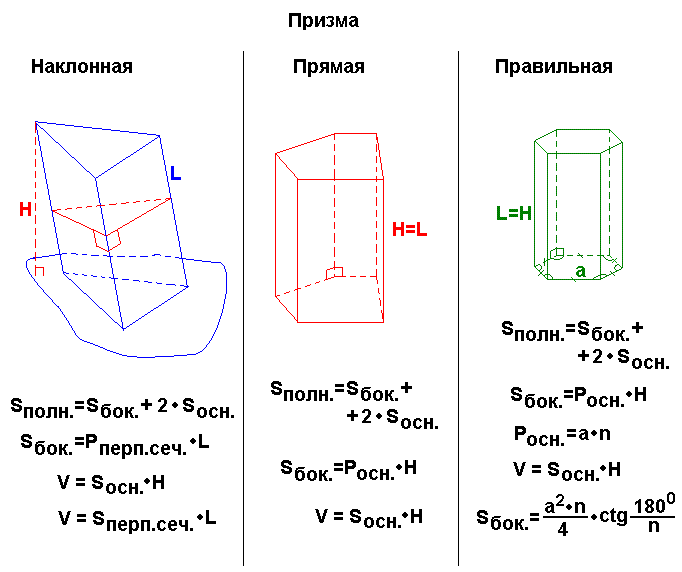
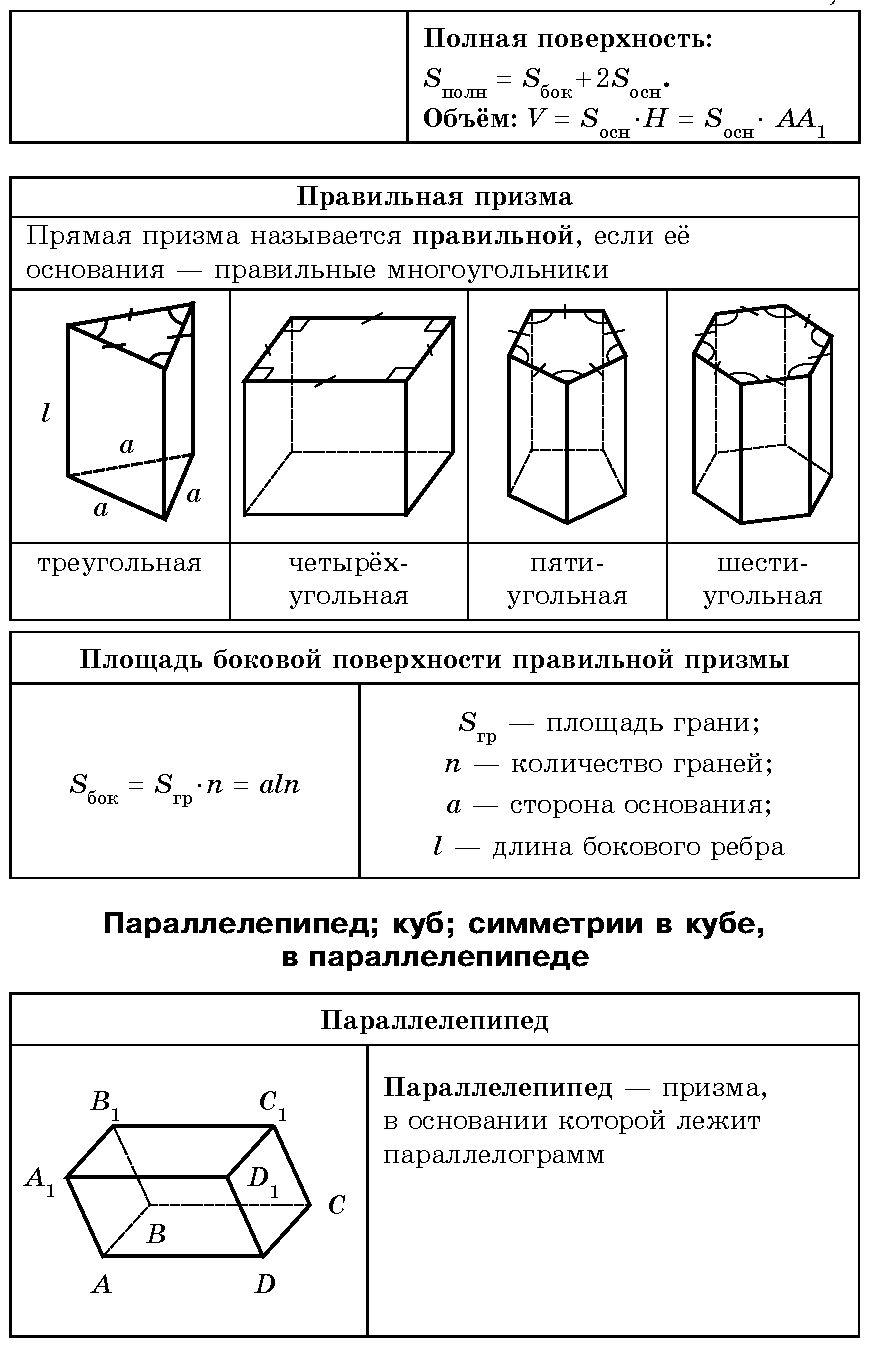
Среди прямых призм выделяется частный вид: правильные призмы.
Прямая призма называется правильной,
если ее основания-правильные многоугольники.

У правильной призмы все боковые грани равные прямоугольники.
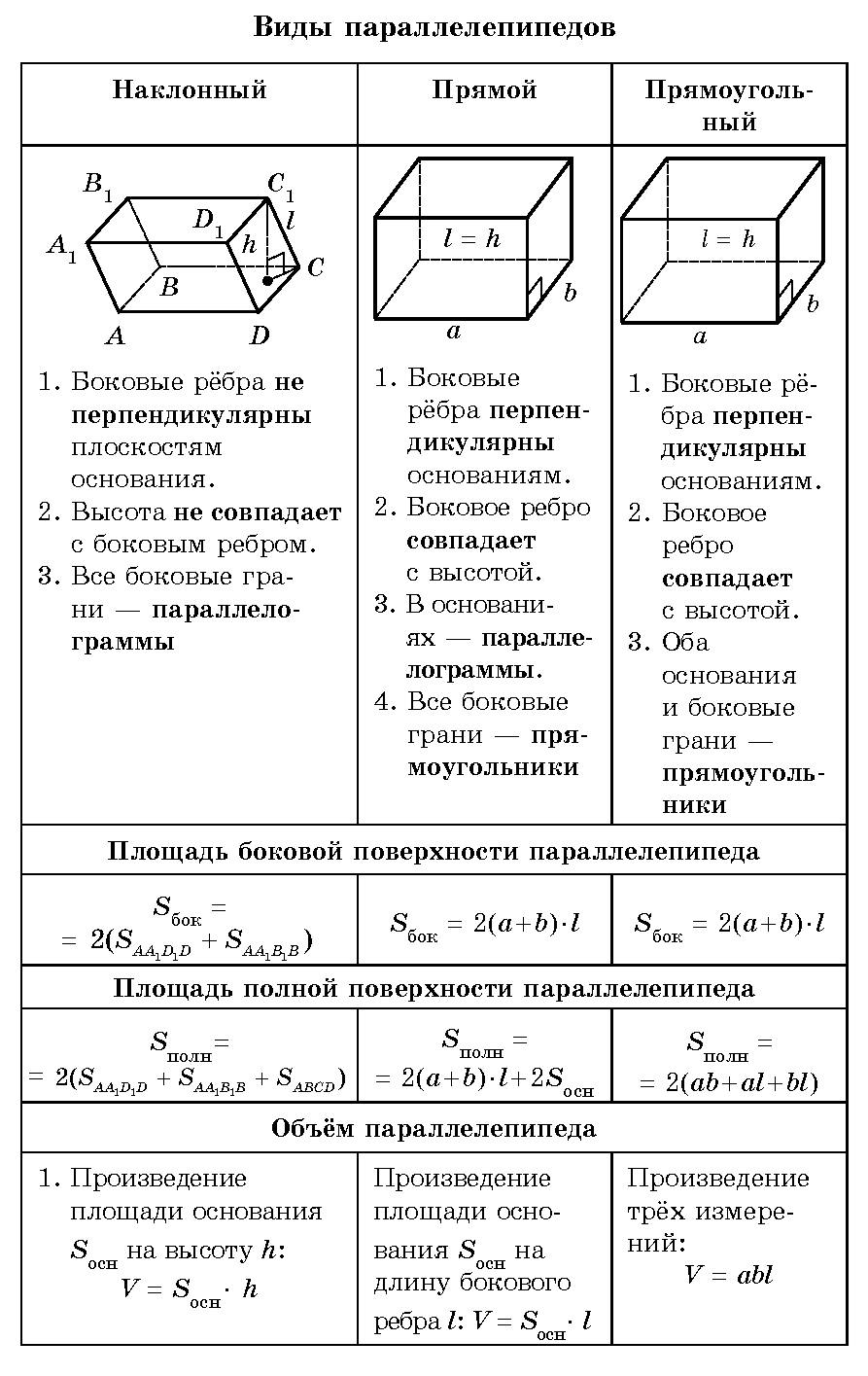
Частным случаем призмы является параллелепипед.
Параллелепипед
Параллелепипед
— это четырехугольная призма, в основании которой лежит параллелограмм (наклонный параллелепипед).Прямой параллелепипед
— параллелепипед, у которого боковые ребра перпендикулярны плоскостям основания.
Прямоугольный параллелепипед
— прямой параллелепипед, основанием которого является прямоугольник.
Свойства и теоремы:
Некоторые свойства параллелепипеда аналогичны известным свойствам параллелограмма.Прямоугольный параллелепипед, имеющий равные измерения, называются кубом
.У куба все грани равные квадраты.Квадрат диагонали, равен сумме квадратов трех его измерений
 ,
,
где d — диагональ квадрата; a — сторона квадрата.
Представление о призме дают:
- различные архитектурные сооружения;
- детские игрушки;
- упаковочные коробки;
- дизайнерские предметы и т.д.


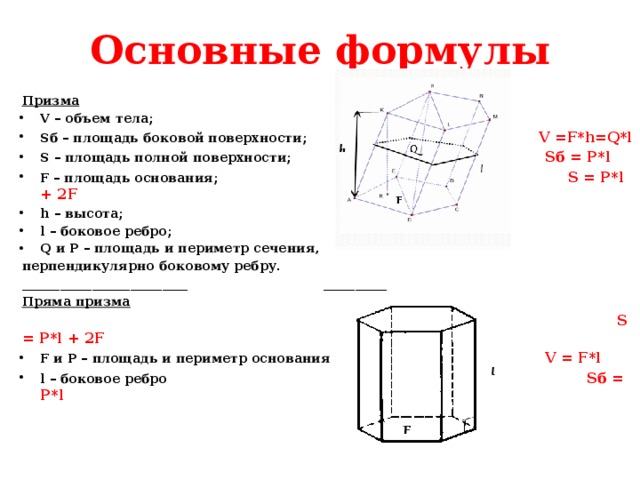
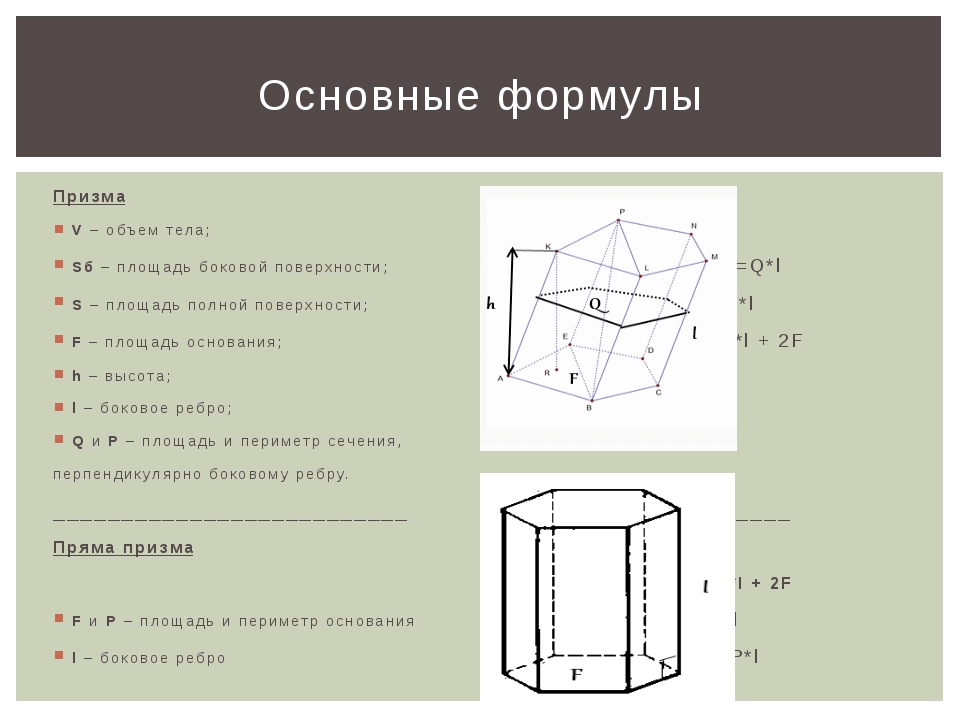
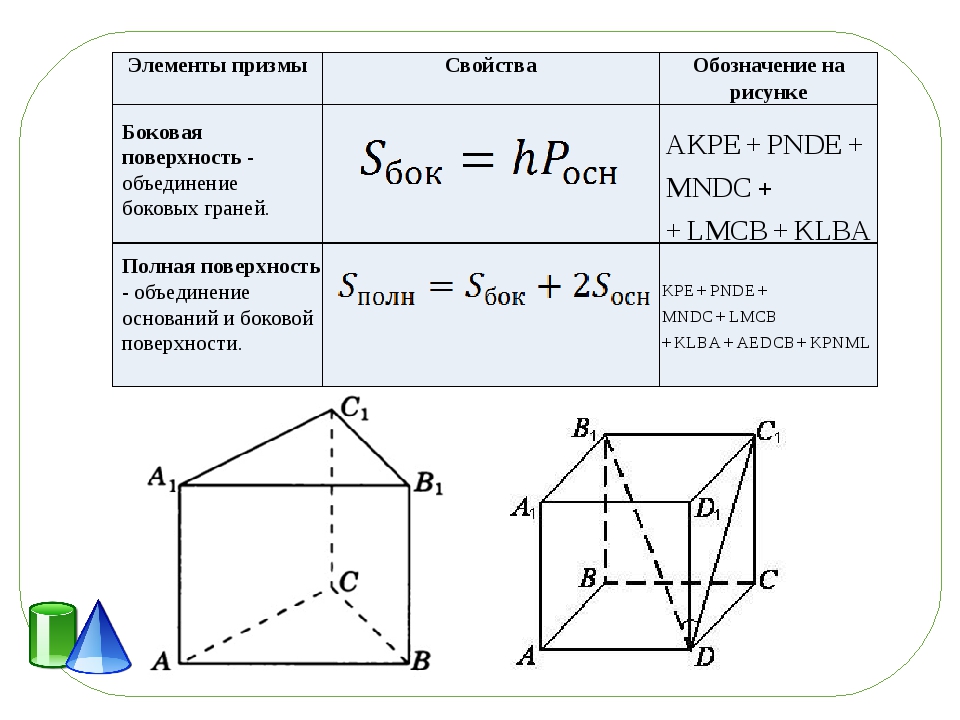
Площадь полной и боковой поверхности призмы
Площадь полной поверхности призмы
называется сумма площадей всех ее гранейПлощадь боковой поверхности
называется сумма площадей ее боковых гранейТ.к. основания призмы — равные многоугольник, то их площади равны. Поэтому
S полн = S бок + 2S осн
,
где S полн
— площадь полной поверхности,S бок
-площадь боковой поверхности, S осн
— площадь основания
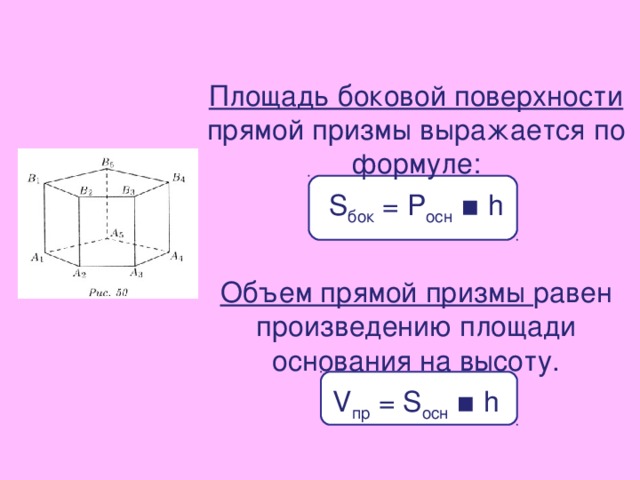
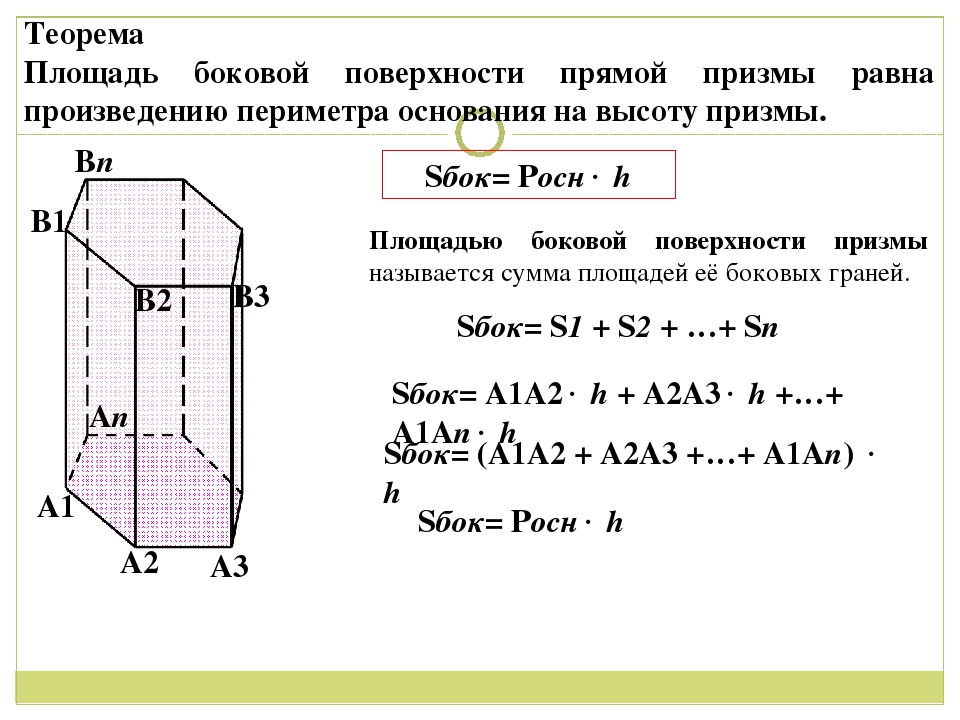
Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы
.
S бок
= P осн * h,
где S бок
-площадь боковой поверхности прямой призмы,
P осн — периметр основания прямой призмы,
h — высота прямой призмы, равная боковому ребру.
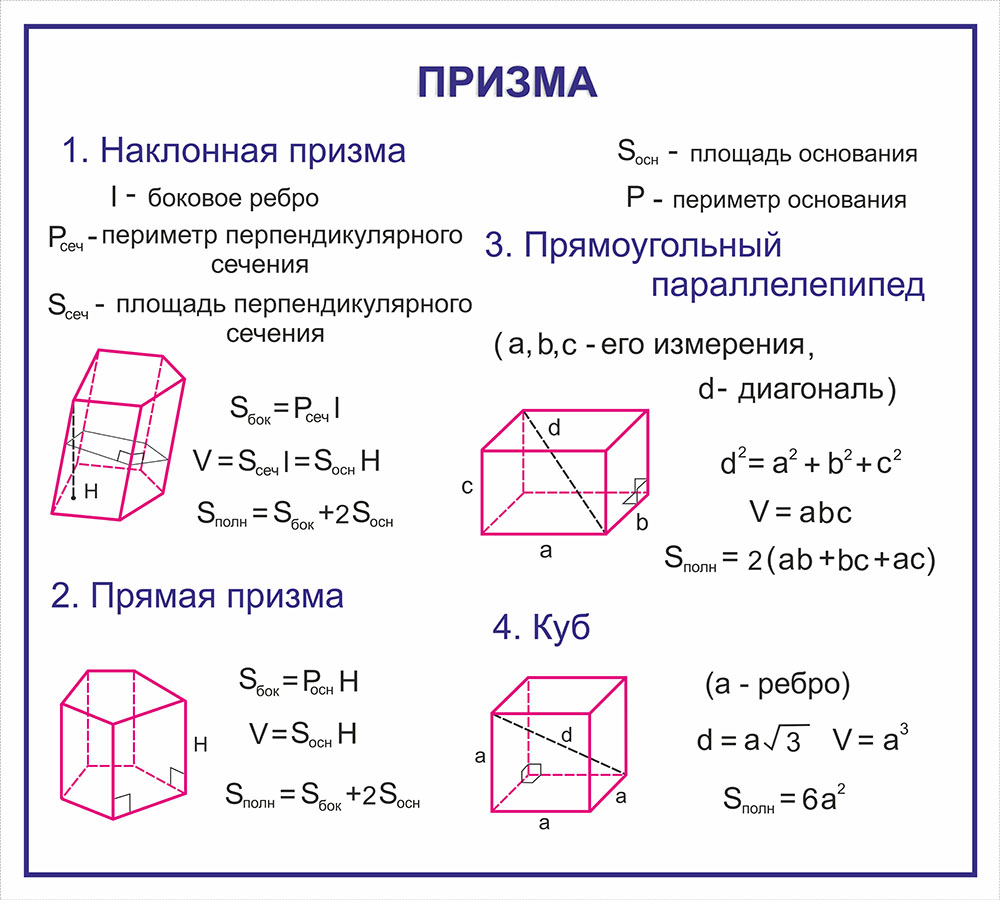
Площадь поверхности призмы
Формулу для площади поверхности любой призмы можно записать, если для начала сделать ее развертку и проанализировать, из каких сторон состоит изучаемая фигура. Поскольку любая призма имеет два n-угольных основания и n параллелограммов, значит, складывая все площади этих фигур, можно получить искомый результат.

Задача вычисления площади поверхности облегчается, если призма является прямой. В такой фигуре все боковые стороны — это прямоугольники, площадь которых легко найти, зная высоту фигуры и длины сторон основания.
Общую для площади призм формулу можно привести только для случая правильной фигуры. Напомним, что правильные призмы состоят из равносторонних и равноугольных оснований и одинаковых прямоугольников боковой поверхности. Для площади основания призмы формула носит универсальный характер:
Площадь произвольной боковой грани вычисляется так:
Теперь остается сложить записанные выражения, учитывая количество сторон фигуры, чтобы получить искомую формулу для площади S всей поверхности призмы:
Как видно, для вычисления величины S правильной призмы достаточно знать длину стороны основания, количество его вершин и высоту фигуры.
Если призма является наклонной, то рассчитать для нее площадь боковой поверхности можно, если вычислить периметр среза Psr, плоскость которого будет перпендикулярна всем боковым граням, а затем умножить этот периметр на длину бокового ребра c. То есть:
Добавив к величине Sb две площади основания So, мы получим площадь всей поверхности S наклонной фигуры.

Диагонали призмы
Все диагонали шестиугольной призмы можно разделить на два типа:
- те, которые лежат в плоскостях ее граней;
- те, которые принадлежат всему объему фигуры.
Рисунок ниже показывает все эти диагонали.
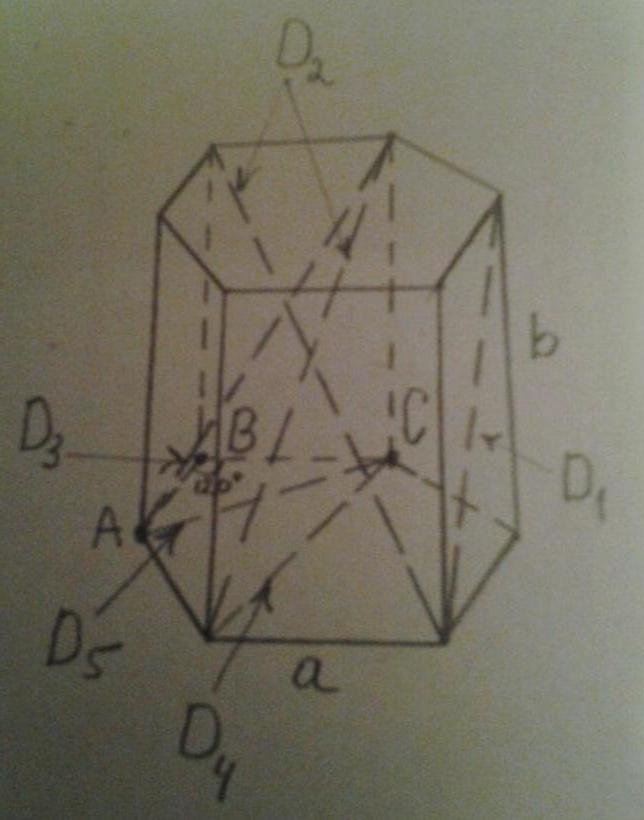
Видно, что D1 — это диагональ боковой стороны, D2 и D3 — диагонали всей призмы, D4 и D5 — диагонали основания.
Длины диагоналей боковых сторон между собой равны. Вычислить их легко, используя всем известную теорему Пифагора. Обозначим символом a длину стороны шестиугольника, символом b — длину бокового ребра. Тогда диагональ имеет длину:
Диагональ D4 также легко определяется. Если вспомнить, что правильный шестиугольник вписывается в окружность радиусом a, то D4 является диаметром этой окружности, то есть получим следующую формулу:
Диагональ D5 основания найти несколько сложнее. Для этого следует рассмотреть равносторонний треугольник ABC (см. рис.). Для него AB = BC = a, угол ABC равен 120o. Если из этого угла опустить высоту (она же будет биссектрисой и медианой), тогда половина основания AC будет равно:
Сторона AC является диагональю D5, поэтому получаем:
Теперь остается найти диагонали D2 и D3 правильной шестиугольной призмы. Для этого нужно увидеть, что они являются гипотенузами соответствующих прямоугольных треугольников. Воспользовавшись теоремой Пифагора, получаем:
Таким образом, самой большой диагональю для любых значений a и b является D2.
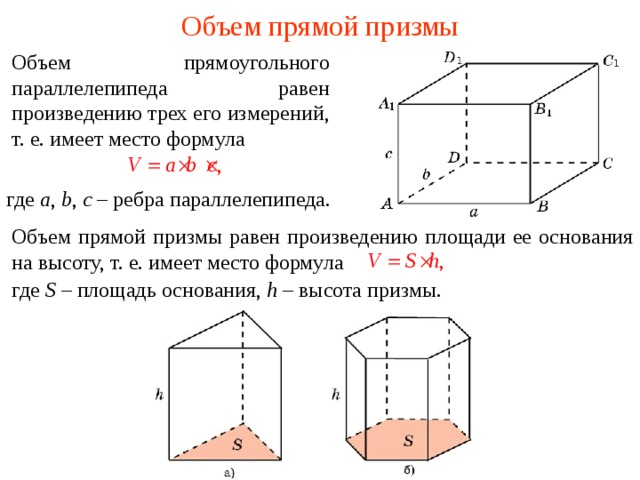
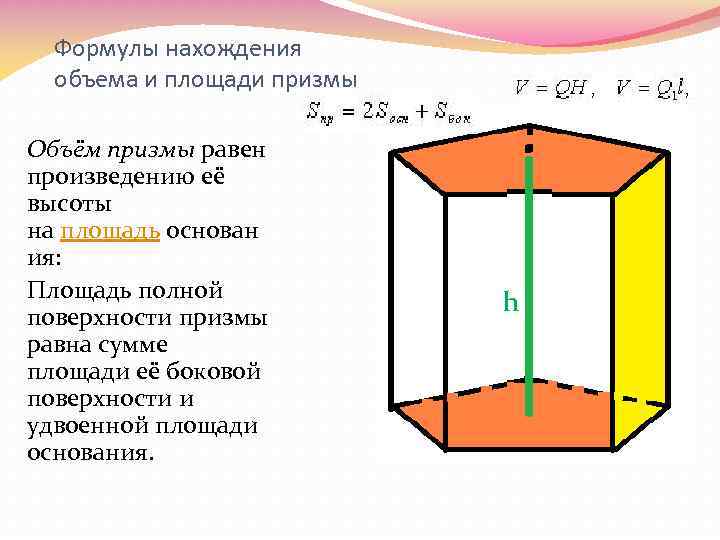
Объем призмы

После того как была получена формула для площади шестиугольного основания, вычислить объем, заключенный в рассматриваемую призму, проще простого. Для этого следует лишь умножить площадь одного основания (шестиугольника) на высоту фигуры, длина которой равна длине бокового ребра. Получаем формулу:
Отметим, что произведение основания на высоту дает значение объема абсолютно любой призмы, включая наклонную. Однако в последнем случае расчет высоты осложняется, поскольку она уже не будет равна длине бокового ребра. Что касается шестиугольной правильной призмы, то значение ее объема является функцией двух переменных: сторон a и b.
Какая фигура называется призмой?
В геометрии дается следующее определение призме: это объемная фигура, ограниченная двумя многоугольными одинаковыми сторонами, которые параллельны друг другу, и некоторым числом параллелограммов. Рисунок ниже показывает пример призмы, соответствующий данному определению.

Мы видим, что два красных пятиугольника равны друг другу и находятся в двух параллельных плоскостях. Пять розовых параллелограммов соединяют эти пятиугольники в цельный объект — призму. Два пятиугольника называются основаниями фигуры, а ее параллелограммы — это боковые грани.
Призмы бывают прямые и наклонные, которые также называют прямоугольными и косоугольными. Разница между ними заключается в углах между основанием и боковыми гранями. Для прямоугольной призмы все эти углы равны 90o.
По количеству сторон или вершин многоугольника в основании говорят о призмах треугольных, пятиугольных, четырехугольных и так далее. Причем если этот многоугольник является правильным, а сама призма прямой, то такую фигуру называют правильной.
Приведенная на предыдущем рисунке призма является пятиугольной наклонной. Ниже же изображена пятиугольная прямая призма, которая является правильной.

Все вычисления, включая методику определения диагоналей призмы, удобно выполнять именно для правильных фигур.
О какой призме пойдет речь?
Призма шестиугольная — это фигура, образованная двумя многоугольниками, имеющими шесть сторон и шесть углов, и шестью параллелограммами, соединяющими отмеченные шестиугольники в единое геометрическое образование.
На рисунке изображен пример этой призмы.

Отмеченный красным цветом шестиугольник называется основанием фигуры. Очевидно, что число ее оснований равно двум, причем оба они идентичны. Желто-зеленоватые грани призмы называются ее боковыми сторонами. На рисунке они представлены квадратами, но в общем случае они являются параллелограммами.
Шестиугольная призма может быть наклонной и прямой. В первом случае углы между основанием и боковыми сторонами не являются прямыми, во втором они равны 90o. Также эта призма может быть правильной и неправильной. Правильная шестиугольная призма обязательно должна быть прямой и иметь правильный шестиугольник в основании. Приведенная выше призма на рисунке этим требованиям удовлетворяет, поэтому она называется правильной. Далее в статье будем изучать только ее свойства, как общий случай.
Связанные многогранники и мозаики
| Многоугольник | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Мозаика | ||||||||||||
| Конфигурация | 3.4.4 | 4.4.4 | 5.4.4 | 6.4.4 | 7.4.4 | 8.4.4 | 9.4.4 | 10.4.4 | 11.4.4 | 12.4.4 | 17.4.4 | ∞.4.4 |
| n | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| Название | {2} || t{2} | {3} || t{3} | {4} || t{4} | {5} || t{5} | {6} || t{6} |
| Купол | Диагональный купол | Трёхскатный купол | Четырёхскатный купол | Шестискатный купол(плоский) | |
| Связанныеоднородныемногогранники | Треугольная призма | Кубооктаэдр | Ромбокубо-октаэдр | Ромбоикосо-додекаэдр |
Симметрии
Призмы топологически являются частью последовательности однородных усечённых многогранников с конфигурациями вершин (3.2n.2n) и .
| Варианты симметрии *n32 усечённых мозаик: 3.2n.2n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия*n32 | Сферическая | Компактная гиперболич. | Параком-пактная | Некомпактная гиперболич. | |||||||
| *232 | *332 | *432 | *532 | *632 | *732 | *832… | *∞32 | ||||
| Усечённыефигуры | |||||||||||
| 3.4.4 | 3.6.6 | 3.8.8 | 3.10.10 | 3.24i.24i | 3.18i.18i | 3.12i.12i | |||||
| Разделённыефигуры | |||||||||||
| V3.4.4 | V3.6.6 | V3.8.8 | V3.10.10 | V3.16.16 | V3.∞.∞ |
Призмы топологически являются частью последовательности скошенных многогранников с вершинными фигурами (3.4.n.4) и мозаик на гиперболической плоскости. Эти вершинно транзитивные фигуры имеют (*n32) зеркальную .
| Варианты симметрии *n42 расширенных мозаик: 3.4.n.4 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия*n32 | Компактнаягиперболическая | Паракомпактная | ||||||
| *232 | *332 | *432 | *532 | *632 | *732 | *832… | *∞32 | |
| Фигура | ||||||||
| 3.4.2.4 | 3.4.3.4 | 3.4.4.4 | 3.4.5.4 |
Существует 4 однородных соединения треугольных призм:
- , , , .
Соты
Существует 9 однородных сот, включающих ячейки в виде треугольных призм:
- ,
- ,
- повёрнутые треугольные призматические соты,
- ,
- треугольные призматические соты,
- треугольно-шестиугольные призматические соты,
- усечённые шестиугольные призматические соты,
- ромботришестиугольные призматические соты,
- плосконосые шестиугольные призматические соты,
- удлинённые треугольные призматические соты.
Связанные многогранники
Треугольная призма является первым многогранником в ряду . Каждый последующий содержит в качестве вершинной фигуры предыдущий многогранник. идентифицировал эту серию в 1900 как содержащую все фасеты правильных многомерных многогранников, все симплексы и ортоплексы (правильные треугольники и квадраты для случая треугольных призм). В нотации Коксетера треугольная призма задаётся символом −121.
| в пространстве размерности n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Пространство | Конечное | Евклидово | Гиперболическое | |||||
| ГруппаКоксетера | E₃=A₂A₁ | E₄=A₄ | E₅=D₅ | E₆ | E₈ | E₉ = E~8{\displaystyle {\tilde {E}}_{8}} = E₈+ | E₁₀ = T¯8{\displaystyle {\bar {T}}_{8}} = E₈++ | |
| ДиаграммаКоксетера | ||||||||
| Порядок | 12 | 120 | 192 | 51,840 | 2,903,040 | 696,729,600 | ∞ | |
| Граф | — | — | ||||||
| Name | −121 |
Призматические многогранники
Призматический многогранник — это обобщение призмы в пространствах размерности 4 и выше. n-мерный призматический многогранник конструируется из двух (n − 1)-мерных многогранников, перенесённых в следующую размерность.
Элементы призматического n-мерного многогранника удваиваются из элементов (n − 1)-мерного многогранника, затем создаются новые элементы следующего уровня.
Возьмём n-мерный многогранник с элементами fi{\displaystyle f_{i}} (i-мерная грань, i = 0, …, n). Призматический (n+1{\displaystyle n+1})-мерный многогранник будет иметь 2fi+f−1{\displaystyle 2f_{i}+f_{-1}} элементов размерности i (при f−1={\displaystyle f_{-1}=0}, fn=1{\displaystyle f_{n}=1}).
По размерностям:
- Берём многоугольник с n вершинами и n сторонами. Получим призму с 2n вершинами, 3n рёбрами и 2+n{\displaystyle 2+n} гранями.
- Берём многогранник с v вершинами, e рёбрами и f гранями. Получаем (4-мерную) призму с 2v вершинами, 2e+v{\displaystyle 2e+v} рёбрами, 2f+e{\displaystyle 2f+e} гранями и 2+f{\displaystyle 2+f} ячейками.
- Берём 4-мерный многогранник с v вершинами, e рёбрами, f гранями и c ячейками. Получаем (5-мерную) призму с 2v вершинами, 2e+v{\displaystyle 2e+v} рёбрами, 2f+e{\displaystyle 2f+e} (2-мерными) гранями, 2c+f{\displaystyle 2c+f} ячейками и 2+c{\displaystyle 2+c} гиперячейками.
Однородные призматические многогранники
Правильный n-многогранник, представленный символом Шлефли {p, q, …, t}, может образовать однородный призматический многогранник размерности (n + 1), представленный прямым произведением двух символов Шлефли: {p, q, …, t}×{}.
По размерностям:
- Призма из 0-мерного многогранника — это отрезок, представленный пустым символом Шлефли {}.
- Призма из 1-мерного многогранника — это прямоугольник, полученный из двух отрезков. Эта призма представляется как произведение символов Шлефли {}×{}. Если призма является квадратом, запись можно сократить: {}×{} = {4}.
Пример: Квадрат, {}×{}, два параллельных отрезка, соединённые двумя другими отрезками, сторонами.
-
многоугольная призма — это 3-мерная призма, полученная из двух многоугольников (один получен параллельным переносом другого), которые связаны прямоугольниками. Из правильного многоугольника {p} можно получить однородную n-угольную призму, представленную произведением {p}×{}. Если p = 4, призма становится кубом: {4}×{} = {4, 3}.
Пример: Пятиугольная призма, {5}×{}, два параллельных пятиугольника связаны пятью прямоугольными сторонами.
- 4-мерная призма, полученная из двух многогранников (один получен параллельным переносом другого), со связывающими 3-мерными призматическими ячейками. Из правильного многогранника {p, q} можно получить однородную 4-мерную призму, представленную произведением {p, q}×{}. Если многогранник является кубом и стороны призмы тоже кубы, призма превращается в тессеракт: {4, 3}×{} = {4, 3, 3}.
Пример: додекаэдральная призма, {5, 3}×{}, два параллельных додекаэдра, соединённых 12 пятиугольными призмами (сторонами).
- …
Призматические многогранники более высоких размерностей также существуют как прямые произведения двух любых многогранников. Размерность призматического многогранника равна произведению размерностей элементов произведения. Первый пример такого произведения существует в 4-мерном пространстве и называется дуопризмами, которые получаются произведением двух многоугольников. Правильные дуопризмы представляются символом {p}×{q}.
| Многоугольник | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Мозаика | ||||||||||||
| Конфигурация | 3.4.4 | 4.4.4 | 5.4.4 | 6.4.4 | 7.4.4 | 8.4.4 | 9.4.4 | 10.4.4 | 11.4.4 | 12.4.4 | 17.4.4 | ∞.4.4 |