Конусность и уклон: построение, расчет, обозначение

От ровного листа до круглой обечайки:

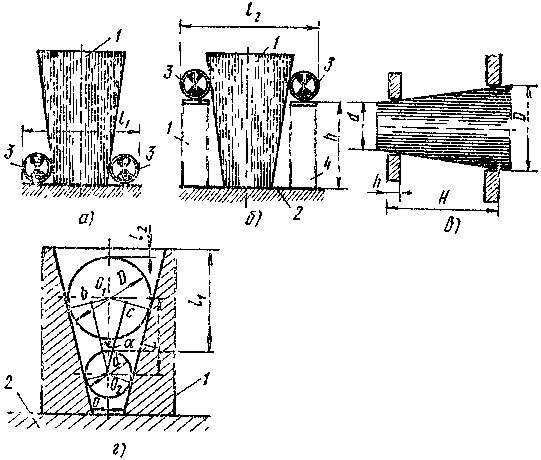
Вальцы с асимметричным расположением валков (рис.11) производят практически полную гибку обечайки. Наиболее современными являются четырехвалковые машины (рис.12), на которых за один цикл осуществляется вальцовка и подгибка краев. Радиус гибки обечаек проверяют шаблонами. Возможные дефекты вальцовки цилиндрических обечаек приведены на рис.14.

Также способы получения нужной формы бывают разные.

Гибка конических обечаек производится несколькими способами:

1) Установкой под углом среднего валка у симметричных трехвалковых машин и бокового валка у асимметричных трехвалковых и четырехвалковых вальцев (рис.15). 2) Гибкой по средней линии последовательно по различным участкам (рис.16) на вальцах. Сначала осуществляют подгибку кромок, затем гнут середину заготовки на каждом участке с переустановками. Такой способ приводит к повышенному износу оборудования. 3) Гибка обечаек на вальцах со сменными коническими валками. Этот способ оправдан в серийном и массовом производстве. 4) Безвальцевым способом для листа толщиной до 20 мм. На рис. 17 показан метод свертывания. Кромки 3 и 4 заготовки закрепляют в опорах 2 и 5, сводят друг к другу, одновременно поворачивают опоры в разных направлениях. Далее кромки конической обечайки соединяют на прихватках и снимают со станка. 5) Наиболее производительным способом является изготовление конических обечаек в штампах (рис.18). Перед сваркой частей обечаек производят их предварительную фиксацию для исключения деформации элементов и обеспечения сварочных зазоров. Совмещение кромок обычно производится струбцинами и сборочными кольцами для тонкого листа (рис.19). На одну обечайку устанавливается две струбцины по торцам. Цилиндричность обечаек обеспечивается специальными приспособлениями с домкратами, распирающими деталь. При сборке габаритных деталей используются стяжные планки и клиновые соединения (рис.20).

Типы конусов

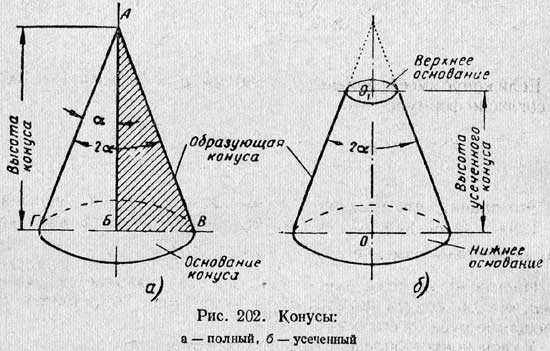
• Прямой конус — конус, основание которого имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром; при этом прямая, соединяющая вершину и центр основания, называется осью конуса.
• Косой (или наклонный) конус — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
• Круговой конус — конус, основание которого является кругом.
• Конус вращения, или прямой круговой конус (часто под конусом подразумевают именно его) — конус, который можно получить вращением (то есть тело вращения) прямоугольного треугольника вокруг прямой, содержащей катет треугольника (эта прямая является осью конуса).
• Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом: последние два имеют бесконечный объём.
• Усечённый конус или конический слой — часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием.
• Равносторонний конус — конус вращения, образующая которого равна диаметру основания.

Как сделать дымник – защиту для трубы?

Чтобы в дымовую трубу не попадали осадки, чтобы она не разрушалась льдом, её нужно защитить дымником. Мастера-жестянщики могут изготовить дымник на трубу самых причудливых форм, иногда на дымник устанавливают флюгер, указывающий направление ветра. Но сделать дымник простой конструкции на дымоходную трубу из металла или кирпича можно и своими руками.

Монтаж дымников

С давних времен дымники защищали дымоходы домов, не потеряли они своей актуальности и в наши дни. Если дровяные печи в домах сегодня редкость, то почти в каждом загородном доме есть камин, вытяжную трубу которого необходимо оградить от попадания в неё атмосферных осадков, птиц, осенней листвы и других посторонних предметов.

Нуждаются в такой же защите и все остальные трубы, выходящие на крышу: вентиляционные и дымовые трубы газовых отопительных приборов. Кроме защитной и декоративной функции, дымники способны выполнять ещё одну: они улучшают циркуляцию горячего воздуха в каминах и печах. Разберемся, как сделать дымник на трубу своими руками.

Виды дымников

Дымники могут отличаться друг от друга формой крыши, материалом изготовления, наличием дополнительных конструктивных элементов. Поэтому, прежде чем приступить к выполнению работ своими руками, стоит познакомиться с их разновидностями.

Формы крыши дымников

Достаточно внимательно посмотреть на крыши домов в какой-нибудь деревне или загородном поселке, чтобы убедиться в том, что человеческая фантазия неистощима на разные выдумки. Дымовые трубы украшают дымники самых разных форм, а некоторые умельцы приспосабливают вместо них дырявые чугунки, чайники, ведра и даже молочные фляги.

Если же вы хотите сделать настоящий красивый дымник своими руками, вам будет интересно узнать о том, какую форму ему можно придать. Различают следующие формы крыш дымников:

• Шатровая.
• Сводчатая (полуцилиндрическая).
• Двускатная.
• Четырехскатная (вальмовая).
• Четырехщипцовая.
• Шпилеобразная.
• Плоская и т. д.

На фотографиях ниже вы можете увидеть некоторые из перечисленных вариантов.

Дымник с вальмовой крышей

Дымник с четырехщипцовой крышей

Материалами для изготовления дымников чаще всего служат оцинкованная или нержавеющая сталь, листовая медь. Они могут иметь полимерное покрытие различных оттенков для защиты от коррозии.

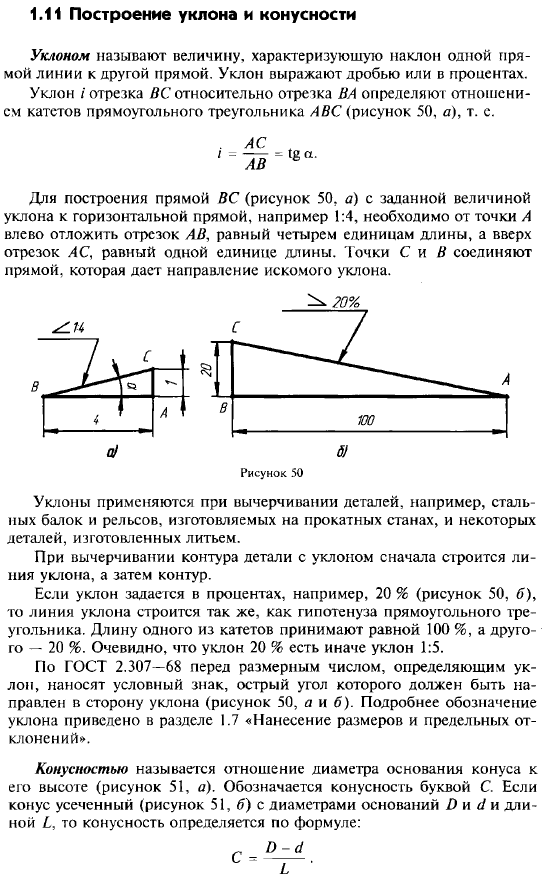
Развёртка

Развёртка прямого кругового конуса

Прямой круговой конус как тело вращения образован прямоугольным треугольником, вращающимся вокруг одного из катетов, где h — высота конуса от центра основания до вершины — является катетом прямоугольного треугольника, вокруг которого происходит вращение. Второй катет прямоугольного треугольника r — радиус в основании конуса. Гипотенузой прямоугольного треугольника является l — образующая конуса.

В создании развёртки конуса могут использоваться всего две величины r и l. Радиус основания r определяет в развертке круг основания конуса, а сектор боковой поверхности конуса определяет образующая боковой поверхности l, являющаяся радиусом сектора боковой поверхности. Угол сектора φ{\displaystyle \varphi } в развёртке боковой поверхности конуса определяется по формуле:

φ = 360°·(r/l).

Свойства

V=13SH,{\displaystyle V={1 \over 3}SH,}

где S — площадь основания, H — высота. Таким образом, все конусы, опирающиеся на данное основание (конечной площади) и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.

• Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от основания.
• Телесный угол при вершине прямого кругового конуса равен

2π(1−cos⁡α2),{\displaystyle 2\pi \left(1-\cos {\alpha \over 2}\right),}

где α — угол раствора конуса.

Площадь боковой поверхности прямого кругового конуса равна

S=πRt,{\displaystyle S=\pi Rt,}

а в общем случае

S=tl2,{\displaystyle S={\frac {tl}{2}},}

где R — радиус основания, t=R2+H2{\displaystyle t={\sqrt {R^{2}+H^{2}}}} — длина образующей, l{\displaystyle l} — длина границы основания.

Полная площадь поверхности (то есть сумма площадей боковой поверхности и основания) равна

S=πR(t+R),{\displaystyle S=\pi R(t+R),}

для прямого кругового конуса и

S=tl2+S,{\displaystyle S={\frac {tl}{2}}+S,}

для произвольного, где S{\displaystyle S} — площадь основания.

Объём кругового (не обязательно прямого) конуса равен

V=13πR2H.{\displaystyle V={1 \over 3}\pi R^{2}H.}

Для усечённого кругового конуса (не обязательно прямого) объём равен:

V=13πH(R2+Rr+r2),{\displaystyle V={1 \over 3}\pi H(R^{2}+Rr+r^{2}),}

где R{\displaystyle R} и r{\displaystyle r}  — радиусы соответственно нижнего и верхнего оснований, H{\displaystyle H} — высота от плоскости нижнего основания,до верхнего основания.

Для произвольного усечённого конуса (не обязательно прямого и кругового) объём равен:

V=13(H2S2−H1S1),{\displaystyle V={1 \over 3}(H_{2}S_{2}-H_{1}S_{1}),}

где S1{\displaystyle S_{1}} и S2{\displaystyle S_{2}}  — площади соответственно верхнего (ближнего к вершине) и нижнего оснований, H1{\displaystyle H_{1}} и H2{\displaystyle H_{2}}  — расстояния от плоскости соответственно верхнего и нижнего основания до вершины.

Пересечение плоскости с прямым круговым конусом является одним из конических сечений (в невырожденных случаях — эллипсом, параболой или гиперболой, в зависимости от положения секущей плоскости).

Свойства

V=13SH,{\displaystyle V={1 \over 3}SH,}

где S — площадь основания, H — высота. Таким образом, все конусы, опирающиеся на данное основание (конечной площади) и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.

• Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от основания.
• Телесный угол при вершине прямого кругового конуса равен

2π(1−cos⁡α2),{\displaystyle 2\pi \left(1-\cos {\alpha \over 2}\right),}

где α — угол раствора конуса.

Площадь боковой поверхности прямого кругового конуса равна

S=πRt,{\displaystyle S=\pi Rt,}

а в общем случае

S=tl2,{\displaystyle S={\frac {tl}{2}},}

где R — радиус основания, t=R2+H2{\displaystyle t={\sqrt {R^{2}+H^{2}}}} — длина образующей, l{\displaystyle l} — длина границы основания.

Полная площадь поверхности (то есть сумма площадей боковой поверхности и основания) равна

S=πR(t+R),{\displaystyle S=\pi R(t+R),}

для прямого кругового конуса и

S=tl2+S,{\displaystyle S={\frac {tl}{2}}+S,}

для произвольного, где S{\displaystyle S} — площадь основания.

Объём кругового (не обязательно прямого) конуса равен

V=13πR2H.{\displaystyle V={1 \over 3}\pi R^{2}H.}

Для усечённого кругового конуса (не обязательно прямого) объём равен:

V=13πH(R2+Rr+r2),{\displaystyle V={1 \over 3}\pi H(R^{2}+Rr+r^{2}),}

где R{\displaystyle R} и r{\displaystyle r}  — радиусы соответственно нижнего и верхнего оснований, H{\displaystyle H} — высота от плоскости нижнего основания,до верхнего основания.

Для произвольного усечённого конуса (не обязательно прямого и кругового) объём равен:

V=13(H2S2−H1S1),{\displaystyle V={1 \over 3}(H_{2}S_{2}-H_{1}S_{1}),}

где S1{\displaystyle S_{1}} и S2{\displaystyle S_{2}}  — площади соответственно верхнего (ближнего к вершине) и нижнего оснований, H1{\displaystyle H_{1}} и H2{\displaystyle H_{2}}  — расстояния от плоскости соответственно верхнего и нижнего основания до вершины.

Пересечение плоскости с прямым круговым конусом является одним из конических сечений (в невырожденных случаях — эллипсом, параболой или гиперболой, в зависимости от положения секущей плоскости).

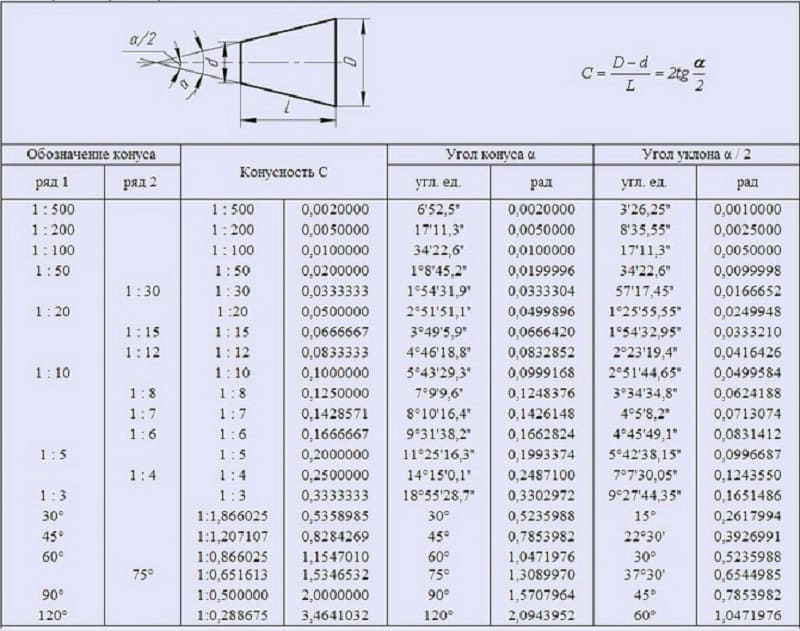
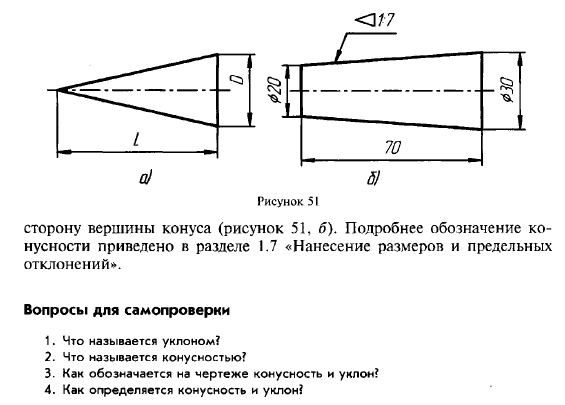
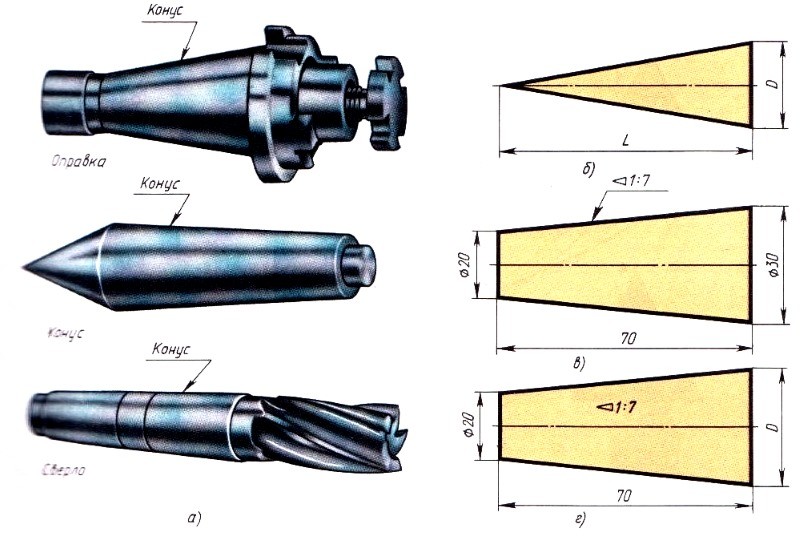
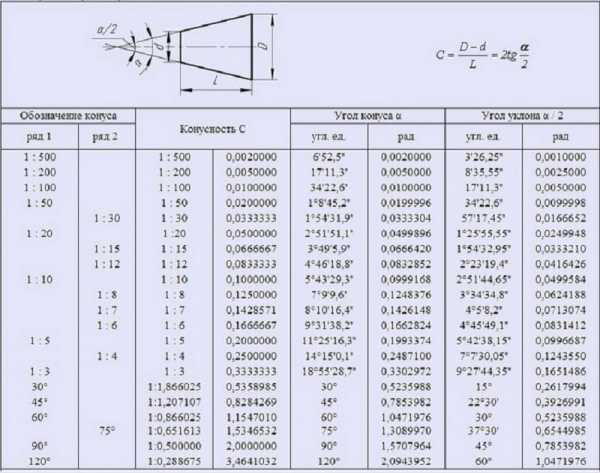
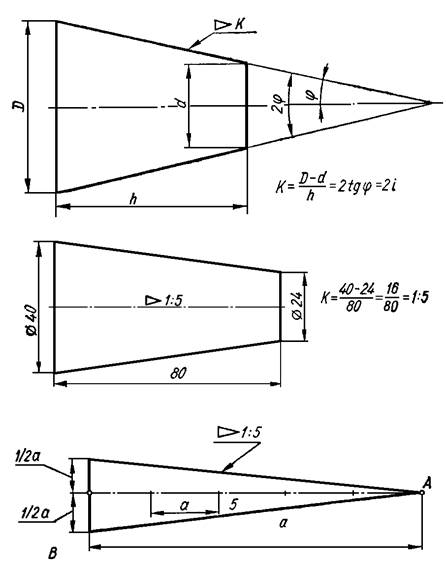
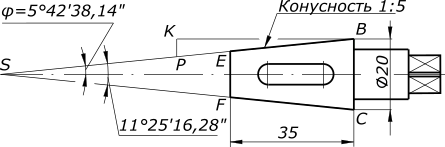
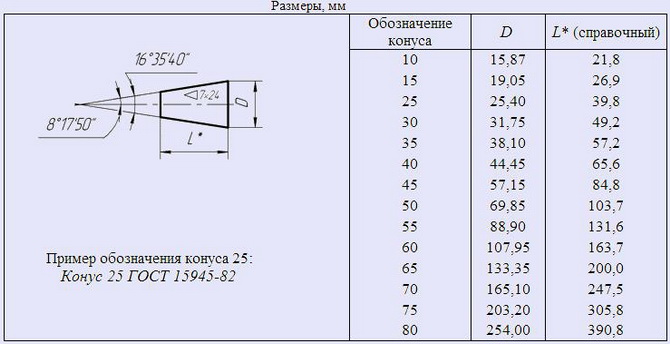
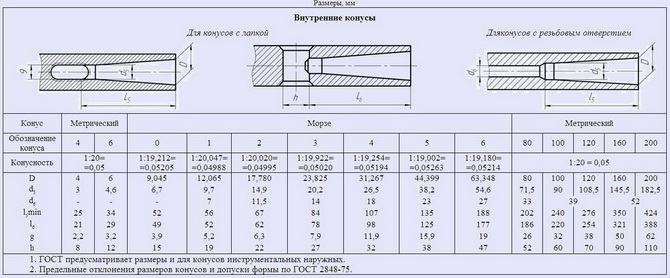
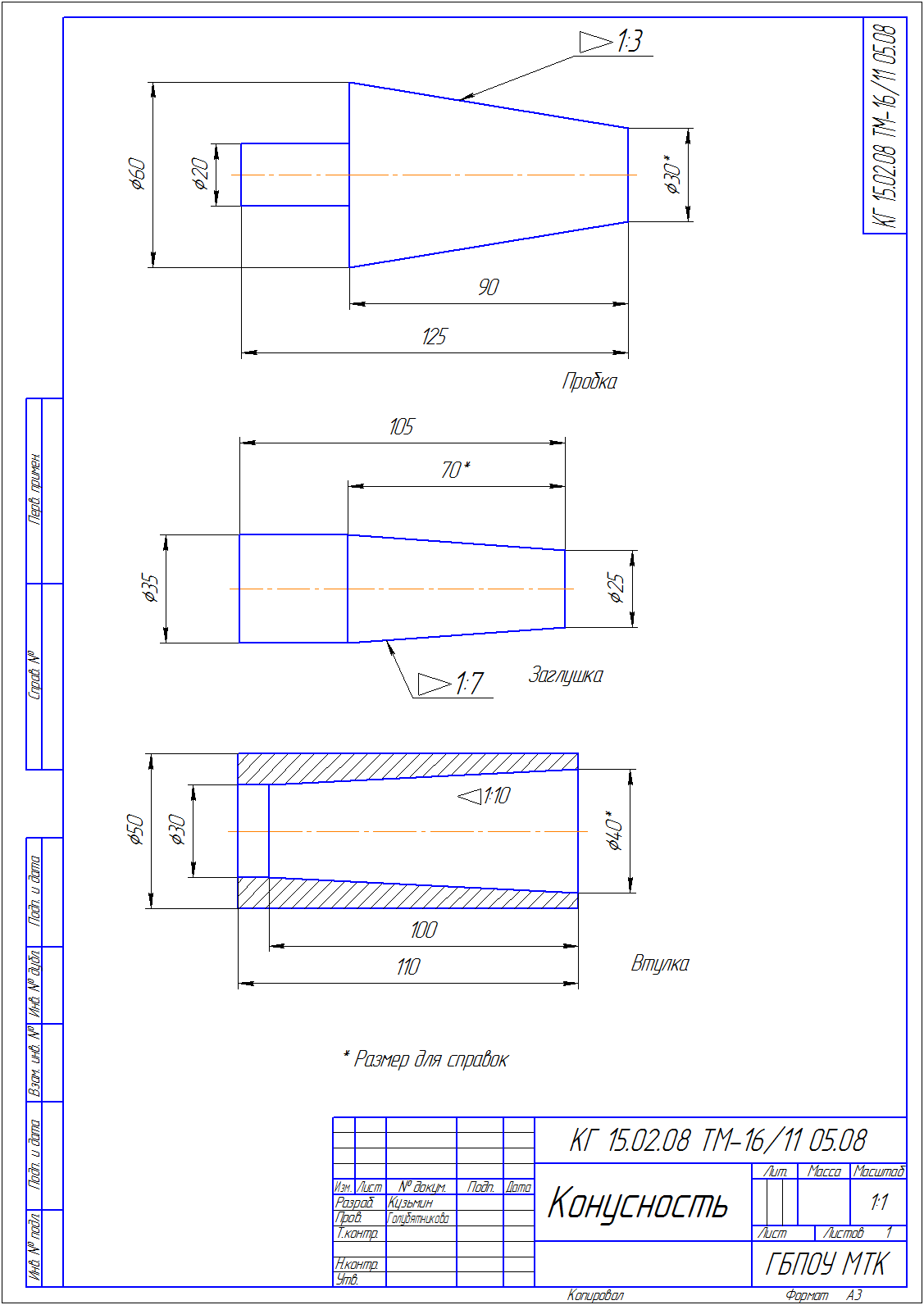
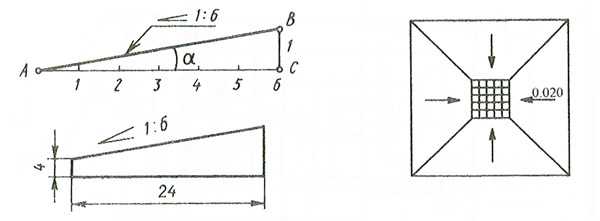
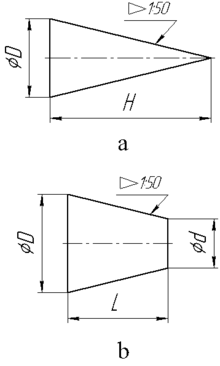
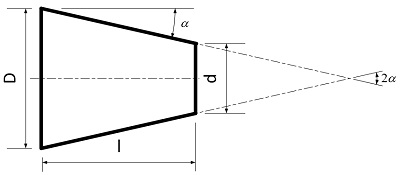
Обозначение конусности на чертеже

При создании технической документации должны учитываться все установленные стандарты, так как в противном случае она не может быть использована в дальнейшем

Рассматривая обозначение конусности на чертежах следует уделить внимание следующим моментам:

1. Отображается диаметр большого основания. Рассматриваемая фигура образуется телом вращения, которому свойственен диаметральный показатель. В случае конуса их может быть несколько, а изменение показателя происходит плавно, не ступенчато. Как правило, у подобной фигуры есть больший диаметр, а также промежуточной в случае наличия ступени.
2. Наносится диаметр меньшего основания. Меньшее основание отвечает за образование требуемого угла.
3. Рассчитывается длина конуса. Расстояние между меньшим и большим основанием является показателем длины.
4. На основании построенного изображения определяется угол. Как правило, для этого проводятся соответствующие расчеты. В случае определения размера по нанесенному изображению при применении специального измерительного прибора существенно снижается точность. Второй метод применяется в случае создания чертежа для производства неответственных деталей.

Простейшее обозначение конусности предусматривает также отображения дополнительных размеров, к примеру, справочную. В некоторых случаях применяется знак конусности, который позволяет сразу понят о разности диаметров.

Выделяют достаточно большое количество различных стандартов, которые касаются обозначения конусности. К особенностям отнесем следующее:

1. Угол может указываться в градусах дробью или в процентах. Выбор проводится в зависимости от области применения чертежа. Примером можно назвать то, что в машиностроительной области указывается значение градуса.
2. В машиностроительной области в особую группу выделяют понятие нормальной конусности. Она варьирует в определенном диапазоне, может составлять 30, 45, 60, 75, 90, 120°. Подобные показатели свойственны большинству изделий, которые применяются при сборке различных механизмов. При этом выдержать подобные значения намного проще при применении токарного оборудования. Однако, при необходимости могут выдерживаться и неточные углы, все зависит от конкретного случая.
3. При начертании основных размеров применяется чертежный шрифт. Он характеризуется довольно большим количеством особенностей, которые должны учитываться. Для правильного отображения используется табличная информация.
4. Для начала указывается значок конусности от которого отводится стрелка и отображается величина. Особенности отображения во многом зависит от того, какой чертеж. В некоторых случаях наносится большое количество различных размеров, что существенно усложняет нанесение конусности. Именно поэтому предусмотрена возможность использования нескольких различных методов отображения подобной информации.

На чертеже рассматриваемый показатель обозначается в виде треугольника. При этом требуется цифровое значение, которое может рассчитываться при применении различных формул.

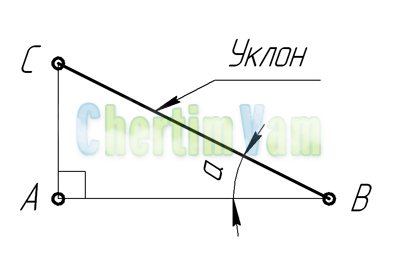
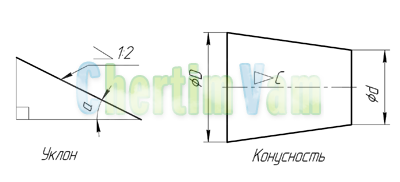
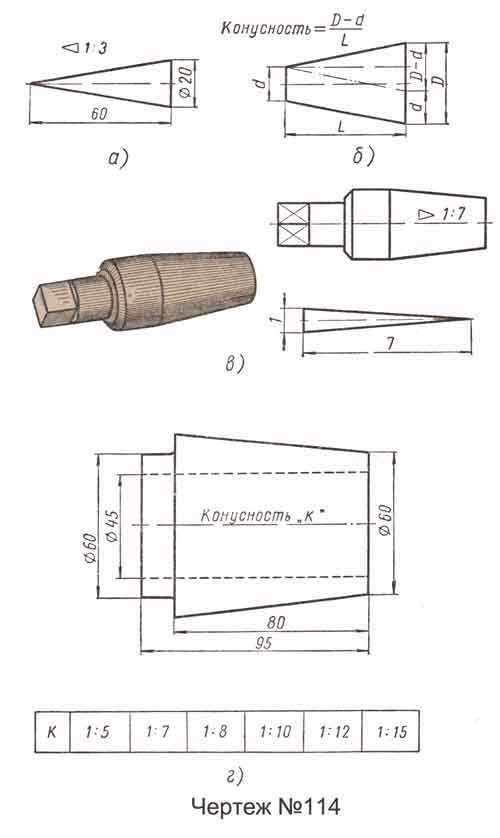
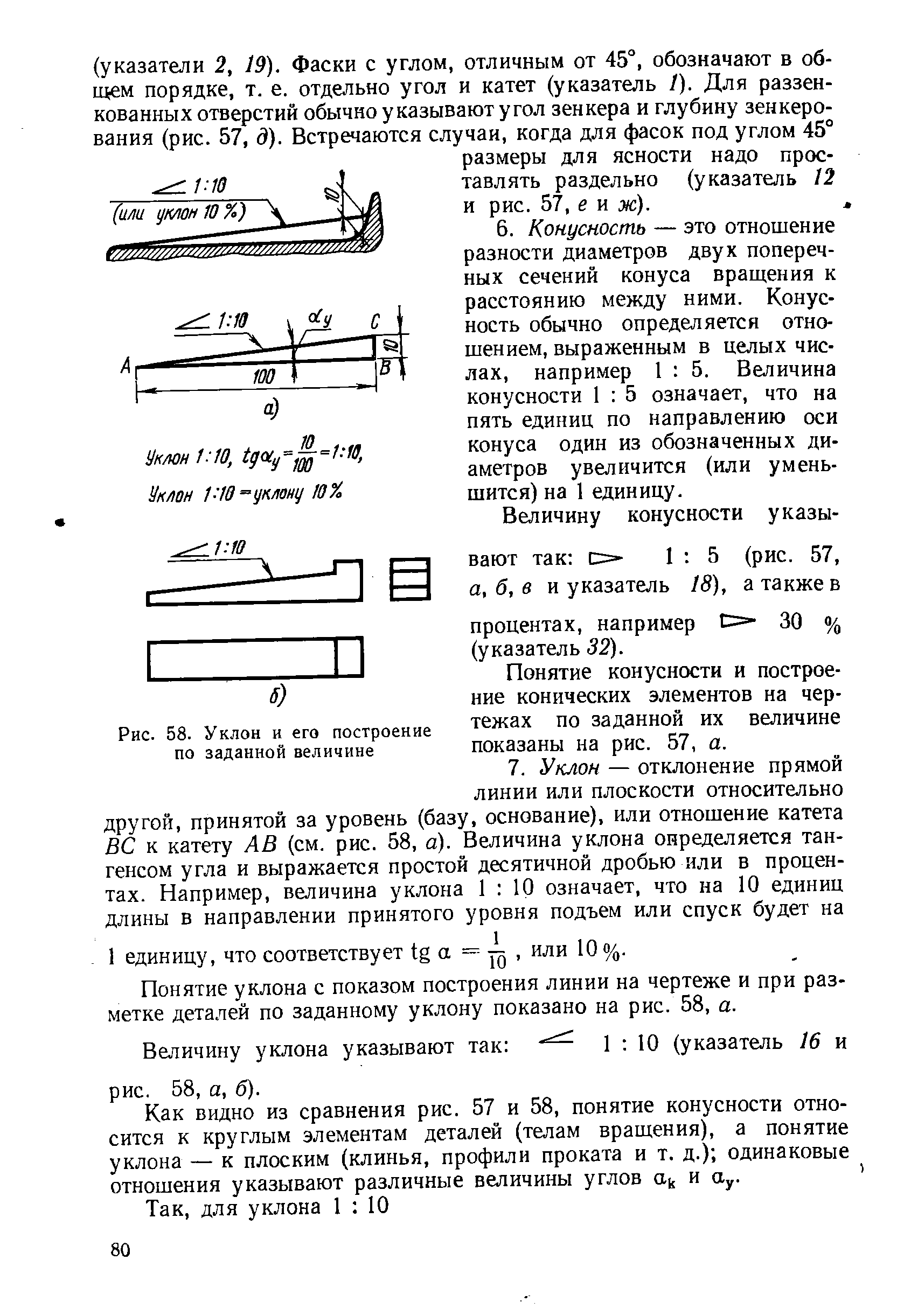
Значение конусности

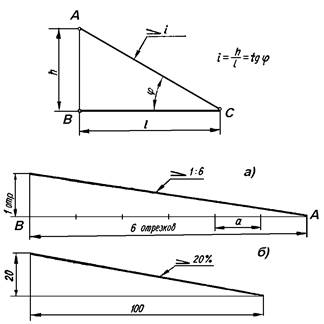
Рассматривая конусность следует учитывать, что этот показатель напрямую связан с уклоном. Этот параметр определяет отклонение прямой лини от вертикального ил горизонтального положения. При этом конусность 1:3 или конусность 1:16 существенно отличается. Определение уклона характеризуется следующими особенностями:

1. Под уклоном подразумевается отношение противолежащего катета прямоугольного треугольника к прилежащему. Этот параметр еще называют тангенс угла.
2. Для расчета примеряется следующая формула: i=AC/AB=tga.

Рассчитать этот показатель можно самым различным образом, наибольшее распространение получила формула K=D/h. В некоторых случаях обозначение проводится в процентах, так как этот переменный показатель применяется для определения всех других параметров.

Рассматривая конусность 1:7 и другой показатель следует также учитывать особенности отображения информации на чертеже. Чаще всего подобное отображение проводится при создании технической документации в машиностроительной области.

Презентация на тему: » Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус.» — Транскрипт:

1

Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус

2

Понятие конуса Рассмотрим окружность L с центром О и прямую ОР, перпендикулярную к плоскости этой поверхности. Через точку Р и каждую точку окружности проведём прямую. Поверхность, образованная этими прямыми, называется конической поверхностью, а сами прямые – образующими конической поверхности. L О Р

3

Точка Р называется вершиной, а прямая ОР – осью конической поверхности. Понятие конуса L О Р вершина ось конической поверхности

4

Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Конус О L

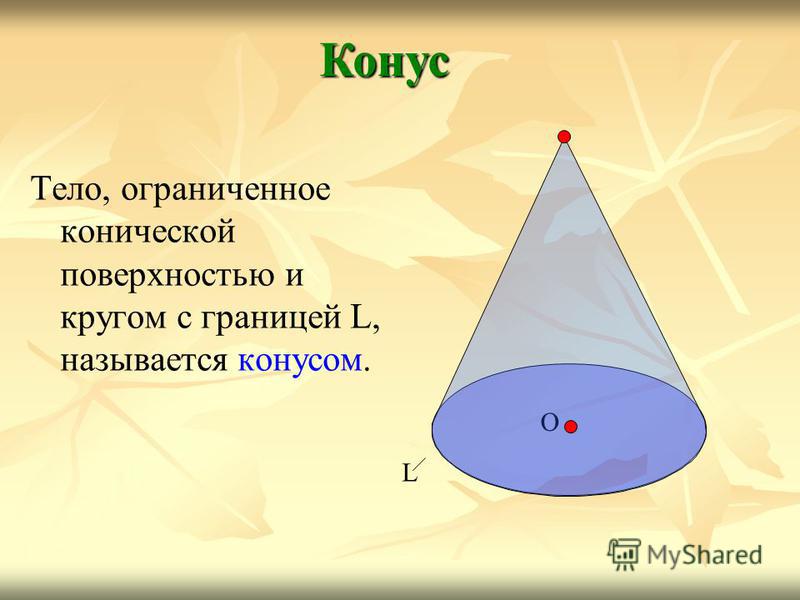
5

Круг называется основанием конуса, вершина конической поверхности – вершиной конуса, отрезки образующих, заключённые между вершиной и основанием, — образующими конуса, а образованная ими часть конической поверхности – боковой поверхностью конуса. Конус О L

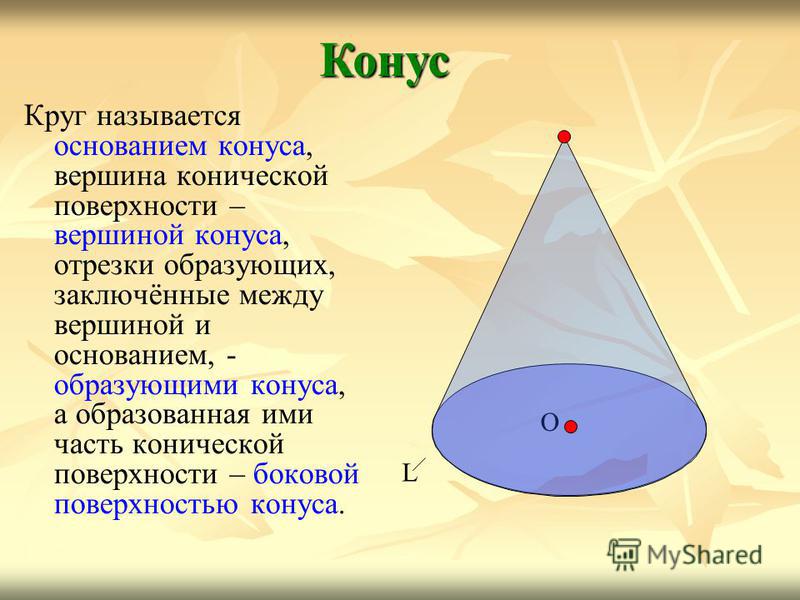
6

Конус О L Р ось конуса вершина конуса образующие конуса боковая поверхность конуса основание конуса

7

Ось конической поверхности называется осью конуса, а её отрезок, заключённый между вершиной и основанием, — высотой конуса.Конус О L Р ось конуса высота конуса

8

Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов. Получение конуса

9

Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Это сечение называется осевым. Сечение конуса О Р

10

Если секущая плоскость перпендикулярна к оси ОР конуса, то сечение конуса представляет собой круг с центром О 1, расположенным на оси конуса. Радиус r 1 этого круга равен, где r – радиус основания конуса. Сечение конуса Р О М r О1О1 М1М1 r1r1

11

Проводя различные сечения одного и того же кругового конуса, причём любого, можно получить эллипс, параболу и гиперболу. При надлежащем наклоне секущей плоскости удаётся получить все типы конических сечений. Если считать, что конус не заканчивается в вершине, а простирается за неё, тогда у некоторых сечений образуются две ветви. Сечение конуса

12

За площадь боковой поверхности конуса принимается площадь её развёртки. Площадь боковой поверхности конуса Развёртка боковой поверхности конуса: А В Р А L А В Р L r

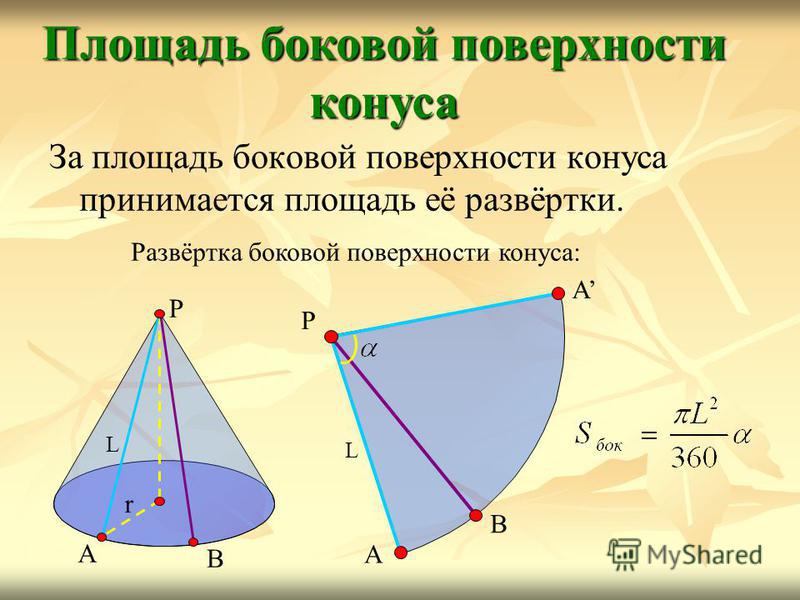
13

Выразим через L и r. Так как длина дуги АВА равна, то, откуда Площадь боковой поверхности конуса А В Р А L Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

14

Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Площадь полной поверхности конуса А В Р L r S кон = r 2 + rL S кон = r(r + L)

15

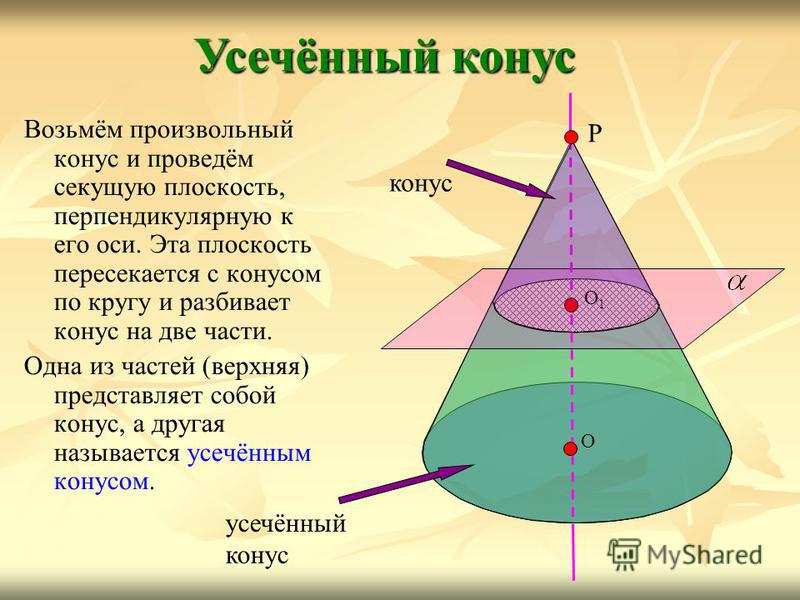
Возьмём произвольный конус и проведём секущую плоскость, перпендикулярную к его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей (верхняя) представляет собой конус, а другая называется усечённым конусом. Усечённый конус Р О О1О1 конус усечённый конус

16

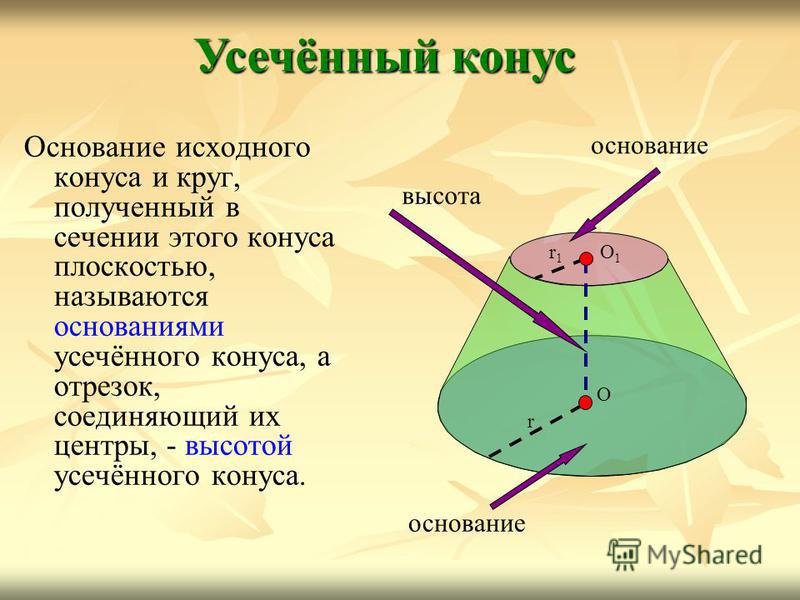
Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усечённого конуса, а отрезок, соединяющий их центры, — высотой усечённого конуса. Усечённый конус О1О1 r1r1 r О основание высота

17

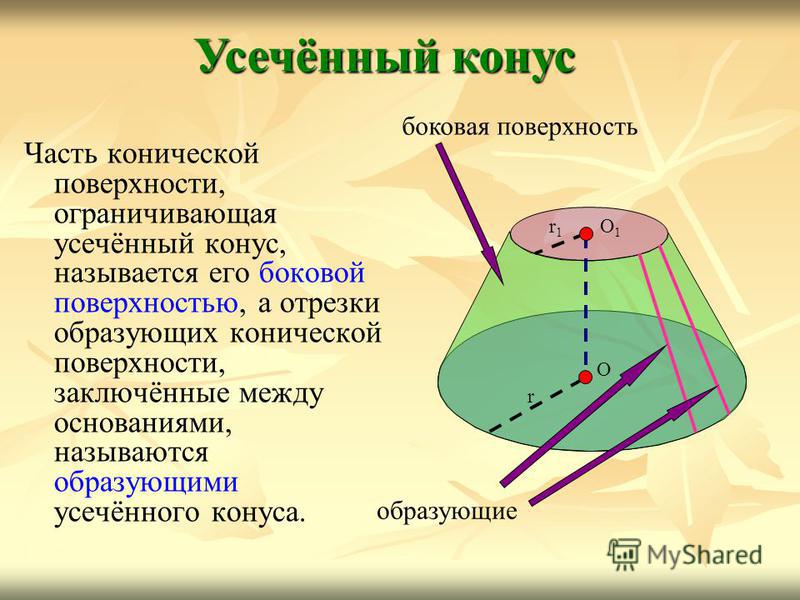
Часть конической поверхности, ограничивающая усечённый конус, называется его боковой поверхностью, а отрезки образующих конической поверхности, заключённые между основаниями, называются образующими усечённого конуса. Усечённый конус О1О1 r1r1 r О боковая поверхность образующие

18

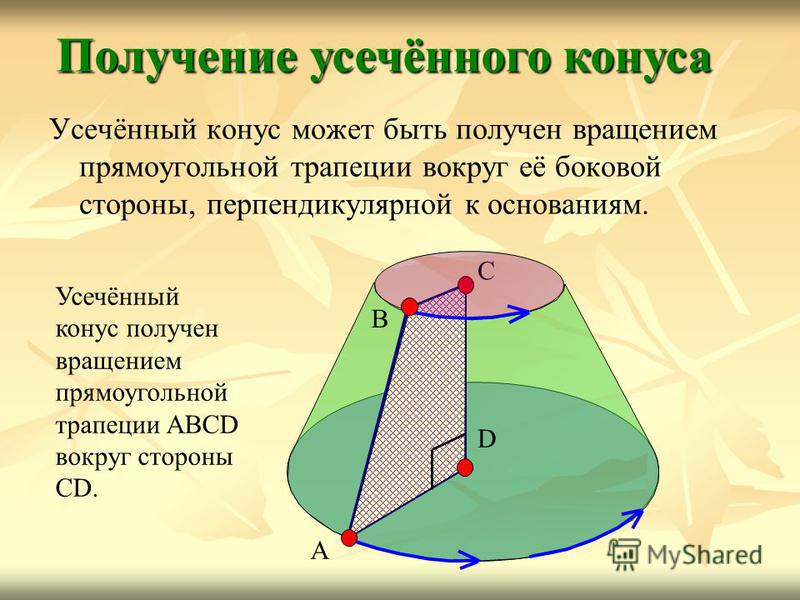
Усечённый конус может быть получен вращением прямоугольной трапеции вокруг её боковой стороны, перпендикулярной к основаниям. Получение усечённого конуса A B C D Усечённый конус получен вращением прямоугольной трапеции ABCD вокруг стороны CD.

19

Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую: где r и r 1 – радиусы оснований, L – образующая усечённого конуса. Площадь боковой поверхности усечённого конуса О1О1 r1r1 r О L

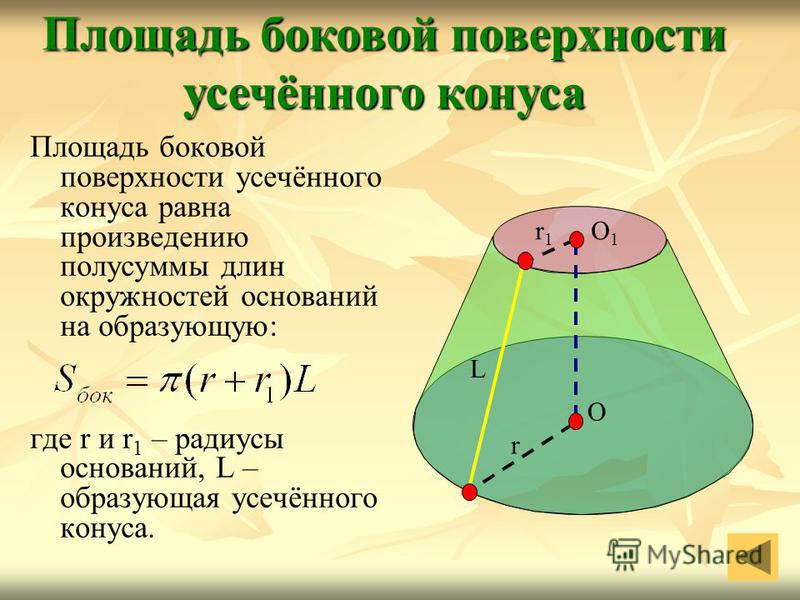
Развертка наклонного конуса

Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).

Алгоритм

1. Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
2. Определяем натуральные величины ребер пирамиды, используя вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S.
   Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’₁ занимает положение, при котором она параллельна фронтальной плоскости π₂. Соответственно, S’’5’’₁ – натуральная величина S5.
3. Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S16, S65, S54, S43, S32, S21. Построение каждого треугольника выполняется по трем сторонам. Например, у △S16 длина S1=S’’1’’, S6=S’’6’’₁, 16=1’6’.

Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.

Перенос линии с поверхности конуса на развертку

Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.

Алгоритм

1. Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
2. Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’₁, SC=S’’C’’₁.
3. Находим положение точек A, B, C на соответствующих им ребрах пирамиды, откладывая на развертке отрезки SA=S’’A’’, SB=S’’B’’₁, SC=S’’C’’₁.
4. Соединяем точки A, B, Cплавной линией.

Калькуляторы расчета размеров развертки конуса

Несколько слов о рассчитываемых параметрах

Понять принцип расчета будет несложно, разобравшись со следующей схемой:

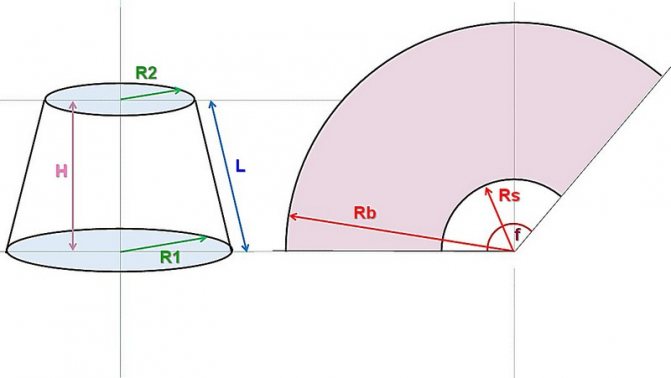
Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты и построение становятся даже проще.

Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.

Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.

Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L

Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.

Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:

Задача на определение площади и объема усеченного конуса

Ниже на рисунке изображен усеченный конус и приведены его линейные параметры. Необходимой найти площадь поверхности и объем фигуры.

Начнем решать задачу с определения величины V. Ее вычисление не представляет никакого труда, поскольку известны все необходимые параметры. Подставляя их в формулу для V, получаем:

Найденное значение соответствует 0,76 литра.

Чтобы найти площадь поверхности S, следует сначала вычислить длину образующей g фигуры. Она будет равна:

Значение образующей g мы округлили до сотых. Теперь можно воспользоваться формулой для площади S:

Заметим, что формулы для V и S, которые мы использовали при решении задачи, справедливы только для круглого прямого усеченного конуса. В случае наклонной фигуры или же фигуры с некруглыми основаниями этими формулами пользоваться нельзя.

Площади боковой и полной поверхностей усеченного конуса

Рис. 12. Конус с вве­ден­ны­ми обо­зна­че­ни­я­ми

Най­дем пло­щадь бо­ко­вой по­верх­но­сти усе­чен­но­го ко­ну­са. Пусть ос­но­ва­ния усе­чен­но­го ко­ну­са имеют ра­ди­у­сы  и , а об­ра­зу­ю­щая равна  (см. рис. 12).

Рис. 13. Обо­зна­че­ние об­ра­зу­ю­щей от­се­чен­но­го ко­ну­са

Най­дем пло­щадь бо­ко­вой по­верх­но­сти усе­чен­но­го ко­ну­са как раз­ность пло­ща­дей бо­ко­вых по­верх­но­стей ис­ход­но­го ко­ну­са и от­се­чен­но­го. Для этого обо­зна­чим через  об­ра­зу­ю­щую от­се­чен­но­го ко­ну­са (см. рис. 13).

Тогда ис­ко­мая .

Рис. 14. По­доб­ные тре­уголь­ни­ки

Оста­лось вы­ра­зить .

За­ме­тим, что из по­до­бия тре­уголь­ни­ков , от­ку­да  (см. рис. 14).

Можно было бы вы­ра­зить , раз­де­лив на раз­ность ра­ди­у­сов, но нам это не нужно, ведь в ис­ко­мом вы­ра­же­нии как раз фи­гу­ри­ру­ет про­из­ве­де­ние . Под­ста­вив вме­сто него , окон­ча­тель­но имеем: .

Неслож­но те­перь по­лу­чить и фор­му­лу для пло­ща­ди пол­ной по­верх­но­сти. Для этого до­ста­точ­но до­ба­вить пло­ща­ди двух кру­гов ос­но­ва­ний: .

Фигура конус усеченный

Он также является фигурой вращения, только вместо прямоугольного треугольника следует вращать прямоугольную трапецию. На рисунке ниже показан усеченный конус.

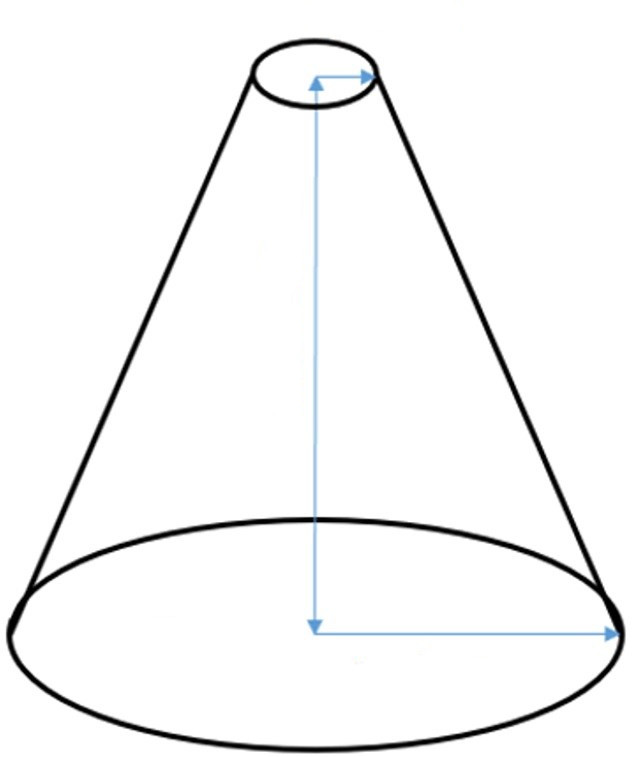
Здесь синие стрелки показывают прямоугольную трапецию. Длина вертикальной стрелки является высотой h фигуры, длины двух других синих стрелок — это радиусы оснований конуса. В отличие от цилиндра, основания усеченного конуса имеют разную площадь. Обозначим их радиусы r₁ и r₂. Четвертая наклонная к основанию сторона трапеции является образующей или генератрисой. Как и для обычного конуса, для усеченного все генератрисы равны друг другу и образуют боковую поверхность фигуры.

Заметим, что усеченный конус получил такое название потому, что его можно получить не только вращением трапеции, но и с помощью отсечения плоскостью верхней части круглого прямого конуса.

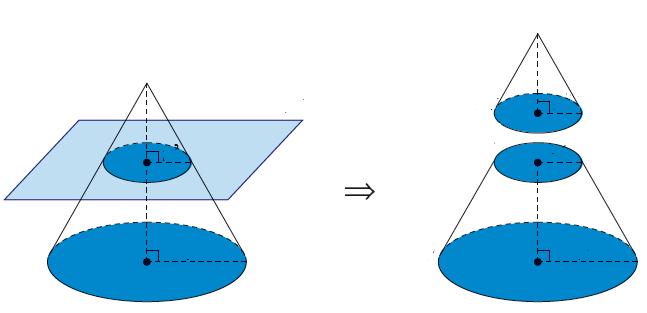
Площадь боковой поверхности усеченного конуса через направляющую и радиусы его оснований

При нахождении площади боковую поверхность усеченного конуса целесообразней рассматривать как разность боковой поверхности конуса и боковой поверхности отсеченного конуса.
Пусть от данного конуса AMB отсекли конус A`MB`. Необходимо вычислить боковую площадь усеченного конуса AA`B`B. Известно, что радиусы его оснований AO=R, A`O`=r, образующая равна L.Обозначим MB` за x. Тогда боковая поверхность конуса A`MB` будет равна πrx. А боковая поверхность конуса AMB будет равна πR(L+x).
Тогда боковую поверхность усеченного конуса AA`B`B можно выразить через разность боковой поверхности конуса AMB и конуса A`MB`:
Треугольники OMB и O`MB`– подобны по равенству углов ∠{MOB} = ∠{MO`B`} и ∠{OMB} = ∠{O`MB`}. Из подобия этих треугольников следует:
Воспользуемся производной пропорции. Имеем:
Отсюда находим x:
Подставив это выражение в формулу площади боковой поверхности, имеем: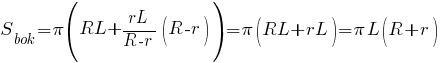
Таким образом, площадь боковой поверхности усеченного конуса равна произведению числа π на его направляющую и сумму радиусов его оснований.
Формула площади боковой поверхности усеченного конуса имеет следующий вид:

Пример расчета площади боковой поверхности усеченного конуса, если известны его радиус и образующая
Радиус большего основания, образующая и высота усеченного конуса равны 7, 5 и 4 см соответственно. Найдите площадь боковой поверхности конуса.
Осевое сечение усеченного конуса представляет собой равнобедренную трапецию, с основаниями 2R и 2r. Образующая усеченного конуса, являющаяся боковой стороной трапеции, высота, опушенная на большое основание и разность радиусов основания усеченного конуса, образуют египетский треугольник. Это прямоугольный треугольник с соотношением сторон 3:4:5. По условию задачи образующая равна 5, а высота – 4, тогда разность радиусов основания усеченного конуса будет равна 3.
Имеем:
L=5
R=7
R=4
Формула площади боковой поверхности усеченного конуса имеет следующий вид:
Подставив значения, имеем:

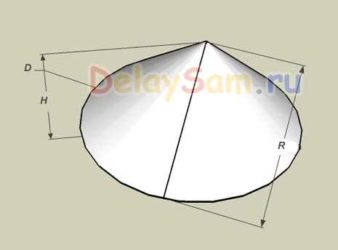
Колпак на дымоход своими руками

Хозяева домов зачастую прибегают к использованию элементов в виде различных колпаков и зонтов, служащих, как это кажется на первый взгляд, для украшения дымовых труб. В то же время такие насадки не только улучшают эстетическое восприятие строения, но и обеспечивают полезную функциональность. Обычно так называемый козырек для дымохода изготавливается собственными силами, так как для этого не требуется серьезных знаний и умений. Хотя наряду с простой конструкцией этих элементов встречаются достаточно замысловатые поделки, которые проблематично соорудить без соответствующего опыта.

Конструктивные особенности

Колпак на дымоход представляет собой устройство, предназначенное для защиты трубы от попадания влаги. Внешний вид таких козырьков может быть различен, что имеет зависимость как от предпочтений хозяина дома, так и от конфигурации трубы.

Колпаки на трубу дымохода включают в себя:

• зонтик – устанавливаемая на вершине колпака защита от осадков, посторонних предметов и проникновения птиц, внешний вид которой имеет форму пирамиды, конуса или соответствует другой геометрии;
• фартук – часть колпака, отвечающая за защиту верха трубы от стекающей с зонтика воды. Обычно установка этого элемента производится при оснащении прямоугольной или квадратной трубы. В результате гарантируется увеличение срока службы дымохода, так как удается практически исключить вероятность появления коррозии и грибка;
• кронштейны – крепежные элементы, представляющие собой металлические полоски, которые позволяют соединить козырек и фартук. Непосредственное крепление в данном случае производится за счет использования сварки.

Имейте в виду! Собрать колпак для дымохода вполне реально самому, но только в том случае, если вы хотите установить достаточно простой флюгарок. Модели, отличающиеся большей сложностью в плане конструктивных особенностей, гораздо выгоднее заказать или купить.

При наличии выбора лучше всего отдать предпочтение тем моделям, которые оборудованы открывающейся крышкой. Это позволит проводить профилактический осмотр дымохода и его чистку без каких-либо проблем, что связано с комфортом доступа.

Колпак на дымоход долгого срока использования может быть изготовлен только из железа, устойчивого к коррозии: оцинкованная сталь, алюминий и медь. В последнем случае предлагаемый металл обладает ярко выраженным декоративным характером, так как его переливы на солнце могут придать вашем дому определенную респектабельность.

Одевают оголовок на трубу дымохода чтобы гасить искры. Это одно из его предназначений. Поэтому качество железа должно быть хорошим, тем самым оно долго не прогорит.

Виды

В связи с тем, что дымоходы отличаются разнообразием форм и размеров, производители колпаков также предлагают широкий ассортимент продукции. Если вы решите украсить свое жилище и продлить срок жизни дымохода, то придется выбирать среди большого ассортимента флюгарок:

1. Стандартные – зонт на дымоход в виде пирамидки, для изготовления которой используется листовой металл, а крепление к фартуку осуществляется посредством кронштейнов.
2. Четырехскатные – устанавливается преимущественно на прямоугольные трубы, выполненные из кирпича. По форме соотносится с вальмовой крышей с четырьмя скатами.
3. С полукруглым зонтиком – визуально отличается красотой, но обеспечивает недостаточную тягу. Преимущественно используется для установки на дымоходах домов, которые построены по европейским стандартам.
4. Плоские – часто можно встретить на зданиях в стиле модерн. Имеет прямоугольную форму и отличается таким недостатком, как повышенная нагрузка на кронштейны, что в некоторых случаях приводит к их деформации. Это связано с плоской крышей колпака, которая не дает возможность скатываться снегу. Данный факт определяет возникновение упомянутой проблемы.
5. Круглые с конусообразным зонтиком – модели без капельника, устанавливаемые на выполненные из нержавейки дымоходы круглого сечения.

Усеченные конусы

      Рассмотрим с   S,     SO,     r   и   h.   Плоскость   β,   и расположенная на  S,   пересекает конус по кругу радиуса   r₁   с центром в точке   O₁   (рис. 2).

Рис.2

      Из   SOA   и   SO₁A₁   можно выразить радиус   r₁   через известные величины   r, h   и   h₁:

      Таким образом, плоскость   β   делит конус на две части: конус с осью   SO₁   и радиусом основания   r₁,   а также вторую часть, называемую усеченным конусом (рис. 3).

Рис.3

      Усеченный конус ограничен двумя основаниями: кругом с центром в точке   O   радиуса   r   на плоскости   α   и кругом с центром в точке   O₁ радиуса   r₁   на плоскости   β,   а также боковой поверхностью усеченного конуса, которая представляет собой часть боковой поверхности исходного конуса, заключенную между плоскостями   α   и   β.   Полная поверхность усеченного конуса состоит из двух оснований усеченного конуса и его боковой поверхности. Часть каждой образующей исходного конуса, которая заключена между плоскостями   α   и   β,   называют образующей усеченного конуса. Например, на рисунке 3 одной из образующих усеченного конуса является отрезок   AA₁.

      Высотой усеченного конуса называют оснований усеченного конуса. У усеченного конуса, изображенного на рисунке 2, высота равна   h – h₁.