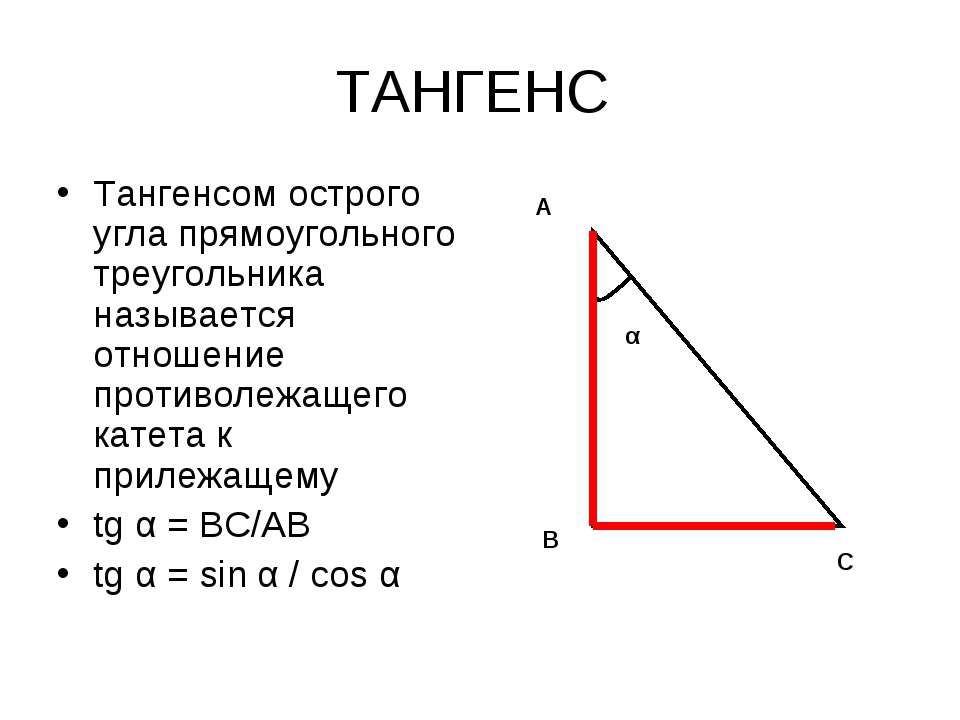
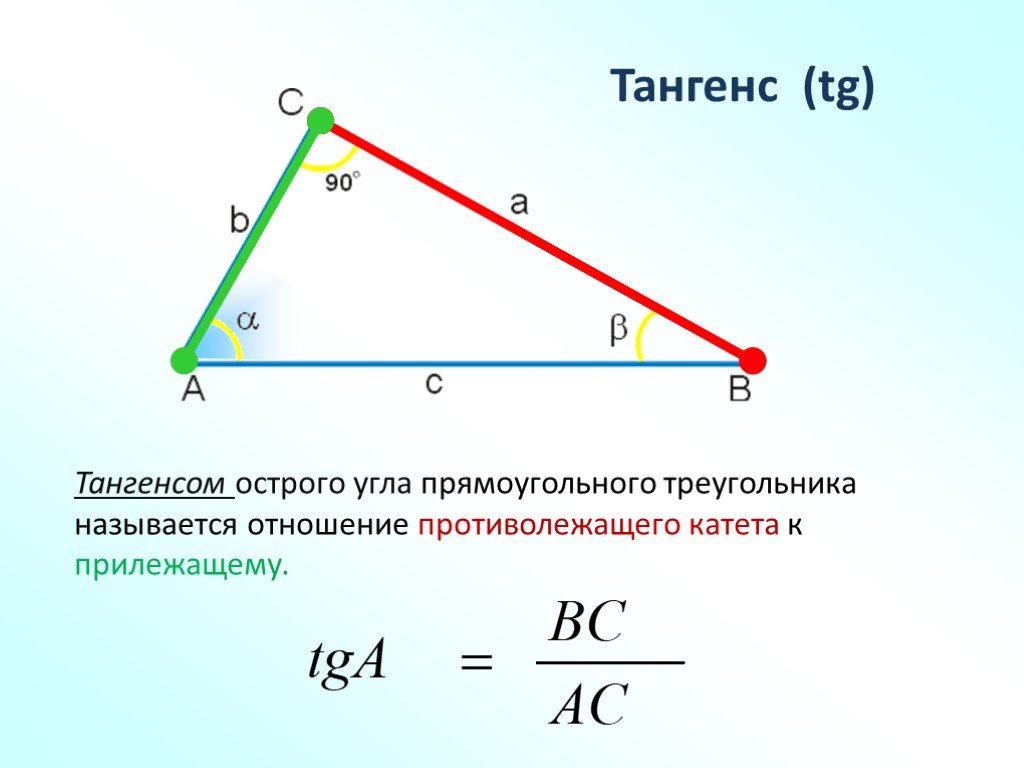
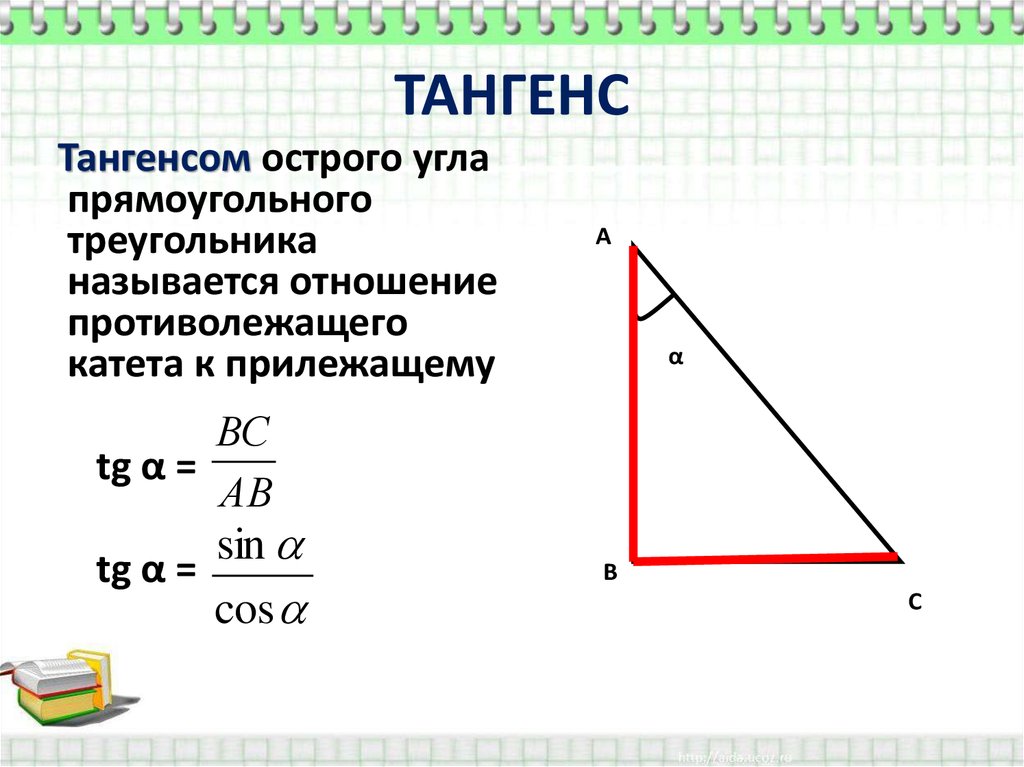
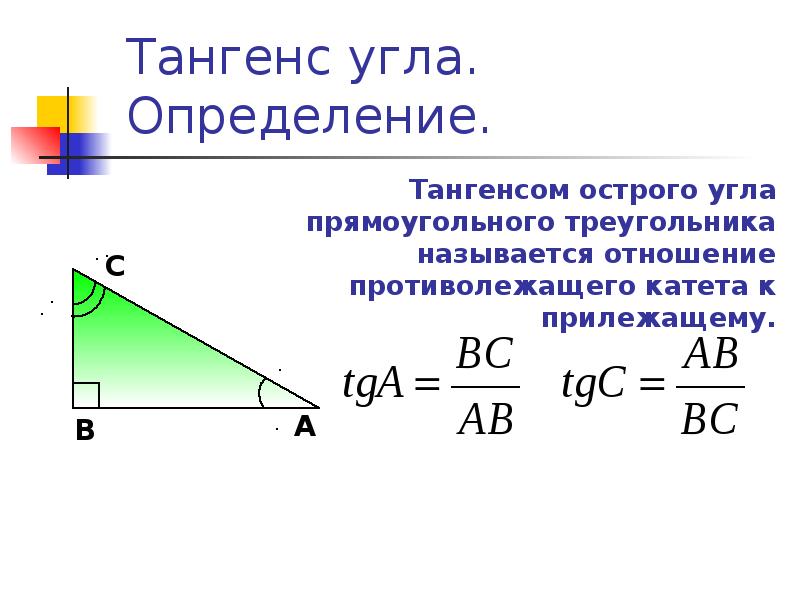
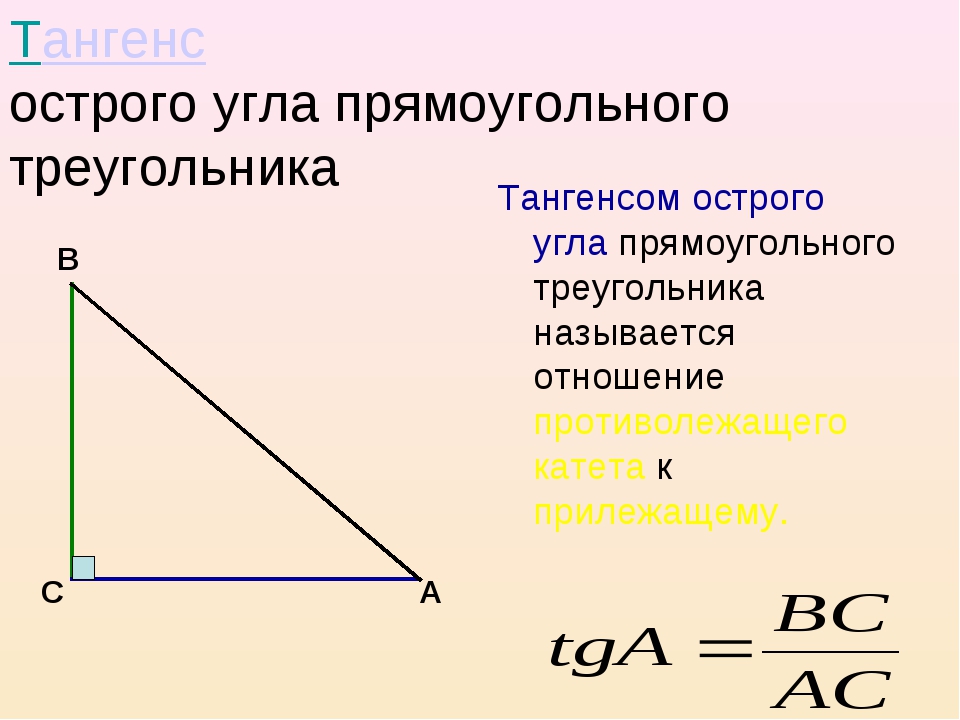
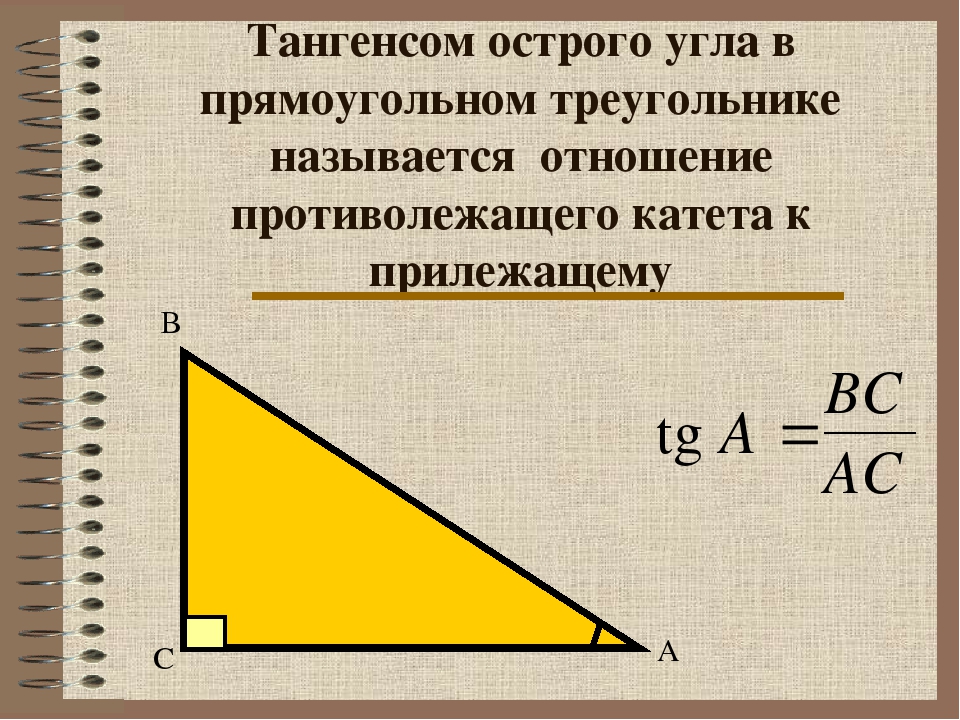
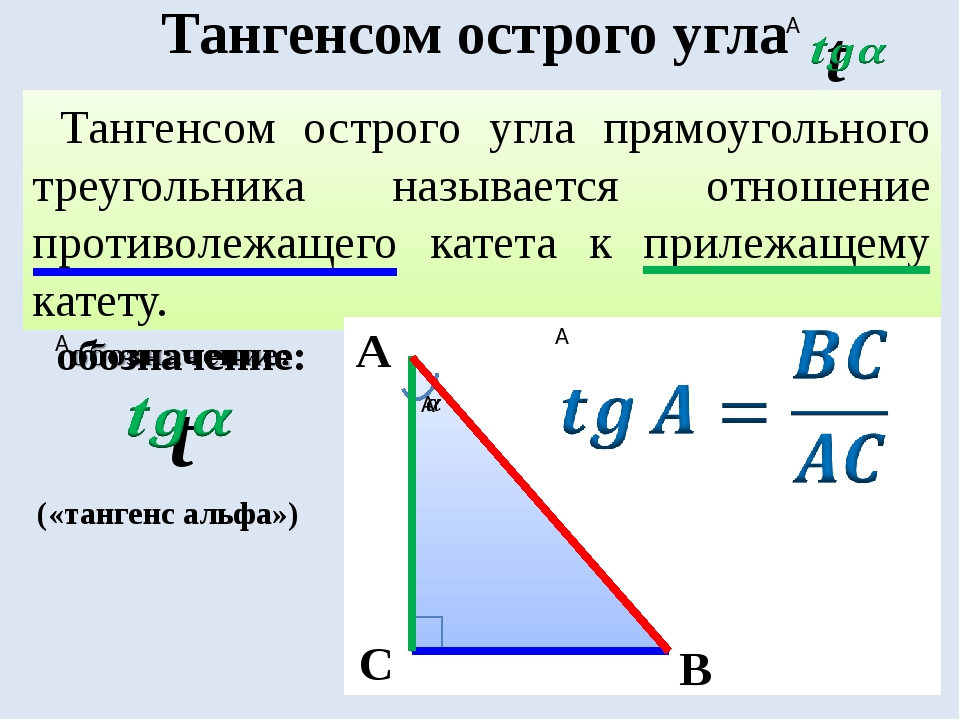
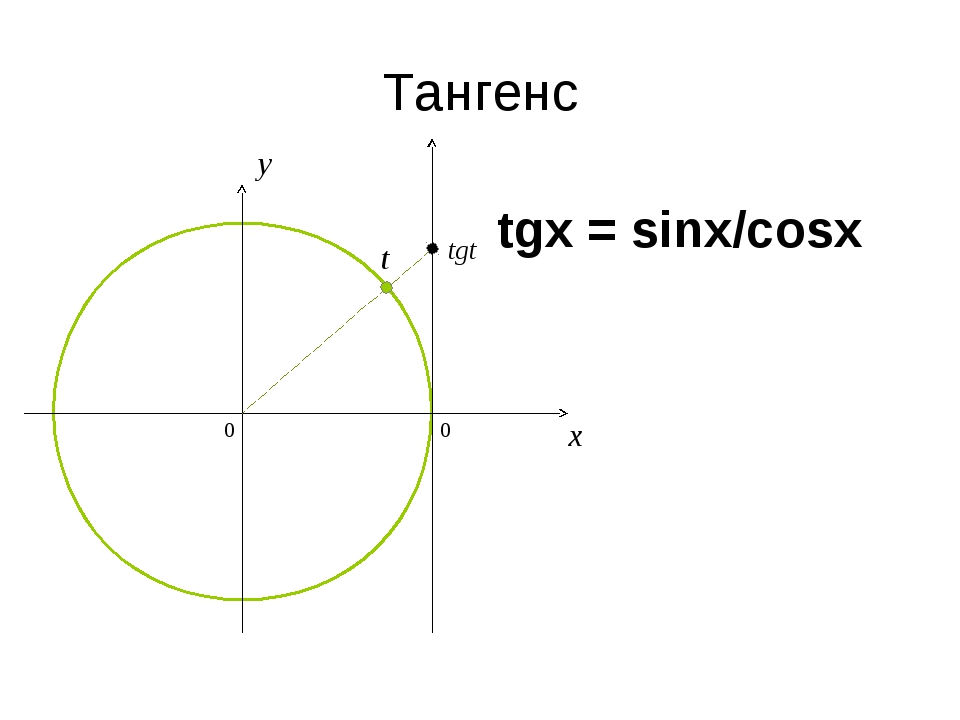
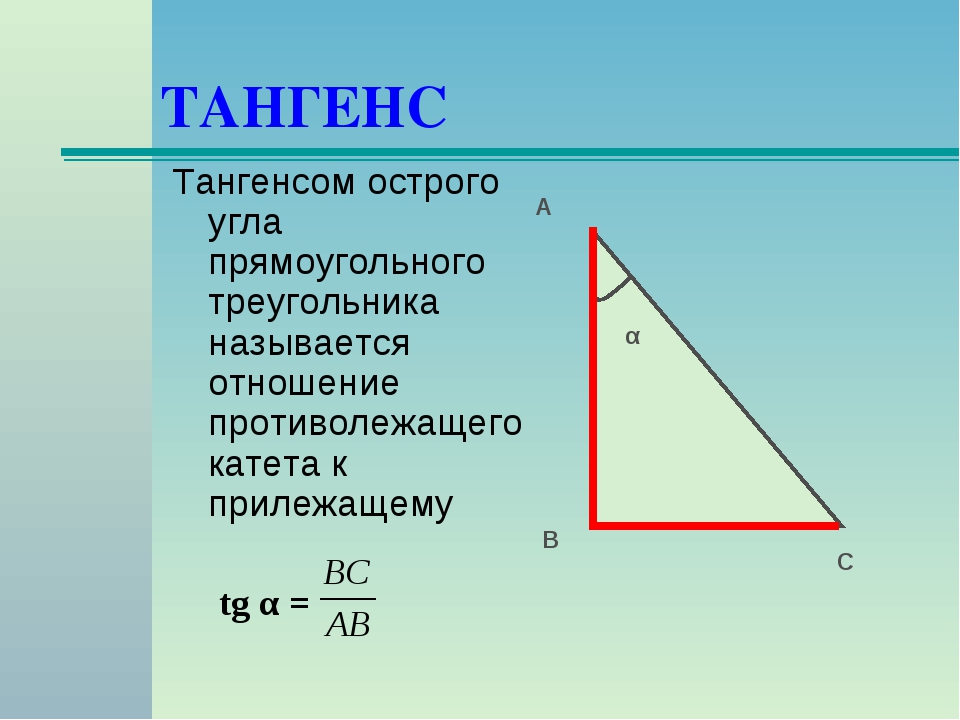
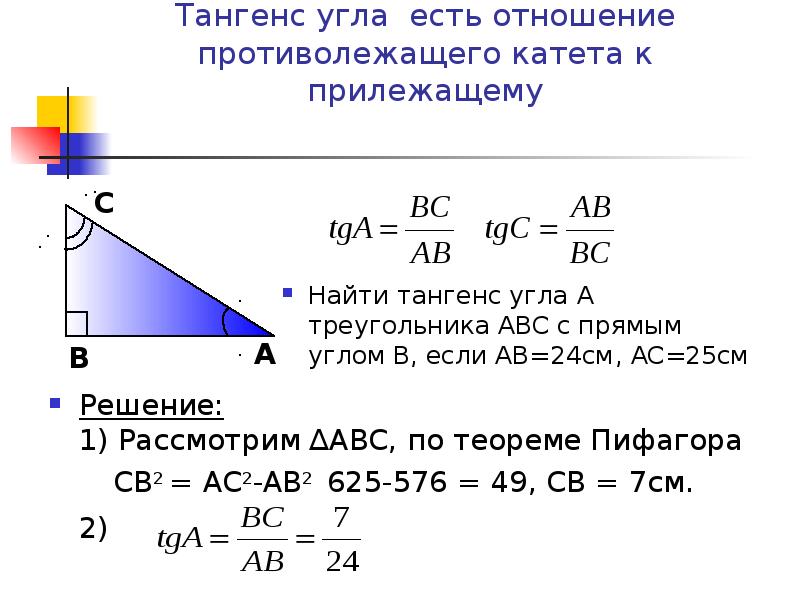
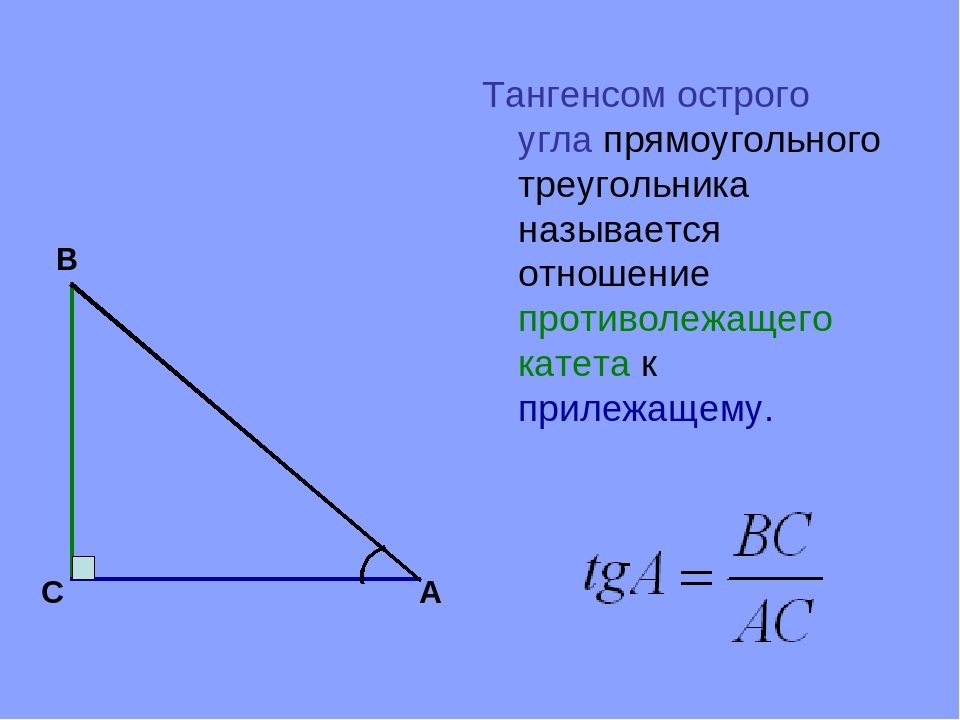
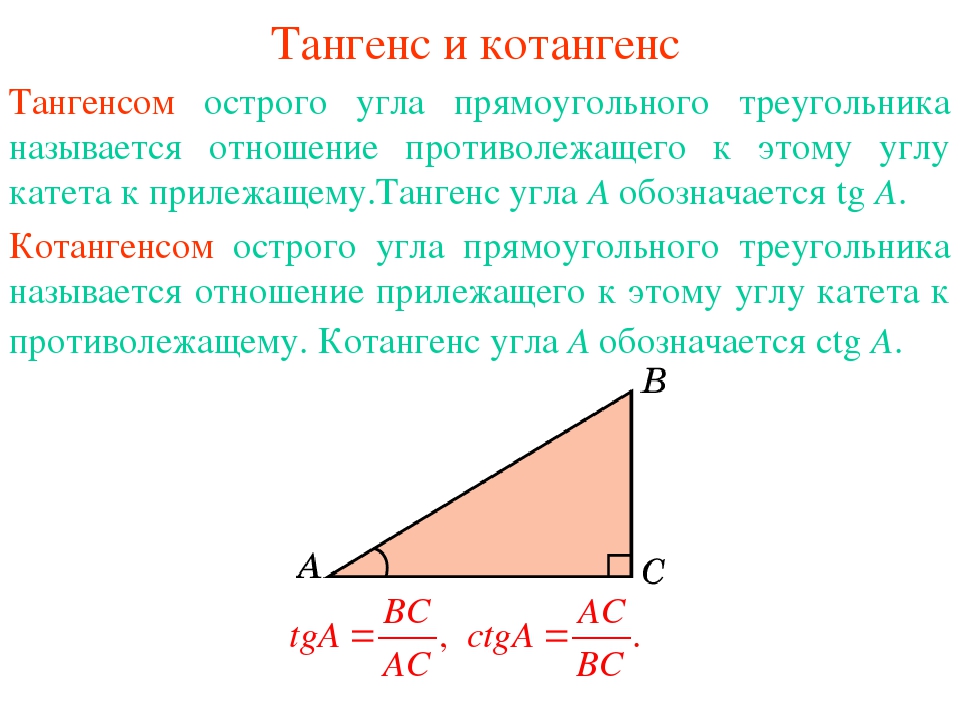
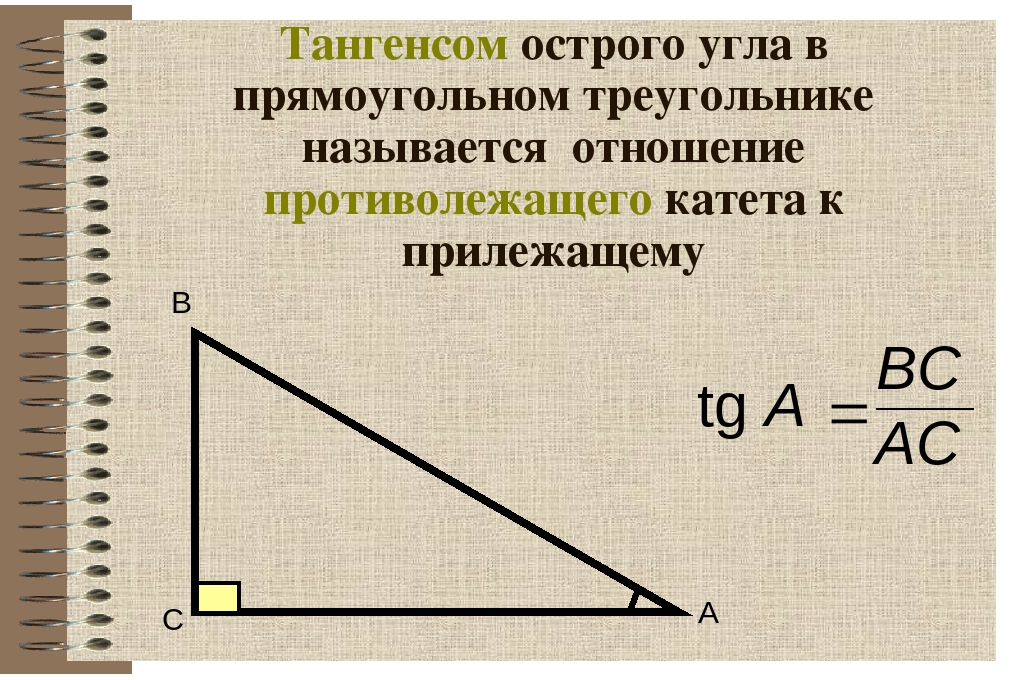
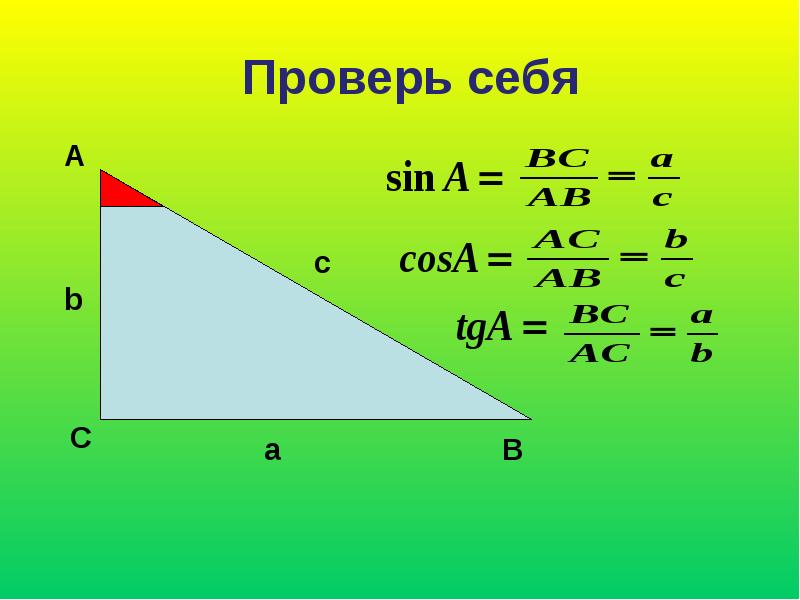
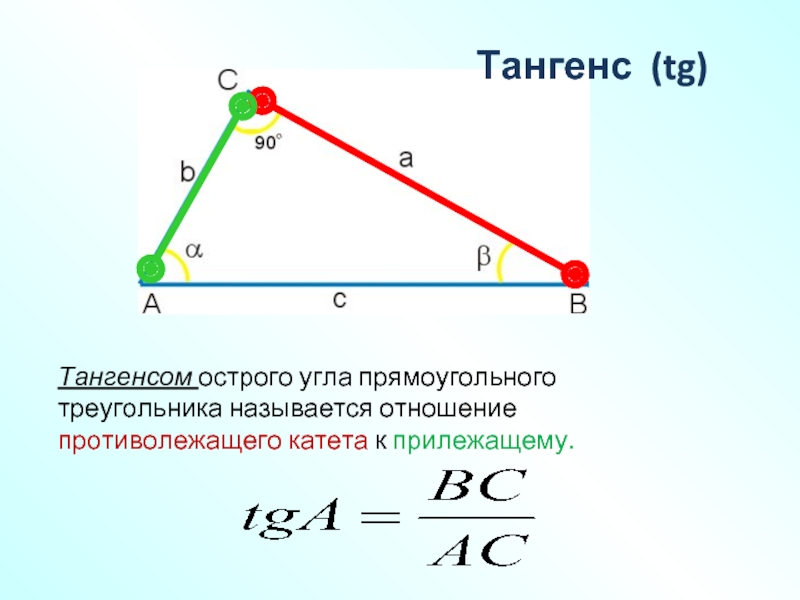
Вычисление тангенса числа или любого угла
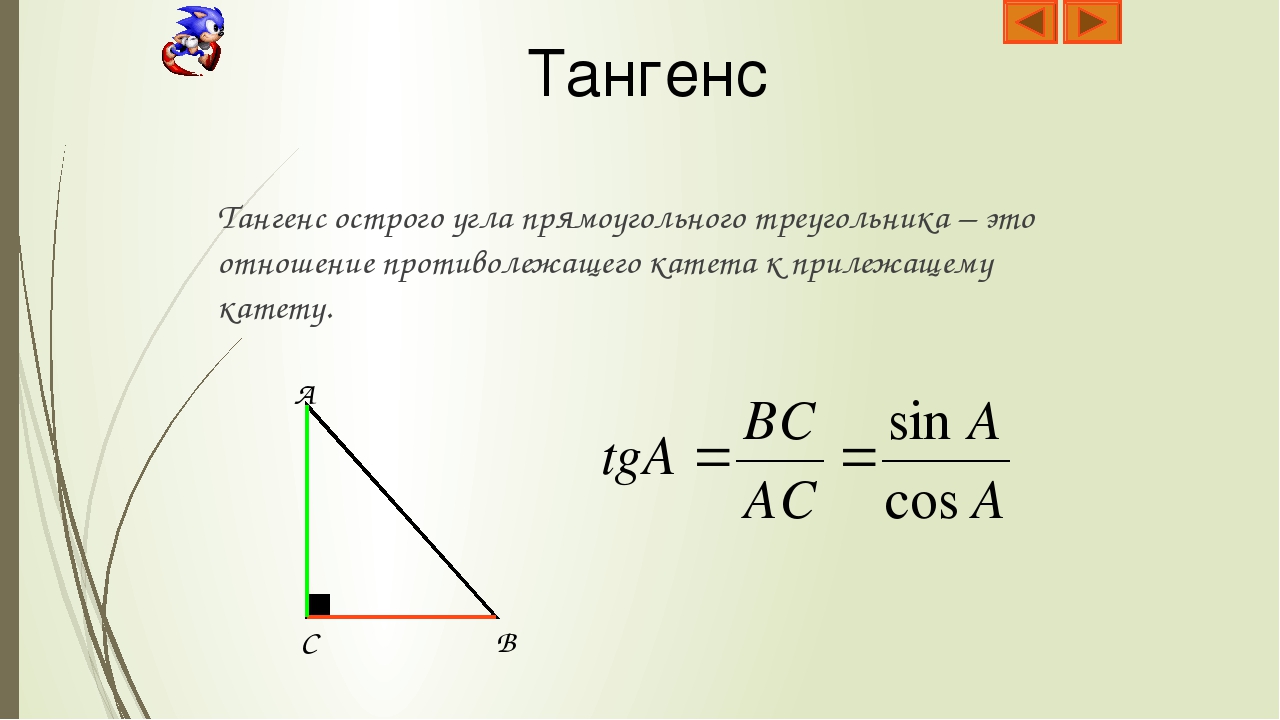
\(tg\: t=\)\(\frac{sin\:t}{cos\:t}\)
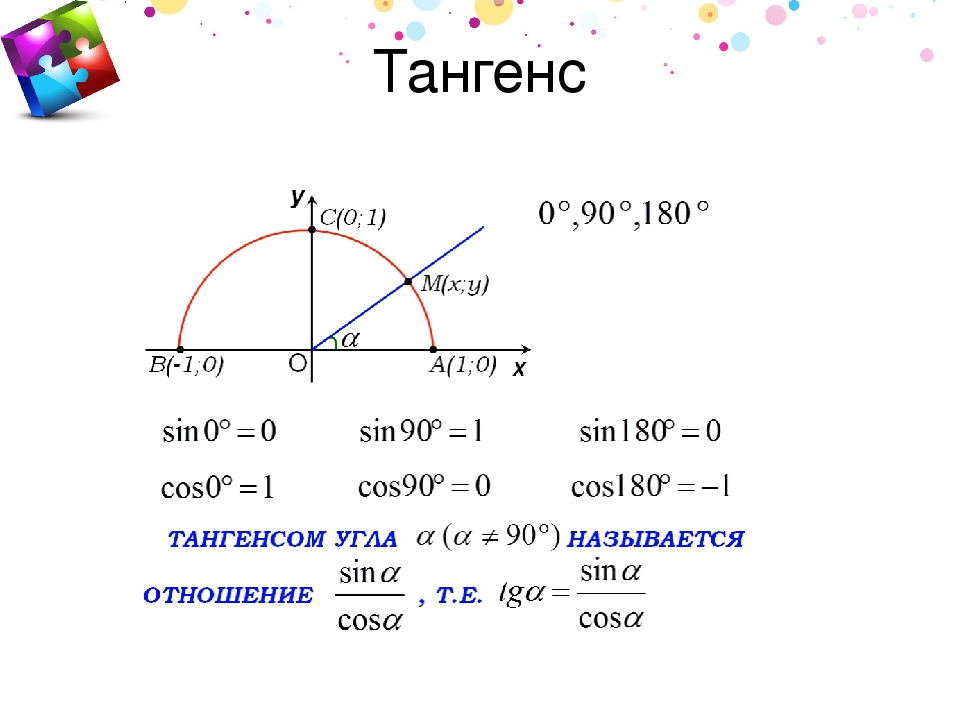
Пример. Вычислите \(tg\:0\).Решение: Чтобы найти тангенс нуля нужно найти сначала синус и косинус \(0\). И то, и другое найдем с помощью тригонометрического круга:
Точка \(0\) на числовой окружности совпадает с \(1\) на оси косинусов, значит \(cos\:0=1\). Если из точки \(0\) на числовой окружности провести перпендикуляр к оси синусов, то мы попадем в точку \(0\), значит \(sin\:0=0\). Получается: \(tg\:0=\)\(\frac{sin\:0}{cos\:0}\) \(=\)\(\frac{0}{1}\)\(=0\).
Ответ: \(0\).
Пример. Вычислите \(tg\:(-765^\circ)\).Решение: \(tg\: (-765^\circ)=\)\(\frac{sin\:(-765^\circ)}{cos\:(-765^\circ)}\)
Что бы вычислить синус и косинус \(-765^°\). Отложим \(-765^°\) на тригонометрическом круге. Для этого надо повернуть в отрицательную сторону на \(720^°\) , а потом еще на \(45^°\).

\(sin(-765^°)=-\frac{\sqrt{2}}{2}\);
\(cos(-765^°)=\frac{\sqrt{2}}{2}\) ;
получается \(tg(-765^°)= -\frac{\sqrt{2}}{2} ∶ \frac{\sqrt{2}}{2}=-1\).
Ответ: \(-1\).
Пример. Вычислите \(tg\:\frac{π}{3}\).Решение: \(tg\: \frac{π}{3}=\)\(\frac{sin\:\frac{π}{3}}{cos\:\frac{π}{3}}\). Опять находим синус пи на 3 и косинус пи на 3 (хоть с помощью тригонометрического круга, хоть по таблице):
\(sin(\frac{π}{3})=\frac{\sqrt{3}}{2}\);
\(cos(\frac{π}{3})=\frac{1}{2}\) ;
получается \(tg(\frac{π}{3})= \frac{\sqrt{3}}{2} ∶ \frac{1}{2}= \frac{\sqrt{3}}{2} \cdot \frac{2}{1}=\sqrt{3}\).
Ответ: \(\sqrt{3}\).
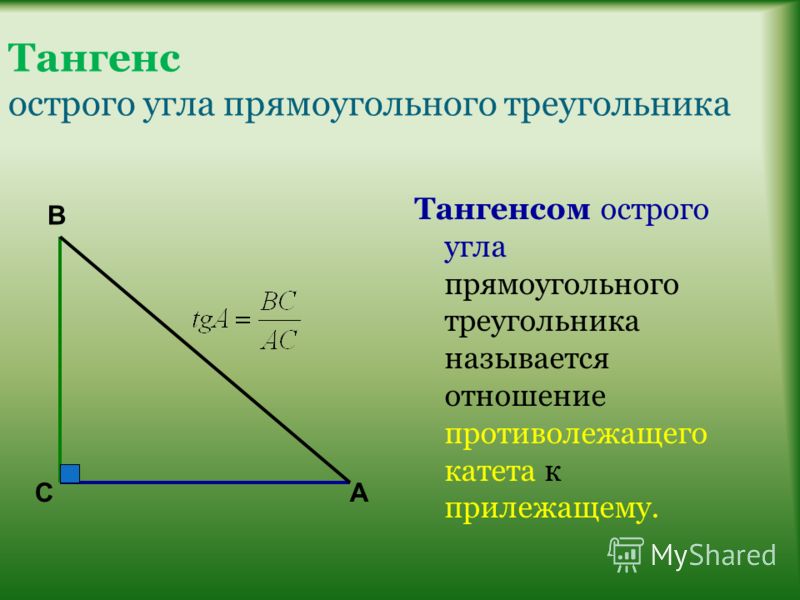
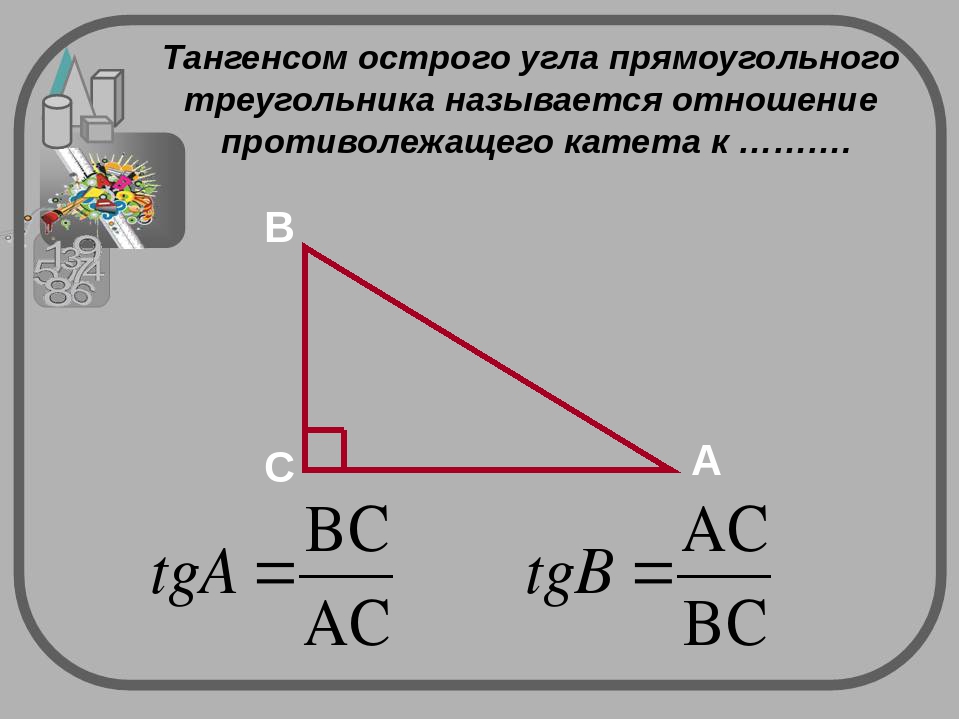
Однако можно определять тангенс и напрямую через тригонометрический круг — для этого надо на нем построить дополнительную ось:

Ось тангенсов – это фактически копия оси синусов, только сдвинутая. Поэтому все числа на ней расставляются так же как на оси синусов.
Чтобы определить тангенс с помощью числовой окружности, нужно:
1) Отметить соответствующую аргументу тангенса точку на числовой окружности.
2) Провести прямую через эту точку и начало координат и продлить её до оси тангенсов.
3) Найти координату пересечения этой прямой и оси тангенсов.
Пример. Вычислите \(tg\:\frac{π}{4}\).Решение:
1)Отмечаем \(\frac{π}{4}\) на окружности.

2) Проводим через данную точку и начало координат прямую.

3) В данном случае координату долго искать не придется – она равняется \(1\).
Ответ: \(1\).
Пример. Вычислите \(tg\: 45°\) и \(tg\: (-240°)\).Решение:
Для угла \(45°\) (\(∠KOA\)) тангенс будет равен \(1\), потому что именно в таком значении сторона угла, проходящая через начало координат и точку \(A\), пересекает ось тангесов. А для угла \(-240°\) (\(∠KOB\)) тангенс равен \(-\sqrt{3}\) (приблизительно \(-1,73\)).

Значения для других часто встречающихся в практике углов смотри в тригонометрической таблице.
Таблица тангенсов от 0° до 180°
| tg(1°) |
0.0175 |
| tg(2°) |
0.0349 |
| tg(3°) |
0.0524 |
| tg(4°) |
0.0699 |
| tg(5°) |
0.0875 |
| tg(6°) |
0.1051 |
| tg(7°) |
0.1228 |
| tg(8°) |
0.1405 |
| tg(9°) |
0.1584 |
| tg(10°) |
0.1763 |
| tg(11°) |
0.1944 |
| tg(12°) |
0.2126 |
| tg(13°) |
0.2309 |
| tg(14°) |
0.2493 |
| tg(15°) |
0.2679 |
| tg(16°) |
0.2867 |
| tg(17°) |
0.3057 |
| tg(18°) |
0.3249 |
| tg(19°) |
0.3443 |
| tg(20°) |
0.364 |
| tg(21°) |
0.3839 |
| tg(22°) |
0.404 |
| tg(23°) |
0.4245 |
| tg(24°) |
0.4452 |
| tg(25°) |
0.4663 |
| tg(26°) |
0.4877 |
| tg(27°) |
0.5095 |
| tg(28°) |
0.5317 |
| tg(29°) |
0.5543 |
| tg(30°) |
0.5774 |
| tg(31°) |
0.6009 |
| tg(32°) |
0.6249 |
| tg(33°) |
0.6494 |
| tg(34°) |
0.6745 |
| tg(35°) |
0.7002 |
| tg(36°) |
0.7265 |
|
| tg(37°) |
0.7536 |
| tg(38°) |
0.7813 |
| tg(39°) |
0.8098 |
| tg(40°) |
0.8391 |
| tg(41°) |
0.8693 |
| tg(42°) |
0.9004 |
| tg(43°) |
0.9325 |
| tg(44°) |
0.9657 |
| tg(45°) |
1 |
| tg(46°) |
1.0355 |
| tg(47°) |
1.0724 |
| tg(48°) |
1.1106 |
| tg(49°) |
1.1504 |
| tg(50°) |
1.1918 |
| tg(51°) |
1.2349 |
| tg(52°) |
1.2799 |
| tg(53°) |
1.327 |
| tg(54°) |
1.3764 |
| tg(55°) |
1.4281 |
| tg(56°) |
1.4826 |
| tg(57°) |
1.5399 |
| tg(58°) |
1.6003 |
| tg(59°) |
1.6643 |
| tg(60°) |
1.7321 |
| tg(61°) |
1.804 |
| tg(62°) |
1.8807 |
| tg(63°) |
1.9626 |
| tg(64°) |
2.0503 |
| tg(65°) |
2.1445 |
| tg(66°) |
2.246 |
| tg(67°) |
2.3559 |
| tg(68°) |
2.4751 |
| tg(69°) |
2.6051 |
| tg(70°) |
2.7475 |
| tg(71°) |
2.9042 |
| tg(72°) |
3.0777 |
|
| tg(73°) |
3.2709 |
| tg(74°) |
3.4874 |
| tg(75°) |
3.7321 |
| tg(76°) |
4.0108 |
| tg(77°) |
4.3315 |
| tg(78°) |
4.7046 |
| tg(79°) |
5.1446 |
| tg(80°) |
5.6713 |
| tg(81°) |
6.3138 |
| tg(82°) |
7.1154 |
| tg(83°) |
8.1443 |
| tg(84°) |
9.5144 |
| tg(85°) |
11.4301 |
| tg(86°) |
14.3007 |
| tg(87°) |
19.0811 |
| tg(88°) |
28.6363 |
| tg(89°) |
57.29 |
| tg(90°) |
∞ |
| tg(91°) |
-57.29 |
| tg(92°) |
-28.6363 |
| tg(93°) |
-19.0811 |
| tg(94°) |
-14.3007 |
| tg(95°) |
-11.4301 |
| tg(96°) |
-9.5144 |
| tg(97°) |
-8.1443 |
| tg(98°) |
-7.1154 |
| tg(99°) |
-6.3138 |
| tg(100°) |
-5.6713 |
| tg(101°) |
-5.1446 |
| tg(102°) |
-4.7046 |
| tg(103°) |
-4.3315 |
| tg(104°) |
-4.0108 |
| tg(105°) |
-3.7321 |
| tg(106°) |
-3.4874 |
| tg(107°) |
-3.2709 |
| tg(108°) |
-3.0777 |
|
| tg(109°) |
-2.9042 |
| tg(110°) |
-2.7475 |
| tg(111°) |
-2.6051 |
| tg(112°) |
-2.4751 |
| tg(113°) |
-2.3559 |
| tg(114°) |
-2.246 |
| tg(115°) |
-2.1445 |
| tg(116°) |
-2.0503 |
| tg(117°) |
-1.9626 |
| tg(118°) |
-1.8807 |
| tg(119°) |
-1.804 |
| tg(120°) |
-1.7321 |
| tg(121°) |
-1.6643 |
| tg(122°) |
-1.6003 |
| tg(123°) |
-1.5399 |
| tg(124°) |
-1.4826 |
| tg(125°) |
-1.4281 |
| tg(126°) |
-1.3764 |
| tg(127°) |
-1.327 |
| tg(128°) |
-1.2799 |
| tg(129°) |
-1.2349 |
| tg(130°) |
-1.1918 |
| tg(131°) |
-1.1504 |
| tg(132°) |
-1.1106 |
| tg(133°) |
-1.0724 |
| tg(134°) |
-1.0355 |
| tg(135°) |
-1 |
| tg(136°) |
-0.9657 |
| tg(137°) |
-0.9325 |
| tg(138°) |
-0.9004 |
| tg(139°) |
-0.8693 |
| tg(140°) |
-0.8391 |
| tg(141°) |
-0.8098 |
| tg(142°) |
-0.7813 |
| tg(143°) |
-0.7536 |
| tg(144°) |
-0.7265 |
|
| tg(145°) |
-0.7002 |
| tg(146°) |
-0.6745 |
| tg(147°) |
-0.6494 |
| tg(148°) |
-0.6249 |
| tg(149°) |
-0.6009 |
| tg(150°) |
-0.5774 |
| tg(151°) |
-0.5543 |
| tg(152°) |
-0.5317 |
| tg(153°) |
-0.5095 |
| tg(154°) |
-0.4877 |
| tg(155°) |
-0.4663 |
| tg(156°) |
-0.4452 |
| tg(157°) |
-0.4245 |
| tg(158°) |
-0.404 |
| tg(159°) |
-0.3839 |
| tg(160°) |
-0.364 |
| tg(161°) |
-0.3443 |
| tg(162°) |
-0.3249 |
| tg(163°) |
-0.3057 |
| tg(164°) |
-0.2867 |
| tg(165°) |
-0.2679 |
| tg(166°) |
-0.2493 |
| tg(167°) |
-0.2309 |
| tg(168°) |
-0.2126 |
| tg(169°) |
-0.1944 |
| tg(170°) |
-0.1763 |
| tg(171°) |
-0.1584 |
| tg(172°) |
-0.1405 |
| tg(173°) |
-0.1228 |
| tg(174°) |
-0.1051 |
| tg(175°) |
-0.0875 |
| tg(176°) |
-0.0699 |
| tg(177°) |
-0.0524 |
| tg(178°) |
-0.0349 |
| tg(179°) |
-0.0175 |
| tg(180°) |
-0 |
|
Таблица тангенсов углов от 271° до 360°
| tg(271°) = -57.28996tg(272°) = -28.63625tg(273°) = -19.08114tg(274°) = -14.30067tg(275°) = -11.43005tg(276°) = -9.51436tg(277°) = -8.14435tg(278°) = -7.11537tg(279°) = -6.31375tg(280°) = -5.67128tg(281°) = -5.14455tg(282°) = -4.70463tg(283°) = -4.33148tg(284°) = -4.01078tg(285°) = -3.73205tg(286°) = -3.48741tg(287°) = -3.27085tg(288°) = -3.07768tg(289°) = -2.90421tg(290°) = -2.74748tg(291°) = -2.60509tg(292°) = -2.47509tg(293°) = -2.35585tg(294°) = -2.24604tg(295°) = -2.14451tg(296°) = -2.0503tg(297°) = -1.96261tg(298°) = -1.88073tg(299°) = -1.80405tg(300°) = -1.73205tg(301°) = -1.66428tg(302°) = -1.60033tg(303°) = -1.53986tg(304°) = -1.48256tg(305°) = -1.42815tg(306°) = -1.37638tg(307°) = -1.32704tg(308°) = -1.27994tg(309°) = -1.2349tg(310°) = -1.19175tg(311°) = -1.15037tg(312°) = -1.11061tg(313°) = -1.07237tg(314°) = -1.03553tg(315°) = -1 |
tg(316°) = -0.96569tg(317°) = -0.93252tg(318°) = -0.9004tg(319°) = -0.86929tg(320°) = -0.8391tg(321°) = -0.80978tg(322°) = -0.78129tg(323°) = -0.75355tg(324°) = -0.72654tg(325°) = -0.70021tg(326°) = -0.67451tg(327°) = -0.64941tg(328°) = -0.62487tg(329°) = -0.60086tg(330°) = -0.57735tg(331°) = -0.55431tg(332°) = -0.53171tg(333°) = -0.50953tg(334°) = -0.48773tg(335°) = -0.46631tg(336°) = -0.44523tg(337°) = -0.42447tg(338°) = -0.40403tg(339°) = -0.38386tg(340°) = -0.36397tg(341°) = -0.34433tg(342°) = -0.32492tg(343°) = -0.30573tg(344°) = -0.28675tg(345°) = -0.26795tg(346°) = -0.24933tg(347°) = -0.23087tg(348°) = -0.21256tg(349°) = -0.19438tg(350°) = -0.17633tg(351°) = -0.15838tg(352°) = -0.14054tg(353°) = -0.12278tg(354°) = -0.1051tg(355°) = -0.08749tg(356°) = -0.06993tg(357°) = -0.05241tg(358°) = -0.03492tg(359°) = -0.01746tg(360°) = 0 |
Таблица тангенсов от 181° до 360°
| tg(181°) |
0.0175 |
| tg(182°) |
0.0349 |
| tg(183°) |
0.0524 |
| tg(184°) |
0.0699 |
| tg(185°) |
0.0875 |
| tg(186°) |
0.1051 |
| tg(187°) |
0.1228 |
| tg(188°) |
0.1405 |
| tg(189°) |
0.1584 |
| tg(190°) |
0.1763 |
| tg(191°) |
0.1944 |
| tg(192°) |
0.2126 |
| tg(193°) |
0.2309 |
| tg(194°) |
0.2493 |
| tg(195°) |
0.2679 |
| tg(196°) |
0.2867 |
| tg(197°) |
0.3057 |
| tg(198°) |
0.3249 |
| tg(199°) |
0.3443 |
| tg(200°) |
0.364 |
| tg(201°) |
0.3839 |
| tg(202°) |
0.404 |
| tg(203°) |
0.4245 |
| tg(204°) |
0.4452 |
| tg(205°) |
0.4663 |
| tg(206°) |
0.4877 |
| tg(207°) |
0.5095 |
| tg(208°) |
0.5317 |
| tg(209°) |
0.5543 |
| tg(210°) |
0.5774 |
| tg(211°) |
0.6009 |
| tg(212°) |
0.6249 |
| tg(213°) |
0.6494 |
| tg(214°) |
0.6745 |
| tg(215°) |
0.7002 |
| tg(216°) |
0.7265 |
|
| tg(217°) |
0.7536 |
| tg(218°) |
0.7813 |
| tg(219°) |
0.8098 |
| tg(220°) |
0.8391 |
| tg(221°) |
0.8693 |
| tg(222°) |
0.9004 |
| tg(223°) |
0.9325 |
| tg(224°) |
0.9657 |
| tg(225°) |
1 |
| tg(226°) |
1.0355 |
| tg(227°) |
1.0724 |
| tg(228°) |
1.1106 |
| tg(229°) |
1.1504 |
| tg(230°) |
1.1918 |
| tg(231°) |
1.2349 |
| tg(232°) |
1.2799 |
| tg(233°) |
1.327 |
| tg(234°) |
1.3764 |
| tg(235°) |
1.4281 |
| tg(236°) |
1.4826 |
| tg(237°) |
1.5399 |
| tg(238°) |
1.6003 |
| tg(239°) |
1.6643 |
| tg(240°) |
1.7321 |
| tg(241°) |
1.804 |
| tg(242°) |
1.8807 |
| tg(243°) |
1.9626 |
| tg(244°) |
2.0503 |
| tg(245°) |
2.1445 |
| tg(246°) |
2.246 |
| tg(247°) |
2.3559 |
| tg(248°) |
2.4751 |
| tg(249°) |
2.6051 |
| tg(250°) |
2.7475 |
| tg(251°) |
2.9042 |
| tg(252°) |
3.0777 |
|
| tg(253°) |
3.2709 |
| tg(254°) |
3.4874 |
| tg(255°) |
3.7321 |
| tg(256°) |
4.0108 |
| tg(257°) |
4.3315 |
| tg(258°) |
4.7046 |
| tg(259°) |
5.1446 |
| tg(260°) |
5.6713 |
| tg(261°) |
6.3138 |
| tg(262°) |
7.1154 |
| tg(263°) |
8.1443 |
| tg(264°) |
9.5144 |
| tg(265°) |
11.4301 |
| tg(266°) |
14.3007 |
| tg(267°) |
19.0811 |
| tg(268°) |
28.6363 |
| tg(269°) |
57.29 |
| tg(270°) |
— ∞ |
| tg(271°) |
-57.29 |
| tg(272°) |
-28.6363 |
| tg(273°) |
-19.0811 |
| tg(274°) |
-14.3007 |
| tg(275°) |
-11.4301 |
| tg(276°) |
-9.5144 |
| tg(277°) |
-8.1443 |
| tg(278°) |
-7.1154 |
| tg(279°) |
-6.3138 |
| tg(280°) |
-5.6713 |
| tg(281°) |
-5.1446 |
| tg(282°) |
-4.7046 |
| tg(283°) |
-4.3315 |
| tg(284°) |
-4.0108 |
| tg(285°) |
-3.7321 |
| tg(286°) |
-3.4874 |
| tg(287°) |
-3.2709 |
| tg(288°) |
-3.0777 |
|
| tg(289°) |
-2.9042 |
| tg(290°) |
-2.7475 |
| tg(291°) |
-2.6051 |
| tg(292°) |
-2.4751 |
| tg(293°) |
-2.3559 |
| tg(294°) |
-2.246 |
| tg(295°) |
-2.1445 |
| tg(296°) |
-2.0503 |
| tg(297°) |
-1.9626 |
| tg(298°) |
-1.8807 |
| tg(299°) |
-1.804 |
| tg(300°) |
-1.7321 |
| tg(301°) |
-1.6643 |
| tg(302°) |
-1.6003 |
| tg(303°) |
-1.5399 |
| tg(304°) |
-1.4826 |
| tg(305°) |
-1.4281 |
| tg(306°) |
-1.3764 |
| tg(307°) |
-1.327 |
| tg(308°) |
-1.2799 |
| tg(309°) |
-1.2349 |
| tg(310°) |
-1.1918 |
| tg(311°) |
-1.1504 |
| tg(312°) |
-1.1106 |
| tg(313°) |
-1.0724 |
| tg(314°) |
-1.0355 |
| tg(315°) |
-1 |
| tg(316°) |
-0.9657 |
| tg(317°) |
-0.9325 |
| tg(318°) |
-0.9004 |
| tg(319°) |
-0.8693 |
| tg(320°) |
-0.8391 |
| tg(321°) |
-0.8098 |
| tg(322°) |
-0.7813 |
| tg(323°) |
-0.7536 |
| tg(324°) |
-0.7265 |
|
| tg(325°) |
-0.7002 |
| tg(326°) |
-0.6745 |
| tg(327°) |
-0.6494 |
| tg(328°) |
-0.6249 |
| tg(329°) |
-0.6009 |
| tg(330°) |
-0.5774 |
| tg(331°) |
-0.5543 |
| tg(332°) |
-0.5317 |
| tg(333°) |
-0.5095 |
| tg(334°) |
-0.4877 |
| tg(335°) |
-0.4663 |
| tg(336°) |
-0.4452 |
| tg(337°) |
-0.4245 |
| tg(338°) |
-0.404 |
| tg(339°) |
-0.3839 |
| tg(340°) |
-0.364 |
| tg(341°) |
-0.3443 |
| tg(342°) |
-0.3249 |
| tg(343°) |
-0.3057 |
| tg(344°) |
-0.2867 |
| tg(345°) |
-0.2679 |
| tg(346°) |
-0.2493 |
| tg(347°) |
-0.2309 |
| tg(348°) |
-0.2126 |
| tg(349°) |
-0.1944 |
| tg(350°) |
-0.1763 |
| tg(351°) |
-0.1584 |
| tg(352°) |
-0.1405 |
| tg(353°) |
-0.1228 |
| tg(354°) |
-0.1051 |
| tg(355°) |
-0.0875 |
| tg(356°) |
-0.0699 |
| tg(357°) |
-0.0524 |
| tg(358°) |
-0.0349 |
| tg(359°) |
-0.0175 |
| tg(360°) |
-0 |
|