Свойства
Основные свойства
Все приведенные ниже основные свойства возведения в степень выполняются для натуральных, целых, рациональных и вещественных чисел. Для комплексных чисел, в силу многозначности комплексной операции, они выполняются только в случае натурального показателя степени.
- a1=a{\displaystyle a^{1}=a}
- (ab)n=anbn{\displaystyle \left(ab\right)^{n}=a^{n}b^{n}}
- (ab)n=anbn{\displaystyle \left({a \over b}\right)^{n}={{a^{n}} \over {b^{n}}}}
- anam=an+m{\displaystyle a^{n}a^{m}=a^{n+m}}
- anam=an−m{\displaystyle \left.{a^{n} \over {a^{m}}}\right.=a^{n-m}}
- (an)m=anm{\displaystyle \left(a^{n}\right)^{m}=a^{nm}}.
Запись anm{\displaystyle a^{n^{m}}} не обладает свойством ассоциативности (сочетательности), то есть, в общем случае,(an)m≠a(nm){\displaystyle (a^{n})^{m}\neq a^{\left({n^{m}}\right)}} Например, (22)3=43=64{\displaystyle (2^{2})^{3}=4^{3}=64}, а 2(23)=28=256{\displaystyle 2^{\left({2^{3}}\right)}=2^{8}=256}. В математике принято считать запись anm{\displaystyle a^{n^{m}}} равнозначной a(nm){\displaystyle a^{\left({n^{m}}\right)}}, а вместо (an)m{\displaystyle (a^{n})^{m}} можно писать просто anm{\displaystyle a^{nm}}, пользуясь предыдущим свойством. Впрочем, некоторые языки программирования не придерживаются этого соглашения.
Возведение в степень не обладает свойством коммутативности (переместительности): вообще говоря, ab≠ba{\displaystyle a^{b}\neq b^{a}}, например, 25=32{\displaystyle 2^{5}=32}, но 52=25.{\displaystyle 5^{2}=25.}
Таблица натуральных степеней небольших чисел
| n | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
|---|---|---|---|---|---|---|---|---|---|
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3 | 9 | 27 | 81 | 243 | 729 | 2 187 | 6 561 | 19 683 | 59 049 |
| 4 | 16 | 64 | 256 | 1024 | 4 096 | 16 384 | 65 536 | 262 144 | 1 048 576 |
| 5 | 25 | 125 | 625 | 3125 | 15 625 | 78 125 | 390 625 | 1 953 125 | 9 765 625 |
| 6 | 36 | 216 | 1296 | 7 776 | 46 656 | 279 936 | 1 679 616 | 10 077 696 | 60 466 176 |
| 7 | 49 | 343 | 2401 | 16 807 | 117 649 | 823 543 | 5 764 801 | 40 353 607 | 282 475 249 |
| 8 | 64 | 512 | 4096 | 32 768 | 262 144 | 2 097 152 | 16 777 216 | 134 217 728 | 1 073 741 824 |
| 9 | 81 | 729 | 6561 | 59 049 | 531 441 | 4 782 969 | 43 046 721 | 387 420 489 | 3 486 784 401 |
| 10 | 100 | 1000 | 10 000 | 100 000 | 1 000 000 | 10 000 000 | 100 000 000 | 1 000 000 000 | 10 000 000 000 |
Степень с отрицательным показателем и её свойства
Число в минусовой степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:
|
Чтобы разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с одинаковыми основаниями.
Деление степеней с разными основаниями, но одинаковыми показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
Поэтому если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
a3÷a6=a3 — 6 = a-3
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
Обозначение
История
В Европе сначала степень записывали как произведение — например, x4{\displaystyle x^{4}} изображалось как xxxx.{\displaystyle xxxx.} Первые попытки сокращённой записи осуществили в XVII веке Пьер Эригон и шотландский математик Джеймс Юм, они записывали x4{\displaystyle x^{4}} в виде x4{\displaystyle x4} и xIV{\displaystyle x^{IV}} соответственно. Начиная с Декарта, степень обозначали «двухэтажной» записью вида ab{\displaystyle a^{b}}.
Значок степени
С появлением компьютеров и компьютерных программ возникла проблема, состоящая в том, что в тексте компьютерных программ невозможно записать степень в «двухэтажном» виде. В связи с этим изобрели особые значки для обозначения операции возведения в степень. Первым таким значком были две звёздочки: «», используемые в языке Фортран. В появившемся несколько позже языке Алгол использовался значок стрелки: «» (стрелки Кну́та). В языке Бейсик предложен символ «» («циркумфлекс»), который приобрёл наибольшую популярность; его часто используют при написании формул и математических выражений не только в языках программирования и компьютерных системах, но и в простом тексте. Примеры:
- ; ; ; .
Случается, что циркумфлекс используют и при написании сложных, громоздких математических выражений и формул на бумаге (особенно с громоздким показателем).
Иногда в компьютерных системах и языках программирования значок возведения в степень имеет левую ассоциативность, в отличие от принятого в математике соглашения о правой ассоциативности возведения в степень.
То есть некоторые языки программирования (например, программа Excel) могут воспринимать запись , как , тогда как другие системы и языки (например, Haskell, Perl, Wolfram|Alpha и многие другие) обработают эту запись справа налево: ,
как это принято в математике: abc=a(bc){\displaystyle a^{b^{c}}=a^{\left({b^{c}}\right)}}.
Некоторые знаки возведения в степень в языках программирования и компьютерных системах:
- : Алгол, некоторые диалекты Бейсика;
- : Бейсик, J, MATLAB, R, Microsoft Excel, TeX, bc, Haskell, Lua, MathML и большинство систем компьютерной алгебры;
- : Haskell, D;
- : Ада, Bash, Кобол, Фортран, FoxPro, Gnuplot, OCaml, Perl, PL/I, PHP, Python, REXX, Ruby, SAS, Seed7, Tcl, ABAP, Haskell, , VHDL, ECMAScript, AutoHotkey;
- : APL.
Во многих языках программирования (например, в Си и Паскале) отсутствует операция возведения в степень и для этой цели используют функции.
В словаре Д.Н. Ушакова
СТЕ́ПЕНЬ, степени, мн. степени, степеней, ·жен.1. Сравнительная величина, сравнительное количество, сравнительный размер, сравнительное качество чего-нибудь. Степень культурности. Высокая степень мастерства. Степень родства (количество рождений, связывающих двух лиц с общим предком). Предусмотреть степень опасности. Степень знания.2. только ед. В ·косв
в соединении с прилагательными образует выражения, обозначающие важность, значительность чего-нибудь или отношение к чему-нибудь, характеризуемые прилагательным. В высшей степени (очень, чрезвычайно)
В значительной степени *****5. Произведение равных множителей, результат повторного умножения числа на самого себя (мат.). Возведение в степень. Показатель степени. Икс в пятой степени.6. То же, что степень сравнения (см. ниже» title=’что такое ниже, значение слова ниже в словаре Ушакова’>ниже; грам.). Сравнительная степень. Превосходная степень.• Степень сравнения (грам.) — форма качественных имен прилагательных и наречий, указывающая на степень качества, выражаемую данным прилагательным или наречием.
Натуральная степень
Число c{\displaystyle c} называется n-й степенью числа a{\displaystyle a}, если
- c=a⋅a⋅…⋅a⏟n{\displaystyle c=\underbrace {a\cdot a\cdot …\cdot a} _{n}}.
Свойства:
- (ab)n=anbn{\displaystyle \left(ab\right)^{n}=a^{n}b^{n}}
- (ab)n=anbn{\displaystyle \left({a \over b}\right)^{n}={{a^{n}} \over {b^{n}}}}
- anam=an+m{\displaystyle a^{n}a^{m}=a^{n+m}}
- anam=an−m{\displaystyle \left.{a^{n} \over {a^{m}}}\right.=a^{n-m}}
- (an)m=anm{\displaystyle \left(a^{n}\right)^{m}=a^{nm}}
- запись anm{\displaystyle a^{n^{m}}} не обладает свойством ассоциативности (сочетательности), то есть в общем случае левая ассоциативность не равна правой ассоциативности (an)m≠a(nm){\displaystyle (a^{n})^{m}\neq a^{\left({n^{m}}\right)}}, результат будет зависеть от последовательности действий, например, (22)3=43=64{\displaystyle (2^{2})^{3}=4^{3}=64}, а 2(23)=28=256{\displaystyle 2^{\left({2^{3}}\right)}=2^{8}=256}. Принято считать запись anm{\displaystyle a^{n^{m}}} равнозначной a(nm){\displaystyle a^{\left({n^{m}}\right)}}, а вместо (an)m{\displaystyle (a^{n})^{m}} можно писать просто anm{\displaystyle a^{nm}}, пользуясь предыдущим свойством. Впрочем некоторые языки программирования не придерживаются этого соглашения (см. );
- возведение в степень не обладает свойством коммутативности (переместительности): вообще говоря, ab≠ba{\displaystyle a^{b}\neq b^{a}}, например, 25=32{\displaystyle 2^{5}=32}, но 52=25{\displaystyle 5^{2}=25}.
Существует алгоритм быстрого возведения в степень, выполняющий возведение в степень за меньшее, чем в определении, число умножений.
Вещественная степень
Пусть a⩾,r{\displaystyle a\geqslant 0,r} — вещественные числа, причём r{\displaystyle r} — иррациональное число. Определим значение ar{\displaystyle a^{r}} следующим образом.
Как известно, любое вещественное число можно приблизить, сверху и снизу, двумя рациональными числами, то есть можно подобрать для r{\displaystyle r} рациональный интервал p,q{\displaystyle } с любой степенью точности. Тогда общая часть всех соответствующих интервалов ap,aq{\displaystyle } состоит из одной точки, которая и принимается за ar{\displaystyle a^{r}}.
Другой подход основан на теории рядов и логарифмов (см. ).
Потенцирование
Потенцирование (от нем. potenzieren — возведение в степень) — это нахождение числа по известному значению его логарифма, то есть решение уравнения:
- loga x=b{\displaystyle \log _{a}~x=b}
Из определения логарифма вытекает, что x=ab{\displaystyle x=a^{b}}. Таким образом, возведение a в степень b может быть названо другими словами «потенцированием b по основанию a».
Ноль в степени ноль
Выражение {\displaystyle 0^{0}} (ноль в нулевой степени) многие учебники считают неопределённым и лишённым смысла. Некоторые авторы предлагают принять соглашение о том, что это выражение равно 1. В частности, тогда разложение в ряд экспоненты:
- ex=1+∑n=1∞xnn!{\displaystyle e^{x}=1+\sum _{n=1}^{\infty }{x^{n} \over n!}}
можно записать короче:
- ex=∑n=∞xnn!.{\displaystyle e^{x}=\sum _{n=0}^{\infty }{x^{n} \over n!}.}
В любом случае соглашение =1{\displaystyle 0^{0}=1} чисто символическое, и оно не может использоваться ни в алгебраических, ни в аналитических преобразованиях из-за разрывности функции в этой точке.
Порядок действий в примерах со степенями
Вычисление значения называется действием возведения в степень. Это действие третьей ступени.
Запомните!
В выражениях со степенями, не содержащими скобки, сначала выполняют
вовзведение в степень, затем умножение и деление, а в
конце сложение и вычитание.
Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках,
а потом оставшиеся действия в том же порядке слева направо.
Пример. Вычислить:
Для облегчения решения примеров полезно знать и пользоваться
таблицей степеней, которую вы можете бесплатно скачать на нашем сайте.
Для проверки своих результатов вы можете воспользоваться на нашем сайте калькулятором
«Возведение в степень онлайн».
Употребление в устной речи
Запись an{\displaystyle a^{n}} обычно читается как «a в n{\displaystyle n}-й степени» или «a в степени n». Например, 104{\displaystyle 10^{4}} читается как «десять в четвёртой степени», 1032{\displaystyle 10^{3/2}} читается как «десять в степени три вторых (или: полтора)».
Для второй и третьей степени существуют специальные названия: возведение в квадрат и в куб соответственно. Так, например, 102{\displaystyle 10^{2}} читается как «десять в квадрате», 103{\displaystyle 10^{3}} читается как «десять в кубе». Такая терминология возникла из древнегреческой математики. Древние греки формулировали алгебраические конструкции на языке геометрической алгебры. В частности, вместо употребления слова «умножение» они говорили о площади прямоугольника или об объёме параллелепипеда: вместо a2{\displaystyle a^{2}}, a3{\displaystyle a^{3}} древние греки говорили «квадрат на отрезке a», «куб на a». По этой причине четвёртую степень и выше древние греки избегали.
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n-раз подряд»
an — степень,
где
a — основание степени
n — показатель степени
Соответственно, an= a·a·a·a…·a
Читается такое выражение, как a в степени n
Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) на само себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число — она решается довольно просто:
23 = 2·2·2, где
2 — основание степени
3 — показатель степени
Действия, конечно, можно выполнять и на калькуляторе. Их выбор велик, а доступность иногда на расстоянии одного клика в онлайн
Всё это безусловно можно использовать, но сейчас нам важно подробно разобрать принцип работы, чтобы не упасть в грязь лицом на контрольной по математике
Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.Задачка про миллион: представьте, что у вас есть миллион рублей. В начале каждого года вы зарабатываете на нем еще два. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.
Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:
3·3·3·3 = 81. То есть получается, что три в степени четыре равно 81.
Математики заскучали и решили все упростить:
34 = 81
Ответ: через четыре года у вас будет 81 миллион.
Комплексная степень
Сначала покажем, как вычисляется экспонента ez{\displaystyle e^{z}}, где e — число Эйлера, z — произвольное комплексное число, z=x+yi{\displaystyle z=x+yi}.
- ez=exeyi=ex(cosy+isiny)=excosy+iexsiny.{\displaystyle e^{z}=e^{x}e^{yi}=e^{x}(\cos y+i\sin y)=e^{x}\cos y+ie^{x}\sin y.}
Теперь рассмотрим общий случай ab{\displaystyle a^{b}}, где a,b{\displaystyle a,b} оба являются комплексными числами. Проще всего это сделать, представив a{\displaystyle a} в экспоненциальной форме и используя тождество ab=eb Ln(a){\displaystyle a^{b}=e^{b\ \operatorname {Ln} (a)}}, где Ln{\displaystyle \operatorname {Ln} } — комплексный логарифм:
- ab=(reθi)b=(eLn(r)+θi)b=e(Ln(r)+θi)b.{\displaystyle a^{b}=(re^{{\theta }i})^{b}=(e^{\operatorname {Ln} (r)+{\theta }i})^{b}=e^{(\operatorname {Ln} (r)+{\theta }i)b}.}
Следует иметь в виду, что комплексный логарифм — многозначная функция, так что, вообще говоря, комплексная степень определена неоднозначно.
Употребление в устной речи
Запись an{\displaystyle a^{n}} обычно читается как «a в n{\displaystyle n}-ой степени» или «a в степени n». Например, 104{\displaystyle 10^{4}} читается как «десять в четвёртой степени», 1032{\displaystyle 10^{3/2}} читается как «десять в степени три вторых (или: полтора)».
Для второй и третьей степени существуют специальные названия: возведение в квадрат и в куб соответственно. Так, например, 102{\displaystyle 10^{2}} читается как «десять в квадрате», 103{\displaystyle 10^{3}} читается как «десять в кубе». Такая терминология возникла из древнегреческой математики. Древние греки формулировали алгебраические конструкции на языке геометрической алгебры (англ.)русск.. В частности, вместо употребления слова «умножение» они говорили о площади прямоугольника или об объёме параллелепипеда: вместо a2{\displaystyle a^{2}}, a3{\displaystyle \ a^{3}} древние греки говорили «квадрат на отрезке a», «куб на a». По этой причине четвёртую степень и выше древние греки избегали.
В разговорной речи иногда говорят, например, что a3{\displaystyle a^{3}} — это «a умноженное само на себя три раза», имея в виду, что берётся три множителя a{\displaystyle a}. Это не совсем точно, и может привести к двусмысленности, так как количество операций умножения будет на одну меньше: a3=a⋅a⋅a{\displaystyle a^{3}=a\cdot a\cdot a} (три множителя, но две операции умножения). Часто когда говорят, «a умноженное само на себя три раза», имеют в виду количество умножений, а не множителей, то есть a4{\displaystyle a^{4}}.
Чтобы избежать двусмысленности, можно говорить, к примеру: третья степень — это когда «число три раза входит в умножение».
Вариации и обобщения
Возведение в степень с натуральным показателем можно определить не только для чисел, но и для нечисловых объектов, для которых определено умножение — например, к матрицам, линейным операторам, множествам (относительно декартова произведения, см. декартова степень).
Обычно эта операция рассматривается в некотором мультипликативном моноиде M{\displaystyle M} (полугруппе с единицей) и определяется индуктивно для любого x∈M{\displaystyle x\in M}:
- x=x{\displaystyle x^{0}=x}
- xn+1=xnx{\displaystyle x^{n+1}=x^{n}x}, где n⩾{\displaystyle n\geqslant 0}
- Если n<,{\displaystyle n<0,} то xn{\displaystyle x^{n}} определён только для обратимых элементов x.{\displaystyle x.}
Особенную ценность представляет применение возведения в степень к группам и полям, где возникает прямой аналог отрицательных степеней.
Гипероператор возведения в степень — тетрация.
Порядок действий в примерах со степенями
Вычисление значения называется действием возведения в степень. Это действие третьей ступени.
Запомните!
В выражениях со степенями, не содержащими скобки, сначала выполняют
вовзведение в степень, затем умножение и деление, а в
конце сложение и вычитание.
Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках,
а потом оставшиеся действия в том же порядке слева направо.
Пример. Вычислить:
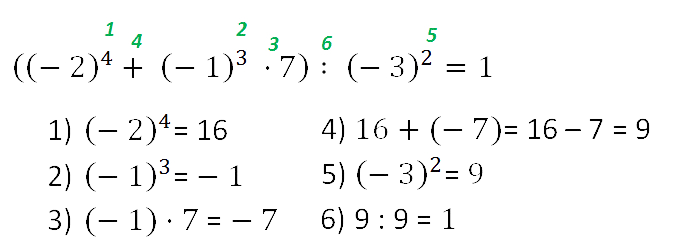
Для облегчения решения примеров полезно знать и пользоваться
таблицей степеней, которую вы можете бесплатно скачать на нашем сайте.
Для проверки своих результатов вы можете воспользоваться на нашем сайте калькулятором
«Возведение в степень онлайн».
Примечания
- Ван дер Варден. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции / Пер. с голл. И. Н. Веселовского. — М., 1959. — С. 165-167. — 456 с.
- Румовский С. Я. Сокращения математики. — Directmedia, 2014. — С. 80. — ISBN 978-5-4458-1644-7.
- , с. 130—131.
- Комментарии
- Термин впервые встречается у швейцарского математика Иоганна Рана (1659 год).
- Для целой степени.
- Для неотрицательной целой степени.
- Поддерживает отрицательные степени, в отличие от , реализованной только как последовательное умножение.
- Для степени, представленной числом с плавающей запятой — реализовано через логарифм.
- Описан в стандарте EcmaScript 7 (ECMA-262, 7th edition), принятом в июне 2016 года.
- В JavaScript изначально присутствует метод .
В словаре Ожегова
СТЕПЕНЬ, -и, мн. -и, -ей, ж. 1. Мера, сравнительная величина чего-н. С. подготовленности. С. загрязнения. 2. То же, что звание (в 1 знач.), а также (устар.) ранг, чин. Ученая с. доктора наук. Достичь высоких степеней. 3. обычно с порядк. числит. Разряд, категория. Орден Отечественной войны 1-й и 2-й степени. Орден Славы 3-й степени. 4. В математике: число (или величина), получающееся повторным умножением другого числа (или величины) на самого себя. Возведение в с. 5. В математике: то же, что показатель степени. * В высшей степени — очень, весьма. В высшей степени осмотрителен. В слабой степени- недостаточно, слабо. Признаки проявляются в слабой степени. До известной (некоторой, какой-то) степени — отчасти, в какой-то мере. До известной степени он прав. До какой степени — в какой мере, насколько. До какой степени можно доверять этому человеку? До такой степени что, в знач. союза — так сильно что, до того что. Освоился до такой степени, что может работать самостоятельно. Степень сравнения — в грамматике: форма прилагательного и наречия, указывающая на большую по сравнению с чем-н. степень (в 1 знач.), меру признака, напр. веселее, умнее, лучше, хуже. и прил. степенной, -ая, -ое (к 4 знач.).
Примечания
- ↑ Степень // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1985. — Т. 5. — С. 221.
- Ван дер Варден. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции / Пер. с голл. И. Н. Веселовского. — М., 1959. — С. 165—167. — 456 с.
- , с. 140—141.
- ↑ , с. 182—184.
- ↑ Выгодский М. Я. Справочник по высшей математике. — 12-е изд.. — М.: Наука, 1977. — С. 597 (подстрочное примечание 3). — 872 с.
- Антилогарифм / Математический энциклопедический словарь, М.: Советская энциклопедия, 1988, стр. 73.
- , §290—297.
- , §164.
- ↑ , с. 130—131.
- , §298—301, 307—309.
- Комментарии
- В разговорной речи иногда говорят, например, что a3{\displaystyle a^{3}} — «a умноженное само на себя три раза», имея в виду, что берётся три множителя a{\displaystyle a}. Это не совсем точно и может привести к двусмысленности, так как количество операций умножения будет на одну меньше: a3=a⋅a⋅a{\displaystyle a^{3}=a\cdot a\cdot a} (три множителя, но две операции умножения). Часто, когда говорят «a умноженное само на себя три раза», имеют в виду количество умножений, а не множителей, то есть a4.{\displaystyle a^{4}.} См. . Чтобы избежать двусмысленности, можно говорить, к примеру: третья степень — это когда «число три раза входит в умножение».
- Термин впервые встречается у швейцарского математика Иоганна Рана (1659 год).
- Для целой степени.
- Для неотрицательной целой степени.
- Поддерживает отрицательные степени, в отличие от , реализованной только как последовательное умножение.
- Для степени, представленной числом с плавающей запятой — реализовано через логарифм.
- Описан в стандарте EcmaScript 7 (ECMA-262, 7th edition), принятом в июне 2016 года.
- ↑ В JavaScript изначально присутствует метод .
Возведение в степень отрицательного числа
Основание степени (число, которое возводят в степень) может быть любым
числом — положительным, отрицательным или нулём.
Запомните!
При возведении в степень положительного числа
получается положительное число.
При возведении нуля в натуральную степень получается ноль.
При возведении в степень отрицательного числа в результате может получиться
как положительное число, так и отрицательное число. Это зависит от того чётным или
нечётным числом был показатель степени.
Рассмотрим примеры возведения в степень отрицательных чисел.

Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень,
то получается отрицательное число. Так как произведение
нечётного количество отрицательных сомножителей отрицательно.
Если же отрицательное число возводится в чётную степень, то получается положительное число.
Так как произведение чётного количество отрицательных сомножителей положительно.
Запомните!
Отрицательное число, возведённое в
чётную степень, есть число
положительное.
Отрицательное число, возведённое в
нечётную степень, — число
отрицательное.
Квадрат любого числа есть положительное число или нуль, то есть: при любом .
Обратите внимание!
При решении примеров на возведение в степень часто делают ошибки, забывая, что записи
и
это разные выражения. Результаты возведения
в степень данных выражений будут разные.
Вычислить означает найти значение четвёртой степени отрицательного числа.
В то время как найти «» означает, что пример нужно решать в 2 действия:
- Возвести в четвёртую степень положительное число .
- Поставить перед полученным результатом знак «минус» (то есть выполнить
действие вычитание).
Пример. Вычислить:
История
Обозначение
В Европе сначала степень величины записывали словесными сокращениями (q или Q обозначало квадрат, c или C — куб, bq или qq — биквадрат, то есть 4-я степень и т. д.) или как произведение — например, x4{\displaystyle x^{4}} изображалось как xxxx.{\displaystyle xxxx.} Отред записывал x5−15×4{\displaystyle x^{5}-15x^{4}} следующим образом: 1qc−15qq{\displaystyle 1qc-15qq} (если неизвестная всего одна, ей часто не присваивался буквенный значок). Немецкая школа коссистов для каждой степени неизвестной предлагала особый готический значок.
В XVII веке постепенно стала преобладать идея явно указывать показатель степени. Жирар (1629 год) для возведения в степень числа ставил показатель в круглых скобках перед этим числом, а если числа правее показателя не было, то это значило, что подразумевается наличие неизвестного в указанной степени; например, (2)2+1(2){\displaystyle (2)2+1(2)} у него означало 22+x2{\displaystyle 2^{2}+x^{2}}. Варианты размещения показателя степени предлагали Пьер Эригон и шотландский математик Джеймс Юм, они записывали x4{\displaystyle x^{4}} в виде x4{\displaystyle x4} и xIV{\displaystyle x^{IV}} соответственно.
Современная запись показателя степени — правее и выше основания — введена Декартом в его «Геометрии» (1637), правда, только для натуральных степеней, больших 2 (возведение в квадрат ещё долгое время обозначалось по-старому, произведением). Позднее Валлис и Ньютон (1676) распространили декартову форму записи степени на отрицательные и дробные показатели, трактовка которых к этому времени уже была известна из трудов Орема, Шюке, Стевина, Жирара и самого Валлиса. К началу XVIII столетия альтернативы для записи степеней «по Декарту», как выразился Ньютон в «Универсальной арифметике», «вышли из моды» (out of fashion). Показательная функция, то есть возведение в переменную степень, появилась сначала в письмах, а потом и в трудах Лейбница (1679). Возведение в мнимую степень обосновал Эйлер (1743).
Запись возведения в степень в языках программирования
С появлением компьютеров и компьютерных программ возникла проблема, состоящая в том, что в тексте компьютерных программ невозможно записать степень в «двухэтажном» виде. В связи с этим изобрели особые значки для обозначения операции возведения в степень. Первым таким значком были две звёздочки: «», используемые в языке Фортран. В появившемся несколько позже языке Алгол использовался значок стрелки: «» (стрелки Кну́та). В языке Бейсик предложен символ «» («циркумфлекс»), который приобрёл наибольшую популярность; его часто используют при написании формул и математических выражений не только в языках программирования и компьютерных системах, но и в простом тексте. Примеры:
- ; ; ; .
Иногда в компьютерных системах и языках программирования значок возведения в степень имеет левую ассоциативность, в отличие от принятого в математике соглашения о правой ассоциативности возведения в степень.
То есть некоторые языки программирования (например, программа Excel) могут воспринимать запись , как , тогда как другие системы и языки (например, Haskell, Perl, Wolfram|Alpha и многие другие) обработают эту запись справа налево: , как это принято в математике: abc=a(bc){\displaystyle a^{b^{c}}=a^{\left(b^{c}\right)}}.
Некоторые знаки возведения в степень в языках программирования и компьютерных системах:
- : Алгол, некоторые диалекты Бейсика;
- : Бейсик, J, MATLAB, R, Microsoft Excel, TeX, bc, Haskell, Lua, MathML и большинство систем компьютерной алгебры;
- : Haskell, D;
- : Ада, Bash, Кобол, Фортран, FoxPro, Gnuplot, OCaml, Perl, PL/I, PHP, Python, REXX, Ruby, SAS, Seed7, Tcl, ABAP, Haskell, , VHDL, ECMAScript, AutoHotkey, JavaScript;
- : APL.
Во многих языках программирования (например, в Java, Си и Паскале) отсутствует операция возведения в степень, и для этой цели используют стандартные функции.
Возведение в степень отрицательного числа
Основание степени (число, которое возводят в степень) может быть любым
числом — положительным, отрицательным или нулём.
Запомните!
При возведении в степень положительного числа
получается положительное число.
При возведении нуля в натуральную степень получается ноль.
При возведении в степень отрицательного числа в результате может получиться
как положительное число, так и отрицательное число. Это зависит от того чётным или
нечётным числом был показатель степени.
Рассмотрим примеры возведения в степень отрицательных чисел.
Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень,
то получается отрицательное число. Так как произведение
нечётного количество отрицательных сомножителей отрицательно.
Если же отрицательное число возводится в чётную степень, то получается положительное число.
Так как произведение чётного количество отрицательных сомножителей положительно.
Запомните!
Отрицательное число, возведённое в
чётную степень, есть число
положительное.
Отрицательное число, возведённое в
нечётную степень, — число
отрицательное.
Квадрат любого числа есть положительное число или нуль, то есть: при любом .
Обратите внимание!
При решении примеров на возведение в степень часто делают ошибки, забывая, что записи
и
это разные выражения. Результаты возведения
в степень данных выражений будут разные.
Вычислить означает найти значение четвёртой степени отрицательного числа.
В то время как найти «» означает, что пример нужно решать в 2 действия:
- Возвести в четвёртую степень положительное число .
- Поставить перед полученным результатом знак «минус» (то есть выполнить
действие вычитание).
Пример. Вычислить:

























































