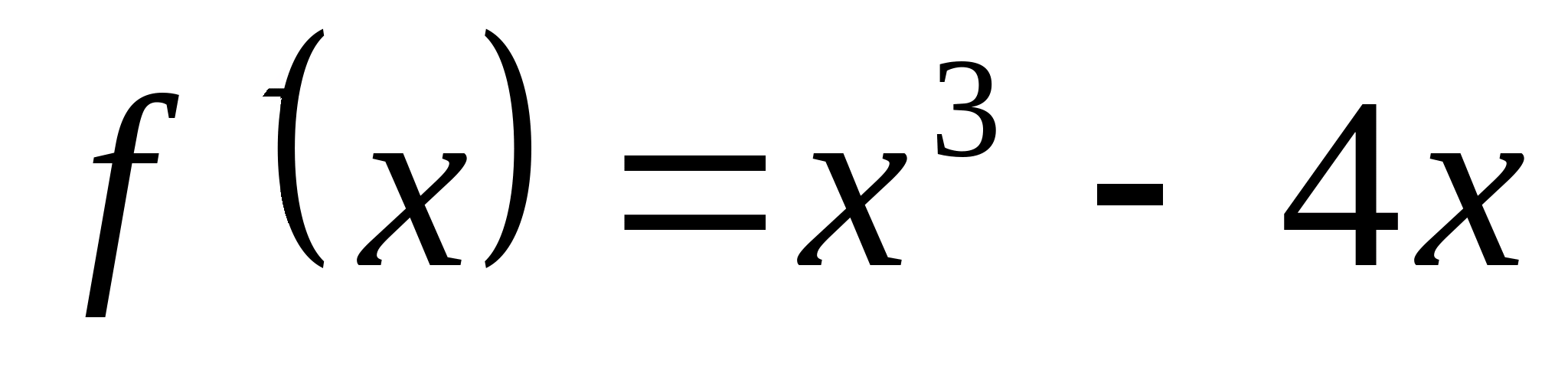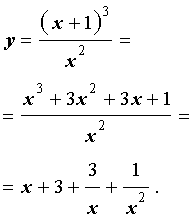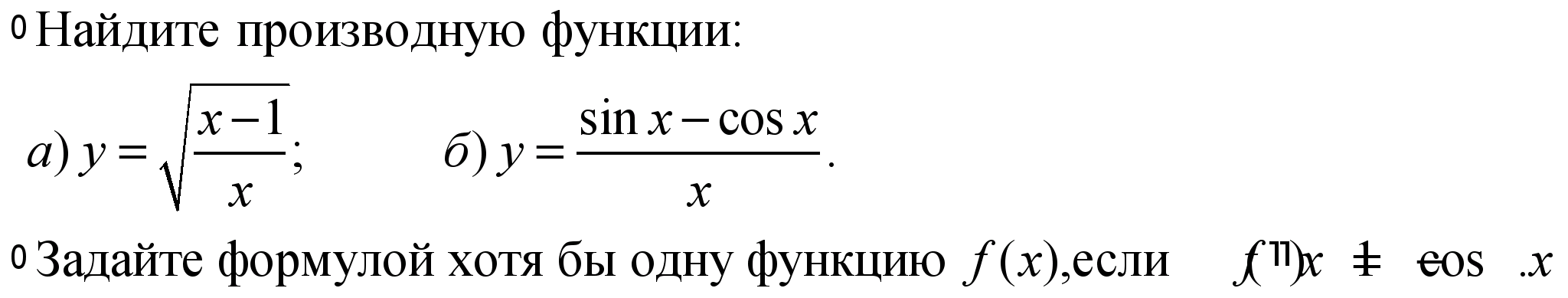Подготовка школьников к егэ (справочник по математике - элементы математического анализа - исследование поведения функций с помощью производной

Истоки математического анализа

А теперь перенесёмся из античных времён в более позднюю эпоху. Интересно, что к осознанию основ математического анализа подтолкнула Кеплера в XVII веке встреча с продавцом вина. Торговец был настолько сведущ в своей профессии, что легко мог определить объём находящегося в бочке напитка, просто опуская туда железный жгут. Размышляя над подобным курьёзом, знаменитый учёный сумел решить для себя эту дилемму. Оказывается, искусные бочары тех времён наловчились изготавливать сосуды таким образом, чтобы при определённой высоте и радиусе окружности скрепляющих колец они имели максимальную вместимость.

Это стало для Кеплера поводом для дальнейших размышлений. Бочары пришли к оптимальному решению методом долгого поиска, ошибок и новых попыток, передавая свой опыт из поколения в поколение. Но Кеплер хотел ускорить процесс и научиться делать то же самое в короткий срок путём математических вычислений. Все его наработки, подхваченные коллегами, превратились в известные ныне теоремы Ферма и Ньютона — Лейбница.

Строительство Карфагена

Существует легенда, сюжет которой построен на решении одной из экстремальных задач. Результатом делового подхода, который продемонстрировала финикийская царевна, обратившаяся за помощью к мудрецам, стало строительство Карфагена. Земельный участок для этого древнего и прославленного города подарил Дидоне (так звали правительницу) вождь одного из африканских племён. Площадь надела не показалась ему вначале очень большой, так как по договору должна была покрываться воловьей шкурой. Но царевна повелела своим воинам разрезать её на тонкие полосы и составить из них ремень. Он получился настолько длинным, что охватил участок, где уместился целый город.

Прямой метод отыскания точек условного экстремума.

Предположим, что из системы уравнений \eqref{ref1} можно выразить какие-либо $m$ переменных $x_{i}$ через остальные переменные. Тогда, подставив вместо соответствующих переменных $x_{i}$ их выражения через остальные $n-m$ переменных в функцию $f_{0}(x)$, получим функцию $F$ от $n-m$ переменных.

Задача о нахождении точек экстремума функции $f_{0}(x)$ при наличии связей \eqref{ref1} сведется к задаче нахождения обычного (безусловного) экстремума функции $F$, зависящей от $n-m$ переменных.

Пример 1.

Найти точки условного экстремума функции $z = 1-x^{2}-y^{2}$, если $x+y = 1$.

$\vartriangle$ Уравнение связи $x+y = 1$ легко разрешается относительно переменной $y$, а именно $y = 1-x$. Подставив это выражение для $y$ в функцию $z = 1-x^{2}-y^{2}$, получаем, что $z = 1-x^{2}-(1-x)^{2} = 2x-2x^{2}$. Функция $2x-2x^{2}$ имеет максимум при $x = \frac{1}{2}$. Точка $(\frac{1}{2}, \frac{1}{2})$ является точкой условного максимума функции $z(x, y)$ при наличии связи $x+y = 1$, причем $z_{\max} = \displaystyle\frac{1}{2}$. $\blacktriangle$

Замечание 1.

Прямой метод нахождения условного экстремума редко бывает эффективным ввиду трудности разрешения уравнений связей относительно какой-либо группы переменных.

Возрастание и убывание функции на интервале.

Определение возрастающей функции.

Функция y=f(x) возрастает на интервале X, если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Определение убывающей функции.

Функция y=f(x) убывает на интервале X, если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.

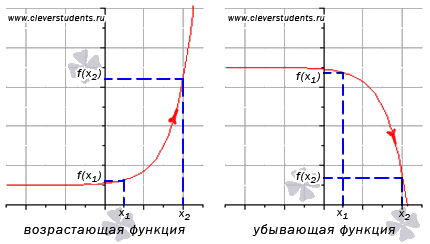
Исследование поведения функций с помощью производной

ЗАМЕЧАНИЕ: если функция определена и непрерывна в концах интервала возрастания или убывания (a;b), то есть при x=a и x=b, то эти точки включаются в промежуток возрастания или убывания. Это не противоречит определениям возрастающей и убывающей функции на промежутке X.

К примеру, из свойств основных элементарных функций мы знаем, что y=sinx определена и непрерывна для всех действительных значений аргумента. Поэтому, из возрастания функции синуса на интервале мы можем утверждать о возрастании на отрезке .

План анализа функции

Первое, что необходимо сделать, так это провести поверхностное исследование функции, в ходе которого мы найдем область определения. Итак, начнем по порядку. Область определения — это совокупность тех значений, которыми функция задается. Проще говоря, это те числа, которые можно использовать в функции вместо х. Для того чтобы определить область определения, необходимо просто взглянуть на запись. К примеру, очевидно, что у функции у (х) = х3 + х2 — х + 43 область определения — множество действительных чисел. Ну а с функцией наподобие (х2 — 2х)/х все немного иначе. Поскольку число в знаменателе не должно равняться 0, то областью определения данной функции будут все действительные числа, помимо нуля.

Далее необходимо найти так называемые нули функции. Это те значения аргумента, при которых вся функция принимает значения ноль. Для этого необходимо приравнять функцию к нулю, подробно ее рассмотреть и совершить некоторые преобразования. Возьмём уже знакомую нам функцию у(х) = (х2 — 2х)/х. Из школьного курса мы знаем, что дробь равна 0 тогда, когда числитель равен нулю. Поэтому знаменатель мы отбрасываем и начинаем работать с числителем, приравнивая его к нулю. Получаем х2 — 2х = 0 и выносим х за скобочки. Отсюда х (х — 2) = 0. В итоге получаем, что наша функция равна нулю тогда, когда х равняется 0 или же 2.

Понятие наибольшего и наименьшего значений

Определение 5

Функция $y=f(x)$, которая имеет областью определения множество $X$, имеет наибольшее значение в точке $x’\in X$, если выполняется

Определение 6

Функция $y=f(x)$, которая имеет областью определения множество $X$, имеет наименьшее значение в точке $x’\in X$, если выполняется

Чтобы найти наименьшее и наибольшее значение заданной функции на каком либо отрезке необходимо произвести следующие действия:

Найти $f'(x)$;
Найти точки, в которых $f’\left(x\right)=0$;
Найти точки, в которых $f'(x)$ не будет существовать;
Выкинуть из точек, найденных в пунктах 2 и 3 те, которые не лежат в отрезке $$;
Вычислить значения в оставшихся точках и на концах $$;
Выбрать из этих значений наибольшее и наименьшее.

Пример исследования поведения функции

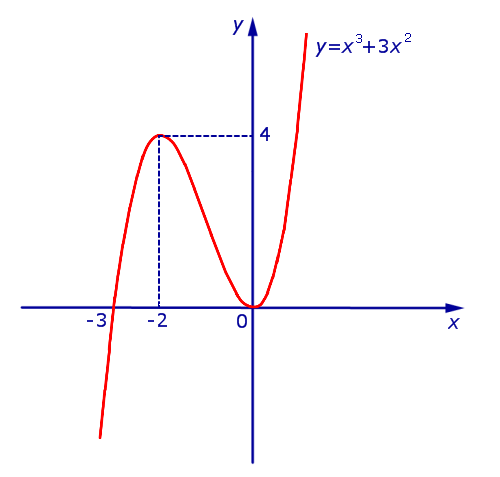
Пример. Найти интервалы , и функции

y = | x3 + 3×2 |

(1)

Решение. Исследуем сначала на , и функцию

y₁ = x3 + 3×2

(2)

и построим ее . Для этого представим формулу (2) в виде

y₁ = x2 (x + 3)

и заметим, что

а) y₁ = 0 при x = 0 и x = – 3 ,

б) y₁ > 0 при x > – 3 ; y₁ < 0 при x < – 3 .

Теперь вычислим производную функции (2):

(3)

и разложим на множители правую часть формулы (3):

(4)

На рисунке 8 при помощи метода интервалов изобразим на числовой оси знаки производной (4)

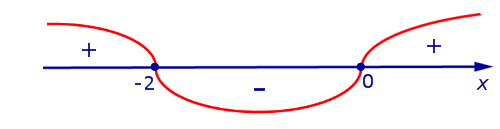
Рис.8

Поскольку решением неравенства

3x (x + 2) > 0

является множество

(5)

то в соответствии с функция y₁ на каждом из интервалов и .

С другой стороны, поскольку решением неравенства

3x (x + 2)

является интервал

(– 2, 0),

(6)

то в соответствии с функция y₁ на интервале (– 2, 0) .

Так как решениями уравнения

3x (x + 2) = 0

являются точки

x = – 2; x = 0;

(7)

то эти точки являются функции y₁ .

Поскольку при переходе через точку x = – 2 y₁ меняет знак с «+» на «–» (рис. 8), то в соответствии с точка x = – 2 является функции y₁ , при этом

y₁ (– 2) = 4 .

При переходе через точку x = 0 y₁ меняет знак с «–» на «+» (рис. 8), поэтому в соответствии с точка x = 0 является функции y₁, при этом

y₁ (0) = 0 .

Заметим, что при анализе поведения функции по знакам ее производной, удобно использовать следующую диаграмму, на которой стрелками указаны интервалы возрастания и убывания функции (рис. 9).

Рис.9

Теперь мы можем построить y₁ (рис. 10).

Рис.10

Перейдем к построению y = | x3 + 3×2 | .

В силу определения модуля, справедливо равенство

Из этого равенства вытекает, что, если мы часть y₁ = x3 + 3×2 (рис. 10), лежащую в нижней полуплоскости, оставив без изменения часть этого графика, лежащую в верхней полуплоскости, то мы получим график функции y = | x3 + 3×2 | (рис.11) .

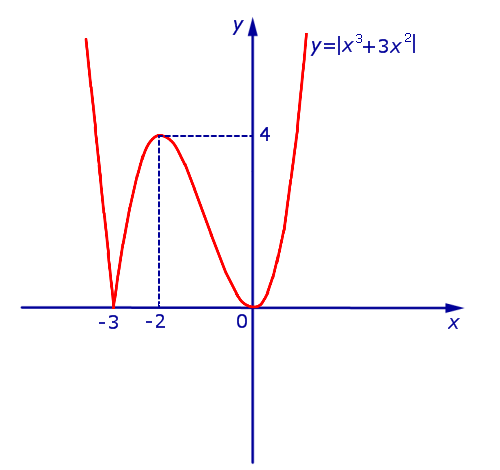
Рис.11

В точке x = – 3 производная функции y = | x3 + 3×2 | не существует. Во всех остальных точках числовой оси производная функции y = | x3 + 3×2 | существует.

Точки x = – 3 и x = 0 являются , причем y ( – 3) = y (0) = 0 .

Точка x = – 2 является , причем y ( – 2) = 4 .

Функция y = | x3 + 3×2 | на каждом из интервалов (– 3, – 2) и .

Функция y = | x3 + 3×2 | на каждом из интервалов и (– 2, 0).

Экстремумы функции

Определение 1

Точки $x_0$ называются точками экстремума функции, если они являются точками максимума и минимума для функции $f(x)$.

Определение 2

Точка $x_0$ называется точкой максимума функции $f(x)$, если существует такая окрестность данной точки, что для всех $x$ из этой окрестность выполняется неравенство $f(x)\le f(x_0)$.

Определение 3

Точка $x_0$ называется точкой максимума функции $f(x)$, если существует такая окрестность данной точки, что для всех $x$ из этой окрестность выполняется неравенство $f(x)\ge f(x_0)$.

Понятие экстремума функции тесно связано с понятием критической точки функции. Введем её определение.

Определение 4

$x_0$ называется критической точкой функции $f(x)$, если:

1) $x_0$ — внутренняя точка области определения;

2) $f’\left(x_0\right)=0$ или не существует.

Для понятия экстремума можно сформулировать теоремы о достаточных и необходимых условиях его существования.

Теорема 1

Необходимое условие экстремума

Если функция $y=f(x)$ имеет экстремум в точке $x_0$, то либо $f’\left(x_0\right)=0$, либо производная в точке $x_0$ не существует.

Теорема 2

Достаточное условие экстремума

Пусть точка $x_0$ является критической для функции $y=f(x)$ и лежит в интервале $(a,b)$. Пусть на каждом интервале $\left(a,x_0\right)\ и\ (x_0,b)$ производная $f'(x)$ существует и сохраняет постоянный знак. Тогда:

1) Если на интервале $(a,x_0)$ производная $f’\left(x\right)>0$, а на интервале $(x_0,b)$ производная $f’\left(x\right)

2) Если на интервале $(a,x_0)$ производная $f’\left(x\right)0$, то точка $x_0$ — точка минимума для данной функции.

3) Если и на интервале $(a,x_0)$, и на интервале $(x_0,b)$ производная $f’\left(x\right) >0$ или производная $f’\left(x\right)

Данная теорема проиллюстрирована на рисунке 1.

Рисунок 1. Достаточное условие существования экстремумов

Примеры экстремумов (Рис. 2).

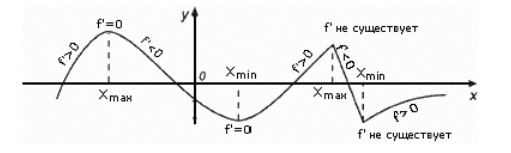Рисунок 2. Примеры точек экстремумов

Несколько замечаний о методе множителей Лагранжа.

Задачи об отыскании экстремумов функций (как числовых, так и функций более общей природы) при наличии ограничений являются весьма распространенными. Теория экстремальных задач интенсивно развивается и находит широкий круг приложений. Здесь были рассмотрены ограничения типа равенств, задаваемые достаточно гладкими функциями (гладкие связи). Метод множителей Лагранжа имеет глубокие обобщения и на более общий случай, когда ограничения задаются системой равенств и неравенств при помощи недифференцируемых в обычном смысле функций.

В конкретных прикладных вопросах множители Лагранжа имеют содержательную интерпретацию. Так, в механике множители Лагранжа задают реакции связей, а в математической экономике — цены на продукты производства. Широко развиты приближенные методы решения экстремальных задач, использующие современную вычислительную технику.

Движение

Предположим, некоторый объект движется по прямой, равномерно набирая скорость. В этот период изменение координаты тела графически представляет собой некую кривую, которую математик назвал бы ветвью параболы. При этом функция постоянно возрастает, так как показатели координаты с каждой секундой изменяются всё быстрей. График скорости демонстрирует поведение производной, значение которой также увеличивается. А значит, движение не имеет критических точек.

Так бы и продолжалось бесконечно долго. Но если тело вдруг решит затормозить, остановиться и начать двигаться в другом направлении? В данном случае показатели координаты начнут уменьшаться. А функция перейдёт критическое значение и из возрастающей превратится в убывающую.

На этом примере снова можно понять, что точки экстремума на графике функции появляются в моменты, когда она перестаёт быть монотонной.

Достаточные условия для существования экстремума функции

В следующем утверждении, доказательство которого выходит за рамки школьного курса математики и в нашем справочнике не приводится, сформулированы достаточные условия для .

Утверждение 3. Рассмотрим f (x) , в интервале (a, b), содержащем точку x , которой существует в каждой точке этого интервала, кроме, быть может, самой точки x .

а). Если для точек выполнено условие:

f ‘ (x) > 0 при x и f ‘ (x) < 0 при x > x,

то точка x является функции f (x) (рис. 6).

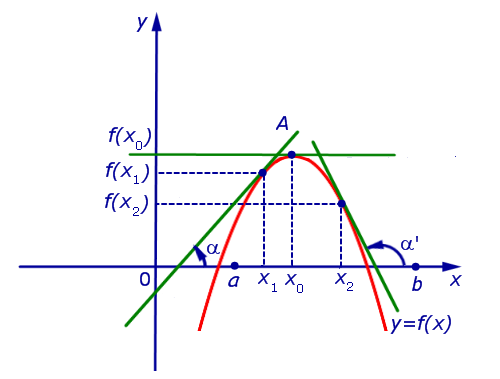
Рис.6

б). Если для точек выполнено условие:

f ‘ (x) < 0 при x < x и f ‘ (x) > 0 при x > x,

то точка x является функции f (x) (рис. 7).

Рис.7

Замечание 2. Условия а) и б) часто формулируют так: «Если при переходе через точку x меняет знак с «+» на «–» , то точка x является функции. Если при переходе через точку x меняет знак с «–» на «+» , то точка x является функции».

Достаточные условия возрастания и убывания функции.

На основании достаточных условий (признаков) возрастания и убывания функции находятся промежутки возрастания и убывания функции.

Вот формулировки признаков возрастания и убывания функции на интервале:

если производная функции y=f(x) положительна для любого x из интервала X, то функция возрастает на X;
если производная функции y=f(x) отрицательна для любого x из интервала X, то функция убывает на X.

Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:

найти область определения функции;
найти производную функции;
решить неравенства и на области определения;
к полученным промежуткам добавить граничные точки, в которых функция определена и непрерывна.

Рассмотрим пример нахождения промежутков возрастания и убывания функции для разъяснения алгоритма.

Пример.

Найти промежутки возрастания и убывания функции .

Решение.

На первом шаге нужно найти область определения функции. В нашем примере выражение в знаменателе не должно обращаться в ноль, следовательно, .

Переходим к нахождению производной функции:

Для определения промежутков возрастания и убывания функции по достаточному признаку решаем неравенства и на области определения. Воспользуемся обобщением метода интервалов. Единственным действительным корнем числителя является x = 2, а знаменатель обращается в ноль при x=0. Эти точки разбивают область определения на интервалы, в которых производная функции сохраняет знак. Отметим эти точки на числовой прямой. Плюсами и минусами условно обозначим интервалы, на которых производная положительна или отрицательна. Стрелочки снизу схематично показывают возрастание или убывание функции на соответствующем интервале.

Таким образом, и .

В точке x=2 функция определена и непрерывна, поэтому ее следует добавить и к промежутку возрастания и к промежутку убывания. В точке x=0 функция не определена, поэтому эту точку не включаем в искомые интервалы.

Приводим график функции для сопоставления с ним полученных результатов.

Ответ:

функция возрастает при , убывает на интервале (0;2].

Экстремумы функции

Для того чтобы ввести понятие наибольшего и наименьшего значения функций, вначале познакомимся с таким понятием, как экстремумы функций. Это понятие нам будет необходимо не для самого определения значений таких функций, а для построения схемы нахождения таких промежутков для конкретно заданных функций.

Определение 1

Точка $x’$ входящая в область определения функции называется точкой экстремума, если она либо будет точкой максимума, либо будет точкой минимума для функции $f(x)$.

Определение 2

Точка $x’$ будет называться точкой максимума для введенной функции $f(x)$, если у она имеет такую окрестность, что для всех точек $x$, которые входят в эту окрестность, будет верно $f(x)\le f(x'{\rm \ })$.

Определение 3

Точка $x_0$ будет называться точкой минимума для введенной функции $f(x)$, если она имеет такую окрестность, что для всех точек $x$, которые входят в эту окрестность, будет верно $f(x)\ge f(x'{\rm \ })$.

Чтобы полностью разобраться в данном понятии, далее введем понятие критической точки функции.

Определение 4

Точка $x’$ будет называться критической точкой для данной функции $f(x)$, если выполняются два следующих условия:

Точка $x’$ является внутренней точкой для области определения данной функции;
$f’\left(x'{\rm \ }\right)=0$ или не существует.

Сформулируем без доказательства теоремы о необходимом (теорема 1) и достаточном (теорема 2) условии для существования точки экстремума.

Теорема 1

Если $y=f(x)$ имеет экстремум в точке $x_0$, то либо её производная в ней равняется нулю, либо производная в ней не существует.

Теорема 2

Пусть точка $x’$ будет критической для $y=f(x)$ и принадлежит интервалу $(a,b)$, причем на каждом интервале $\left(a,x'{\rm \ }\right)\ и\ (x'{\rm \ },b)$ производная $f'(x)$ существует и сохраняет один и тот же знак. В этом случае:

Если в $(a,x'{\rm \ })$ $f’\left(x\right) >0$, а в $(x'{\rm \ },b)$ $f’\left(x\right)
Если в $(a,x'{\rm \ })$ $f’\left(x\right)0$, то $x’$ —будет точкой минимума для этой функции.
Если и в $(a,x'{\rm \ })$, и в $(x'{\rm \ },b)$ производная $имеет\ один\ и\ тот\ же\ постоянный\ знак$, то $x’$ не будет точкой экстремума для этой функции.

На рисунке 1 мы можем наглядно увидеть смысл теоремы 2.

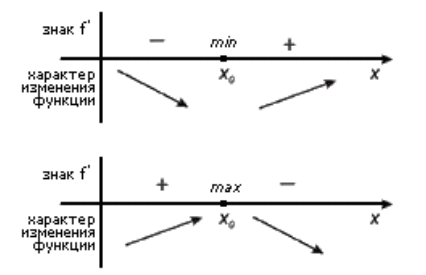Рисунок 1.

Примеры точек экстремумов вы можете видеть на рисунке 2.

Рисунок 2.

Примеры задач на исследования функций на возрастание, убывание и наличие точек экстремумов

Пример 1

Исследовать функцию на возрастание и убывание, и наличие точек максимумов и минимумов: $f(x)={2x}^3-15x^2+36x+1$

Так как первые 6 пунктов совпадают, проведем для начала их.

1) Область определения — все действительные числа;

2) $f’\left(x\right)=6x^2-30x+36$;

3) $f’\left(x\right)=0$;

\ \ \

4) $f'(x)$ существует во всех точках области определения;

5) Координатная прямая:

Рисунок 3.

6) Определить знак производной $f'(x)$ на каждом промежутке:

\ \[f’\left(x\right)7) Изобразим все на одном рисунке:

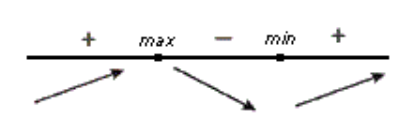Рисунок 4.

Получаем:

Функция возрастает, при $\left(-\infty ,2\right)\ (3,+\infty )$, функция убывает, при $\left(2,3\right)$.

Точка $x=2$ — точка максимума, точка $x=3$ — точка минимума.

Точки экстремума, экстремумы функции.

Точку называют точкой максимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство . Значение функции в точке максимума называют максимумом функции и обозначают .

Точку называют точкой минимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называют минимумом функции и обозначают .

Под окрестностью точки понимают интервал , где — достаточно малое положительное число.

Точки минимума и максимума называют точками экстремума, а значения функции, соответствующие точкам экстремума, называют экстремумами функции.

Не путайте экстремумы функции с наибольшим и наименьшим значением функции.

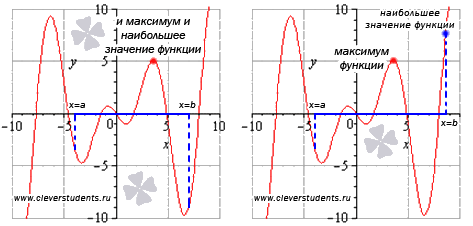
На первом рисунке наибольшее значение функции на отрезке достигается в точке максимума и равно максимуму функции, а на втором рисунке – наибольшее значение функции достигается в точке x=b, которая не является точкой максимума.

Задачи на нахождения экстремума функции

Пример 2. Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, четвертой стороной примыкала к стене. Для этого имеется a погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?

Решение. Обозначим стороны площадки через x и y. Площадь площадки равна S = xy. Пусть y — это длина стороны, примыкающей к стене. Тогда по условию должно выполняться равенство 2x +y =a. Поэтому y = a — 2x и S =x(a — 2x), где
0 ≤x ≤a/2 (длина и ширина площадки не могут быть отрицательными).
S ‘ = a — 4x, a — 4x = 0 при x = a/4, откуда
y = a — 2×a/4 = a/2. Поскольку x = a/4 — единственная критическая точка, проверим, меняется ли знак производной при переходе через эту точку. При x < a/4, S ‘ > 0, a при x > a/4, S ‘< 0, значит, в точке x = a/4 функция S имеет максимум. Значение функции S(a/4) = a/4(a — a/2) = a2 /8 (кв. ед). Поскольку S непрерывна на [0,a/2] и ее значения на концах S(0) и S(a/2) равны нулю, то найденное значение будет наибольшим значением функции. Таким образом, наиболее выгодным соотношением сторон площадки при данных условиях задачи является y = 2x.

Пример 3. Требуется изготовить закрытый цилиндрический бак вместимостью V=16p ≈ 50 м3. Каковы должны быть размеры бака (радиус R и высота Н), чтобы на его изготовление пошло наименьшее количество материала?

Решение. Площадь полной поверхности цилиндра равна S = 2pR(R+Н). Мы знаем объем цилиндра V = pR2Н Þ Н = V/pR2 =16p/pR2 = 16/R2. Значит, S(R) = 2p(R2+16/R). Находим производную этой функции:
S ‘ (R) = 2p(2R- 16/R2) = 4p (R- 8/R2). S ‘(R) = 0 при R3 = 8, следовательно,
R = 2, Н = 16/4 = 4.

Пример 4. Найти экстремумы функцииf(x) = 2×3 — 15×2+ 36x — 14.

Решение. Так как f ‘(x) = 6×2 — 30x +36 = 6(x -2)(x — 3), то критические точки функции x₁ = 2 и x₂ = 3. Экстремумы могут быть только в них. Так как при переходе через x₁ = 2 производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через x₂ = 3 производная меняет знак минус на плюс, поэтому в точке x₂ = 3 у функции минимум. Вычислив значения функции при
x₁ = 2 и x₂ = 3, найдем экстремумы функции: максимумf(2) = 14 и минимумf(3) = 13.

Пример 5. Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, четвертой стороной примыкала к стене. Для этого имеется c погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?

Решение. Обозначим стороны площадки через x и y. Площадь площадки равна S = xy. Пусть y — это длина стороны, примыкающей к стене. Тогда по условию должно выполняться равенство 2x +y =c. Поэтому y = c — 2x и S = x(c — 2x), где
0 ≤x ≤c/2 (длина и ширина площадки не могут быть отрицательными). S ‘ = c — 4x, c — 4x = 0 при x = c/4, откуда
y = c — 2c/4 = c/2. Поскольку x = c/4 — единственная критическая точка, проверим, меняется ли знак производной при переходе через неё. Приx < c/4, S ‘ > 0, при x >c/4 S ‘< 0, значит, при x=c/4 функция S имеет максимум. Значение функции S(c/4) = c/4(c — c/2) = c2 /8 (кв. ед). Поскольку S непрерывна на [0,c/2] и ее значения на концах S(0) и S(c/2) равны нулю, то найденное значение будет наибольшим значением функции. Таким образом, наиболее выгодным соотношением сторон площадки при данных условиях задачи является y = 2x.

«Подозрительные» на наличие экстремума точки функции.Теорема Ферма

Определение 4.Стационарной точкой функции называют такую точку, в которой функции равна нулю.

Определение 5.Критической точкой функции называют такую точку, в которой функции равна нулю или не существует.

Таким образом, если точка x является критической точкой функции, то точка x либо является стационарной точкой функции, либо производная функции в точке x не существует.

Теорема Ферма. Если точка x является f (x) , то точка x является критической точкой функции f (x) .

Доказательство. Если в точке x у функции y = f (x) не существует , то точка x является критической точкой по определению. Докажем, что если в точке x у функции y = f (x) существует , то точка x является стационарной, то есть f ‘ (x) = 0 .

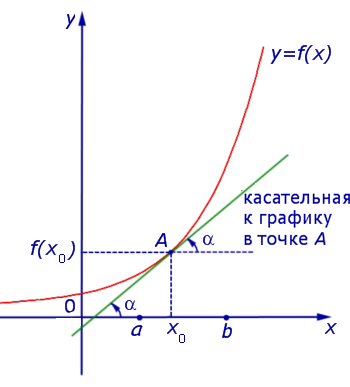
Предположим сначала, что точка x является y = f (x) (рис. 5).

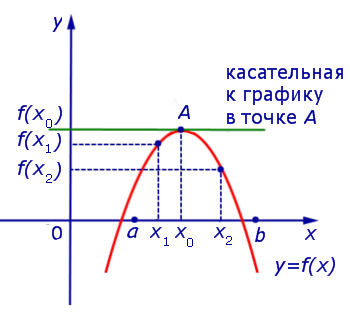
Рис.5

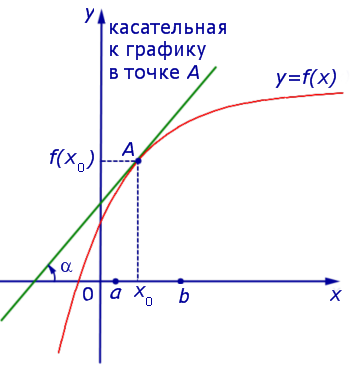
Поскольку x – точка максимума, то для любой точки x₁ такой, что x₁x , выполнено неравенство f (x₁) < f (x) , поэтому

Точно так же, для любой точки x₂ такой, что x₂ > x , выполнено неравенство f (x₂) < f (x) , поэтому

Таким образом, в случае, когда точка x является y = f (x), выполнено равенство f ‘ (x) = 0 . Касательная к графику функции y = f (x) в точке A= (x; f (x)) параллельна оси Ox.

Совершенно аналогично доказывается, что и в случае, когда точка x является y = f (x), выполнено равенство f ‘ (x) = 0 .

Замечание 1. Из утверждения 2 следует, что (точки максимумов и точки минимумов) нужно искать лишь среди критических точек функции, так как в других (некритических) точках экстремумов быть не может. По этой причине критические точки функции часто называют точками, подозрительными на экстремум.

Угол наклона

Легко можно определить по рисунку, как изменяется производная функции. Если прямые линии графика с течением времени идут вверх, то она положительна. И чем они круче, тем большее значение принимает производная, так как растет угол наклона. В периоды убывания эта величина принимает отрицательные значения, в точках экстремума обращаясь в ноль, а график производной в последнем случае рисуется параллельно оси ОХ.

Любой другой процесс следует рассматривать аналогичным образом. Но лучше всего об этом понятии может рассказать перемещение различных тел, наглядно показанное на графиках.

Оптимальное решение

Не стоит объяснять, насколько может оказаться важным в выполнении практических заданий выбор оптимального решения. Ведь путей достижения цели бывает много, а наилучший выход, как правило, — всего один. Это бывает крайне необходимо, к примеру, при конструировании судов, космических кораблей и самолётов, архитектурных сооружений для нахождения оптимальной формы данных рукотворных объектов.

Быстроходность средств передвижения во многом зависит от грамотного сведения к минимуму сопротивления, которое они испытывают при перемещении по воде и воздуху, от перегрузок, возникающих под действием гравитационных сил и многих других показателей. Кораблю на море необходимы такие качества, как устойчивость во время шторма, для речного судна важна минимальная осадка. При расчётах оптимальной конструкции точки экстремума на графике наглядно могут дать представление о наилучшем решении сложной проблемы. Задачи такого плана часто решаются в экономике, в хозяйственных областях, во множестве других жизненных ситуаций.