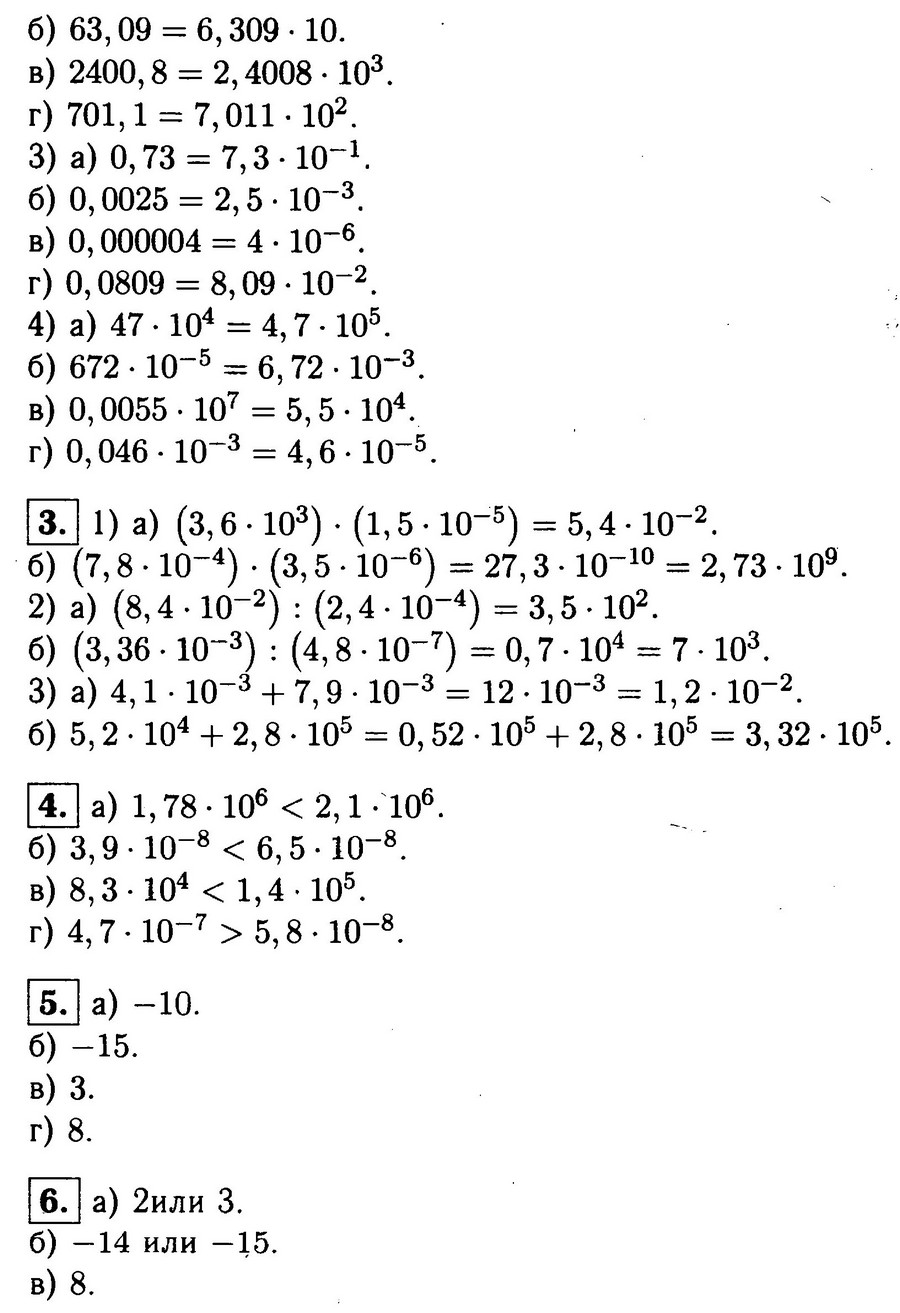Стандартный вид числа. 8-й класс

Экспоненциальная запись числа в компьютере

Представление чисел в приложениях

Основная масса прикладных программ для компьютера обеспечивает представление чисел в удобной для восприятия человеком форме, т.е. в десятичной системе счисления.

На компьютере (в частности в языках программирования высокого уровня) числа в экспоненциальном формате (его ещё называют научным) принято записывать в виде MEp,
где:

M — мантисса,

E — экспонента (от англ. «exponent»), означающая «·10» («…умножить на десять в степени…»),

p — порядок.

Например:

1,602176565E-19=1,602176565⋅10−19{\displaystyle {\text{1,602176565E-19}}=1{,}602176565\cdot 10^{-19}} (элементарный заряд в Кл);

1,380650424E-23=1,380650424⋅10−23{\displaystyle {\text{1,380650424E-23}}=1{,}380650424\cdot 10^{-23}} (Постоянная Больцмана в Дж/К);

6,02214129E23=6,02214129⋅1023{\displaystyle {\text{6,02214129E23}}=6{,}02214129\cdot 10^{23}} (число Авогадро).

В программировании часто используют символ «+» для неотрицательного порядка и ведущие нули, а в качестве десятичного разделителя — точку:

1.048576E+06=1048576; 3.14E+00=3,14{\displaystyle {\text{1.048576E+06}}=1\,048\,576;~{\text{3.14E+00}}=3,14}.

Для улучшения читаемости иногда используют строчную букву e: 6,02214129e23{\displaystyle {\text{6,02214129e23}}}

Внутренний формат представления чисел

Внутренний формат представления вещественных чисел в компьютере тоже является экспоненциальным, но основанием степени выбрано число 2 вместо 10. Это связано с тем, что все данные в компьютере представлены в двоичной форме (битами). Под число отводится определённое количество компьютерной памяти (часто это 4 или 8 байт). Там содержится следующая информация.

Знаковый бит (он обычно занимает старшее место), который указывает знак числа. Установленный бит говорит о том, что число отрицательное (исключение может составлять число ноль — иногда он тоже может иметь установленный знаковый бит).
Порядок — целое число, которое задаёт нужную степень двойки. Обычно это не истинная величина порядка, а сдвинутая на некоторую константу таким образом, чтобы число было неотрицательным. Так, наименьший возможный порядок (он отрицательный) представлен числом 0.
Мантисса (обычно за исключением старшего бита, который всегда установлен в нормализованном числе).

Более подробно форматы представления чисел описаны стандартом IEEE 754-2008.

Когда применять стандартную запись

По идее, стандартная запись числа должна сделать дробные вычисления еще проще. Но на практике заметный выигрыш получается только при выполнении операции сравнения. Потому что сравнение чисел, записанных в стандартном виде, выполняется так:

Сравнить степени десятки. Наибольшим будет то число, у которого эта степень больше;
Если степени одинаковые, начинаем сравнивать значащие цифры — как в обычных десятичных дробях. Сравнение идет слева направо, от старшего разряда к младшему. Наибольшим будет то число, в котором очередной разряд окажется больше;
Если степени десятки равны, а все разряды совпадают, то сами дроби тоже равны.

Разумеется, все это верно только для положительных чисел. Для отрицательных чисел все знаки меняются на противоположные.

Замечательно свойство дробей, записанных в стандартном виде, заключается в том, что к их значащей части можно приписывать любое количество нулей — как слева, так и справа. Аналогичное правило существует для других десятичных дробей (см. урок «Десятичные дроби »), но там есть свои ограничения.

8,0382 · 10 6 и 1,099 · 10 25 . Оба числа положительные, причем у первого степень десятки меньше, чем у второго (6
1,76 · 10 3 и 2,5 · 10 −4 . Числа снова положительные, причем степень десятки у первого из них больше, чем у второго (3 > −4). Следовательно, 1,76 · 10 3 > 2,5 · 10 −4 ;
2,215 · 10 11 и 2,64 · 10 11 . Числа положительные, степени десятки совпадают. Смотрим на значащую часть: первые цифры тоже совпадают (2 = 2). Различие начинается на второй цифре: 2
−1,3975 · 10 3 и −3,28 · 10 4 . Это отрицательные числа. У первого степень десятки меньше (3 −3,28 · 10 4 ;
−1,0015 · 10 −8 и −1,001498 · 10 −8 . Снова отрицательные числа, причем степени десятки совпадают. Также совпадают и первые 4 разряда значащей части (1001 = 1001). На 5 разряде начинается отличие, а именно: 5 > 4. Поскольку исходные числа отрицательные, заключаем: −1,0015 · 10 −8

Хотели бы вы научиться записывать огромные или очень маленькие числа в простой форме? Эта статья содержит необходимые объяснения и очень четкие правила о том, как это сделать. Теоретический материал поможет разобраться в этой довольно легкой теме.

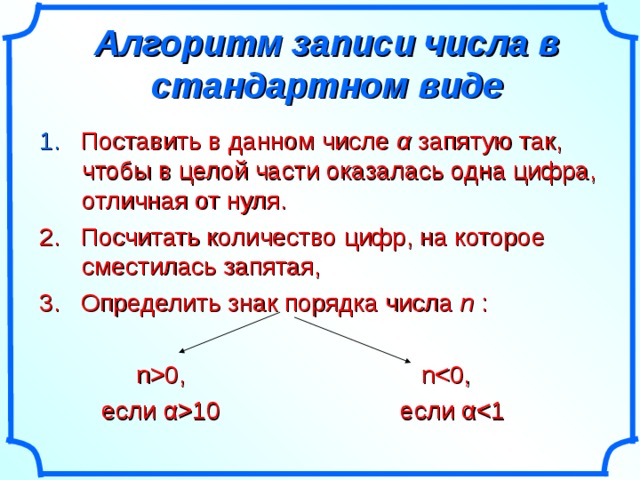
Нормализованная запись

Любое данное число может быть записано в виде M⋅10p{\displaystyle M\cdot 10^{p}} многими путями; например 350 может быть записано как 3,5⋅102{\displaystyle 3{,}5\cdot 10^{2}} или 35⋅101{\displaystyle 35\cdot 10^{1}}.

В нормализованной научной записи порядок p{\displaystyle p} выбирается такой, чтобы абсолютная величина M{\displaystyle M} оставалась не меньше единицы, но строго меньше десяти (1≤|M|<10{\displaystyle 1\leq |M|<10}). Например, 350 записывается как 3,5⋅102{\displaystyle 3{,}5\cdot 10^{2}}. Этот вид записи, называемый также стандартным видом, позволяет легко сравнивать два числа. Кроме того, он удобен для десятичного логарифмирования: целая часть логарифма, записанного «в искусственной форме», равна порядку числа, дробная часть логарифма определяется из таблицы только по мантиссе, что было крайне важным до массового распространения калькуляторов в 1970-х годах.

В инженерной нормализованной записи (в том числе в информатике), мантисса обычно выбирается в пределах ,1<|a|⩽1{\displaystyle 0{,}1<|a|\leqslant 1}: 350=,35⋅103{\displaystyle 350=0,35\cdot 10^{3}}[источник не указан 360 дней].

В некоторых калькуляторах, как опция, может быть использована запись с мантиссой 1≤|a|<1000{\displaystyle 1\leq |a|<1000} и с порядком, кратным 3, так, например, 3,52⋅10−8{\displaystyle 3{,}52\cdot 10^{-8}} записывается как 35,2⋅10−9{\displaystyle 35{,}2\cdot 10^{-9}}. Такая запись проста для чтения (640⋅106{\displaystyle 640\cdot 10^{6}} легче прочесть, как «640 миллионов», чем 6,4⋅108{\displaystyle 6{,}4\cdot 10^{8}}) и удобна для выражения физических величин в единицах измерения с десятичными приставками: кило-, микро-, тера- и так далее.

Когда применять стандартную запись

Сравнить степени десятки. Наибольшим будет то число, у которого эта степень больше;
Если степени одинаковые, начинаем сравнивать значащие цифры — как в обычных десятичных дробях. Сравнение идет слева направо, от старшего разряда к младшему. Наибольшим будет то число, в котором очередной разряд окажется больше;
Если степени десятки равны, а все разряды совпадают, то сами дроби тоже равны.

Замечательно свойство дробей, записанных в стандартном виде, заключается в том, что к их значащей части можно приписывать любое количество нулей — как слева, так и справа. Аналогичное правило существует для других десятичных дробей (см. урок «Десятичные дроби»), но там есть свои ограничения.

8,0382 · 106 и 1,099 · 1025. Оба числа положительные, причем у первого степень десятки меньше, чем у второго (6 < 25). Значит, 8,0382 · 106 < 1,099 · 1025;
1,76 · 103 и 2,5 · 10−4. Числа снова положительные, причем степень десятки у первого из них больше, чем у второго (3 > −4). Следовательно, 1,76 · 103 > 2,5 · 10−4;
2,215 · 1011 и 2,64 · 1011. Числа положительные, степени десятки совпадают. Смотрим на значащую часть: первые цифры тоже совпадают (2 = 2). Различие начинается на второй цифре: 2 < 6, поэтому 2,215 · 1011 < 2,64 · 1011;
−1,3975 · 103 и −3,28 · 104. Это отрицательные числа. У первого степень десятки меньше (3 < 4), поэтому (в силу отрицательности) само число будет больше: −1,3975 · 103 > −3,28 · 104;
−1,0015 · 10−8 и −1,001498 · 10−8. Снова отрицательные числа, причем степени десятки совпадают. Также совпадают и первые 4 разряда значащей части (1001 = 1001). На 5 разряде начинается отличие, а именно: 5 > 4. Поскольку исходные числа отрицательные, заключаем: −1,0015 · 10−8 < −1,001498 · 10−8.

Тест на тему «Значащая часть числа»
Умножение и деление десятичных дробей
Пробный ЕГЭ 2012. Вариант 7 (без производных)
Метод координат в пространстве
Задача B8: отрезки и углы в треугольниках
Задача B5: метод узлов