Соотношение

Содержание

Серьезные отношения для нас

Для большинства людей главным является не только вопрос, что такое серьезные отношения, но еще и то, как построить настоящие отношения. Психологи советуют смотреть на ситуацию со стороны. Любые отношение начинаются с влюбленности (психология любви). Социальность в характере любимого человека практически не замечается. Если же какие отрицательные черты и проявляются, то существует убеждения, что от них можно избавиться. Почему-то, каждый верит, что любимого человека можно изменить и сделать таким, каким его хочется видеть.

Психологи называют это одной из главных ошибок, которую можно допустить вначале любых отношений. Для того чтобы создавать по-настоящему серьезные отношения, требуется реально смотреть на отрицательные черты, а также то, как любимый человек ведет себя с другими. Следует четко понимать, что все это будет присутствовать дальше в семейной жизни.

Для того чтобы создать настоящие серьезные отношения, необходимо постоянно прислушиваться к себе. Нужно четко понимать то, что в этот момент и создаются те отношения и жизнь, о которой так все мечтают. В обязательном порядке следует оговаривать любые непонимания. Таким образом, исчезнут любые сомнения в проблемных ситуациях.

Наиболее часто мы можем наблюдать за тем, как создаются и развиваются отношения у представителей звездного мира, а также всех, кто постоянно находится на виду. Британский актер Патрик Стюарт много раз повторял, что любовь является самой сильной со всех страстей. Она завладевает не только телом, но еще и сердцем, головой. Это один из наиболее лаконичных ответов на вопрос, что такое серьезные отношения. Такой же позиции придерживаются и многие другие знаменитости, которые постоянно скрывают свою личную жизнь от окружающих.

Обозначения и термины

Соотношение чисел A и B можно представить как:

• отношение A к B
• A:B
• долю A (рациональное число), которая представляет собой результат деления A на B
• AB{\displaystyle {\tfrac {A}{B}}}

Числа A и B в данном контексте иногда называют членами (terms), где A — антецедент, а B — консеквент.

Пропорция, выражающая равенство соотношений A:B и C:D, записывается как
A:B=C:D или A:B::C:D. Читается:

A относится к B как C относится к D.

И в данном случае, A, B, C, D называются членами пропорции. A и D — крайние члены пропорции, а B и C — средние члены. Равенство трёх и более соотношений называется непрерывной пропорцией (continued proportion, ряд отношений).

Иногда в соотношениях три и более членов. Например, размеры предмета с сечением два к четырём и длиной десять сантиметров составят 2:4:10.

Пропорции

Если два или более количества, состоящих в пропорциональном соотношении, являются всеми количествами, задействованными в конкретной ситуации, например, два яблока и три апельсина в корзине, в которой нет других фруктов, то можно сказать, что «целое» содержит пять частей, состоящих из двух частей яблок и трёх частей апельсинов. В данном случае, 25{\displaystyle {\tfrac {2}{5}}}, или 40 % целого, — это яблоки, а 35{\displaystyle {\tfrac {3}{5}}}, или 60 % целого, — это апельсины. Такое сравнение определённого количества с «целым» иногда называют пропорцией. Пропорции иногда выражают в процентах, как указано выше.

Другие применения

• Соотношения часто используются для простых растворов в химии и биологии (степень разбавления).
• Шансы выигрыша в играх выражают в виде соотношения.
• Возможны соотношения количеств, измеряемых в разных единицах измерения.

Обозначения и термины

Соотношение чисел A и B можно представить как:

• отношение A к B
• A:B
• долю A (рациональное число), которая представляет собой результат деления A на B
• AB{\displaystyle {\tfrac {A}{B}}}

Числа A и B в данном контексте иногда называют членами (terms), где A — антецедент, а B — консеквент.

Пропорция, выражающая равенство соотношений A:B и C:D, записывается как
A:B=C:D или A:B::C:D. Читается:

A относится к B как C относится к D.

И в данном случае, A, B, C, D называются членами пропорции. A и D — крайние члены пропорции, а B и C — средние члены. Равенство трёх и более соотношений называется непрерывной пропорцией (continued proportion, ряд отношений).

Иногда в соотношениях три и более членов. Например, размеры предмета с сечением два к четырём и длиной десять сантиметров составят 2:4:10.

Свойство отношения

Отношение не изменится если его члены умножить или разделить на одно и тоже число.

Это одно из важнейших свойств отношения следует из свойства частного. Мы знаем, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится. А поскольку отношение является ничем иным как делением, то свойство частного работает и для него.

Вернемся к отношению девочек к мальчикам (10 : 5). Данное отношение показало, что на каждого мальчика приходится две девочки. Проверим, как работает свойство отношения, а именно попробуем умножить или разделить его члены на одно и то же число.

В нашем примере удобнее разделить члены отношения  на их наибольший общий делитель (НОД).

НОД членов 10 и 5 это число 5. Поэтому можно разделить члены отношения на число 5

Получили новое отношение . Это есть отношение два к одному (2:1). Данное отношение, как и прошлое отношение 10:5 показывает, что на одного мальчика приходятся две девочки.

На рисунке показано отношение 2 : 1 (два к одному). Как и в прошлом отношении 10 : 5 на одного мальчика приходятся две девочки. Другими словами, отношение не изменилось.

Пример 2. В одном классе 10 девочек и 5 мальчиков. В другом классе 20 девочек и 10 мальчиков. Во сколько раз в первом классе девочек больше мальчиков? Во сколько раз во втором классе девочек больше мальчиков?

В обоих классах девочек  в два раза больше мальчиков, поскольку отношения    и    равны одному и тому же числу.

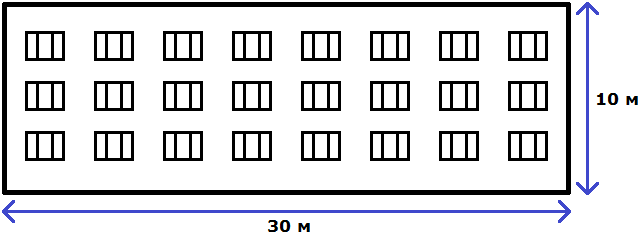
Свойство отношения позволяет строить различные модели, которые имеют схожие параметры с реальным объектом. Предположим, что многоквартирный дом имеет ширину 30 метров и высоту 10 метров.

Чтобы нарисовать на бумаге похожий дом, нужно рисовать его в таком же отношении 30 : 10.

Разделим оба члена этого отношения на число 10. Тогда получим отношение 3 : 1. Это отношение равно 3, как и предыдущее отношение равно 3

Переведем метры в сантиметры. 3 метра это 300 сантиметров, а 1 метр это 100 сантиметров

3 м = 300 см

1  м = 100 см

Имеем отношение 300 см : 100 см. Разделим члены этого отношения на 100. Получим отношение 3 см : 1 см. Теперь можно нарисовать дом с шириной 3 см и высотой 1 см

Конечно нарисованный дом намного меньше реального дома, но неизменным осталось отношение ширины и высоты. Это позволило нам нарисовать дом, максимально похожий на реальный

Отношение можно понимать и другим образом. Изначально было сказано, что у реального дома ширина составляет 30 метров, а высота 10 метров. Итого получается 30+10, то есть 40 метров.

Эти 40 метров можно понимать, как 40 частей. Отношение 30 : 10 говорит о том, что 30 частей приходится на ширину, а 10 частей на высоту.

Далее члены отношения 30 : 10 были разделены на 10. В результате получилось отношение 3 : 1. Это отношение можно понимать, как 4 части, три из которых приходится на ширину, одна — на высоту. В этом случае обычно требуется узнать сколько конкретно метров приходится на ширину и высоту.

Другими словами, нужно узнать сколько метров приходится на 3 части и сколько метров приходится на 1 часть. Сначала надо узнать сколько метров приходится на одну часть. Для этого общие 40 метров нужно разделить на 4, поскольку в отношении 3 : 1 всего четыре части

40 м : 4 = 10 м

Далее с помощью умножения определяют сколько метров приходятся на ширину и высоту. Члены, которые даны в отношении используют в качестве сомножителя.

Определим сколько метров приходится на ширину:

10 м × 3 = 30 м

Определим сколько метров приходится на высоту:

10 м × 1 = 10 м

Шаги

Метод 1 из 2:

Запись соотношений

1. 1

   Обозначение соотношений. При написании соотношений используют следующие символы: косая черта (/), двоеточие (:), или предлог «к». Например, если вы хотите записать соотношение для выражения «на вечеринке на каждые пять мужчин приходятся три женщины», то сделайте это так:

   • 5 мужчин/3 женщинам
   • 5 мужчин:3 женщинам
   • 5 мужчин к 3 женщинам

2. 2

   Запишите значение первой данной величины слева от символа соотношения.

   Пример: 20 г муки.

   Не забывайте про величины, с которыми вы работаете (мужчины или женщины, куры или козы, метры или сантиметры).

3. 3

   Запишите значение второй данной величины справа от символа соотношения.

   Пример: 20 г муки/8 г сахара.

   Не забывайте про величины, с которыми вы работаете.

4. 4

   Упростите соотношение (по желанию). Для этого разделите оба члена (числа) соотношения на наибольший общий делитель (НОД), то есть наибольшее число, на которое делятся оба члена соотношения. (Процесс упрощения соотношения аналогичен процессу упрощения дроби.)

   • В нашем примере найдите НОД чисел 20 и 8. Для этого запишите все делители этих чисел (делители – числа, которые делят данное число без остатка). Затем найдите наибольший делитель, который присутствует в списке делителей как 20, так и 8. Вот как это делается:
     • 20: 1, 2, 4, 5, 10, 20
     • 8: 1, 2, 4, 8
   • В нашем примере НОД=4. Чтобы упростить соотношение, разделите 20 и 8 на 4:
   • 20/4 = 5
   • 8/4 = 2

5. 5

   Преобразуйте соотношение в проценты (по желанию). Для этого выполните следующие действия:

   • Разделите первое число на второе. Пример: 5/2 = 2,5.
   • Умножьте полученный результат на 100. Пример: 2,5*100 = 250.
   • Напишите знак процента: 250%.
   • Это означает, что на 1 единицу сахара приходится 2,5 единицы муки; аналогично, для приготовления блюда нужно взять 250% сахара (по сравнению с мукой).

Метод 2 из 2:

Дополнительная информация о соотношениях

1. 1

   Порядок членов в соотношении не имеет значения. Выражение «5 яблок к 3 грушам» аналогично выражению «3 груши к 5 яблокам». Таким образом, 5 яблок/3 грушами = 3 груши/5 яблокам.

2. 2

   Соотношение может быть использовано для описания вероятности. Например, вероятность выбросить число 2 на одной игральной кости составляет 1/6, или один из шести. Примечание: если вы используете соотношение для описания вероятности, то порядок членов имеет значение.

3. 3

   Вы можете увеличивать или уменьшать соотношение. При упрощении соотношения вы уменьшаете его, но вы можете и увеличивать соотношение. Например, вы знаете, что для приготовления 100 г макарон нужно 2 стакана воды (соотношение: 2 стакана воды/100 г макарон). Если вы хотите узнать, сколько стаканов воды требуется для приготовления 200 г макарон, разделите 200 на 100 и получите 2. Затем полученное значение умножьте на 2 стакана (2*2=4). Таким образом, увеличенное соотношение запишется так: 4 стакана воды/200 г макарон (то есть для приготовления 200 г макарон требуется 4 стакана воды).

Деление в данном отношении

Иногда приходится делить какую-либо величину на части в заданном отношении, например, разделить 30 конфет в отношении 3:2, разделить 30 кг сахара в отношении
7:6 и т.д.

Запомните правило: чтобы разделить число в отношении a:b необходимо:
1. Сложить члены отношения a и b.
2. Разделить число на сумму a и b .
3. Умножить частное на a ∙ a.
4. Умножить частное на b ∙ b.

Вы можете воспользоваться калькулятором деления числа в данном отношении и получить подробное решение.

Приведем примеры на деление числа в данном отношении:

Пример 1. Разделить число 16 в отношении 6:3
1) = 10,6667
2) = 5,3333
Ответ: 10,6667; 5,3333

Пример 2. Разделить число 370 в отношении 15:27
1) = 132,1429
2) = 237,85
Ответ: 132,1429; 237,85

Пример 3. Разделить дробь в отношении 4:3
1)
2)
Ответ:

Пример 4. Пусть необходимо разделить 30 конфет между двумя мальчиками в отношении 2:3.
Решение:
1) = 12
2) = 18
Значит, первому мальчику нужно дать 12 конфет, а второму 18.

Пример 5. Мария Ивановна и Анастасия Михайловна сложили деньги, чтобы закупить семена укропа. Мария Ивановна потратила 26 рублей, а Анастасия
Михайловна 135 рублей. Спустя время урожай укропа собрали и продали. Выручка составила 750 рублей. Как Мария Ивановна и Анастасия Михайловна должны поделить вырученные деньги?
Решение: чтобы разделить деньги между женщинами, необходимо разделить 750 рублей в том отношении, в котором они эти деньги вложили в урожай укропа,
то есть 26:135, следовательно:
1) Мария Ивановна получит = 121,118 руб.
2) Анастасия Михайловна = 628,881 руб.

Пример 6. Пусть необходимо разделить 100 кг сахара между тремя столовыми в отношении 2:6:12.
Решение:
1) = 10
2) = 30
3) = 60
Ответ: первая столовая получит 10 кг сахара, вторая 30 кг сахара и третья 60 кг сахара.

Поделиться публикацией

Пропорции

Если два или более количества, состоящих в пропорциональном соотношении, являются всеми количествами, задействованными в конкретной ситуации, например, два яблока и три апельсина в корзине, в которой нет других фруктов, то можно сказать, что «целое» содержит пять частей, состоящих из двух частей яблок и трёх частей апельсинов. В данном случае, 25{\displaystyle {\tfrac {2}{5}}}, или 40 % целого, — это яблоки, а 35{\displaystyle {\tfrac {3}{5}}}, или 60 % целого, — это апельсины. Такое сравнение определённого количества с «целым» иногда называют пропорцией. Пропорции иногда выражают в процентах, как указано выше.

Другие применения

• Соотношения часто используются для простых растворов в химии и биологии (степень разбавления).
• Шансы выигрыша в играх выражают в виде соотношения.
• Возможны соотношения количеств, измеряемых в разных единицах измерения.

Несколько членов отношения

Если в отношении дано несколько членов, то их можно понимать как части от чего-либо.

Пример 1. Куплено 18 яблок. Эти яблоки разделили между мамой, папой и дочкой в отношении 2 : 1 : 3. Сколько яблок получил каждый?

Отношение 2 : 1 : 3 говорит о том, что мама получила 2 части, папа — 1 часть, дочка — 3 части. Другими словами, каждый член отношения 2 : 1 : 3 это определенная часть от 18 яблок:

Если сложить члены отношения 2 : 1 : 3, то можно узнать сколько всего частей имеется:

2 + 1 + 3 = 6 (частей)

Узнаем сколько яблок приходится на одну часть. Для этого 18 яблок разделим на 6

18 : 6 = 3 (яблока на одну часть)

Теперь определим сколько яблок получил каждый. Умножая три яблока на каждый член отношения 2 : 1 : 3, можно определить сколько яблок получила мама, сколько получил папа и сколько получила дочка.

Узнаем сколько яблок получила мама:

3 × 2 = 6 (яблок)

Узнаем сколько яблок получил папа:

3 × 1 = 3 (яблока)

Узнаем сколько яблок получила дочка:

3 × 3 = 9 (яблок)

Пример 2. Новое серебро (альпака) — это сплав никеля, цинка и меди в отношении 3 : 4 : 13. Сколько килограммов каждого металла нужно взять, чтобы получить 4 кг нового серебра?

4 килограмма нового серебра будет содержать 3 части никеля, 4 части цинка и 13 частей меди. Сначала узнаем сколько всего частей будет в четырех килограммах серебра:

3 + 4 + 13 = 20 (частей)

Определим сколько килограммов будет приходиться на одну часть:

4 кг : 20 = 0,2 кг

Определим сколько килограммов никеля будет содержáться в 4 кг нового серебра. В отношении 3 : 4 : 13 указано, что три части сплава содержат никель. Поэтому умножаем 0,2 на 3:

0,2 кг × 3 = 0,6 кг никеля

Теперь определим сколько килограммов цинка будет содержáться в 4 кг нового серебра. В отношении 3 : 4 : 13 указано, что четыре части сплава содержат цинк. Поэтому умножаем 0,2 на 4:

0,2 кг × 4 = 0,8 кг цинка

Теперь определим сколько килограммов меди будет содержáться в 4 кг нового серебра. В отношении 3 : 4 : 13 указано, что тринадцать частей сплава содержат медь. Поэтому умножаем 0,2 на 13:

0,2 кг × 13 = 2,6 кг меди

Значит, чтобы получить 4 кг нового серебра, нужно взять 0,6 кг никеля, 0,8 кг цинка и 2,6 кг меди.

Пример 3. Латунь — это сплав меди и цинка, массы которых относятся как 3 : 2. Для изготовления куска латуни требуется 120 г меди. Сколько требуется цинка для изготовления этого куска латуни?

Определим сколько граммов сплава приходится на одну часть. В условии сказано, что для изготовления куска латуни требуется 120 г меди. Также сказано, что три части сплава содержат медь. Если разделить 120 на 3, мы узнаем сколько граммов сплава приходится на одну часть:

120 : 3 = 40 граммов на одну часть

Теперь определим сколько требуется цинка для изготовления куска латуни. Для этого 40 граммов умножим на 2, поскольку в отношении 3 : 2 указано, что две части содержат цинк:

40 г × 2 = 80 граммов цинка

Пример 4. Взяли два сплава золота и серебра. В одном количество этих металлов находится в отношении 1 : 9, а в другом 2 : 3. Сколько нужно взять каждого сплава, чтобы получить 15 кг нового сплава, в котором золото и серебро относилось бы как 1 : 4?

Решение

15 кг нового сплава должны состоять в отношении 1 : 4. Это отношение говорит о том, что на одну часть сплава будет приходиться золото, а на четыре части будет приходиться серебро. Всего же частей пять. Схематически это можно представить следующим образом

Определим массу одной части. Для этого сначала сложим все части (1 и 4), затем массу сплава разделим на количество этих частей

1 + 4 = 5 15 кг : 5 = 3 кг

Одна часть сплава будет иметь массу 3 кг. Тогда в 15 кг нового сплава будет содержáться 3 × 1 = 3 кг золота и серебра 3 × 4 = 12 кг серебра.

Поэтому для получения сплава массой 15 кг нам нужно 3 кг золота и 12 кг серебра.

Теперь ответим на вопрос задачи — «Сколько нужно взять каждого сплава?»

Первого сплава мы возьмем 10 кг, поскольку золото и серебро в нём находятся в отношении 1 : 9. То есть этот первый сплав даст нам 1 кг золота и 9 кг серебра.

Второго сплава мы возьмем 5 кг, поскольку золото и серебро находятся в нём в отношении 2 : 3. То есть этот второй сплав даст нам 2 кг золота и 3 кг серебра.

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках