Сравнение смешанного числа и натурального числа
Разберемся, как сравнить смешанное число и натуральное число.
Справедливо такое правило сравнения смешанного числа с натуральным числом: если целая часть смешанного числа меньше данного натурального числа, то смешанное число меньше данного натурального числа, а если целая часть смешанного числа больше или равна данному смешанному числу, то смешанное число больше данного натурального числа.
Разберем примеры сравнения смешанного числа и натурального числа.
Пример.
Сравните числа 6 и .
Решение.
Целая часть смешанного числа равна 9. Так как она больше натурального числа 6, то .
Ответ:
.
Пример.
Дано смешанное число и натуральное число 34, какое из чисел меньше?
Решение.
Целая часть смешанного числа меньше числа 34 (11<34), поэтому .
Ответ:
смешанное число меньше, чем число 34.
Пример.
Выполните сравнение числа 5 и смешанного числа .
Решение.
Целая часть данного смешанного числа равна натуральному числу 5, следовательно, данное смешанное число больше, чем 5.
Ответ:
.
В заключение этого пункта отметим, что любое смешанное число больше единицы. Это утверждение следует из правила сравнения смешанного числа и натурального числа, а также из того, что целая часть любого смешанного числа либо больше 1, либо равна 1.
Умножение целого числа на дробь
Любое целое число можно умножить на дробь. Для этого достаточно умножить это число на числитель дроби.
Например, умножим число 5 на дробь . Чтобы решить этот пример, нужно число 5 умножить на числитель дроби
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Если имеются пять целых пицц и мы возьмём от этого количества половину, то у нас окажется две целые пиццы и половина пиццы:

Пример 2. Найти значение выражения
Умножим число 3 на числитель дроби
В ответе получилась неправильная дробь , но мы выделили её целую часть и получили 2.
Также, можно было сократить эту дробь. Получился бы тот же результат. Выглядело бы это следующим образом:

Если имеются три целые пиццы и мы возьмём от этого количества две третьих, то у нас окажется две целые пиццы:
Пример 3. Найти значение выражения
Этот пример решается так же, как и предыдущие. Целое число и числитель дроби нужно перемножить:
Пример 4. Найти значение выражения
Умножим число 3 на числитель дроби
Деление смешанного числа на целое число
Чтобы разделить смешанное число на целое число, нужно смешанное число перевести в неправильную дробь, затем умножить эту дробь на число, обратное делителю.
Например, разделим на 2. Чтобы решить этот пример, нужно делимое перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.
Переведём смешанное число в неправильную дробь, получим .
Теперь умножаем на число, обратное числу 2. Обратное числу 2 это дробь
Допустим, имеется одна целая и половина пиццы:

Разделим это количество пиццы поровну на две части. Для этого сначала разделим на две части целую пиццу:

Затем разделим поровну на две части и половину:

Теперь если мы сгруппируем эти кусочки на две группы, то получим по пиццы в каждой группе:

Поэтому значение выражения равно
Пример 2. Найти значение выражения
Переведём делимое в неправильную дробь, получим . Теперь умножаем на число, обратное числу 4. Обратное числу 4 это дробь .
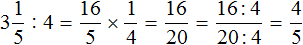
Сложение целого и смешанного числа
Встречаются задачи, в которых нужно сложить целое и смешанное число. Например, сложить 2 и смешанное число . В этом случае целые части складываются отдельно, а дробная часть остаётся без изменения:
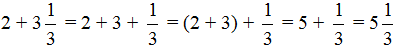
Здесь смешанная дробь была развёрнута в ходе решения, затем целые части были сгруппированы и сложены. В конце целая и дробная части были свёрнуты. В результате получили ответ .
Попробуем изобразить это решение в виде рисунка. Если к двум целым пиццам прибавить три целые и треть пиццы, то получятся пять целых и треть пиццы:
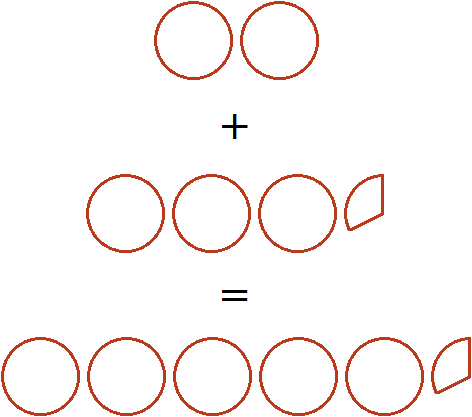
Пример 2. Найти значение выражения
В этом примере, как и в предыдущем, нужно сложить целые части:

Осталось свернуть целую и дробную части, но дело в том, что дробная часть представляет собой неправильную дробь. Сначала нужно выделить целую часть в этой неправильной дроби. Затем целую часть этой дроби прибавить к 4, а дробную часть оставить без изменения. Продолжим данный пример на новой строке:
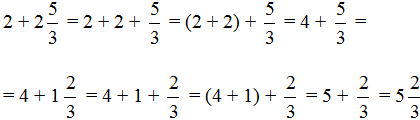
Умножение смешанного числа на дробь
Чтобы умножить смешанное число на дробь, нужно смешанное число перевести в неправильную дробь, затем выполнить перемножение обыкновенных дробей.
Пример 1. Найти значение выражения
Переведём смешанное число в неправильную дробь. После перевода это число превратится в дробь . Затем можно будет умножить эту дробь на
Допустим, имеются одна целая и половина пиццы:

Умножить эти куски на означает взять от них две трети. Чтобы взять от них две трети, сначала разделим их на три равные части. Разделим пополам ту пиццу, которая слева. Тогда у нас получится три равных куска:

Теперь если мы возьмем (два куска из трёх имеющихся), то получим одну целую пиццу. Для наглядности закрасим эти два куска:
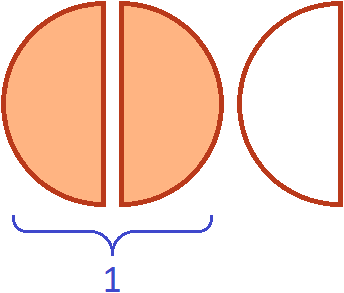
Поэтому значение выражения было равно 1
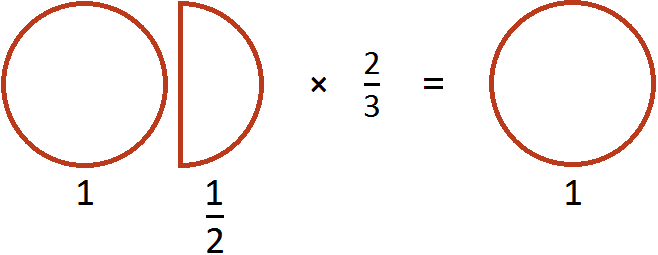
Деление дроби на целое число
Чтобы разделить дробь на целое число, нужно данную дробь умножить на число, обратное делителю. Таким делением мы занимались в прошлом уроке. Вспомним ещё раз.
Пример 1. Разделим дробь на число 2
Чтобы разделить дробь на 2, нужно данную дробь умножить на число, обратное числу 2. А обратное числу 2 это дробь
Пусть имеется половина пиццы:
Разделим её поровну на две части. Тогда каждая получившаяся часть будет одной четвертой пиццы:
Поэтому значение выражения равно
Пример 2. Найти значение выражения
Чтобы решить этот пример, нужно дробь умножить на число, обратное числу 2. Обратное числу 2 это дробь
Пример 3. Найти значение выражения
Умножаем первую дробь на число, обратное числу 3. Обратное числу 3 это дробь

Сложение смешанных чисел
Встречаются задачи, в которых требуется сложить смешанные числа. Например, найти значение выражения . Чтобы решить этот пример, нужно целые и дробные части сложить по отдельности.
Для начала запишем смешанные числа в развёрнутом виде:
Применим сочетательный закон сложения. Сгруппируем целые и дробные части по отдельности:
Вычислим целые части: 2 + 3 = 5. В главном выражении заменяем выражение в скобках (2 + 3) на полученную пятёрку:
Теперь вычислим дробные части. Это сложение дробей с разными знаменателями. Как складывать такие дроби мы уже знаем:

Получили . Теперь в главном выражении заменяем дробные части на полученную дробь
Теперь свернем полученное смешанное число:
Таким образом, значение выражения равно . Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:

Подобные примеры нужно решать быстро, не останавливаясь на подробностях. Находясь в школе, нам пришлось бы записать решение этого примера следующим образом:
Если в будущем увидите такое короткое решение, не пугайтесь. Вы уже понимаете, что откуда взялось.
Пример 2. Найти значение выражения
Запишем смешанные числа в развёрнутом виде:
Сгруппируем целые и дробные части по отдельности:
Вычислим целые части: 5 + 3 = 8. В главном выражении заменяем выражение в скобках (5 + 3) на полученное число 8
Теперь вычислим дробные части:

Получили смешанное число . Теперь в главном выражении заменяем выражение в скобках на полученное смешанное число
Получили выражение . В данном случае число 8 надо прибавить к целой части смешанного числа . Для этого смешанное число можно временно развернуть, чтобы было понятнее, что с чем складывать:
Сложим целые части. Получаем 9
Сворачиваем готовый ответ:
Таким образом, значение выражения равно .
Полное решение этого примера выглядит следующим образом:

Для решения подобных примеров существует универсальное правило. Выглядит оно следующим образом:
Чтобы сложить смешанные числа, надо:
- привести дробные части этих чисел к общему знаменателю;
- отдельно выполнить сложение целых и дробных частей.
Если при сложении дробных частей получилась неправильная дробь, выделить целую часть в этой дроби и прибавить ее к полученной целой части.
Применение готовых правил допустимо в том случае, если суть темы полностью понятна. Решение по-шаблону, поглядывая в другие подобные примеры, приводит к ошибкам на обнаружение которых уходит дополнительное время. Поэтому, сначала разумнее понять тему, а затем пользоваться готовым правилом.
Пример 3. Найти значение выражения
Воспользуемся готовым правилом. Приведём дробные части к общему знаменателю, затем по отдельности сложим целые и дробные части:

Зачем нужны смешанные числа?
Помимо записи результатов, смешанные числа очень часто применяются в примерах с десятичными дробями. Ни один отсчет, исследование или расчеты не обходятся без применения десятичных дробей. А довольствоваться только дробями от минус бесконечности до 0 невозможно. Поэтому и применяют смешанные числа в расчетах. При этом отдельного правила смешанных чисел нет.
Что мы узнали?
Мы вспомнили, какие бывают дроби. Поговорили о каждой из них в отдельности. Выделили смешанные числа. Рассказали, откуда смешанные числа могут появиться в задачах и как правильно записывать ответы дробных примеров. Пояснили, для чего нужны смешанные числа в современном мире.
Связь между смешанными числами и неправильными дробями
Проследить связь между смешанными числами и неправильными дробями лучше всего на примерах.
Пусть на подносе лежит торт и еще 3/4 такого же торта. То есть, по смыслу сложения на подносе находится 1+3/4 торта. Записав последнюю сумму в виде смешанного числа, констатируем, что на подносе находится торта. Теперь целый торт разрежем на 4 равные доли. В результате на подносе окажется 7/4 торта. Понятно, что «количество» торта при этом не изменилось, поэтому .
Из рассмотренного примера явно видна такая связь: любое смешанное число можно представить в виде неправильной дроби.
А теперь пусть на подносе находятся 7/4 торта. Сложив из четырех долей целый торт, на подносе окажется 1+3/4, то есть, торта. Отсюда видно, что .
Из этого примера понятно, что неправильную дробь можно представить в виде смешанного числа. (В частном случае, когда числитель неправильной дроби делится нацело на знаменатель, неправильную дробь можно представить в виде натурального числа, например, , так как 8:4=2).
Перевод смешанного числа в неправильную дробь
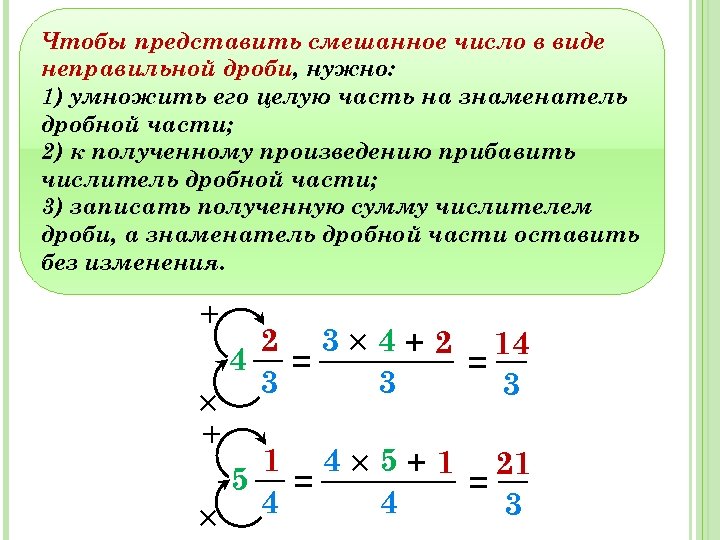
Для выполнения различных действий со смешанными числами оказывается полезным навык представления смешанных чисел в виде неправильных дробей. В предыдущем пункте мы выяснили, что любое смешанное число можно перевести в неправильную дробь. Пришло время разобраться, как осуществляется такой перевод.
Запишем алгоритм, показывающий как перевести смешанное число в неправильную дробь:
- Во-первых, записываем данное смешанное число в виде суммы целой части и дробной части числа, то есть, как .
- Во-вторых, целую часть исходного смешанного числа заменяем дробью со знаменателем 1, то есть, заменяем n на дробь n/1 (при необходимости смотрите ).
- Наконец, складываем обыкновенные дроби n/1 и a/b, в результате получаем искомую неправильную дробь, равную исходному смешанному числу.
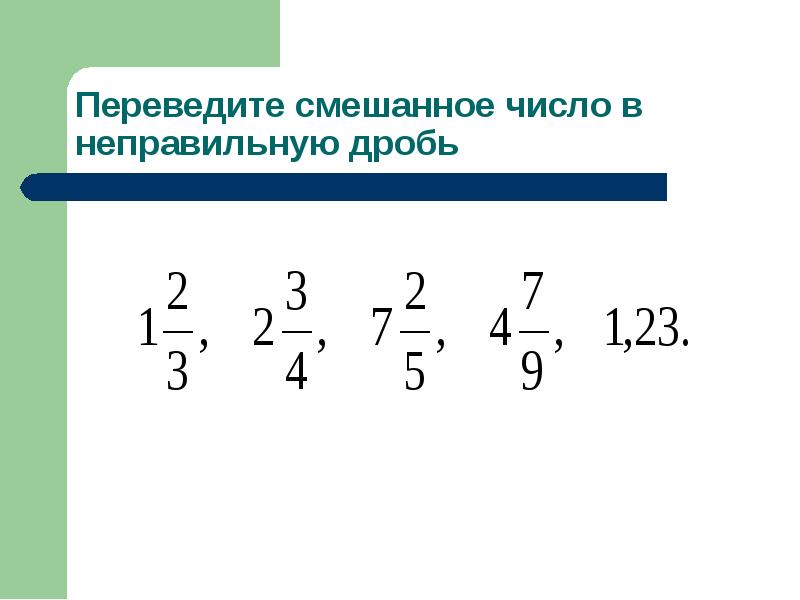
Рассмотрим пример перевода смешанного числа в неправильную дробь.
Пример.
Представьте смешанное число в виде неправильной дроби.
Решение.
Выполним все необходимые шаги алгоритма.
Смешанное число равно сумме его целой и дробной части: .
Записав число 5 как 5/1, последняя сумма примет вид .
Чтобы закончить перевод исходного смешанного числа в неправильную дробь, осталось выполнить : .
Краткая запись всего решения такова: .
Ответ:
.
Итак, чтобы осуществить перевод смешанного числа в неправильную дробь, нужно выполнить следующую цепочку действий: . В итоге получена формула перевода смешанного числа в неправильную дробь , которую мы и будем использовать в дальнейшем.
Пример.
Запишите смешанное число в виде неправильной дроби.
Решение.
Воспользуемся формулой для перевода смешанного числа в неправильную дробь. В этом примере n=15, a=2, b=5. Таким образом, .
Ответ:
.
Деление целого числа на смешанное число
Встречаются задачи, в которых требуется разделить целое число на смешанное число. Например, разделим 2 на .
Чтобы решить этот пример, нужно делитель перевести в неправильную дробь. Затем умножить число 2 на дробь, обратную делителю.
Переведём делитель в неправильную дробь, получим . Затем умножим 2 на дробь, обратную дроби . Обратная для дроби это дробь
Допустим, имеются две целые пиццы:

Зададим вопрос «Сколько раз (одна целая и половина пиццы) содержится в двух целых пиццах?». Похожий пример мы решали ранее, когда учились .
В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:

А оставшаяся половина это треть от , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества
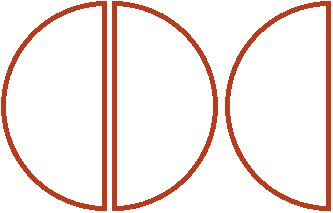
Поэтому значение выражения равно
Пример 2. Найти значение выражения
Переводим делитель в неправильную дробь, получаем . Теперь умножаем число 5 на дробь, обратную дроби . Обратная для дроби это дробь
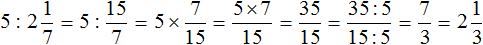
Сначала мы получили ответ , затем сократили эту дробь на 5, и получили , но этот ответ нас тоже не устроил, поскольку он представлял собой неправильную дробь. Мы выделили в этой неправильной дроби целую часть. В результате получили ответ
Откуда появляются смешанные дроби?
Вариантов возникновения в задаче смешанных дробей всего 2:
- Пример изначально дан с использованием смешанных дробей
- В результате решения примера или задачи появилась неправильная дробь. Проблема в том, что неправильную дробь в ответ записывать нежелательно. В промежуточных действиях ответы пишут так, как удобно решающему, но конечный результат должен быть максимально упрощен. Если возможно вынесение целой части в дроби – ее выносят. Это негласное правило хорошего тона в математике. Неправильная запись результата не всегда считается ошибкой, но лучше все же выделять целую часть.
Дробь. Правильные и неправильные дроби. Смешанные числа

Дробь. Числитель и знаменатель дроби
ОПРЕДЕЛЕНИЕ 1. Дробью называют одну или несколько одинаковых долей (частей) предмета или некоторой величины.
Дробь записывают при помощи двух натуральных чисел, одно из которых стоит над горизонтальной чертой, а второе – под нею.
ОПРЕДЕЛЕНИЕ 2. Число, стоящее над чертой, называют числителем дроби. Число, стоящее под чертой, называют знаменателем дроби.Числитель и знаменатель называют членами дроби.
Знаменатель дроби показывает, на сколько одинаковых долей мы делим предмет или величину, а числитель дроби показывает, сколько таких долей взято.
Например, дробь
у которой числитель равен 8 , а знаменатель равен 17 , означает, что предмет или величину мы делим на 17 равных долей (частей) и берем 8 таких долей.
ПРИМЕР 1. В классе 25 учеников, из которых посещают театральный кружок. Сколько учеников ходят в театральный кружок?
РЕШЕНИЕ. Для решения примера нужно 25 учеников разделить на 5 частей и взять 2 таких части.
ОТВЕТ. 10 учеников.
ПРИМЕР 2. Турист в первый день похода прошел намеченного маршрута, а во второй день – оставшиеся 24 километра. Сколько всего километров прошел турист?
РЕШЕНИЕ. Весь маршрут разделен на 7 равных частей, 3 из которых турист прошел в первый день (рис. 1).
| 1 день |
| 1 день |
| 1 день |
| 2 день |
| 2 день |
| 2 день |
| 2 день |
Рис. 1
Из рисунка 1 видно, что 24 километра составляют 4 из 7 частей маршрута. Таким образом, 1 часть маршрута равна
24 : 4 = 6 (км) ,
а весь маршрут равен
(км) .
ОТВЕТ. 42 километра.
ЗАМЕЧАНИЕ. Если не указано, от какого предмета или какой величины берется дробь, то считают, что дробь взята от числа 1 .
Термин дробь имеет синонимы: простая дробь, обыкновенная дробь, рациональная дробь, дробное число.
Правильные и неправильные дроби. Смешанные числа
ОПРЕДЕЛЕНИЕ 3. Если у дроби числитель меньше знаменателя, то ее называют правильной дробью. В противном случае – неправильной дробью.
Из этого определения, в частности, вытекает, что правильная дробь меньше единицы, а неправильная — больше единицы или равна единице.
ПРИМЕР 3
– правильная дробь, и – неправильные дроби.
Неправильную дробь всегда можно представить в виде суммы целого числа и правильной дроби. Эту операцию называют выделением целой части из неправильной дроби и осуществляют при помощи числителя неправильной дроби на знаменатель.
ПРИМЕР 4 .
Число является примером смешанного числа. Целое число 2 и правильную дробь называют целой и дробной частью смешанного числа соответственно.
Любое смешанное число всегда можно обратить в неправильную дробь, например,
Основное свойство дроби, сокращение дробей, несократимая дробь
Основным свойством дроби называют следующее
УТВЕРЖДЕНИЕ. Дробь превращается в равную дробь, если её числитель и знаменатель умножить или разделить на одно и то же число.
ОПРЕДЕЛЕНИЕ 4. Операцию, при которой числитель и знаменатель дроби делят на одно и то же число, называют сокращением дроби.
ПРИМЕР 5.
ОПРЕДЕЛЕНИЕ 5. Если числитель и знаменатель дроби не имеют , то такую дробь называют несократимой.
При помощи сокращений любую дробь можно превратить в равную ей несократимую дробь.
Сравнение смешанных чисел
Сравнение смешанных чисел можно свести к сравнению обыкновенных дробей. Для этого достаточно .
Для примера, сравним смешанное число и смешанное число , представив их в виде неправильных дробей. Имеем и . Так сравнение исходных смешанных чисел сводится к и . Так как , то .
Сравнение смешанных чисел через сравнение равных им дробей является не лучшим решением. Гораздо удобнее использовать следующее правило сравнения смешанных чисел: больше то смешанное число, целая часть которого больше, если же целые части равны, то больше то смешанное число, дробная часть которого больше.
Рассмотрим, как происходит сравнение смешанных чисел по озвученному правилу. Для этого разберем решения примеров.
Пример.
Сравните смешанные числа и .
Решение.
Целая часть смешанного числа меньше целой части смешанного числа (5<31 смотрите сравнение натуральных чисел), поэтому .
Ответ:
.
Пример.
Какое из смешанных чисел и больше?
Решение.
Целые части сравниваемых смешанных чисел равны, поэтому сравнение сводится к сравнению дробных частей и . Так как , то . Таким образом, смешанное число больше, чем смешанное число .
Ответ:
.
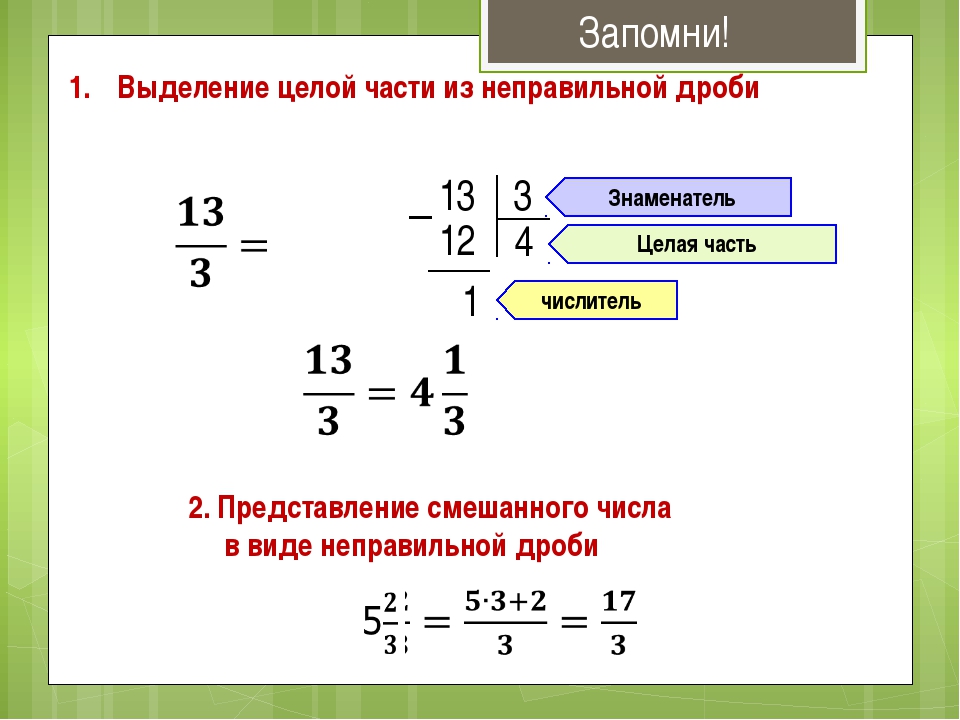
Выделение целой части из неправильной дроби
В ответе не принято записывать неправильную дробь. Неправильную дробь предварительно заменяют либо равным ей натуральным числом (когда числитель делится нацело на знаменатель), либо проводят так называемое выделение целой части из неправильной дроби (когда числитель не делится нацело на знаменатель).
Определение.
Выделение целой части из неправильной дроби – это замена дроби равным ей смешанным числом.
Осталось узнать, как можно выделить целую часть из неправильной дроби.
Это очень просто: неправильная дробь a/b равна смешанному числу вида , где q — неполное частное, а r – остаток от деления a на b. То есть, целая часть равна неполному частному от деления a на b, а остаток равен числителю дробной части.
Докажем это утверждение.
Для этого достаточно показать, что . Переведем смешанное в неправильную дробь так, как мы это делали в предыдущем пункте: . Так как q – неполное частное, а r – остаток от деления a на b, то справедливо равенство a=b·q+r (при необходимости смотрите деление с остатком). Следовательно, , поэтому , что и требовалось показать.
Итак, правило выделения целой части из неправильной дроби a/b таково:
- делим с остатком a на b, при этом будет найдено неполное частное q и остаток r;
- записываем смешанное число , которое равно исходной дроби a/b.
Рассмотрим решение примера.
Пример.
Выделите целую часть из дроби 104/7.
Решение.
Выполним деление столбиком:
Так деление числителя a=118 на знаменатель b=7 дает неполное частное q=16 и остаток r=6.
Таким образом, неправильная дробь 118/7 равна смешанному числу .
Ответ:
.
Для полноты картины рассмотрим, как неправильная дробь a/b, числитель которой делится нацело на знаменатель, заменяется натуральным числом.
Пусть a:b=c. Вспомнив про , мы можем записать следующие равенства , то есть, неправильную дробь a/b можно заменить натуральным числом c.
Например, в ответе вместо неправильной дроби 27/3 записывают равное ей натуральное число 9, так как .
Список литературы.
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика: учебник для 5 кл. общеобразовательных учреждений.
- Виленкин Н.Я. и др. Математика. 6 класс: учебник для общеобразовательных учреждений.
Некогда разбираться?
Что такое смешанная дробь?
Смешанная дробь это дробь, у которой есть две части: целая и дробная. При этом дробная часть обязательно не должна равняться нулю.
Целая часть, равная нулю, есть у любой обыкновенной дроби.
Всего существует 4 вида дробей:
- Обыкновенные или правильные. Это дроби, записанные с помощью дробной черты. Числитель такого числа всегда меньше знаменателя, а саму дробь всегда можно заменить операцией деления, в которой делимым будет числитель, а делителем знаменатель.
- Неправильные дроби. Это числа, в которых числитель больше знаменателя. Они могут возникать в результате сложении или вычитания чисел, а могут быть даны в неправильном виде в задаче или примере.
- Смешанные дроби.
-
Десятичные дроби. Это дроби, знаменатель которых представлен степенью числа 10.
Записываются десятичные дроби в строку с помощью разделительной запятой. Количество знаков после запятой обозначает степень, в которую нужно возвести 10, чтобы получить знаменатель дроби.
Смешанная дробь может быть записана в десятичном виде, так же, как и обыкновенная. А вот неправильную дробь в строку записать невозможно. И главное, нельзя забывать, что смешанные дроби и смешанные числа это одно и то же.
Вычитание смешанных чисел
Встречаются задачи, в которых требуется вычесть из одного смешанного числа другое смешанное число. Например, найдём значение выражения:
Чтобы решить этот пример, нужно смешанные числа и перевести в неправильные дроби, затем выполнить вычитание дробей с разными знаменателями:

Если от трёх целых пицц вычесть две целые и треть пиццы, то останутся одна целая и одна шестая пиццы:

Пример 2. Найти значение выражения
Переводим смешанные числа и в неправильные дроби и выполняем вычитание дробей с разными знаменателями:

К вычитанию смешанных чисел мы ещё вернёмся. В вычитании дробей есть немало тонкостей, которым новичок пока не готов. Например, возможен случай, когда уменьшаемое может оказаться меньше вычитаемого. Это может вывести нас в мир отрицательных чисел, которых мы ещё не изучали.
А пока изучим умножение смешанных чисел. Благо оно не такое сложное, как сложение и вычитание.
Умножение смешанных чисел
Встречаются задачи, в которых требуется перемножить смешанные числа. Например, перемножить и . Чтобы решить этот пример, нужно перевести эти смешанные числа в неправильные дроби, затем выполнить умножение неправильных дробей:
Попробуем разобраться в этом примере с помощью рисунка. Допустим, имеются одна целая и половина пиццы:
Теперь разберемся со смешанным множителем . Этот множитель означает, что одну целую и половину пиццы нужно взять 2 раза и еще раза.
С множителем 2 всё понятно, он означает что одну целую и половину пиццы нужно взять два раза. Давайте возьмём два раза целую пиццу и половину:
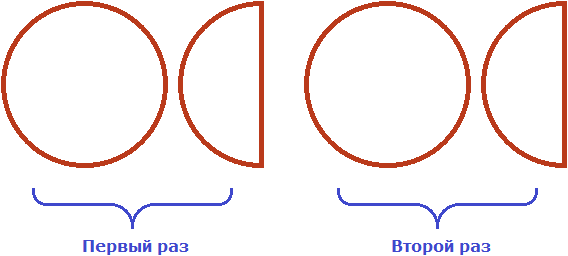
Но ещё осталось взять от изначальной целой пиццы и половины, ведь множителем было смешанное число . Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:
Мы разделили нашу целую пиццу и половину на равные части, и теперь можем сказать, что является половиной от этих кусков. Половиной от этих кусков является пиццы. Это можно хорошо увидеть, если мы упорядочим наши равные кусочки следующим образом:
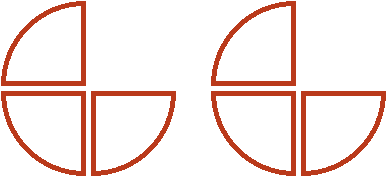
А если смотреть на изначальную целую пиццу и половину с точки зрения такого порядка, как на этом рисунке, то половиной от них является пиццы.
Поэтому значение выражения равно
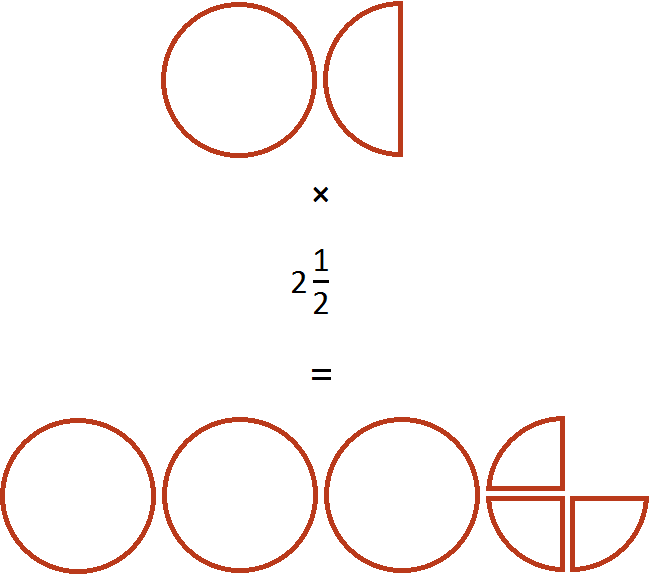
Пример 2. Найти значение выражения
Переводим смешанные числа в неправильные дроби и перемножаем эти неправильные дроби. Если в ответе получится неправильная дробь, выделим в ней целую часть:

Деление целого числа на дробь
Чтобы разделить целое число на дробь, нужно это целое число умножить на дробь, обратную делителю.
Например, разделим число 3 на дробь . Здесь число 3 — это делимое, а дробь — делитель.
Чтобы решить этот пример, нужно число 3 умножить на дробь, обратную дроби . А обратная дробь для дроби это дробь . Поэтому умножаем число 3 на дробь
Допустим, имеются три целые пиццы:

Если мы зададим вопрос «cколько раз (половина пиццы) содержится в трёх пиццах», то ответом будет «шесть раз».
Действительно, если мы разделим каждую пиццу пополам, то у нас получится шесть половинок:
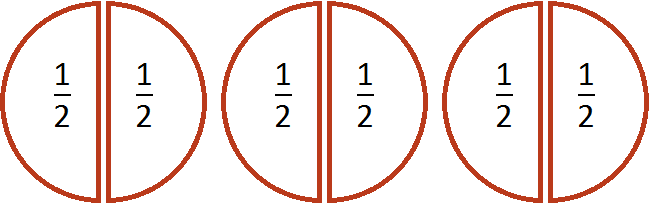
Поэтому значение выражения равно 6.
Пример 2. Найти значение выражения
Чтобы решить этот пример, нужно число 2 умножить на дробь, обратную дроби . А обратная дробь для дроби это дробь
Допустим, имеются две целые пиццы:

Зададим вопрос «Сколько раз пиццы содержится в этих двух пиццах?» Чтобы ответить на этот вопрос, выделим целую часть в дроби . После выделения целой части в этой дроби получим
Теперь поставим вопрос так: «Сколько раз (одна целая и половина пиццы) содержится в двух пиццах?».
Чтобы ответить на этот вопрос, нужно найти в двух пиццах такое количество пиццы, которое изображено на следующем рисунке:

В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:

А оставшаяся половина это треть от , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества

Поэтому значение выражения равно
Пример 3. Найти значение выражения
Чтобы решить этот пример, нужно число 5 умножить на дробь, обратную дроби . А обратная дробь для дроби это дробь . Поэтому умножаем число 5 на
Дробь это 2 целых и . Проще говоря, две целые и четверть пиццы:

А выражение определяет сколько раз содержится в пяти целых пиццах. Ответом было смешанное число .
То есть пиццы содержится в пяти целых пиццах раза.
Давайте нащупаем в пяти пиццах два раза по

Белым цветом осталось не выделено две четверти. Эти две четверти представляют собой от , которые не вместились. Двумя девятыми они являются по той причине, что в пиццы каждую целую пиццу можно разделить на четыре части. Тогда каждый кусок будет девятой частью от этого количества, а два куска соответственно двумя из девяти
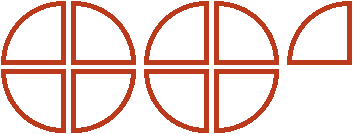
Поэтому значение выражения равно
Сложение целого числа и правильной дроби
Встречаются задачи, в которых требуется сложить целое число и правильную дробь. Например, сложить число 2 и дробь . Чтобы решить этот пример, нужно число 2 представить в виде дроби . Затем сложить дроби с разными знаменателями:

А теперь внимательно посмотрим на этот пример. Смотрим на его начало и на его конец. Начало у него выглядит так: , а конец так: . Различие в том, что в первом случае число 2 и дробь соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что это свёрнутая форма записи смешанного числа, а — развёрнутая.
Когда перед нами смешанное число вида , мы должны понимать, что знак сложения опущен.
Какой можно сделать вывод? Если потребуется сложить целое число и правильную дробь, можно опустить плюс и записать целое число и дробь вместе.
Значит значение выражения равно
Если к двум целым пиццам прибавить половину пиццы, то получится две целые пиццы и ещё половина пиццы:
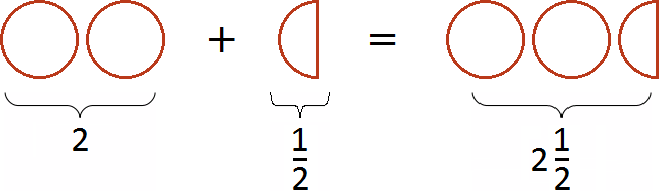
Пример 2. Найти значение выражения
Представим число 3 в виде дроби . Затем сложим дроби с разными знаменателями:
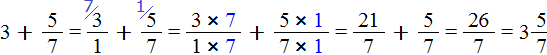
Это первый способ. Второй способ намного проще. Можно поставить знак равенства и записать целую и дробную часть вместе. То есть опустить знак сложения:
Пример 3. Найти значение выражения
Можно записать вместе число 2 и дробь , но этот ответ не будет окончательным, поскольку в дроби можно выделить целую часть.
Поэтому в данном примере сначала нужно выделить целую часть в дроби . Пять вторых это две целых и одна вторая:
Теперь в главном выражении вместо дроби запишем смешанное число

Получили новое выражение . В этом выражении смешанное число запишем в развёрнутом виде:
Применим сочетательный закон сложения. Сложим две двойки, получим 4:
Теперь свернём полученное смешанное число:
Это окончательный ответ. Подробное решение этого примера можно записать следующим образом:

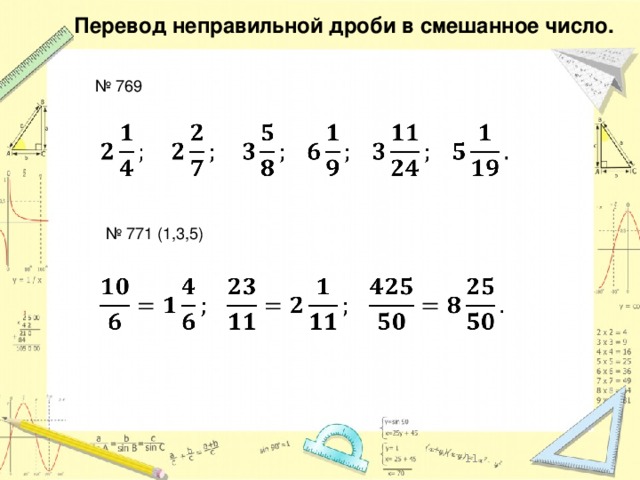
Превращение неправильной дроби в смешанную
Чтобы преобразовать неправильную дробь в смешанную, в ней нужно выделить целую часть.
Чтобы этого добиться, мы задаем себе вопрос – сколько раз знаменатель целиком «помещается» в числителе?Например, пусть нам нужно представить как смешанную дробь \(\frac{13}{5}\). Сколько раз пятерка «помещается» в тринадцати? Два раза. Третий раз уже «не влезет». Значит, целая часть будет равна двойке, а дробная – остатку, то есть \(\frac{3}{5}\). Оформляем: \(\frac{13}{5}\)\(=\)\(\frac{10 + 3}{5}\)\(=\)\(\frac{10}{5}\)\(+\)\(\frac{3}{5}\)\(=2+\)\(\frac{3}{5}\)\(=2\)\(\frac{3}{5}\). Вот еще примеры с верным преобразованием:
\(\frac{37}{11}\)\(=\)\(\frac{33 + 4}{11}\)\(=\)\(\frac{33}{11}\)\(+\)\(\frac{4}{11}\)\(=3+\)\(\frac{4}{11}\)\(=3\)\(\frac{4}{11}\)\(\frac{26}{3}\)\(=\)\(\frac{24 + 2}{3}\)\(=\)\(\frac{24}{3}\)\(+\)\(\frac{2}{3}\)\(=8+\)\(\frac{2}{3}\)\(=8\)\(\frac{2}{3}\)
А вот пример неправильного выделения целой части:
\(\frac{7}{2}\)\(=\)\(\frac{4 + 3}{2}\)\(=\)\(\frac{4}{2}\)\(+\)\(\frac{3}{2}\)\(=2+\)\(\frac{3}{2}\)\(=2\)\(\frac{3}{2}\)
В чем ошибка? В том, что дробная часть должна быть правильной дробью. А здесь не так — значит целая часть выделена не полностью. Действительно, ведь двойка в семерке нацело помещается три раза, а не два. Поэтому верным будет вот такое выделение:
\(\frac{7}{2}\)\(=\)\(\frac{6 + 1}{2}\)\(=\)\(\frac{6}{2}\)\(+\)\(\frac{1}{2}\)\(=3+\)\(\frac{1}{2}\)\(=3\)\(\frac{1}{2}\)