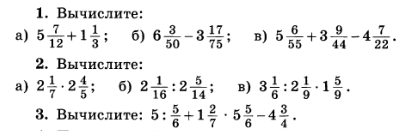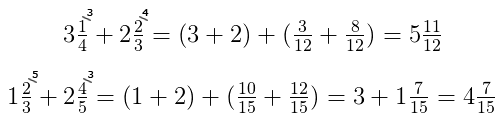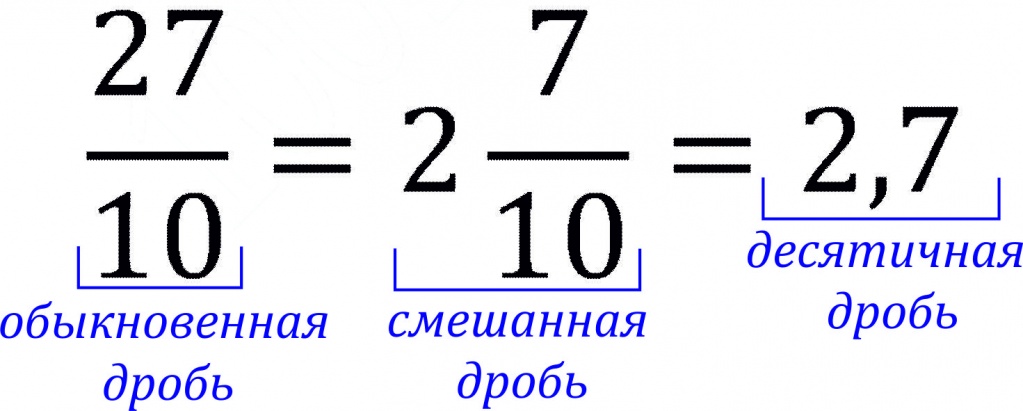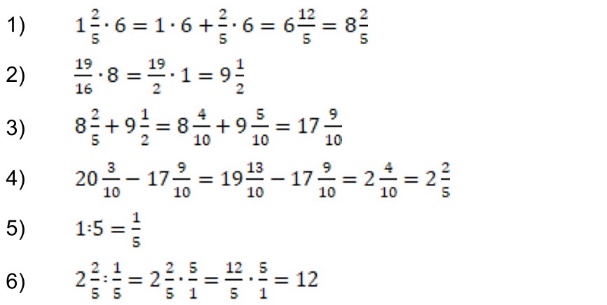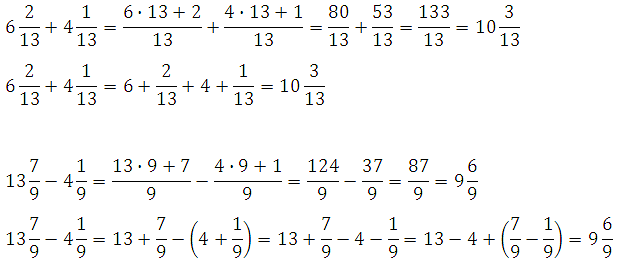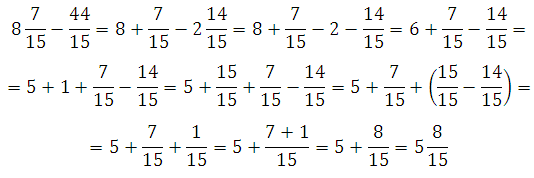Смешанная дробь. действия со смешанными дробями

Суть дроби

Перед тем, как узнать что такое дробь, ребенок должен познакомиться с понятием доля. Здесь лучше всего подойдет ассоциативный метод.

Представьте целый торт, который поделили на несколько равных частей, допустим на четыре. Тогда каждый кусочек торта, можно назвать долей. Если взять один из четырех кусков торта, то он будет одной четвертой долей.

Доли бывают разные, потому что, целое можно поделить на совершенно разное количество частей. Чем больше долей в целом, тем они меньше, и наоборот.

Чтобы доли можно было обозначить, придумали такое математическое понятие, как обыкновенная дробь. Дробь позволит нам записать столько долей, сколько потребуется.

Составными частями дроби являются числитель и знаменатель, которые разделены дробной чертой либо наклонной чертой. Многие дети не понимают их смысла, поэтому и суть дроби им не понятна. Дробная черта обозначает деление, здесь нет ничего сложного.

Знаменатель принято записывать снизу, под дробной чертой или справа от накл.черты. Он показывает количество долей целого. Числитель, он записывается сверху над дробной чертой или слева от накл.черты, определяет сколько долей взяли.К примеру дробь 4/7. В данном случае 7-это знаменатель, показывает, что есть всего 7 долей, а числитель 4 указывает на то, что из семи долей взяли четыре.

Основные доли и их запись в дробях:

Помимо обыкновеной, существует еще и десятичная дробь.

Сложение смешанного числа и правильной дроби

Сложение смешанного числа $a\frac{b}{c}$ и правильной дроби $\frac{d}{e}$ выполняет прибавлением к данной дроби дробной части данного смешанного числа:

Пример 7

Выполнить сложение правильной дроби $\frac{4}{15}$ и смешанного числа $3\frac{2}{5}$.

Решение.

Воспользуемся формулой сложения смешанного числа и правильной дроби:

По признаку деления на число \textit{5 }можно определить, что дробь $\frac{10}{15}$ — сократима. Выполним сокращение и найдем результат сложения:

Итак, результатом сложения правильной дроби $\frac{4}{15}$ и смешанного числа $3\frac{2}{5}$ будет $3\frac{2}{3}$.

Ответ: $3\frac{2}{3}$

Общие сведения

Смешанная дробь — число, состоящее из целого значения и обыкновенного дробного выражения. Они образуются в результате операции деления. Последняя состоит из трех элементов, а именно: делимого, делителя и частного. Чтобы понять смысл смешанного числа, нужно разобрать дробные величины. К ним относятся следующие виды:

Обыкновенные.
Десятичные.

Обыкновенная дробь образуется посредством комбинации делимого и делителя, т. е. состоит всего из двух элементов. В этом случае частное имеет вид десятичного дробного тождества. Иными словами, десятичная дробь — величина, полученная при делении числителя на знаменатель.

Обыкновенные дробные выражения бывают двух видов: правильными и неправильными. У первых величина числителя меньше знаменателя, а у вторых — наоборот. Десятичные дроби делятся на 3 типа: с фиксированным количеством знаков после запятой, бесконечные периодические и непериодические.

У периодических дробных величин после запятой математические символы повторяются через определенный период, который указывается в круглых скобках. Например, число 4,(3) читается следующим образом: четыре целых и три в периоде.

Следует отметить, что бесконечные непериодические дробные выражения в их полном виде невозможно записать на листе бумаги, поскольку количество разрядов достигает бесконечности. Далее необходимо рассмотреть сокращение дробей, поскольку операция применяется для оптимизации конвертации неправильного дробного тождества в смешанное число.

Свойства дробей

Дроби, как и любые числовые выражения, обладают определенными свойствами. К ним относятся:

Если от числителя отнять одно значение, а затем его прибавить, дробь не изменится, т. е. (Q+T-T)/Z=Q/Z.
При умножении и делении на эквивалентное число величина дробного тождества не изменится, т. е. (Q*T)/(Z*Т)=Q/Z.

Первое утверждение проверить очень просто. Для этой цели нужно решить следующий пример, прибавив и отняв от числителя одно и то же значение: 7/8. Доказательство имеет такой вид:

Записать дробь: 7/8.
Взять произвольный коэффициент: 5.
Отнять, а затем прибавить его к числителю: (7−5+5)/8.
Числа «-5» и «5» являются противоположными. Их сумма равна 0, т. е. 5−5=0.
Если прибавить нуль к любому числу, получится искомая величина: 5+0=5.
Математические преобразования исходной дроби: (7−5+5)/8=/8=(7+0)/8.
Результат совпадает с искомым значением: 7/8=7/8.

Второе утверждение доказывается таким же простым способом на дроби ½. Для этого нужно решить пример (1*8)/(2*8) по следующему нестандартному алгоритму:

Записать дробное тождество: ½.
Коэффициент — общий множитель: 8. Последний необходимо представить в виде обыкновенной дроби: 8/8.
Величина «8/8» эквивалентна единице, которую можно умножить на любое число без потери значения выражения.
Расписать дробное значение: (½) * (8/8) = (½) * 1 = ½.
Сравнить результат и исходное значение: ½ = ½.
Утверждение доказано.

Некоторые ученики делают большую ошибку, отнимая (прибавляя) к числителю и знаменателю одну величину. Чтобы они не путали 2 утверждения сокращения, нужно привести пример и решить его:

Записать искомое значение: ½.
Коэффициент: 3.
Прибавить значение «3» к числителю и знаменателю: (1+3)/(2+3)=4/5.
Превратить искомое значение и величину в третьем пункте в десятичные дроби: 0,5 и 0,8.
Сравнить: 0,5 < 0,8.

Упрощение выражений

Преобразование любого арифметического выражения начинается с упрощения. Последнее применяется для уменьшения расчетов, при которых возникают ошибки. Упростить выражение — значит, сделать его более читабельным и предоставить возможность дальнейшего применения при расчетах. Иными словами, каждый результат должен «подгоняться» под мировой стандарт. Для сокращения дробей обыкновенного типа рекомендуется использовать такие правила:

Вынесения общего множителя за скобки и сокращение на него.
Формулы сокращенного умножения.
Приведение подобных слагаемых.

Первое правило позволяет найти единый множитель всего дробного выражения. После этого его можно будет разделить на одно и то же число. Формулы сокращенного умножения применяются также для реализации первого правила. Суть метода заключается в использовании специальных соотношений. Например, математическое выражение «1−25t 2 » выглядит таким образом: (1−5t)(1+5t).

После раскрытия скобок реализовывается третье правило — приведение подобных слагаемых. Они группируются по наличию однотипных элементов. Например, выражение 4t-4+t+t 2 −3+2t 2 имеет следующие одинаковые компоненты, которые группируются в скобках: (2t 2 +t 2 )+(4t+t)-(4+3). Если приводить подобные элементы, выражение упрощается, т. е. 3t 2 +5t-7.

Нахождение целого числа по дроби

Зная часть числа и сколько это составляет от целого числа, можно найти изначальное целое число. Это обратная задача к той, которую мы рассматривали в предыдущей теме. Там мы искали дробь от числа, деля это число на знаменатель дроби, и полученный результат умножая на числитель дроби.

А сейчас наоборот, зная дробь и сколько это составляет от числа, найти изначальное целое число.

Например, если длины линейки составляют шесть сантиметров и нам говорят найти длину всей линейки, то мы должны понимать, что от нас требуют найти изначальное целое число (длину всей линейки) по дроби . Давайте решим эту задачу.

Требуется найти длину всей линейки по дроби . Известно, что длины всей линейки составляют 6 см.

Мы уже знаем каким образом получились эти 6 см. Имелась какая-то длина, её разделили на пять частей, поскольку знаменатель дроби это число 5. Затем было взято две части от пяти частей, поскольку числитель дроби это число 2.

Чтобы узнать длину всей линейки, сначала нужно узнать длину одной части. Как это узнать? Попробуем догадаться, внимательно изучив следующий рисунок:

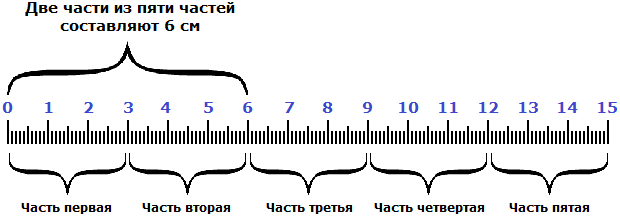
Если две части длины линейки составляют 6 см, то нетрудно догадаться, что одна часть составляет 3 см. А чтобы получить эти 3 см, надо 6 разделить на 2

6 см : 2 = 3 см

Итак, мы нашли длину одной части. Одна часть из пяти или длины линейки составляет 3 см. Если частей всего пять, то для нахождения длины линейки, нужно взять три сантиметра пять раз. Другими словами, умножить 3 см на число 5

3 см × 5 = 15

Мы нашли длину линейки. Она составляет 15 сантиметров. Это можно увидеть на следующем рисунке.

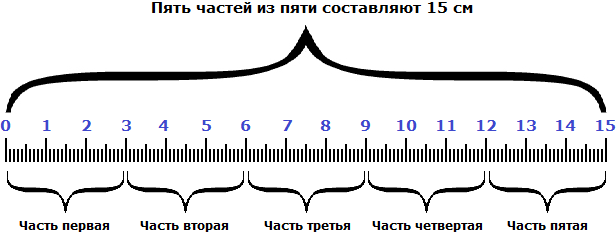
Видно, что пять частей из пяти или составляют пятнадцать сантиметров.

Чтобы легче было находить число по его дроби, можно пользоваться следующим правилом:

Чтобы найти число по его дроби, нужно известное число разделить на числитель дроби, и полученный результат умножить на знаменатель дроби.

Пример 2. Число 20 это от всего числа. Найдите это число.

Знаменатель дроби показывает, что число, которое мы должны найти, разделено на пять частей. Если этого числа составляет число 20, то для нахождения всего числа, сначала нужно найти (одну часть из пяти) от всего числа. Для этого 20 надо разделить на числитель дроби

20 : 4 = 5

Мы нашли от всего числа. Эта часть равна 5. Чтобы найти всё число, нужно полученный результат 5 умножить на знаменатель дроби

5 × 5 = 25

Мы нашли от всего числа. Другими словами, нашли всё число, которое от нас требовали найти. Это число 25.

Пример 3. Десять минут это времени приготовления каши. Найдите общее время приготовления каши.

Знаменатель дроби показывает, что общее время приготовления каши разделено на три части. Если времени приготовления каши составляет десять минут, то для нахождения общего времени приготовления, нужно сначала найти времени приготовления. Для этого 10 нужно разделить на числитель дроби

10 мин : 2 = 5 мин

Мы нашли времени приготовления каши. времени приготовления каши составляют пять минут. Для нахождения общего времени приготовления, нужно 5 минут умножить на знаменатель дроби

5 мин × 3 = 15 мин

Мы нашли времени приготовления каши, то есть нашли общее время приготовления. Оно составляет 15 минут.

Пример 4. массы мешка цемента составляет 30 кг. Найти общую массу мешка.

Знаменатель дроби показывает, что общая масса мешка разделена на четыре части. Если массы мешка составляет 30 кг то для того, чтобы найти общую массу мешка нужно сначала найти массы мешка. Для этого 30 надо разделить на числитель дроби .

30кг : 2 = 15кг

Мы нашли массы мешка. массы мешка составляет 15 кг. Теперь, чтобы найти общую массу мешка, надо 15кг умножить на знаменатель дроби

15кг × 4 = 60кг

Мы нашли массы мешка. Другими словами, нашли общую массу мешка. Общая масса мешка цемента составляет 60 кг.

Шаги

Метод 1 из 2:

Деление

1

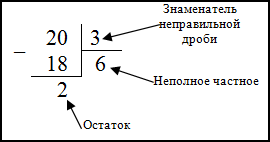
Рассмотрите неправильную дробь. Например, дробь 15/₄

Если вы не знаете, что такое дробь или операция деления, перейдите к следующему разделу.

является неправильной, потому что ее числитель (15) больше знаменателя (4).
2

Перепишите дробь в виде операции деления. Разделите числитель на знаменатель в столбик.
X
Источник информации

Помните, что числитель (делимое) всегда делится на знаменатель (делитель). В нашем примере: 15 ÷ 4.
3

Найдите результат деления. Сначала изучите деление в столбик, если не знаете, что это такое. Записывайте процесс деления в столбик, чтобы лучше понять его.
- Разделите первую цифру числителя на знаменатель. В нашем примере разделите 1 на 4. 1 не делится на 4 нацело, поэтому рассмотрите первые две цифры.
- Разделите первые две цифры числителя на знаменатель. В нашем примере разделите 15 на 4. Вы получите 3 с некоторым остатком.
- Запишите 3 под делителем (в нашем примере под 4). Это целое число ответа.
4

Найдите остаток. Если числа не делятся нацело, получится некоторый остаток. Вычислите его следующим образом:
X
Источник информации
- Умножьте целое число ответа на делитель. В нашем примере: 3 х 4.
- Результат умножения запишите под делимым. В нашем примере: 3 х 4 = 12, поэтому под 15 напишите 12.
- Вычтите результат умножения из делимого. В нашем примере: 15 — 12 = 3. Это остаток.
5

Запишите смешанное число. Смешанное число состоит из целого числа и правильной дроби. Разделив числитель на знаменатель, вы получили все необходимые значения.
- Целое число смешанного числа равно целому числу ответа. В нашем примере это число 3.
- Числитель дроби равен остатку. В нашем примере это число 3.
- Знаменатель дроби равен знаменателю исходной неправильной дроби. В нашем примере это число 4.
- Запишите смешанное число: 33/₄.

Метод 2 из 2:

Без деления

1

Запишите дробь. Неправильная дробь – это любая дробь, числитель (верхнее число) которой больше знаменателя (нижнее число). Например, 3/₂ является неправильной дробью, так как 3 больше 2.
- Верхнее число дроби называется числителем, а нижнее – знаменателем.
- Этот метод не применим к большим числам. Если числитель намного больше знаменателя, воспользуйтесь методом, изложенным в первом разделе.
2

Запомните, какие дроби равны единице. Например, 2 ÷ 2 = 1 и 4 ÷ 4 = 1, то есть любое число, деленное само на себя, равно единице. Например, 2/₂ = 1, 4/₄ = 1, 397/₃₉₇ = 1.
3

Разбейте дробь на две дроби. Одна из дробей должна быть равна целому числу. В нашем примере:
- 3/₂, где знаменатель (нижнее число) равен 2.
- Дробь 2/₂ равна 1, так как числитель равен знаменателю. Поэтому эта дробь является одной из двух дробей, на которые разбивается исходная неправильная дробь.
- Запишите это так: 3/₂ = 2/₂ + ?/₂.
4

Найдите вторую дробь. То есть нужно найти цифру, которую можно подставить вместо вопросительного знака. Не волнуйтесь, если не умеете складывать и вычитать дроби. Когда знаменатели (нижние числа) равны, числители можно просто сложить или вычесть. Ниже представлен пошаговый процесс для нашего примера 3/₂ = 2/₂ + ?/₂:
- Рассмотрите только числители (верхние числа). В нашем примере 3 = 2 + «?». Какую цифру можно подставить вместо вопросительного знака? Какое число нужно прибавить к 2, чтобы получить 3?
- Ответ: 1, так как 3 = 2 + 1.
- Теперь запишите сумму дробей так: 3/₂ = 2/₂ + 1/₂.
5

Упростите дробь. Теперь вы знаете, что исходная неправильная дробь равна сумме двух дробей: 2/₂ + 1/₂. Здесь 2/₂ = 1 (так как числитель равен знаменателю), поэтому вместо дроби 2/₂ можно написать 1: 1 + 1/₂, а эта сумма представляет собой смешанное число! Таким образом, задача решена.
- Теперь можно проигнорировать знак «+» и в ответе написать 11/₂.
- Смешанное число включает как целое число, так и правильную дробь.
  X
  Источник информации
6

Повторите описанные действия, если дробь все еще неправильная. Иногда вторая дробь также является неправильной (то есть ее числитель больше знаменателя). В этом случае преобразуйте ее в смешанное число, а затем к его целой части прибавьте 1. Рассмотрим следующий пример: 7/₃:
- 7/₃ = 3/₃ + ?/₃
- 7 = 3 + ?
- 7 = 3 + 4
- 7/₃ = 3/₃ + 4/₃
- 7/₃ = 1 + 4/₃
- Здесь вторая дробь также является неправильной, поэтому на время забудьте про 1 и преобразуйте эту дробь в смешанное число: 4/₃ = 3/₃ + ?/₃
- 4 = 3 + ?
- 4 = 3 + 1
- 4/₃ = 3/₃ + 1/₃
- 4/₃ = 1 + 1/₃
- Здесь вторая дробь является правильной. Поэтому к полученной 1 прибавьте 1, про которую вы на время забыли: 1 + 1 + 1/₃ = 21/₃.

Превращение дробей

По смыслу неправильные выражения представляют собой целую и дробную часть, записанную в виде отношения. Поэтому любую смешанную дробь можно превратить в правильную, и наоборот. Деление целого числа на такое же можно объяснить так. Пусть нужно разделить четыре на пять. Значит, единицу понадобится разделить на пять равных частей, то есть 1 / 5. Четыре же единицы дадут 1 / 5 + 1/ 5 + 1 / 5 + 1 / 5 = 4 / 5. В этом случае получается правильное выражение. Но бывает, что числитель количественно превышает знаменатель. Значит, для более понятной формы записи нужно из такого выражения выделить целую часть.

Например, нужно преобразовать число 25 / 8. Это действие подразумевает нахождение целых единиц, содержащихся в выражении. Рассуждать нужно следующим образом. Одна единица может быть представлена как 8 / 8, две — 16 / 8, три — 24 / 8. Значит, число состоит из трёх единиц и оставшейся 1 / 8 части. Поэтому записать его можно так: 3 (1 / 8).

Поняв смысл такого перехода, можно выполнить превращение и в обратную сторону. Чтобы разобраться, как это сделать лучше, проще рассмотреть пример. Пусть имеется смешанное число 4 (5/8), его нужно превратить в неправильную дробь. Иными словами, определить, сколько восьмых долей содержится в четырёх и пяти восьмых. Так как одной единице соответствует 8 / 8, то четырём – 8 * 4 / 8 = 32 / 8. Соответственно в четырёх и 5 / 8 будет 37 / 8 долей.

Такого вида преобразования часто приходится выполнять при решении примеров с дробями в 5 классе. Поэтому понять принцип превращения лучше всего на конкретное задание. При этом можно использовать следующий алгоритм:

перемножить единицы целой части со знаменателем дробного числа;
сложить полученное произведение и числитель дроби;
результат сложения записать в числитель, а знаменатель оставить без изменений.

Итак, пусть имеется выражение 3 (5 / 7). Так как фактически это сумма трёх и пяти седьмых, то следуя алгоритму, можно решение расписать так: 3 + 5 / 7 = (3 * 7 + 5) / 7 = (21 + 5) / 7 = 26 / 7. Аналогичный результат мог быть получен при простом сложении двух частей смешанного числа: 3 / 1 + 5 / 7 = (3 * 7) / 1 * 7 + 5 / 7 = 21 / 7 + 5 / 7 = (21 + 5) / 7 = 26 / 7. Первый вариант, конечно же, более удобен. Его можно выразить формулой: a (c / d) = (a * d + c) / d.

Нахождение дроби от числа

Мы уже говорили, что дробь это часть от чего-либо. Эта часть может быть чем угодно. Например, от пиццы это половина пиццы:

Но применение дробей не заканчивается на одной пицце. Например, можно узнать сколько составляет от десяти сантиметров:

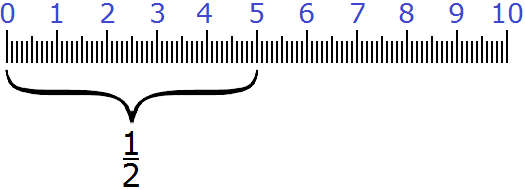
Как вы уже догадались от десяти сантиметров составляют пять сантиметров. Ведь это простейшая дробь, которая означает половину от чего-то. У нас было десять сантиметров. Мы разделили эти десять сантиметров пополам и получили пять сантиметров.

Попробуем узнать, сколько составляет от одного часа. Вспоминаем, что час это 60 минут. Нам нужно найти (половину) от 60 минут. Нетрудно догадаться, что половина от 60 минут это 30 минут. Значит от одного часа составляет 30 минут или полчаса.

Попробуем найти от одного центнера. Центнер это 100 кг. Требуется найти (половину) от 100 кг. Нетрудно догадаться, что половина от 100 кг это 50 кг. Значит от одного центнера составляют 50 кг.

Поскольку мы занимаемся математикой, значит в большинстве случаев будем иметь дело с числами. Например, найдём от числа 12.

Итак, нужно найти половину от числа 12. Нетрудно догадаться, что половиной от числа 12 является число 6. Значит числа 12 составляет число 6.

Чтобы легче было находить дробь от числа, можно пользоваться следующим правилом:

Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.

Попробуем проследить весь процесс работы этого правила. Для примера возьмём десять сантиметров:

Пусть требуется найти от этих десяти сантиметров. Читаем первую часть правила:

Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби

Итак, делим десять сантиметров на знаменатель дроби . Знаменатель этой дроби равен числу 2. Поэтому делим десять сантиметров на 2

10 см : 2 = 5 см

Читаем вторую часть правила:

и полученный результат умножить на числитель дроби

Итак, умножаем пять сантиметров на числитель дроби . Числитель дроби в данном случае единица. Поэтому умножаем пять сантиметров на единицу:

5 см × 1 = 5 см

Мы нашли от десяти сантиметров. Видим, что от десяти сантиметров составляют пять сантиметров:

Почему же после деления числа на знаменатель дроби приходиться умножать полученный результат на числитель дроби? Дело в том, что знаменатель дроби показывает на сколько частей что-либо разделено, а числитель показывает сколько частей было взято.

В нашем примере десять сантиметров были разделены на две части (пополам), и из этих частей была взята одна часть. Умножая одну часть на числитель дроби, мы тем самым указываем сколько частей мы берём от чего-то. То есть умножив пять сантиметров на числитель дроби , мы тем самым указали, что берем одну часть из двух.

Пример 2. Найти от 10 см.

Применим правило нахождения дроби от числа:

Сначала делим 10 сантиметров на знаменатель дроби

10 см : 5 = 2 см

Получили два сантиметра. Этот результат нужно умножить на числитель дроби

2 см × 2 = 4 см

Мы нашли от десяти сантиметров. Видим, что от десяти сантиметров составляют четыре сантиметра.

Весь процесс решения можно увидеть на следующем рисунке:

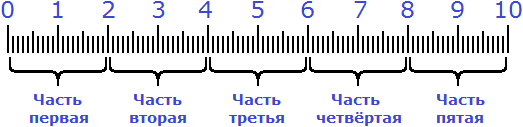
Сначала десять сантиметров были разделены на пять равных частей. Затем было взято две части из этих пяти частей:

Пример 3. Найти от числа 56.

Чтобы найти от числа 56, нужно это число разделить на знаменатель дроби , и полученный результат умножить на числитель дроби .

Итак, сначала делим число 56 на знаменатель дроби

56 : 8 = 7

Теперь умножаем полученное результат на числитель дроби

7 × 3 = 21

Получили ответ 21. Значит от числа 56 составляет 21.

Пример 4. Найти от одного часа.

Один час это 60 минут. Задание можно понимать, как нахождение от 60 минут.

Сначала разделим 60 минут на знаменатель дроби

60 мин : 4 = 15 мин

Теперь умножим полученные 15 минут на числитель дроби

15 мин × 2 = 30 мин

Получили в ответе 30 минут. Значит от одного часа составляют тридцать минут или полчаса.

Пример 5. Найти от одного метра.

Один метр это сто сантиметров. Сначала разделим 100 см на знаменатель дроби

100 см : 5 = 20 см

Теперь умножим полученные 20 см на числитель дроби

20 см × 4 = 80 см

Получили ответ 80 см. Значит от одного метра составляют 80 см.

Сложение дробей, объяснение

Давайте более подробно разберем, как складывать обыкновенные и десятичные дроби.

Как видно на изображении выше, у дроби одна третья и две третьих общий знаменатель три. Значит требуется сложить только числители единицу и два, а знаменатель оставить без изменения. В итоге получается сумма три третьих. Такой ответ, когда числитель и знаменатель дроби равны, можно записать как 1, так как 3:3 = 1.

Требуется найти сумму дробей две третьих и две девятых. В этом случае знаменатели различны, 3 и 9. Чтобы выполнить сложение, нужно подобрать общий. Есть очень простой способ. Выбираем наибольший знаменатель, это 9. Проверяем делится ли он на 3. Так как 9:3 = 3 без остатка, следовательно 9 подходит как общий знаменатель.

Следующим шагом находим дополнительные множители для каждого числителя. Для этого общий знаменатель 9 делим поочередно на знаменатель каждой дроби, полученные числа и будут допол. множ. Для первой дроби: 9:3 = 3, дописываем к числителю первой дроби 3. Для второй дроби: 9:9 = 1, единицу можно не дописывать, так как при умножении на нее получится то же самое число.

Теперь умножаем числители на их дополнительные множители и складываем результаты. Полученная сумма дробь восемь девятых.

Сложение десятичных дробей выполняется по тому же правилу, что и сложение натуральных чисел. В столбик, разряд записывается под разрядом. Единственное отличие в том, что в десятичных дробях нужно правильно поставить запятую в результате. Для этого дроби записываются запятая под запятой, и в сумме требуется лишь снести запятую вниз.

Найдем сумму дробей 38, 251 и 1, 56. Чтобы было удобнее выполнять действия, мы уровняли количество десятичных знаков справа, добавив 0.

Складываем дроби не обращая внимания на запятую. А в полученной сумме просто опускаем запятую вниз. Ответ: 39, 811.

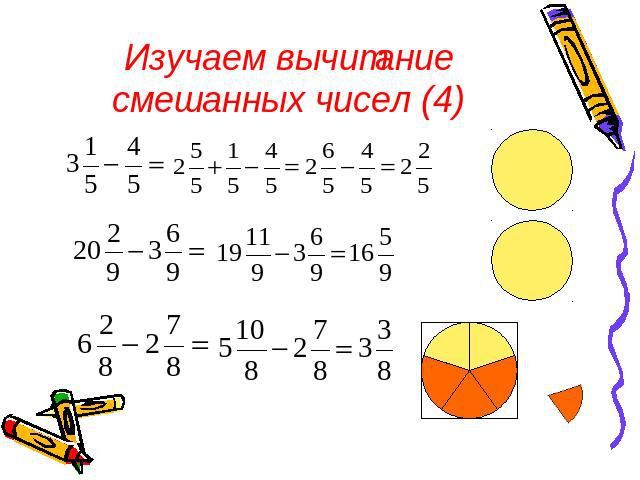
Сложение смешанных чисел

Встречаются задачи, в которых требуется сложить смешанные числа. Например, найти значение выражения . Чтобы решить этот пример, нужно целые и дробные части сложить по отдельности.

Для начала запишем смешанные числа в развёрнутом виде:

Применим сочетательный закон сложения. Сгруппируем целые и дробные части по отдельности:

Вычислим целые части: 2 + 3 = 5. В главном выражении заменяем выражение в скобках (2 + 3) на полученную пятёрку:

Теперь вычислим дробные части. Это сложение дробей с разными знаменателями. Как складывать такие дроби мы уже знаем:

Получили . Теперь в главном выражении заменяем дробные части на полученную дробь

Теперь свернем полученное смешанное число:

Таким образом, значение выражения равно . Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:

Подобные примеры нужно решать быстро, не останавливаясь на подробностях. Находясь в школе, нам пришлось бы записать решение этого примера следующим образом:

Если в будущем увидите такое короткое решение, не пугайтесь. Вы уже понимаете, что откуда взялось.

Пример 2. Найти значение выражения

Запишем смешанные числа в развёрнутом виде:

Сгруппируем целые и дробные части по отдельности:

Вычислим целые части: 5 + 3 = 8. В главном выражении заменяем выражение в скобках (5 + 3) на полученное число 8

Теперь вычислим дробные части:

Получили смешанное число . Теперь в главном выражении заменяем выражение в скобках на полученное смешанное число

Получили выражение . В данном случае число 8 надо прибавить к целой части смешанного числа . Для этого смешанное число можно временно развернуть, чтобы было понятнее, что с чем складывать:

Сложим целые части. Получаем 9

Сворачиваем готовый ответ:

Таким образом, значение выражения равно .

Полное решение этого примера выглядит следующим образом:

Для решения подобных примеров существует универсальное правило. Выглядит оно следующим образом:

Чтобы сложить смешанные числа, надо:

привести дробные части этих чисел к общему знаменателю;
отдельно выполнить сложение целых и дробных частей.

Если при сложении дробных частей получилась неправильная дробь, выделить целую часть в этой дроби и прибавить ее к полученной целой части.

Применение готовых правил допустимо в том случае, если суть темы полностью понятна. Решение по-шаблону, поглядывая в другие подобные примеры, приводит к ошибкам на обнаружение которых уходит дополнительное время. Поэтому, сначала разумнее понять тему, а затем пользоваться готовым правилом.

Пример 3. Найти значение выражения

Воспользуемся готовым правилом. Приведём дробные части к общему знаменателю, затем по отдельности сложим целые и дробные части:

Деление целого числа на дробь

Чтобы разделить целое число на дробь, нужно это целое число умножить на дробь, обратную делителю.

Например, разделим число 3 на дробь . Здесь число 3 — это делимое, а дробь — делитель.

Чтобы решить этот пример, нужно число 3 умножить на дробь, обратную дроби . А обратная дробь для дроби это дробь . Поэтому умножаем число 3 на дробь

Допустим, имеются три целые пиццы:

Если мы зададим вопрос «cколько раз (половина пиццы) содержится в трёх пиццах», то ответом будет «шесть раз».

Действительно, если мы разделим каждую пиццу пополам, то у нас получится шесть половинок:

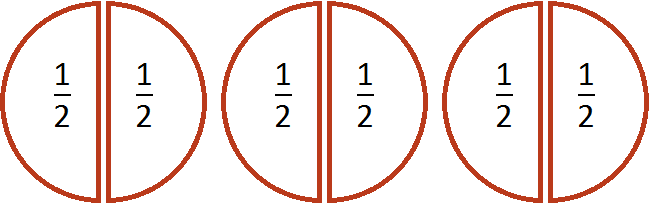
Поэтому значение выражения равно 6.

Пример 2. Найти значение выражения

Чтобы решить этот пример, нужно число 2 умножить на дробь, обратную дроби . А обратная дробь для дроби это дробь

Допустим, имеются две целые пиццы:

Зададим вопрос «Сколько раз пиццы содержится в этих двух пиццах?» Чтобы ответить на этот вопрос, выделим целую часть в дроби . После выделения целой части в этой дроби получим

Теперь поставим вопрос так: «Сколько раз (одна целая и половина пиццы) содержится в двух пиццах?».

Чтобы ответить на этот вопрос, нужно найти в двух пиццах такое количество пиццы, которое изображено на следующем рисунке:

В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:

А оставшаяся половина это треть от , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества

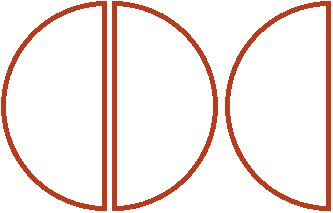
Поэтому значение выражения равно

Пример 3. Найти значение выражения

Чтобы решить этот пример, нужно число 5 умножить на дробь, обратную дроби . А обратная дробь для дроби это дробь . Поэтому умножаем число 5 на

Дробь это 2 целых и . Проще говоря, две целые и четверть пиццы:

А выражение определяет сколько раз содержится в пяти целых пиццах. Ответом было смешанное число .

То есть пиццы содержится в пяти целых пиццах раза.

Давайте нащупаем в пяти пиццах два раза по

Белым цветом осталось не выделено две четверти. Эти две четверти представляют собой от , которые не вместились. Двумя девятыми они являются по той причине, что в пиццы каждую целую пиццу можно разделить на четыре части. Тогда каждый кусок будет девятой частью от этого количества, а два куска соответственно двумя из девяти

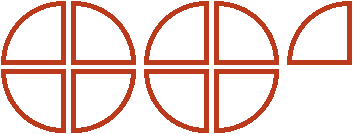
Поэтому значение выражения равно

Сравнение дробей 6 класс

Чтобы сравнить дроби, нужно запомнить два простых правила.

Правило 1. Если знаменатели разные

Смотрим на знаменатели, они не совпадают. Значит нужно найти общий.
Для дробей общим знаменателем будет 12.
Делим 12 сначала на нижнюю часть первой дроби: 12 : 12 = 1 (это доп. множитель для 1-й дроби).
Теперь 12 делим на 3, получаем 4 — доп. множитель 2-й дроби.
Умножаем полученные цифры на числители, чтобы преобразовать дроби: 1 х 7 = 7 (первая дробь: 7/12); 4 х 2 = 8 (вторая дробь: 8/12).
Теперь можем сравнивать: 7/12 и 8/12. Получилось: 7/12 < 8/12.

Чтобы представлять дроби лучше, можно для наглядности использовать рисунки, где предмет делится на части (к примеру, торт). Если требуется сравнить 4/7 и 2/3, то в первом случае торт делят на 7 частей и выбирают 4 из них. Во втором — делят на 3 части и берут 2. Невооруженным взглядом будет понятно, что 2/3 будет больше 4/7.