Системы с нелинейными уравнениями

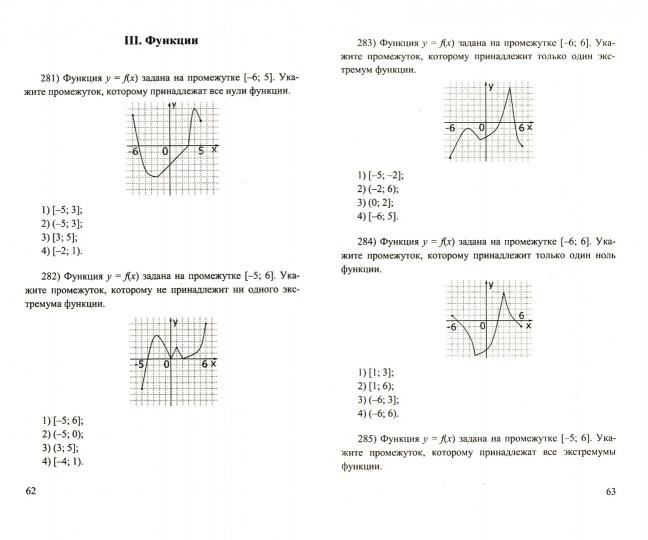
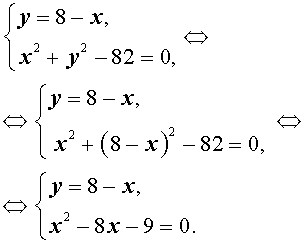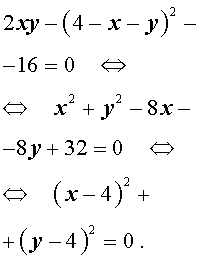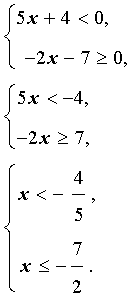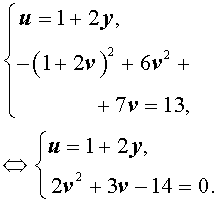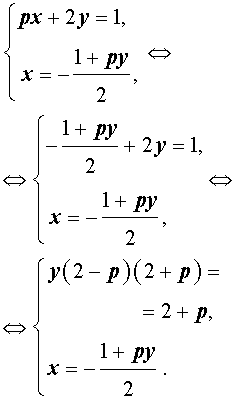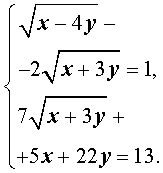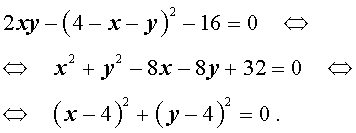Основные виды

Понятно, что разнообразных уравнений бесконечно много. Естественно, и составленных с их использованием систем уравнений также бесконечно много. Поэтому, для удобства изучения и работы с системами уравнений есть смысл их разделить на группы по схожим характеристикам, а дальше перейти к рассмотрению систем уравнений отдельных видов.

Первое подразделение напрашивается по числу уравнений, входящих в систему. Если уравнений два, то можно сказать, что перед нами система двух уравнений, если три – то система трех уравнений, и т.д. Понятно, что не имеет смысла говорить о системе одного уравнения, так как в этом случае по сути мы имеем дело с самим уравнением, а не с системой.

Следующее деление базируется на числе переменных, участвующих в записи уравнений системы. Если переменная одна, то мы имеем дело с системой уравнений с одной переменной (еще говорят с одной неизвестной), если две – то с системой уравнений с двумя переменными (с двумя неизвестными), и т.д. Например, — это система уравнений с двумя переменными x и y.

При этом имеется в виду число всех различных переменных, участвующих в записи. Они не обязательно должны все сразу входить в запись каждого уравнения, достаточно их наличия хотя бы в одном уравнении. К примеру, — это система уравнений с тремя переменными x, y и z. В первом уравнение переменная x присутствует явно, а y и z – неявно (можно считать, что эти переменные имеют числовой коэффициент нуль), а во втором уравнении есть x и z, а переменная y явно не представлена. Другими словами, первое уравнение можно рассматривать как , а второе – как x+0·y−3·z=0.

Третий момент, в котором различаются системы уравнений, это вид самих уравнений.

В школе изучение систем уравнений начинается с систем двух линейных уравнений с двумя переменными . То есть, такие системы составляют два линейных уравнения. Вот пара примеров: и . На них и познаются азы работы с системами уравнений.

При решении более сложных задач можно столкнуться и с системами трех линейных уравнений с тремя неизвестными.

Дальше в 9 классе в системы двух уравнений с двумя переменными добавляются нелинейные уравнения, по большей части целые уравнения второй степени, реже – более высоких степеней. Эти системы называют системами нелинейных уравнений, при необходимости уточняют число уравнений и неизвестных. Покажем примеры таких систем нелинейных уравнений: и .

А дальше в системах встречаются и дробно рациональные уравнения, к примеру, . Их обычно называют просто системами уравнений, не уточняя, каких именно уравнений. Здесь стоит заметить, что наиболее часто про систему уравнений говорят просто «система уравнений», а уточнения добавляют лишь при необходимости.

В старших классах по мере изучения материала в системы проникают иррациональные, тригонометрические, логарифмические и показательные уравнения : , , .

Если заглянуть еще дальше в программу первых курсов ВУЗов, то основной упор сделан на исследование и решение систем линейных алгебраических уравнений (СЛАУ), то есть, уравнений, в левых частях которых многочлены первой степени, а в правых – некоторые числа. Но там, в отличие от школы, уже берутся не два линейных уравнения с двумя переменными, а произвольное число уравнений с произвольным числом переменных, зачастую не совпадающим с числом уравнений .

Что называется решением системы уравнений?

К системам уравнений непосредственно относится термин «решение системы уравнений». В школе дается определение решения системы уравнений с двумя переменными :

Определение.

Решением системы уравнений с двумя переменными называется пара значений этих переменных, обращающая каждое уравнение системы в верное числовое равенство, другими словами, являющаяся решением каждого уравнения системы.

Например, пара значений переменных x=5, y=2 (ее можно записать как (5, 2)) является решением системы уравнений по определению, так как уравнения системы при подстановке в них x=5, y=2 обращаются в верные числовые равенства 5+2=7 и 5−2=3 соответственно. А вот пара значений x=3, y=0 не является решением этой системы, так как при подстановке этих значений в уравнения, первое из них обратится в неверное равенство 3+0=7.

Аналогичные определения можно сформулировать и для систем с одной переменной, а также для систем с тремя, четырьмя и т.д. переменными.

Определение.

Решением системы уравнений с одной переменной будет значение переменной, являющееся корнем всех уравнений системы, то есть, обращающее все уравнения в верные числовые равенства.

Приведем пример. Рассмотрим систему уравнений с одной переменной t вида . Число −2 является ее решением, так как и (−2)2=4, и 5·(−2+2)=0 – верные числовые равенства. А t=1 – не является решением системы, так как подстановка этого значения даст два неверных равенства 12=4 и 5·(1+2)=0.

Определение.

Решением системы с тремя, четырьмя и т.д. переменными называется тройка, четверка и т.д. значений переменных соответственно, обращающая в верные равенства все уравнения системы.

Так по определению тройка значений переменных x=1, y=2, z=0 – решение системы , так как 2·1=2, 5·2=10 и 1+2+0=3 — верные числовые равенства. А (1, 0, 5) не является решением этой системы, так как при подстановке этих значений переменных в уравнения системы второе из них обращается в неверное равенство 5·0=10, да и третье тоже 1+0+5=3.

Заметим, что системы уравнений могут не иметь решений, могут иметь конечное число решений, например, одно, два, …, а могут иметь бесконечно много решений. В этом Вы убедитесь по мере углубления в тему.

Учитывая определения системы уравнений и их решений можно заключить, что решение системы уравнений представляет собой пересечение множеств решений всех ее уравнений.

В заключение приведем несколько связанных определений:

Определение.

Система уравнений называется несовместной, если она не имеет решений, в противном случае система называется совместной.

Определение.

Система уравнений называется неопределенной, если она имеет бесконечно много решений, и определенной, если имеет конечное число решений, либо не имеет их вообще.

Эти термины вводятся, например, в учебнике , однако в школе применяются довольно редко, чаще их можно услышать в высших учебных заведениях.

Дальше не помешает познакомиться с равносильными системами уравнений, а уже потом можно будет переходить к процессу нахождения решений систем уравнений.

Список литературы.

1. Алгебра: учеб. для 7 кл. общеобразоват. учреждений / ; под ред. С. А. Теляковского. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : ил. — ISBN 978-5-09-019315-3.
2. Алгебра: 9 класс: учеб. для общеобразоват. учреждений / ; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2009. — 271 с. : ил. — ISBN 978-5-09-021134-5.
3. Мордкович А. Г. Алгебра. 7 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. — 17-е изд., доп. — М.: Мнемозина, 2013. — 175 с.: ил. ISBN 978-5-346-02432-3.
4. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 13-е изд., стер. — М.: Мнемозина, 2011. — 222 с.: ил. ISBN 978-5-346-01752-3.
5. Мордкович А. Г. Алгебра и начала математического анализа. 11 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А. Г. Мордкович, П. В. Семенов. — 2-е изд., стер. — М.: Мнемозина, 2008. — 287 с.: ил. ISBN 978-5-346-01027-2.
6. Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
7. А. Г. Курош. Курс высшей алгебры.
8. Ильин В. А., Позняк Э. Г. Аналитическая геометрия: Учеб.: Для вузов. – 5-е изд. – М.: Наука. Физматлит, 1999. – 224 с. – (Курс высшей математики и мат. физики). – ISBN 5-02-015234 – X (Вып. 3)

Некогда разбираться?

Решение систем методом Гаусса

В высшей математике способ Гаусса изучают совместно с методом Крамера, а процесс поиска решения систем так и называется метод решения Гаусса — Крамера. Данные способы используют при нахождении переменных систем с большим количеством линейных уравнений.

Метод Гаусса очень похож на решения с помощью подстановок и алгебраического сложения, но более систематичен. В школьном курсе решение способом Гаусса применяется для систем из 3 и 4 уравнений. Цель метода состоит в приведении системы к виду перевернутой трапеции. Путем алгебраических преобразований и подстановок находится значение одной переменной в одном из уравнении системы. Второе уравнение представляет собой выражение с 2-мя неизвестными, ну а 3 и 4 — соответственно с 3-мя и 4-мя переменными.

После приведения системы к описанному виду, дальнейшее решение сводится к последовательной подстановке известных переменных в уравнения системы.

В школьных учебниках для 7 класса пример решения методом Гаусса описан следующим образом:

Как видно из примера, на шаге (3) было получено два уравнения 3x₃-2x₄=11 и 3x₃+2x₄=7. Решение любого из уравнений позволит узнать одну из переменных x_n.

Теорема 5, о которой упоминается в тексте, гласит что если одно из уравнений системы заменить равносильным, то полученная система будет также равносильна исходной.

Метод Гаусса труден для восприятия учеников средней школы, но является одним из наиболее интересных способов для развития смекалки детей, обучающихся по программе углубленного изучения в математических и физических классах.

Для простоты записи вычислений принято делать следующим образом:

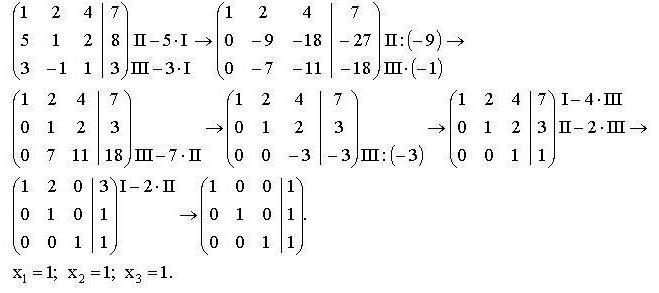
Коэффициенты уравнений и свободные члены записываются в виде матрицы, где каждая строка матрицы соотносится с одним из уравнений системы. Вертикальная черта отделяет левую часть уравнения от правой. Римскими цифрами обозначаются номера уравнений в системе.

Сначала записывают матрицу, с которой предстоит работать, затем все действия проводимые с одной из строк. Полученную матрицу записывают после знака «стрелка» и продолжают выполнять необходимые алгебраические действия до достижения результата.

В итоге должна получиться матрица в которой по одной из диагоналей стоят 1, а все другие коэффициенты равны нулю, то есть матрицу приводят к единичному виду. Нельзя забывать производить вычисления с цифрами обеих частей уравнения.

Данный способ записи менее громоздкий и позволяет не отвлекаться на перечисление многочисленных неизвестных.

Свободное применение любого способа решения потребует внимательности и определенного опыта. Не все методы имеют прикладной характер. Какие-то способы поиска решений более предпочтительны в той иной области деятельности людей, а другие существуют в целях обучения.

Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное

      Пример 7. Решить систему уравнений

(10)

      Решение. Совершим над системой (10) следующие преобразования:

• второе уравнение системы оставим без изменений;
• к первому уравнению, умноженному на   5 ,   прибавим второе уравнение, умноженное на   3 ,   и запишем полученный результат вместо первого уравнения системы (10).

      В результате система (10) преобразуется в ей систему (11), в которой первое уравнение является

(11)

     Решим

3×2 + 17xy + 10y2 = 0 ,

рассматривая его как относительно неизвестного   x :

.

      В случае, когда   x = – 5y ,   из второго уравнения системы (11) получаем уравнение

5y2 = – 20 ,

которое корней не имеет.

      В случае, когда

,

из второго уравнения системы (11) получаем уравнение

,

Ответ:   (– 2 ; 3) ,   (2 ; – 3)

Уравнения с двумя переменными

Порою в ур-нии содержится не одна, а две переменных. Такие ур-ния мы уже . Приведем несколько примеров уравнений с двумя переменными:

2х – 5у = 8

4t3– 6ht = h4

– 14z + 5v/z = 8

В абсолютном большинстве таких задач для обозначения переменных используют буквы х и у. Решение указывают в виде пары чисел, причем на первом месте пишут значение х, а на втором – значение у. Например, несложно убедиться, что пара чисел (– 1; 3) является решением ур-ния

х(х – у) = 4.

Для этого надо лишь вместо х подставить (– 1), а вместо у – число 3:

(– 1)(– 1 – 3) = 4

4 = 4

Получили верное равенство. Заметим, что пара (– 1; 3) является не единственным решением ур-ния. Например, пара (2; 0) также обращает ур-ние в верное рав-во:

2(2 – 0) = 4

4 = 4

У ур-ний с двумя неизвестными, как и у ур-ний с одной неизвестной, можно определить степень. Для этого надо представить их в таком виде, когда слева записан многочлен, а справа – ноль. Тогда степень ур-ния будет равна степени многочлена. Так как ур-ние содержит две переменных, то для обозначения такого многочлена используется запись Р(х; у).

Пример. Определите степень уравнения

х(х2 + у) = х + 1

Решение. Раскроем скобки слева, а потом перенесем все слагаемые в одну сторону:

х(х2 + у) = х + 1

х3 + ху = х + 1

х3 + ху – х – 1 = 0

В левой части стоит многочлен третьей степени (подробнее об определении степени полинома можно узнать из ). Поэтому и степень ур-ния равна 3.

Ответ: 3

Об этой статье

wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали авторы-волонтеры. Количество просмотров этой статьи: 304 921.

Категории: Математика

English:Solve Systems of Equations

Português:Resolver um Sistema de Equações

Español:resolver sistemas de ecuaciones

Français:résoudre un système d’équations

Italiano:Risolvere dei Sistemi di Equazioni

Nederlands:Een stelsel van vergelijkingen oplossen

中文:解方程组

Bahasa Indonesia:Menyelesaikan Sistem Sistem Persamaan

Печать

Алгебра 7-9 классы. 11. Способы решения систем линейных уравнений

Подробности

Категория: Алгебра 7-9 классы

https://youtube.com/watch?v=8mbiYVE6kYY

 СПОСОБ ПОДСТАНОВКИ

Решим систему уравнений:

Выразим из первого уравнения у через х:

Подставив во второе уравнение вместо у выражение , получим систему:

Докажем, что системы (1) и (2) имеют одни и те же решения.Пусть некоторая пара значений х и у является решением системы (1). При этих значениях х и у уравнение обращается в верное равенство. Заменив в нем значение у равным ему значением выражения , мы снова получим верное равенство. Значит, каждое решение системы (1) является решением системы (2).Аналогично доказывается, что каждое решение системы (2) является решением системы (1).Таким образом, системы (1) и (2) имеют одни и те же решения. Такие системы называются равносильными.В системе (2) второе уравнение содержит только одну переменную. Решим это уравнение:

Соответствующее значение у можно найти, подставив вместо х число 1 в первое уравнение системы (1). Удобнее, однако, воспользоваться формулой

Пара (1; 4) — решение системы (1).Способ, с помощью которого мы решили систему (1), называют способом подстановки. При решении этим способом сначала из какого-нибудь уравнения выражают одну переменную через другую. Полученное выражение подставляют в другое уравнение, в результате чего приходят к уравнению с одной переменной. Решают это уравнение. Затем находят соответствующее значение второй переменной.На рисунке 66 построены графики уравнений и . Они пересекаются в точке (1; 4). Через эту точку проходит и график уравнения т. е. прямая х = 1. Мы видим, что системы (1) и (2) имеют одно и то же решение.

Покажем применение способа подстановки еще на одном примере. Решим систему:

Выразим из второго уравнения х через у:

Подставим в первое уравнение вместо х выражение

Решим полученное уравнение с одной переменной у:

Подставим в уравнение вместо у число 4,5:

Ответ: х=—3, у = 4,5.

 СПОСОБ СЛОЖЕНИЯ

Рассмотрим еще один способ решения систем уравнений — способ сложения. При решении систем этим способом, как и при решении способом подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.Пример 1. Решим систему:

 В уравнениях системы коэффициенты при у — противоположные числа. Сложив почленно левые и правые части уравнения, получим уравнение с одной переменной:

Заменим одно из уравнений системы (1), например первое, уравнением . Получим систему:

Решим систему (2). Из уравнения находим, что . Подставив это значение х в уравнение , получим уравнение с переменной у:Решим это уравнение:

Пара (11; —9) — решение системы (2). Она является также решением системы (1), так как системы (1) и (2) равносильны. В этом можно убедиться с помощью рассуждений, аналогичных тем, которые были проведены в предыдущем пункте при решении систем способом подстановки.На рисунке 67 изображены графики уравнений 2x + 3у =  — 5 и х — Зу = 38.

График уравнения , т. е. прямая , проходит через точку их пересечения. Из рисунка видно, что система (2) имеет то же решение, что и система (1).

Пример 2. Решим систему:

Почленное сложение уравнений системы не приводит к исключению одной из переменных. Однако если умножить все члены первого уравнения на — 2, а второе уравнение оставить без изменений, то коэффициенты при х в полученных уравнениях будут противоположными числами:

Теперь почленное сложение приведет к уравнению с одной переменной . Из этого уравнения находим, что . Подставив во второе уравнение вместо у число —2, найдем значение х:

Ответ: х = 6, у= — 2.

Пример 3. Решим систему

Подберем множители к уравнениям так, чтобы коэффициенты при у стали противоположными числами. С этой целью умножим каждый член первого уравнения на 3, а второго на 7. Получим систему:

Сложив уравнения почленно, получим:

Отсюда

Подставив это значение х в уравнение , найдем, что у = 19.Ответ: х=—14, у —19.

Варианты нахождения обратной матрицы

Формула нахождения обратной матрицы довольно проста: K-1= 1 / |K|, где K-1 — обратная матрица, а |K| — определитель матрицы. |K| не должен быть равен нулю, тогда система имеет решение.

Определитель легко вычисляется для матрицы «два на два», необходимо лишь помножить друг на друга элементы по диагонали. Для варианта «три на три» существует формула |K|=a₁b₂c₃ + a₁b₃c₂ + a₃b₁c_{2 +} a₂b₃c₁ + a₂b₁c₃ + a₃b₂c₁. Можно воспользоваться формулой, а можно запомнить что необходимо взять по одному элементу из каждой строки и каждого столбца так, чтобы в произведении не повторялись номера столбцов и строк элементов.

Система линейных уравнений с двумя переменными

Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.

Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и является верным числовым равенством.

Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент — его графиком будет прямая линия.

Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0: 

1. Дать переменной ? конкретное значение x = x₁, и найти значение y = y₁ при

ax₁ + by + c = 0.

1. Дать ? другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.
2. Построить на координатной плоскости xOy точки: (x₁; y₁); (x₂; y₂).
3. Проводим прямую через эти две точки и вуаля — график готов. 

График уравнения с двумя переменными

Очень часто ур-ние с 2 переменными имеет бесконечное число решений. Их удобно изображать в виде графика, ведь каждой паре чисел (х₁; у₁) соответствует точка на координатной плоскости с координатами х₁ и у₁.

Проще всего строить график уравнения с двумя переменными в том случае, когда удается выразить переменную у через х. Например, пусть надо построить график ур-ния

6х + 3у = 9

Выразим неизвестную величину у через х, то есть попытаемся получить ф-цию у = у(х):

6х + 3у = 9

3у = 9 – 6х

у = 3 – 2х

Построим график ф-ции у = 3 – 2х. Он одновременно будет являться и графиком ур-ния 6х + 3у = 9:

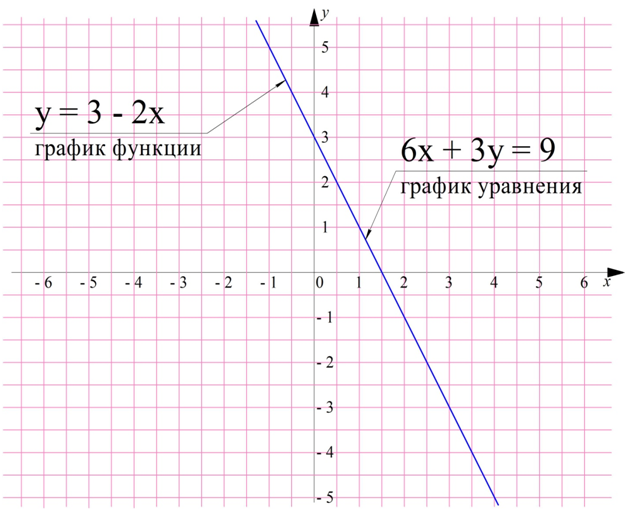
Не всегда можно так преобразовать ур-ние, чтобы получилась ф-ция у = у(х). Действительно, по определению функции, каждому значению аргумента должно соответствовать только одно значение ф-ции. Однако рассмотрим пример ур-ния

х – у2 = 0

Можно убедиться, что его обращают в верное рав-во пары чисел (1; 1) и (1; – 1):

12 – 12 = 0

12 – (– 1)2 = 0

Получается, что одному значению х(х = 1) соответствует сразу 2 значения у (у = 1 и у = –1). Это значит, что графиком такого ур-ния не может являться ф-ция у = у(х)

В данном случае возможно выразить х через у. Перенесем слагаемое у2 вправо:

х = у2

Получили «перевернутую ф-цию» х = х(у), где не у зависит от х, а х от у. Ф-ция является квадратичной, а потому ее графиком будет парабола:

Так как х и у в ф-ции поменялись местами, то ось параболы стала не вертикальной, а горизонтальной.

Встречаются случаи, когда из ур-ния невозможно получить ни ф-циюу(х), ни ф-цию х(у). Рассмотрим ур-ние

х2 + у2 = 25

Его решениями являются пары чисел (0; 5) и (0; – 5). То есть значению х = 0 соответствует два значения у (5 и – 5), поэтому не получиться записать ф-циюу(х). С другой стороны, решениями ур-ния являются также пары (5; 0) и (– 5; 0), то есть значению у = 0 также соответствует два значения х (– 5 и 5), поэтому и записать ф-цию х(у) не удастся. Вообще данное ур-ние является частным случаем ур-ния

х2 + у2 = R2

где R– некоторое постоянное число, или параметр. Оно называется уравнением окружности, потому что его графиком как раз и является окружность.

Докажем это утверждение. Пусть на координатной плоскости есть точка А с произвольными координатами (х; у):

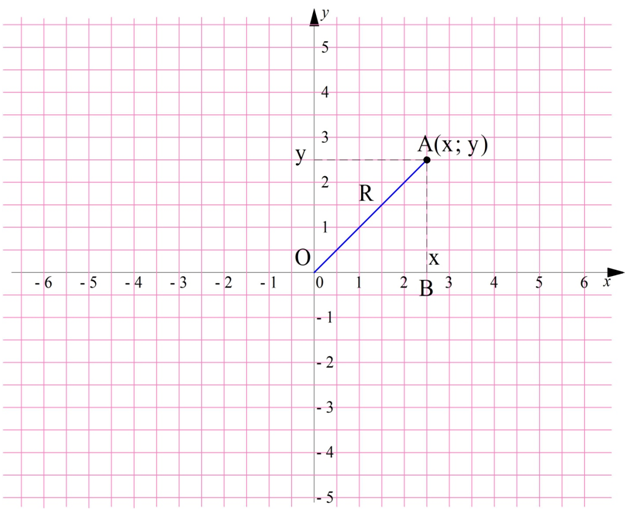
Опустим из А перпендикуляр на ось Ох в точку В. Получили прямоугольный треугольник ОАВ. Его катет ОВ равен у, а катет АВ = х. По теореме Пифагора можно найти длину гипотенузы ОА, которая и является расстоянием от О до А:

ОА2 = ОВ2 + АВ2 = х2 + у2

Окружность радиусом R– это множество точек, удаленных от центра на расстояние R. То есть расстояние ОА равно R, то точка А лежит на окружности радиусом R c центром в О:

х2 + у2 = ОА2 = R2

Таким образом, координаты любой точки, лежащей на расстоянии Rот центра, удовлетворяют ур-нию

х2 + у2 = R2

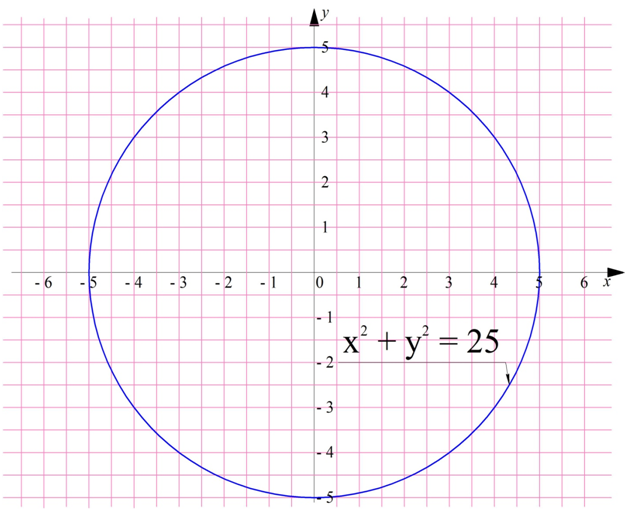
В частности, графиком ур-ния

х2 + у2 = 25

является окружность с радиусом 5 (так как 25 = 52)

Онлайн-курсы по математике помогут подготовиться к ОГЭ наилучшим образом

Метод сложения

Очевидно, что не всегда в ур-нии можно выразить одну переменную через другую. Такую ситуацию можно, например, наблюдать в сис-ме

Однако здесь в каждом ур-нии есть слагаемое 6у2, взятое с разными знаками. За счет этого сис-му можно решить методом сложения, ведь при сложении левых частей ур-ний слагаемые 6у2 и (– 6у2) сократятся, что позволит исключить переменную у из ур-ния. Для этого надо сложить по отдельности левые и правые части ур-ний и получить новое ур-ние:

(3х2 – 6у2 + 3х) + (– 2х2 + 6у2) = –18 + 22

3х2 – 6у2 + 3х – 2х2 + 6у2 = 4

х2 + 3х = 4

х2 + 3х – 4 = 0

Получили ур-ние, не содержащее у. Его можно решить как обычное квадратное ур-ние:

D = b2– 4ас = 32 – 4•1•(– 4) = 9 + 16 = 25

х₁ = (– 3 – 5)/2 = – 4

х₂ = (– 3 + 5)/2 = 1

Нашли два значения х. Подставляя его второе ур-ние, получим

при х = – 4:

– 2•(– 4)2 + 6у2 = 22

6у2 = 22 + 32

у2 = 9

у₁ = 3 или у₂ = – 3

при х = 1:

– 2•12 + 6у2 = 22

6у2 = 22 + 2

у2 = 4

у₃ = – 2 или у₄ = 2

Имеем 4 решения сис-мы (– 4; 3), (– 4; – 3), (1; – 2), (1; 2).

Мы рассмотрели простейший случай использования метода сложения уравнений, когда ур-ния сис-мы можно сложить сразу. Однако порою их надо сначала умножить на какие-то числа, и лишь потом складывать.

Пример. Укажите решение для сис-мы:

Решение. Сразу складывать эти ур-ния нет смысла, потому что при этом не исчезнет ни одна переменная. Напомним, что обе части любого ур-ния можно умножить на число, не равное нулю, и в результате получится равносильное ур-ние. Поэтому второе ур-ние умножим на (– 2):– 4х2+ 2у2 = – 2

А вот теперь есть смысл сложить его с первым ур-нием, так как у них есть слагаемые 2у2 с противоположными знаками:

(3х2 – 2у2) + (– 4х2 + 2у2) = 1 – 2

–х2 = – 1

х2 = 1

х = – 1 или х = 1

Полученные значения х будем подставлять в другое ур-ние, например, в 2х2 – у2 = 1 (на самом деле можно выбрать любое другое из ур-ний сис-мы).

При х = – 1:

2(– 1)2 – у2 = 1

у2 = 1

у₁ = – 1 или у₂ = 1

Теперь подставим х = 1:

2•12 – у2 = 1

у2 = 1

у₃ = – 1 или у₄ = 1

В итоге получаем 4 решения: (– 1; – 1), (– 1; 1), (1; – 1) и (1; 1)

Ответ:(– 1; – 1), (– 1; 1), (1; – 1), (1; 1).

Порою метод сложения и метод подстановки следует использовать одновременно.

Пример. Решите систему методом сложения:

Решение: постараемся избавиться от слагаемых с буквенной частью ху. Для этого умножим второе ур-ние на (– 2):

– 2х – 2у – 2ху = 12

Сложим его с первым ур-нием:

(3х + у + 2ху) + (– 2х – 2у – 2ху) = – 6 + 12

х – у = 6

исключить переменную не удалось, однако мы получили линейное ур-ние. Выразим из него у:

у = х – 6

х + у + ху = – 6

х + (х – 6) + х(х – 6) = – 6

х2 – 4х – 6 = – 6

х2 – 4х = 0

х(х – 4) = 0

х = 0 или х – 4 = 0

х₁ = 0 или х₂ = 4

Подставим полученные результаты в выражение у = х – 6

у₁ = х₁ – 6 = 0 – 6 = – 6

у₂ = х₂ – 6 = 4 – 6 = – 2

Получили два решения: (0; – 6) и (4; – 2).

Ответ: (0; – 6) и (4; – 2).

Только усвоенная информация становится знанием. В этом вам помогут онлайн-курсы