Система отсчёта

Неинерциальные системы отсчёта

С планетой Земля связывают и инерциальные, и неинерциальные системы отсчёта. При этом нужно понимать, что допущение о том, что Земля – инерционная система, по космическим масштабам очень грубое. Тем не менее, этого грубого приближения достаточно для описания многих процессов, проходящих на поверхности планеты. В частности, движение сухопутного транспорта, движение шаров на биллиардном столе и т. д. точно описывается в этом приближении.

Земля движется вокруг собственной оси. Это движение необходимо учитывать, например, при запуске космических аппаратов. В системе отсчёта, связанной с Землёй, ракета, стартовавшая вертикально, совершает также видимое движение в горизонтальном направлении. Это логично: место старта ракеты смещается вместе со всей поверхностью планеты из-за её вращения. Подобные отклонения траектории, свойственные неинерциальным системам, чисто математически описывают с помощью инерциальных сил (сил, которых на самом деле не существует, но принятие которых в расчёт помогает чисто формально отнести систему отсчёта к числу инерциальных). В данном случае математически видимое отклонение ракеты от прямой траектории описывается силой Кориолиса, которая якобы действует на неё.

В классической механике

Классическая механика постулирует следующие два принципа:

время абсолютно, то есть промежутки времени между любыми двумя событиями одинаковы во всех произвольно движущихся системах отсчёта;
пространство абсолютно, то есть расстояние между двумя любыми материальными точками одинаково во всех произвольно движущихся системах отсчёта.

Эти два принципа позволяют записывать уравнение движения материальной точки относительно любой неинерциальной системы отсчёта, в которой не выполняется первый закон Ньютона.

Уравнение движения материальной точки в неинерциальной системе отсчёта может быть представлено в виде:

ma→r=F→−ma→e−ma→k{\displaystyle m{\vec {a}}_{r}={\vec {F}}-m{\vec {a}}_{e}-m{\vec {a}}_{k}},

или в развёрнутом виде:

ma→r=F→+2mv→r×ω→−mdv→dt+mω2r→⊥−mdω→dt×r→{\displaystyle m{\vec {a}}_{r}={\vec {F}}+2m\left-m{\frac {d{\vec {v_{0}}}}{dt}}+m\omega ^{2}{\vec {r}}_{\perp }-m\left},

где m{\displaystyle \ m} — масса тела, a→r{\displaystyle \ {\vec {a}}_{r}}, v→r{\displaystyle {\vec {v}}_{r}} — ускорение и скорость тела относительно неинерциальной системы отсчёта, F→{\displaystyle \ {\vec {F}}} — сумма всех внешних сил, действующих на тело, a→e{\displaystyle \ {\vec {a}}_{e}} — переносное ускорение тела, a→k{\displaystyle \ {\vec {a}}_{k}} — кориолисово ускорение тела, ω{\displaystyle \omega } — угловая скорость вращательного движения неинерциальной системы отсчёта вокруг мгновенной оси, проходящей через начало координат, v→{\displaystyle {\vec {v_{0}}}} — скорость движения начала координат неинерциальной системы отсчёта относительно какой-либо инерциальной системы отсчёта.

Это уравнение может быть записано в привычной форме второго закона Ньютона, если ввести силы инерции:

F→e=−ma→e{\displaystyle {\vec {F}}_{e}=-m{\vec {a}}_{e}} — переносная сила инерции
F→k=−ma→k{\displaystyle {\vec {F}}_{k}=-m{\vec {a}}_{k}} — сила Кориолиса

В неинерциальных системах отсчета возникают силы инерции. Появление этих сил является признаком неинерциальности системы отсчета.

Определение

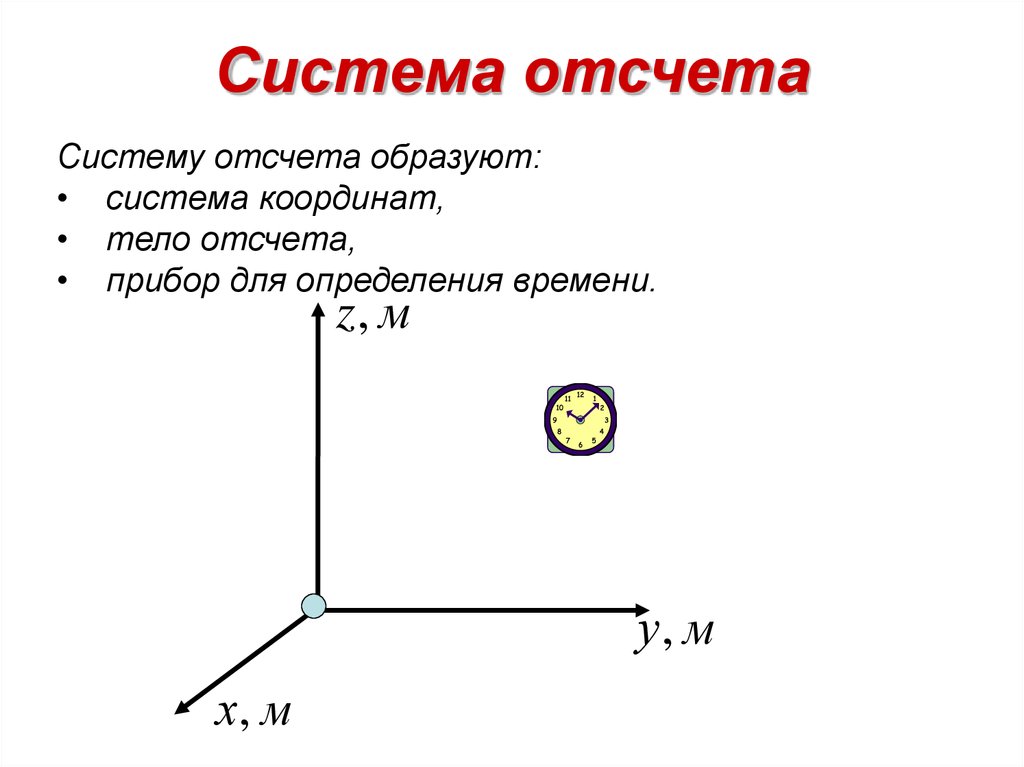
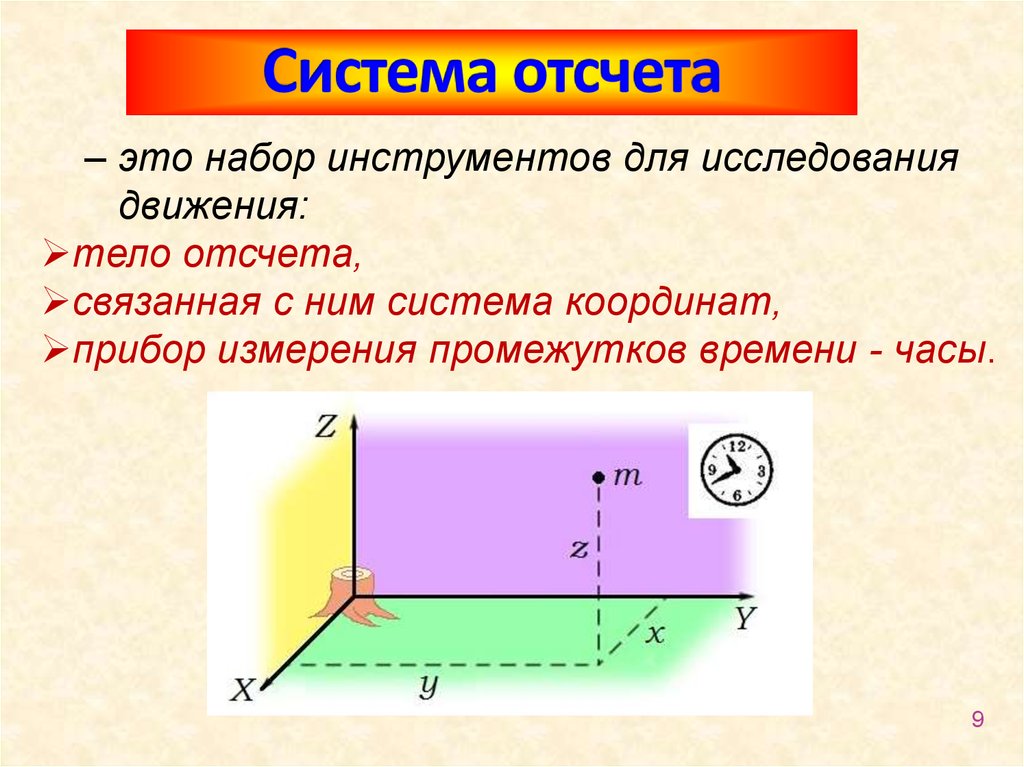
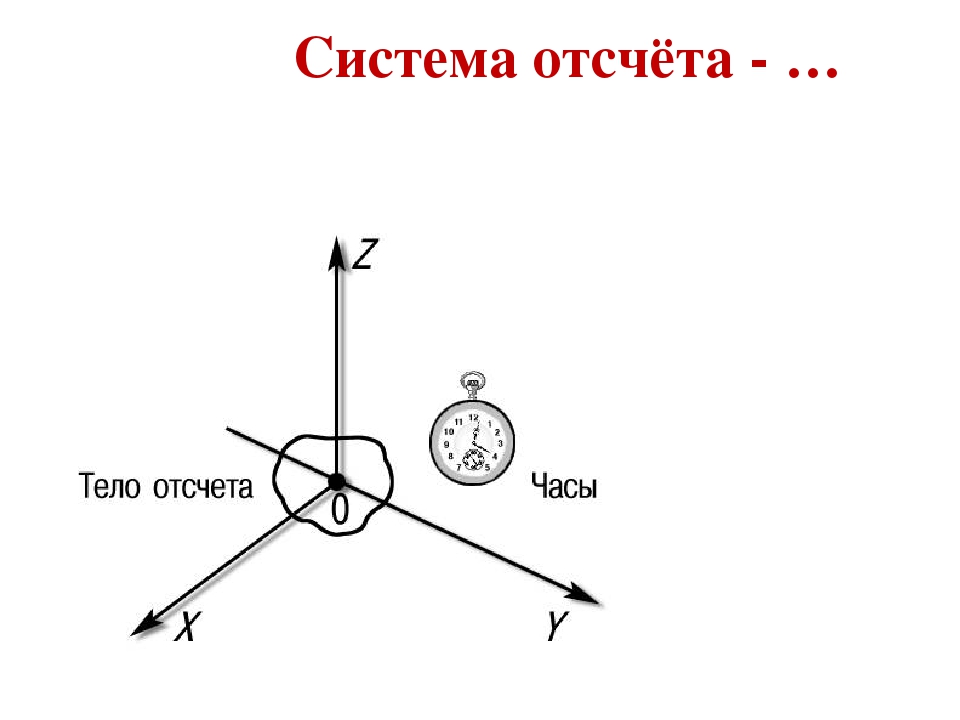
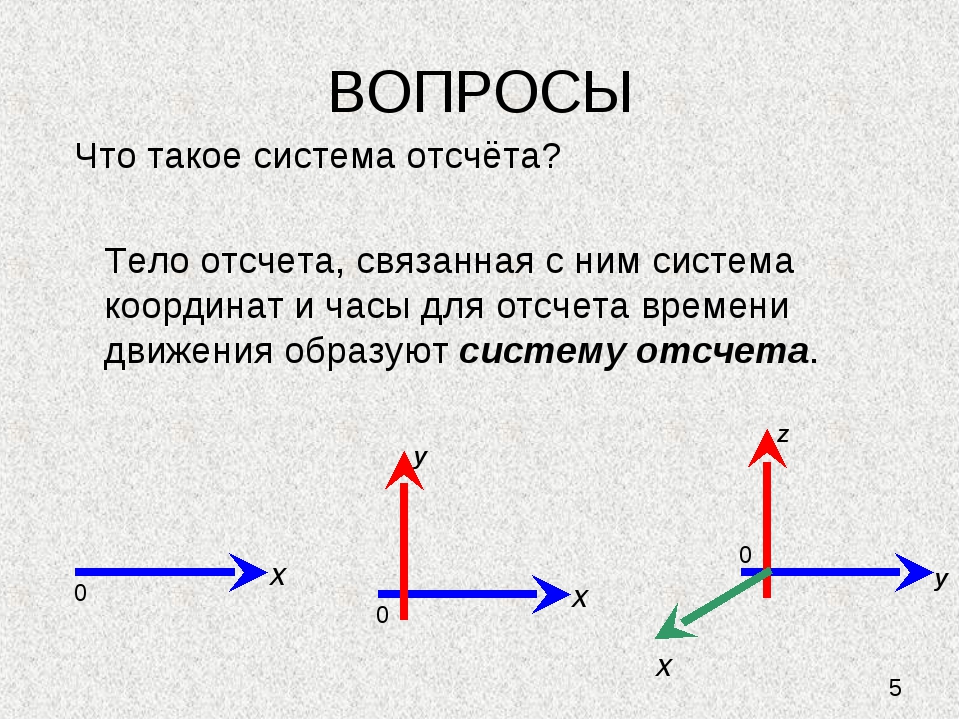
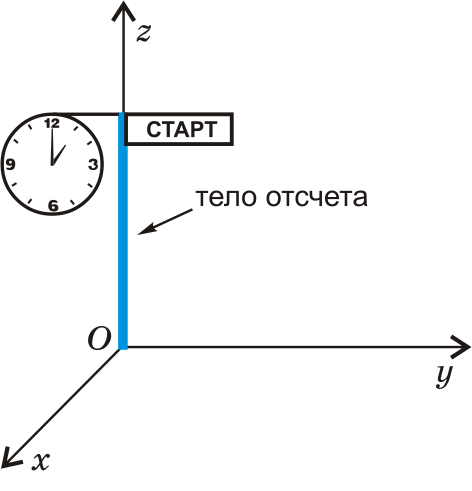
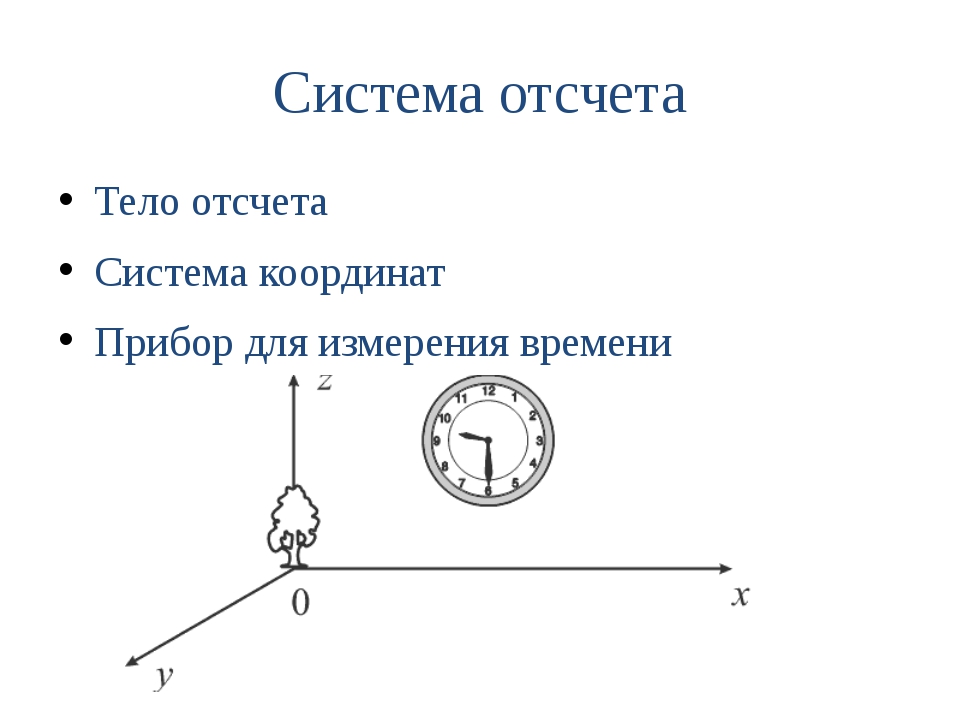
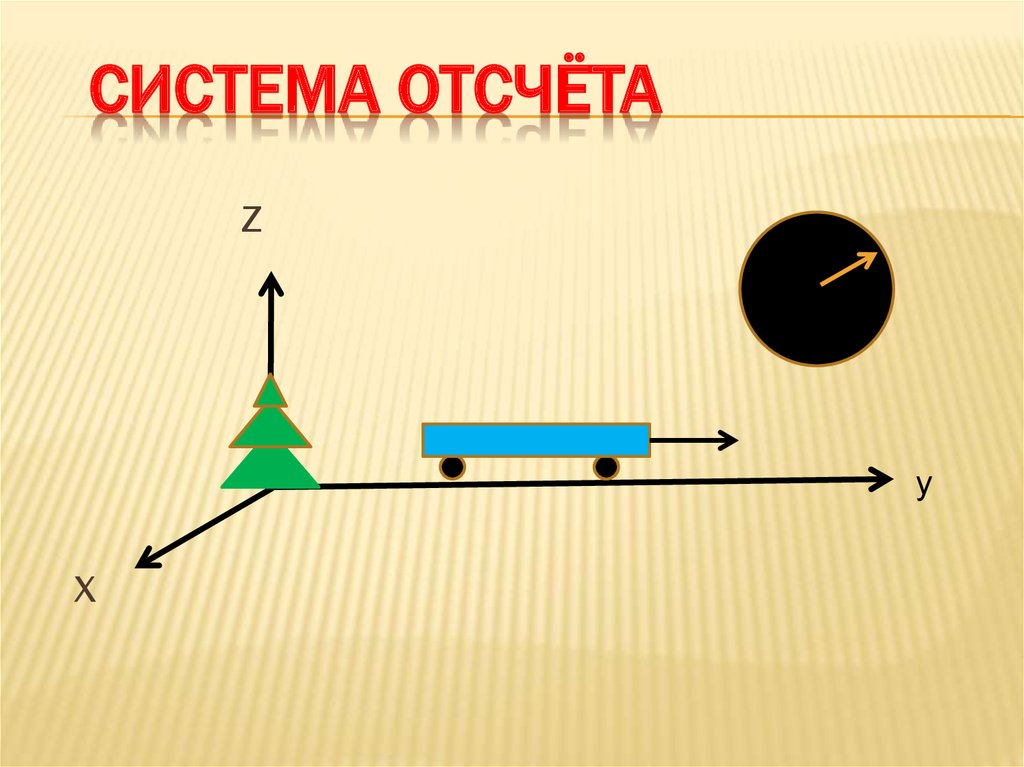
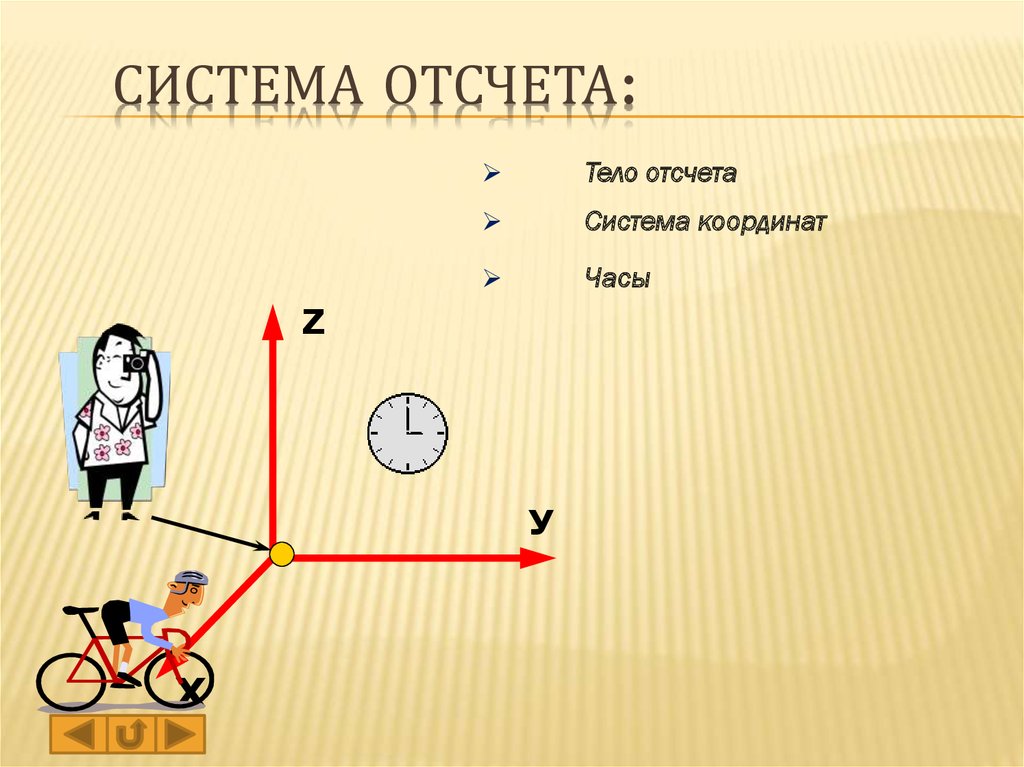
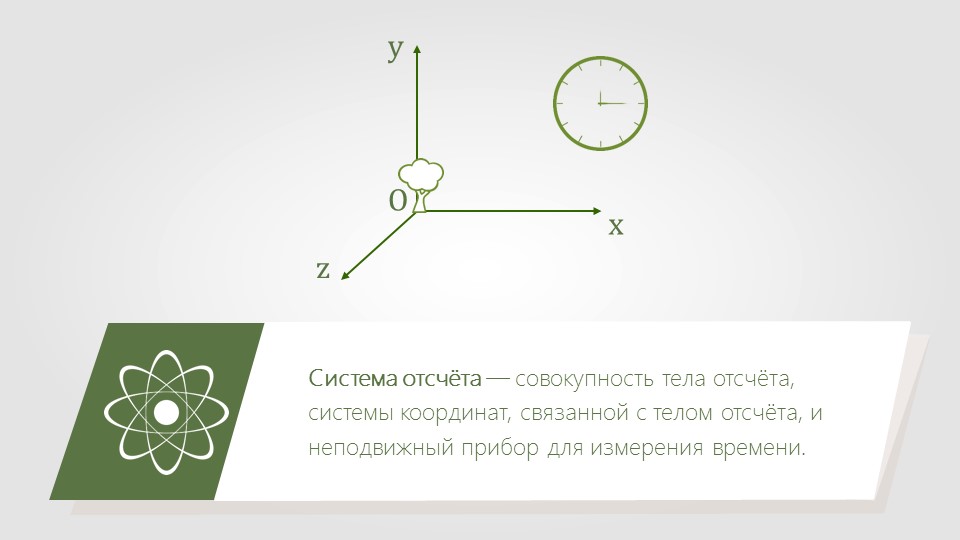
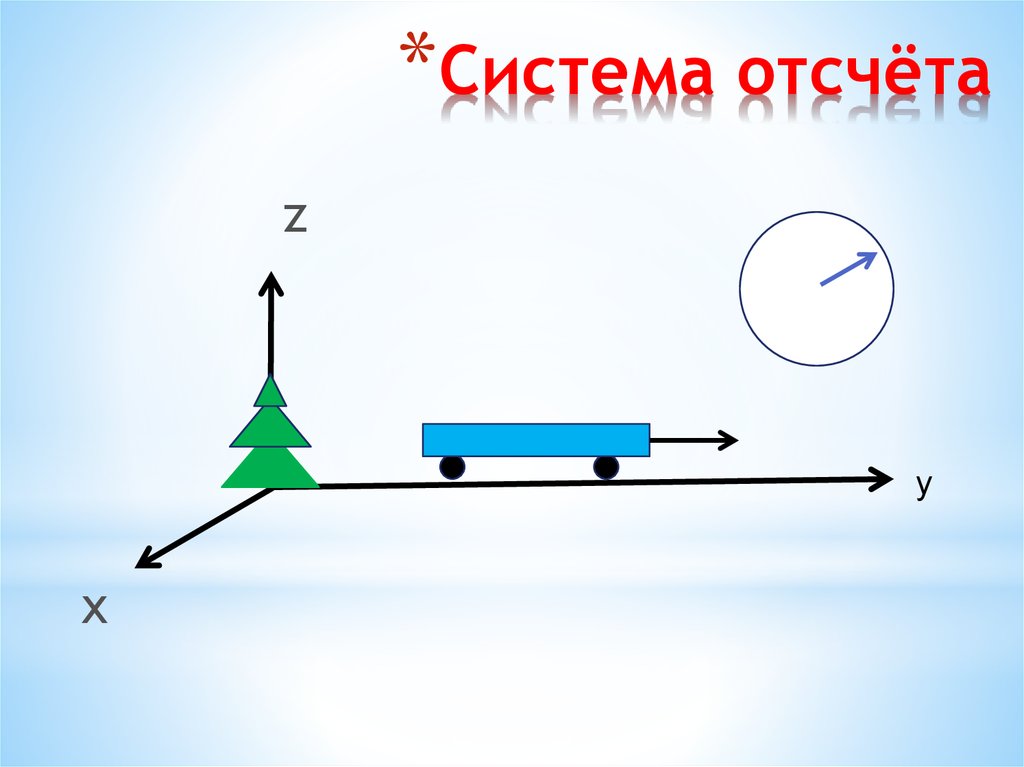
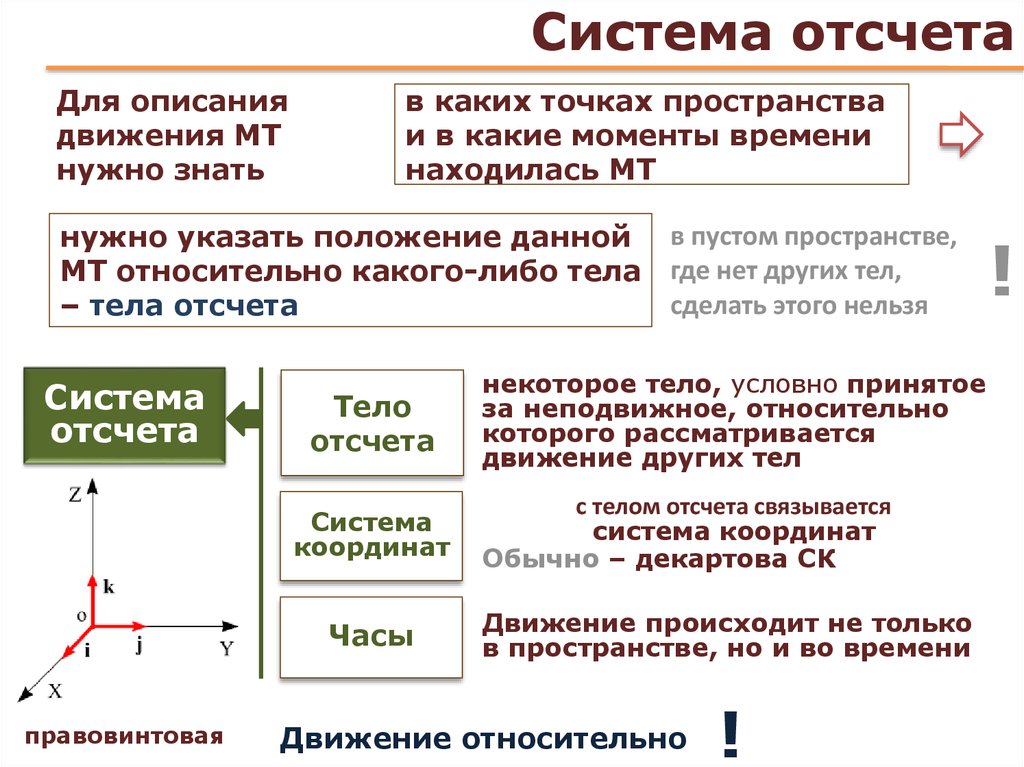
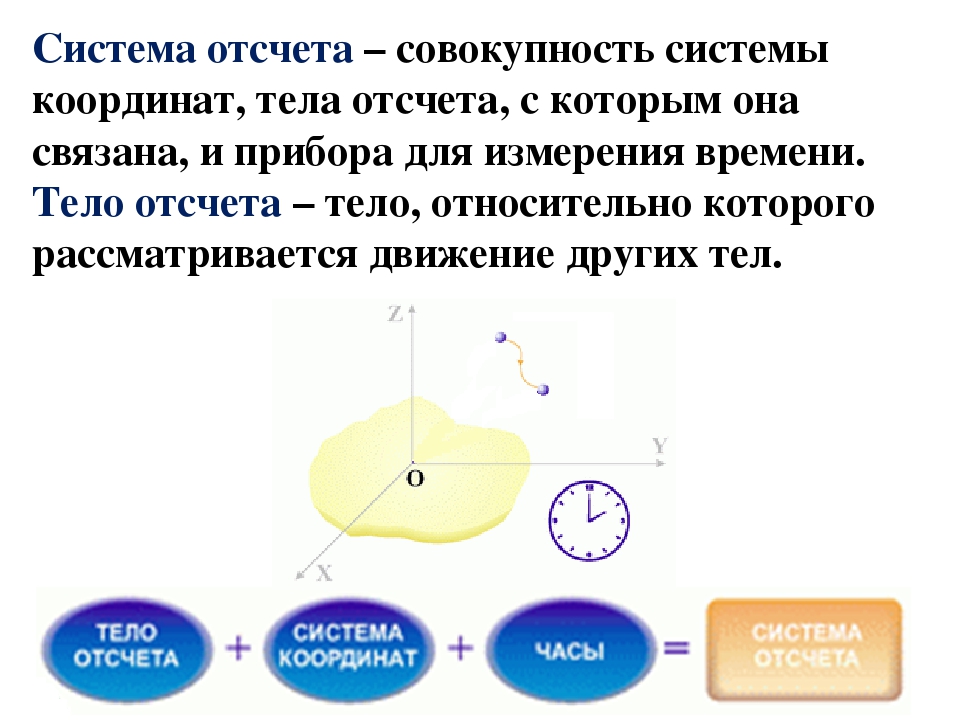
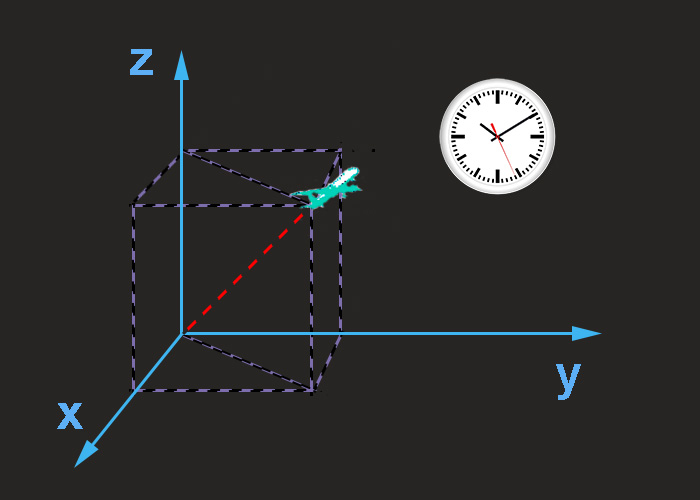
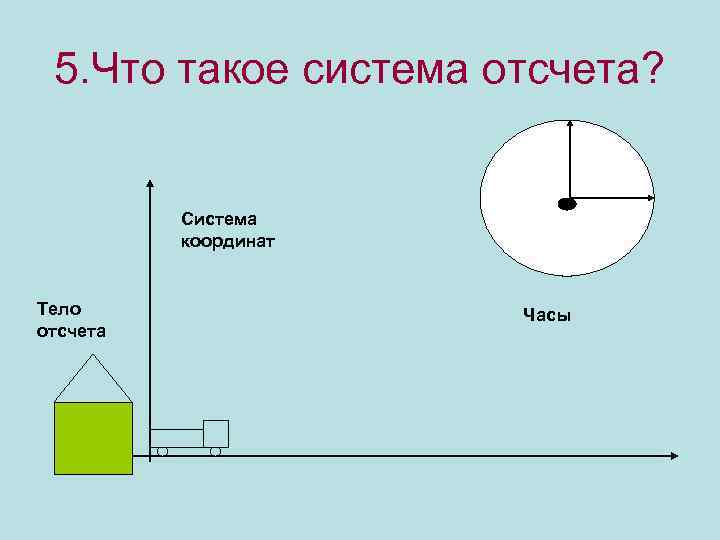
Система отсчета в физике включает в себя тело отсчета, связанные с ним оси координат и прибор для измерения времени. Тело отсчета — это точка, от которой отсчитывают положение всех остальных точек. Она может быть выбрана в любом месте пространства. Иногда в качестве начальной точки выбирают несколько тел.

Что такое система координат? Она дает возможность однозначно определить положение точки относительно начальной точки. Каждой точке пространства сопоставляются числа (одно или несколько), которые откладываются на координатных осях.

Пример — шахматная доска. Каждая клетка обозначается буквой и цифрой, по одной оси идут буквы, по другой цифры. Благодаря им мы можем однозначно описать положение фигуры.

Наиболее распространенные в физике виды координат — это:

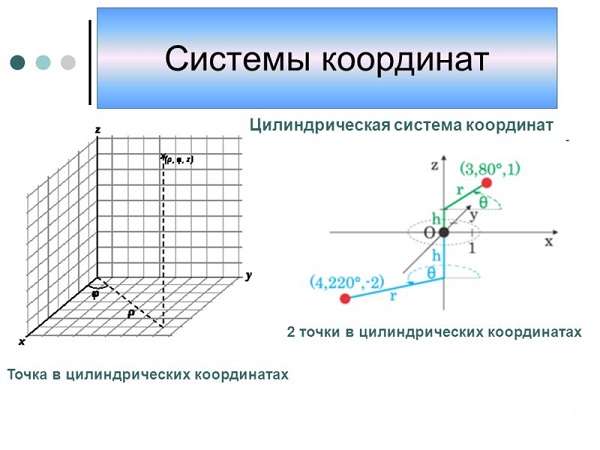
прямоугольные, или декартовы — угол между осями прямой, используются две (на плоскости) или три (в трехмерном пространстве) оси,
полярные — на плоскости, где в качестве координат используется расстояние от центра r и угол относительно полярной оси (полярный угол),
цилиндрические — расширение полярных на трехмерное пространство, добавляется ось z, перпендикулярная r и плоскости, в которой лежит полярный угол,
сферические — трехмерные, используются два угла и расстояние от центра, так построены географические и астрономические координаты.

Существует множество других вариантов координат. Можно переходить из одних в другие, преобразуя координаты с помощью уравнений.

Понятие системы отсчета (СО) включает прибор для измерения времени, другими словами, часы. Он необходим, чтобы рассматривать движение точки — изменение ее положения со временем.

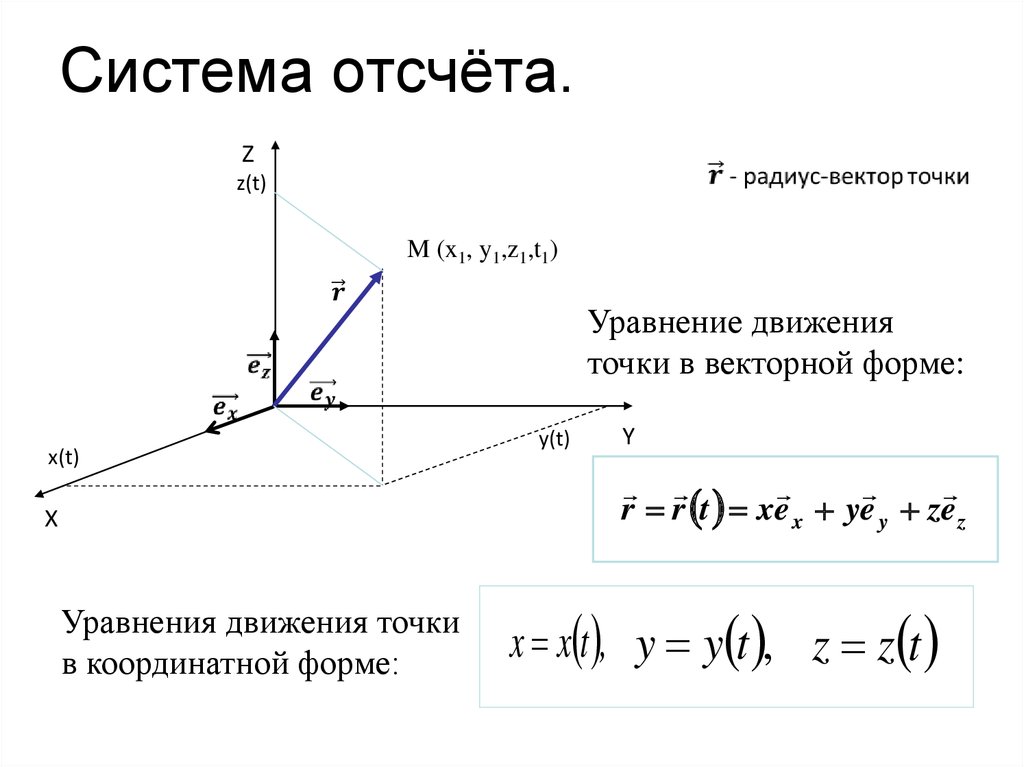
Изменения положения точки относительно выбранной СО описываются уравнениями движения. Они показывают, как изменяется положение точки с течением времени.

Абсолютная система отсчёта

Часто в физике какую-либо систему отсчета считают наиболее удобной (привилегированной) в рамках решения данной задачи — это определяется простотой расчётов либо записи уравнений динамики тел и полей в ней. Обычно такая возможность связана с симметрией задачи.

С другой стороны, ранее считалось, что существует некая «фундаментальная» система отсчёта, простота записи в которой законов природы выделяет её из всех остальных систем. Так, Ньютон считал выделенной системой отсчёта абсолютное пространство, а физики XIX века полагали что, система, относительно которой покоится эфир электродинамики Максвелла, является привилегированной, и поэтому она была названа абсолютной системой отсчёта (АСО). Окончательно предположения о существовании привилегированной системы отсчёта были отвергнуты теорией относительности. В современных представлениях никакой абсолютной системы отсчёта не существует, так как законы природы, выраженные в тензорной форме, имеют один и тот же вид во всех системах отсчёта — то есть во всех точках пространства и во все моменты времени. Это условие — — является одним из проверяемых оснований физики.

Иногда абсолютной системой отсчета называют систему, связанную с реликтовым излучением, то есть инерциальную систему отсчета, в которой реликтовое излучение не имеет .

Материальная точка

Не нужно описывать движение каждой точки тела и тогда, когда его размеры очень малы по сравнению с расстоянием, которое оно проходит. Например, корабль, преодолевающий океан. Астрономы при описании движения планет и небесных тел друг относительно друга не учитывают их размеров и их собственное движение. Несмотря на то, что, например, Земля громадная, относительно расстояния до Солнца она ничтожно мала.

Нет необходимости рассматривать движение каждой точки тела, когда они не влияют на движение тела всего целиком. Такое тело можно представлять точкой. Все вещество тела как бы сосредотачиваем в точку. Получаем модель тела, без размеров, но она имеет массу. Это и есть материальная точка.

Одно и то же тело при одних его движениях можно считать материальной точкой, при других — нельзя. Например, когда мальчик идет из дома в школу и при этом проходит расстояние 1 км, то в этом движении его можно считать материальной точкой. Но когда тот же мальчик выполняет зарядку, то точкой его считать уже нельзя.

Рассмотрим движущихся спортсменов

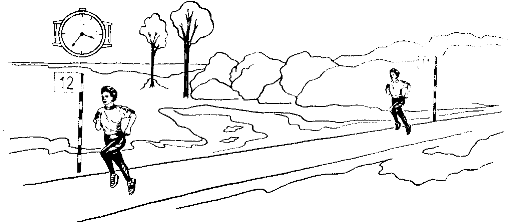
В этом случае можно спортсмена моделировать материальной точкой

В случае прыжка спортсмена в воду (рисунок справа) нельзя моделировать его в точку, так как от любого положения рук и ног зависит движение всего тела

Упражнения

Мимо стоящего велосипедиста проезжает колонна движущихся с одинаковой скоростью машин. Движется ли каждая из машин относительно велосипедиста? Движется ли машина относительно другой машин? Движется ли велосипедист относительно машины?

Относительно велосипедиста каждая машина движется. Машина относительно другой машины покоится. Велосипедист движется относительно машины.

Из центра горизонтально расположенного вращающегося диска по его поверхности пущен шарик. Каковы траектории шарика относительно Земли и диска?

Относительно Земли — спираль, относительно диска — прямая.

Чему равно перемещение какой-либо точки, находящейся на краю диска радиусом R при его повороте относительно подставки на 60? на 180? Решить в системах отсчета, связанных с подставкой и диском.

В системе отсчета, связанной с подставкой, перемещения равны R и 2R. В системе отсчета, связанной с диском, перемещение все время равно нулю.

Почему дождевые капли в безветренную погоду оставляют наклонные прямые полосы на стеклах равномерно движущегося поезда?

В системе отсчета, связанной с Землей, траектория капли — вертикальная линия. В системе отсчета, связанной с поездом, движение капли по стеклу есть результат сложения двух прямолинейных и равномерных движений: поезда и равномерного падения капли в воздухе. Поэтому след капли на стекле наклонный.

Каким образом можно определить скорость бега, если тренироваться на беговой дорожке со сломанным автоматическим определением скорости? Ведь относительно стен зала не пробегаешь ни одного метра.

Определить скорость беговой ленты относительно стен зала.

Эскалатор метро движется вверх со скоростью 0,75 м/с. а) С какой скоростью и в каком направлении надо идти по эскалатору, чтобы быть все время на уровне одного из фонарей освещения туннеля? б) С какой скоростью относительно поднимающейся лестницы надо было бы передвигаться, чтобы опускаться вниз со скоростью пассажиров, неподвижно стоящих на другой опускающейся лестнице?

а) Вниз со скоростью 0,75 м/с; б) 1,5 м/с

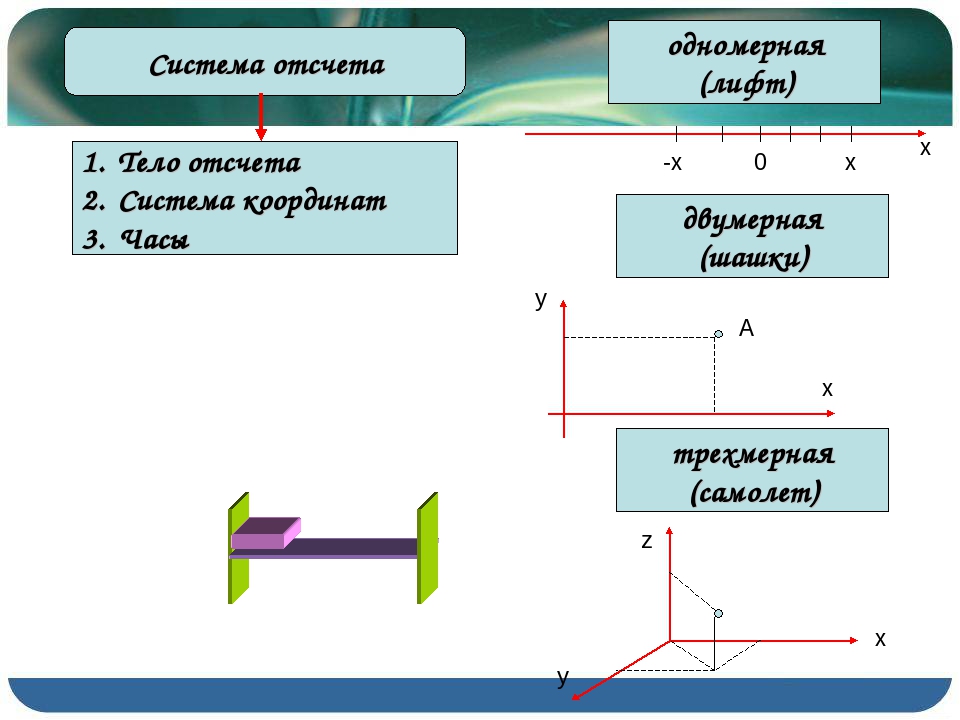
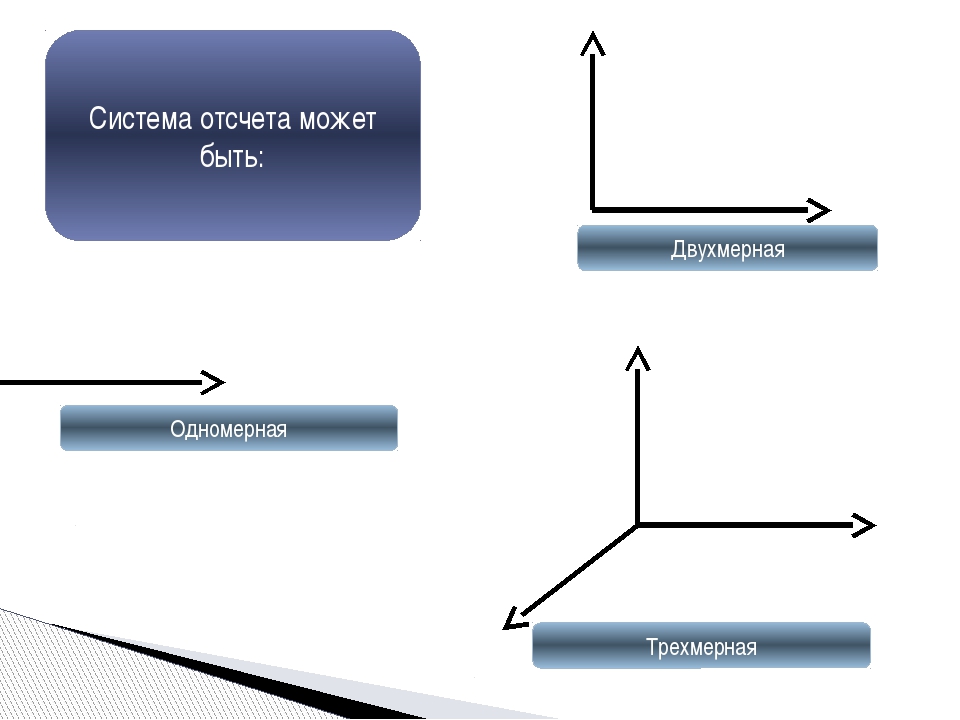
Какую систему координат следует выбрать (одномерную, двухмерную, трехмерную) для определения положения таких тел: 1. трактор в поле; 2. поезд; 3. люстра в комнате; 4. лифт; 5. подводная лодка; 6. шахматная фигура

1. двухмерную;
2. одномерную;
3. двухмерную;
4. одномерную;
5. трехмерную;
6. двухмерную

Основные свойства

Под однородностью в физике принято понимать тождественность всех точек в пространстве

Этот фактор имеет в физике немаловажное значение. Во всех точках Земли и Солнечной системы в целом законы Ньютона в физики действуют абсолютно идентично

Благодаря этому начало отсчёта может быть размещено в любой удобной точке. И если исследователь поворачивает сетку координат вокруг начальной точки, при этом никакие другие параметры задачи не будут изменяться. Все направления, которые начинаются от этой точки, имеют абсолютно тождественные свойства. Такая закономерность называется изотропностью пространства.

Относительность движения

Прямолинейное равномерно ускоренное движение в одной инерциальной системе в общем случае будет параболическим в другой равномерно двигающейся инерциальной системе отсчёта.

Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта.

Движущиеся тела изменяют своё положение относительно других тел в пространстве с течением времени. Положение автомобиля, мчащегося по шоссе, изменяется относительно указателей на километровых столбах, положение корабля, плывущего в море недалеко от берега, меняется относительно береговой линии, а о движении самолёта, летящего над землей, можно судить по изменению его положения относительно поверхности Земли. Можно показать, что одно и то же тело при одном и том же движении может одновременно по-разному перемещаться относительно разных тел.

Таким образом говорить о том, что какое-то тело движется, можно лишь тогда, когда ясно, относительно какого другого тела — тела отсчета, изменилось его положение.

Относительность движения

Виды систем отсчёта

Существует несколько видов — подвижные и неподвижные, инерциальные и неинерциальные.

Если такая совокупность координат и времени требуется для проведения кинематических исследований, в этом случае все подобные структуры являются равноправными. Если же речь идёт о решении динамических задач, предпочтение отдаётся инерциальным разновидностям – в них движение имеет более простые характеристики.

Инерциальные системы отсчёта

Инерциальными называют такие совокупности, в которых физическое тело сохраняет состояние покоя или продолжает равномерно передвигаться, если на него не воздействуют внешние силы или суммарное воздействие этих сил равняется нулю. В этом случае на тело действует инерция, что и даёт название системе.

Существование таких совокупностей подчиняется первому закону Ньютона.
Именно в таких сетках возможно наиболее простое описание движения тел.
По существу, инерциальная структура — это всего лишь идеальна математическая модель. Найти такую структуру в физическом мире не представляется возможным.

Одна и та же совокупность в одном случае может считаться инерциальной, а в другом будет признана неинерциальной. Это происходит в тех случаях, когда погрешность в результате неинерциальности слишком ничтожна и ею можно свободно пренебречь.

Неинерциальные системы отсчёта

Отличительной чертой неинерциальной системы является то, что она перемещается по отношению к инерциальной с некоторым ускорением. В этом случае законы Ньютона могут утратить свою силу и требуют введения дополнительных переменных. Без этих переменных описание такой совокупности будет недостоверным.

Проще всего рассматривать неинерциальную систему на примере. Такая характеристика движения характерна для всех тел, которые имеют сложную траекторию движения. Наиболее ярким примером такой системы можно считать вращение планет, в том числе и Земли.

Движение в неинерциальных системах отсчёта впервые изучено Коперником. Именно он доказал, что движение с участием нескольких сил может быть весьма сложным. До этого считалось, что движение Земли относится к инерциальным и описывалось оно законами Ньютона.

Положение предметов в пространстве. Тело отсчета.

Предлагаю игру: выбрать предмет в комнате и описать его местонахождение. Выполнить это так, чтобы угадывающий не смог ошибиться. Вышло? А что выйдет из описания, если другие тела не использовать? Останутся выражения: «слева от…», «над …» и подобное. Положение тела можно задать только относительно какого-нибудь другого тела.

Местонахождение клада: «Стань у восточного угла крайнего дома села лицом на север и, пройдя 120 шагов, повернись лицом на восток и пройди 200 шагов. В этом месте вырой яму в 10 локтей и найдешь 100 слитков золота». Клад найти невозможно, иначе его давно откопали бы. Почему? Тело, относительно которого совершается описание не определено, неизвестно в каком селе находится тот самый дом. Необходимо точно определиться с телом, которое возьмется за основу нашего будущего описания. Такое тело в физике называется телом отсчета. Его можно выбрать произвольно. Например, попробуйте выбрать два различных тела отсчета и относительно их описать местонахождение компьютера в комнате. Выйдет два непохожих друг на друга описания.

Инерциальные системы

Инерциальными называются системы отсчёта, в которых тело при отсутствии действия на него сил (или при суммарном значении сил, действующих на него, равном нулю) либо сохраняет состояние покоя, либо продолжает равномерное прямолинейное движение (то есть движется по инерции, отсюда и название). Существование таких систем отсчёта постулируется первым законом Ньютона. Именно такие системы подходят для наиболее простого описания движения тел.

Инерциальная система является лишь идеальной математической моделью. Физически найти такую систему отсчёта невозможно. Для описания различных процессов используются разные системы отсчёта. Кроме того, в одних случаях система отсчёта может считаться инерциальной, а в других – неинерциальной. Дело в том, что иногда погрешность вычислений, вызванная неинерциальностью системы, незначительна, и ею можно пренебречь.

Абсолютная система отсчёта

Связь с реальными системами отсчёта

Абсолютно инерциальные системы представляют собой математическую абстракцию и в природе не существуют. Однако существуют системы отсчёта, в которых относительное ускорение достаточно удалённых друг от друга тел (измеренное по эффекту Доплера) не превышает 10−10 м/с², например, Международная небесная система координат в сочетании с Барицентрическим динамическим временем дают систему, относительные ускорения в которой не превышают 1,5·10−10 м/с² (на уровне 1σ). Точность экспериментов по анализу времени прихода импульсов от пульсаров, а вскоре — и астрометрических измерений, такова, что в ближайшее время должно быть измерено ускорение Солнечной системы при её движении в гравитационном поле Галактики, которое оценивается в 2⋅10−10{\displaystyle 2\cdot 10^{-10}} м/с².

С разной степенью точности и в зависимости от области использования инерциальными системами можно считать системы отсчёта, связанные с: Землёй, Солнцем, неподвижные относительно звёзд.

Виды систем отсчета

В зависимости от того, какие задачи надо решить, можно выбрать те или иные системы отсчета.

Инерциальная и неинерциальная

СО бывают инерциальные и неинерциальные

Понятие инерциальной СО важно для кинематики — раздела физики, изучающего движение тел

Инерциальная СО движется прямолинейно с неизменной скоростью относительно окружающих тел. Окружающие предметы на нее не воздействуют. Если она стоит на месте — это тоже частный случай равномерного прямолинейного движения. Такие СО имеют следующие свойства:

инерциальная СО, которая движется относительно другой инерциальной СО, также будет инерциальной;
все законы физики выполняются в разных ИСО одинаково и имеют одинаковую форму записи;
координаты и время в разных ИСО в классической механике связаны преобразованиями Галилея;
в специальной теории относительности вместо них пользуются преобразованиями Лоренца, а скорость не может превышать некоторую постоянную (скорость света с).

Пример инерциальной СО — гелиоцентрическая, с центром в Солнце. СО, связанная с землей, инерциальной не будет. Наша планета движется вокруг солнца криволинейно, кроме того, на нее действует гравитация Солнца. Однако для многих задач этим ускорением и воздействием Солнца можно пренебречь. Это задачи, где «место действия» — поверхность Земли. Например, если нам нужно найти скорость снаряда, выпущенного из пушки, влияние Солнца и вращение Земли нас не интересует.

Неинерциальная СО подвергается воздействию других предметов, поэтому движется с ускорением. К неинерциальным относятся и вращающиеся СО. В неинерциальных СО законы Ньютона не выполняются, но можно описывать перемещение теми же уравнениями, что и в ИСО, если ввести дополнительные силы.

Система центра масс и лабораторная

В механике также используется система центра масс (центра инерции), сокращенно с.ц.м. или с.ц.и. В качестве начала координат в такой СО выбирают центр масс нескольких объектов. Сумма их импульсов в такой СО равна нулю.

Применяют с.ц.и. чаще всего в задачах рассеяния. Задачи такого типа решают в механике и ядерной физике, например, это задачи о столкновении частиц в ускорителях.

В таких задачах также используют лабораторную СО. Она противоположна с.ц.и. В ЛСО положение частиц определяют относительно покоящейся мишени, на которой рассеиваются другие частицы.

Относительность движения

Абсолютная система отсчёта

Инерциальная система отсчета

Первый закон Ньютона утверждает (это с той или иной степенью точности можно проверить на опыте) о том, что инерциальные системы существуют в действительности. Этот закон механики ставит в особое, привилегированное положение инерциальные системы отсчета.

Системы отсчета, в которых выполняется первый закон Ньютона, называют инерциальными.

Или

Инерциальные системы отсчета – это системы, относительно которых материальная точка при отсутствии на нее внешних воздействий или их взаимной компенсации покоится или движется равномерно и прямолинейно.

Инерциальных систем существует бесконечное множество. Система от-счета, связанная с поездом, идущим с постоянной скоростью по прямолинейному участку пути, – тоже инерциальная система (приближенно), как и система, связанная с Землей. Все инерциальные системы отсчета образуют класс систем, которые движутся друг относительно друга равномерно и прямолинейно. Ускорения какого-либо тела в разных инерциальных системах одинаковы.

Как установить, что данная система отсчета является инерциальной? Это можно сделать только опытным путем. Наблюдения показывают, что с очень высокой степенью точности можно считать инерциальной системой отсчета гелиоцентрическую систему, у которой начало координат связано с Солнцем, а оси направлены на определенные «неподвижные» звезды. Системы отсчета, жестко связанные с поверхностью Земли, строго говоря, не являются инерциальными, так как Земля движется по орбите вокруг Солнца и при этом вращается вокруг своей оси. Однако при описании движений, не имеющих глобального (т.е. всемирного) масштаба, системы отсчета, связанные с Землей, можно с достаточной точностью считать инерциальными.

С гораздо большей точностью можно считать инерциальной систему отсчета, в которой начало координат совмещено с центром Солнца, а координатные оси направлены к неподвижным звездам. Эту систему отсчета называют гелиоцентрической.

Инерциальными являются системы отсчета, которые движутся равномерно и прямолинейно относительно какой-либо инерциальной системы отсчета.

Галилей установил, что никакими механическими опытами, поставлен-ными внутри инерциальной системы отсчета, невозможно установить, покоится эта система или движется равномерно и прямолинейно. Это утверждение носит название принципа относительности Галилея или механического принципа относительности.

Этот принцип был впоследствии развит А. Эйнштейном и является одним из постулатов специальной теории относительности. Инерциальные системы отсчета играют в физике исключительно важную роль, так как, согласно принципу относительности Эйнштейна, математическое выражение любою закона физики имеет одинаковый вид в каждой инерциальной системе отсчета. В дальнейшем мы будем пользоваться только инерциальными системами (не упоминая об этом каждый раз).

Системы отсчета, в которых первый закон Ньютона не выполняется, называют неинерциальными.

К таким системам относится любая система отсчета, движущаяся с ускорением относительно инерциальной системы отсчета.

В механике Ньютона законы взаимодействия тел формулируются для класса инерциальных систем отсчета.

Примером механического эксперимента, в котором проявляется неинерциальность системы, связанной с Землей, служит поведение маятника Фуко. Так называется массивный шар, подвешенный на достаточно длинной нити и совершающий малые колебания около положения равновесия. Если бы система, связанная с Землей, была инерциальной, плоскость качаний маятника Фуко оставалась бы неизменной относительно Земли. На самом деле плоскость качаний маятника вследствие вращения Земли поворачивается, и проекция траектории маятника на поверхность Земли имеет вид розетки (рис. 1).

Рис. 1

О том, что телу свойственно сохранять не любое движение, а именно прямолинейное, свидетельствует, например, следующий опыт (рис. 2). Шарик, двигавшийся прямолинейно по плоской горизонтальной поверхности, сталкиваясь с преградой, имеющей криволинейную форму, под действием этой преграды вынужден двигаться по дуге. Однако когда шарик доходит до края преграды, он перестает двигаться криволинейно и вновь начинает двигаться по прямой. Обобщая результаты упомянутых (и аналогичных им) наблюдений, можно сделать вывод, что если на данное тело не действуют другие тела или их действия взаимно компенсируются, это тело покоится или же скорость его движения остается неизменной относительно системы отсчета, неподвижно связанной с поверхностью Земли.

Рис. 2

Наглядные примеры

Более наглядное представление о силах инерции дают примеры систем отсчета, связанные с транспортным средством. Представьте биллиардный стол, расположенный в вагоне поезда, идущего прямо и с постоянной скоростью. Пассажиры могут играть за этим столом, не ощущая движения. Но, как только поезд резко затормозит, ускорится, или повернёт, все почувствуют толчок, и шары начнут двигаться. Тем не менее, в системе отсчёта, связанной с поездом, физически не было никаких источников силы, которые привели к сложившейся ситуации. Эта «несуществующая сила» и является тем, что называют силой инерции.