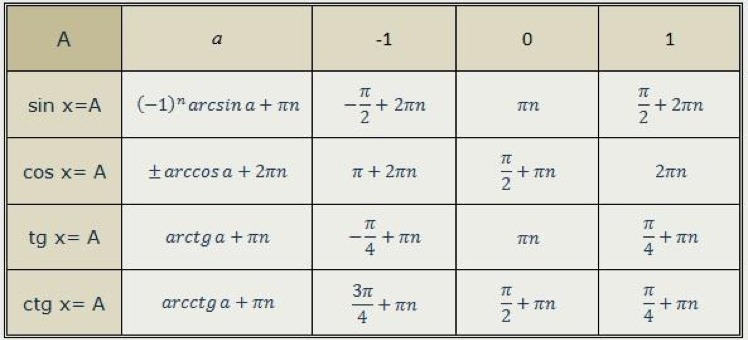
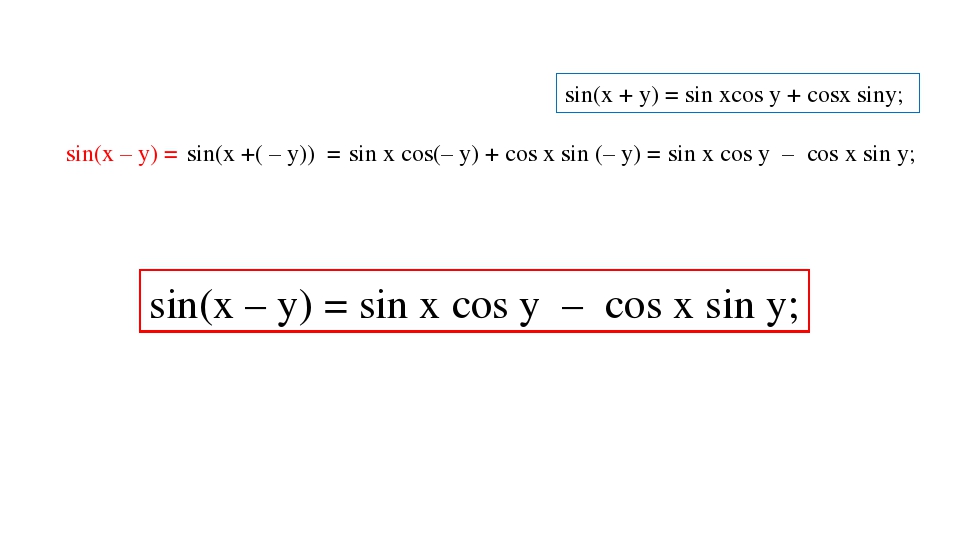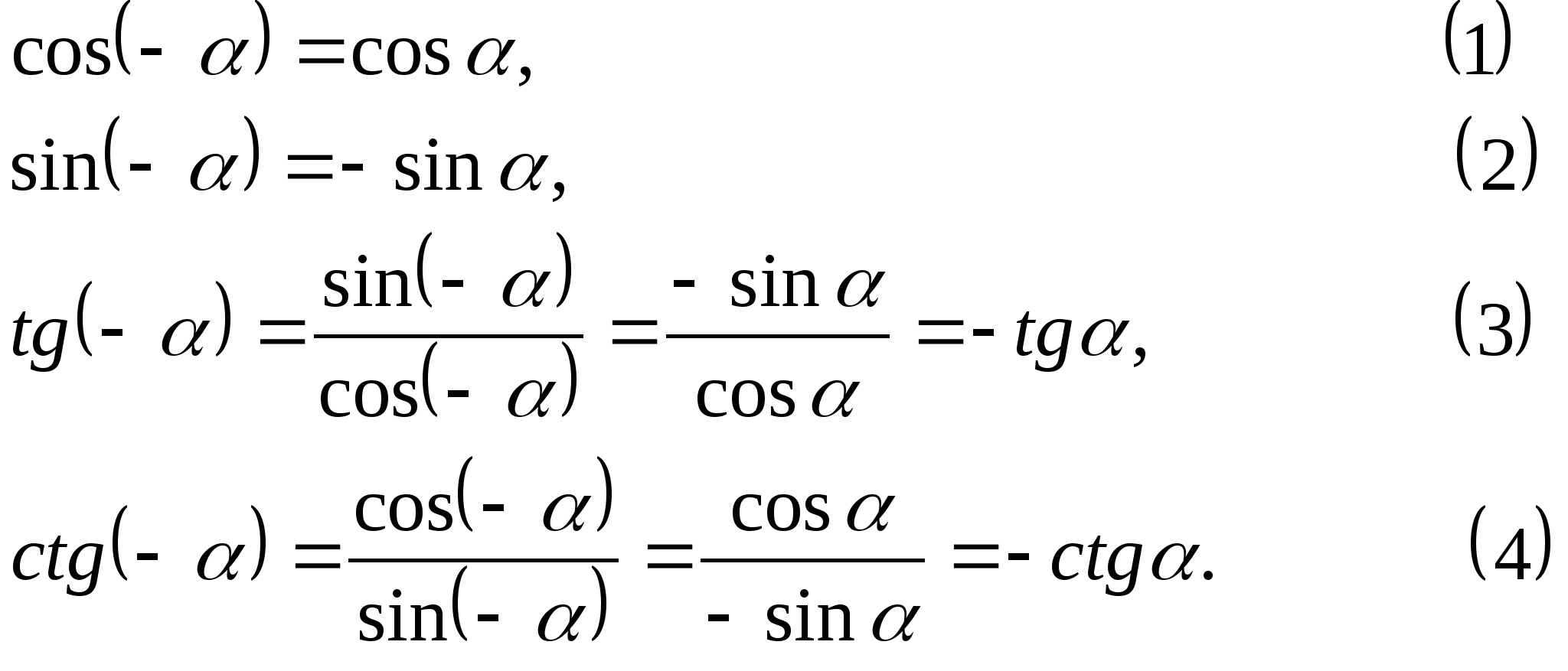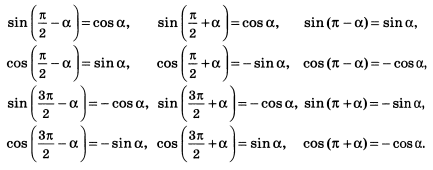Синус (sin x) и косинус (cos x)

Как найти косинус, синус, тангенс и котангенс

Почему-то у многих тригонометрия вызывает страх, ведь еще со школьной скамьи большинство не понимало, чем отличается косинус от синуса, и вообще как можно найти тангенс или котангенс. Но найти все эти тригонометрические функции совсем не сложно, особенно, если руководствоваться нижеприведенной инструкцией.

Инструкция:

Начнем с определения косинуса. Косинусом называют одну из тригонометрических функций, которая обычно обозначается как «сos».
Если говорить про косинус острого угла в прямоугольном треугольнике, то он равен отношению катета, который выходит из данного угла (его еще часто называют прилежащим катетом) к гипотенузе.

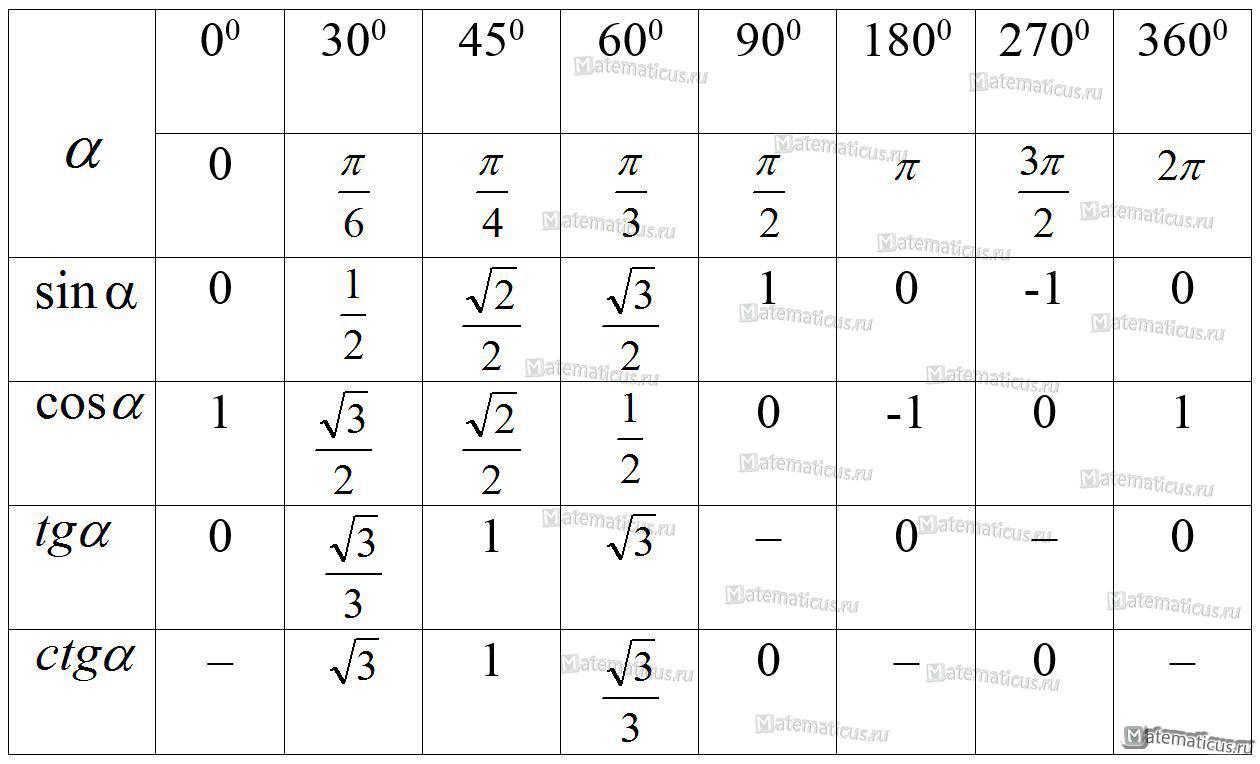
Если говорить про значения косинусов для самых популярных углов, то они будут выглядеть следующим образом:

— косинус 0 = единице;— косинус 30 = числу ПИ, поделенному на шесть (или квадратному корню из трех, поделенному на два);— косинус 45 = числу ПИ, поделенному на четыре (или квадратному корню из двух, поделенному на два);— косинус 60 = числу ПИ, поделенному на три (или половине);— косинус 90 = числу ПИ, поделенному на два (или нулю);— косинус 180 = числу ПИ (или минус единице);— косинус 270 = числу ПИ, умноженному на три и поделенному на два (или нулю).
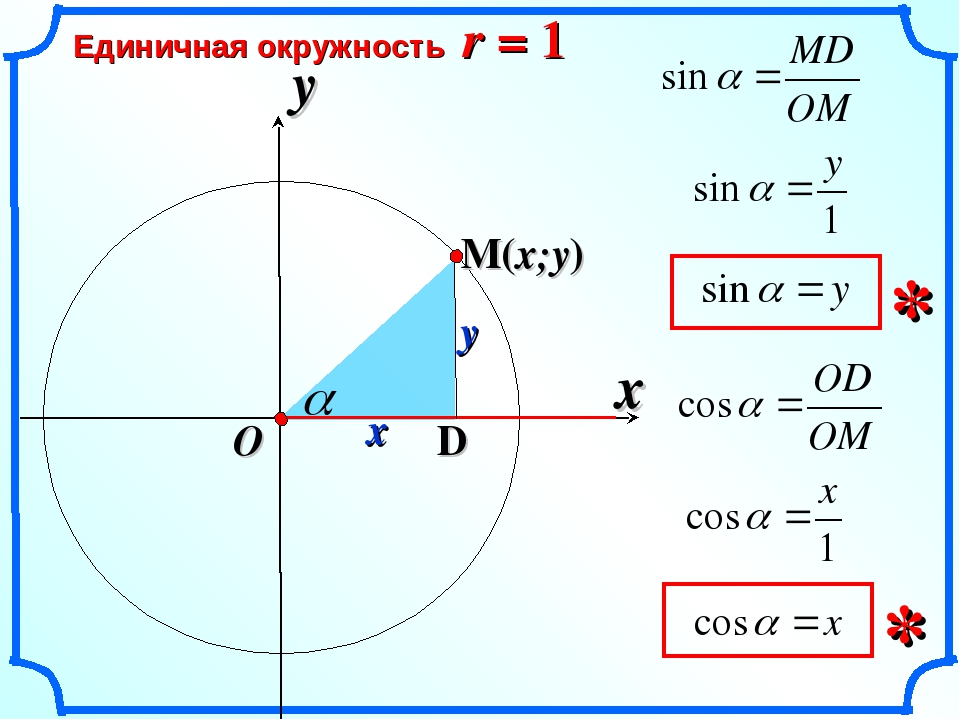
Синусом называют одну из тригонометрических функций, которая обычно обозначается как «sіn». Если говорить про синус острого угла в прямоугольном треугольнике, то он равен отношению катета, который лежит напротив данного угла (его еще часто называют противолежащим катетом) к гипотенузе. Если говорить про значения синусовдля самых популярных углов, то они будут выглядеть следующим образом:
— синус 0 = нулю;— синус 30 = числу ПИ, поделенному на шесть (или половине);— синус 45 = числу ПИ, поделенному на четыре (или квадратному корню из двух, поделенному на два);— синус 60 = числу ПИ, поделенному на три (или квадратному корню из трех, поделенному на два);— синус 90 = числу ПИ, поделенному на два (или единице);— синус 180 = числу ПИ (или нулю);— синус 270 = числу ПИ, умноженному на три и поделенному на два (или минус единице).
Тангенсом называют одну из тригонометрических функций, которая обычно обозначается как «tg» или «tan». Если говорить про тангенс острого угла в прямоугольном треугольнике, то он равен отношению катета, который лежит напротив данного угла к катету, который выходит из него. Кроме этого, если Вы знаете синус и косинус угла, то путем деления одного значения на другое («синус / косинус») Вы сможете найти и тангенс. Если говорить про значения тангенсов для самых популярных углов, то они будут выглядеть следующим образом:
— тангенс 0 = нулю;— тангенс 30 = числу ПИ, поделенному на шесть (или квадратному корню из трех, поделенному на три);— тангенс 45 = числу ПИ, поделенному на четыре (или единице);— тангенс 60 = числу ПИ, поделенному на три (или квадратному корню из трех);— тангенс 90 = числу ПИ, поделенному на два (или стремится к «+∞» бесконечности);— тангенс 180 = числу ПИ (или нулю);— тангенс 270 = числу ПИ, умноженному на три и поделенному на два (или стремится к «–∞» бесконечности);— тангенс 360 = двум ПИ (или нулю).
Котангенсом называют одну из тригонометрических функций, которая обычно обозначается как «сtg». Если говорить про котангенс острого угла в прямоугольном треугольнике, то он равен отношению катета, который выходит из данного угла к катету, который лежит напротив него. Если говорить про значения котангенсовдля самых популярных углов, то они будут выглядеть следующим образом:
— котангенс 0 стремится к бесконечности;— котангенс 30 = квадратному корню из трех;— котангенс 45 = единице;— котангенс 60 = одной третьей квадратного корня из трех;— котангенс 90 = нулю.

Похожие инструкции

Формула объема параллелепипеда

Параллелепипед – это объемная геометрическая фигура, многогранник (или призма) с шестью гранями, в…

Как найти длину круга

Многое, что нас окружает в обычной жизни, выполнено в форме окружности, именно поэтому у многих возникает…

Решить уравнение

Очень часто мы сталкиваемся с уравнениями различного рода, ведь с их помощью можно высчитать нужные нам…

Как найти объем пирамиды

Заглянем в будущее

Тригонометрия, изучаемая в школе, имеет дело с прямолинейной системой координат, где, как бы это странно ни звучало, прямая – это прямая.

Но есть и более сложные способы работы с пространством: сумма углов треугольника здесь будет больше 180 градусов, а прямая в нашем представлении будет выглядеть как самая настоящая дуга.

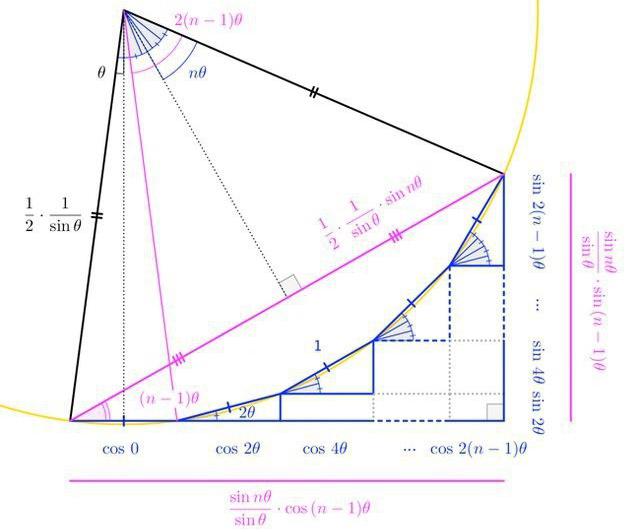
Перейдем от слов к делу! Возьмите яблоко. Сделайте ножом три надреза, чтобы при взгляде сверху получался треугольник. Выньте получившийся кусок яблока и посмотрите на «рёбра», где заканчивается кожура. Они вовсе не прямые. Фрукт в ваших руках условно можно назвать круглым, а теперь представьте, какими сложными должны быть формулы, с помощью которых можно найти площадь вырезанного куска. А ведь некоторые специалисты решают такие задачи ежедневно.

Рубрика «Вопросы и ответы»

Первый раз, изучая синусы, я упустил несколько вещей:

Синус вообще-то 1-мерный.

Синус движется в одном измерении. Правда. Мы часто рисуем синус, изменяющийся во времени, а иногда и «предмет», описывающий своим движением синус, тоже куда-то движется, но это уже опционально! Скачок в одном направлении — вполне себе полноценная волна синусоиды.

Окружности — это пример синусных волн.

Окружности и квадраты — это комбинации базовых элементов (синусов и прямых отрезков). Но окружности не являются основой синусоиды, как и квадрат не является составной частью прямой.

Что показывают значения синуса?

Синус принимает значения от -1 до 1. Он начинается с 0, возрастает до 1.0 (максимум), падает до -1.0 (минимум) и снова возвращается в нейтральную точку, к нулю. Я также вижу синус как процент от 100% (полный вперёд!) до -100% (полный обратный ход).

Что означает вводное значение ‘x’ в функции sin(x)?

Каверзный вопрос. Поскольку это цикл и х — вводный параметр, он означает, как далеко мы прошли по окружности.

Рассмотрим пример с линиями:

Мы бродим по квадрату. За 10 секунд мы проходим каждую сторону.
Спустя 1 секунду, вы прошли 10% от одной стороны
Спустя 5 секунд, вы прошли одну сторону на 50%
Через 10 секунд вы пройдете всю сторону.

В линейном движении есть парочка сюрпризов. Рассмотрим теперь синус (сфокусируемся на цикле «от 0 до максимума»):

Мы путешествуем по синусоиде, стартуя с 0 (нейтральная точка) до 1.0 (максимум). И на этот путь у нас ушло 10 секунд.
Спустя 5 секунд мы…прошли 70%! Синус очень быстрый на старте, и потихоньку замедляется к вершине. Так что большую часть пути мы пройдем за первые 5 секунд.
И еще 5 секунд нам потребуется на то, чтобы пройти с 70% до 100% пути. А отрезок с 98% до 100% занимает почти целую секунду!

Несмотря на высокую начальную скорость, синус замедляет свой рост, так что мы очень плавно касаемся точки максимума и разворачиваемся назад. Эта плавность и делает синус синусом.

Если вам очень интересны подробности, нажмите «show stats» в симуляторе. Вы увидите процент выполнения полного цикла, мини-цикла (с 0 до 1.0) и текущее значение. Остановите движение (кнопка Stop), попереключайтесь между линейным и синусоидальным движением, чтобы сравнить значения.

Маленькая проверка: Что будет дальше, 10% линейного цикла или 10% синусного? Правильный ответ — синусного.

Помните, в самом начале синус максимально ускорен. Ко времени достижения 50% цикла, синус движется со средней скоростью линейного цикла и, более того, замедляется (пока не достигнет максимума и не развернется).

Так что x — это «количество вашего цикла». Какого цикла?

Зависит от контекста.

Базовый вариант: ‘x’ — это градусы, и полный цикл состоит из 360 градусов
Продвинутый вариант: ‘x’ — это радианы (они более натуральные!) и полный цикл составляет полный проход по единичной окружности (2*π радиан)

Поэкспериментируйте со значением х здесь:

Но опять же, циклы зависят от окружностей! Можем ли мы как-то вырваться из-под их тирании?

Принятые обозначения

\( \sin^2 x \equiv (\sin x)^2; \)\( \quad \sin^3 x \equiv (\sin x)^3; \)\( \quad \sin^n x \equiv (\sin x)^n \)\( \sin^{-1} x \equiv \arcsin x \)\( (\sin x )^{-1} \equiv \dfrac1{\sin x} \equiv \cosec x \).

\( \cos^2 x \equiv (\cos x)^2; \)\( \quad \cos^3 x \equiv (\cos x)^3; \)\( \quad \cos^n x \equiv (\cos x)^n \)\( \cos^{-1} x \equiv \arccos x \)\( (\cos x )^{-1} \equiv \dfrac1{\cos x} \equiv \sec x \).

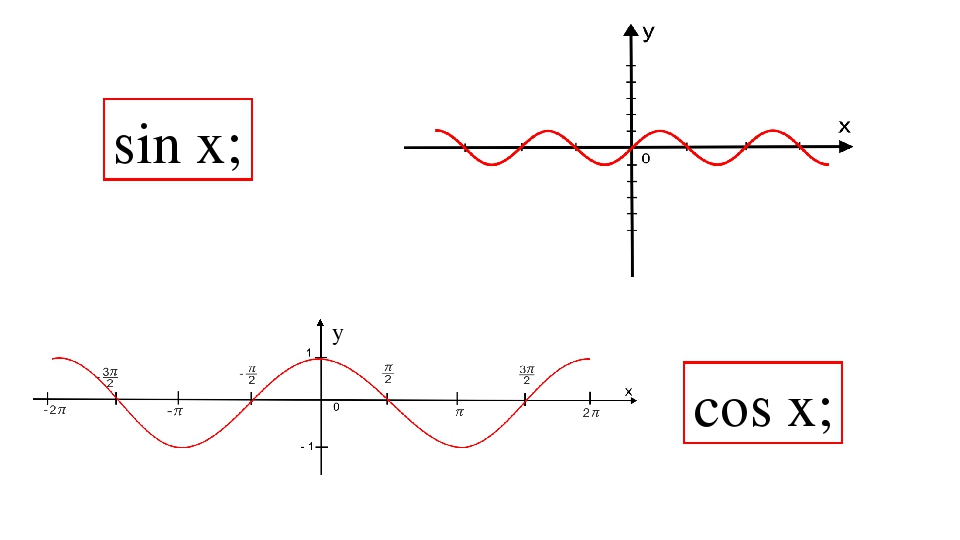
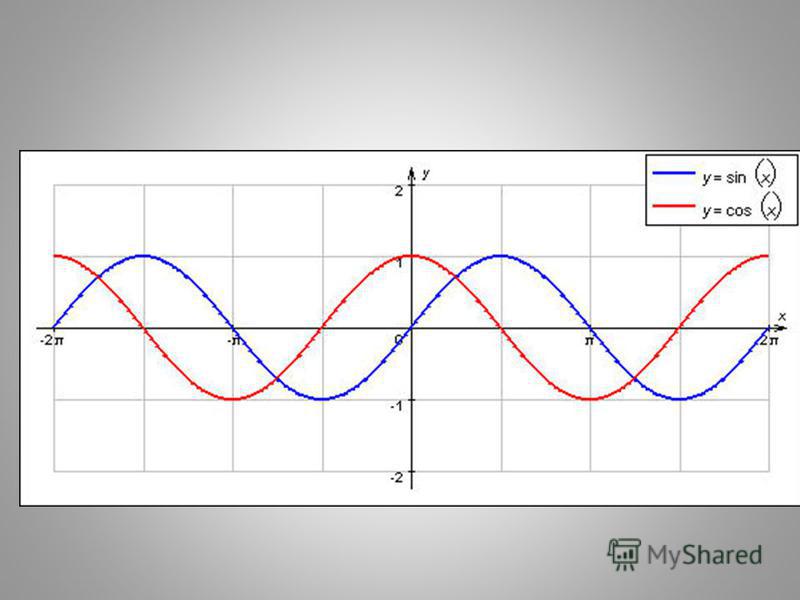
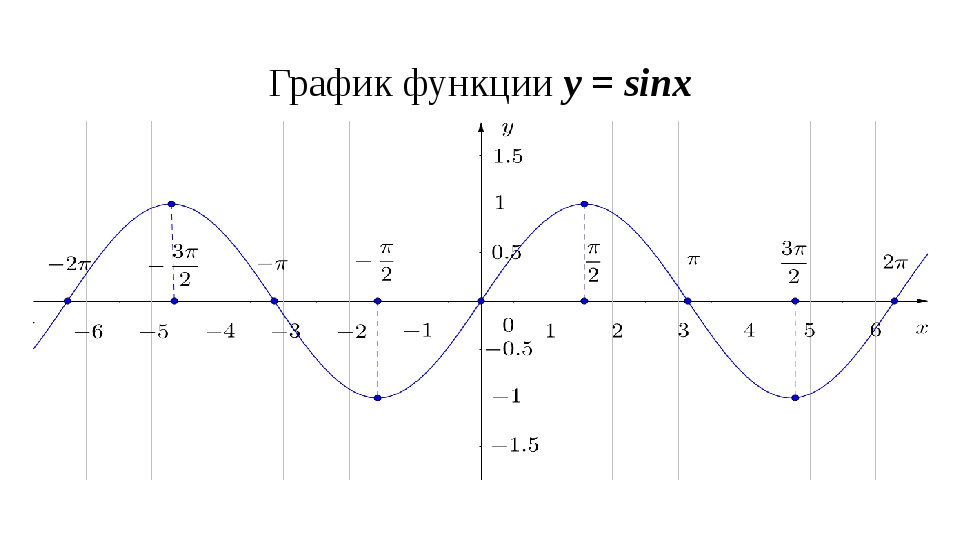
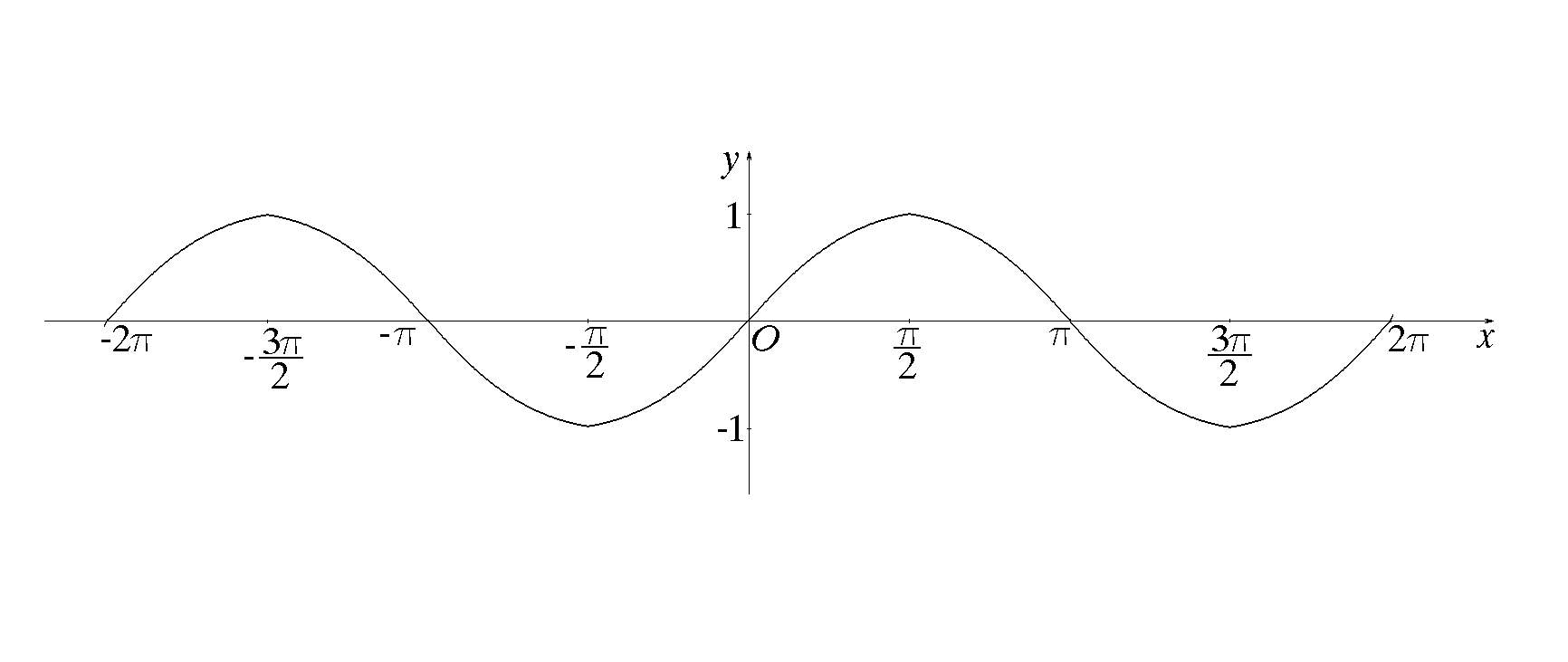
Функции y = sin x и y = cos x периодичны с периодом 2π.

\( \sin(x + 2\pi) = \sin x; \quad \)\( \cos(x + 2\pi) = \cos x \)

Функция синус – нечетная. Функция косинус – четная.

\( \sin( -x ) = — \sin x; \quad \)\( \cos( -x ) = \cos x \)

Области определения и значений, экстремумы, возрастание, убывание

Основные свойства синуса и косинуса представлены в таблице (n — целое).

	\( \small -\dfrac{\pi}2 + 2\pi n \)\( \small < x < \)\( \small \dfrac{\pi}2 + 2\pi n \)	\( \small -\pi + 2\pi n \)\( \small < x < \)\( \small 2\pi n \)
Убывание	\( \small \dfrac{\pi}2 + 2\pi n \)\( \small < x < \)\( \small \dfrac{3\pi}2 + 2\pi n \)	\( \small 2\pi n \)\( \small < x < \)\( \pi + \small 2\pi n \)
Максимумы, \( \small x = \)\( \small \dfrac{\pi}2 + 2\pi n \)	\( \small x = 2\pi n \)
Минимумы, \( \small x = \)\( \small -\dfrac{\pi}2 + 2\pi n \)	\( \small x = \)\( \small \pi + 2\pi n \)
Нули, \( \small x = \pi n \)	\( \small x = \dfrac{\pi}2 + \pi n \)
Точки пересечения с осью ординат, x = 0	y = 0	y = 1

Покопаемся в расчётах

Давайте опишем синус с помощью вычислений. Как в случае с e, мы можем разбить синус на маленькие части:

Начнем с 0 и дорастем до единичной скорости
В каждый момент времени мы будем замедляться из-за отрицательного ускорения

И как обо всем этом думать? Посмотрите, как каждое наше действие изменяет расстояние от центра:

Наш первый скачок увеличивает расстояние линейно: у (расстояние от центра) = х (затраченное время)
В любой момент, мы чувствуем возвращающую силу -х. Мы интегрируем дважды, чтобы обратить отрицательное ускорение в расстояние:

Понимание того, как ускорение влияет на расстояние, похоже на наблюдение за тем, как прибавки влияют на ваш банковский счёт. «Прибавка» должна изменять ваш доход, а ваш доход изменяет состояние вашего банковского счёта (два интеграла «по команде»).

Так что после «х» секунд, мы уже догадаемся, что синус это «х» (начальный импульс) минус x^3/3! (эффект ускорения):

Что-то не так — синус не спадает! В случае с е мы видели, что «проценты приносят свои проценты», в случае с синусом происходит то же самое. «Возвращающая сила» меняет наше расстояние на -x^3/3!, что создает другую возвращающую силу. Рассмотрите пружину: если отпустить пружину с грузиком внизу, то толчок будет достаточно большим, чтобы создать другой толчок, который потянет грузик обратно вверх, а потом снова вниз. Ох уж эти неугомонные пружины!

Нам нужно рассмотреть каждую возвращающую силу:

y = x — это наше изначальное движение, которое создает возвращающую силу удара:
y = -x^3/3!, которая создает возвращающую силу удара:
y = x^5/5!, которая создает возвращающую силу удара:
y = -x^7/7!, которая создает возвращающую силу удара…

Точь-в-точь как е, синус можно описать бесконечным уравнением:

Я видел эту формулу много раз, но до меня дошел ее смысл только когда я представил синус как комбинацию начального импульса и возвращающих сил. Начальный импульс (y = x, растет вверх) в итоге превосходит возвращающая сила (которая толкает нас вниз), и эта сила в свою очередь постепенно компенсируется своей возвращающей силой (что снова толкает нас вверх), и так далее.

Пара интересных заметок:

Рассматривайте «возвращающую силу» как «положительный или отрицательный процент». Так проще понять связь синуса и е в формуле Эйлера. Синус ведет себя как е, кроме моментов, когда он начинает зарабатывать отрицательный процент. Тут нам еще надо поучиться :).
Для маленьких чисел «y = x» — неплохое предположение для синуса. Мы просто берем начальный импульс и игнорируем возвращающие силы.

Обратные функции

Обратными функциями к синусу и косинусу являются арксинус и арккосинус, соответственно.

Арксинус, arcsin

\( y = \arcsin x \) \( \left\{ -1 \leqslant x \leqslant 1; \; — \dfrac{\pi}2 \leqslant y \leqslant \dfrac{\pi}2 \right\} \)\( \sin( \arcsin x ) = x \) \( \{ -1 \leqslant x \leqslant 1 \} \)\( \arcsin( \sin x ) = x \) \( \left\{ — \dfrac{\pi}2 \leqslant x \leqslant \dfrac{\pi}2 \right\} \)

Арккосинус, arccos

\( y = \arccos x \) \( \left\{ -1 \leqslant x \leqslant 1; \; 0 \leqslant y \leqslant \pi \right\} \)\( \cos( \arccos x ) = x \) \( \{ -1 \leqslant x \leqslant 1 \} \)\( \arccos( \cos x ) = x \) \( \{ 0 \leqslant x \leqslant \pi \} \)

Использованная литература: И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

ТригонометрияМатематика Тригонометрия Формулы Теория

В вашем браузере отключен Javascript. Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Геометрия. Синус, косинус и тангенс —

В уроке рассматривается нахождение синуса, косинуса и тангенса острого угла прямоугольного треугольника. Серия видеоуроков по элементарной математике для подгот

YouTube

Синус, косинус, тангенс, котангенс. Поддержать канал: http://donationalerts.ru/r/valeryvolkov Тригонометрия, урок 1. Соотношения между сторонами и углами прямо

YouTube

Доступно о том, зачем нужны тригонометрические функции. Предварительно нужно посмотреть мои видеоуроки о функции, градусах и радианах: https://www.youtube.com/w

YouTube

Видео сайтов http://school-pro.ru, http://um-razum.ru В данном ролике показано, что такое синус угла и рассмотрены значения синусов основных углов.

YouTube

В этом видео рассказывается о теореме Пифагора, приводятся примеры решения задач. *** Это видео — русская версия видео «The Pythagorean Theorem» Академии Хан

YouTube

Как за 1 минуту запомнить таблицу значений углов sin cos tg ctg http://horoshist-center.ru/ http://horoshist-center.com/

YouTube

Отдельные разделы тригонометрии рассеяны по всему школьному курсу математики. А мы собрали их все вместе: от исчисления углов в прямоугольном треугольнике до те

YouTube

В этом видео показаны два определения тригонометрических функций (синус, косинус, тангенс, котангенс): простейшее или историческое (для острого угла в прямоугол

YouTube

Даются геометрические определения синуса, косинуса, тангенса в прямоугольном треугольнике

YouTube

Интересное видео в простой и доступной форме раскрывает такие понятия как синус, косинус, тангенс и котангенс угла в прямоугольном треугольнике. Благодаря уроку

YouTube

Как не запоминать синусы, косинусы, тангенсы и котангенсы «легких» углов и почему катет напротив угла в 30 градусов равен половине гипотенузы. Дистанционные зан

YouTube

Тригонометрия — это легко и просто, даже для чайников. Например, табличные значения синуса и косинуса легко запомнить с помощью пальцев левой руки.

YouTube

Практическое нахождение косинуса синуса и тангенса с помощью СОКИ ТОИ

YouTube

Пример. Найти значение выражения: Решение: https://www.youtube.com/watch?v=nPBhGWFGkBo Катет и гипотенуза прямоугольного треугольника равны Решение математики онлайн http://you

YouTube

Простой способ запоминания значений тригонометрических функций.

YouTube

Школа-студия Народного учителя СССР Шаталова В.Ф. сохраняет лучшие традиции педагогической науки, а также уроки Народных учителей СССР и их последователей.

YouTube

все уроки по ГЕОМЕТРИИ — https://www.youtube.com/playlist?list=PLBnDGoKqP7bY_V8lEYj_3d3AenlZrYfgW по ФИЗИКЕ — https://www.youtube.com/playlist?list=PLBnDGoKqP7b

YouTube

Определение 2: Бесконечный ряд

Я спрятал слона в комнате: как мы вообще вычисляем синус? Мой калькулятор, что, каждый раз рисует окружность и замеряет его?

Рад вам поведать, как можно вычислить синус без окружностей.

Синус — это ускорение в сторону, противоположную тому, где вы находитесь.

Пользуясь нашим примером с банковским счётом: представьте, что ваш шеф каждую неделю решил менять вашу зарплату на сумму, противоположную текущей на вашем банковском счёте. Если у вас сейчас есть 50 рублей, на следующей неделе шеф выдаст на 50 рублей меньше. Конечно, поскольку ваш доход будет 75 рублей, вы всё еще будете в плюсе (75 — 50) но в итоге ваш баланс уменьшится, поскольку «прибавки» шефа превзойдут ваши доходы.

Но не отчаивайтесь! Как только баланс становится отрицательным (скажем, у вас -50 рублей), ваш босс выдаст вам на целых 50 рублей больше. Затем снова баланс станет отрицательным (с его ростом шеф выдает всё меньше денег), и так будет продолжаться постоянно. Баланс будет то положительный, то нулевой, то отрицательный.

Этот пример также поясняет, почему в нейтральной точке (в 0) скорость синуса максимальна: когда вы на максимуме, вы начинаете падать и собирать всё больше «отрицательных прибавок», которые довольно быстро тянут вас к 0. После прохождения 0 вы начинаете получать наиболее значительные положительные прибавки и замедляетесь., потому что как только уходите в плюс, шеф опять начинает отнимать от вашей зарплаты.

Между прочим: поскольку синус — это ускорение, обратное к вашему текущему положению, а окружность сделана из горизонтальной и вертикальной синусоиды… вы поняли! Круговое движение может быть описано как «постоянное движение в направлении, противоположном текущей позиции, по направлению к горизонтальному и вертикальному центру».

Неизбежная окружность

У окружности есть синус. Да. Но увидеть синус внутри окружности — это всё равно, что получить из омлета яйца обратно, когда все они хорошенько друг с другом перемешаны!

Давайте помедленнее. В симуляторе установите такие параметры: vertical:none и horizontal: sine*. Видите, как смайлик движется вперёд-назад? Это и есть движение синуса. Небольшой фокус: обычно синус начинает свой цикл на нейтральной срединной точке и бежит к максимуму. На этот раз мы начинаем в максимуме и падаем к срединной точке. Синус, который «стартует на максимуме», называется косинусом, и это просто версия синуса (как горизонтальная прямая является версией вертикальной прямой)

Настало время для обеих синусных волн: установите параметры vertical:sine и horizontal:sine*. И… у нас получилась окружность!

Горизонтальные и вертикальные «прыжки» в сумме дали круговое движение. В большинстве учебников рисуют окружность и пытаются извлечь из нее синус, но я предпочитаю обратный подход: начать с простого горизонтального или вертикального движения и добавить противоположное.

π без картинок

Представьте себе слепого пришельца, который может различать только тени света и темноты. Можете ли вы объяснить ему, что такое π? Довольно сложно пояснить в такой ситуации понятие длины окружности, верно?

Давайте вернемся немного назад. Синус — это циклическая функция. Это означает, что значит ее значения должны…повторяться! Синус начинается с 0, идет к 1, к 0, к -1, к 0 и так далее.

Давайте определим π как время, за которое синус поднимается с 0 до 1, и обратно возвращается к 0. Вау! Теперь и мы используем π без всяких окружностей!

Синус — это плавное передвижение вперёд-назад
π — это время движения синуса с 0 до 1 и обратно до 0
n * π (0 * π, 1 * π, 2 * π и т.д.) — это момент времени, в котором синус равен 0
2 * π, 4 * π, 6 * π и т.д. — полные периоды синуса.

Ага! Вот почему π встречается в таком количестве формул! π не «принадлежит» окружностям больше, чем 0 или 1 — π касается возвращения синуса в центр! Окружность — это пример фигуры, которая повторяется и возвращается в центр каждые 2*π единиц. Но вибрации, скачки и т.д. возвращаются к центру каждый π!

Вопрос: если π — это половина естественного периода, почему оно длится вечно (является иррациональным числом)?

Можно я отвечу вопросом на вопрос, А почему длина диагонали «единичной окружности» равна квадратному корню из 2, который также уходит в бесконечность?

Но да, я понимаю, что это философски не удобно, когда природа ведет себя произвольно. Но что поделаешь…

Тригонометрические функции в жизни

Обращали ли вы внимание, что самый короткий маршрут самолёта из точки А в точку Б на поверхности нашей планеты имеет ярко выраженную форму дуги? Причина проста: Земля имеет форму шара, а значит, с помощью треугольников многого не вычислишь – здесь приходится использовать более сложные формулы

Не обойтись без синуса/косинуса острого угла в любых вопросах, связанных с космосом. Интересно, что здесь сходится целое множество факторов: тригонометрические функции требуются при расчётах движения планет по окружностям, эллипсам и различным траекториям более сложных форм; процесса запуска ракет, спутников, шаттлов, отстыковки исследовательских аппаратов; наблюдении за далёкими звёздами и изучении галактик, до которых человек в обозримом будущем добраться не сможет.

В целом поле для деятельности человека, владеющего тригонометрией, очень широко и, по-видимому, со временем будет только расширяться.

Теоремы

В базовой тригонометрии существует две основные теоремы: синусов и косинусов.

Первая гласит, что отношение каждой стороны треугольника к синусу противолежащего угла одинаково. Вторая – что квадрат любой стороны можно получить, если сложить квадраты двух оставшихся сторон и вычесть удвоенное их произведение, умноженное на косинус лежащего между ними угла.

Таким образом, если в теорему косинусов подставить значение угла в 90 градусов, мы получим… теорему Пифагора. Теперь, если требуется высчитать площадь фигуры, не являющейся прямоугольным треугольником, можно больше не переживать – две рассмотренные теоремы существенно упростят решение задачи.

Единицы измерения

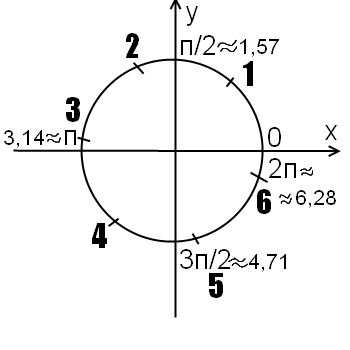
Почему число Пи равняется именно 3,14? Помните ли вы, что это за значение? Это количество радиусов, умещающихся в дуге на половине окружности. Если диаметр круга – 2 сантиметра, длина окружности составит 3,14*2, или 6,28.

Второй момент: возможно, вы замечали сходство слов «радиан» и «радиус». Дело в том, что один радиан численно равен величине угла, отложенного из центра окружности на дугу длиной в один радиус.

Теперь совместим полученные знания и поймем, почему сверху на оси координат в тригонометрии пишется «Пи пополам», а слева – «Пи». Это угловая величина, измеренная в радианах, ведь полукруг – это 180 градусов, или 3,14 радиана. А там, где есть градусы, есть синусы и косинусы. Треугольник же легко провести от нужной точки, отложив отрезки к центру и на ось координат.

Определение 3: Дифференциальное уравнение

Мы описали поведение синуса определенными уравнениями. Вкратце это будет выглядеть так:

Эта красота означает следующее:

Наша текущая позиция — y

Наше ускорение (2-я производная, или у”) — обратно нашей текущей позиции (-y)

Это справедливо и для синуса, и для косинуса. Сначала я просто ненавидел это определение; оно такое непохожее на нашу визуализацию. Я не понимал, что оно описывало суть синуса: «ускорение, обратное текущей позиции».

И вспомните как синус и е связаны? Ну, e^x можно описать уравнением:

То же уравнение с положительным знаком («ускорение равно текущей позиции»)! Когда синус — это «высота окружности», очень тяжело проследить связь с е.

Одним из моих серьезнейших математических сожалений является то, что я еще не изучил дифференциальные уравнения. Но я хочу это сделать, и подозреваю, что правильное понимание синуса и экспоненты сыграют в этом решающую роль.

Синус против прямых

Не забывайте разделять идеи и примеры: квадрат — это лишь пример сочетания линий. А синус как понятие совсем не является «частью окружности».

Давайте рассмотрим синус в симуляторе.

Смайлик начнет свой путь:

Нажмите start. Давай, смайлик, беги! Заметили это плавное движение вперёд-назад? Этот смайлик и есть синус. В таком же стиле вибрируют струны, сжимаются и разжимаются пружины, вращается маятник… и еще очень много разных тел движутся.
Измените «vertical» на «linear». Большая разница — видите, какими резкими стали движения на краях амплитуды?

Давайте рассмотрим различия на видео:

https://youtube.com/watch?v=WAyTK6jF5o8

Движение linear постоянно: мы движемся с постоянной скоростью и резко меняем направление. Это неестественное движение, как танцуют в стиле «робот» (на 0:07 движения танцора очень плавные, а на 00:38 он показывает уже стробоскопический эффект).
Синус меняет свою скорость: начинает двигаться быстро, замедляется, останавливается, а затем снова ускоряется. Ох уж эти очаровательные переходы в танце! (на 0:12 и 0:23 можно увидеть настоящую человеческую синусоиду, а на 00:47 — естественная упругость).

К сожалению, в учебниках танцы не показывают в качестве примера синусоиды. Авторам больше нравится представлять синусоиду изменяющейся во времени (установите «horizontal» в графе «timeline»):

(Википедия)

Проклятие. Вот этот схематический график нам всегда и показывали. Вы по нему представляете, что такое синус? Примерно также, как если бы вас заставили представить ловкость кота по изображению его скелета. Давайте сначала изучим синус в движении, а потом, конечно, изобразим его на графике.

Основные формулы, содержащие синус и косинус

Формулы синуса и косинуса суммы и разности

\( \sin(x + y) = \sin x \cos y + \cos x \sin y \) \( \sin(x — y) = \sin x \cos y — \cos x \sin y \) \( \cos(x + y) = \cos x \cos y — \sin x \sin y \) \( \cos(x — y) = \cos x \cos y + \sin x \sin y \)

\( \sin( 2x ) = 2 \sin x \cos x \) \( \cos( 2x ) = \cos^2 x — \sin^2 x = \)\( 2 \cos^2 x — 1 = 1 — 2 \sin^2 x \) \( \cos\left( \dfrac{\pi}2 — x \right) = \sin x \) ; \( \sin\left( \dfrac{\pi}2 — x \right) = \cos x \) \( \cos( x + \pi ) = — \cos x \) ; \( \sin( x + \pi ) = — \sin x \)

Формулы произведения синусов и косинусов

\( \sin x \cos y = \)\( \dfrac12 {\Large } \) \( \sin x \sin y = \)\( \dfrac12 {\Large } \) \( \cos x \cos y = \)\( \dfrac12 {\Large } \)

\( \sin x \cos y = \dfrac12 \sin 2x \) \( \sin^2 x = \dfrac12 {\Large } \) \( \cos^2 x = \dfrac12 {\Large } \)

Формулы суммы и разности

\( \sin x + \sin y = 2 \, \sin \dfrac{x+y}2 \, \cos \dfrac{x-y}2 \) \( \sin x — \sin y = 2 \, \sin \dfrac{x-y}2 \, \cos \dfrac{x+y}2 \) \( \cos x + \cos y = 2 \, \cos \dfrac{x+y}2 \, \cos \dfrac{x-y}2 \) \( \cos x — \cos y = 2 \, \sin \dfrac{x+y}2 \, \sin \dfrac{y-x}2 \)

Выражение синуса через косинус

Далее мы полагаем, что \( n \) – целое число.

\( \sin x = \cos\left( \dfrac{\pi}2 — x \right) = \)\( \cos\left( x — \dfrac{\pi}2 \right) = — \cos\left( x + \dfrac{\pi}2 \right) \)\( \sin^2 x = 1 — \cos^2 x \)\( \sin x = \sqrt{1 — \cos^2 x} \) \( \{ 2 \pi n \leqslant x \leqslant \pi + 2 \pi n \} \)\( \sin x = — \sqrt{1 — \cos^2 x} \) \( \{ -\pi + 2 \pi n \leqslant x \leqslant 2 \pi n \} \).

Выражение косинуса через синус

\( \cos x = \sin\left( \dfrac{\pi}2 — x \right) = \)\( — \sin\left( x — \dfrac{\pi}2 \right) = \sin\left( x + \dfrac{\pi}2 \right) \)\( \cos^2 x = 1 — \sin^2 x \)\( \cos x = \sqrt{1 — \sin^2 x} \) \( \{ -\pi/2 + 2 \pi n \leqslant x \leqslant \pi/2 + 2 \pi n \} \)\( \cos x = — \sqrt{1 — \sin^2 x} \) \( \{ \pi/2 + 2 \pi n \leqslant x \leqslant 3\pi/2 + 2 \pi n \} \).

Выражение через тангенс

\( \sin^2 x = \dfrac{\tg^2 x}{1+\tg^2 x} \)\( \cos^2 x = \dfrac1{1+\tg^2 x} \).

При \( — \dfrac{\pi}2 + 2 \pi n < x < \dfrac{\pi}2 + 2 \pi n \)\( \sin x = \dfrac{\tg x}{ \sqrt{1+\tg^2 x} } \)\( \cos x = \dfrac1{ \sqrt{1+\tg^2 x} } \).

При \( \dfrac{\pi}2 + 2 \pi n < x < \dfrac{3\pi}2 + 2 \pi n \) : \( \sin x = — \dfrac{\tg x}{ \sqrt{1+\tg^2 x} } \)\( \cos x = — \dfrac1{ \sqrt{1+\tg^2 x} } \).

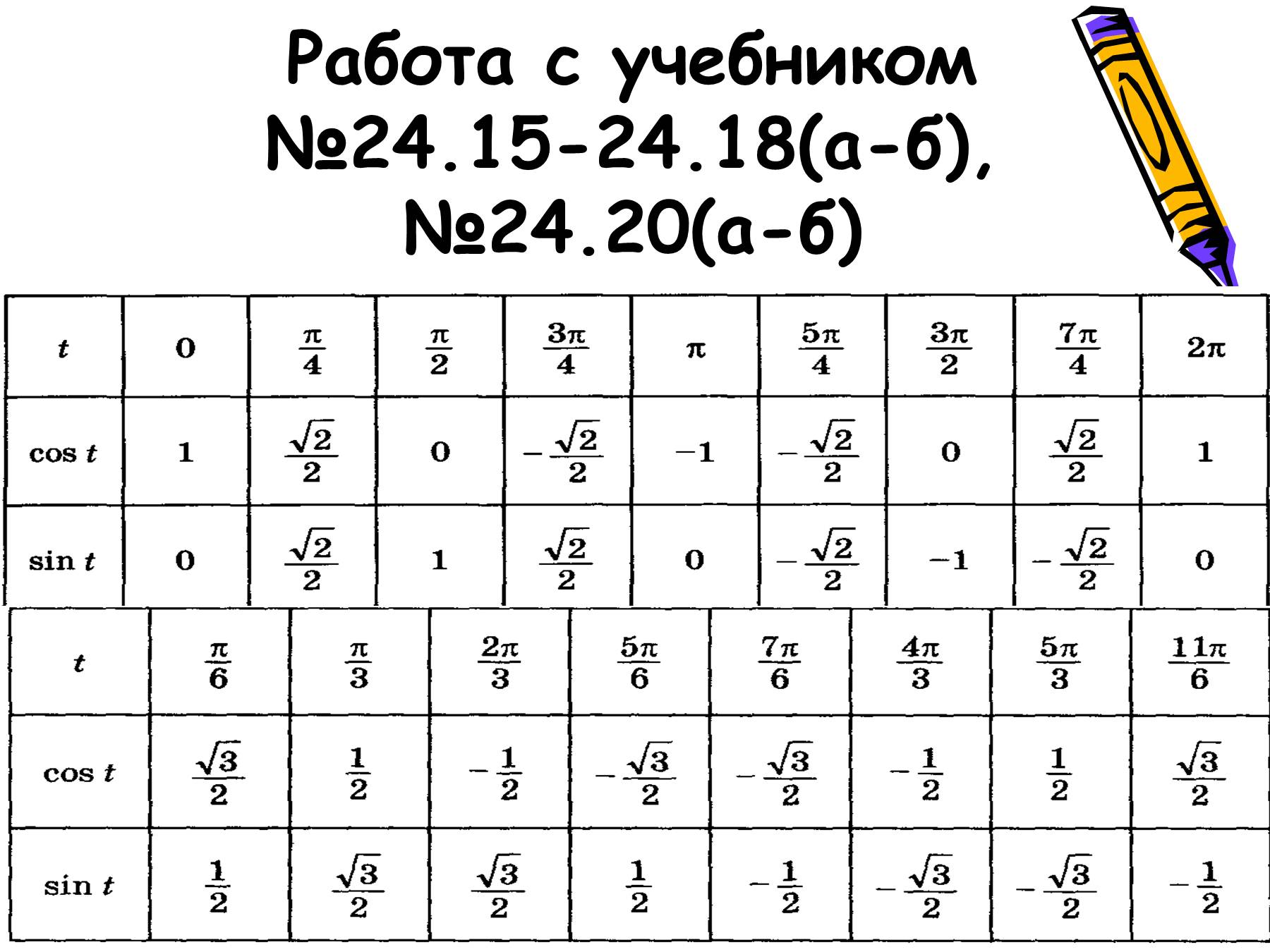
Табличные значения синуса и косинуса

Нулевой угол \( \LARGE 0^{\circ } \)

Абсцисса точки равна 1, ордината точки равна . Следовательно,

cos 0 = 1 sin 0 = 0

Рис 4. Нулевой угол

Угол \( \LARGE \frac{\pi}{6} = 30^{\circ } \)

Мы видим прямоугольный треугольник с единичной гипотенузой и острым углом 30°. Как известно, катет, лежащий напротив угла 30°, равен половине гипотенузы1; иными словами, вертикальный катет равен 1/2 и, стало быть,

Горизонтальный катет находим по теореме Пифагора (или, что то же самое, находим косинус по основному тригонометрическому тождеству):

1 Почему так получается? Разрежьте равносторонний треугольник со стороной 2 вдоль его высоты! Он распадётся на два прямоугольных треугольника с гипотенузой 2, острым углом 30° и меньшим катетом 1.

Рис 5. Угол π / 6

Угол \( \LARGE \frac{\pi}{4} = 45^{\circ } \)

В данном случае прямоугольный треугольник является равнобедренным; синус и косинус угла 45° равны друг другу. Обозначим их пока через x. Имеем:

откуда \( x=\frac{\sqrt{2} }{2} \). Следовательно,

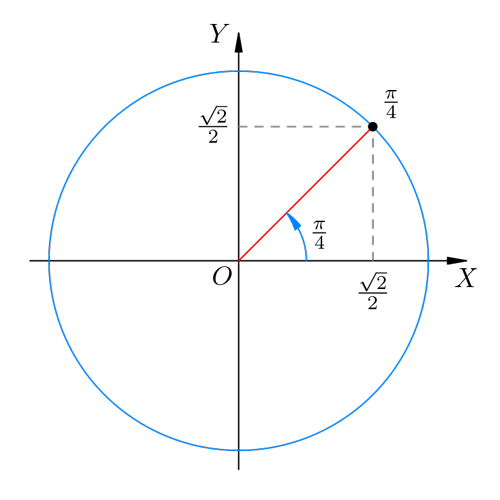Рис 5. Угол π / 4

Насколько быстр синус?

Я вас немного запутал. Сначала я сказал: «представьте, что синусу нужно 10 секунд, чтобы добраться с 0 до максимума». А сейчас я говорю, что ему надо π секунд, чтобы добраться с 0 до максимума и обратно спуститься к 0. Что происходит?

sin(x) — это базовая синусная волна, которой действительно требуется π единиц времени, чтобы пройти путь с 0 до максимума и опять до 0 (или 2*π, чтобы обойти свой полный период)
sin(2x) — это синусоида, которая движется вдвое быстрее
sin(x/2) — это синусоида, которая движется вдвое медленее базовой

Так что мы используем sin(n*x) , чтобы сделать синус, который будет двигаться так быстро, как нам нужно. Очень часто слово «синусоида» используется для указания общей формы волны, а не конкретной скорости.

Синус любого угла

Благодаря единичному кругу можно определять тригонометрические функции не только острого угла, но и тупого, отрицательного, и даже большего, чем \(360°\) (полный оборот). Как это делать — проще один раз увидеть, чем \(100\) раз услышать, поэтому смотрите картинку.

Теперь пояснение: пусть нужно определить \(sin∠КОА\) с градусной мерой в \(150°\). Совмещаем точку О с центром окружности, а сторону ОК – с осью \(x\). После этого откладываем \(150°\) против часовой стрелки. Тогда ордината точки А покажет нам \(\sin⁡∠KOA\).

Если же нас интересует угол с градусной мерой, например, в \(-60°\) (угол КОВ), делаем также, но \(60°\) откладываем по часовой стрелке.

И, наконец, угол больше \(360°\) (угол КОС) — всё аналогично тупому, только пройдя по часовой стрелке полный оборот, отправляемся на второй круг и «добираем нехватку градусов». Конкретно в нашем случае угол \(405°\) отложен как \(360° + 45°\).

Несложно догадаться, что для откладывания угла, например, в \(960°\), надо сделать уже два оборота (\(360°+360°+240°\)), а для угла в \(2640°\) — целых семь.

Как вы могли заменить, и синус числа, и синус произвольного угла определяется практически одинаково. Изменяются только способ нахождения точки на окружности.