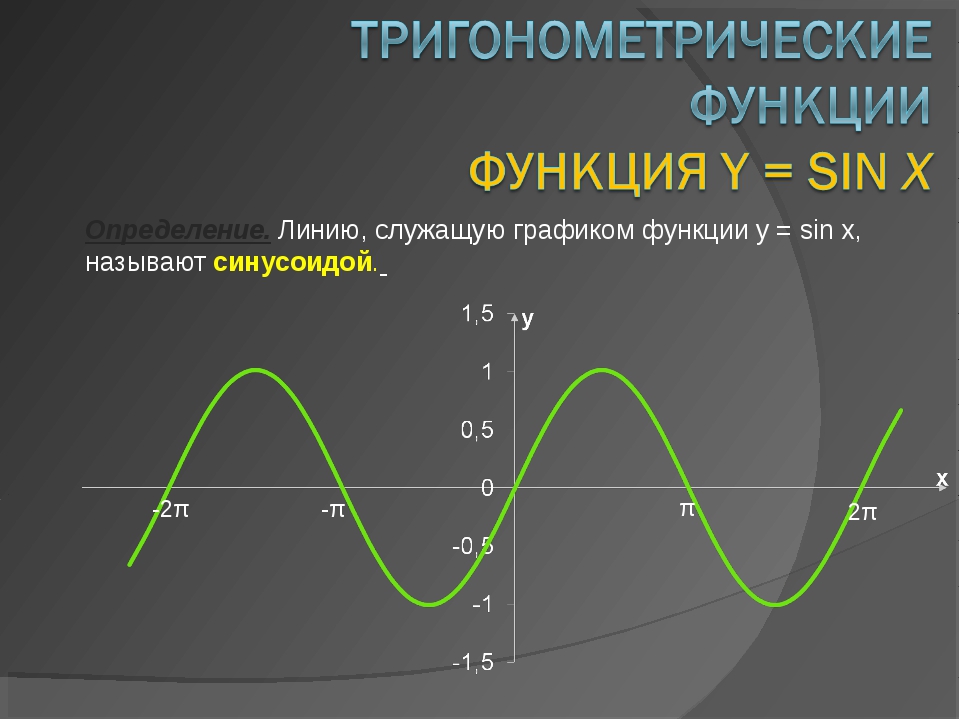
Формулы понижения степени.
Из формул кратного аргумента выводятся формулы:
| sin2a = (1 – cos 2a)/2; | cos2a = (1 + cos 2a)/2; |
| sin3a = (3 sin a – sin 3a)/4; | cos3a = (3 cosa + cos 3a)/4. |
С помощью этих формул тригонометрические уравнения можно приводить к уравнениям более низких степеней. Таким же образом можно вывести и формулы понижения для более высоких степеней синуса и косинуса.
| Производные и интегралы тригонометрических функций | |
| (sin x)` = cos x; | (cos x)` = –sin x; |
| (tg x)` = ; | (ctg x)` = – ; |
| т sin x dx = –cos x + C; | т cos x dx = sin x + C; |
| т tg x dx = –ln |cos x| + C; | т ctg x dx = ln |sin x| + C; |
Каждая тригонометрическая функция в каждой точке своей области определения непрерывна и бесконечно дифференцируема. Причем и производные тригонометрических функций являются тригонометрическими функциями, а при интегрировании получаются так же тригонометрические функции или их логарифмы. Интегралы от рациональных комбинаций тригонометрических функций всегда являются элементарными функциями.
Формулы приведения.
По этим формулам значение тригонометрической функции аргумента a, где p/2 a p, можно привести к значению функции аргумента a, где 0 a p/2, как той же, так и дополнительной к ней.
| Аргумент b
Функция |
– a | + a | p – a | p + a | + a | + a | 2p – a |
| sin b | cos a | cos a | sin a | –sin a | –cos a | –cos a | –sin a |
| cos b | sin a | –sin a | –cos a | –cos a | –sin a | sin a | cos a |
Поэтому в таблицах тригонометрических функций даются значения только для острых углов, причем достаточно ограничиться, например, синусом и тангенсом. В таблице даны только наиболее употребительные формулы для синуса и косинуса. Из них легко получить формулы для тангенса и котангенса. При приведении функции от аргумента вида kp/2 ± a, где k – целое число, к функции от аргумента a:
1) название функции сохраняется, если k четное, и меняется на «дополнительное», если k нечетное;
2) знак в правой части совпадает со знаком приводимой функции в точке kp/2 ± a, если угол a острый.
Например, при приведении ctg (a – p/2) убеждаемся, что a – p/2 при 0 a p/2 лежит в четвертом квадранте, где котангенс отрицателен, и, по правилу 1, меняем название функции: ctg (a – p/2) = –tg a.
Четность и периодичность.
Функция называется четной, если f(–x) = f(x). Функции косинус и секанс – четные, а синус, тангенс, котангенс и косеканс – функции нечетные:
| sin (–α) = – sin α | tg (–α) = – tg α |
| cos (–α) = cos α | ctg (–α) = – ctg α |
| sec (–α) = sec α | cosec (–α) = – cosec α |
Свойства четности вытекают из симметричности точек Pa и Р—a(рис. 14) относительно оси х.При такой симметрии ордината точки меняет знак ((х; у)переходит в (х; –у)). Все функции – периодические, синус, косинус, секанс и косеканс имеют период 2p,а тангенс и котангенс – p:
| sin (α + 2kπ) = sin α | cos (α + 2kπ) = cos α |
| tg (α + kπ) = tg α | ctg (α + kπ) = ctg α |
| sec (α + 2kπ) = sec α | cosec (α + 2kπ) = cosec α |
Периодичность синуса и косинуса следует из того, что все точки Pa + 2kp, где k = 0, ±1, ±2,…, совпадают, а периодичность тангенса и котангенса – из того, что точки Pa + kpпоочередно попадают в две диаметрально противоположные точки окружности, дающие одну и ту же точку на оси тангенсов.
Основные свойства тригонометрических функций могут быть сведены в таблицу:
| Функция | Область определения | Множество значений | Четность | Участки монотонности (k = 0, ± 1, ± 2,…) |
| sin x | –Ґ x Ґ | нечетная | возрастает при x О ((4k – 1) p /2, (4k + 1) p /2),убывает при x О ((4k + 1) p /2, (4k + 3) p/2) | |
| cos x | –Ґ x Ґ | четная | Возрастает приx О ((2k – 1) p, 2kp),убывает приx О (2kp, (2k + 1) p) | |
| tg x | x № p/2 + pk | (–Ґ, +Ґ) | нечетная | возрастает приx О ((2k – 1) p /2, (2k + 1) p /2) |
| ctg x | x № pk | (–Ґ, +Ґ) | нечетная | убывает приx О (kp, (k + 1) p) |
| sec x | x № p/2 + pk | (–Ґ, –1] И [+1, +Ґ) | четная | Возрастает приx О (2kp, (2k + 1) p),убывает приx О ((2k – 1) p, 2kp) |
| cosec x | x № pk | (–Ґ, –1] И [+1, +Ґ) | нечетная | возрастает приx О ((4k + 1) p /2, (4k + 3) p/2),убывает приx О ((4k – 1) p /2, (4k + 1) p /2) |
Тригонометрические функции комплексного аргумента
определяются как аналитические продолжения соответствующих тригонометрических функций действительного аргумента в комплексную плоскость. Так, sin z и cos z могут быть определены с помощью рядов для sin x и cos x,если вместо x поставить z:
,
.
Эти ряды сходятся по всей плоскости, поэтому sin z и cos z – целые функции.
Тангенс и котангенс определяются формулами:
,
.
Функции tg z и ctg z – мероморфные функции. Полюсы tg z и sec z – простые (1-го порядка) и находятся в точках z = p/2 + pn, полюсы ctg z и cosec z – также простые и находятся в точках z = pn, n = 0, ±1, ±2,…
Все формулы, справедливые для тригонометрических функций действительного аргумента, справедливы и для комплексного. В частности,
sin (–z) = –sin z,
cos (–z) = cos z,
tg (–z) = –tg z,
ctg (–z) = –ctg z,
т.е. четность и нечетность сохраняются. Сохраняются и формулы
sin (z + 2p) = sin z, (z + 2p) = cos z, (z + p) = tg z, (z + p) = ctg z,
т.е. периодичность также сохраняется, причем периоды такие же, как и для функций действительного аргумента.
Тригонометрические функции могут быть выражены через показательную функцию от чисто мнимого аргумента:
;
;
.
Обратно, eiz выражается через cos z и sin z по формуле:
eiz = cos z + i sin z
Эти формулы носят название формул Эйлера. Леонард Эйлер вывел их в 1743.
Тригонометрические функции также можно выразить через гиперболические функции:
z = –i sh iz, cos z = ch iz, z = –i th iz.
где sh, ch и th – гиперболические синус, косинус и тангенс.
Тригонометрические функции комплексного аргумента z = x + iy, где x и y – действительные числа, можно выразить через тригонометрические и гиперболические функции действительных аргументов, например:
sin (x + iy) = sin x ch y + i cos x sh y;
cos (x + iy) = cos x ch y + i sin x sh y.
Синус и косинус комплексного аргумента могут принимать действительные значения, превосходящие 1 по абсолютной величине. Например:
Если неизвестный угол входит в уравнение как аргумент тригонометрических функций, то уравнение называется тригонометрическим.Такие уравнения настолько часто встречаются, что методы ихрешения очень подробно и тщательно разработаны. С помощью различных приемов и формул тригонометрические уравнения сводят к уравнениям вида f(x) = a, где f – какая-либо из простейших тригонометрических функций: синус, косинус, тангенс или котангенс. Затем выражают аргумент x этой функции через ее известное значение а.
Поскольку тригонометрические функции периодичны, одному и тому же а из области значений отвечает бесконечно много значений аргумента, и решения уравнения нельзя записать в виде одной функции от а.Поэтому в области определения каждой из основных тригонометрических функций выделяют участок, на котором она принимает все свои значения, причем каждое только один раз, и находят функцию, обратную ей на этом участке. Такие функции обозначают, приписывая приставку агс (дуга) к названию исходной функции, и называют обратными тригонометрическимифункциями или просто аркфункциями.
Представление тригонометрических функций в виде степенных рядов и бесконечных произведений.
Все тригонометрические функции допускают разложение в степенные ряды. При этом функции sin x b cos x представляются рядами. сходящимися для всех значений x:
Эти ряды можно использовать для получения приближенных выражений sin x и cos x при малых значениях x:
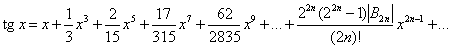
при |x| p/2;

при 0 x| p
(Bn – числа Бернулли).
Функции sin x и cos x могут быть представлены в виде бесконечных произведений:
 (эта формула была получена Эйлером в 1740);
(эта формула была получена Эйлером в 1740);
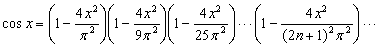
Тригонометрическая система 1, cos x, sin x, cos 2x, sin 2x, ¼, cos nx, sin nx, ¼, образует на отрезке [–p, p] ортогональную систему функций, что дает возможность представления функций в виде тригонометрических рядов.
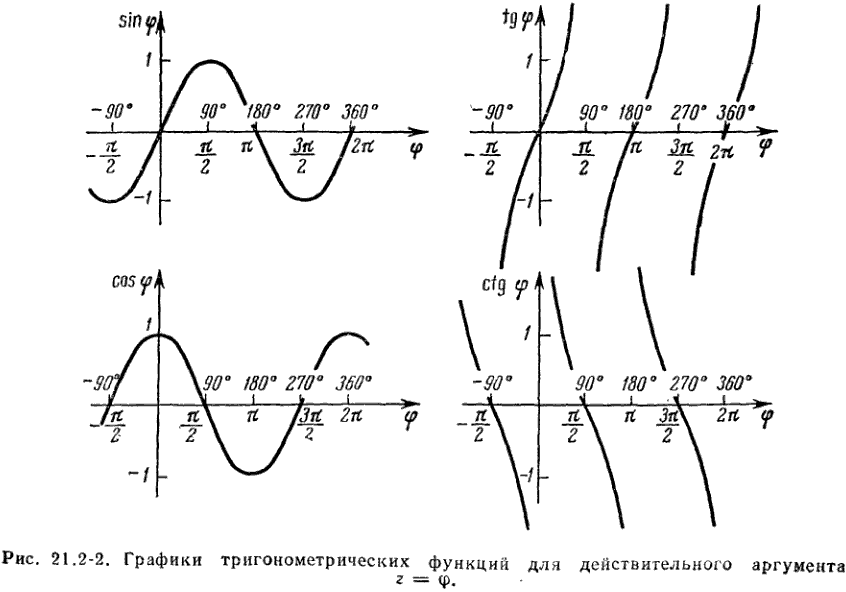
Функция у = cos х.
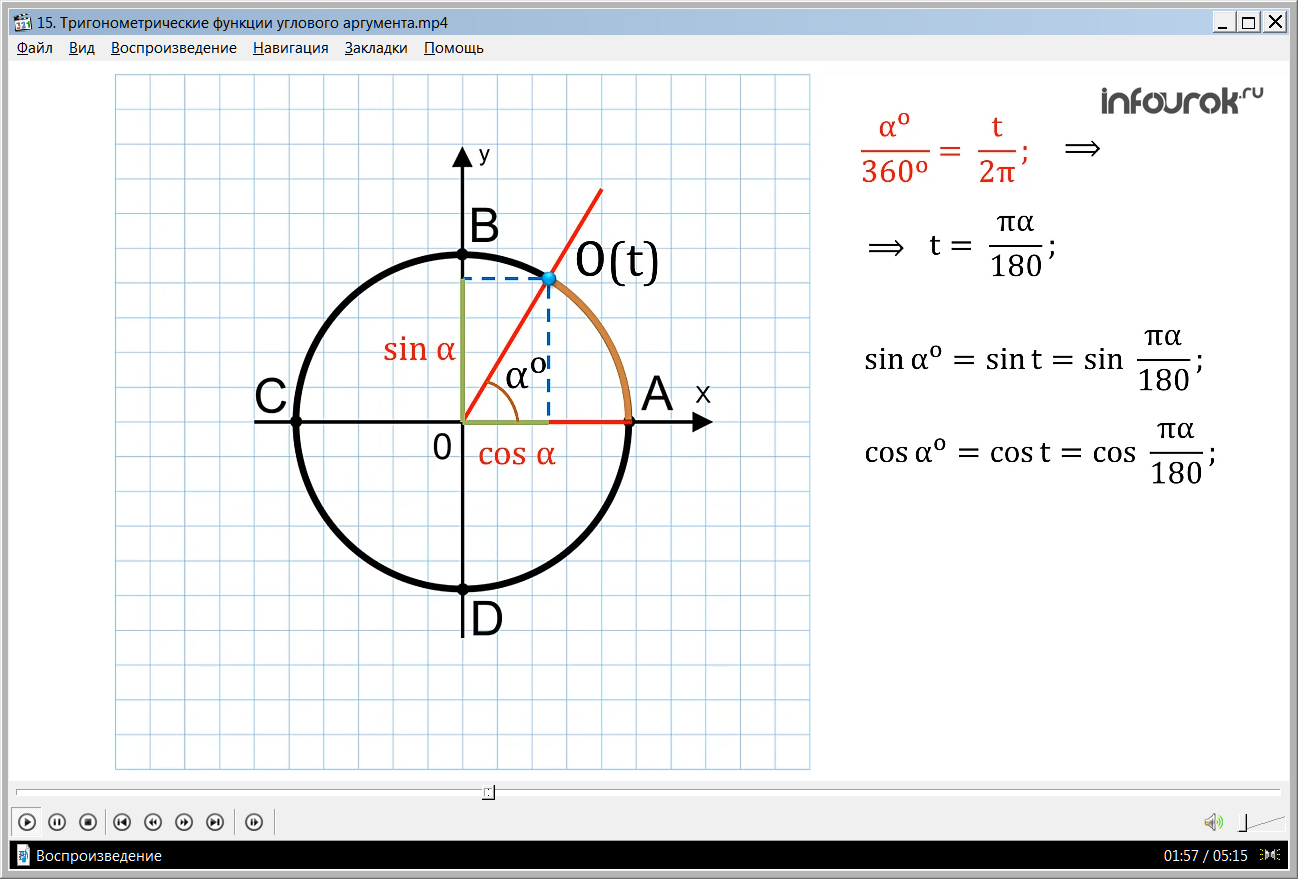
Если построить единичную окружность с центром в начале координат, и задать произвольное значение аргумента xи отсчитать от оси Ox угол x0,то этому углу на единичной окружности соответствует некоторая точка A (рис. 1)а ее проекцией на ось Ох будет точка М.Длина отрезка ОМ равна абсолютной величине абсциссы точки A. Данному значению аргумента xсопоставлено значение функции y =cos xкак абсциссы точки А.Соответственно точка В (x; у)принадлежит графику функции у = cos х (рис. 2).Если точка А находится правее оси Оу,токосинус будет положителен, если же левее – отрицателен. Но в любом случае точка А не может покинуть окружность. Поэтому косинус лежит в пределах от –1 до 1:
–1 = cos x = 1.
Дополнительный поворот на любой угол, кратный 2p, возвращает точку A на то же место. Поэтому функция у = cos x периодическая, ее период равен 2p:
cos (x + 2p) = cos x.
Если взять два значения аргумента, равные по абсолютной величине, но противоположные по знаку, x и –x,найти на окружности соответствующие точки Ax и А-x.Как видно на рис. 3их проекцией на ось Ох является одна и та же точка М.Поэтому
cos (–x) = cos (x),
т.е. косинус – четная функция, f(–x) = f(x).
Значит, можно исследовать свойства функции y = cos х на отрезке [0, p], а затем учесть ее четность и периодичность.
При х = 0 точка А лежит на оси Ох,ее абсцисса равна 1, а потому cos 0 = 1. С увеличением х точка А передвигается по окружности вверх и влево, ее проекция, естественно, только влево, и при х = p/2 косинус становится равен 0. Точка A в этот момент поднимается на максимальную высоту, а затем продолжает двигаться влево, но уже снижаясь. Ее абсцисса все убывает, пока не достигнет наименьшего значения, равного –1 при х = p. Таким образом, на отрезке [0, p] функция у = cos х монотонно убывает от 1 до –1 (рис. 4, 5).
Из четности косинуса следует, что на отрезке [–p, 0] функция монотонно возрастает от –1 до 1, принимая нулевое значение при х = –p/2. Если взять несколько периодов, получится волнообразная кривая (рис. 6).
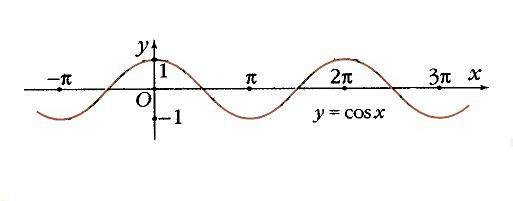
Итак, функция y = cos x принимает нулевые значения в точках х = p/2 + kp,где k – любое целое число. Максимумы, равные 1, достигаются в точках х = 2kp, т.е. с шагом 2p, а минимумы, равные –1, в точках х = p + 2kp.