Шар что это? значение слова шар

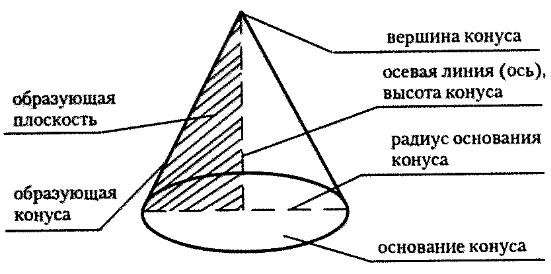
Основные геометрические формулы

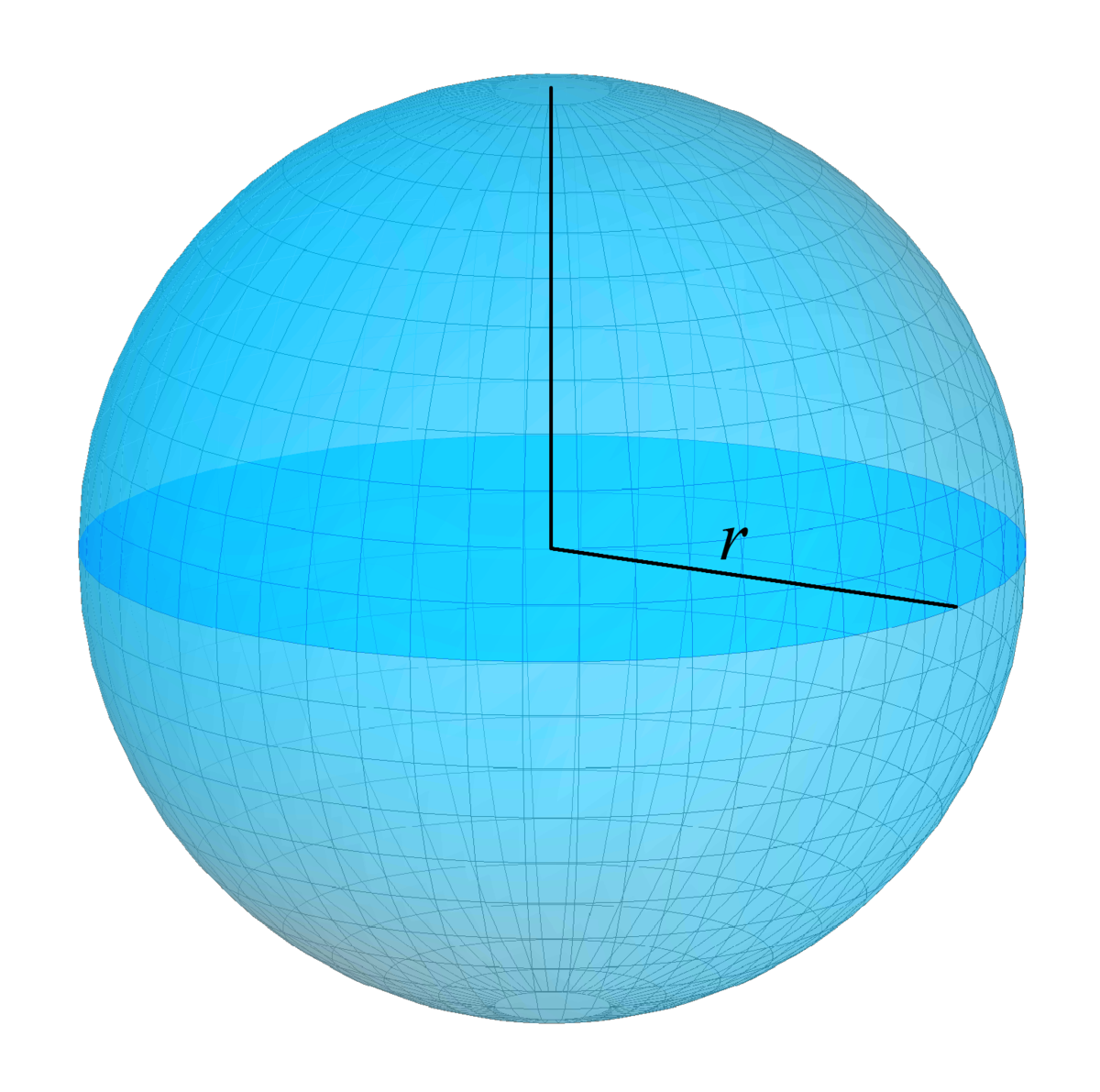
Площадь поверхности S{\displaystyle S} и объём V{\displaystyle V} шара радиуса r{\displaystyle r} (и диаметром d=2r{\displaystyle d=2r}) определяются формулами:

S= 4πr2{\displaystyle S=\ 4\pi r^{2}}

S= πd2{\displaystyle S=\ \pi d^{2}}

V=43πr3{\displaystyle V={\frac {4}{3}}\pi r^{3}}

Доказательство

Возьмём четверть круга радиуса R с центром в точке (;){\displaystyle \left(0;0\right)}. Уравнение окружности этого круга : x2+y2=R2{\displaystyle x^{2}+y^{2}=R^{2}}, откуда y2=R2−x2{\displaystyle y^{2}=R^{2}-x^{2}}.

Функция y=R2−x2,x∈(;R){\displaystyle y={\sqrt {R^{2}-x^{2}}},x\in (0;R)} непрерывная, убывающая, неотрицательная. При вращении четверти круга вокруг оси Ox образуется полушар, следовательно:

12V=π∫R(R2−x2)dx=π⋅(R2x−x33)|R=π⋅(R3−R33)=23πR3{\displaystyle {1 \over 2}V=\pi \int \limits _{0}^{R}(R^{2}-x^{2})dx=\pi \cdot {\Bigl .}\left(R^{2}x-{\frac {x^{3}}{3}}\right){\Bigr |}_{0}^{R}=\pi \cdot (R^{3}-{\frac {R^{3}}{3}})={\frac {2}{3}}\pi R^{3}}

Откуда V=43πR3{\displaystyle V={\frac {4}{3}}\pi R^{3}} Ч. т. д.

V=πd36{\displaystyle V={\frac {\pi d^{3}}{6}}}

Доказательство

d=2r,V=43πr3=43π(d2)3=43πd38=πd36{\displaystyle d=2r,V={4 \over 3}\pi r^{3}={4 \over 3}\pi \left({d \over 2}\right)^{3}={4 \over 3}\pi {\frac {d^{3}}{8}}={\frac {\pi d^{3}}{6}}} Ч. т. д.

Понятие шара в метрическом пространстве естественно обобщает понятие шара в евклидовой геометрии.

В словаре Фасмера Макса

I I, род. п. -а, болг. шар «шар» (Младенов 691); неубедительны попытки сближения с шар II, якобы первонач. в данном случае «пятно» (напр., Брандт, РФВ 24, 190; Ильинский, ИОРЯС 24, 1, 136). Последний привлекает сюда же хоро́ший. Ошибочно и сравнение с греч, κάρη «голова», др.-инд. c̨íras ср. р. «голова, вершина», авест. sarah- (ср. р.) – то же, вопреки Горяеву (ЭС 419).II II «краска», церк., русск.-цслав. шаръ «краска», шарити «красить», шаръчи «художник» (Ио. Леств., ХII в.; см. Срезн. III, 1582), ст.-слав. шаръ χρῶμα (Супр.), болг. шар «пятно; пестрый», сербохорв. ша̏ра «пестрота», ша́рац «конь пегой масти», словен. šа̑r м., šárа ж. «пестрый, пятнистый», šárа ж. «пестрота». Распространение этого слова говорит в пользу раннего заимствования из тюрк.; ср. чув. sărlа «красить», sără «краска». Арним (ZfslPh 9, 406) предполагал заимствование из тюрк. sаrуɣ «белый» или «желтый». Невероятна реконструкция праформы и.-е. *ki̯āro- и сравнение с си́зый, вопреки Петерссону (ВSl Wortst. 28).III III «морской пролив; залив», беломорск. (Даль, Ончуков), печорск. (Подв.); коми šаr «морской пролив», которое Калима (FUF 18, 46 и сл.) считает источником, не отмечено у Вихм. – Уотилы. Шренк у Калимы (там же) считает источником коми šоr «ручей», родственное венг. ár «поток» (Паасонен, KSz. 16, 57).

Значение слова Шар по словарю Символизма:

Шар — Олицетворяет как Солнце, так и Луну, поэтому игры с шарами связаны как с солярными, так и с лунными ритуалами и празднествами. Символизируют могущество богов разбрасывать по небесам планеты, метеориты и звезды. Золотые шары — атрибуты Гарпий и эмблема святого Николая из Миры. Шар, как и сфера , означает мир, вечность, самодовлеющюю власть над вселенной, силу и императорское достоинство. Обычно его держат в левой руке как символ далеко простирающейся власти божества или суверена. Шар, водруженный на основание, означает Небо, ограничение или предел. В алхимии коронованный шар — это философский камень, который иногда называют Великим Королем. В христианстве шар, увенчанный крестом, означает правление Христа над миром, а также преобладание веры в Христа. В христианском искусстве Бог-Отец иногда изображается стоящим на шаре. Эмблема святого Карла Великого. В греко-римской мифологии шар СИУ волировал удачу, судьбу, ассоциируясь с Тихэ (Фортуной), стоящей на шаре. Шар и компас — эмблемы Урании. Синий шар — атрибут Зевса (Юпитера), как бога Небес, а также Аполлона и Кибелы.

В чем различие

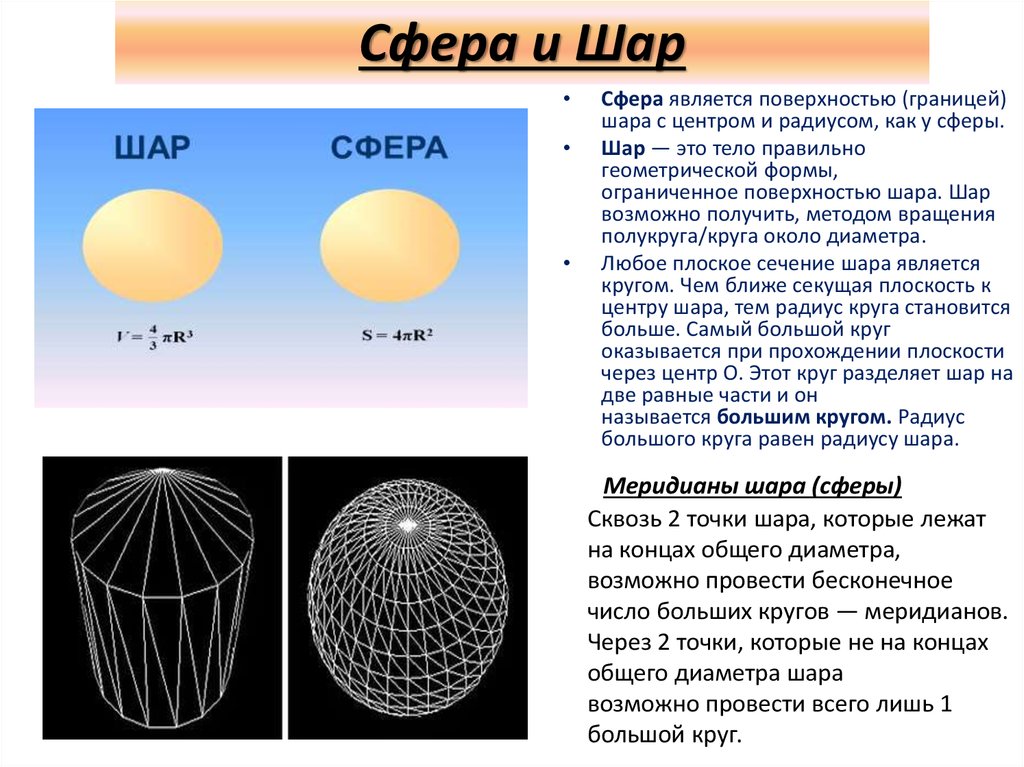
Тогда возникает вопрос, а чем отличается шар от сферы кроме определения? Дело в том, что различия шара и сферы куда более размыты, нежели различия круга и окружности. Сфера так же имеет объем и площадь поверхности.

Пожалуй, кроме определения, разница заключается в том, что в задачах никогда не находят объем сферы. Как правило, ищут объем шара. Это не значит, что у сферы нет объема. Это трехмерная фигура, поэтому объем у нее есть.

Просто проводится аналогия с окружностью, у которой нет площади. Это не правило, но скорее традиция, которую нужно запомнить: в геометрии не приветствуется формулировка объем сферы.

Еще одно отличие, которое можно считать более или менее значимым: секущая плоскость сферы: окружность, которая не имеет внутреннего пространства, но имеет длину. Секущая плоскость шара: круг, который имеет площадь и не имеет длины окружности. Поэтому стоит быть аккуратным в формулировках задачи, чтобы не было ошибок из-за подобных мелочей.

Что мы узнали?

Мы узнали, что такое сфера и шар. Поговорили об их сходствах и различии. Узнали, что различий у этих фигур почти нет. Решили, что не стоит приводить такую формулировку, как объем сферы.

Вопрос 1 из 10

Начать тест(новая вкладка)

Шар

Шар и сфера – это аналог круга и окружности в плоскости. Шар представляет собой фигуру, полученную вращением полукруга вокруг одной точки.

Шар имеет площадь поверхности: $S=4pir^2$

Радиус это отрезок, соединяющий центр шара и любую из точек на его поверхности.

Формула объема шара$V={4pir^3\over3}$

Объем показывает, какое пространство занимает фигура. Чтобы понять, что такое объем нужно представить себе фигуру полой. Тогда объем это количество воды, которое можно налить в эту фигуру

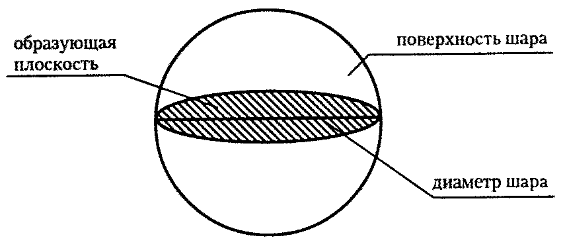
Шар, как и любую другую трехмерную фигуру, можно рассечь плоскостью. Секущей плоскостью шара является круг, центр которого можно найти, опустив из центра шара перпендикуляр на окружность.

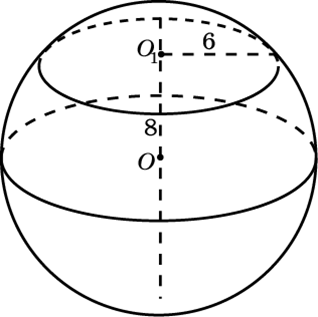
Рис. 2. Сечение шара.

Хоть в школьном курсе такие ситуации не случаются, но нужно понимать, что шар может быть рассечен плоскостью под углом. Но даже в этом примере, секущая плоскость останется шаром.

В словаре Энциклопедии

геометрическое тело, получающееся при вращении круга вокруг своего диаметра. Шар ограничен сферой; центр этой сферы называется центром шара, а ее радиус — радиусом шара. Объем шара V = 4/3*п*R3,площадь его поверхности S = 4*П*R2,где R — радиус шара.—название морских проливов на севере Европейской части России (напр., Маточкин Шар); некоторых речных рукавов.—(Char) Рене (1907-88) , французский поэт. На рубеже 20-30-х гг. близок к сюрреализму (сборник стихов «Молот без хозяина» 1934). Активный участник Движения Сопротивления, опыт которого — как бы пограничного бытия — обобщил в книге стихов в прозе «Листки Гипноса» (1946). Сосредоточенности бодрствующего разума сочетал с темной, до конца не расшифрованной метафористикой первичных стихий: книги стихов в прозе «Архипелаг слова» (1962), «Спящие окна и ход на крышу» (1979).

Лучшие ранние сорта черешни с описанием и фото

Примеры

Br(x)={x∈R∣|x−x|<r}=(x−r,x+r),{\displaystyle B_{r}(x_{0})=\{x\in {\mathbb {R} }\mid |x-x_{0}|<r\}=\left(x_{0}-{r},x_{0}+{r}\right),}

Dr(x)={x∈R∣|x−x|≤r}=x−r,x+r.{\displaystyle D_{r}(x_{0})=\{x\in {\mathbb {R} }\mid |x-x_{0}|\leq r\}=\left.}

— открытый и замкнутый отрезок соответственно.

если d=2{\displaystyle d=2} (пространство — плоскость), то
Br((x0,y0))={(x,y)∈R2∣(x−x0)2+(y−y0)2

— открытый и замкнутый диск соответственно.

если d=3{\displaystyle d=3}, то
Br((x0,y0,z0))={(x,y,z)∈R3∣(x−x0)2+(y−y0)2+(z−z0)2

— открытый и замкнутый стереометрический шар соответственно.

В иных метриках шар может иметь иную геометрическую форму. Например, определим в евклидовом пространстве Rd{\displaystyle \mathbb {R} ^{d}} метрику следующим образом:
ρ(x,y)=∑i=1d‖xi−yi‖,x=(x1,…,xd)⊤,y=(y1,…,yd)⊤∈Rd.{\displaystyle \rho (x,y)=\sum \limits _{i=1}^{d}\|x_{i}-y_{i}\|,\quad x=(x_{1},\ldots ,x_{d})^{\top },y=(y_{1},\ldots ,y_{d})^{\top }\in \mathbb {R} ^{d}.}

Тогда

если d=2{\displaystyle d=2}, то Ur(x){\displaystyle U_{r}(x_{0})} — это открытый квадрат с центром в точке x{\displaystyle x_{0}} и сторонами длины 2{\displaystyle {\sqrt {2}}}, расположенными по диагонали к координатным осям.
если d=3{\displaystyle d=3}, то Ur(x){\displaystyle U_{r}(x_{0})} — это открытый трёхмерный октаэдр.

Примеры

Br(x)={x∈R∣|x−x|<r}=(x−r,x+r),{\displaystyle B_{r}(x_{0})=\{x\in {\mathbb {R} }\mid |x-x_{0}|<r\}=\left(x_{0}-{r},x_{0}+{r}\right),}

Dr(x)={x∈R∣|x−x|≤r}=x−r,x+r.{\displaystyle D_{r}(x_{0})=\{x\in {\mathbb {R} }\mid |x-x_{0}|\leq r\}=\left.}

— открытый и замкнутый отрезок соответственно.

если d=2{\displaystyle d=2} (пространство — плоскость), то
Br((x0,y0))={(x,y)∈R2∣(x−x0)2+(y−y0)2

— открытый и замкнутый диск соответственно.

если d=3{\displaystyle d=3}, то
Br((x0,y0,z0))={(x,y,z)∈R3∣(x−x0)2+(y−y0)2+(z−z0)2

— открытый и замкнутый стереометрический шар соответственно.

Тогда

если d=2{\displaystyle d=2}, то Ur(x){\displaystyle U_{r}(x_{0})} — это открытый квадрат с центром в точке x{\displaystyle x_{0}} и сторонами длины 2{\displaystyle {\sqrt {2}}}, расположенными по диагонали к координатным осям.
если d=3{\displaystyle d=3}, то Ur(x){\displaystyle U_{r}(x_{0})} — это открытый трёхмерный октаэдр.

Свойства

Шар является открытым множеством в топологии, порождённой метрикой ρ{\displaystyle \rho }.
Замкнутый шар — замкнутым множеством в топологии, порождённой метрикой ρ{\displaystyle \rho }.
По определению такой топологии открытые шары с центрами в любой точке X{\displaystyle X} являют собой её базу.
Очевидно, Br(x)⊂Dr(x){\displaystyle B_{r}(x_{0})\subset D_{r}(x_{0})}. Однако, вообще говоря, замыкание открытого шара может не совпадать с замкнутым шаром: Br(x)¯≠Dr(x).{\displaystyle {\overline {B_{r}(x_{0})}}\neq D_{r}(x_{0}).}
Например: пусть (X,ρ){\displaystyle (X,\rho )} — дискретное метрическое пространство, и X{\displaystyle X} состоит из более, чем двух точек. Тогда для любого x∈X{\displaystyle x\in X} имеем:

B1(x)={x},B1(x)¯={x},D1(x)=X.{\displaystyle B_{1}(x)=\{x\},\;{\overline {B_{1}(x)}}=\{x\},\;D_{1}(x)=X.}

Примеры

Br(x)={x∈R∣|x−x|<r}=(x−r,x+r),{\displaystyle B_{r}(x_{0})=\{x\in {\mathbb {R} }\mid |x-x_{0}|<r\}=\left(x_{0}-{r},x_{0}+{r}\right),}

Dr(x)={x∈R∣|x−x|≤r}=x−r,x+r.{\displaystyle D_{r}(x_{0})=\{x\in {\mathbb {R} }\mid |x-x_{0}|\leq r\}=\left.}

— открытый и замкнутый отрезок соответственно.

если d=2{\displaystyle d=2} (пространство — плоскость), то
Br((x0,y0))={(x,y)∈R2∣(x−x0)2+(y−y0)2

— открытый и замкнутый диск соответственно.

если d=3{\displaystyle d=3}, то
Br((x0,y0,z0))={(x,y,z)∈R3∣(x−x0)2+(y−y0)2+(z−z0)2

— открытый и замкнутый стереометрический шар соответственно.

Тогда

если d=2{\displaystyle d=2}, то Ur(x){\displaystyle U_{r}(x_{0})} — это открытый квадрат с центром в точке x{\displaystyle x_{0}} и сторонами длины 2{\displaystyle {\sqrt {2}}}, расположенными по диагонали к координатным осям.
если d=3{\displaystyle d=3}, то Ur(x){\displaystyle U_{r}(x_{0})} — это открытый трёхмерный октаэдр.

Трехмерное пространство

Большая часть геометрических построений производится в плоскости, но в старших классах начинают изучать трехмерные фигуры. Двухмерное пространство имеет только две характеристики: длину и ширину. В трехмерных областях добавляется высота. В математике 6 класса изучаются отдельные 3д фигуры.

На плоскости фигуру характеризовала площадь и периметр. В трехмерных объектах к ним прибавляется объем.

Рис. 1. Трехмерное пространство.

Кроме того, имеется ряд специфических свойств 3д фигур. Их может пересекать прямая и плоскость, могут имеется секущие плоскости, которые принимают формы других фигур.

Применение 3д фигур для составления задач значительно усложняет их, но в то же время делает куда более интересными. Приведем определения шара и сферы, после чего попробуем выделить различия этих фигур.

В словаре Ожегова

ШАР, -а и (с колич. числит.) -а, мн. -ы. -ов, м. 1.В математике: часть пространства, ограниченная сферой. Радиус шара. 2. Предмет такой формы. Биллиардный ш. Ш.-зонд (наполненный водородом резиновый шар для исследования атмосферы). Баллотировочные шары (черные и белые шары, использовавшиеся при тайном голосовании; стар.). * Земной шар — планета Земля. Воздушный шар — 1) летательный аппарат легче воздуха, поднимаемый вверх легким газом, заполняющим его шарообразную оболочку. Путешествие на воздушном шаре; 2) надувная игрушка — прозрачная цветная оболочка, заполняемая легким газом. Воздушный ш. на ниточке. Гирлянды воздушных шаров (на празднествах). Пробный шар (книжн.) — действие, имеющее целью предварительно проверить, испытать что-н. Хоть шаром покати (разг.) — ничего нет, совершенно пусто. Черный шар — черный баллотировочный шар, выражающий несогласие, также вообще выражение несогласия при тайном голосовании. I) умелый, шарик, -а, м. (ко 2 знач.). || прил. шаровой, -ая, -ое (к 1 знач.).