Бизнес и финансы
БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством
Об определении
Формальное введение понятия площадь и объём можно найти в статье мера Жордана, здесь мы приводим лишь намётки определения с комментариями.
Площадь — это вещественнозначная функция, определённая на определённом классе фигур евклидовой плоскости и удовлетворяющая четырём условиям:
- Положительность — площадь неотрицательна;
- Нормировка — квадрат со стороной единица имеет площадь 1;
- Конгруэнтность — конгруэнтные фигуры имеют равную площадь;
- Аддитивность — площадь объединения двух фигур без общих внутренних точек равна сумме площадей.
При этом определённый класс должен быть замкнут относительно пересечения и объединения, а также относительно движений плоскости и включать в себя все многоугольники. Из этих аксиом следует монотонность площади, то есть
Если одна фигура принадлежит другой фигуре, то площадь первой не превосходит площади второй:
Чаще всего за «определённый класс» берут множество квадрируемых фигур.
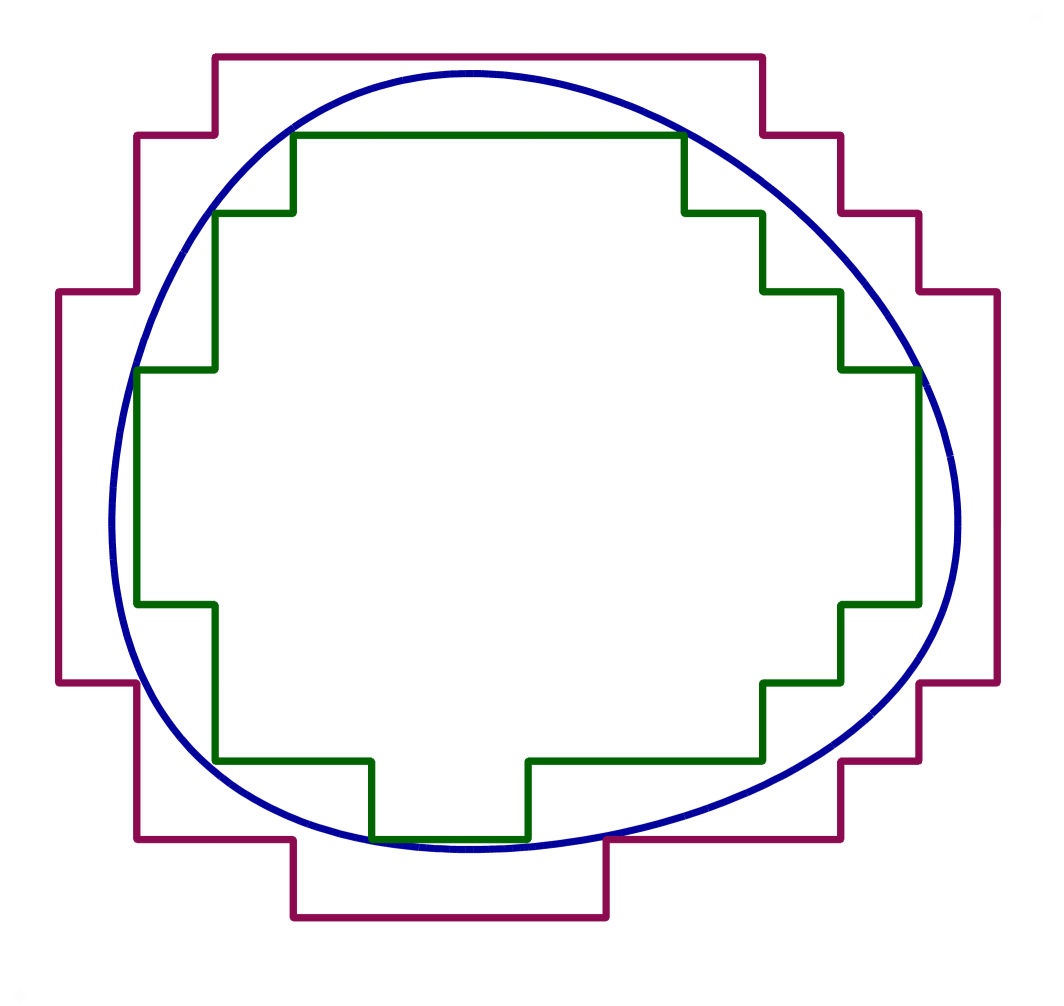
Фигура F{\displaystyle F} называется квадрируемой, если для любого ε>{\displaystyle \varepsilon >0} существует пара многоугольников P{\displaystyle P} и Q{\displaystyle Q}, такие что P⊂F⊂Q{\displaystyle P\subset F\subset Q} и S(Q)−S(P)<ε{\displaystyle S(Q)-S(P)<\varepsilon }, где S(P){\displaystyle S(P)} обозначает площадь P{\displaystyle P}.
- Примеры квадрируемых фигур
- многоугольники;
- любая фигура, ограниченная спрямляемой кривой, в частности круг;
- фигура ограниченная снежинкой Коха, хотя её граница не спрямляема.
Визуальный способ
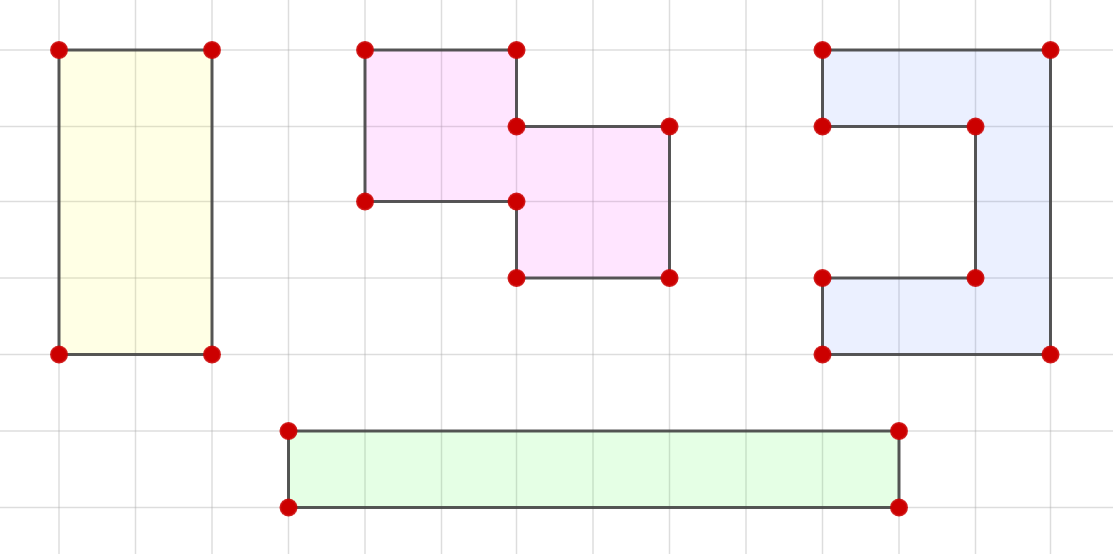
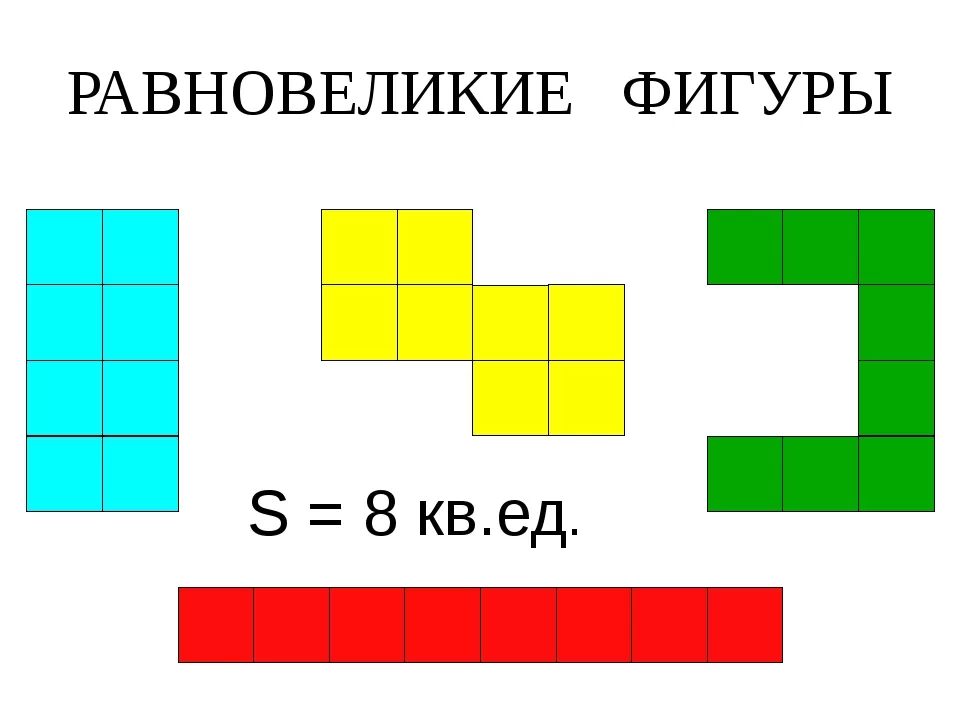
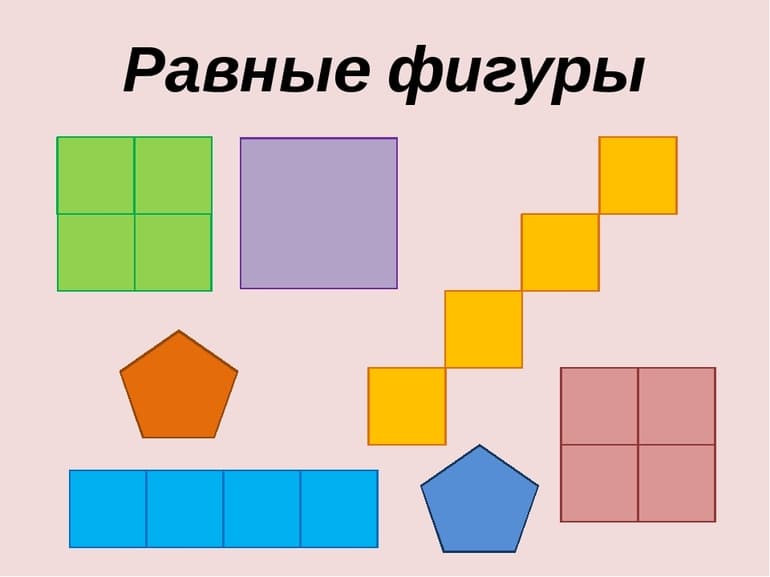
Существует также наглядный, но неточный способ. Нужно взять листок в клеточку и нарисовать на нём многоугольники. Если рисунок получился большой — не страшно, так будет только проще в дальнейшем. Следующий шаг — посчитать количество клеток, которое заняла каждая фигура и сравнить. Если оно равно, равновеликость доказана. Опять же метод не точный, но для введения в концепцию площадей и их «равности» подойдёт.
Иногда встречается словосочетание «равносоставленная фигура». Такими называют произвольные многоугольники, которые можно составить друг из друга путём разрезания одного из них на одинаковые объекты и перекладывания. Например, если прямоугольник 4 на 1 нарезать на одинаковые части — квадраты 1 на 1, то из полученных маленьких квадратов можно составить один большой со стороной 2. Но это не более чем забавное свойство некоторых фигур и в геометрии фактически почти не используется.
Предыдущая
ГеометрияДиагональ прямоугольного параллелепипеда — свойства, формулы и примеры
Следующая
ГеометрияРавнобедренный треугольник — свойства, признаки и формулы
Равность правильных фигур
Частным и самым простым для сравнения является случай, когда многоугольник по условию правильный. Так называется фигура с одинаковыми сторонами и углами. Например, равносторонний треугольник и квадрат
Важно не забывать проверить равны ли углы, так как не каждая фигура правильная. Тот же ромб по определению имеет 4 совпадающие по длине стороны, но разные углы
При сравнении правильных многоугольников достаточно указать, что, хотя бы одна сторона фигуры равна стороне у другой. Это будет достаточное условие для доказательства «равности».
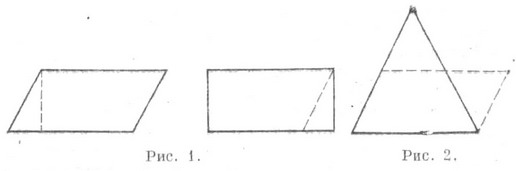
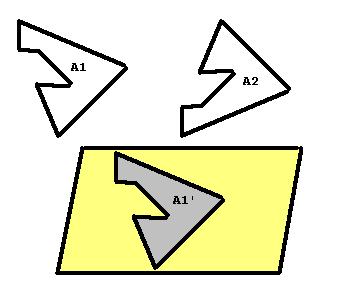
Самым простым и наглядным способом сверки двух фигур будет не геометрический с помощью правил, а путём наложения рисунков друг на друга. Разумеется, что он не претендует на точность, но изобразить параллелограмм и наложить его на другой нагляднее, чем сравнивать, например, углы. Понятно, что так можно только ознакомиться с концепцией «равности» и показать, какие фигуры называются равными, для упрощения в дальнейшем решения задач, но доказывать что-либо нельзя, ввиду неточности метода.
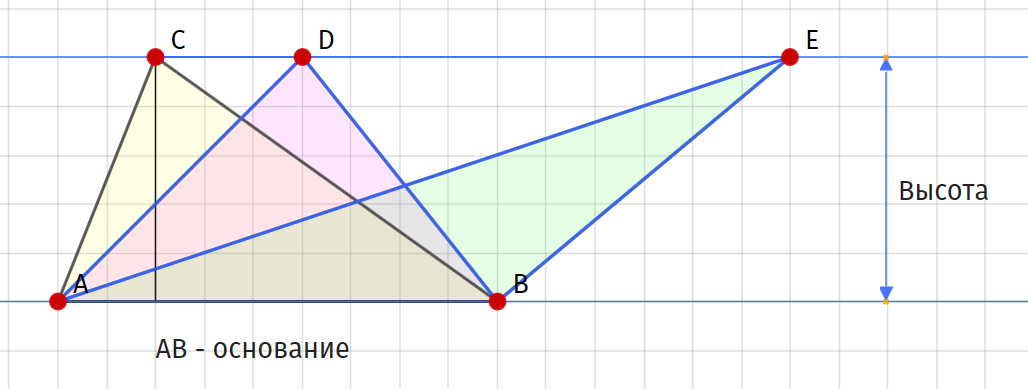
Если при сравнении двух тел оказывается, что их площади равны, такие тела (многоугольники) являются равновеликими. Как и в случае с прошлым, это определение звучит несложно. Проблемы могут начаться непосредственно при вычислении площадей. Самый простой многоугольник — треугольник. Для вычисления его площади существует множество способов.
Формулы[ | код]
| Фигура | Формула | Комментарий |
|---|---|---|
| Правильный треугольник | 34⋅a2{\displaystyle {\tfrac {\sqrt {3}}{4}}{\cdot }a^{2}} | a{\displaystyle a} — длина стороны треугольника. |
| Треугольник | p⋅(p−a)⋅(p−b)⋅(p−c){\displaystyle {\sqrt {p{\cdot }(p-a){\cdot }(p-b){\cdot }(p-c)}}} | Формула Герона. p{\displaystyle p} — полупериметр, a{\displaystyle a}, b{\displaystyle b} и c{\displaystyle c} — длины сторон треугольника. |
| Треугольник | 12⋅a⋅b⋅sinγ{\displaystyle {\tfrac {1}{2}}{\cdot }a{\cdot }b{\cdot }\sin \gamma } | a{\displaystyle a} и b{\displaystyle b} — две стороны треугольника, а γ{\displaystyle \gamma } — угол между ними. |
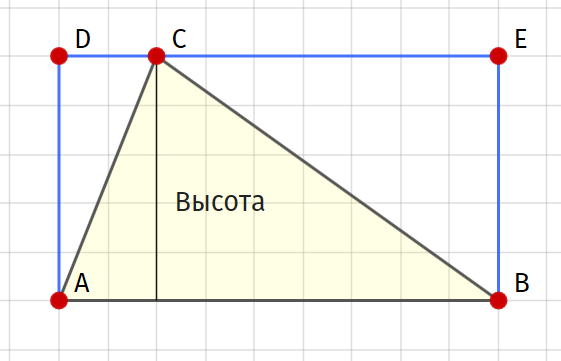
| Треугольник | 12⋅b⋅h{\displaystyle {\tfrac {1}{2}}{\cdot }b{\cdot }h} | b{\displaystyle b} и h{\displaystyle h} — сторона треугольника и высота, проведённая к этой стороне. |
| Квадрат | a2{\displaystyle a^{2}} | a{\displaystyle a} — длина стороны квадрата. |
| Прямоугольник | a⋅b{\displaystyle a{\cdot }b} | a{\displaystyle a} и b{\displaystyle b} — длины сторон прямоугольника. |
| Ромб | a2⋅sinα,12bc{\displaystyle a^{2}{\cdot }\sin \alpha ,{\tfrac {1}{2}}bc} | a{\displaystyle a} — сторона ромба, α{\displaystyle \alpha } — внутренний угол, b,c{\displaystyle b,c} — диагонали. |
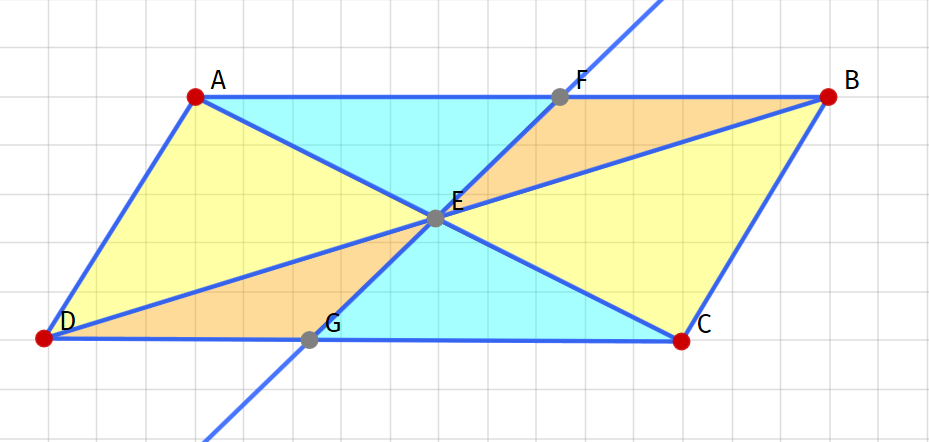
| Параллелограмм | b⋅h{\displaystyle b{\cdot }h} | b{\displaystyle b} — длина одной из сторон параллелограмма, а h{\displaystyle h} — высота, проведённая к этой стороне. |
| Трапеция | 12⋅(a+b)⋅h{\displaystyle {\tfrac {1}{2}}{\cdot }(a+b){\cdot }h} | a{\displaystyle a} и b{\displaystyle b} — длины параллельных сторон, а h{\displaystyle h} — расстояние между ними (высота). |
| Четырёхугольник | 12⋅m⋅n⋅sinϕ{\displaystyle {\tfrac {1}{2}}{\cdot }m{\cdot }n{\cdot }\sin \phi } | n{\displaystyle n} и m{\displaystyle m} — длины диагоналей, и ϕ{\displaystyle \phi } — угол между ними. |
| Правильный шестиугольник | 3⋅32⋅a2{\displaystyle {\tfrac {3{\cdot }{\sqrt {3}}}{2}}{\cdot }a^{2}} | a{\displaystyle a} — длина стороны шестиугольника. |
| Правильный восьмиугольник | 2⋅(1+2)⋅a2{\displaystyle 2{\cdot }(1+{\sqrt {2}}){\cdot }a^{2}} | a{\displaystyle a} — длина стороны восьмиугольника. |
| Правильный многоугольник | n⋅a24⋅tan(πn){\displaystyle {\frac {n{\cdot }a^{2}}{4{\cdot }\tan(\pi /n)}}} | a{\displaystyle a} — длина стороны многоугольника, а n{\displaystyle n} — количество сторон многоугольника. |
| 12⋅a⋅p{\displaystyle {\tfrac {1}{2}}{\cdot }a{\cdot }p} | a{\displaystyle a} — апофема (или радиус вписанной в многоугольник окружности), а p{\displaystyle p} — периметр многоугольника. | |
| Произвольный многоугольник | 12|∑i=n−1det(xixi+1yiyi+1)|{\displaystyle {1 \over 2}\left|\sum _{i=0}^{n-1}\det {\begin{pmatrix}x_{i}&x_{i+1}\\y_{i}&y_{i+1}\end{pmatrix}}\right|} | Формула площади Гаусса. (xi,yi){\displaystyle (x_{i},y_{i})} — координаты вершин n{\displaystyle n}-угольника, (xn,yn)=(x,y){\displaystyle (x_{n},y_{n})=(x_{0},y_{0})} |
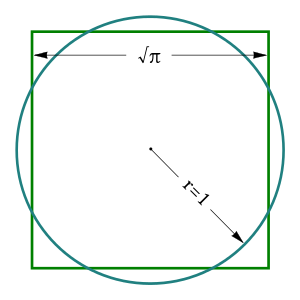
| Круг | π⋅r2{\displaystyle \pi {\cdot }r^{2}} или π⋅d24{\displaystyle {\frac {\pi {\cdot }d^{2}}{4}}} | r{\displaystyle r} — радиус окружности, а d{\displaystyle d} — её диаметр. |
| Сектор круга | 12⋅r2⋅θ{\displaystyle {\tfrac {1}{2}}{\cdot }r^{2}{\cdot }\theta } | r{\displaystyle r} и θ{\displaystyle \theta } — соответственно радиус и угол сектора (в радианах). |
| Эллипс | π⋅a⋅b{\displaystyle \pi {\cdot }a{\cdot }b} | a{\displaystyle a} и b{\displaystyle b} — большая и малая полуоси эллипса. |
Справочная информация
ДокументыЗаконыИзвещенияУтверждения документовДоговораЗапросы предложенийТехнические заданияПланы развитияДокументоведениеАналитикаМероприятияКонкурсыИтогиАдминистрации городовПриказыКонтрактыВыполнение работПротоколы рассмотрения заявокАукционыПроектыПротоколыБюджетные организацииМуниципалитетыРайоныОбразованияПрограммыОтчетыпо упоминаниямДокументная базаЦенные бумагиПоложенияФинансовые документыПостановленияРубрикатор по темамФинансыгорода Российской Федерациирегионыпо точным датамРегламентыТерминыНаучная терминологияФинансоваяЭкономическаяВремяДаты2015 год2016 годДокументы в финансовой сферев инвестиционной