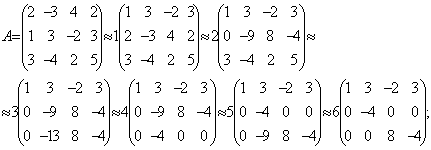Как определить ранг матрицы: примеры
Пример 1
Определить ранг матрицы $A=\left(\begin{array}{ccc} {-2} & {1} & {4} \\ {1} & {0} & {3} \\ {1} & {2} & {3} \end{array}\right)$.
Решение:
Отметим, что ранг исходной матрицы не может быть более 3.
Среди миноров первого порядка имеются миноры не равные нулю, например, $M_{1} =\left|-2\right|=-2$. Рассмотрим миноры второго порядка.
$M_{2} =\left|\begin{array}{cc} {-2} & {1} \\ {1} & {0} \end{array}\right|=-2\cdot 0-1\cdot 1=0-1=-1\ne 0$
Выполним окаймление минора второго порядка и получим минор третьего порядка.
$M_{3} =\left|\begin{array}{ccc} {-2} & {1} & {4} \\ {1} & {0} & {3} \\ {1} & {2} & {3} \end{array}\right|=-2\cdot 0\cdot 3+1\cdot 3\cdot 1+1\cdot 2\cdot 4-1\cdot 0\cdot 4-1\cdot 1\cdot 3-2\cdot 3\cdot (-2)=3+8-0-3+12=20\ne 0$
Следовательно, ранг рассматриваемой матрицы равен 3.
Пример 2
Определить ранг матрицы $A=\left(\begin{array}{ccccc} {1} & {2} & {3} & {0} & {1} \\ {0} & {1} & {2} & {3} & {4} \\ {2} & {3} & {1} & {4} & {5} \\ {0} & {0} & {0} & {0} & {0} \end{array}\right)$.
Решение:
Отметим, что ранг исходной матрицы не может быть более 4 (строк 4, столбцов 5).
Среди миноров первого порядка имеются отличные от нуля, например, $M_{1} =\left|1\right|=1$. Рассмотрим миноры второго порядка.
$M_{2} =\left|\begin{array}{cc} {1} & {2} \\ {0} & {1} \end{array}\right|=1\cdot 1-0\cdot 2=1-0=1\ne 0$
Выполним окаймление минора второго порядка и получим минор третьего порядка.
$M_{3} =\left|\begin{array}{ccc} {1} & {2} & {3} \\ {0} & {1} & {2} \\ {2} & {3} & {1} \end{array}\right|=1\cdot 1\cdot 1+2\cdot 2\cdot 2+0\cdot 3\cdot 3-2\cdot 1\cdot 3-0\cdot 1\cdot 2-2\cdot 3\cdot 1=1+8+0-6-0-6=-3\ne 0$
Выполним окантовывание минора третьего порядка и получим минор четвертого порядка.
$M_{4} =\left|\begin{array}{cccc} {1} & {2} & {3} & {0} \\ {0} & {1} & {2} & {3} \\ {2} & {3} & {1} & {4} \\ {0} & {0} & {0} & {0} \end{array}\right|=0$ (содержит нулевую строку)
$M_{5} =\left|\begin{array}{cccc} {1} & {2} & {3} & {1} \\ {0} & {1} & {2} & {4} \\ {2} & {3} & {1} & {5} \\ {0} & {0} & {0} & {0} \end{array}\right|=0$ (содержит нулевую строку)
Все миноры четвертого порядка матрицы равны нулю, следовательно, ранг рассматриваемой матрицы равен 3.
Нахождение ранга матрицы посредством элементарных преобразований сводится к приведению матрицы к диагональному (ступенчатому) виду. Ранг полученной в результате преобразований матрицы равен числу ненулевых диагональных элементов.
Пример 3
Определить ранг матрицы $A=\left(\begin{array}{ccc} {-2} & {1} & {4} \\ {1} & {0} & {3} \\ {1} & {2} & {3} \end{array}\right)$.
Решение:
Поменяем местами первую и вторую строки матрицы А:
$A=\left(\begin{array}{ccc} {-2} & {1} & {4} \\ {1} & {0} & {3} \\ {1} & {2} & {3} \end{array}\right)\sim \left(\begin{array}{ccc} {1} & {0} & {3} \\ {-2} & {1} & {4} \\ {1} & {2} & {3} \end{array}\right)$
Умножим первую строку матрицы В на число 2 и сложим со второй строкой:
$\left(\begin{array}{ccc} {1} & {0} & {3} \\ {-2} & {1} & {4} \\ {1} & {2} & {3} \end{array}\right)\sim \left(\begin{array}{ccc} {1} & {0} & {3} \\ {0} & {1} & {10} \\ {1} & {2} & {3} \end{array}\right)$
Умножим первую строку матрицы С на число -1 и сложим с третьей строкой:
$\left(\begin{array}{ccc} {1} & {0} & {3} \\ {0} & {1} & {10} \\ {1} & {2} & {3} \end{array}\right)\sim \left(\begin{array}{ccc} {1} & {0} & {3} \\ {0} & {1} & {10} \\ {0} & {2} & {0} \end{array}\right)$
Умножим вторую строку матрицы D на число -2 и сложим с третьей строкой:
$\left(\begin{array}{ccc} {1} & {0} & {3} \\ {0} & {1} & {10} \\ {0} & {2} & {0} \end{array}\right)\sim \left(\begin{array}{ccc} {1} & {0} & {3} \\ {0} & {1} & {10} \\ {0} & {0} & {-20} \end{array}\right)$
$\left(\begin{array}{ccc} {1} & {0} & {3} \\ {0} & {1} & {10} \\ {0} & {0} & {-20} \end{array}\right)$ — матрица ступенчатого вида
Количество ненулевых диагональных элементов равно 3, следовательно, $rang=3$.
Нахождение ранга матрицы.
Определение
Матрица размеров m \times n называется упрощенной (или имеет упрощенный вид), если некоторые r ее столбцов являются первыми r столбцами единичной матрицы порядка m и, в случае m > r, ее последние (m-r) строк — нулевые.
Утверждение 5.
Каждую матрицу с помощью элементарных преобразований строк можно превратить в упрощенную матрицу.
Если матрица нулевая, то она уже упрощенная (r=0). В общем случае применим метод Гаусса. В мы превратили квадратную невырожденную матрицу элементарными преобразованиями строк в единичную матрицу. Это — частный случай доказываемого утверждения. То обстоятельство, что матрица невырождена, использовалось, когда мы в очередной строке преобразованной матрицы находили ненулевой элемент.
В общем случае ненулевой элемент может не найтись, то есть очередная строка окажется нулевой. Все встречающиеся нулевые строки будем переставлять на последние места и будем продолжать преобразования так, как при доказательстве утверждения, на которое ссылались выше.
Преобразования закончатся, когда либо будут исчерпаны все строки, либо останутся только нулевые строки. При этом не существенно, квадратная матрица или нет. Конечно, может случиться, что некоторые столбцы не будут превращены в столбцы единичной матрицы, но это нам и не требуется. Пусть всего в столбцы единичной матрицы преобразовано r столбцов. Если остались строки ниже r-й, они нулевые, иначе преобразования можно продолжить. Предложение доказано.
Пусть мы привели матрицу A к упрощенному виду, и в упрощенной матрице A’, столбцы \boldsymbol{a}_{j_{1}},…, \boldsymbol{a}_{j_{r}}\ (j_{1} <…< j_{r}) превращены в столбцы единичной матрицы \boldsymbol{e}_{1},…, \boldsymbol{e}_{r}. Можно считать, что \boldsymbol{a}_{j_{k}} \rightarrow \boldsymbol{e}_{k} для всех k=1,…, r. Это достигается перестановкой строк.
Рассмотрим упрощенную матрицу A’. В ней есть невырожденная подматрица порядка r, а невырожденных подматриц большего порядка, очевидно, нет. Следовательно, ранг матрицы равен r, а подматрица базисная.
Из этого следует, что \mathbf{Rg}\,A=r, так как ранг не изменился при элементарных преобразованиях. За базисную подматрицу в A можно принять подматрицу, расположенную в столбцах с номерами j_{1},…, j_{r} и строках, которые после перестановок попали на места 1,…, r в упрощенной матрице. Это видно из того, что, преобразуя матрицу, мы не прибавляли к пересекающим ее строкам никаких строк, которые ее не пересекают.
Таким образом, если мы не знали ранга матрицы и ее базисной подматрицы, то приведя ее к упрощенному виду, мы их определим. С другой стороны, имеет место
Утверждение 6.
Какова бы ни была базисная подматрица матрицы A, элементарными преобразованиями строк можно привести A к такому упрощенному виду, в котором базисные столбцы будут первыми столбцами единичной матрицы.
Действительно, небазисные строки можно обратить в нулевые, вычитая из них подходящие линейные комбинации базисных. После этого можно превратить базисную подматрицу в единичную так, как это было сделано . (Элементарные преобразования производятся, конечно, над полными строками.)
Определение ранга матрицы и необходимые дополнительные понятия.
Прежде чем озвучить определение ранга матрицы, следует хорошо разобраться с понятием минора, а нахождение миноров матрицы подразумевает умение вычисления определителя. Так что рекомендуем при необходимости вспомнить теорию статьи методы нахождения определителя матрицы, свойства определителя.
Возьмем матрицу А порядка . Пусть k – некоторое натуральное число, не превосходящее наименьшего из чисел m и n, то есть, .
Определение.
Минором k-ого порядка матрицы А называется определитель квадратной матрицы порядка , составленной из элементов матрицы А, которые находятся в заранее выбранных k строках и k столбцах, причем расположение элементов матрицы А сохраняется.
Другими словами, если в матрице А вычеркнуть (p–k) строк и (n–k) столбцов, а из оставшихся элементов составить матрицу, сохраняя расположение элементов матрицы А, то определитель полученной матрицы есть минор порядка k матрицы А.
Разберемся с определением минора матрицы на примере.
Рассмотрим матрицу .
Запишем несколько миноров первого порядка этой матрицы. К примеру, если мы выберем третью строку и второй столбец матрицы А, то нашему выбору соответствует минор первого порядка . Иными словами, для получения этого минора мы вычеркнули первую и вторую строки, а также первый, третий и четвертый столбцы из матрицы А, а из оставшегося элемента составили определитель. Если же выбрать первую строку и третий столбец матрицы А, то мы получим минор .
Проиллюстрируем процедуру получения рассмотренных миноров первого порядка
и .
Таким образом, минорами первого порядка матрицы являются сами элементы матрицы.
Покажем несколько миноров второго порядка. Выбираем две строки и два столбца. К примеру, возьмем первую и вторую строки и третий и четвертый столбец. При таком выборе имеем минор второго порядка . Этот минор также можно было составить вычеркиванием из матрицы А третьей строки, первого и второго столбцов.
Другим минором второго порядка матрицы А является .
Проиллюстрируем построение этих миноров второго порядка и .
Аналогично могут быть найдены миноры третьего порядка матрицы А. Так как в матрице А всего три строки, то выбираем их все. Если к этим строкам выбрать три первых столбца, то получим минор третьего порядка
Он также может быть построен вычеркиванием последнего столбца матрицы А.
Другим минором третьего порядка является
получающийся вычеркиванием третьего столбца матрицы А.
Вот рисунок, показывающий построение этих миноров третьего порядка и .
Для данной матрицы А миноров порядка выше третьего не существует, так как .
Сколько же существует миноров k-ого порядка матрицы А порядка ?
Число миноров порядка k может быть вычислено как , где и — число сочетаний из p по k и из n по k соответственно.
Как же построить все миноры порядка k матрицы А порядка p на n?
Нам потребуется множество номеров строк матрицы и множество номеров столбцов . Записываем все сочетания из p элементов по k (они будут соответствовать выбираемым строкам матрицы А при построении минора порядка k). К каждому сочетанию номеров строк последовательно добавляем все сочетания из n элементов по k номеров столбцов. Эти наборы сочетаний номеров строк и номеров столбцов матрицы А помогут составить все миноры порядка k.
Разберем на примере.
Пример.
Найдите все миноры второго порядка матрицы .
Решение.
Так как порядок исходной матрицы равен 3 на 3, то всего миноров второго порядка будет  .
.
Запишем все сочетания из 3 по 2 номеров строк матрицы А: 1, 2; 1, 3 и 2, 3. Все сочетания из 3 по 2 номеров столбцов есть 1, 2; 1, 3 и 2, 3.
Возьмем первую и вторую строки матрицы А. Выбрав к этим строкам первый и второй столбцы, первый и третий столбцы, второй и третий столбцы, получим соответственно миноры
Для первой и третьей строк при аналогичном выборе столбцов имеем
Осталось ко второй и третьей строкам добавить первый и второй, первый и третий, второй и третий столбцы:
Итак, все девять миноров второго порядка матрицы А найдены.
Сейчас можно переходить к определению ранга матрицы.
Определение.
Ранг матрицы – это наивысший порядок минора матрицы, отличного от нуля.
Ранг матрицы А обозначают как Rank(A). Можно также встретить обозначения Rg(A) или Rang(A).
Из определений ранга матрицы и минора матрицы можно заключить, что ранг нулевой матрицы равен нулю, а ранг ненулевой матрицы не меньше единицы.
Формулы Крамера
Дана система трех
уравнений с тремя неизвестными
(1)
Основную роль
играют следующие четыре определителя:
,
,,.
Определитель Dназывается определителем системы (1).
ОпределителиDx,Dy,Dzполучаются из определителяDзаменой свободными членами элементов
соответственно первого, второго и
третьего столбцов.
Возможны следующие
случаи.
Случай 1 (D¹0).
В этом случае существует единственное
решение системы, и оно может быть найдено
по следующим формулам, которые называются
формулами Крамера.
Случай
2 (D=0).
В этом случае решение системы может не
существовать или система может иметь
бесконечное число решений. Например,
система
не
имеет решения, а система
имеет
бесконечное число решений.
Решение
систем линейных уравнений с помощью
обратной матрицы и метод Гаусса
рассмотреть самостоятельно.
Системы
линейных однородных уравнений
Пусть
дана система линейных однородных
уравнений
.
Однородная
система всегда совместна (),
она имеетнулевое
(тривиальное)
решение
.
Теорема
1. Для того,
чтобы система однородных уравнений
имела ненулевые решения, необходимо и
достаточно, чтобы ранг ее основной
матрицы был меньше числа неизвестных,
т.е.
.
Теорема
2. Для того,
чтобы однородная система n
линейных уравнений с n
неизвестными имела ненулевые решения,
необходимо и достаточно, чтобы ее
определитель был равен нулю.
Координаты
точки на прямой и плоскости. Деление
отрезка в данном отношении.
Аналитическая
геометрия изучает геометрические образы
алгебраическими методами. Аппаратом
аналитической геометрии является метод
координат, разработанный Декартом в
XVII веке. В основе метода координат лежит
понятие системы координат.
Две взаимно
перпендикулярные оси ОхиОу, имеющие общее начало
О и одинаковую масштабную единицу,
образуют прямоугольную систему координат.
ОсьОхназывается осью
абсцисс, осьОу– осью
ординат.
В
прямоугольной системе координат Охуточку М, имеющую координатых и у,
обозначаютМ(х; у), гдех– абсцисса
точки, ау– её ордината.
Пусть в прямоугольной
системе координат заданы точки М1(х1,
у1)иМ2(х2;у2).
Расстояние между ними определяется по
формуле:
(1)
Теорема. Для
любых трех точек А(х1;у1),В(х2;у2)
и С(х3;у3), не лежащих на одной
прямой, площадь S треугольника АВС
вычисляется по формуле
(2)
Пусть на плоскости
дан произвольный отрезок М1М2и пустьМ– любая точка этого отрезка,
отличная от точкиМ2(рис.1).
Координаты точки
М(х;у)делящей отрезок между точкамиМ1(х1;у1)иМ2(х2;у2)в заданном отношенииλ, определяются
по формулам:
(3)
При
λ=1получаем формулы для координат
середины отрезка:
(4)
у
М2(х2;у2)
М1(х1;у1)
М(х;у)
ρ М
О Р1Р Р2хOφ
рис.1
рис.2
В полярной системе
координат положение точки М на плоскости
определяется её расстоянием |ОМ|=ρот полюсаО(ρ–полярный
радиус-вектор точки) и угломφ,
образованным отрезкомОМс полярной
осьюОЕ(рис.2). Уголφсчитается
положительным при отсчете от полярной
оси против часовой стрелки.
Прямоугольные
координаты хиуточкиМи
её полярные координатыρиφсвязаны следующими формулами
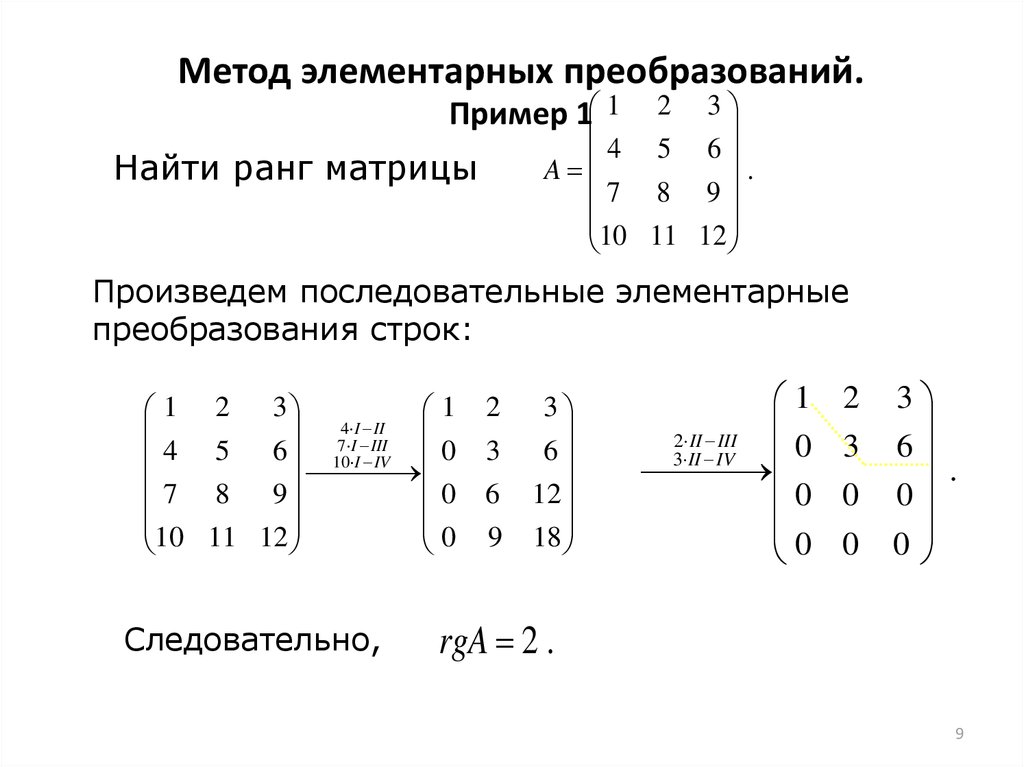
Определение ранга матрицы.
Определение
Пусть в матрице A существует линейно независимая система из r строк, и нет линейно независимой системы из большего числа строк. Тогда мы будем говорить, что строчный ранг матрицы A равен r. Нулевая матрица не содержит никакой линейно независимой системы строк, и ее строчный ранг по определению равен нулю.
Аналогично определяется столбцовый ранг матрицы. Он равен r_{1}, если есть линейно независимая система из r_{1} столбцов, и нет линейно независимой системы из большего числа столбцов. Столбцовый ранг нулевой матрицы по определению равен нулю.
Утверждение 1.
Система из r строк линейно независима тогда и только тогда, когда в этих строках найдется невырожденная подматрица порядка r.
1^{\circ}. Пусть r строк линейно зависимы. Рассмотрим произвольную подматрицу порядка r, расположенную в этих строках. Если строки линейно зависимы, то также линейно зависимы (с теми же коэффициентами) и отрезки этих строк, составляющие подматрицу, и подматрица является вырожденной.
2^{\circ}. Обратное утверждение докажем по индукции. Одна строка линейно независима, если она не нулевая. В этом случае она содержит ненулевой элемент, составляющий невырожденную подматрицу порядка 1.
Пусть теперь даны r линейно независимых строк. Первые r-1 из них также линейно независимы, и по предположению индукции содержат невырожденную подматрицу порядка r-1. Пусть j_{1},…, j_{r-1} — номера столбцов этой подматрицы. Рассмотрим отрезок r-й строки, расположенный под подматрицей, то есть составленный из элементов с номерами j_{1},…, j_{r-1}. По следствию из этот отрезок раскладывается в линейную комбинацию строк подматрицы. Коэффициенты этой линейной комбинации обозначим \alpha_{1},…, \alpha_{r-1}.
Теперь будем рассматривать полные строки. Вычтем из последней строки линейную комбинацию предыдущих с теми же коэффициентами \alpha_{1},…, \alpha_{r-1}. Это обратит в нуль j_{1},…, j_{r-1}-й элементы r-й строки, но не всю строку, так как строки линейно независимы. Таким образом, в преобразованной r-й строке есть ненулевой элемент a_{j}^{r}, и его номер j отличен от номеров j_{1},…, j_{r-1}.
В преобразованной матрице рассмотрим столбцы, имеющие номера j_{1},…, j_{r-1}, j. (Мы для удобства пишем j на последнем месте, хотя в действительности столбцы располагаются в порядке возрастания номеров.) Легко видеть, что эти столбцы линейно независимы. Действительно, пусть \tag{1} \alpha_{1}\boldsymbol{a}_{j_{1}}+…+\alpha_{r-1}\boldsymbol{a}_{j_{r-1}}+\alpha \boldsymbol{a}_{j}=\boldsymbol{o} их нулевая линейная комбинация. Тогда для последних элементов столбцов \alpha_{1}0+…+\alpha_{r-1}0+\alpha a_{j}^{r}=0. Так как a_{j}^{r} \neq 0, отсюда следует \alpha=0, и мы получаем \alpha_{1}\boldsymbol{a}_{j_{1}}+…+\alpha_{r-1}\boldsymbol{a}_{j_{r-1}}=\boldsymbol{o}. Если бы среди коэффициентов этой линейной комбинации были отличные от нуля, то столбцы с номерами j_{1},…, j_{r-1} были бы линейно зависимы. Это противоречило бы тому, что исходная подматрица порядка n-1 невырождена. Таким образом, все коэффициенты в равны нулю, и столбцы с номерами j_{1},…, j_{r-1}, j линейно независимы. Отсюда следует, что составленная ими подматрица порядка r невырождена.
Невырождена соответствующая подматрица и в непреобразованной матрице, так как элементарными преобразованиями мы превратили ее в невырожденную матрицу. Это заканчивает доказательство.
Определение
В матрице A размеров m \times n подматрица порядка r называется базисной, если она невырождена, а все квадратные подматрицы большего порядка, если они существуют, вырождены.
Столбцы и строки матрицы A, на пересечении которых стоит базисная подматрица, называются базисными столбцами и строками A.
В силу утверждения 1 базисные столбцы и строки линейно независимы.
Определение
Рангом матрицы называется порядок базисной подматрицы или, иначе, самый большой порядок, для которого существуют невырожденные подматрицы. Ранг нулевой матрицы по определению считают нулем.
Отметим два очевидных свойства ранга.
Свойство 1
\bullet Ранг матрицы не меняется при транспонировании, так как при транспонировании матрицы все ее подматрицы транспонируются, и при этом невырожденные подматрицы остаются невырожденными, а вырожденные — вырожденными.
Свойство 2
\bullet Если A’ — подматрица матрицы A, то ранг A’ не превосходит ранга A, так как любая невырожденная подматрица, входящая в A’, входит и в A.
Ранг линейного отображения
рассматривается
☞
.
☞
ЗДЕСЬ.
Источники
. Бохер М. Введение в высшую алгебру. М.-Л. ГТТИ, 1933
. Kronecker L. Bemerkungen zur Determinanten-Theorie. J. reine angew. Math. Bd. 72, 1870, S. 152-175
Для упрощения геометрических интерпретаций мы всегда — если только не обговорено иное — ищем только вещественные решения.
Строгое определение слова система нигде в литературе я не нашел — как-то стыдливо это понятие обходится. Можно понимать его как множество — с теми только поправками, что в системе, в отличие от множества, допускается повторение объектов, и они, как правило, пронумерованы.
Основные теоремы.
Из утверждения 1 прямо следует теорема о ранге матрицы:
Теорема 1.
Ранг любой матрицы равен ее строчному рангу и ее столбцовому рангу.
Действительно, если строчный ранг A равен r, то в A найдется линейно независимая система из r строк, а значит, и невырожденная подматрица порядка r. Если при этом есть p > r различных строк A, то они линейно зависимы, и любая подматрица порядка p в них вырождена. Столбцовый ранг равен строчному рангу A^{T}, значит, и рангу A^{T}, а потому — рангу A.
Таким образом, мы видим, что все три определения на самом деле определяют одно и то же число, и впредь не будем их различать. Будем говорить ранг матрицы и обозначать его \mathbf{Rg}\,A.
Из теоремы о ранге матрицы мы получаем теорему о базисном миноре, на которую существенно опирается все дальнейшее изложение. Слово “минор” означает “детерминант подматрицы”. В частности, базисный минор — это детерминант базисной подматрицы. О детерминантах будет речь в следующем параграфе, а здесь это слово можно воспринимать просто как составную часть названия теоремы.
Теорема 2.
Каждый столбец матрицы раскладывается в линейную комбинацию ее базисных столбцов.
Каждый из базисных столбцов, разумеется, раскладывается по базисным: для этого достаточно взять его самого с коэффициентом 1, а остальные с нулевыми коэффициентами.
Пусть теперь \boldsymbol{a}_{j} — не базисный столбец. Базисные столбцы обозначим через \boldsymbol{a}_{i_{1}},…, \boldsymbol{a}_{i_{r}}. По теореме о ранге матрицы любые r+1 столбцов линейно зависимы, и найдутся такие коэффициенты, что \alpha_{1}\boldsymbol{a}_{i_{1}}+…+\alpha_{r}\boldsymbol{a}_{i_{r}}+\alpha \boldsymbol{a}_{j}=\boldsymbol{o}. При этом мы можем быть уверены, что \alpha \neq 0, так как иначе это равенство означало бы линейную зависимость базисных столбцов. Деля на \alpha, мы получаем нужное нам разложение \boldsymbol{a}_{j}=-\alpha^{-1}\alpha_{1}\boldsymbol{a}_{i_{1}}-…-\alpha^{-1}\alpha_{r}\boldsymbol{a}_{i_{r}}.
Следствие.
Каждая строка матрицы раскладывается по ее базисным строкам.
Матричный метод решения систем линейных уравнений.
Матричный
метод применим к решению систем уравнений,
где число уравнений равно числу
неизвестных. Метод удобен для решения
систем невысокого порядка. Метод
основан на применении свойств умножения
матриц. Пусть дана система уравнений:
Составим
матрицы: A
= ; B
= ; X
= .
Систему уравнений можно записать: AX
= B.
Сделаем следующее преобразование:
A-1AX
= A-1B,
т.к. А-1А
= Е, то ЕХ
= А-1В
Х = А-1В
Для применения данного метода
необходимо находить обратную матрицу,
что может быть связано с вычислительными
трудностями при решении систем высокого
порядка.
Пример.
Решить систему уравнений: Х
= ,
B
= ,
A
= Найдем
обратную матрицу А-1.
= det
A
= 5(4-9)
+ 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30. M11
= =
-5; M21
= =
1; M31
= =
-1; M12
= M22
= M32
= M13
= M23
= M33
= A-1
= ;
Cделаем
проверку: AA-1
=  =E.
=E.
Находим матрицу Х. Х = =
А-1В
= =
.
Метод
Крамера. (Габриель
Крамер (1704-1752) швейцарский математик)
Данный метод также применим только в
случае систем линейных уравнений, где
число переменных совпадает с числом
уравнений. Кроме того, необходимо ввести
ограничения на коэффициенты системы.
Необходимо, чтобы все уравнения были
линейно независимы, т.е. ни одно уравнение
не являлось бы линейной комбинацией
остальных. Для этого необходимо, чтобы
определитель матрицы системы не равнялся
0. det
A
0; Действительно, если какое- либо
уравнение системы есть линейная
комбинация остальных, то если к элементам
какой- либо строки прибавить элементы
другой, умноженные на какое- либо число,
с помощью линейных преобразований можно
получить нулевую строку. Определитель
в этом случае будет равен нулю.
Теорема.
(Правило Крамера):
Теорема.
Система из n
уравнений с n
неизвестными в
случае, если определитель матрицы
системы не равен нулю, имеет единственное
решение и это решение находится по
формулам: xi
= i,
где
= detA,
а i
– определитель матрицы, получаемой из
матрицы системы заменой столбца i
столбцом свободных членов bi.
i
=
Пример.
A
= ; 1=
; 2=
; 3=
;
x1
= 1/detA;
x2
= 2/detA; x3
= 3/detA;
Пример. Найти
решение системы уравнений:
=
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30; 1
= =
(28 – 48) – (42 – 32) = -20 – 10 = -30. x1
= 1/
= 1; 2
= =
5(28 – 48) – (16 – 56) = -100 + 40 = -60. x2
= 2/
= 2; 3
= =
5( 32 – 42) + (16 – 56) = -50 – 40 = -90. x3
= 3/
= 3. Как видно, результат совпадает с
результатом, полученным выше матричным
методом. Если система однородна,
т.е. bi
= 0, то при 0
система имеет единственное нулевое
решение x1
= x2
= … = xn
= 0. При
= 0 система имеет бесконечное множество
решений. Для самостоятельного
решения: ; Ответ:
x
= 0; y
= 0; z
= -2.
Метод
Гаусса. (Карл Фридрих
Гаусс (1777-1855) немецкий математик) В
отличие от матричного метода и метода
Крамера, метод Гаусса может быть применен
к системам линейных уравнений с
произвольным числом уравнений и
неизвестных. Суть метода заключается
в последовательном исключении неизвестных.
Рассмотрим систему линейных уравнений:
Разделим
обе части 1–го уравнения на a11
0, затем: 1) умножим на а21
и вычтем из второго уравнения 2) умножим
на а31
и вычтем из третьего уравнения и
т.д. Получим: , где
d1j
= a1ja11,j
= 2, 3, …, n+1.
dij= aij
– ai1d1ji
= 2, 3, … , n; j
= 2, 3, … , n+1.
Далее
повторяем эти же действия для второго
уравнения системы, потом – для третьего
и т.д.
Пример.
Решить систему линейных уравнений
методом Гаусса. Составим
расширенную матрицу системы. А* = 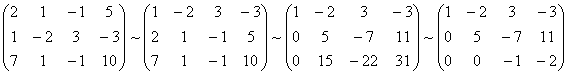 Таким
Таким
образом, исходная система может быть
представлена в виде: ,
откуда получаем: x3
= 2; x2
= 5; x1
= 1.
Пример.
Решить систему методом Гаусса. Составим
расширенную матрицу системы.  Таким
Таким
образом, исходная система может быть
представлена в виде: ,
откуда получаем: z
= 3; y
= 2; x
= 1. Полученный ответ совпадает с
ответом, полученным для данной системы
методом Крамера и матричным методом.
Для самостоятельного решения: Ответ:
{1, 2, 3, 4}.
Предел
функции при стремлении аргумента к
бесконечности.
Определение.
Число А называется пределом
функции f(x)
при х,
если для любого числа >0
существует такое число М>0, что для
всех х, х>M
выполняется неравенство
При
этом предполагается, что функция f(x)
определена в окрестности бесконечности.
Записывают:
Графически можно представить:
|
|
Аналогично можно определить пределы
для
любого х>M
и
для
любого х<M.











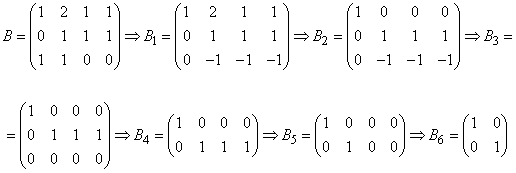


![Algebra2:rank [vf]](https://rusinfo.info/wp-content/uploads/5/f/e/5fe9e773f7800a01cd94b1ea0a3bcba6.gif)