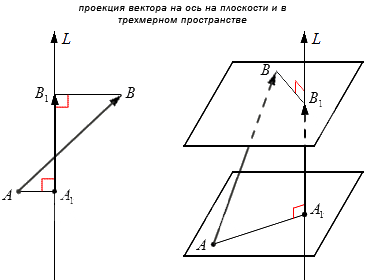
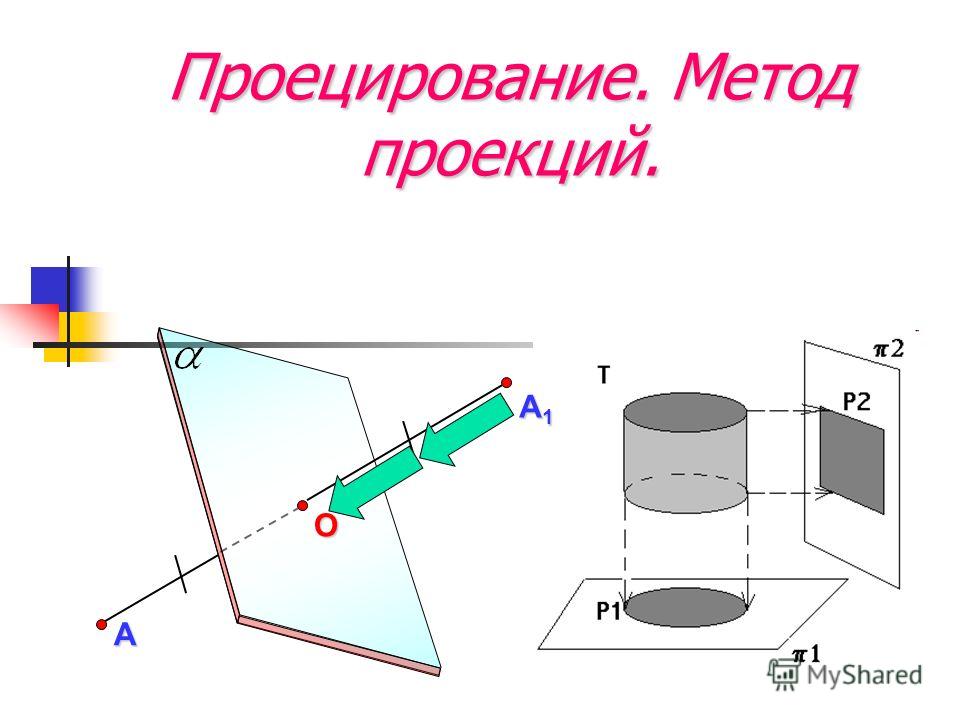
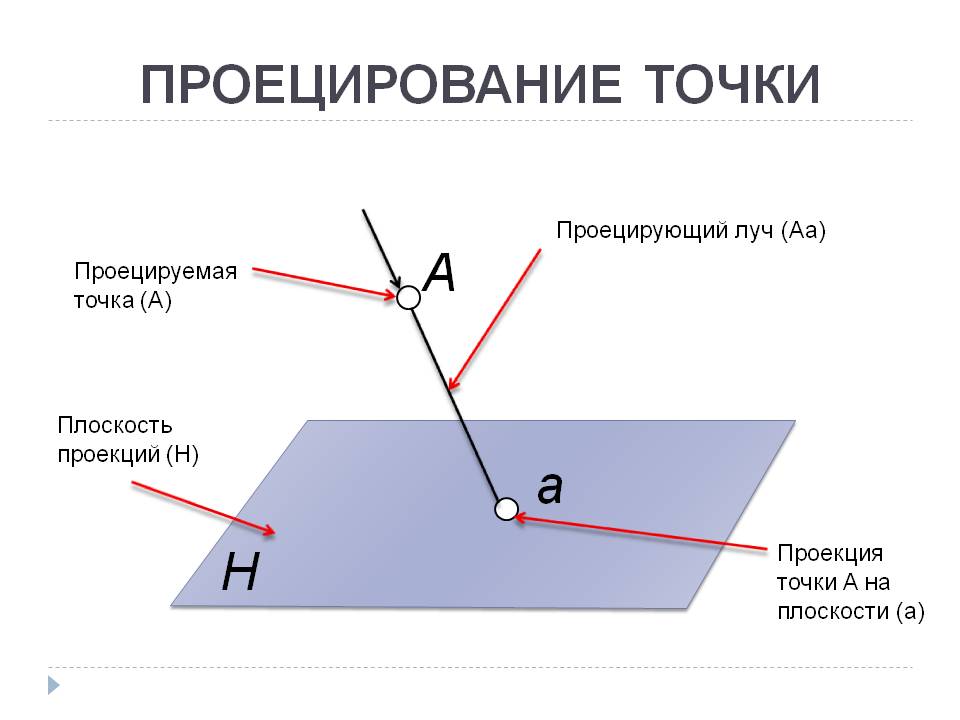
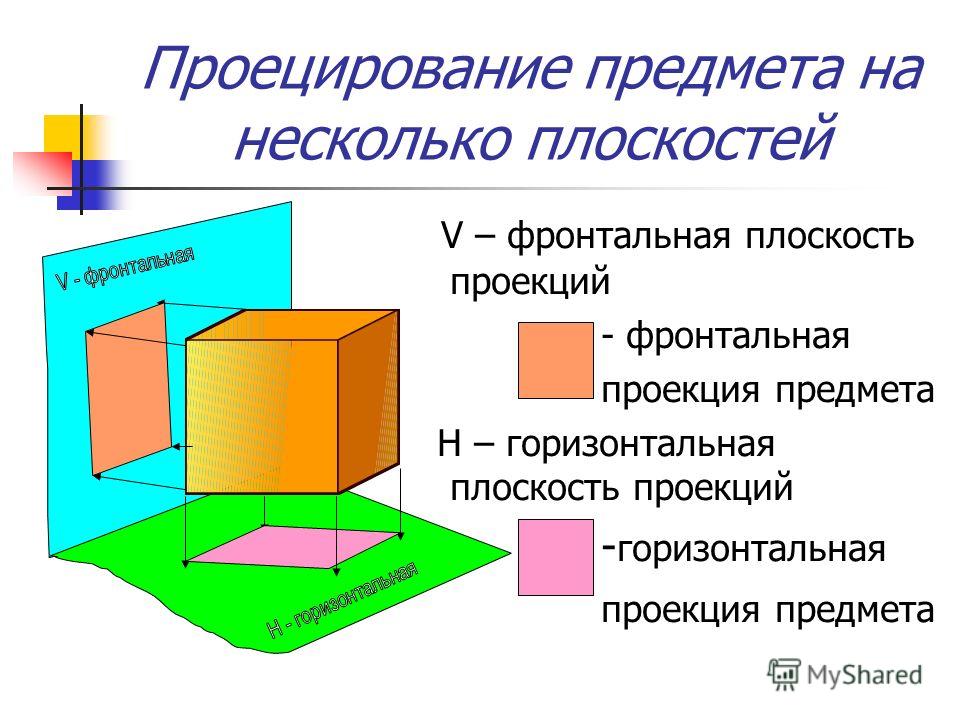
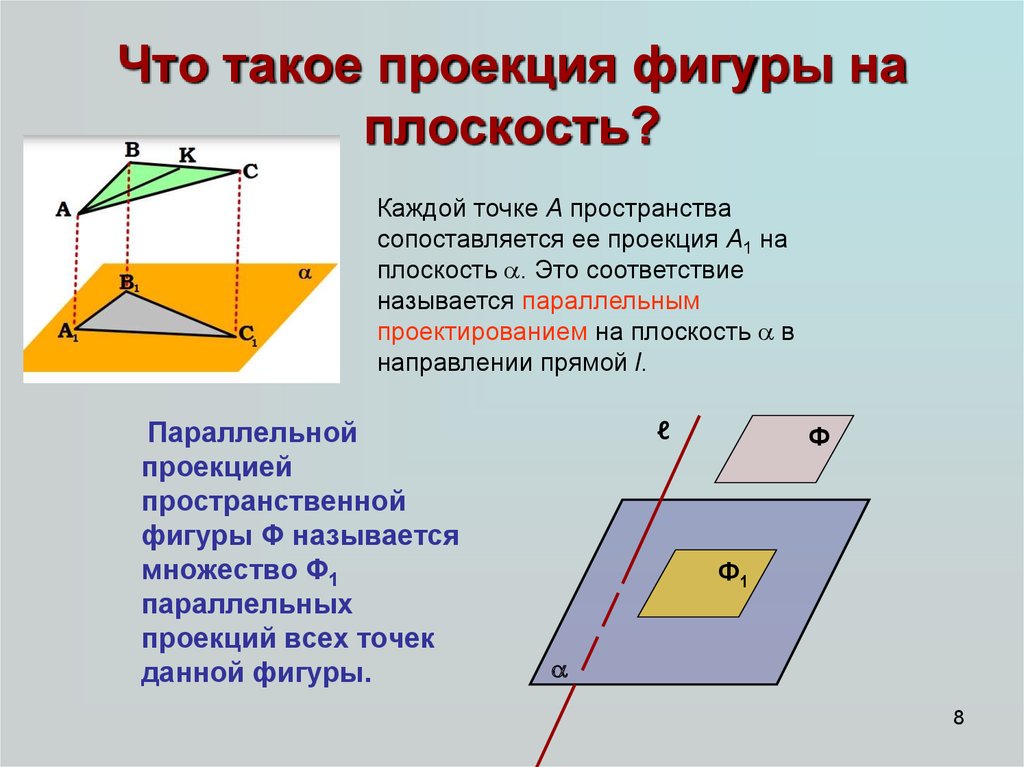
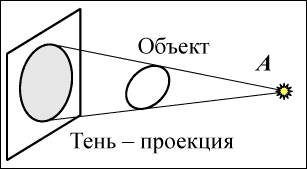
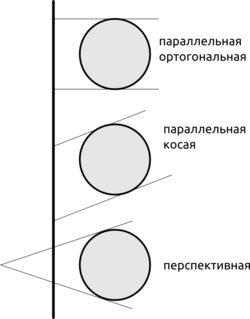
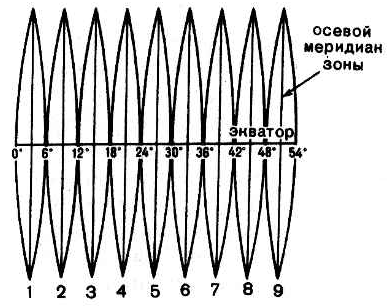
Проекция что это? значение слова проекция

Понятие проекции

Итак, есть несколько основных значений этого термина. В классическом психоанализе, наследии Фрейда, проекции – это защитный механизм, который свидетельствует о наличии в психике человека некоего конфликта, находящегося в подавленном состоянии. В ходе работы этого механизма человек приписывает свои эмоции, чувства и мысли другим. При этом он отрицает тот факт, что на самом деле это его собственные ощущения. Так, перед важным докладом человек может волноваться и думать про аудиторию «Я неприятен им», хотя на самом деле люди не испытывают к докладчику негативных эмоций. Он сам перекладывает свои неприятные ощущения на них. Таким образом, человек воспринимает собственные эмоции и мысли как нечто, приходящее к нему извне, к чему он отношения не имеет и повлиять на это не может.

Соответственно, в понимании психоаналитиков такое проецирование различных проявлений своей психики на других является одним из показателей невроза (причиной невроза, в свою очередь, являются внутренние конфликты между сознательной и бессознательной составляющими психики).

С другой стороны, в некоторых психологических теориях проекция – это естественный механизм, присущий человеческой психике изначально. Таким образом, проекцию рассматривают не только как проявление невроза, но и как нормальный процесс.

Как формируется проекция?

Проекция относится к одному из механизмов психологической защиты. Это понятие возникло в рамках психоанализа, и ввел его основоположник этого учения Зигмунд Фрейд в 1894 году. Он считал, что личность прибегает к психологическим защитам для того, чтобы справиться с различными болезненными переживаниями. Они помогают сохранить психическое здоровье и целостность личности путем искажения реальности. Одним из таких механизмов является интроекция – когда личность присваивает нечто внешнее как нечто внутреннее. Проекция же является ее противоположностью: в этом случае нечто внутреннее приписывается внешней среде.

По мнению Зигмунда Фрейда, принцип формирования проекций примерно следующий. Если в нас есть какое-то качество (например, агрессивность), которое с детства нам запрещают проявлять, то мы его вытесняем, но отчетливо видим эту черту в окружающих. И для этого другим людям вовсе не обязательно обладать этим качеством в действительности. Считается, что около 80% того, что мы думаем о других людях,– наши собственные проекции, и не более того.

Так, например, скованной сексуальными запретами женщине кажется, что к ней все пристают, а мужчина, вожделеющий других женщин, яростно ревнует свою жену, у которой нет и мысли об измене.

Психика не может распознавать в других людях и событиях то, что не содержится в ней самой. Чем ярче, чаще и эмоциональнее мы реагируем на то или иное качество в других, тем больше соответствующих тенденций содержится в нашем уме. Мы просто получаем безошибочное указание на свою собственную «специализацию».

Что такое проекция

Знаете, как работает проектор? Он переносит изображение с фотопленки на экран. Также и человек нередко переносит, проецирует свои чувства, мысли, желания на других. Чаще всего это неприятные мысли и желания. Стыд и чувство вины – тяжелые переживания, и человек стремится избавиться от них, чтобы не травмировать свою психику. Причем не просто выносит свои грехи и темные помыслы из своего сознания, а наделяет ими других людей. Так ему проще – не нужно обвинять себя, ведь другие ничем не лучше, а даже и хуже.

Так, наиболее ревнивыми всегда бывают мужья, которые сами не прочь изменить жене. Но раз у них подобные мысли и желания возникают, то у женщины они тоже должны быть? И в этом есть своя, хоть и извращенная, логика. А жена, обвиняющая мужа в лишних тратах на «его прихоти и игрушки», сама не слишком экономна. Ей же так хочется эти туфли или блузку, но муж нисколько ее не лучше. А осуждая своих соседей или коллег, мы вспоминаем прежде всего те неприятные качества, которые присущи нам самим.

Вы скажете: это плохо, и я так никогда не делаю. Нет, не тешьте себя иллюзиями, все так делают, и вы тоже.

Как это работает

Защитный механизм проекции присущ всем людям и формируется в самом раннем детстве. Он рождается из запретов, которые диктует нам социум. В процессе воспитания складываются и закрепляются в сознании представления о плохом и хорошем, о дозволенном и недопустимом. Ребенок очень рано начинает понимать, что проявлять агрессию, обижать слабых, оскорблять других людей, отбирать игрушки – это плохо. Чем старше становится человек, тем больше запретов диктует ему общество. Они создают условия для негативных переживаний, ведь даже желать запретное – это плохо, недопустимо. И человек стремится защититься от этих неприятных эмоций, выйти из внутреннего конфликта между желаемым и допустимым. Вот и возникает известная всем реакция: «Ты сам(а), виноват(а)!»

Проекция – один из древнейших видов психологической защиты, и механизм ее прост. Он всегда работает по следующей схеме:

Индивид ощущает дискомфорт, стыд, раздражение, причиной которых являются запретные желания и его неправильное, с точки зрения социальных норм, поведение.
Стремясь избавиться от негативных эмоций, человек выносит неприемлемые желания и побуждения за пределы своего сознания.
Приписывает эти побуждения другим людям, чтобы не было самому так стыдно, ведь «все такие, все так делают».

Поэтому «старые девы», озабоченные своими «неправильными» мыслями и желаниями, так энергично борются с «развратом» молодежи. А пьяница в моменты трезвости с гневом клеймит позором соседа-алкоголика.

Механизм проекции подливает масло и в огонь межнациональных конфликтов, потому что чаще всего представители одной нации обвиняют своих врагов в грехах, присущих им самим. И чем больше этих грехов, тем агрессивнее становятся люди. Чаще всего мы обвиняем тех, кого сами же обидели. Почему? Чтобы не было стыдно и чтобы не чувствовать себя виноватыми.

Громче всех обвиняют чиновников в воровстве те люди, которые и сами бы не прочь погреть руки, но этой возможности не имеют. И отвергая собственные желания, эти обличители проецируют их на тех, у кого такая возможность есть.

Проекция и эмпатия

Проекция связана не только с постыдными мыслями и асоциальными желаниями

Процесс переноса эмоциональных состояний лежит в основе такого важного социально-психологического явления, как эмпатия. Под эмпатией в психологии понимается способность человека переживать те же чувства, что и его партнер

Это сострадание, сочувствие, которое основано на личном эмоциональном опыте. Именно этот опыт индивид и переносит на других людей, представляя, что они должны чувствовать в знакомой ему ситуации. Поэтому страдания или радость другого может понять только тот, кто сам страдал и радовался.

Без способности проецировать свой эмоциональный опыт невозможно взаимопонимание. Хотя не всегда проекция отражает объективное состояние дел. Мы можем сопереживать человеку, думать, как ему плохо, ведь в схожей ситуации нам было очень тяжело. Но это не значит, что тот человек действительно страдает. Люди-то разные, и обстоятельства, в которых они оказываются, тоже разные. Но чем более эмоционально близки индивиды, тем более точно они понимают состояние друг друга.

Определение слова «Проекция» по БСЭ:

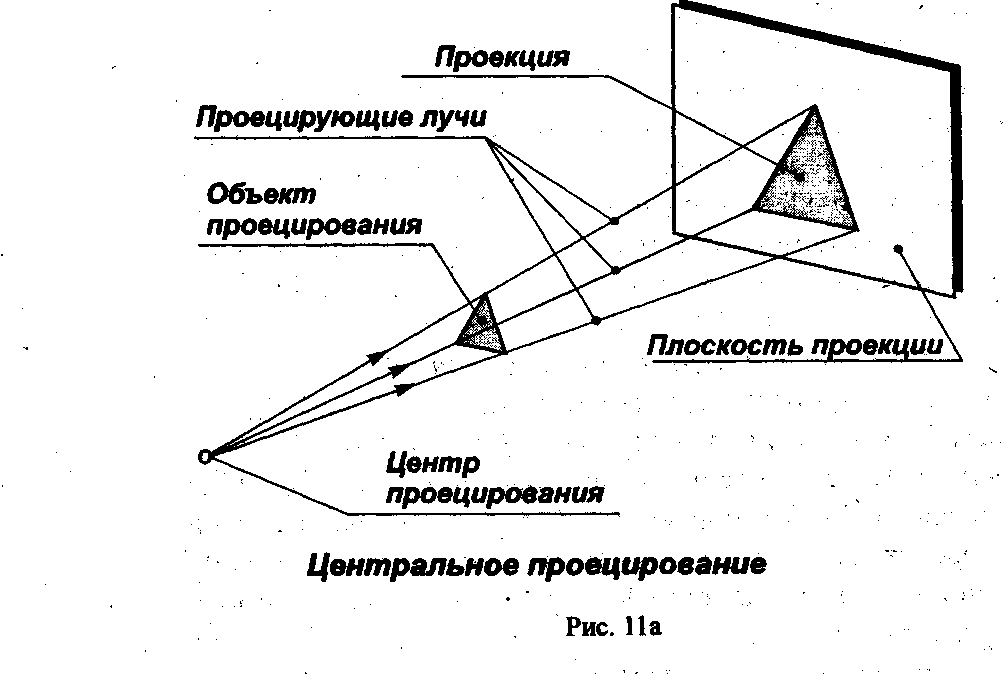
Проекция — Проекция (от лат. projectio — бросание вперёд, выбрасывание)геометрический термин, связанный с операцией проектирования (проецирования), которую можно определить следующим образом (см. рис. 1): выбирают произвольную точку S пространства в качестве центра проектирования и плоскость П, не проходящую через точку S, в качестве плоскости проекций (картинной плоскости). Чтобы спроектировать точку A (прообраз) пространства на плоскость П, через центр проекций S(«глаз») проводят прямую SA до её пересечения в точке А с плоскостью П. Точку А (образ) и называется проекцией точки A. Проекцией фигуры F называется совокупность П. всех её точек. Прямая линия, не проходящая через центр П., проектируется в виде прямой. Описанная П. носит название центральной или конической. Она существенно зависит от выбора центра проекций S. При проектировании точек данной плоскости П на плоскость П (см. рис. 2) встречаются следующие затруднения. На плоскости П имеются такие точки, для которых не существует образов на плоскости П. Такова, например, точка В, если проектирующая прямая SB параллельна плоскости П. Для устранения этого затруднения, происходящего от свойств евклидова пространства, последнее пополняют бесконечно удалёнными элементами (несобственными элементами).Именно, принимают, что параллельные прямые BS и РА пересекаются в бесконечно удалённой точке B. тогда её можно считать образом точки В на плоскости П. Аналогично бесконечно удалённая точка C является прообразом точки C (см. рис. 2). Благодаря введению бесконечно удалённых элементов, между точками плоскости П и точками плоскости П устанавливается взаимно однозначное соответствие, осуществляемое при помощи центральной П. Такое соответствие носит название перспективной коллинеации.Большое практическое значение имеет вид проектирования, при котором центром П. является бесконечно удалённая точка пространства S_&infin. (см. рис. 3). При этом все проектирующие прямые параллельны и П. называется параллельной или цилиндрической. Взаимно однозначное соответствие между точками плоскостей П и П, установленное при помощи параллельного проектирования, называется перспективно-аффинным или родственным (см. Аффинные преобразования).В черчении широко применяется частный вид параллельного проектирования, когда плоскость П. расположена перпендикулярно (ортогонально) к направлению проектирования. П. в этом случае называется прямоугольной или ортогональной.Центральные и параллельные (в частности, ортогональные) П. широко используют в начертательной геометрии, причём получаются различные виды изображений (перспективные, аксонометрические и др.). Специальные виды проектирования на плоскость, сферу и др. поверхности применяются в географии, астрономии, кристаллографии, топографии и т.д. Таковы Картографические проекции, гномонические проекции, стереографические проекции и др. Об ортогональной проекции направленных отрезков (векторов) см. в ст. Векторное исчисление.Н. Ф. Четверухин.Рис. 1.Рис. 2.Рис. 3.

Проекция — в психологии, восприятие собственных психических процессов как свойств внешнего объекта в результате бессознательного перенесения на него своих внутренних импульсов и чувств. П. играет большую роль в процессе формирования психики в раннем детском возрасте, когда отсутствует чёткая дифференциация между«Я» и внешним миром, и лежит в основе архаичных, антропоморфных представлений о мире, характеризующих ранние стадии развития человеческого сознания (см. Анимизм, Антропоморфизм). С патологическими формами П. связано возникновение ряда психических заболеваний (Паранойя, фобия, Мания), когда резко искажается восприятие внешнего мира при сохранении иллюзии контроля над собственным поведением. Механизм П. используется в диагностических целях в т. н. проективных Тестах (тест Роршаха и др.) для выявления скрытых мотиваций и побуждений.

Проекция из произвольного пространства на его подпространство

Проекция в этом смысле (упомянутая во введении в пункте 2) — широко применяется в линейной алгебре (подробнее, см.: Проекция (линейная алгебра)), но на практике не только в достаточно абстрактных контекстах, но и при работе с векторами любой природы, размерности и степени абстракции, и даже в элементарной геометрии, а также — очень широко — при использовании прямолинейных координат (как прямоугольных или аффинных).

Отдельно следует упомянуть проекцию точки на прямую и проекцию вектора на прямую (на направление).

Ортогональная проекция на прямую и на направление

Чаще всего используется ортогональная проекция.

Ортогональная проекция P{\displaystyle P} точек u,v,w,x{\displaystyle u,v,w,x} на прямую m{\displaystyle m}

Термин проекция в этом смысле употребляется и в отношении самой операции проецирования, и в отношении её результата (при операции проецирования на прямую образы точки, вектора, множества точек называются проекцией точки, вектора, множества точек на эту прямую).

Элементарное описание ортогональной проекции точки на прямую сводится к тому, что из точки на прямую следует опустить перпендикуляр, и его пересечение с прямой даст образ точки (проекцию точки на эту прямую). Это определение работает и на плоскости, и в трёхмерном пространстве, и в пространстве любой размерности.

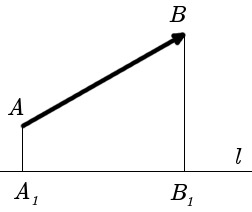
Элементарное определение проекции вектора на прямую легче всего дать, представив вектор направленным отрезком. Тогда на прямую можно спроецировать его начало и его конец, и направленный отрезок от проекции начала к проекции конца исходного вектора даст его проекцию на прямую.

Проекцией вектора на некоторое направление обычно называют число, совпадающее по абсолютной величине с длиной проекции этого вектора на прямую, определяющую это направление; знак же числа выбирается так, что оно считается положительным, когда направление этой проекции совпадает с данным направлением, и отрицательным, когда направление противоположно.

Последнее определение очень просто заменить на эквивалентное с использованием скалярного произведения: если направление задаётся единичным вектором e, то проекция любого вектора a на это направление равно скалярному произведению a•e.
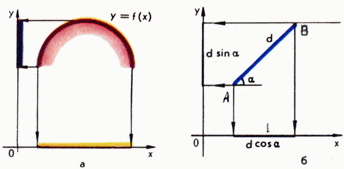
Это же можно переписать |a|cos α{\displaystyle |\mathbf {a} |\mathrm {cos} \ \alpha }, где |a|{\displaystyle |\mathbf {a} |} — длина вектора a{\displaystyle \mathbf {a} }, α{\displaystyle \alpha } — угол между вектором a{\displaystyle \mathbf {a} } и направлением, на которое ищется проекция.

Неортогональная проекция на прямую и на направление

Неортогональная проекция используется реже, к тому же даже при использовании, особенно в элементарных контекстах, этот термин не всегда используется.

Преобразование T является косоугольной проекцией вдоль k на прямую m. U=m и V=k

Проще всего неортогональную проекцию на прямую можно задать, задав саму эту прямую и плоскость (в двумерном случае — вместо плоскости другую прямую, в случае n-мерного пространства — гиперплоскость размерности (n-1)), пересекающую прямую. Проекция точки определяется как пересечение плоскости (гиперплоскости), содержащей эту точку и параллельную плоскости, задающей проекцию.

В случае, когда плоскость (гиперплоскость), задающая проекцию, ортогональна прямой, мы получаем ортогональную проекцию (это может быть её альтернативным определением). Поэтому собственно для неортогональной проекции надо потребовать, чтобы эта ортогональность отсутствовала.

Для неортогональной проекции вектора на прямую и на направление определения получаются, исходя из приведённого определения проекции точки, прямо аналогично тому, как это было описано в параграфе об ортогональной проекции.

Надо, правда, иметь в виду, что по умолчанию под проекцией вектора на прямую или на направление понимается всё же ортогональная проекция.

Тем не менее понятие неортогонального проецирования может быть полезным (по крайней мере, если не бояться терминологической путаницы) для введения косоугольных координат и работы с ними (через них может быть в принципе довольно легко определено понятие координат точки и координат вектора в этом случае).

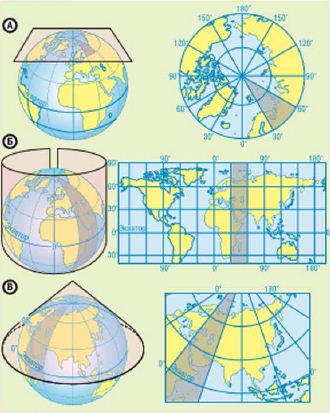
Классификация географических проекций по геометрической фигуре, являющейся вспомогательной поверхностью

На плоскость эллипсоид проектируют при помощи геометрических фигур, а поверхности, на которые он проектируется, могут быть секущими (разрезающей) фигуру или касательными (соприкасается, но не разрезает глобус) к ней. При этом на полученной карте касательные и секущие линии (стандартные) представлены неискажёнными.

Проекции также бывают по-разному ориентированы.

Нормальными называют проекции, в которых оси вспомогательной поверхности совмещаются с осью земного эллипсоида или шара, а спроектированная поверхность размещается касательно к полюсу.
Поперечными – ось располагают под прямым углом к оси Земли.
Наклонными – под любым другим (непрямым) углом к оси Земли.

Поверхности, которые могут быть развёрнуты на плоскость или лист без растяжений, разрыва или усадки, называются разрабатываемыми поверхностями. Ими являются цилиндр, конус и плоскость. Поэтому по вспомогательной поверхности проекции делятся на:

цилиндрические – вспомогательная поверхность – боковая цилиндра, касательная к эллипсоиду или секущая эллипсоида. Меридианы изображаются равностоящими параллельными прямыми, а параллели – прямыми, перпендикулярными меридианам. Пример – нормальная равноугольная цилиндрическая проекция Меркатора.

Псевдоцилиндрическая проекция

конические – боковая поверхность секущей или касательной конуса. Конической называется любая проекция, в которой меридианы представлены прямыми линиями, выходящими из одного центра и равноудаляющимися к периферии, а параллели – дуги, центрированные на вершине. При построении картографы чаще выбирают 2 основные параллели, которые могут быть секущими или касательными. Искажения масштаба и формы на них низкие. К северу и югу от стандартных параллелей расстояния растягиваются, а между стандартными параллелями расстояния сжимаются. Может использоваться и одна стандартная параллель, тогда с удалением от неё расстояния растягиваются. Применяется для территорий, вытянутых вдоль параллелей, например, все карты России построены в конических проекциях.
псевдоконические – проекции, где центральный меридиан – прямая, остальные меридианы кривые линии, а параллели – прямые, промежутки между которыми уменьшаются к полюсам.
азимутальные – вспомогательной поверхностью служит секущая или касательная плоскость. Параллели на них – полные окружности. Меридианы – их радиусы. По меридианам такая проекция является равнопромежуточной и сохраняет вдоль них главный масштаб. Именно разновидностью азимутальной проекции является первая известная на Земле гномическая проекция.

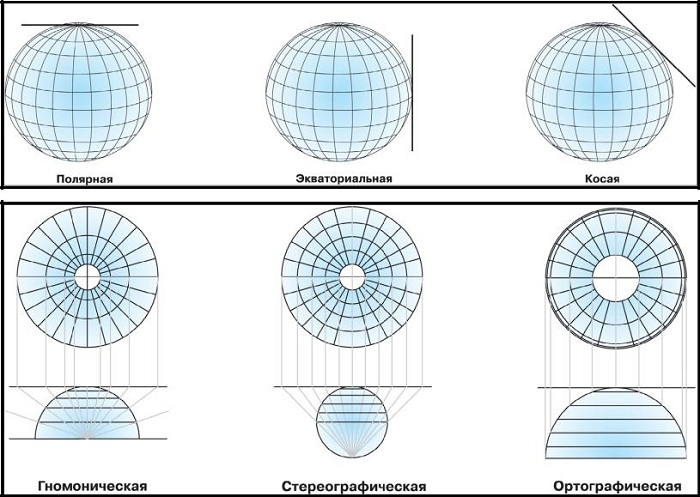Типы азимутальных проекций

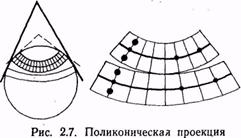
поликонические – боковые вспомогательные поверхности нескольких касательных конусов, каждая из которых затем разворачивается на плоскость. Экватор и средний меридиан – перпендикулярные прямые, параллели – дуги, выпуклостью направленные к экватору, меридианы – кривые малой кривизны, направленные выпуклой стороной от центрального меридиана.
условные – те, что ни входят ни в один из выше перечисленных классов. Параллели и меридианы на них являются кривыми очень разного вида.

Полное название проекций может быть следующим: косая азимутальная равновеликая, нормальная равноугольная цилиндрическая, произвольная поликоническая и т.д.

Проекция из произвольного пространства на его подпространство

Отдельно следует упомянуть проекцию точки на прямую и проекцию вектора на прямую (на направление).

Ортогональная проекция на прямую и на направление

Чаще всего используется ортогональная проекция.

Ортогональная проекция P{\displaystyle P} точек u,v,w,x{\displaystyle u,v,w,x} на прямую m{\displaystyle m}

Последнее определение очень просто заменить на эквивалентное с использованием скалярного произведения: если направление задаётся единичным вектором e, то проекция любого вектора a на это направление равно скалярному произведению a•e.
Это же можно переписать |a|cos α{\displaystyle |\mathbf {a} |\mathrm {cos} \ \alpha }, где |a|{\displaystyle |\mathbf {a} |} — длина вектора a{\displaystyle \mathbf {a} }, α{\displaystyle \alpha } — угол между вектором a{\displaystyle \mathbf {a} } и направлением, на которое ищется проекция.

Неортогональная проекция на прямую и на направление

Преобразование T является косоугольной проекцией вдоль k на прямую m. U=m и V=k

Как связаны проекция и эмпатия

Стоит отметить, что в психологии проекция – это не всегда негативные эмоции. Часто она идет рука об руку с эмпатией. По определению это способность человека сопереживать, сочувствовать, испытывать те же чувства, ощущения, что и собеседник. Это сострадание, которое всегда связано с личным опытом. Человек понимает, как чувствует себя его оппонент в той или иной ситуации, потому что сам пережил похожую. Не зря говорят, что понять человека можно, пройдя путь в его обуви.

Без проекции сложно достигнуть успеха во взаимоотношениях с другими людьми. Однако не всегда она бывает объективной. Вы смотрите на ситуацию со своей стороны. Думаете, что вам понятны чувства человека. Это ошибка. На самом деле он испытывает совсем другое. Ведь все люди разные. Вы не знаете, что происходит у них внутри.

На 100% понять друг друга смогут только эмоционально близкие люди.