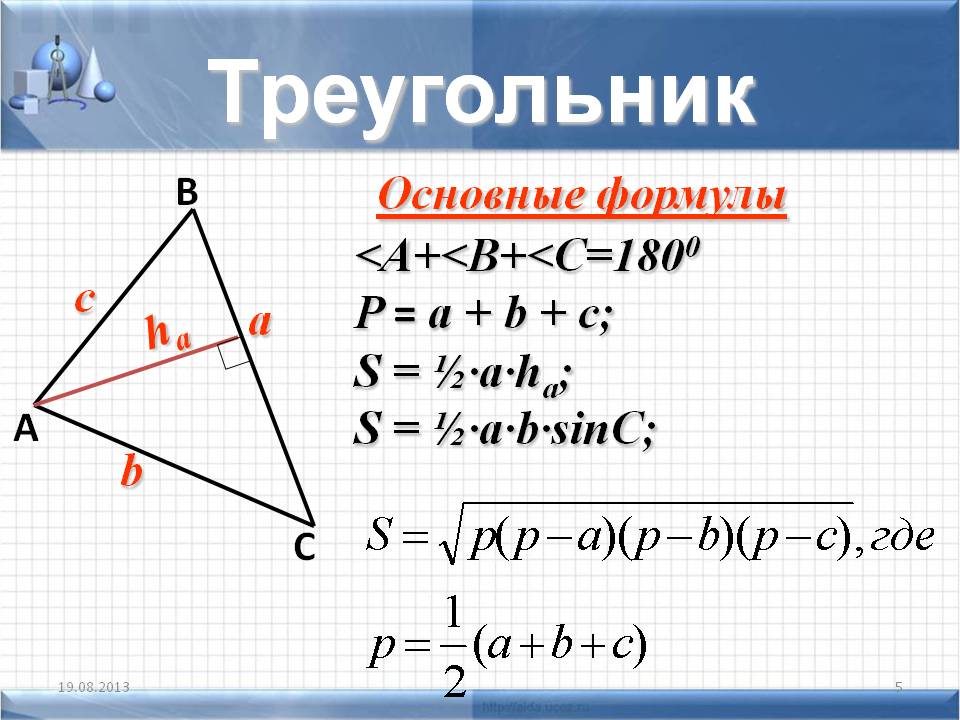
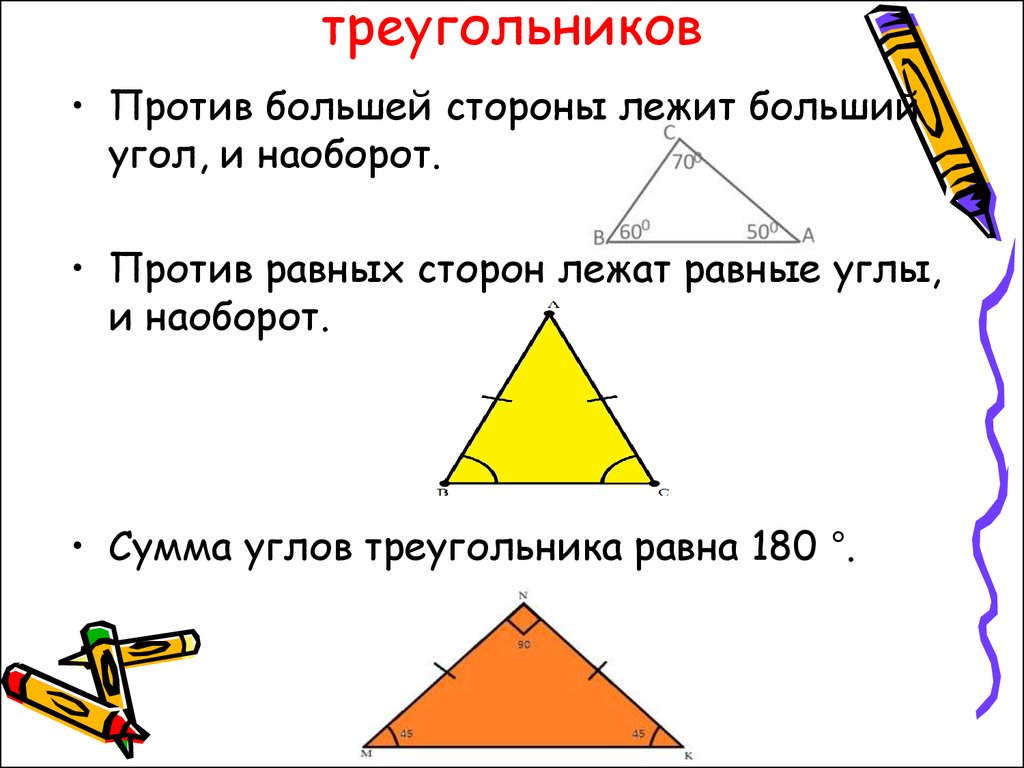
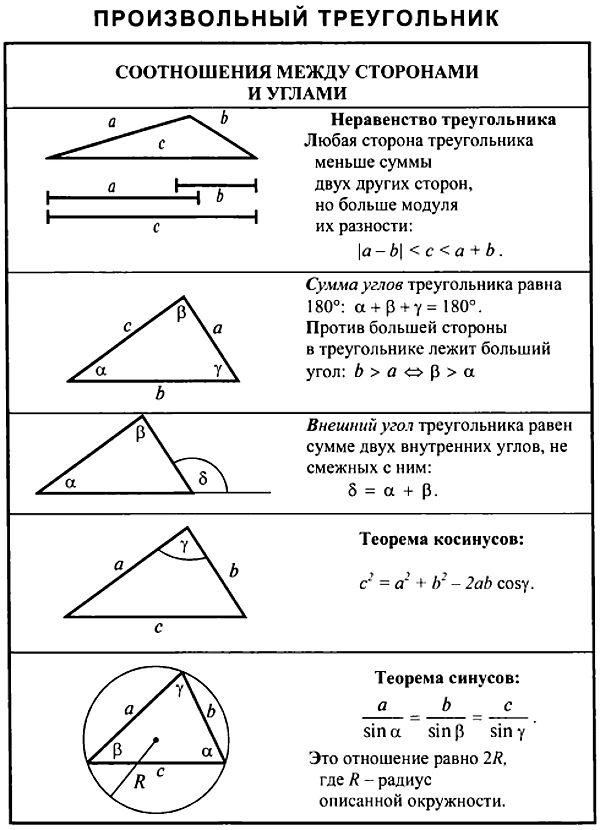
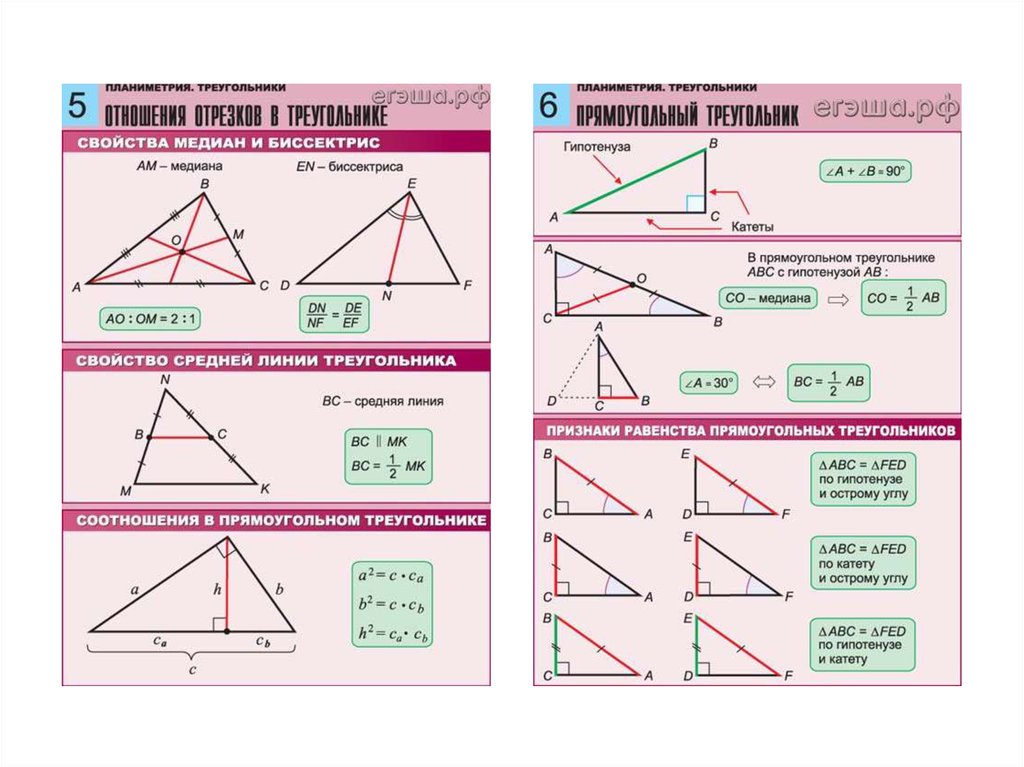
Основные свойства целых треугольников
Целочисленные треугольники с заданным периметром
Любая тройка положительных чисел может стать сторонами треугольника, необходимо лишь удовлетворение неравенства треугольника — самая длинная сторона должна быть короче суммы двух других сторон. Каждая такая тройка задаёт единственный (с точностью до конгруэнтности) треугольник. Так что число целочисленных треугольников с периметром p равно числу разбиений p на три положительные части, удовлетворяющие неравенству треугольника. Эти числа являются ближайшими к p2⁄48 для чётных p и к (p + 3)2⁄48 для нечётных. Это также означает, что число целочисленных треугольников с чётным периметром p = 2n равно числу с нечётным периметром p = 2n — 3. Таким образом, нет треугольников с периметрами 1, 2 и 4, имеется по одному с периметрами 3, 5, 6 и 8, и по два с периметрами 7 и 10. Последовательность числа целочисленных треугольников с периметрами p, начиная с p = 1:
- 0, 0, 1, 0, 1, 1, 2, 1, 3, 2, 4, 3, 5, 4, 7, 5, 8, 7, 10, 8 … (последовательность A005044 в OEIS)
Целочисленные треугольники с заданной большей стороной
Число целочисленных треугольников (с точностью до конгруэнции[неизвестный термин]) с заданной наибольшей стороной c равно числу троек (a, b, c), таких, что a + b > c и a ≤ b ≤ c. Это значение равно Ceiling[(c + 1)⁄2] * Floor[(c + 1)⁄2]. Для чётных c это равно удвоенному треугольному числу c⁄2(c⁄2 + 1), а для нечётных c это равно квадрату (c + 1)2⁄4. Это означает, что число целочисленных треугольников с наибольшей стороной c превышает число целочисленных треугольников с наибольшей стороной c−2 на c. Последовательность числа неконгруэнтных целочисленных треугольников с наибольшей стороной c, начиная с c = 1:
- 1, 2, 4, 6, 9, 12, 16, 20, 25, 30, 36, 42, 49, 56, 64, 72, 81, 90 … (последовательность A002620 в OEIS)
Число целочисленных треугольников (с точностью до конгруэнции) с данной наибольшей стороной c, вершины которого лежат на или внутри полуокружности диаметра c, равно числу троек (a, b, c), таких, что a + b > c , a2 + b2 ≤ c2 и a ≤ b ≤ c. Это число совпадает с числом целочисленных треугольников с тупым или прямым углом с наибольшей стороной c. Последовательность числа таких треугольников, начинающаяся с c = 1:
- 0, 0, 1, 1, 3, 4, 5, 7, 10, 13, 15, 17, 22, 25, 30, 33, 38, 42, 48 … (последовательность A236384 в OEIS)
Разница между последними двумя последовательностями даёт число целочисленных треугольников с острыми углами (с точностью до конгруэнции) с наибольшей стороной c. Последовательность числа остроугольных треугольников, начиная с c = 1:
- 1, 2, 3, 5, 6, 8, 11, 13, 15, 17, 21, 25, 27, 31, 34, 39, 43, 48, 52 … (последовательность A247588 в OEIS)
Площадь целочисленного треугольника
По формуле Герона, если T — площадь треугольника, а длины сторон равны a, b и c, то
- 4T=(a+b+c)(a+b−c)(a−b+c)(−a+b+c).{\displaystyle 4T={\sqrt {(a+b+c)(a+b-c)(a-b+c)(-a+b+c)}}.}
Поскольку все множители под знаком корня в правой части формулы являются целыми числами, все целочисленные треугольники должны иметь целочисленное значение величины 16T2.
Углы целочисленного треугольника
По теореме косинусов любой угол целочисленного треугольника имеет рациональный косинус.
Если углы любого треугольника образуют арифметическую прогрессию, то один из его углов должен быть 60°. Для целочисленных треугольников оставшиеся углы должны также иметь рациональные косинусы и метод генерации таких треугольников приведён ниже. Однако, за исключением тривиального случая равностороннего треугольника, не существует целочисленных треугольников, углы которого образуют геометрическую или гармоническую прогрессию. Это потому, что углы должны быть рациональными углами вида πp⁄q с рациональными 0 < p⁄q < 1. Но все углы целочисленных треугольников должны иметь рациональные косинусы, а это может произойти только в случае, когда p⁄q = 1⁄3 , то есть целочисленный треугольник является равносторонним.
Деление стороны высотой
Любая высота, опущенная из вершины на противоположную сторону или её продолжение, делит эту сторону (или продолжение) на отрезки рациональной длины.
Формулы равностороннего треугольника:
Пусть a – длина стороны равностороннего треугольника, h – высота (l – биссектриса, m – медиана) равностороннего треугольника, проведенная к каждой стороне, α – угол равностороннего треугольника, α = 60°, R – радиус описанной окружности, r – радиус вписанной окружности (см. Рис. 6).
Рис. 6. Равносторонний треугольник
Формула радиуса вписанной окружности (r):
.
Формула радиуса описанной окружности (R):
,
.
Формулы периметра (Р) равностороннего треугольника:
 .
.
Формулы площади (S) равностороннего треугольника:
 .
.
Формулы высоты (h), медианы (m) и биссектрисы (l) треугольника:
.
Примечание: Фото https://www.pexels.com, https://pixabay.com
Как возможно научиться писать тексты и зарабатывать на этом удаленно? Например, можете пройти курс «Копирайтинг от А до Я», который подойдет даже начинающим авторам.
Другие записи:
карта сайта
Коэффициент востребованности
7 397
Ссылки
- Herbert Bailey, Duane DeTemple. Squares inscribed in angles and triangles // Mathematics Magazine. — 1998. — Вып. 71(4).
- T. Barnard, J. Silvester. Circle theorems and a property of the (2,3,4) triangle // Mathematical Gazette. — 2001. — Вып. 85, July.
- H. F. Blichfeldt. On Triangles with Rational Sides and Having Rational Areas // Annals of Mathematics. — 1896—1897. — Т. 11, вып. 1/6.
- Bart De Bruyn. On a Problem Regarding the n-Sectors of a Triangle // Forum Geometricorum. — 2005. — Вып. 5.
- R. H. Buchholz, J. A. MacDougall. Heron Quadrilaterals with sides in Arithmetic or Geometric progression // Bull. Austral. Math. Soc.. — 1999. — Т. 59.
- R. H. Buchholz, J. A. MacDougall. Cyclic Polygons with Rational Sides and Area. — CiteSeerX Penn State University, 2001.
- Bob Burn. Triangles with a 60° angle and sides of integer length // Mathematical Gazette. — 2003. — Вып. 87, March.
- John R. Carlson. Determination of Heronian triangles // San Diego State College. — 1970.
- R. D. Carmichael. The Theory of Numbers and Diophantine Analysis. — Dover, 1959.
- J. H. Conway, R. K. Guy. The Book of Numbers. — Springer-Verlag, 1996. — С. 201, 228-239 The only rational triangle.
- M. N. Deshpande. Some new triples of integers and associated triangles // Mathematical Gazette. — 2002. — Вып. 86, November.
- L. E. Dickson. History of the Theory of Numbers. — 2005. — Т. 2.
- J. Gilder. Integer-sided triangles with an angle of 60° // Mathematical Gazette. — 1982. — Вып. 66, December.
- John F. Jr. Goehl. More integer triangles with R/r = N // Forum Geometricorum. — 2012. — Вып. 12.
- John F. Jr. Goehl. Pythagorean triangles with square of perimeter equal to an integer multiple of area // Forum Geometricorum. — 2009. — Вып. 9.
Jan Friche. On Heron Simplices and Integer Embedding // Ernst-Moritz-Arndt Universät Greiswald Publication. — 2002. — Вып. 2 Jan.
Michael D. Hirschhorn. Commensurable triangles // Mathematical Gazette. — 2011. — Вып. 95, March.
- Ross Honsberger. Mathematical Gems III. — Washington, DC: Mathematical Association of America, 1973. — Т. 1. — (Dolciani mathematical expositions). — ISBN 0-88385-301-9.
- Jörg Jahnel. When is the (Co)Sine of a Rational Angle equal to a rational number?. — Cornell Univ. archive, 2010.
- N. Lord. A striking property of the (2,3,4) triangle // Mathematical Gazette. — 1998. — Вып. 82, March.
- D. MacHale. That 3,4,5 triangle again // Mathematical Gazette. — 1989. — Вып. 73, March.
Allan J. MacLeod. Integer triangles with R/r = N // Forum Geometricorum. — 2010. — Вып. 10.
- Susan H. Marshall, Alexander R. Perlis. Heronian tetrahedra are lattice tetrahedra. — University of Arizona, 2012.
- Douglas W. Mitchell. Heron triangles with ∠B=2∠A // Mathematical Gazette. — 2007. — Вып. 91, July.
- Douglas W. Mitchell. The 2:3:4, 3:4:5, 4:5:6, and 3:5:7 triangles // Mathematical Gazette. — 2008. — Вып. 92, July.
- Douglas W. Mitchell. Perpendicular Bisectors of Triangle Sides // Forum Geometricorum. — 2013. — Вып. 13.
- Tom Jenkyns, Eric Muller. Triangular Triples from Ceilings to Floors. — American Mathematical Monthly. — 2000.
- Richard Parris. College Mathematics Journal. — 2007. — Вып. 38(5), November.
- Emrys Read. On integer-sided triangles containing angles of 120° or 60° // Mathematical Gazette. — 2006. — Вып. 90, July.
- K.R.S Sastry. Integer-sided triangles containing a given rational cosine // Mathematical Gazette. — 1984. — Вып. 68, December.
- K. R. S. Sastry. Construction of Brahmagupta n-gons // Forum Geometricorum. — 2005. — Вып. 5.
- K. Selkirk. Integer-sided triangles with an angle of 120° // Mathematical Gazette. — 1983. — Вып. 67, December.
Wacław Sierpiński. Pythagorean Triangles. — orig. ed. 1962. — Dover Publications, 2003. — ISBN 978-0-486-43278-6.
- Roger Voles. Integer solutions of a−2+b−2=d−2 // Mathematical Gazette. — 1999. — Вып. 83, July.
- Jennifer Richinick. The upside-down Pythagorean Theorem // Mathematical Gazette. — 2008. — Вып. 92, July.
- William Wynne Willson. A generalisation of the property of the 4, 5, 6 triangle // Mathematical Gazette. — 1976. — Вып. 60, June.
- Paul Yiu. Heron triangles which cannot be decomposed into two integer right triangles. — 41st Meeting of Florida Section of Mathematical Association of America, 2008.
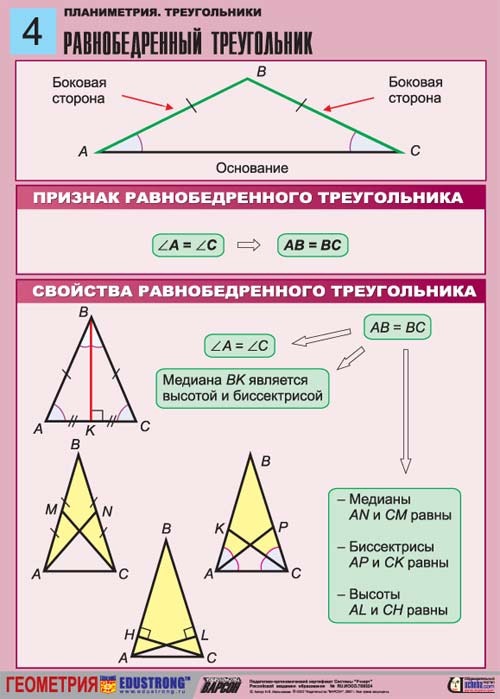
Свойства равностороннего треугольника:
1. В равностороннем треугольнике все стороны равны между собой.
2. В равностороннем треугольнике углы равны и составляют 60°.
3. В равностороннем треугольнике каждая медиана, проведенная к каждой стороне, является биссектрисой и высотой, и они равны между собой.
В равностороннем треугольнике биссектриса, проведенная к каждой стороне, является медианой и высотой, и они равны между собой.
В равностороннем треугольнике высота, проведенная к каждой стороне, является биссектрисой и медианой, и они равны между собой.
Рис. 2. Равносторонний треугольник
АK = BF = CD
4. В равностороннем треугольнике высоты, биссектрисы, медианы и серединные перпендикуляры пересекаются в одной точке, которая называется центром равностороннего треугольника. Она же является центром вписанной и описанной окружностей.
Рис. 3. Равносторонний треугольник
R – радиус описанной окружности, r – радиус вписанной окружности
5. В равностороннем треугольнике радиус описанной окружности в два раза больше радиуса вписанной.
6. Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, если считать от вершин.
Рис. 4. Равносторонний треугольник
AO : OK = BO : OА = CO : OD = 2 : 1
Ответы знатоков
Andy Green:
Правильный треугольник
Правильный треугольник или равносторонний треугольник — это правильный многоугольник с тремя сторонами, первый из правильных многоугольников. Все стороны правильного треугольника равны между собой, а все углы равны 60° (или π / 3).
В силу определения правильный треугольник также является равнобедренным.
Юлия:
это треугольник, у которого все стороны равны
Larisa:
Когда все стороны равны
это правильный многоугольник с тремя сторонами, первый из правильных многоугольников. Все стороны правильного треугольника равны между собой, а все углы равны 60°
Nick Storozhev:
равносторонний
Peny Crape:
Все стороны правильного треугольника равны между собой, а все углы равны 60° (или π / 3).
Dream Milkshake:
Правильные геометрические фигуры — это такие фигуры, у которых все стороны равны и все углы равны 60 градусов. А правильный треугольник — это простейший равносторонний треугольник. Могу показать пример четырёх правильных геометрических фигур: правильного шестиугольника, правильного треугольника, правильного четырёхугольника и правильного пятиугольника на чистом белом листе без клеток. Ещё могу сказать, чтобы начертить такие правильные фигуры нужно использовать линейку, циркуль и транспортир. Одно из самых сложных начертить правильный пятиугольник! Ещё надо мне сказать, что в равностороннем треугольнике высота является и биссектрисой, и медианой, ведь речь шла о правильном треугольнике, а не о правильных геометрических фигурах. Надеюсь мой ответ вам понравится!Картинку с четырьмя фигурами ты увидишь ниже. Вот пример четырёх правильных геометрических фигур: правильного шестиугольника, правильного треугольника, правильного четырёхугольника и правильного пятиугольника на чистом белом листе без клеток. Также разные ответы можно получить на сайте Википедии.
Алексей Александров:
Правильный треугольник
Правильный треугольник или равносторонний треугольник — это правильный многоугольник с тремя сторонами, первый из правильных многоугольников. Все стороны правильного треугольника равны между собой, а все углы равны 60° (или π / 3).
В силу определения правильный треугольник также является равнобедренным
Ассоль Счастье:
Правильный — это равносторонний треугольник. Соответственно неправильный треугольник — не равносторонний, т. е. треугольник, у которого хотя бы одна сторона не равна двум другим!) )
Исходя из геометрических определений делаем вывод: неправильный треугольник; — это когда рост; и соответственно «угол»(ум) , влюбленных друг в друга особей, не совпадаюДЪ)))))))))))) )
Продолжая далее логическое размышление, (такое софпадение нереально) ; приходим к выводу, что ФСЕ; треугольники яфляюцца НЕПРАФИЛЬНЫМИ!)))))))))))))) ;
Андрей Минеев:
Групповой
Акварелька:
Однобедренный..
Vera vep:
С шестью углами
сергей пышкин:
однополый
че че гевара OLD:
Любовный
Павел Замятин:
Все треугольники как треугольники, а этот тупой.
Сергей Евтихов:
Енто пять 3,14доров.
❧Ǻλȅભŷ∮ķǻ☙:
Круглый…. как яйцо _))))
⁂ Галина Купина⁂:
не равносторонний, не равнобедренный
НИКого:
Которого и нет))
Собакевич:
Муж, жена и два её любовника
Владимир Юрьевич:
Это когда пришёл к любовнице, а у неё в гостях бывший муж с другом.
Attiny13:
тип гибридизации spd physic.kemsu /pub/library/learn_pos/Udin_ModelChemSoed/HTML/soder/2/2_4
Типы тетраэдров.
Правильный тетраэдр — это такая правильная треугольная пирамида, каждая из граней которой оказывается равносторонним треугольником.
У правильного тетраэдра каждый двугранный угол при рёбрах и каждый трёхгранный угол при вершинах имеют одинаковую величину.
Тетраэдр состоит из 4 граней, 4 вершин и 6 ребер.
Правильный тетраэдр — это один из 5-ти правильных многогранников.
Кроме правильного тетраэдра, заслуживают внимания такие типы тетраэдров:
— Равногранный тетраэдр, у него каждая грань представляет собой треугольник. Все грани-треугольники такого тетраэдра равны.
— Ортоцентрический тетраэдр, у него каждая высота, опущенная из вершин на противоположную грань, пересекается с остальными в одной точке.
— Прямоугольный тетраэдр, у него каждое ребро, прилежащее к одной из вершин, перпендикулярно другим ребрам, прилежащим к этой же вершине.
— Каркасный тетраэдр — тетраэдр, который таким условиям:
- есть сфера, которая касается каждого ребра,
- суммы длин ребер, что скрещиваются равны,
- суммы двугранных углов при противоположных ребрах равны,
- окружности, которые вписаны в грани, попарно касаются,
- каждый четырехугольник, образующийся на развертке тетраэдра, — описанный,
- перпендикуляры, поставленные к граням из центров окружностей, в них вписанных, пересекаются в одной точке.
— Соразмерный тетраэдр, бивысоты у него одинаковы.
— Инцентрический тетраэдр, у него отрезки, которые соединяют вершины тетраэдра с центрами окружностей, которые вписаны в противоположные грани, пересекаются в одной точке.
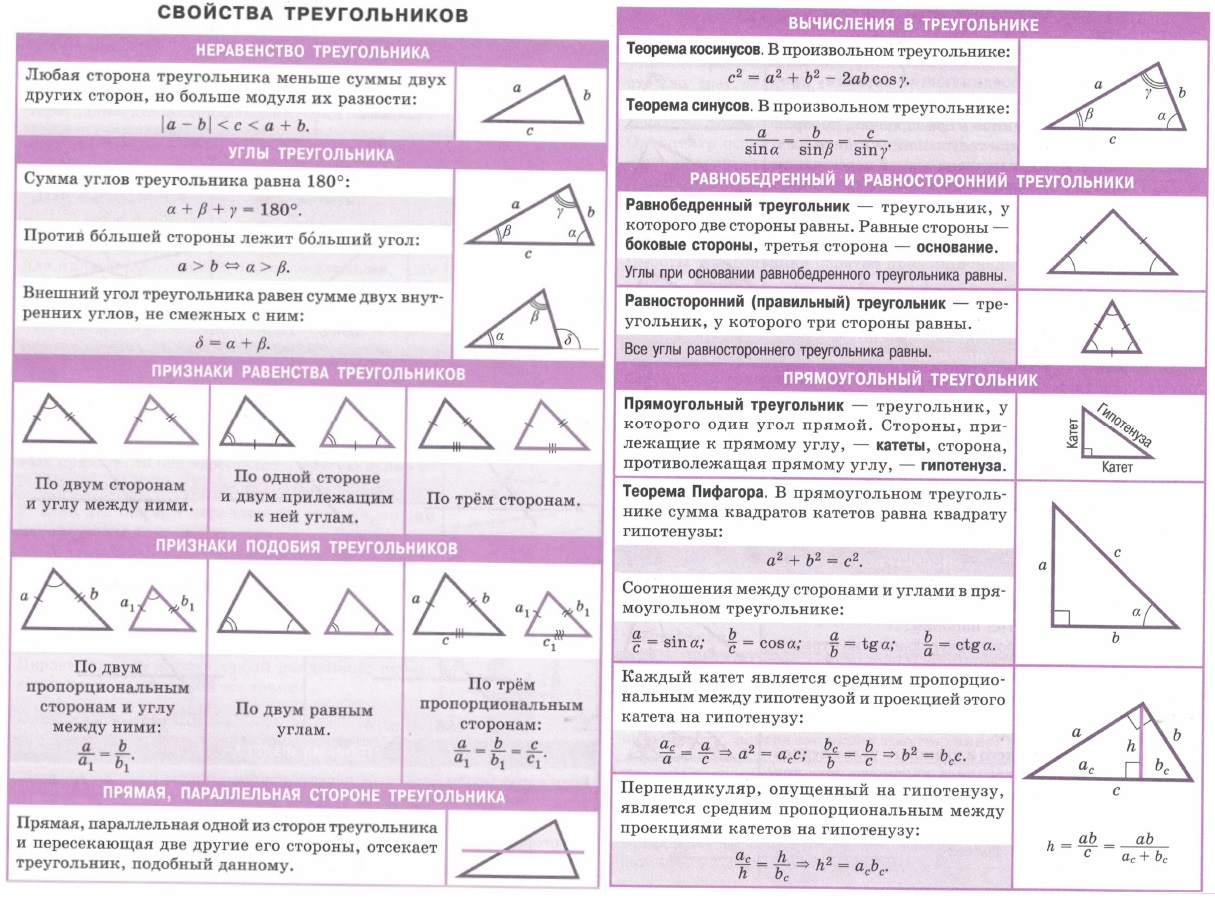
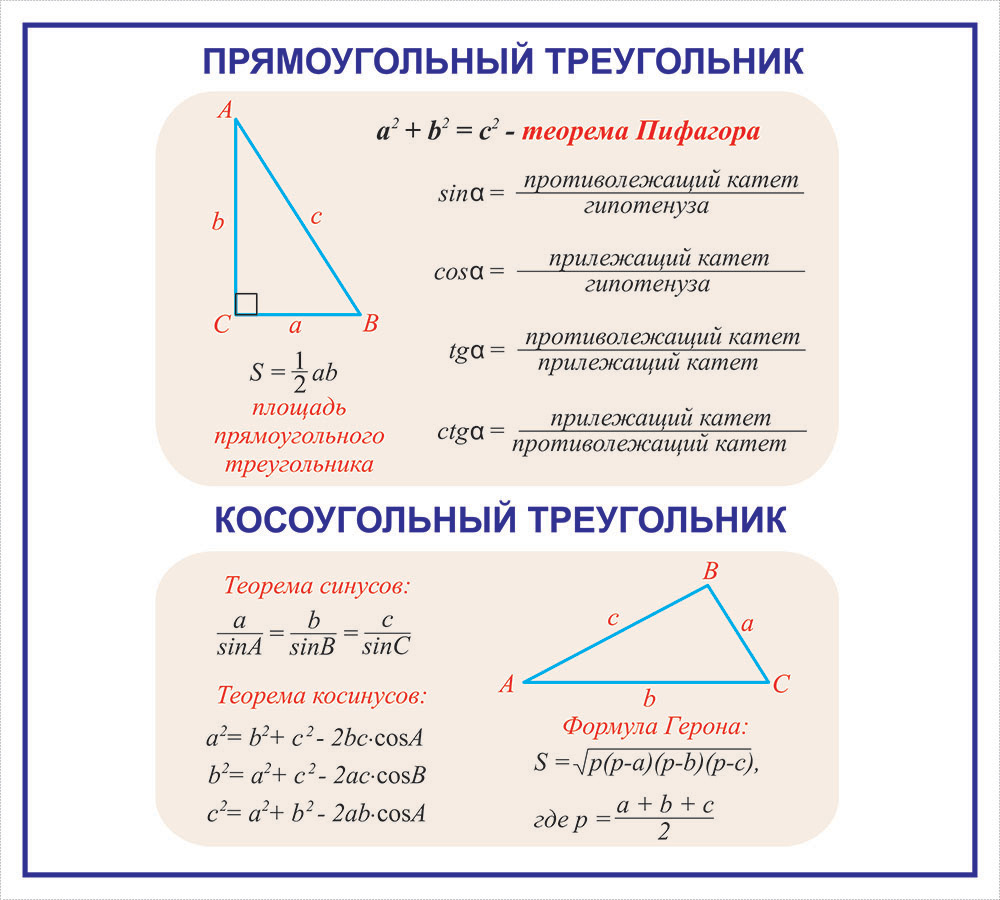
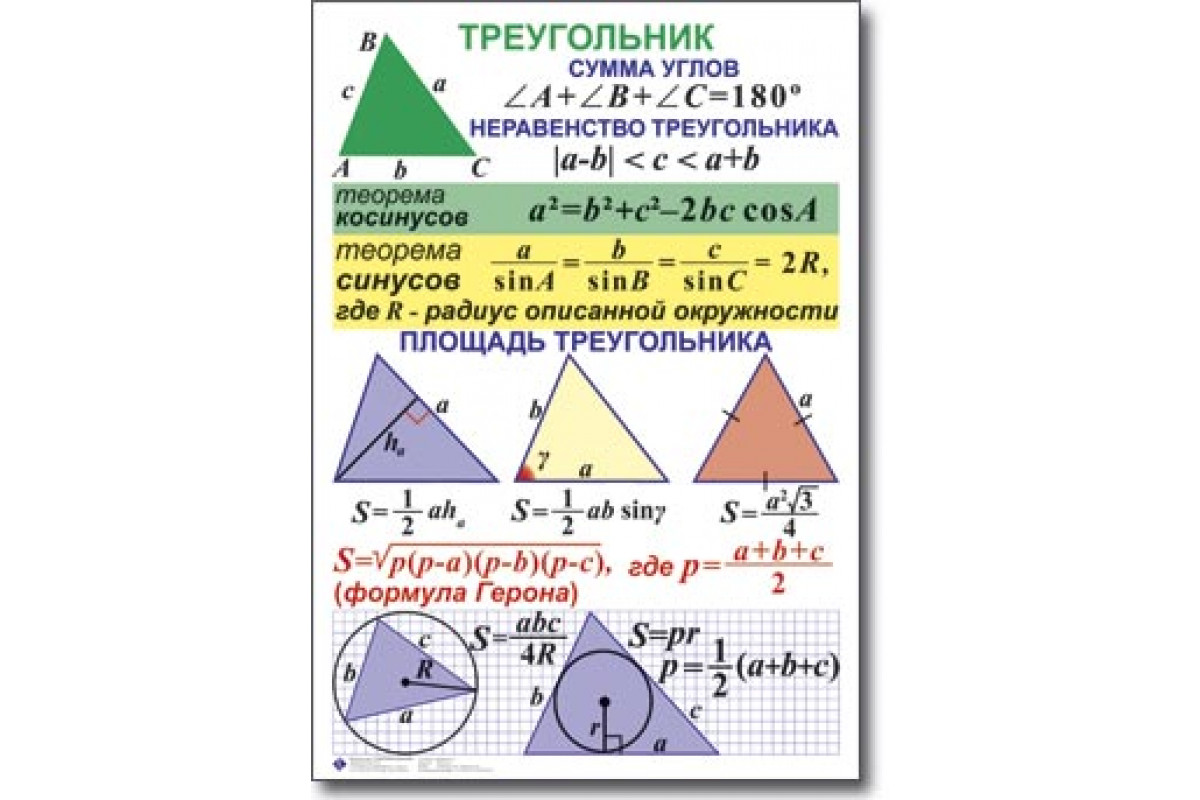
Формулы площади треугольника
-
Формула площади треугольника по стороне и высотеПлощадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
S = 12
S = 12
S = 12 -
Формула площади треугольника по трем сторонам
S = √()()()
где = + + 2 — полупериметр треугльника.
-
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.S = 12
S = 12
S = 12 -
Формула площади треугольника по трем сторонам и радиусу описанной окружности
S = 4R -
Формула площади треугольника по трем сторонам и радиусу вписанной окружностиПлощадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
S = ·
Свойства
Правильный тетраэдр состоит из четырёх правильных треугольников.
Пусть a — сторона правильного треугольника, R — радиус описанной окружности, r — радиус вписанной окружности.
Радиус вписанной окружности правильного треугольника, выраженный через его сторону:
- r=36a{\displaystyle r={\frac {\sqrt {3}}{6}}a}
Радиус описанной окружности правильного треугольника, выраженный через его сторону:
- R=33a{\displaystyle R={\frac {\sqrt {3}}{3}}a}
Периметр правильного треугольника:
- P=3a=33R=63r{\displaystyle P=3a=3{\sqrt {3}}R=6{\sqrt {3}}r}
Высоты, медианы и биссектрисы правильного треугольника:
- h=m=l=32a{\displaystyle h=m=l={\frac {\sqrt {3}}{2}}a}
Площадь правильного треугольника рассчитывается по формулам:
- S=34a2=334R2=33r2=336P2{\displaystyle S={\frac {\sqrt {3}}{4}}a^{2}={\frac {3{\sqrt {3}}}{4}}R^{2}=3{\sqrt {3}}r^{2}={\frac {\sqrt {3}}{36}}P^{2}}
Радиус описанной окружности равен двойному радиусу вписанной окружности:
- R=2r{\displaystyle R=2r}
Правильными треугольниками можно замостить плоскость.
В правильном треугольнике окружность девяти точек совпадает с вписанной окружностью.
- Для равностороннего треугольника T группа движений (самосовмещений) плоскости, переводящих треугольник в себя, состоит из 6 элементов: трёх поворотов на углы 0, 2π⁄3 и 4π⁄3 вокруг точки O, а также трёх симметрий относительно трёх прямых, на которых лежат биссектрисы треугольника (последние являются также его высотами и медианами).
- На описанной окружности произвольного треугольника ABC{\displaystyle ABC} существуют ровно три точки такие, что их прямая Симсона касается окружности Эйлера треугольника ABC{\displaystyle ABC}, причем эти точки образуют правильный треугольник. Стороны этого треугольника параллельны сторонам треугольника Морлея.
- Равносторонний треугольник является одновременно и равноугольным треугольником, то есть у него равны все внутренние углы.
- Равносторонний треугольник является частными случаем равнобедренного треугольника, а именно: дважды равнобедренным треугольником.
Свойства
Правильный тетраэдр состоит из четырёх правильных треугольников.
Пусть a — сторона правильного треугольника, R — радиус описанной окружности, r — радиус вписанной окружности.
Радиус вписанной окружности правильного треугольника, выраженный через его сторону:
- r=36a{\displaystyle r={\frac {\sqrt {3}}{6}}a}
Радиус описанной окружности правильного треугольника, выраженный через его сторону:
- R=33a{\displaystyle R={\frac {\sqrt {3}}{3}}a}
Периметр правильного треугольника:
- P=3a=33R=63r{\displaystyle P=3a=3{\sqrt {3}}R=6{\sqrt {3}}r}
Высоты, медианы и биссектрисы правильного треугольника:
- h=m=l=32a{\displaystyle h=m=l={\frac {\sqrt {3}}{2}}a}
Площадь правильного треугольника рассчитывается по формулам:
- S=34a2=334R2=33r2=336P2{\displaystyle S={\frac {\sqrt {3}}{4}}a^{2}={\frac {3{\sqrt {3}}}{4}}R^{2}=3{\sqrt {3}}r^{2}={\frac {\sqrt {3}}{36}}P^{2}}
Радиус описанной окружности равен двойному радиусу вписанной окружности:
- R=2r{\displaystyle R=2r}
Правильными треугольниками можно замостить плоскость.
В правильном треугольнике окружность девяти точек совпадает с вписанной окружностью.
- Для равностороннего треугольника T группа движений (самосовмещений) плоскости, переводящих треугольник в себя, состоит из 6 элементов: трёх поворотов на углы 0, 2π⁄3 и 4π⁄3 вокруг точки O, а также трёх симметрий относительно трёх прямых, на которых лежат биссектрисы треугольника (последние являются также его высотами и медианами).
- На описанной окружности произвольного треугольника ABC{\displaystyle ABC} существуют ровно три точки такие, что их прямая Симсона касается окружности Эйлера треугольника ABC{\displaystyle ABC}, причем эти точки образуют правильный треугольник. Стороны этого треугольника параллельны сторонам треугольника Морлея.
- Равносторонний треугольник является одновременно и равноугольным треугольником, то есть у него равны все внутренние углы.
- Равносторонний треугольник является частными случаем равнобедренного треугольника, а именно: дважды равнобедренным треугольником.
Свойства
Правильный тетраэдр состоит из четырёх правильных треугольников.
Пусть a — сторона правильного треугольника, R — радиус описанной окружности, r — радиус вписанной окружности.
Радиус вписанной окружности правильного треугольника, выраженный через его сторону:
- r=36a{\displaystyle r={\frac {\sqrt {3}}{6}}a}
Радиус описанной окружности правильного треугольника, выраженный через его сторону:
- R=33a{\displaystyle R={\frac {\sqrt {3}}{3}}a}
Периметр правильного треугольника:
- P=3a=33R=63r{\displaystyle P=3a=3{\sqrt {3}}R=6{\sqrt {3}}r}
Высоты, медианы и биссектрисы правильного треугольника:
- h=m=l=32a{\displaystyle h=m=l={\frac {\sqrt {3}}{2}}a}
Площадь правильного треугольника рассчитывается по формулам:
- S=34a2=334R2=33r2=336P2{\displaystyle S={\frac {\sqrt {3}}{4}}a^{2}={\frac {3{\sqrt {3}}}{4}}R^{2}=3{\sqrt {3}}r^{2}={\frac {\sqrt {3}}{36}}P^{2}}
Радиус описанной окружности равен двойному радиусу вписанной окружности:
- R=2r{\displaystyle R=2r}
Правильными треугольниками можно замостить плоскость.
В правильном треугольнике окружность девяти точек совпадает с вписанной окружностью.
- Для равностороннего треугольника T группа движений (самосовмещений) плоскости, переводящих треугольник в себя, состоит из 6 элементов: трёх поворотов на углы 0, 2π⁄3 и 4π⁄3 вокруг точки O, а также трёх симметрий относительно трёх прямых, на которых лежат биссектрисы треугольника (последние являются также его высотами и медианами).
- На описанной окружности произвольного треугольника ABC{\displaystyle ABC} существуют ровно три точки такие, что их прямая Симсона касается окружности Эйлера треугольника ABC{\displaystyle ABC}, причем эти точки образуют правильный треугольник. Стороны этого треугольника параллельны сторонам треугольника Морлея.
- Равносторонний треугольник является одновременно и равноугольным треугольником, то есть у него равны все внутренние углы.
- Равносторонний треугольник является частными случаем равнобедренного треугольника, а именно: дважды равнобедренным треугольником.
Свойства
Правильный тетраэдр состоит из четырёх правильных треугольников.
Пусть a — сторона правильного треугольника, R — радиус описанной окружности, r — радиус вписанной окружности.
Радиус вписанной окружности правильного треугольника, выраженный через его сторону:
- r=36a{\displaystyle r={\frac {\sqrt {3}}{6}}a}
Радиус описанной окружности правильного треугольника, выраженный через его сторону:
- R=33a{\displaystyle R={\frac {\sqrt {3}}{3}}a}
Периметр правильного треугольника:
- P=3a=33R=63r{\displaystyle P=3a=3{\sqrt {3}}R=6{\sqrt {3}}r}
Высоты, медианы и биссектрисы правильного треугольника:
- h=m=l=32a{\displaystyle h=m=l={\frac {\sqrt {3}}{2}}a}
Площадь правильного треугольника рассчитывается по формулам:
- S=34a2=334R2=33r2=336P2{\displaystyle S={\frac {\sqrt {3}}{4}}a^{2}={\frac {3{\sqrt {3}}}{4}}R^{2}=3{\sqrt {3}}r^{2}={\frac {\sqrt {3}}{36}}P^{2}}
Радиус описанной окружности равен двойному радиусу вписанной окружности:
- R=2r{\displaystyle R=2r}
Правильными треугольниками можно замостить плоскость.
В правильном треугольнике окружность девяти точек совпадает с вписанной окружностью.
- Для равностороннего треугольника T группа движений (самосовмещений) плоскости, переводящих треугольник в себя, состоит из 6 элементов: трёх поворотов на углы 0, 2π⁄3 и 4π⁄3 вокруг точки O, а также трёх симметрий относительно трёх прямых, на которых лежат биссектрисы треугольника (последние являются также его высотами и медианами).
- На описанной окружности произвольного треугольника ABC{\displaystyle ABC} существуют ровно три точки такие, что их прямая Симсона касается окружности Эйлера треугольника ABC{\displaystyle ABC}, причем эти точки образуют правильный треугольник. Стороны этого треугольника параллельны сторонам треугольника Морлея.
- Равносторонний треугольник является одновременно и равноугольным треугольником, то есть у него равны все внутренние углы.
- Равносторонний треугольник является частными случаем равнобедренного треугольника, а именно: дважды равнобедренным треугольником.
Задачи с разными видами треугольников
№1. Дан равнобедренный треугольник. Его периметр известен и равен 90 см. Требуется узнать его стороны. В качестве дополнительного условия: боковая сторона меньше основания в 1,2 раза.
Решение
Значение периметра напрямую зависит от тех величин, которые нужно найти. Сумма всех трех сторон и даст 90 см. Теперь нужно вспомнить признак треугольника, по которому он является равнобедренным. То есть две стороны равны. Можно составить уравнение с двумя неизвестными: 2а + в = 90. Здесь а — боковая сторона, в — основание.
Настала очередь дополнительного условия. Следуя ему, получается второе уравнение: в = 1,2а. Можно выполнить подстановку этого выражения в первое. Получится: 2а + 1,2а = 90. После преобразований: 3,2а = 90. Отсюда а = 28,125 (см). Теперь несложно узнать основание. Лучше всего это сделать из второго условия: в = 1,2 * 28,125 = 33,75 (см).
Для проверки можно сложить три значения: 28,125 * 2 + 33,75 = 90 (см). Все верно.
Ответ: стороны треугольника равны 28,125 см, 28,125 см, 33,75 см.
№2. Сторона равностороннего треугольника равна 12 см. Нужно вычислить его высоту.
Решение. Для поиска ответа достаточно вернуться к тому моменту, где были описаны свойства треугольника. Так указана формула для нахождения высоты, медианы и биссектрисы равностороннего треугольника.
н = а * √3 / 2, где н — высота, а — сторона.
Подстановка и вычисление дают такой результат: н = 6 √3 (см).
Эту формулу необязательно запоминать. Достаточно вспомнить, что высота делит треугольник на два прямоугольных. Причем она оказывается катетом, а гипотенуза в нем — это сторона исходного, второй катет — половина известной стороны. Теперь нужно записать теорему Пифагора и вывести формулу для высоты.
Ответ: высота равна 6 √3 см.
№3. Дан МКР — треугольник, 90 градусов в котором составляет угол К. Известны стороны МР и КР, они равны соответственно 30 и 15 см. Нужно узнать значение угла Р.
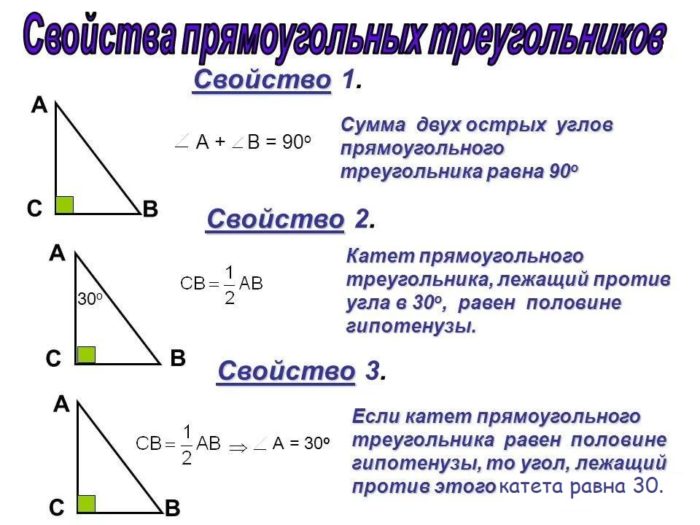
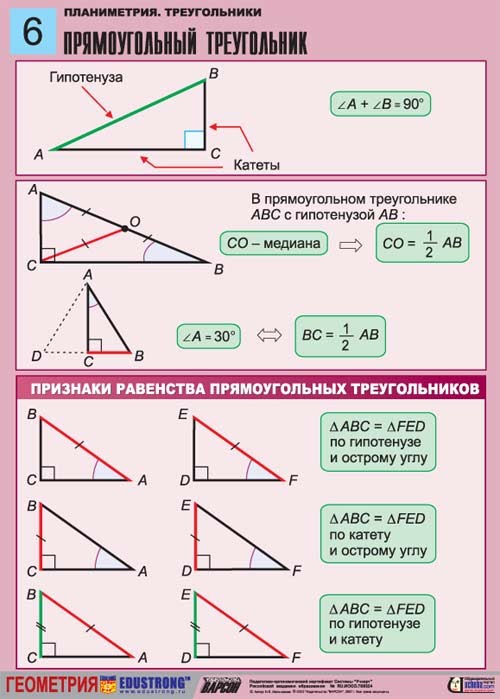
Решение. Если сделать чертеж, то становится ясно, что МР — гипотенуза. Причем она в два раза больше катета КР. Снова нужно обратиться к свойствам. Одно из них как раз связано с углами. Из него понятно, что угол КМР равен 30º. Значит искомый угол Р будет равен 60º. Это следует из другого свойства, которое утверждает, что сумма двух острых углов должна равняться 90º.
Ответ: угол Р равен 60º.
№4. Нужно найти все углы равнобедренного треугольника. Про него известно, что внешний угол от угла при основании равен 110º.
Решение. Поскольку дан только внешний угол, то этим и нужно воспользоваться. Он образует с внутренним углом развернутый. Значит в сумме они дадут 180º. То есть угол при основании треугольника будет равен 70º. Так как он равнобедренный, то второй угол имеет такое же значение. Осталось вычислить третий угол. По свойству, общему для всех треугольников, сумма углов равна 180º. Значит, третий определится как 180º – 70º – 70º = 40º.
Ответ: углы равны 70º, 70º, 40º.
№5. Известно, что в равнобедренном треугольнике угол, лежащий напротив основания, равен 90º. На основании отмечена точка. Отрезок, соединяющий ее с прямым углом, делит его в отношении 1 к 4. Нужно узнать все углы меньшего треугольника.
Решение. Один из углов можно определить сразу. Поскольку треугольник прямоугольный и равнобедренный, то те, что лежат у его основания, будут по 45º, то есть по 90º/2.
Второй из них поможет найти известное в условии отношение. Поскольку оно равно 1 к 4, то частей, на которые он делится получается всего 5. Значит, чтобы узнать меньший угол треугольника нужно 90º/5 = 18º. Осталось узнать третий. Для этого из 180º (суммы всех углов треугольника) нужно вычесть 45º и 18º. Вычисления несложные, и получится: 117º.
Ответ: 18º, 45º, 117º
Некоторые целочисленные треугольники
- Единственный треугольник с последовательными целыми числами в качестве сторон и площади имеет стороны (3,4,5){\displaystyle (3,4,5)} и площадь 6{\displaystyle 6}.
- Единственный треугольник с последовательными целыми числами в качестве сторон и высоты имеет стороны (13,14,15){\displaystyle (13,14,15)} и высоту 12, опущенную на сторону длиной 14.
- Треугольник (3,4,5){\displaystyle (3,4,5)} и кратные ему являются единственными прямоугольными треугольниками с целочисленными сторонами, у которых стороны образуют арифметическую прогрессию .
- Треугольник (4,5,6){\displaystyle (4,5,6)} и кратные ему являются единственными треугольниками с целочисленными сторонами, у которых один угол вдвое больше другого и стороны образуют арифметическую прогрессию .
- Треугольник (3,5,7){\displaystyle (3,5,7)} и кратные ему являются единственными треугольниками с целочисленными сторонами, имеющими угол 120°, и стороны образуют арифметическую прогрессию .
- Единственный целочисленный треугольник с площадью, равной полупериметру имеет стороны (3,4,5){\displaystyle (3,4,5)}.
- Целочисленные треугольники с площадью, равной периметру, имеют только стороны (5, 12, 13), (6,8,10), (6,25,29), (7,15,20) и (9,10,17). Из них только первых два прямоугольные.
- Существуют целочисленные треугольники с тремя рациональными медианами. Самый маленький из них имеет стороны (68, 85, 87). Можно привести ещё (127, 131, 158), (113, 243, 290), (145, 207, 328) и (327, 386, 409).
- Не существует равнобедренных пифагоровых треугольников.
- Единственными примитивными пифагоровыми треугольниками, для которых квадрат периметра кратен площади, являются
- 1) треугольник (3,4,5) с периметром 12, площадью 6 и отношением квадрата периметра к площади 24 — Египетский треугольник
- 2) треугольник (5,12,13) с периметром 30, площадью 30 и отношением квадрата периметра к площади 30
- 3) треугольник (9, 40, 41) с периметром 90, площадью 180 и отношением квадрата периметра к площади 45
Свойства[ | код]
Правильный тетраэдр состоит из четырёх правильных треугольников.
Пусть a — сторона правильного треугольника, R — радиус описанной окружности, r — радиус вписанной окружности.
Радиус вписанной окружности правильного треугольника, выраженный через его сторону:
- r=36a{\displaystyle r={\frac {\sqrt {3}}{6}}a}
Радиус описанной окружности правильного треугольника, выраженный через его сторону:
- R=33a{\displaystyle R={\frac {\sqrt {3}}{3}}a}
Периметр правильного треугольника:
- P=3a=33R=63r{\displaystyle P=3a=3{\sqrt {3}}R=6{\sqrt {3}}r}
Высоты, медианы и биссектрисы правильного треугольника:
- h=m=l=32a{\displaystyle h=m=l={\frac {\sqrt {3}}{2}}a}
Площадь правильного треугольника рассчитывается по формулам:
- S=34a2=334R2=33r2=336P2{\displaystyle S={\frac {\sqrt {3}}{4}}a^{2}={\frac {3{\sqrt {3}}}{4}}R^{2}=3{\sqrt {3}}r^{2}={\frac {\sqrt {3}}{36}}P^{2}}
Радиус описанной окружности равен двойному радиусу вписанной окружности:
- R=2r{\displaystyle R=2r}
Правильными треугольниками можно замостить плоскость.
В правильном треугольнике окружность девяти точек совпадает с вписанной окружностью.
- Для равностороннего треугольника T группа движений (самосовмещений) плоскости, переводящих треугольник в себя, состоит из 6 элементов: трёх поворотов на углы 0, 2π⁄3 и 4π⁄3 вокруг точки O, а также трёх симметрий относительно трёх прямых, на которых лежат биссектрисы треугольника (последние являются также его высотами и медианами).
- На описанной окружности произвольного треугольника ABC{\displaystyle ABC} существуют ровно три точки такие, что их прямая Симсона касается окружности Эйлера треугольника ABC{\displaystyle ABC}, причем эти точки образуют правильный треугольник. Стороны этого треугольника параллельны сторонам треугольника Морлея.
- Равносторонний треугольник является одновременно и равноугольным треугольником, то есть у него равны все внутренние углы.
- Равносторонний треугольник является частными случаем равнобедренного треугольника, а именно: дважды равнобедренным треугольником.
Равносторонний треугольник (понятие, определение):
Равносторонний треугольник – это треугольник, у которого все стороны равны между собой по длине, все углы также равны и составляют 60°.
Равносторонний треугольник называется также правильным или равноугольным треугольником.
По определению, каждый правильный (равносторонний) треугольник также является равнобедренным, но не каждый равнобедренный треугольник – правильным (равносторонним). Иными словами, правильный (равносторонний) треугольник является частным случаем равнобедренного треугольника.
Рис. 1. Равносторонний треугольник
АВ = ВС = АС – стороны треугольника, ∠ АВС = ∠ BАC = ∠ BСA = 60° – углы треугольника