Понятие

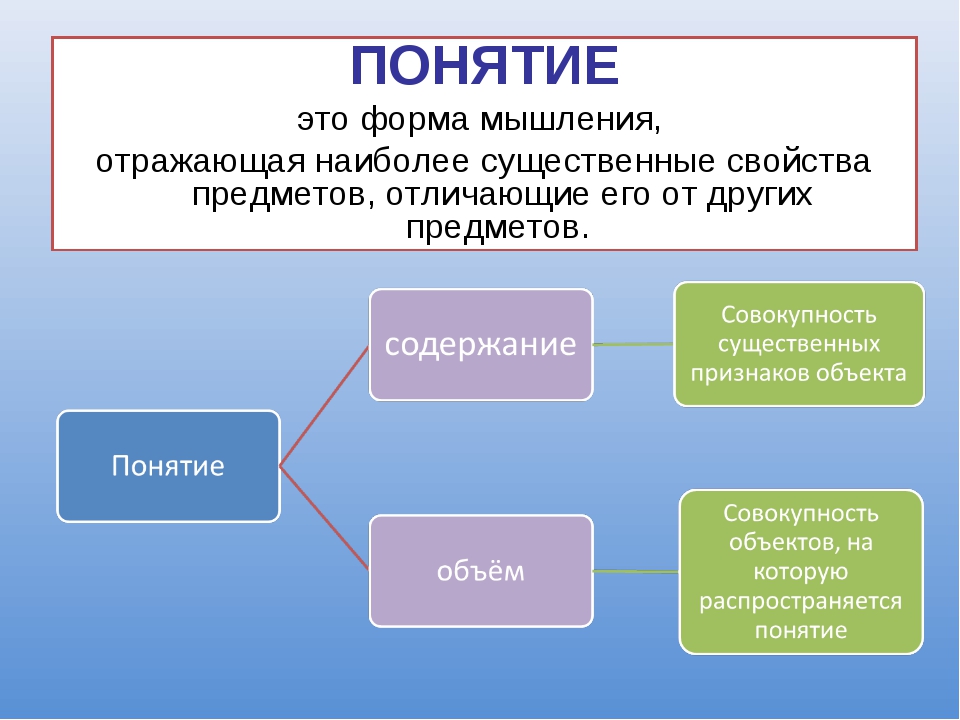
Содержание и объём понятия

Выделяют содержание и объём понятия. Содержанием понятия называется совокупность существенных признаков класса предметов, подпадающих под это понятие. Например, содержание понятия «ромб» образуют следующие два признака: родовой — «быть параллелограммом» и специфический (видовой) — «иметь равные стороны». Объёмом понятия называется совокупность самих предметов (или классов предметов), подпадающих под это понятие. Например, объём понятия «дерево» составляет множество всех деревьев (которые существовали, существуют или будут существовать; реальных и воображаемых), или множество всех разновидностей деревьев.

Между содержанием и объёмом понятия существует обратная зависимость: чем больше содержание понятия, тем меньше его объём. Иными словами, чем больше признаков входит в понятие, тем меньше предметов это понятие охватывает (и наоборот). Например, понятие «лиственное дерево» больше по содержанию, то есть содержит больше признаков, чем понятие «дерево», соответственно объём первого понятия оказывается меньше (у́же), чем объём второго, поскольку лиственные деревья — это часть (или подкласс) всех деревьев (деревьев вообще).

Понятие в теории решения задач

Теория решения задач — теоретический раздел исследований по искусственному интеллекту — предлагает достаточно математически строгую и в то же время наглядную трактовку термина «понятие». Полное математически строгое описание можно найти в монографии Бенерджи.

Можно дать менее строгое, но более лаконичное описание таким образом:

Понятия образуются на основании свойств.
Существует два основных класса свойств — внутренние и внешние. Внешние свойства выявляются непосредственно, их существование постулируется, вопрос об их происхождении не ставится. Внутренние свойства являются ненаблюдаемой непосредственно логической функцией внешних свойств.
При решении задач используются преимущественно внутренние свойства. Использование это состоит в том, что в зависимости от значения свойства выбирается та или иная операция, ведущая к решению задачи.
Понятие в традиционном его понимании — это особый вид внутренних свойств, получаемых в результате логической конъюнкции (логическое И) внешних свойств.
Любое внутреннее свойство можно представить в виде дизъюнкции (логическое ИЛИ) понятий.

В такой трактовке закон обратного отношения действительно оказывается тривиальным следствием определения и одного из законов поглощения A&B->A. Стоит заметить, что закон обратного отношения не имеет места для произвольного свойства.

Бенерджи рассматривает модель задач, в которой задано некоторое множество ситуаций и множество преобразований (операций) одной ситуации в другую. Выделено также подмножество ситуаций, являющихся целью решения. «При этом мы стремимся перевести данную ситуацию в другую допустимую ситуацию, применяя последовательность преобразований, чтобы в конце прийти к целевой ситуации». Понятия в модели Бенерджи применяются для описания как целевого подмножества, так и стратегии выбора преобразований.

Понятия по Бенерджи логично было бы называть «протопонятиями», так как в общенаучном смысле понятия выделяются и фиксируются с помощью термина в ходе решения широкого класса однородных задач, в которых их применение оказалось полезным.

Сравнимые и несравнимые понятия

Кроме того, разные понятия могут быть сравнимыми или несравнимыми. Сравнимыми считаются такие понятия, в содержании которых имеются общие признаки.Несравнимыми принято называть такие понятия, которые по своему содержанию значительно далеки друг от друга. Сравнимыми являются два понятия, которые различаются по содержанию, но совпадают полностью или частично по объему. Тождественными (равнозначными) являются понятия , которые совпадают . понятия, объемы которых совпадают. В качестве примера мы можем рассмотреть квадрат и правильный четырехугольник или куб и правильный шестигранник; Четные числа и числа , кратные двум. Пересекающиеся – понятия, объемы которых совпадают только частично, либо пересекаются. Например, прямоугольник и ромб или число, кратное 2 и число, кратное 3; Месяцы 3 квартала года , и летние месяцы. Одно из понятий может быть подчинено другому. Например, действительные и рациональные числа, или правильный многоугольник и квадрат, или тождественные преобразования и сокращение дроби ; Линейная функция и Константа.

Понятия, пересечение обьемов которых пусто или равно нулю , называют несовметимыми понятиями. Для таких понятий характерно наличие общего рода .

Понятие в истории философии

В русских философских словарях XVIII века (см. Антиох Кантемир и Григорий Теплов) термин «понятие» сближался с «идеей».

Определение понятия у Канта

Под понятием Кант разумел любое общее представление, поскольку последнее фиксировано термином. Отсюда и его определение: «Понятие… есть общее представление или представление того, что обще многим объектам, следовательно — представление, имеющее возможность содержаться в различных объектах»

Определение понятия у Гегеля

Понятие для Гегеля — «прежде всего синоним действительного понимания существа дела, а не просто выражение любого общего, любой одинаковости объектов созерцания. В понятии раскрывается подлинная природа вещи, а не её сходство с другими вещами, и в нём должна поэтому находить своё выражение не только абстрактная общность (это лишь один момент понятия, роднящий его с представлением), а и особенность его объекта. Вот почему формой понятия оказывается диалектическое единство всеобщности и особенности, которое и раскрывается через разнообразные формы суждения и заключения, а в суждении выступает наружу. Неудивительно, что любое суждение ломает форму абстрактного тождества, представляет собою её самоочевиднейшее отрицание. Его форма — А есть В (то есть не‑A)».

Всеобщее понятие выражает не простую абстрактную общность, одинаковость единичных представителей данного класса, но «действительный закон возникновения, развития и исчезновения единичных вещей».

У Энгельса

Понятия суть «сокращения, в которых мы охватываем, сообразно их общим свойствам, множество различных чувственно воспринимаемых вещей» (Ф. Энгельс).

Понятие в психологии

Психология позволяет подойти к изучению понятий эмпирически, исследуя существующие в сознании отношения между понятиями (семантические кластеры, группы, сети), в том числе с помощью математических методов (кластерного и факторного анализа); процессы формирования понятий, в том числе с помощью ; возрастное развитие понятий и т. п.

Методы исследования понятий

В психологии разработано множество методов исследования понятий, таких как ассоциативный эксперимент, метод классификации, метод субъективного шкалирования, семантический дифференциал, метод формирования искусственных понятий.

В некоторых случаях, как, например, в методе семантического радикала, используются также физиологические измерения.

Возрастное развитие понятий

Психологические исследования позволили установить, что понятия не являются неизменными по своей природе сущностями, не зависящими от возраста оперирующего ими субъекта. Овладение понятиями происходит постепенно, и понятия, которыми пользуется ребёнок, отличаются от понятий взрослого человека. Были выявлены различные типы понятий, соответствующие различным возрастным стадиям.

Предпонятия

Ж. Пиаже обнаружил, что на когнитивного развития (2—7 лет) понятия ребёнка представляют собой ещё не истинные понятия, но предпонятия. Предпонятия образны и конкретны, не относятся ни к индивидуальным объектам, ни к классам вещей и связываются друг с другом посредством трансдуктивного рассуждения, представляющего собой переход от частного к частному.

Исследование Выготского — Сахарова

Л. С. Выготский и Л. С. Сахаров в своём классическом исследовании, пользуясь , представляющей собой модификацию , установили типы (они же — возрастные стадии развития) понятий.

Житейские и научные понятия

Основная статья:

Л. С. Выготский, исследуя развитие понятий в детском возрасте, писал о житейских (спонтанных) и научных понятиях. Житейские понятия — приобретаемые и используемые в быту, в повседневном общении слова вроде «стол», «кошка», «дом». Научные понятия — это слова, которые ребёнок узнаёт в школе, термины, встроенные в систему знаний, связанные с другими терминами.

При использовании житейских понятий ребёнок долгое время (до 11-12 лет) осознаёт только предмет, на который они указывают, но не сами понятия, не их значение. Лишь постепенно ребёнок овладевает значением понятий. Согласно взглядам Выготского, развитие спонтанных и научных понятий идёт в противоположных направлениях: спонтанных — к постепенному осознанию их значения, научных — в обратном направлении.

Приходящее с возрастом осознание значений связано с рождающейся систематичностью понятий, то есть с установлением логических отношений между ними. А поскольку научные понятия, которые ребёнок усваивает в процессе обучения, принципиально отличаются от житейских понятий именно тем, что по самой своей природе они должны быть организованы в систему, то — полагает Выготский — их значения и осознаются первыми. Осознанность же значений научных понятий постепенно распространяется и на житейские.

Сравнимые и несравнимые понятия

Кроме того, разные понятия могут быть сравнимыми или несравнимыми. Сравнимыми считаются такие понятия, в содержании которых имеются общие признаки. Несравнимыми принято называть такие понятия, которые по своему содержанию значительно далеки друг от друга. Сравнимыми являются два понятия, которые различаются по содержанию, но совпадают полностью или частично по объему. Тождественными (равнозначными) являются понятия, объемы которых совпадают. В качестве примера мы можем рассмотреть квадрат и правильный четырехугольник или куб и правильный шестигранник; чётные числа и числа, кратные двум. Пересекающиеся – понятия, объемы которых совпадают только частично, или пересекаются. Например, прямоугольник и ромб или число, кратное 2, и число, кратное 3; месяцы третьего квартала года и летние месяцы. Одно из понятий может быть подчинено другому. Например: действительные и рациональные числа; правильный многоугольник и квадрат; тождественные преобразования и сокращение дроби; линейная функция и константа.

Понятия, пересечение объёмов которых пусто или равно нулю, называют несовместимыми понятиями. Для таких понятий характерно наличие общего рода.

Виды понятий

По объёму

По объёму понятия можно разделить на единичные, общие и пустые. В объём единичного понятия входит один-единственный объект (одноэлементный класс) — например, «русский писатель Антон Павлович Чехов», «столица Дании». В объём общего понятия входит более одного объекта (например, «дерево», «химический элемент»). Объём пустого понятия представляет собой пустое множество (например, «вечный двигатель», «круглый квадрат»). Объем общего понятия может быть конечным или бесконечным. Так, понятие «простое число» имеет бесконечный объем, а «простое число, меньше 20» — конечный объем (2,3,5,7,11,13, 17, 19). Кроме того, уменьшая объем общего понятия, мы можем придти к понятию единичному (х – простое число, 35<х<40; получим единичное понятие – число 37).

По содержанию

По содержанию понятия делят на положительные и отрицательные; относительные и безотносительные; собирательные и несобирательные (разделительные); конкретные и абстрактные; эмпирические и теоретические.

1. Положительные понятия фиксируют наличие у предмета какого-либо признака (например, «опрятный человек»), отрицательные указывают на отсутствие этого признака у предмета («неопрятный человек»). Если отрицание «не» или «без» («бес») стало частью слова и без него это слово не употребляется («неряха»), такое понятие также считается положительным.

2. Относительное понятие обозначает предмет, существование которого подразумевает существование некоторого другого предмета («ученик» — «учитель»). Безотносительное понятие обозначает предмет, существующий вне подобной зависимости («человек», «дерево»).

3. Собирательным называется понятие, обозначающее множество однородных предметов, которое мыслится как единое целое («стая», «флот»). Собирательные понятия могут быть общими («лес») или единичными («Созвездие Волопаса»). В отличие от собирательного, несобирательное (разделительное) понятие указывает не на группу, а на отдельный предмет («дерево», «звезда»).

4. Понятие называется конкретным, если оно относится к предмету или классу предметов (например, «дом»), и абстрактным, если оно отражает свойства, признаки предмета, взятые отдельно от него самого (например, «белизна», «доброта»), или отношения между предметами (например, «равенство»).

5. Эмпирические понятия есть понятия о наблюдаемых объектах и их свойствах, а теоретические — о ненаблюдаемых объектах. Если эмпирические понятия вырабатываются на основе непосредственного сравнения общих свойств некоторого класса наличествующих (доступных для изучения) объектов или явлений, то теоретические — на основе опосредованного анализа некоторого класса объектов или явлений при помощи ранее выработанных понятий, концепций и формализмов.

Название любого материального предмета является конкретным эмпирическим понятием, а его непосредственно наблюдаемые свойства выражаются абстрактными эмпирическими понятиями. К конкретным теоретическим понятиям относится, в частности, ряд понятий теоретической физики, например «электрон»; абстрактным теоретическим понятием является, например, «спин».

Виды понятий

По объёму

По объёму понятия можно разделить на единичные, общие и пустые. В объём единичного понятия входит один-единственный объект (одноэлементный класс) — например, «русский писатель Антон Павлович Чехов», «столица Дании». В объём общего понятия входит более одного объекта (например, «дерево», «химический элемент»). Объём пустого понятия представляет собой пустое множество (например, «вечный двигатель», «круглый квадрат»). Объем общего понятия может быть конечным или бесконечным. Так, понятие «простое число» имеет бесконечный объем, а «простое число, меньше 20» — конечный объем (2, 3, 5, 7, 11, 13, 17, 19). Кроме того, уменьшая объем общего понятия, мы можем прийти к понятию единичному (х – простое число, 36<х<38; получим единичное понятие – число 37).

По содержанию

Происхождение понятий

Основная статья: Формирование понятий

Согласно Л. С. Выготскому, понятия является результатом развития категории объектов, которое проходит в четыре этапа в соответствии с возрастанием уровня сложности, обобщенности и специфики функционирования.

Первый уровень — синкретическое обобщение — сделанное на основе случайно возникших признаков.
Второй уровень — комплексное обобщение — сделанное на основе неустойчивых характеристик.
Третий уровень — псевдопонятие (переходная форма от комплексного обобщения к понятию) — обобщение сделано на основе устойчивых и существенных характеристик, но это знание применяется не во всех случаях. В некоторых аспектах человек намеренно остается на этом уровне (к примеру, в определениях критериев принадлежности к тому или иному архитектурному стилю)
Четвертый уровень — истинное понятие — обобщение, сделанное на основе значимых и присутствующих у всех объектов категории признаков. Также иначе называется научным (Л. С. Выготский) или теоретическим (Давыдов В. В.) понятием..

Понятие в истории философии

Определение понятия у Канта

Определение понятия у Гегеля

У Энгельса

Понятие в психологии

Методы исследования понятий

Основная статья: Методы исследования понятий

Возрастное развитие понятий

Психологические исследования позволили установить, что понятия не являются неизменными по своей природе сущностями, не зависящими от возраста оперирующего ими субъекта. Овладение понятиями происходит постепенно, и понятия, которыми пользуется ребёнок, отличаются от понятий взрослого человека. Были выявлены различные типы понятий, соответствующие изменениям понимания пространства с переходом от одной возрастной стадии к другой.

Предпонятия

Основная статья: Предпонятие

Исследование Выготского — Сахарова

Житейские и научные понятия

Основная статья:

Значение слова Смысл по Логическому словарю:

Смысл — — в повседневной речи синоним значения. В логической семантике общее значение языковых выражений расщепляют на две части: предметное значение и С. Предметным значением, денотатом, объемом, экстенсионалом и т. п. некоторого выражения называют тот предмет или класс предметов, которые обозначаются данным выражением. Вместе с тем каждое выражение несет в себе некоторое мысленное которое и называют С. Понять некоторое выражение значит усвоить его С. Если С. усвоен, то мы знаем, к каким объектам относится данное выражение, следовательно, С. выражения задает его денотат. Два выражения могут иметь одно и то же предметное значение, но различаться по С. Напр., выражения «самый большой город в России» и «город, в котором родился А. С. Пушкин» обозначают один и тот же объект — город Москву, однако обладают разными смыслами. Значением предложения обычно считают его истинностное значение — истину или ложь, С. предложения — выражаемую им мысль. Т. о., все истинные предложения имеют одно и то же значение и различаются только своим С.. то же самое относится к ложным предложениям. Анализом проблем, встающих в связи с попытками точно определить понятие С. для различных типов языковых выражений, занимается специальный раздел логической семантики — теория С. (см.: Имя, Значение, Семантика логическая).

Понятие в теории решения задач

Можно дать менее строгое, но более лаконичное описание таким образом:

Понятия образуются на основании свойств.
Существует два основных класса свойств — внутренние и внешние. Внешние свойства выявляются непосредственно, их существование постулируется, вопрос об их происхождении не ставится. Внутренние свойства являются ненаблюдаемой непосредственно логической функцией внешних свойств.
При решении задач используются преимущественно внутренние свойства. Использование это состоит в том, что в зависимости от значения свойства выбирается та или иная операция, ведущая к решению задачи.
Понятие в традиционном его понимании — это особый вид внутренних свойств, получаемых в результате логической конъюнкции (логическое И) внешних свойств.
Любое внутреннее свойство можно представить в виде дизъюнкции (логическое ИЛИ) понятий.