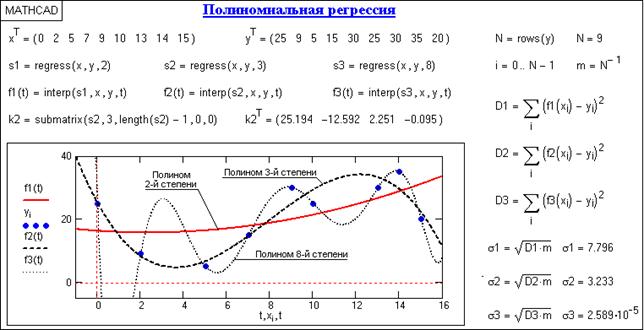
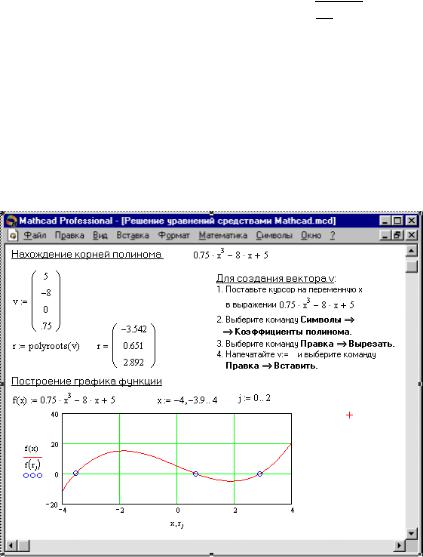
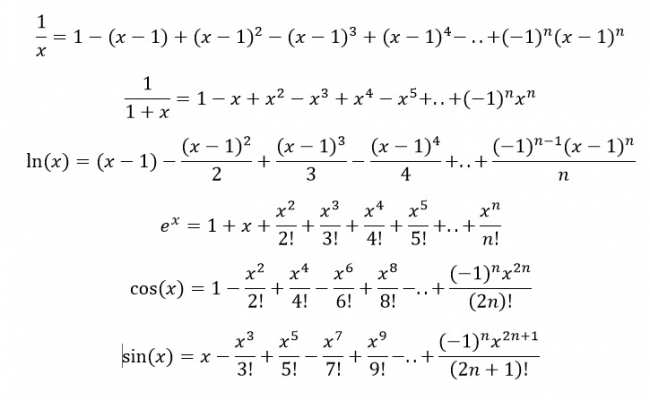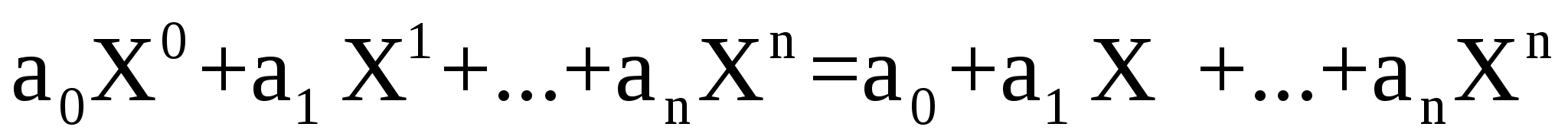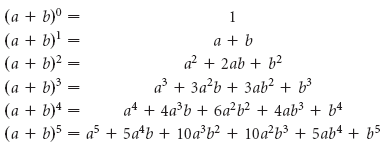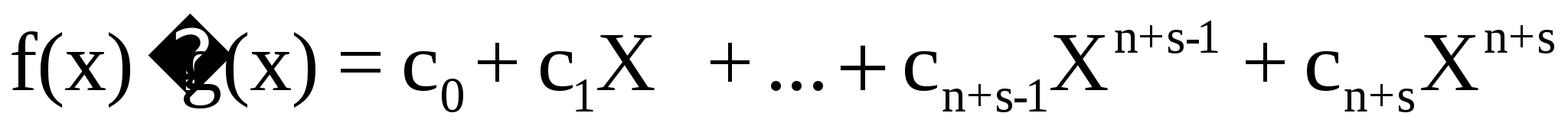Применение полинома одной переменной
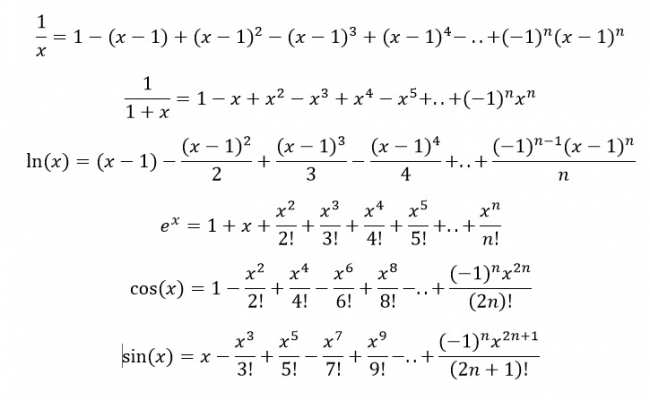
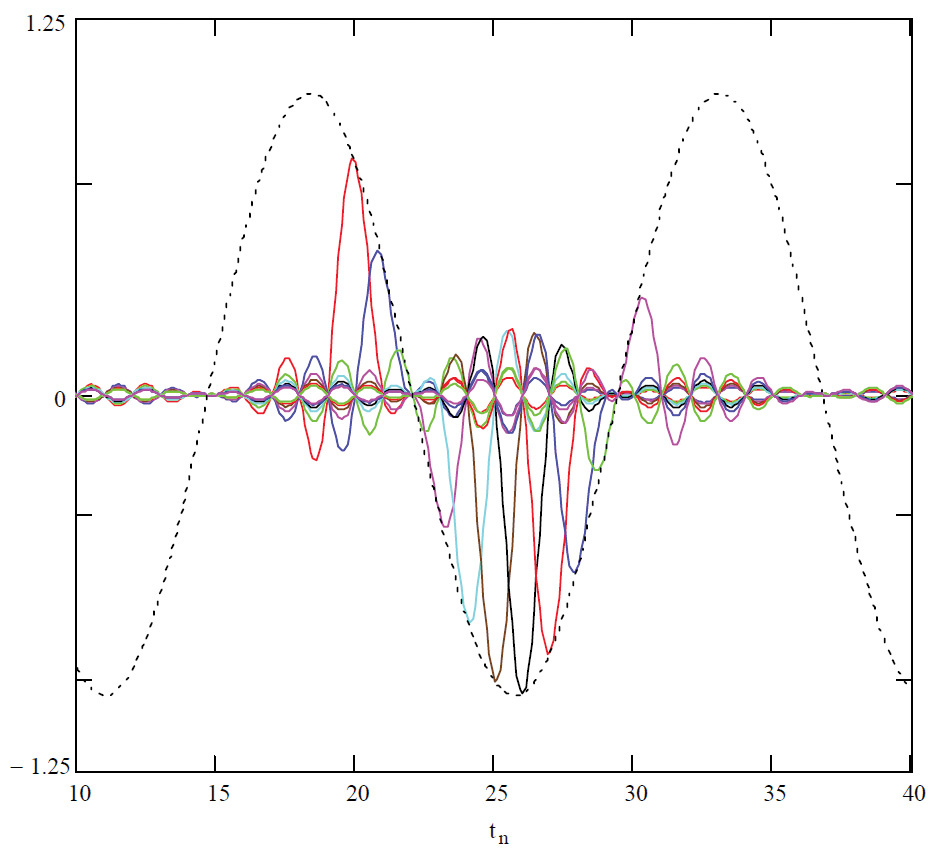
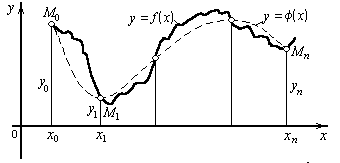
Многочлены одной переменной хорошо приближают непрерывные функции различной сложности от одного аргумента.
Дело в том, что такие полиномы можно рассматривать как частичные суммы степенного ряда, а непрерывную функцию можно представить в виде ряда со сколь угодно малой погрешностью. Ряды разложения функции называют рядами Тейлора, а их частичные суммы в виде полиномов — многочленами Тейлора.
Изучить графически поведение функции, аппроксимировав ее некоторым многочленом, зачастую легче, чем исследовать ту же функцию непосредственно или с помощью ряда.
Легко искать производные многочленов. Для нахождения корней у полиномов 4-й степени и ниже существуют готовые формулы, а для работы с более высокими степенями используются приближенные алгоритмы высокой точности.
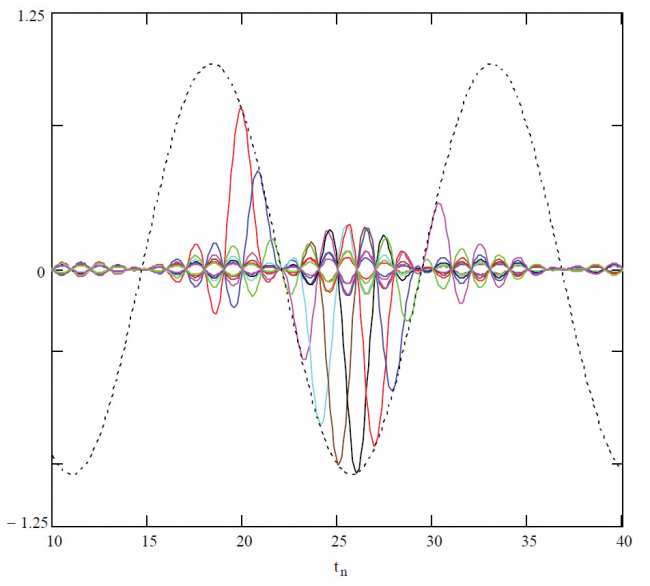
Существует и обобщение описанных многочленов для функций многих переменных.
Классификации полиномов
По степени полинома
Для каждого монома в составе многочлена находят сумму показателей степени i1+i2+…+in. Наибольшую из сумм называют показателем степени полинома, а одночлен, соответствующий этой сумме, — старшим членом.
Кстати, любую константу можно считать многочленом степени ноль.
Приведенные и неприведенные полиномы
Если у старшего члена коэффициент с равен 1, то многочлен приведен, иначе — нет.
Например, выражение х2+2х+1 — приведенный полином, а 2х2+2х+1 — неприведенный.
Однородные и неоднородные полиномы
Если степени всех членов полинома равны, то говорят, что такой полином однороден. Все остальные полиномы считаются неоднородными.
Однородные многочлены: х2-ху+у2, xyz+х3+у3. Неоднородные: х+1, х2+у.
Существуют специальные названия для полинома из двух и трех членов: бином и трехчлен соответственно.
В отдельную категорию выделяют многочлены одной переменной.
Классификации полиномов
По степени полинома
Для каждого монома в составе многочлена находят сумму показателей степени i1+i2+…+in. Наибольшую из сумм называют показателем степени полинома, а одночлен, соответствующий этой сумме, — старшим членом.
Кстати, любую константу можно считать многочленом степени ноль.
Приведенные и неприведенные полиномы
Если у старшего члена коэффициент с равен 1, то многочлен приведен, иначе — нет.
Например, выражение х2+2х+1 — приведенный полином, а 2х2+2х+1 — неприведенный.
Однородные и неоднородные полиномы
Если степени всех членов полинома равны, то говорят, что такой полином однороден. Все остальные полиномы считаются неоднородными.
Однородные многочлены: х2-ху+у2, xyz+х3+у3. Неоднородные: х+1, х2+у.
Существуют специальные названия для полинома из двух и трех членов: бином и трехчлен соответственно.
В отдельную категорию выделяют многочлены одной переменной.
Умножение многочлена на многочлен
Пусть нам надо перемножить два полинома, a+bи c+d. Запишем их произведение:
Заменим выражение a + b переменной k:
Теперь исходное произведение можно выразить как произведение монома и полинома:
Проведем обратное преобразование, заменив k на a + b:
Наконец, раскроем скобки в этом выражении:
Эту формулу можно проиллюстрировать геометрически. Рассмотрим прямоугольник со сторонами a + b и c + d:
Площадь этого прямоугольника, как и любого другого, равна произведению его сторон, то есть(a + b)(c + d).С другой стороны, она состоит из 4 прямоугольников, чьи площади также вычисляются как произведения их сторон, и составляют ac, bc, ad и bd. Поэтому можно записать равенство
Получается, что для умножения многочлена на многочлен нужно перемножать попарно все мономы, входящие в их состав, после чего сложить их.
Если в одном полиноме содержится m слагаемых, а в другом n, то результатом их перемножения окажется новый полином, содержащий m•n мономов (до приведения подобных слагаемых). Для перемножения многочленов также используется метод «фонтанчика».
Пример. Найдем произведение выражений 3a2 – 4ab + b2и 2a– b.
Решение: В первом полиноме содержится 3 монома, а во втором – 2, поэтому после их перемножения мы получим сумму 3•2 = 6 одночленов:
Раскрытие скобок «фонтанчиком» будет выглядеть так:
В результате действительно получилась сумма 6 мономов. Осталось вычислить каждый из них, после чего привести подобные слагаемые:
Заметим, что при перемножении полиномов происходит сложение степеней многочленов. Действительно, в рассмотренном выше примере мы умножили полином второй степени 3a2 – 4ab + b2 на полином первой степени 2a– b, и получили в результате многочлен 3-ей (2+1) степени.
Также возможно умножение многочленов в столбик. Особенно это удобно делать в случае с полиномами с одной переменной.
Пример. Найдите произведение выражений 2×3 + 3×2 +5x + 9 и x2 + 4x + 7.
Решение: Запишем полиномы в столбик, один под другим:
Далее умножим самый правый моном второго многочлена, то есть число 7, на первый полином, и запишем его ниже:
Далее умножим следующий моном, 4х, на первый полином, и запишем результат ещё ниже, причем сместим запись чуть влево, чтобы подобные члены оказались друг под другом:
Также умножим последний одночлен, x2, на первый полином:
Осталось сложить подобные слагаемые (то есть переменные х с одинаковыми степенями), которые записаны друг под другом:
Ещё раз цветом выделим подобные слагаемые и результаты их суммирования:
Ответ: 2х5 + 11х4 + 31х3 + 50х2 + 71х +63.
Особенности чугунных котлов
Следует отметить, что практически каждый чугунный твердотопливный котел может функционировать на дровах и коксе. Стоит он дороже стального изделия, но его характеристики оправдывают такую цену. Дело в том, что для их производства требуется гораздо больше времени, чем на сборку прибора из стали.
Чугунный отопительный котел на твердом топливе более долговечен по сравнению со стальным, он способен выдержать более высокие температуры. Остывает чугун гораздо медленнее, что позволяет экономить топливо.

Кроме этого у чугунных приборов:
- имеется значительное превосходство – это долговечность, поскольку срок их службы достигает 25 лет;
- они занимают меньше места по сравнению со стальными агрегатами;
- чугун более устойчив к коррозийным процессам, чем сталь.
Имеются у этого отопительного оборудования недостатки:
- Твердотопливный котел с чугунным теплообменником чувствителен к механическим воздействиям в виде ударов. Корпус из чугуна при определенной нагрузке может треснуть. По этой причине с ним следует обращаться аккуратно.
- В случае резкого перепада температур чугун может треснуть, поэтому специалисты не рекомендуют охлаждать такие котлы при помощи холодной воды или загружать в разогретую камеру сгорания холодное топливо.
- На нагрев корпуса из этого материала уходит много времени.

Чтобы еще лучше разобраться, в чем отличие между чугунным отопительным котлом и стальным, следует более подробно ознакомиться со свойствами твердотопливных агрегатов из стали:
- ударопрочность приборов особенно актуальна при транспортировке, даже, если они упадут или перевернутся, то с вероятностью 99% можно утверждать, что корпус останется целым, а герметичность камеры сгорания не пострадает;
- стальным котлам не опасны даже большие перепады температуры;
- изделия имеют относительно небольшой вес;
- если в отопительном оборудовании отломался один из элементов, его можно без проблем приварить.

Среди отрицательных моментов нужно отметить восприимчивость к коррозийным процессам, а также отсутствие возможности наращивать мощность.
Бином Ньютона
Знаменитыми полиномами являются полиномы Ньютона, выведенные ученым для нахождения коэффициентов выражения (х+у)n.
Достаточно посмотреть на несколько первых степеней разложения бинома, чтобы убедиться в нетривиальности формулы:
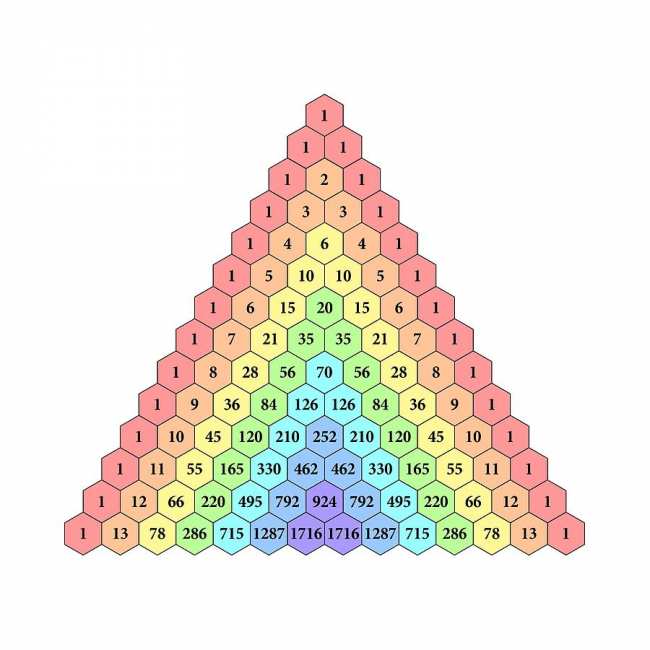
Для каждого коэффициента существует выражение, позволяющее его вычислить. Однако запоминать громоздкие формулы и каждый раз производить необходимые арифметические операции было бы крайне неудобно для тех математиков, которым часто требуются подобные разложения. Им значительно облегчил жизнь треугольник Паскаля.
Фигура строится по следующему принципу. В вершине треугольника пишется 1, а в каждой следующей строке становится на одну цифру больше, по краям ставят 1, а середина строчки заполняется суммами двух соседних чисел из предыдущей.
При взгляде на иллюстрацию все становится понятно.
Разумеется, приведенными примерами, наиболее широко известными, применение многочленов в математике не ограничивается.
Бином Ньютона
Знаменитыми полиномами являются полиномы Ньютона, выведенные ученым для нахождения коэффициентов выражения (х+у)n.
Достаточно посмотреть на несколько первых степеней разложения бинома, чтобы убедиться в нетривиальности формулы:
(х+у)2=х2+2ху+у2;
(х+у)3=х3+3х2у+3ху2+у3;
(х+у)4=х4+4х3у+6х2у2+4ху3+у4;
(х+у)5=х5+5х4у+10х3у2+10х2у3+5ху4+у5.
Для каждого коэффициента существует выражение, позволяющее его вычислить. Однако запоминать громоздкие формулы и каждый раз производить необходимые арифметические операции было бы крайне неудобно для тех математиков, которым часто требуются подобные разложения. Им значительно облегчил жизнь треугольник Паскаля.
Фигура строится по следующему принципу. В вершине треугольника пишется 1, а в каждой следующей строке становится на одну цифру больше, по краям ставят 1, а середина строчки заполняется суммами двух соседних чисел из предыдущей.
При взгляде на иллюстрацию все становится понятно.
Разумеется, приведенными примерами, наиболее широко известными, применение многочленов в математике не ограничивается.
Многочлены, или полиномы
Определение. Множество элементов называется полем, если для этих элементов определены действия: сложение и умножение и выполняются свойства
относительно сложения:
1) коммутативность ;2) ассоциативность ;3) существование нуля: ;4) существование противоположного элемента: ;
относительно умножения:
5) коммутативность ;
6) ассоциативность ;7) существование единицы ;8 ) для любого ненулевого элемента существование обратного .
относительно сложения и умножения:
9) дистрибутивность (распределительный закон) ;10) в поле должно существовать хотя бы два элемента .
Определение. Множество элементов называется кольцом, если для всех его элементов определены операции сложения и умножения, и выполняются свойства:\\
относительно сложения:
1) коммутативность ;2) ассоциативность ;3) существование нуля: ;4) существование противоположного элемента: ;
относительно сложения и умножения:
5) дистрибутивность (распределительный закон) — правосторонний распределительный закон.
5′) дистрибутивность (распределительный закон) — левосторонний распределительный закон.
Поскольку коммутативности умножения не требуется, то распределительных закона два.
Кольцо называется коммутативным, если есть коммутативность умножения, ассоциативным, если ассоциативность, унитарным (или кольцом с единицей), если в нем есть .
Определение. Многочленом (полиномом) называется выражение вида
где — элементы некоторого поля , — буква, — коэффициенты полинома, — старший коэффициент.
Если , то число называется степенью многочлена. Степень нулевого многочлена не будем считать равной какому-либо конкретному числу, но будем считать, что она меньше степени любого ненулевого многочлена.
Обозначение. — степень многочлена .
Условимся считать, что многочлен не меняется, если приписать к нему слагаемое .
Пусть и — многочлены над одним и тем же полем, пусть
Будем говорить, что , если и .
Пример (метод неопределенных коэффициентов). Требуется найти значения такие, чтобы выполнялось равенство
Отсюда .
Можно определить обычным образом сумму, разность, произведение многочленов и доказать, что при этом выполняются обычные законы действий.
Свойства степени многочлена
1) ,2) .
Задачи.
1) Найдите все значения параметров и такие, что многочлены и равны, если
2) Найдите все значения параметров такие, что при всех выполняется равенство
3) Найдите все значения параметров и такие, что многочлен является кубом двучлена .
4) Найдите многочлен третьей степени со старшим коэффициентом единицей и такой, что .
Многочлен и его стандартный вид
Ключевые слова конспекта: Многочлен, стандартный вид многочлена, члены многочлена, полиномы, нуль-многочлен, степень многочлена, приведение подобных слагаемых, старший коэффициент, свободный член многочлена.
Выражение 5a2b – 3ab – 4а3 + 7 представляет собой сумму одночленов 5a2b, –5ab, –4а3 и 7. Такие выражения называют многочленами.
Определение. Многочленом называется сумма одночленов.
Одночлены, из которых составлен многочлен, называют членами многочлена. Например, членами многочлена х3у – 4х2 + 9 являются одночлены х3у, –4х2 и 9.
Многочлен, состоящий из двух членов, называется двучленом, а многочлен, состоящий из трёх членов, — трёхчленом. Одночлен считают многочленом, состоящим из одного члена. Многочлены иногда называют полиномами, а двучлены — биномами (от греческих слов «поли» — «много», «номос» — «член, часть» и латинского «би» — «два, дважды»).
Зная значения переменных, входящих в многочлен, можно вычислить значение многочлена.
Пример 1. Найдём значение многочлена –0,3х2у – х3 + 7у при х = –0,2, у = –1.Имеем:–0,3х2у – х3+7у = –0,3 • (–0,2)2 • (–1) – (–0,2)3 + 7 • (–1) = 0,012 + 0,008 – 7 = –6,98.
Стандартный вид многочлена
В многочлене 13х2у + 4 + 8ху – 6х2у — 9 первый и четвёртый члены имеют одинаковую буквенную часть. Члены многочлена, имеющие одинаковую буквенную часть, называются подобными членами. Подобными членами считаются и слагаемые, не имеющие буквенной части.
Сумму подобных членов многочлена можно заменить одночленом. Такое тождественное преобразование называют приведением подобных членов или приведением подобных слагаемых. Приведение подобных членов основано на переместительном и сочетательном свойствах сложения и распределительном свойстве умножения.
Пример 2. Приведём подобные члены многочлена 13х2у + 4 + 8ху – 6х2у — 9. Имеем: 13х2у + 4 + 8ху – 6х2у – 9 = (13х2у – 6х2у) + 8ху + (4 – 9) = (13 – 6)х2у + 8ху – 5 = 7х2у + 8ху – 5.
В многочлене 7х2у + 8ху – 5 каждый член является одночленом стандартного вида, причём среди них нет подобных членов. Такие многочлены называются многочленами стандартного вида.
Рассмотрим многочлен стандартного вида За3 – 5а3b2 + 7. Его членами являются одночлены третьей, пятой и нулевой степени. Наибольшую из этих степеней называют степенью многочлена. Таким образом, этот многочлен является многочленом пятой степени.
Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.
Пример 3. Определим степень многочлена а6 + 2а2b – а6 + 1. Для этого приведём многочлен к стандартному виду: а6 + 2а2b – а6 + 1 = 2a2b + 1. Степень полученного многочлена равна трём. Значит, и степень заданного многочлена равна трём.
Если многочлен является числом, отличным от нуля, то степень такого многочлена равна 0. Число нуль называют нуль-многочленом. Его степень считается не определённой.
Среди многочленов выделяют многочлены с одной переменной. Многочлен n-й степени с одной переменной в стандартном виде записывается так: ахn + а1хn-1 + а2хn-2 + … + аn-2х2 + аn-1х + аn, где х — переменная, а, a1 а2, …, аn-1, аn — произвольные числа, n ∈ N или n = 0. Коэффициент при хn называют старшим коэффициентом (в нашем случае это а). Слагаемое, не содержащее переменной х, называют свободным членом многочлена (в нашем случае это аn). Например, старший коэффициент многочлена х4 + 2х3– х2 + 3х равен 1, а свободный член равен нулю.
Заметим, что значение многочлена с переменной х при х = 0 равно свободному члену этого многочлена, а при х = 1 — сумме его коэффициентов.
Это конспект по математике на тему «Многочлен и его стандартный вид». Выберите дальнейшие действия:
- Перейти к следующему конспекту:
- Вернуться к списку конспектов по Математике.
- Проверить знания по Математике.
Бином Ньютона
Знаменитыми полиномами являются полиномы Ньютона, выведенные ученым для нахождения коэффициентов выражения (х+у)n.
Достаточно посмотреть на несколько первых степеней разложения бинома, чтобы убедиться в нетривиальности формулы:
Для каждого коэффициента существует выражение, позволяющее его вычислить. Однако запоминать громоздкие формулы и каждый раз производить необходимые арифметические операции было бы крайне неудобно для тех математиков, которым часто требуются подобные разложения. Им значительно облегчил жизнь треугольник Паскаля.
Фигура строится по следующему принципу. В вершине треугольника пишется 1, а в каждой следующей строке становится на одну цифру больше, по краям ставят 1, а середина строчки заполняется суммами двух соседних чисел из предыдущей.
При взгляде на иллюстрацию все становится понятно.
Разумеется, приведенными примерами, наиболее широко известными, применение многочленов в математике не ограничивается.